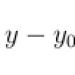Многочлены. Многочлены от одной переменной Многочлен и его члены – определения и примеры

§ 13. Целые функции (многочлены) и их основные свойства. Решение алгебраических уравнений на множестве комплексных чисел 165

13.1. Основные определения 165

13.2. Основные свойства целых многочленов 166

13.3. Основные свойства корней алгебраического уравнения 169

13.4. Решение основных алгебраических уравнений на множестве комплексных чисел 173

13.5. Упражнения для самостоятельной работы 176

Вопросы для самопроверки 178

Глоссарий 178

1. Основные определения

Целой алгебраической функцией илиалгебраическим многочленом (полиномом )аргумента x называется функция следующего вида

Здесьn –степень многочлена (натуральное число или 0),x – переменная (действительная или комплексная),a 0 , a 1 , …, a n –коэффициенты многочлена (действительные или комплексные числа),a 0  0.

Например,

;
;
,
– квадратный трехчлен;

,
;.

Числох 0 такое, чтоP n (x 0)0, называетсянулем функции P n (x ) иликорнем уравнения
.

Например,

его корни
,
,
.

так как
и
.

Замечание (к определению нулей целой алгебраической функции)

В литературе часто нули функции
называются ее корнями. Например, числа
и
называются корнями квадратичной функции
.

1. Основные свойствацелых многочленов

 Тождество (3) справедливо при x 
(илиx  ), следовательно, оно справедливо при
; подставляя
, получима n = b n . Взаимно уничтожим в (3) слагаемые а n и b n и поделим обе части на x :

Это тождество тоже верно при x , в том числе при x = 0, поэтому полагая x = 0, получим а n – 1 = b n – 1 .

Взаимно уничтожим в (3") слагаемые а n – 1 и b n – 1 и поделим обе части на x , в результате получим

Аналогично продолжая рассуждение, получим, что а n – 2 = b n –2 , …, а 0 = b 0 .

Таким образом, доказано, что из тождественного равенства двух целых многочленов следует совпадение их коэффициентов при одинаковых степенях x .

Обратное утверждение справедливо очевидно, то есть если два многочлена имеют одинаковыми все коэффициенты, то они есть одинаковые функции, определенные на множестве
, следовательно, их значения совпадают при всех значениях аргумента
, что и означает их тождественное равенство. Свойство 1 доказано полностью.

Пример (тождественное равенство многочленов)

.

 Запишем формулу деления с остатком: P n (x ) = (x – х 0)∙Q n – 1 (x ) + A ,

где Q n – 1 (x ) - многочлен степени (n – 1), A - остаток, который является числом вследствие известного алгоритма деления многочлена на двучлен «в столбик».

Это равенство верно при x , в том числе при x = х 0 ; полагая
, получим

P n (x 0) = (x 0 – x 0)Q n – 1 (x 0) + A  A = P n (х 0) 

Следствием доказанного свойства является утверждение о делении без остатка многочлена на двучлен, известное как теорема Безу.

 Доказательство теоремы Безу можно провести без использования ранее доказанного свойства о делении целого многочлена
на двучлен
. Действительно, запишем формулу деления многочлена
на двучлен
с остатком А=0:

Теперь учтем, что - это нуль многочлена
, и запишем последнее равенство при
:

Примеры (разложение многочлена на множители с использованием т. Безу)

1) ,так какP 3 (1)0;

2) ,так какP 4 (–2)0;

3) ,так какP 2 (–1/2)0.

Доказательство этой теоремы выходит за рамки нашего курса. Поэтому примем теорему без доказательства.

Поработаем по этой теореме и по теореме Безу с многочленом P n (x ):

после n -кратного применения этих теорем получим, что

где a 0 - это коэффициент приx n в записи многочленаP n (x ).

Если в равенстве (6)k чисел из наборах 1 ,х 2 , …х n совпадают между собой и с числом, то в произведении справа получается множитель (x –) k . Тогда числоx =называетсяk-кратным корнем многочлена P n (x ) , или корнем кратности k . Еслиk = 1, то число
называетсяпростым корнем многочлена P n (x ) .

Примеры (разложение многочлена на линейные множители)

1) P 4 (x ) = (x – 2)(x – 4) 3  x 1 = 2 - простой корень, x 2 = 4 - трехкратный корень;

2) P 4 (x ) = (x – i ) 4  x = i - корень кратности 4.

Согласно определению, многочлен это алгебраическое выражение представляющее собой сумму одночленов.

Для примера: 2*a^2 + 4*a*x^7 - 3*a*b^3 + 4; 6 + 4*b^3 - многочлены, а выражение z/(x - x*y^2 + 4) не является многочленом потому, что оно не является суммой одночленов. Многочлен еще иногда называют полиномом, а одночлены которые входят в состав многочлена членами многочлена или мономами.

Комплексное понятие многочлена

Если многочлен состоит из двух слагаемых, то его называют двучлен, если из трех - трехчлен. Названия четырехчлен, пятичлен и другие не используются, а в таких случаях говорят просто, многочлен. Такие названия, в зависимости от количества слагаемых, ставят все на свои места.

И термин одночлен становится интуитивно понятным. С точки зрения математики, одночлен является частным случаем многочлена. Одночлен это многочлен, который состоит из одного слагаемого.

Так же как и у одночлена, у многочлена есть свой стандартный вид. Стандартным видом многочлена называется такая запись многочлена, при которой все входящие в него в качестве слагаемых одночлены, записаны в стандартном виде и приведены подобные члены.

Стандартный вид многочлена

Процедура приведения многочлена к стандартному виду состоит в том, чтобы привести каждый из одночленов к стандартному виду, а потом все подобные одночлены между собой сложить. Сложение подобных членов многочлена называют приведением подобных.
Например, приведем подобные слагаемые в многочлене 4*a*b^2*c^3 + 6*a*b^2*c^3 - a*b.

Подобными здесь являются слагаемые 4*a*b^2*c^3 и 6*a*b^2*c^3. Суммой этих слагаемых будет одночлен 10*a*b^2*c^3. Следовательно, исходный многочлен 4*a*b^2*c^3 + 6*a*b^2*c^3 - a*b можно переписать в виде 10*a*b^2*c^3 - a*b. Эта запись и будет стандартным видом многочлена.

Из того, что любой одночлен можно привести к стандартному виду, следует также и тот факт, что любой многочлен можно привести к стандартному виду.

Когда многочлен приведен к стандартному виду, можно говорить о таком понятии как степень многочлена. Степенью многочлена называется наибольшая степень одночлена, входящего в данный многочлен.
Так, например, 1 + 4*x^3 - 5*x^3*y^2 - многочлен пятой степени, так как максимальная степень одночлена входящего в многочлен (5*x^3*y^2) пятая.

Например, выражения:

a - b + c , x 2 - y 2 , 5x - 3y - z - многочлены.

Одночлены, входящие в состав многочлена, называются членами многочлена . Рассмотрим многочлен:

7a + 2b - 3c - 11

выражения: 7a , 2b , -3c и -11 - это члены многочлена. Обратите внимание на член -11 . Он не содержит переменной. Такие члены, состоящие только из числа, называются свободными .

Принято считать, что любой одночлен - это частный случай многочлена, состоящий из одно члена. В этом случае одночлен является названием для многочлена с одним членом. Для многочленов, состоящих из двух и трёх членов, тоже есть специальные названия - двучлен и трёхчлен соответственно:

7a - одночлен

7a + 2b - двучлен

7a + 2b - 3c - трёхчлен

Подобные члены

Подобные члены - одночлены, входящие в многочлен, которые отличаются друг от друга только коэффициентом , знаком или совсем не отличаются (противоположные одночлены тоже можно назвать подобными). Например, в многочлене:

члены 3a 2 b , 2a 2 b и -2a 2 b , так же как и члены 5abc 2 и -7abc 2 - это подобные члены.

Приведение подобных членов

Если многочлен содержит подобные члены, то его можно привести к более простому виду путём соединения подобных членов в один. Такое действие называется приведением подобных членов . Первым делом заключим в скобки отдельно все подобные члены:

(3a 2 b + 2a 2 b - 2a 2 b ) + (5abc 2 - 7abc 2)

Чтобы соединить несколько подобных одночленов в один, надо сложить их коэффициенты, а буквенные множители оставить без изменений:

((3 + 2 - 2)a 2 b ) + ((5 - 7)abc 2) = (3a 2 b ) + (-2abc 2) = 3a 2 b - 2abc 2

Приведение подобных членов - это операция замены алгебраической суммы нескольких подобных одночленов одним одночленом.

Многочлен стандартного вида

Многочлен стандартного вида - это многочлен, все члены которого являются одночленами стандартного вида, среди которых нет подобных членов.

Чтобы привести многочлен к стандартному виду, достаточно сделать приведение подобных членов. Например, представьте в виде многочлена стандартного вида выражение:

3xy + x 3 - 2xy - y + 2x 3

Сначала найдём подобные члены:

Если все члены многочлена стандартного вида содержат одну и ту же переменную, то его члены принято располагать от большей степени к меньшей. Свободный член многочлена, если он есть, ставится на последнее место - справа.

Например, многочлен

3x + x 3 - 2x 2 - 7

должен быть записан так:

x 3 - 2x 2 + 3x - 7

Странно, что делается равенство между полиномом и многочленом. Хотя насколько я помню это разные вещи. Многочлен это то, о чём тут пишут. А полином это отношение 2-х многочленов. Посмотрел в словаре перевод на английский слова многочлен увидел, что переводится как polynomial чему был немало удивлён…. Выходит они даже не видят разницу. По поводу 1-го примера… Это всё хорошо, но есть ли способ непосредственного преобразования без ввода неизвестных коэффициентов? Этот метод слишком вычурный… О многочленах можно говорить много. Это выходит далеко за рамки ср школы. Исследования ведутся до сих пор! Т.е. тема многочленов не завершена. Могу ответить на вопрос о корнях в радикалах. В общем случае доказано, что многочлены степени выше 4 не имеют решения в радикалах. И вообще не решаются аналитически. Хотя некоторые виды вполне решаются. Но не все… Уравнение 3-ей степени имеет решение Кардано. У уравнения 4-й степени есть 2 вида формул. Они достаточно сложны и вобщем заранее неясно есть ли действительные решения, они все могут быть комплексными. У многочлена нечётной степени всегда есть хотя бы 1 действ корень. В теории формулы для решения уравнений даже 3-ей или 4-ой степени особого распространения не получили из-за их сложности. И возникает вопрос с тем какие из корней рассматривать. Ведь у уравнения n-ой степени ровно n корней с учётом их кратности. Вот к примеру можно решать методом ньютона численно уравнение. Там всё просто. Пишется итерационная формула и нет проблем. Линейное приближение. С осью OX прямая пересекается только в 1-ой точке. Может не пересекаться, тогда корень комплексный. Но тоже 1-й. Ну понятно, что если многочлен с действительными коэффиициентами имеет комплексный корень, то он так же имеет так же и комплексно сопряжённый. Однако уже в квадратичном приближении(этот метод именуется как метод парабол и др варианты этого метода Мюллера по 2-м предыдущим точкам и т.п) возникают проблемы. Во первых там 2 корня(мб если дискриминант > 0) еакой из них выбирать? Хотя уравнение квадратное. Можно пойти дальше взять кубическое приближение(4-й член в ряде Тейлора, для кв берётся 3) И даже приближение 4-ой степени взяв 5 членов ряда Тейлора. Сходимость будет супер быстрая. Аналитически всё решается! Но я нигде в математической литературе не встречал таких методов. Как правило пользуются методом Ньютона потому что он беспроблемный! И везде где в теории встречаются кубические или уравнения 4-ой степени такое имеет место быть. Хотите, сами попробуйте! Не думаю что вы будете в восторге. Хотя повторяю всё решается аналитически. Просто формулы будут оч сложные. Но не в этом дело. Возникают массы других проблем, не связанных со сложностью.

- многочленами . В этой статье мы изложим все начальные и необходимые сведения о многочленах. К ним, во-первых, относится определение многочлена с сопутствующими определениями членов многочлена, в частности, свободного члена и подобных членов. Во-вторых, остановимся на многочленах стандартного вида, дадим соответствующее определение и приведем их примеры. Наконец, введем определение степени многочлена, разберемся, как ее найти, и скажем про коэффициенты членов многочлена.

Навигация по странице.

Многочлен и его члены – определения и примеры

В 7 классе многочлены изучаются сразу после одночленов, это и понятно, так как определение многочлена дается через одночлены. Дадим это определение, объясняющее что такое многочлен.

Определение.

Многочлен – это сумма одночленов; одночлен считается частным случаем многочлена.

Записанное определение позволяет привести сколько угодно примеров многочленов. Любой из одночленов 5 , 0 , −1 , x , 5·a·b 3 , x 2 ·0,6·x·(−2)·y 12 , и т.п. является многочленом. Также по определению 1+x , a 2 +b 2 и - это многочлены.

Для удобства описания многочленов вводится определение члена многочлена.

Определение.

Члены многочлена – это составляющие многочлен одночлены.

Например, многочлен 3·x 4 −2·x·y+3−y 3 состоит из четырех членов: 3·x 4 , −2·x·y , 3 и −y 3 . Одночлен считается многочленом, состоящим из одного члена.

Определение.

Многочлены, которые состоят из двух и трех членов, имеют специальные названия – двучлен и трехчлен соответственно.

Так x+y – это двучлен, а 2·x 3 ·q−q·x·x+7·b – трехчлен.

В школе наиболее часто приходится работать с линейным двучленом a·x+b , где a и b – некоторые числа, а x – переменная, а также с квадратным трехчленом a·x 2 +b·x+c , где a , b и c – некоторые числа, а x – переменная. Вот примеры линейных двучленов: x+1 , x·7,2−4 , а вот примеры квадратных трехчленов: x 2 +3·x−5 и .

Многочлены в своей записи могут иметь подобные слагаемые . Например, в многочлене 1+5·x−3+y+2·x подобными слагаемыми являются 1 и −3 , а также 5·x и 2·x . Они имеют свое особое название – подобные члены многочлена.

Определение.

Подобными членами многочлена называются подобные слагаемые в многочлене.

В предыдущем примере 1 и −3 , как и пара 5·x и 2·x , являются подобными членами многочлена. В многочленах, имеющих подобные члены, можно для упрощения их вида выполнять приведение подобных членов .

Многочлен стандартного вида

Для многочленов, как и для одночленов, существует так называемый стандартный вид. Озвучим соответствующее определение.

Исходя из данного определения, можно привести примеры многочленов стандартного вида. Так многочлены 3·x 2 −x·y+1 и записаны в стандартном виде. А выражения 5+3·x 2 −x 2 +2·x·z и x+x·y 3 ·x·z 2 +3·z не являются многочленами стандартного вида, так как в первом из них содержатся подобные члены 3·x 2 и −x 2 , а во втором – одночлен x·y 3 ·x·z 2 , вид которого отличен от стандартного.

Заметим, что при необходимости всегда можно привести многочлен к стандартному виду .

К многочленам стандартного вида относится еще одно понятие – понятие свободного члена многочлена.

Определение.

Свободным членом многочлена называют член многочлена стандартного вида без буквенной части.

Иными словами, если в записи многочлена стандартного вида есть число, то его называют свободным членом. Например, 5 – это свободный член многочлена x 2 ·z+5 , а многочлен 7·a+4·a·b+b 3 не имеет свободного члена.

Степень многочлена – как ее найти?

Еще одним важным сопутствующим определением является определение степени многочлена. Сначала определим степень многочлена стандартного вида, это определение базируется на степенях одночленов , находящихся в его составе.

Определение.

Степень многочлена стандартного вида – это наибольшая из степеней входящих в его запись одночленов.

Приведем примеры. Степень многочлена 5·x 3 −4 равна 3 , так как входящие в его состав одночлены 5·x 3 и −4 имеют степени 3 и 0 соответственно, наибольшее из этих чисел есть 3 , оно и является степенью многочлена по определению. А степень многочлена 4·x 2 ·y 3 −5·x 4 ·y+6·x равна наибольшему из чисел 2+3=5 , 4+1=5 и 1 , то есть, 5 .

Теперь выясним, как найти степень многочлена произвольного вида.

Определение.

Степенью многочлена произвольного вида называют степень соответствующего ему многочлена стандартного вида.

Итак, если многочлен записан не в стандартном виде, и требуется найти его степень, то нужно привести исходный многочлен к стандартному виду, и найти степень полученного многочлена – она и будет искомой. Рассмотрим решение примера.

Пример.

Найдите степень многочлена 3·a 12 −2·a·b·c·a·c·b+y 2 ·z 2 −2·a 12 −a 12 .

Решение.

Сначала нужно представить многочлен в стандартном виде:
3·a 12 −2·a·b·c·a·c·b+y 2 ·z 2 −2·a 12 −a 12 = =(3·a 12 −2·a 12 −a 12)− 2·(a·a)·(b·b)·(c·c)+y 2 ·z 2 = =−2·a 2 ·b 2 ·c 2 +y 2 ·z 2 .

В полученный многочлен стандартного вида входят два одночлена −2·a 2 ·b 2 ·c 2 и y 2 ·z 2 . Найдем их степени: 2+2+2=6 и 2+2=4 . Очевидно, наибольшая из этих степеней равна 6 , она по определению является степенью многочлена стандартного вида −2·a 2 ·b 2 ·c 2 +y 2 ·z 2 , а значит, и степенью исходного многочлена. , 3·x и 7 многочлена 2·x−0,5·x·y+3·x+7 .

Список литературы.

• Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 17-е изд. - М. : Просвещение, 2008. - 240 с. : ил. - ISBN 978-5-09-019315-3.
• Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. - 17-е изд., доп. - М.: Мнемозина, 2013. - 175 с.: ил. ISBN 978-5-346-02432-3.
• Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. - 3-е изд. - М.: Просвещение, 2010.- 368 с. : ил. - ISBN 978-5-09-022771-1.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.