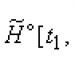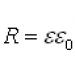Kementerian Pendidikan dan Ilmu Pengetahuan Federasi Rusia
Institusi pendidikan tinggi negeri
pendidikan kejuruan
"Akademi Sosial dan Pedagogis Negara Bagian Tobolsk
mereka. DI. Mendeleev"
Departemen Matematika, TIMOM
Beberapa Persamaan Diophantine
Tugas kursus
mahasiswa tahun ke-3 FMF
Mataev Evgeny Viktorovich
Penasihat ilmiah:
Kandidat Ilmu Fisika dan Matematika A.I. Valitskas
Nilai: ____________
Tobolsk - 2011
Pengantar……………………………………………………………………........2
1. Persamaan Linear Diophantine…………………………………..3
2. Persamaan Diophantinex 2 – kamu 2 = sebuah………………………………….....9
3. Persamaan Diophantinex 2 + kamu 2 = sebuah…………………………………... 12
4. Persamaan x 2 + x + 1 = 3 tahun 2 …………………………………………….. 16
5. Tripel Pythagoras……………………………………………………….. 19
6. Teorema Besar Peternakan………………………………………………23
Kesimpulan……………………………………………………………….…….29
Bibliografi...........………………………………………………..30
PENGANTAR
Persamaan Diophantine adalah persamaan bentuk P(x 1 , … , x n ) = 0 , di mana sisi kiri adalah polinomial dalam variabel x 1 , … , x n Dengan koefisien bilangan bulat. Setiap set yang dipesan (kamu 1 ; … ; kamu n ) bilangan bulat dengan properti P(kamu 1 , … , kamu n ) = 0 disebut solusi (sebagian) dari persamaan Diophantine P(x 1 , … , x n ) = 0 . Menyelesaikan persamaan Diophantine berarti menemukan semua penyelesaiannya, mis. solusi umum persamaan ini.
Tujuan kami adalah mempelajari cara menemukan solusi untuk beberapa persamaan Diophantine, jika solusi ini tersedia.
Untuk melakukan ini, Anda perlu menjawab pertanyaan-pertanyaan berikut:
sebuah. Apakah persamaan Diophantine selalu memiliki solusi, temukan kondisi keberadaan solusi.
b. Apakah ada algoritma yang memungkinkan menemukan solusi untuk persamaan Diophantine.
Contoh: 1. Persamaan diophantine 5 x – 1 = 0 tidak memiliki solusi.
2. Persamaan diophantine 5 x – 10 = 0 punya solusi x = 2 , yang merupakan satu-satunya.
3. persamaan ln x – 8 x 2 = 0 bukan diofantin.
4. Seringkali persamaan bentuk P(x 1 , … , x n ) = Q(x 1 , … , x n ) , di mana P(x 1 , … , x n ) , Q(x 1 , … , x n ) adalah polinomial dengan koefisien bilangan bulat, juga disebut Diophantine. Mereka dapat ditulis dalam bentuk P(x 1 , … , x n ) – Q(x 1 , … , x n ) = 0 , yang merupakan standar untuk persamaan Diophantine.
5. x 2 – kamu 2 = sebuah adalah persamaan Diophantine derajat kedua dengan dua tidak diketahui x dan y untuk setiap bilangan bulat a. Ini memiliki solusi untuk sebuah = 1 , tetapi tidak memiliki solusi untuk sebuah = 2 .
1. Persamaan Diophantine Linier
Membiarkan sebuah 1 , … , sebuah n , DenganZ . Ketik persamaan sebuah 1 x 1 + … + a n x n = c disebut persamaan Diophantine linier dengan koefisien sebuah 1 , … , sebuah n , sisi kanan c dan tidak diketahui x 1 , … , x n . Jika ruas kanan c persamaan Diophantine linier adalah nol, maka persamaan Diophantine tersebut disebut homogen.
Tujuan langsung kami adalah untuk mempelajari bagaimana menemukan solusi khusus dan umum dari persamaan Diophantine linier dalam dua yang tidak diketahui. Jelas, setiap persamaan Diophantine homogen sebuah 1 x 1 + … + a n x n = 0 selalu memiliki solusi tertentu (0; … ; 0).
Jelas bahwa persamaan Diophantine linier, semua koefisiennya sama dengan nol, memiliki solusi hanya jika sisi kanannya sama dengan nol. Secara umum, kami memiliki yang berikut:
Teorema (tentang keberadaan solusi untuk persamaan linear Diophantine). Persamaan diophantine linier sebuah 1 x 1 + … + a n x n = c, yang koefisiennya tidak semuanya sama dengan nol, memiliki solusi jika dan hanya jika GCD(a 1 , … , sebuah n ) | c.
Bukti. Perlunya kondisi ini jelas: GCD(a 1 , … , sebuah n ) | sebuah saya (1 saya n) , jadi GCD(a 1 , … , sebuah n ) | (sebuah 1 x 1 + … + sebuah n x n ) , yang berarti membagi dan
c = sebuah 1 x 1 + … + sebuah n x n .
Membiarkan D= gcd(sebuah 1 , … , sebuah n ) , c =Dt dan sebuah 1 kamu 1 + … + a n kamu n = D – ekspansi linier dari pembagi umum terbesar dari angka sebuah 1 , … , sebuah n. Mengalikan kedua ruas dengan t, kita mendapatkan sebuah 1 (kamu 1 t) + … + a n (kamu n t) = Dt = c, yaitu bilangan bulat
n-ka (x 1 t; … ; x n t) adalah solusi dari persamaan awal dengan n tidak dikenal.
Teorema telah terbukti.
Teorema ini memberikan algoritma konstruktif untuk menemukan solusi tertentu untuk persamaan Diophantine linier.
Contoh: 1. Persamaan diophantine linier 12x+21y=5 tidak memiliki solusi karena gcd(12, 21) = 3 tidak membagi 5 .
2. Temukan solusi khusus dari persamaan Diophantine 12x+21y = 6.
Jelas sekarang gcd(12, 21) = 3 | 6, jadi solusinya ada. Kami menulis ekspansi linier gcd(12, 21) = 3 = 122 + 21(–1). Oleh karena itu, pasangan (2; –1) adalah solusi khusus dari persamaan 12x+21y = 3, dan pasangan (4; –2) adalah solusi khusus dari persamaan asli 12x+21y = 6.
3. Temukan solusi khusus untuk persamaan linier 12x + 21y - 2z = 5.
Karena (12, 21, –2) = ((12, 21), –2) = (3, –2) = 1 | 5 , maka solusinya ada. Mengikuti bukti teorema, pertama-tama kita temukan solusi untuk persamaan (12.21)x–2y=5, dan kemudian, menggantikan ekspansi linier dari pembagi persekutuan terbesar dari masalah sebelumnya, kami memperoleh solusi dari persamaan asli.
Untuk menyelesaikan persamaan 3x - 2y = 5 tuliskan ekspansi linier gcd(3, -2) = 1 = 31 - 21 jelas sekali. Jadi beberapa angka (1; 1) adalah solusi dari persamaan 3 x – 2 kamu = 1 , dan pasangan (5; 5) adalah solusi khusus dari persamaan Diophantine 3x - 2y = 5.
Jadi, (12, 21)5 – 25 = 5 . Mengganti di sini ekspansi linier yang ditemukan sebelumnya (12, 21) = 3 = 122 + 21(–1) , kita mendapatkan (122+21(–1))5 – 25 = 5 , atau 1210 + 21(–5) – 25 = 5 , yaitu triplet bilangan bulat (10; –5; 5) adalah solusi khusus dari persamaan Diophantine asli 12x + 21y - 2z = 5.
Teorema (pada struktur solusi umum persamaan linear Diophantine). Untuk persamaan Diophantine linier sebuah 1 x 1 + … + a n x n = c pernyataan berikut ini benar:
(1) jika = (u 1 ; … ; kamu n ), = (v 1 ; … ; v n ) adalah solusi khususnya, maka perbedaannya (u 1 –v 1 ; … ; kamu n –v n ) adalah solusi khusus dari persamaan homogen yang sesuai sebuah 1 x 1 + … + a n x n = 0 ,
(2) himpunan solusi tertentu dari persamaan homogen linier Diophantine sebuah 1 x 1 + … + a n x n = 0 tertutup di bawah penambahan, pengurangan dan perkalian dengan bilangan bulat,
(3) jika M adalah solusi umum dari persamaan Diophantine linier yang diberikan, dan L adalah solusi umum dari persamaan Diophantine homogen yang sesuai, maka untuk setiap solusi tertentu = (u 1 ; … ; kamu n ) dari persamaan asli, persamaan M = +L .
Bukti. Mengurangi persamaan sebuah 1 v 1 + … + sebuah n v n = c dari kesetaraan sebuah 1 kamu 1 + … + a n kamu n = c, kita mendapatkan sebuah 1 (u 1 –v 1 ) + … + a n (u n –v n ) = 0 , yaitu himpunan
(u 1 –v 1 ; … ; kamu n –v n ) adalah solusi khusus dari persamaan Diophantine homogen linier sebuah 1 x 1 + … + a n x n = 0 . Dengan demikian, telah terbukti bahwa
= (kamu 1 ; … ; kamu n ), = (v 1 ; … ; v n ) ML .
Ini membuktikan pernyataan (1).
Pernyataan (2) dibuktikan dengan cara yang sama:
, L z Z L z L .
Untuk membuktikan (3), pertama-tama kita perhatikan bahwa M+L. Ini mengikuti dari yang sebelumnya: M+L .
Sebaliknya, jika = (l 1 ; … ; aku n ) L dan = (kamu 1 ; … ; kamu n ) M, lalu M:
sebuah 1 (u 1 + aku 1 )+ …+a n (u n + aku n ) = (a 1 kamu 1 + … + a n kamu n )+(a 1 aku 1 + … + a n aku n ) = c + 0 = c.
Lewat sini, + LM, dan akhirnya M = +L .
Teorema telah terbukti.
Teorema terbukti memiliki arti geometris yang jelas. Jika kita mempertimbangkan persamaan linier sebuah 1 x 1 + … + a n x n = c, di mana X saya R, maka, seperti yang diketahui dari geometri, ia menentukan dalam ruang R n hyperplane diperoleh dari pesawat L dengan persamaan homogen sebuah 1 x 1 + … +a n x n =0 melewati titik asal koordinat dengan pergeseran oleh beberapa vektor R n. Lihat permukaan + L juga disebut manifold linier dengan ruang panduan L dan menggeser vektor . Dengan demikian, terbukti bahwa solusi umum M persamaan diophantine sebuah 1 x 1 + … + a n x n = c terdiri dari semua titik dari beberapa manifold linier yang memiliki koordinat bilangan bulat. Dalam hal ini, koordinat vektor pergeseran juga bilangan bulat, dan himpunan L solusi persamaan Diophantine homogen sebuah 1 x 1 + … + a n x n = 0 terdiri dari semua titik dalam ruang panduan dengan koordinat bilangan bulat. Untuk alasan ini, sering dikatakan bahwa himpunan solusi dari persamaan Diophantine arbitrer membentuk manifold linier dengan vektor pergeseran dan ruang terkemuka L.
Contoh: untuk persamaan Diophantine x - y \u003d 1 keputusan bersama M memiliki bentuk (1+y; y), di mana yZ, solusi khususnya =
(1; 0)
, dan solusi umum L persamaan homogen x – y = 0 akan ditulis dalam bentuk (Y y), di mana padaZ. Dengan demikian, kita dapat menggambar gambar berikut, di mana solusi dari persamaan Diophantine asli dan persamaan Diophantine homogen yang sesuai ditunjukkan oleh titik-titik tebal pada manifold linier M dan ruang L masing-masing. 
2. Temukan solusi umum persamaan Diophantine 12x + 21y - 2z = 5.
Solusi pribadi (10; –5; 5) persamaan ini ditemukan sebelumnya, kami menemukan solusi umum dari persamaan homogen 12x + 21y - 2z = 0, setara dengan persamaan Diophantine 12 x + 21 kamu = 2 z.
Agar persamaan ini dapat dipecahkan, perlu dan cukup bahwa kondisinya gcd(12, 21) = 3 | 2z, itu. 3 | z atau z = 3t untuk beberapa bilangan bulat t. Kurangi kedua bagian menjadi 3 , kita mendapatkan 4x + 7y = 2t. Solusi khusus (2; –1) dari persamaan Diophantine 4x+7y= 1 ditemukan pada contoh sebelumnya. Itu sebabnya (4t ; -2t) adalah solusi khusus dari persamaan 4x + 7y = 2t untuk apa saja
t Z. Solusi umum dari persamaan homogen yang sesuai
(7 kamu ; –4 kamu) sudah ditemukan. Jadi, solusi umum persamaan 4x + 7y = 2t seperti: (4t + 7kamu; -2t - 4kamu) , dan solusi umum persamaan homogen 12x + 21y - 2z = 0 akan ditulis seperti ini:
(4t + 7kamu; -2t - 4kamu; 3t).
Sangat mudah untuk memverifikasi bahwa hasil ini sesuai dengan teorema yang dinyatakan di atas tanpa bukti pada solusi persamaan Diophantine homogen sebuah 1 X 1 + … + a n X n = 0 : jika P = , kemudian R dan
(kamu; t) P adalah solusi umum dari persamaan homogen yang dianggap.
Jadi, solusi umum persamaan Diophantine 12x + 21y - 2z = 5 terlihat seperti itu: (10 + 4t + 7kamu; –5 – 2t – 4kamu; 5+3t).
3. Pada contoh persamaan sebelumnya, kami mengilustrasikan metode lain untuk menyelesaikan persamaan Diophantine dalam banyak hal yang tidak diketahui, yang terdiri dari penurunan nilai maksimum modul koefisiennya secara berturut-turut.
12x + 21y - 2z = 5 12x + (102 + 1)y - 2z = 5
12x + y - 2(z - 10y) = 5
Dengan demikian, solusi umum dari persamaan yang dipertimbangkan dapat ditulis sebagai berikut: (x; 5 - 12x + 2u; 50 - 120x + 21u), di mana x, kamu adalah parameter bilangan bulat arbitrer.
2. Persamaan Diophantinex 2 – kamu 2 = sebuah
Contoh: 1. Pada sebuah = 0 kami mendapatkan jumlah solusi yang tak terbatas: x = kamu atau x = – kamu untuk siapa saja kamu Z.
2. Pada sebuah = 1 kita punya x 2 – kamu 2 = 1 (x + kamu)(x – kamu) = 1 . Dengan demikian, angka 1 didekomposisi menjadi produk dari dua faktor bilangan bulat x + kamu dan x – kamu(penting, itu x, kamu- utuh!). Karena nomor 1 hanya dua ekspansi ke dalam produk faktor bilangan bulat 1 = 11 dan 1 = (–1)(–1) , kita mendapatkan dua kemungkinan: .
3. Untuk sebuah = 2 kita punya x 2 – kamu 2 = 2 (x + kamu)(x – kamu) = 2. Melanjutkan dengan cara yang sama dengan yang sebelumnya, kami mempertimbangkan ekspansi
2=12=21=(–1)(–2)=(–2)(–1), kami membuat sistem:, yang, tidak seperti contoh sebelumnya, tidak memiliki solusi. Jadi tidak ada solusi untuk persamaan Diophantine yang dipertimbangkan x 2 – kamu 2 = 2.
4.
Pertimbangan sebelumnya mengarah pada beberapa kesimpulan. Solusi persamaan x 2
–
kamu 2
=
sebuah
sedang dalam dekomposisi sebuah
=
km menjadi produk bilangan bulat dari sistem ![]() .
Sistem ini memiliki seluruh solusi jika dan hanya jika k
+
m
dan k
–
m
genap, yaitu ketika angka k
dan m
paritas yang sama (genap atau ganjil secara bersamaan). Jadi, persamaan Diophantine x 2 – y 2 = a memiliki solusi jika dan hanya jika a dapat diekspansi menjadi perkalian dua faktor bilangan bulat dengan paritas yang sama. Tetap hanya untuk menemukan semua file .
.
Sistem ini memiliki seluruh solusi jika dan hanya jika k
+
m
dan k
–
m
genap, yaitu ketika angka k
dan m
paritas yang sama (genap atau ganjil secara bersamaan). Jadi, persamaan Diophantine x 2 – y 2 = a memiliki solusi jika dan hanya jika a dapat diekspansi menjadi perkalian dua faktor bilangan bulat dengan paritas yang sama. Tetap hanya untuk menemukan semua file .
Teorema (pada persamaanx 2 – kamu 2 = sebuah ). (1) Persamaan x 2 – kamu 2 = 0 memiliki jumlah solusi yang tak terbatas .
(2) Setiap solusi persamaan diperoleh sebagai , di mana sebuah = km adalah penguraian bilangan a menjadi hasil kali dua faktor bilangan bulat dengan paritas yang sama.
(3) Persamaan x 2 – kamu 2 = sebuah memiliki solusi jika dan hanya jika sebuah 2 (mod 4).
Bukti.(1) sudah terbukti.
(2) sudah terbukti.
(3) () Mari pertama persamaan Diophantine x 2 – kamu 2 = sebuah memiliki solusi. Ayo buktikan sebuah 2 (mod 4) . Jika sebuah sebuah = km adalah ekspansi menjadi produk bilangan bulat dengan paritas yang sama, maka untuk genap k dan m kita punya k = 2 aku, m = 2 n dan sebuah = km = 4 ln 0 (mod 4) . Dalam kasus ganjil k, m pekerjaan mereka sebuah juga aneh, perbedaan sebuah – 2 ganjil dan tidak habis dibagi 4 , yaitu lagi
sebuah 2 (mod 4).
() Jika sekarang sebuah 2 (mod 4) , maka kita dapat membangun solusi untuk persamaan x 2 – kamu 2 = sebuah. Memang, jika a ganjil, maka sebuah = 1 sebuah adalah dekomposisi produk dari bilangan bulat ganjil, sehingga adalah solusi dari persamaan Diophantine. Jika a genap, maka mengingat sebuah 2 (mod 4) kita mengerti itu 4 | sebuah, sebuah = 4 b = 2(2 b) adalah dekomposisi produk dari bilangan bulat genap, sehingga adalah solusi dari persamaan Diophantine.
Teorema telah terbukti.
Contoh: 1. Persamaan diophantine x 2 – kamu 2 = 2012 tidak memiliki solusi, karena 2010 = 4502 + 2 2 (mod 4).
2. Persamaan diophantine x 2 – kamu 2 = 2011 memiliki solusi, karena
2011 3 (mod 4). Kami memiliki ekspansi yang jelas
2011 = 12011 = 20111 = (–1)(–2011) = (–2011)(–1),
untuk masing-masing yang kami temukan solusinya (kombinasi karakter apa saja). Tidak ada solusi lain, karena nomor 2011 sederhana (?!).
3. Persamaan Diophantinex 2 + kamu 2 = sebuah
Contoh: 1. 0 = 0 2 + 0 2 , 1 = 0 2 + 1 2 , k 2 = 0 2 + k 2 . Dengan demikian, jelas bahwa setiap persegi dapat direpresentasikan secara sepele sebagai jumlah dari dua persegi.
2. 2 = 1 2 + 1 2 , 5 = 1 2 + 2 2 , 8 = 2 2 + 2 2 , 10 = 1 2 + 3 2 , 13 = 2 2 + 3 2 , 17 = 1 2 + 4 2 , 18 = 3 2 + 3 2 , 20 = 2 2 + 4 2 , …
3. Tidak ada solusi untuk sebuah = 3, 6 = 23, 7, 11, 12 = 2 2 3, 14 = 27, 15 = 35, 19, 21 = 37, 22 = 211, 23, 24 = 32 3 , …
Analisis hasil di atas dapat menunjukkan bahwa tidak adanya solusi entah bagaimana terkait dengan bilangan prima dari bentuk
4 n+3 hadir dalam faktorisasi bilangan yang tidak dapat direpresentasikan sebagai jumlah dari dua kuadrat.
Teorema (tentang representasi bilangan asli dengan jumlah dua kotak). Suatu bilangan asli a dapat dinyatakan sebagai jumlah dari dua kuadrat jika dan hanya jika, dalam ekspansi kanoniknya, bilangan prima berbentuk 4 n + 3 memiliki eksponen genap.
Bukti. Pertama kita buktikan bahwa jika bilangan asli a dapat direpresentasikan sebagai jumlah dari dua kuadrat, maka dalam ekspansi kanoniknya semua bilangan prima berbentuk 4 n + 3 harus memiliki eksponen genap. Misalkan, bertentangan dengan apa yang telah dibuktikan, bahwa sebuah= p 2 k +1 b = x 2 + kamu 2 , di mana
R - bilangan prima bentuk 4 n+3 dan b p. Bayangkan angka X dan pada sebagai
x =Dz, kamu = Dt, di manaD= gcd(x, kamu) = p s w, p w; z, t, s N 0 . Kemudian kita mendapatkan persamaan R 2 k +1 b = D 2 (z 2 + t 2 ) = p 2 s w 2 (z 2 + t 2 ) , yaitu R 2( k – s )+1 b = w 2 (z 2 + t 2 ) . Ada p di ruas kiri persamaan (pangkat ganjil tidak sama dengan nol), yang berarti salah satu faktor di ruas kanan habis dibagi bilangan prima p. Karena p w, kemudian p | (z 2 + t 2 ) , dimana angka z, t saling sederhana. Ini bertentangan dengan lemma berikutnya (?!).
Lemma (tentang pembagian jumlah dua kuadrat dengan bilangan prima dari bentuk
4 n + 3 ). Jika bilangan prima p = 4n+3 membagi jumlah kuadrat dua bilangan asli, kemudian membagi masing-masing bilangan tersebut.
Bukti. Dari sebaliknya. Membiarkan x 2 + kamu 2 0(mod p) , tetapi x0(mod p) atau kamu 0 (mod p) . Karena x dan kamu simetris, mereka dapat dipertukarkan, sehingga kita dapat mengasumsikan bahwa x p.
Lemma (pada modulo reversibilitasp ). Untuk sembarang bilangan bulat x, tidak habis dibagi bilangan prima p, ada modulo elemen terbalik p – bilangan bulat seperti itu 1 kamu < p, Apa xi 1 (mod p).
Bukti. Nomor x koprima dengan p, sehingga kita dapat menulis ekspansi linier KPK(x, p) = 1 = xi + pv (kamu, v Z) . Jelas itu xi1(modp) , yaitu kamu- elemen terbalik ke x modulo p. Jika sebuah kamu tidak memenuhi kendala 1 kamu < p, lalu dibagi kamu dengan sisa pada p, kita dapatkan sisanya r kamu (mod p) , untuk itu xr xi 1 (mod p) dan 0 r < p.
Lemma reversibilitas modulo p terbukti.
Mengalikan Perbandingan x 2 + kamu 2 0 (mod p) per persegi kamu 2 elemen terbalik ke x modulo p, kita mendapatkan 0 = 0u 2 x 2 kamu 2 + y 2 kamu 2 = (xu) 2 + (kamu) 2 1+t 2 (mod p).
Sehingga untuk t = kamu perbandingan selesai t 2 –1 (mod p) , yang kita bawa ke kontradiksi. Sudah jelas itu t p: jika tidak t 0 (mod p) dan 0 t 2 –1 (mod p) , yang tidak mungkin. Dengan teorema Fermat kita memiliki t p –1 1 (mod p), yang bersama-sama dengan t 2 –1 (mod p) dan p = 4 n + 3 mengarah pada kontradiksi:
1 s p-1 = t 4n+3–1 = t 2(2n+1) = (t 2 ) 2n+1 (–1) 2n+1 = -1 (modp).
Kontradiksi yang diperoleh menunjukkan bahwa asumsi tentang x 0 (mod p) tidak benar.
Lemma tentang pembagian jumlah dua kuadrat dengan bilangan prima 4 n+3 terbukti.
Jadi, terbukti bahwa bilangan yang dekomposisi kanoniknya termasuk bilangan prima p = 4 n + 3 pangkat ganjil, tidak dapat direpresentasikan sebagai jumlah dua kuadrat.
Mari kita buktikan bahwa setiap bilangan yang ekspansi kanoniknya adalah bilangan prima p = 4 n + 3 berpartisipasi hanya dalam bahkan kekuatan, dapat direpresentasikan sebagai jumlah dari dua kuadrat.
Gagasan pembuktian didasarkan pada identitas berikut:
(sebuah 2 +b 2 )(c 2 +d 2 ) = (ac – bd) 2 + (iklan + sm) 2 ,
yang dapat diperoleh dari properti modul yang diketahui bilangan kompleks– modul produk sama dengan produk modul. Betulkah,
| z|| t| = | zt| | sebuah + dua|| c + di| = |(sebuah + dua)(c + di)|
|a+bi| 2 |c + di| 2 = |(ac – bd) + (iklan + bc)i| 2
(sebuah 2 +b 2 )(c 2 +d 2 ) = (ac – bd) 2 + (iklan + sm) 2 .
Dari identitas ini dapat disimpulkan bahwa jika dua bilangan u, v dapat direpresentasikan sebagai jumlah dari dua kuadrat: kamu = x 2 + kamu 2 , v = z 2 + t 2 , maka produk mereka uv juga dapat direpresentasikan sebagai jumlah dari dua kuadrat: UV = (xz – yt) 2 + (xt + yz) 2 .
Setiap bilangan asli sebuah > 1 dapat ditulis dalam bentuk sebuah= p 1 … R k m 2 , di mana R saya adalah bilangan prima yang berbeda berpasangan, m N . Untuk melakukan ini, cukup dengan menemukan dekomposisi kanonik , tuliskan setiap derajat dari bentuk r dalam bentuk persegi (r) 2 untuk genap = 2, atau dalam bentuk r = r(r) 2 untuk ganjil = 2 + 1 , lalu kelompokkan secara terpisah kuadrat dan bilangan prima tunggal yang tersisa. Sebagai contoh,
29250 = 23 2 5 3 13 = 2513(35) 2 , m = 15.
Nomor m 2 memiliki representasi sepele sebagai jumlah dari dua kuadrat: m 2 = 0 2 + m 2 . Jika kita membuktikan keterwakilan sebagai jumlah dari dua kuadrat dari semua bilangan prima R saya (1 saya k) , maka dengan menggunakan identitas tersebut juga akan diperoleh representasi bilangan a. Dengan syarat, di antara angka-angka R 1 , … , R k hanya bisa bertemu 2 = 1 2 + 1 2 dan bilangan prima dari bentuk 4 n + 1 . Dengan demikian, tetap mendapatkan representasi dalam bentuk jumlah dua kuadrat bilangan prima p = 4m + 1. Kami memisahkan pernyataan ini menjadi teorema terpisah (lihat di bawah)
Misalnya untuk sebuah = 29250 = 2513(15) 2 berturut-turut kita peroleh:
2 = 1 2 + 1 2 , 5 = 1 2 + 2 2 , 13 = 2 2 + 3 2 ,
25 = (11 – 12) 2 + (12 + 11) 2 = 1 2 + 3 2 ,
2513 = (12 – 33) 2 + (13 + 32) 2 = 7 2 + 9 2 ,
29250 = 2513(15) 2 = (715) 2 + (915) 2 = 105 2 + 135 2 .
Teorema telah terbukti.
4. Persamaanx + x + 1 = 3y
Sekarang mari kita berurusan dengan persamaan x+x+1=Zu. Itu sudah memiliki sejarahnya. Pada tahun 1950, R. Oblat menyarankan bahwa, selain memecahkan
x=y=1. tidak memiliki solusi lain dalam bilangan asli x, y dimana x adalah bilangan ganjil. Pada tahun yang sama, T. Nagel menunjukkan solusinya x= 313, y = 181. Metode yang mirip dengan yang di atas untuk persamaan x+x-2y=0, akan memungkinkan kita untuk menentukan semua solusi persamaan x+x+1=3y (1)
dalam bilangan asli x, pada. Mari kita berpura-pura itu (x, y) adalah solusi persamaan (1) dalam bilangan asli, dan x > 1. Dapat dengan mudah dilihat bahwa persamaan (18) tidak memiliki solusi dalam bilangan asli x, kamu, di mana x = 2, 3. 4, 5, 6, 7, 8, 9; jadi seharusnya x10.
Mari kita tunjukkan itu 12 tahun<7 x+3, 7th>4x+ 2. 4 tahun > 2x+1 . (2)
Jika itu 12 tahun> 7x+3, kita akan memiliki 144 tahun> 49 x+42 x+9 . dan karena, mengingat (18), 144y= 48x+ 48 x + 48 , maka itu akan menjadi X< 6 x +3 9, dari mana
(x-z)< 48 dan, oleh karena itu, mengingat bahwa x> 10, 7 < 148 , yang tidak mungkin. Jadi, pertidaksamaan pertama (2) terbukti.
Jika itu 7 tahun< 4 x+2 , kita akan memiliki 49 tahun< 16 x+ 16 x+4 , dan karena, mengingat (1), 16 x+ 16 x+ 16 = 48 tahun, maka itu akan menjadi 49 tahun< 48u- 12, yang tidak mungkin. Jadi, yang kedua dari pertidaksamaan (2) terbukti, dari mana yang ketiga mengikuti secara langsung. Jadi, pertidaksamaan (2) adalah benar.
Ayo pasang sekarang
w\u003d 7x - 12th + 3,h = -4 x+ 7u-2. (3)
Berdasarkan (2), kami menemukan bahwa w > 0 , h > 0 dan X -w=3(4 kamu-2 x-1)>0 dan maka dari itu, w<х . Menurut (3), kita memiliki w 2 + w+1=3 h 2 dari mana, mengingat (1), kami menerima g(x, y) = (7x - 12y + 3, -4x + 7y -2).
Jadi, kita dapat mengatakan bahwa, berdasarkan solusi apa pun (x, y) persamaan (1) dalam bilangan asli, di mana x > 1, kami mendapatkan solusi baru (w, h) = g(x, y) persamaan (1) dalam bilangan asli w, h di mana w < х (dan karenanya solusi dalam bilangan asli yang lebih kecil). Oleh karena itu, bertindak seperti di atas, kami menemukan bahwa untuk setiap solusi Persamaan (1) dalam bilangan asli x, y, di mana x > 1, ada bilangan asli n sehingga g(x, y) = (l, 1).
Setelah menerima f(x, y) = (7x+12 tahun + 3, 4x+ 7 tahun + 2), (4) kita dapat dengan mudah menemukan bahwa f(g(x, y)) = (x, y) dan karenanya (x, kamu) = f(1,1) Di sisi lain, mudah untuk memeriksa apakah (x, y) adalah solusi persamaan (1) dalam bilangan asli, maka f(x, kamu) ada juga solusi persamaan (1) dalam bilangan asli (masing-masing lebih besar dari X dan pada).
Setelah menerima x=y=1(x, y) = f(1, 1) untuk n=2,3,…..,
kita mendapatkan urutannya { x, kamu} untuk n= 1, 2,….., berisi semua solusi persamaan (1) dalam bilangan asli dan hanya solusi tersebut.
Di sini kita punya (X,kamu)= f(1,1)= f(x, y), oleh karena itu, karena (4), kami memperoleh
x=7x+12 tahun+3,kamu=4x+7y+2 (5) (n=1, 2, ...)
Rumus yang memungkinkan Anda untuk secara konsisten menentukan semua solusi (x, y) persamaan (1) dalam bilangan asli. Dengan cara ini, kami dengan mudah mendapatkan solusi (1,1),(22,13),(313,181),.(4366,2521),(60817,35113),..
Jelas ada jumlah tak terbatas dari solusi ini. Dari persamaan
x=y=1 dan (4) dengan induksi kita dengan mudah menemukan bahwa bilangan-bilangan itu X dengan indeks ganjil adalah ganjil, dengan indeks genap mereka genap, dan angkanya kamu esensi aneh untuk n = 1, 2, ... Untuk mendapatkan semua solusi persamaan (1) dalam bilangan bulat x, y, karena mudah dibuktikan, itu akan mengikuti solusi yang sudah diperoleh (x, y) Ikuti (x, -y) dan (-x-1,±y) untuk n=1, 2, .. .
Jadi di sini kita memiliki, misalnya, lebih banyak solusi seperti itu: (-2,1) (-23,13), (-314,181). A. Rotkevich mencatat bahwa dari semua solusi persamaan (1) dalam bilangan asli x > 1 dan y bisa mendapatkan semua solusi dari persamaan (z+1)-z= y (6)
dalam bilangan asli z, y. Memang, misalkan bilangan asli z, y memenuhi persamaan (5). Menempatkan x=3z+l, kita dapatkan, karena mudah diperiksa, bilangan asli x > 1 dan pada memenuhi persamaan (1).
Di sisi lain, jika bilangan asli x > 1 dan pada memenuhi persamaan (1), maka kita memiliki, karena mudah untuk memeriksa, (x-1)= 3(y-x), maka bilangan tersebut (alami) x-1 dibagi dengan 3 , Akibatnya x-1=3 z, dimana z adalah bilangan asli, dan persamaan 3z=y-x=y3z-1 , yang membuktikan bahwa bilangan z dan pada memenuhi persamaan (6). Jadi, berdasarkan keputusan (22,13),(313,181), (4366,2521) persamaan (1), kami memperoleh solusi (7,13),(104,181),(1455,2521) persamaan (6). Kami juga mencatat di sini bahwa jika bilangan asli z, kamu memenuhi persamaan (6), terbukti bahwa pada adalah jumlah dari dua persegi berturut-turut, misalnya 13=2+3,181=9+10, 2521=35+ 36 . Dengan cara yang sama, seperti sebelumnya untuk persamaan (1), kita dapat menemukan semua solusi persamaan x+(x+1)= kamu dalam bilangan asli x, y, mengambil untuk x > 3 g (x. y) \u003d (3x -2y + 1, 3y - 4x - 2) dan untuk x> 1 f(x, y) = (3x+ 2th+l, 4x + Zu + 2), yang mengarah ke rumus ( x, y)f(3,5) dan kesimpulan bahwa semua solusi persamaan (6) dalam bilangan asli x, y terdapat dalam barisan { x, kamu} untuk n= 1, 2,…., di mana x=3, y=5, danx=3 x+2 kamu+1 . kamu = 4 x+3 kamu+2 (n=1, 2, ...). Sebagai contoh, x \u003d 3 3 + 2 5 + 1 \u003d 20, y \u003d 4 3 + Z 5 + 2 \u003d 29;x=119, y=169:x=69b, y=985;x=4059, y=5741.
Arti geometris dari persamaan yang dipertimbangkan adalah bahwa ia memberikan semua segitiga Pythagoras (persegi panjang dengan sisi alami), yang kakinya dinyatakan oleh bilangan asli yang berurutan. Ada banyak segitiga seperti itu (*).
persamaannya adalah x+(x+1)= kamu, telah terbukti tidak memiliki solusi dalam bilangan asli x, y.
Linier persamaan diophantine
Pekerjaan penelitian dalam aljabar
MOU siswa kelas 9 "Upshinskaya OOSh"
Antonov Yuri
"Jika kamu ingin belajar berenang, maka
dengan berani masuk ke air, dan jika Anda mau
belajar memecahkan masalah, kemudian menyelesaikannya.
D.Poya
Kepala - Sofronova N.A. .

Sebuah tugas
Untuk lantai dengan lebar 3 meter, ada papan dengan lebar 11 cm dan 13 cm. Berapa banyak papan dari kedua ukuran yang Anda butuhkan?
Jika sebuah X - jumlah papan lebar 11 cm, dan pada - jumlah papan lebar 13 cm, maka kita perlu menyelesaikan persamaan:
11 X + 13 tahun = 300

Fitur persamaan 11 x + 13 y \u003d 300: ▪ Koefisien 11, 13, 300 adalah bilangan bulat. ▪ Jumlah yang tidak diketahui melebihi jumlah persamaan. ▪ Solusi dari persamaan ini x dan y harus bilangan bulat bilangan positif
Persamaan aljabar atau sistem persamaan aljabar dengan koefisien bilangan bulat, di mana jumlah yang tidak diketahui melebihi jumlah persamaan dan untuk itu solusi bilangan bulat harus ditemukan, disebut tak tentu atau diofantin, dinamai dari seorang ahli matematika Yunani Diophantus .

Contoh Persamaan Diophantine
1 . Temukan semua pasangan bilangan bulat
x , kamu , yang benar persamaan
2 . Tunjukkan bahwa persamaan
memiliki jumlah solusi yang tak terbatas
bilangan bulat

Objektif:
Untuk mengetahui:
- Jenis apa metode Dengan ada untuk solusi untuk persamaan Diophantine?

Tugas:
- Temukan dan dan pelajari metode solusi linier Persamaan diophantine dalam dua variabel.
- Pertimbangkan kemungkinan teori persamaan Diophantine linier.

kembar tiga Pythagoras
- Persamaan tak tentu dalam bilangan bulat diselesaikan bahkan sebelum Diophantus. Yang sangat menarik adalah, misalnya, persamaan aljabar x 2 + kamu 2 = z 2 , pihak yang mengikat x , pada , z segitiga siku-siku. Bilangan bulat x , kamu dan z , yang merupakan solusi dari persamaan ini, disebut "kembar tiga Pythagoras" .

persamaan Fermat
- Karya-karya Diophantus juga terkait langsung dengan penelitian matematika matematikawan Prancis Pierre de Fermat. Diyakini bahwa karya Fermat yang memulai gelombang baru dalam pengembangan teori bilangan. Dan salah satu masalahnya adalah persamaan Fermat yang terkenal
X n + y n =z n

Tidak ada satu pun matematikawan besar yang lulus teori persamaan Diophantine.
Fermat, Euler, Lagrange, Gauss, Chebyshev meninggalkan jejak yang tak terhapuskan pada teori yang menarik ini.
 1, (Catalana); ax 2 + bxy + su 2 + dx + ey + f \u003d 0, di mana a, b, c, d, e, f adalah bilangan bulat, yaitu persamaan umum tidak homogen tingkat kedua dengan dua yang tidak diketahui (P. Fermat, J Wallis, L. Euler, J. Lagrange dan K. Gauss) "lebar = "640"
1, (Catalana); ax 2 + bxy + su 2 + dx + ey + f \u003d 0, di mana a, b, c, d, e, f adalah bilangan bulat, yaitu persamaan umum tidak homogen tingkat kedua dengan dua yang tidak diketahui (P. Fermat, J Wallis, L. Euler, J. Lagrange dan K. Gauss) "lebar = "640" Contoh persamaan tak tentu diselesaikan oleh matematikawan hebat abad ke-19 dan ke-20: x 2 − ny 2 = 1 , di mana n bukan kuadrat eksak (Fermat, Pell); x z − kamu t = 1 , di mana z , t 1, (Catalana); Oh 2 + b.xy + su 2 + dx + mata + f = 0 , di mana sebuah , b , Dengan , d , e , f - bilangan bulat, yaitu persamaan umum tidak homogen tingkat kedua dengan dua yang tidak diketahui (P. Fermat, J. Vallis, L. Euler, J. Lagrange dan K. Gauss)

Persamaan diophantine di abad ke-20
1900 Kongres Matematika Internasional.
Masalah ke-10 Hilbert
Diberikan persamaan Diophantine dengan sejumlah koefisien bilangan bulat yang tidak diketahui dan rasional. Hal ini diperlukan untuk menghasilkan prosedur yang dapat menentukan dalam sejumlah operasi terbatas apakah persamaan tersebut dapat diselesaikan dalam bilangan bulat rasional.
Matematikawan Rusia Yuri Matiyasevich terbukti :
Masalah ke-10 Hilbert tidak dapat dipecahkan - algoritma yang diperlukan tidak ada.

Apakah selalu mungkin untuk menemukan semua solusi untuk persamaan tak tentu tertentu atau membuktikan tidak adanya seperti itu?
- Masalah penyelesaian persamaan dalam bilangan bulat telah diselesaikan sepenuhnya hanya untuk persamaan tingkat pertama dengan dua atau tiga yang tidak diketahui.
- DE tingkat kedua dengan dua yang tidak diketahui sudah diselesaikan dengan susah payah.
- DE derajat kedua dengan lebih dari dua yang tidak diketahui diselesaikan hanya dalam beberapa kasus khusus, misalnya, persamaan x 2 + kamu 2 = z 2 .
- DE derajat lebih tinggi dari yang kedua, sebagai suatu peraturan, hanya memiliki sejumlah solusi yang terbatas (dalam bilangan bulat).
- Untuk persamaan di atas derajat kedua dengan dua atau lebih yang tidak diketahui, bahkan masalah keberadaan solusi bilangan bulat agak sulit. Misalnya, tidak diketahui apakah persamaan memiliki
x 3 + kamu 3 + z 3 = 30 setidaknya satu solusi bilangan bulat.
- Untuk memecahkan persamaan diferensial individu, dan kadang-kadang untuk persamaan tertentu, seseorang harus menemukan metode baru. Jelas, tidak ada algoritma yang memungkinkan menemukan solusi untuk DE sewenang-wenang.

Persamaan Diophantine Linier
Bentuk umum:
LDE dengan dua variabel:
sebuah X + oleh = c
LDE dengan tiga variabel:
sebuah X + oleh + cz = d

LDE dengan dua yang tidak diketahui
LDE dengan dua variabel:
sebuah X + oleh = c
Solusi:
x = x 0 - bt
pada = pada 0 + pada
Homogen:
sebuah X + oleh = 0
Solusi:
x = - bt
pada = pada

Menemukan solusi pribadi
Metode solusi:
- Beberapa metode.
- Penerapan algoritma Euclid.
- Metode iterasi.
- Metode keturunan.
- Metode untuk mempertimbangkan sisa dari pembagian

Beberapa metode
selesaikan persamaannya 11 x + 2 y = 69
Kami mencari jumlah yang sama dengan 69: 55 + 14 = 69 Solusi khusus dari persamaan
X 0 = 5, y 0 = 7

Penerapan algoritma Euclid
selesaikan persamaannya 4 x + 7 y = 16
- Mari kita cari gcd dari angka 4 dan 7 menggunakan algoritma Euclid: gcd(4,7) = 1
- Ayo nyatakan angkanya 1 melalui koefisien sebuah = 4 dan b =7 menggunakan teorema ekspansi linier GCD:
KPK ( sebuah, b ) = au+bv .
- Kita peroleh: 1 = 4 2 + 7 ∙ (-1) kamu = 2, v = -1
- Solusi khusus dari persamaan: X 0 = 2 ∙ 16 = 32,
pada 0 = -1 ∙ 16 = -16

metode pencacahan
selesaikan persamaannya 7 x + 12 y = 100
- 7x + 12y = 100
- 7x \u003d 100 - 12th
- 100 - 12 tahun kelipatan 7
Solusi khusus dari persamaan: X 0 = 4, y 0 = 6
100-12u

Metode pelepasan: 3x+8y=60
Cepat
variabel X
melalui pada
Cepat
variabel X
melalui t
Menjawab:
Penyelidikan:

Metode untuk mempertimbangkan sisa dari pembagian
- Selesaikan persamaan dalam bilangan bulat 3x - 4 tahun \u003d 1
- 3 x = 4 y + 1
- Ruas kiri persamaan habis dibagi 3, jadi ruas kanan harus habis dibagi 3. Pembagian dengan 3 menghasilkan sisa 0, 1, dan 2.
- Mari kita pertimbangkan 3 kasus.
3x = 4 3p + 1 = 12p + 1
y=3p+1
Tidak habis dibagi 3
3x = 4 (3p + 1) +1 = 12p + 3
y=3p+2
Tidak habis dibagi 3
3 x = 4 (3p + 2) +1 = 12p + 9
3x=3(4p+3)
x = 4 p + 3
Menjawab:
habis dibagi 3
x = 4 p + 3 ; y=3p+2

Kemungkinan teori LDE Temukan semua solusi bilangan bulat dari suatu persamaan X 2 + 5 tahun 2 + 34z 2 + 2xy - 10xz - 22uz =0

Apa yang diberikan proyek itu kepada saya?
- Memperoleh wawasan tentang bekerja pada proyek penelitian.
- Dia berkenalan dengan sejarah perkembangan persamaan Diophantine dan biografi Diophantus.
- Mempelajari metode untuk memecahkan LDE dengan dua dan tiga yang tidak diketahui.
- memecahkan sekelompok masalah yang bersifat praktis, dan juga terjadi di olimpiade, ujian untuk kursus sekolah dasar
- Memperoleh keterampilan untuk memecahkan masalah non-standar.
Saya pikir di masa depan saya akan terus mempelajari persamaan Diophantine tingkat kedua dan metode untuk menyelesaikannya.
DAFTAR SUMBER YANG DIGUNAKAN
- Matematika dalam konsep, definisi dan istilah. Bagian 1. Sebuah panduan untuk guru. Ed. L.V. Sabinina. M., "Pencerahan", 1978. -320 hal. (Perpustakaan seorang guru matematika.) Di belakang buku judul: O.V. Manturov, Yu.K. Solntsev, Yu.I. Sorokin, N.G. Fedin.
- Nagibin F.F., Kanin E.S. Kotak Matematika: Panduan Siswa. – Edisi ke-4, direvisi. dan tambahan - M.: Pencerahan, 1984. - 160-an., sakit.
- N.P. Tuchnin. Bagaimana cara mengajukan pertanyaan? (Tentang kreativitas matematika anak sekolah): Buku untuk siswa. - M.: Pendidikan, 1993. - 192 hal., sakit.
- S.N.Olekhnik, Yu.V.Nesterenko, M.K.Potapov Masalah menghibur kuno. –M.: Bustard, 2002. -176s., sakit.
- Ya.I. Perelman. Aljabar yang menghibur. - M.: Nauka, 1975. - 200-an., sakit.
- Sumber daya pemilu: http :// www.yugzone.ru /x/ diofant-i-diofantovy-uravneniya / I.G. Bashmakova "Persamaan Diophantine dan Diophantine".
- Sumber daya pemilu: http :// www.goldenmuseum.com /1612Hilbert_eng.html Masalah ke-10 Hilbert: sejarah penemuan matematika (Diophantus, Fermat, Hilbert, Julia Robinson, Nikolai Vorobyov, Yuri Matiyasevich).
- Sumber daya elektoral: http://ru.wikipedia.org/wiki/ Persamaan diophantine.
- Sumber daya pemilu: http :// revolusi.allbest.ru / matematika /d00013924.html Persamaan Diophantine Linier Belov Denis Vladimirovich.
- Sumber daya pemilu: http :// revolusi.allbest.ru / matematika /d00063111.html Persamaan Diophantine Linier
- Sumber daya pemilu: http ://portfolio.1september.ru/work.php?id=570768 Zyuryukina Olga. Persamaan tak tentu dalam bilangan bulat atau persamaan Diophantine.
- Sumber daya pemilu: http ://portfolio.1september.ru/work.php?id=561773 Arapov Alexander. Diophantus dan persamaannya.
- Sumber daya pemilu: http :// en.wikipedia.org / wiki / algoritma Euclid.
Hari ini saya mengusulkan untuk merenungkan beberapa masalah matematika yang menarik.
Yaitu, mari kita lakukan pemanasan dengan menyelesaikan persamaan linier berikut:
"Apa yang sulit?" - Anda bertanya. Memang hanya satu persamaan dan sebanyak empat tidak diketahui. Oleh karena itu, tiga variabel bebas, dan yang terakhir bergantung padanya. Jadi mari kita ekspresikan dengan cepat! Misalnya melalui variabel , maka himpunan penyelesaiannya adalah sebagai berikut:
di mana adalah himpunan setiap bilangan real.
Nah, solusinya ternyata terlalu sepele. Kemudian kita akan memperumit tugas kita dan membuatnya lebih menarik.
Mari kita ingat tentang persamaan linear dengan koefisien bilangan bulat dan akar bilangan bulat, yang sebenarnya adalah sejenis persamaan Diophantine. Secara khusus, kami akan memaksakan pada persamaan kami pembatasan yang sesuai pada koefisien bilangan bulat dan akar. Koefisien untuk yang tidak diketahui sudah bilangan bulat (), tetapi yang tidak diketahui itu sendiri harus dibatasi sebagai berikut:
di mana adalah himpunan bilangan bulat.
Sekarang solusi yang diperoleh di awal artikel tidak akan berfungsi, karena kita berisiko mendapatkannya sebagai bilangan rasional (pecahan). Jadi bagaimana Anda memecahkan persamaan ini? khusus dalam bilangan bulat?
Tertarik untuk memecahkan masalah ini, saya bertanya di bawah cat.
Dan kami melanjutkan dengan Anda. Mari kita coba membuat beberapa transformasi dasar dari persamaan yang diinginkan:
Masalahnya masih terlihat tidak dapat dipahami, dalam kasus seperti itu matematikawan biasanya membuat semacam substitusi. Mari kita memukulnya dengan Anda:
Wow, kami telah mencapai hasil yang menarik! Koefisien dengan kami sekarang sama dengan satu, yang berarti bahwa Anda dan saya dapat mengungkapkan yang tidak diketahui ini dalam hal sisa yang tidak diketahui dalam persamaan ini tanpa pembagian (yang kita berdosa di awal artikel). Ayo lakukan:
Biarkan saya perhatikan bahwa ini memberi tahu kita bahwa tidak peduli apa pun itu (dalam kerangka persamaan Diophantine), mereka akan tetap menjadi bilangan bulat, dan ini baik-baik saja.
Mengingat bahwa itu adil untuk mengatakan itu. Dan mengganti hasil yang diperoleh di atas, kita mendapatkan:
Di sini kita juga melihat bahwa tidak peduli apa pun itu, mereka akan tetap menjadi bilangan bulat, dan ini masih baik-baik saja.
Kemudian sebuah ide cemerlang muncul di benak: jadi mari kita deklarasikan sebagai variabel bebas, dan kita akan mengekspresikannya melalui mereka! Bahkan, kami sudah melakukannya. Tetap hanya untuk menulis jawabannya ke dalam sistem solusi:
Sekarang Anda dapat melihatnya dalam sistem keputusan tidak ada pembagian di mana pun, yang berarti bahwa solusi akan selalu bilangan bulat. Mari kita coba mencari solusi khusus untuk persamaan asli, dengan asumsi, misalnya, bahwa:
Substitusi ke persamaan awal:
Sama, keren! Mari kita coba lagi dengan contoh lain, ya?
Di sini kita melihat koefisien negatif, itu dapat memberi kita cukup banyak masalah, jadi mari kita singkirkan dosa dengan menggantinya, maka persamaannya adalah sebagai berikut:
Seperti yang kita ingat, tugas kita adalah membuat transformasi sedemikian sehingga dalam persamaan kita ada yang tidak diketahui dengan koefisien satuannya (untuk kemudian mengungkapkannya melalui sisanya tanpa pembagian). Untuk melakukan ini, kita harus kembali mengambil sesuatu "keluar dari kurung", yang tercepat adalah mengambil koefisien dari persamaan yang paling dekat dengan kesatuan. Namun, Anda perlu memahami bahwa hanya angka yang merupakan beberapa koefisien persamaan (tidak lebih, tidak kurang) yang dapat dikeluarkan dari kurung, jika tidak, kita akan menemukan tautologi / kontradiksi atau pecahan (dengan kata lain, itu tidak mungkin variabel bebas muncul di suatu tempat kecuali untuk perubahan terakhir). Jadi:
Kami memperkenalkan pengganti, maka kami mendapatkan:
Sekali lagi, kami mengeluarkannya dari braket dan akhirnya kami mendapatkan yang tidak diketahui dalam persamaan dengan koefisien satuan:
Kami memperkenalkan pengganti, maka:
Mari kita ungkapkan kesepian kita yang tidak diketahui dari sini:
Oleh karena itu, apa pun yang kita ambil, itu akan tetap menjadi bilangan bulat. Kemudian kita temukan dari rasio:
Demikian pula, kami menemukan dari hubungan:
Dalam hal ini, sistem solusi kami telah matang - kami telah menyatakan secara mutlak semua yang tidak diketahui tanpa menggunakan pembagian, sehingga menunjukkan bahwa solusinya pasti bilangan bulat. Juga, jangan lupa bahwa , dan kita perlu memperkenalkan substitusi terbalik. Maka sistem penyelesaian akhir adalah sebagai berikut:
Jadi, tetap menjawab pertanyaan - dapatkah persamaan serupa diselesaikan dengan cara ini? Jawaban: tidak, jika persamaan pada prinsipnya tidak dapat diselesaikan. Hal ini terjadi dalam kasus di mana istilah bebas tidak habis dibagi oleh GCD dari semua koefisien untuk yang tidak diketahui. Dengan kata lain, diberikan persamaan:
Untuk menyelesaikannya dalam bilangan bulat, cukup memenuhi kondisi berikut:
(di mana adalah pembagi persekutuan terbesar).
Bukti
Pembuktian tidak dipertimbangkan dalam kerangka artikel ini, karena ini adalah alasan untuk artikel terpisah. Anda dapat melihatnya, misalnya, dalam buku luar biasa karya V. Sierpinsky "Tentang penyelesaian persamaan dalam bilangan bulat" di 2.
Meringkas hal di atas, kami menulis algoritme tindakan untuk menyelesaikan persamaan Diophantine linier dengan sejumlah yang tidak diketahui:
Sebagai kesimpulan, perlu dikatakan bahwa dimungkinkan untuk menambahkan pembatasan pada setiap suku persamaan dalam bentuk pertidaksamaan di atasnya (kemudian sistem pertidaksamaan ditambahkan ke sistem solusi, yang menurutnya jawabannya perlu disesuaikan), dan juga menambahkan hal lain yang menarik. Anda juga tidak boleh lupa bahwa algoritma solusinya ketat dan dapat ditulis dalam bentuk program komputer.
Peter bersamamu
Terima kasih atas perhatian Anda.
Soal 1. Katakanlah gurita dan bintang laut hidup di akuarium. Gurita memiliki 8 kaki, dan bintang laut memiliki 5. Total ada 39 kaki. Berapa banyak hewan yang ada di akuarium?
Larutan. Misalkan x adalah jumlah bintang laut dan y adalah jumlah gurita. Kemudian semua gurita memiliki 8 kaki, dan semua bintang memiliki 5 kaki. Mari kita buat persamaan: 5x + 8y = 39.
Perhatikan bahwa jumlah hewan tidak dapat dinyatakan sebagai bilangan bulat atau negatif. Oleh karena itu, jika x adalah bilangan bulat non-negatif, maka y \u003d (39 - 5x) / 8 juga harus bilangan bulat dan bukan negatif, yang berarti bahwa ekspresi 39 - 5x harus habis dibagi 8 tanpa sisa. Pencacahan opsi menunjukkan bahwa ini hanya mungkin jika x = 3, maka y = 3. Jawaban: (3; 3).
Persamaan bentuk ax + bu = c disebut Diophantine, diambil dari nama matematikawan Yunani kuno Diophantus dari Alexandria. Diophantus hidup, tampaknya, pada abad ke-3. n. e., sisa fakta biografinya yang kita ketahui habis oleh puisi teka-teki seperti itu, menurut legenda, terukir di batu nisannya:
Abu makam Diophantus diletakkan; kagumi dia dan batunya
Usia orang yang sudah meninggal akan memberitahunya dengan seni yang bijaksana.
Atas kehendak para dewa, ia menjalani seperenam dari hidupnya sebagai seorang anak.
Dan dia bertemu setengah dari keenam dengan bulu di pipinya.
Baru ketujuh berlalu, dia bertunangan dengan pacarnya.
Bersamanya, setelah menghabiskan lima tahun, seorang bijak menunggu putranya;
Putra kesayangannya hanya menjalani separuh hidup ayahnya.
Dia diambil dari ayahnya oleh kuburan awalnya.
Dua kali dua tahun orang tua meratapi kesedihan yang berat,
Di sini saya melihat batas hidup saya yang menyedihkan.
Berapa tahun Diophantus dari Alexandria hidup?
Tugas 2. Ada paku di gudang dalam kotak 16,17 dan 40 kg. Dapatkah seorang penjaga toko memberikan 100 kg paku tanpa membuka kotaknya? (metode pencacahan langsung)
Mari kita menganalisis metode penyelesaian sehubungan dengan satu yang tidak diketahui.
Tugas 3. Ada 96 lukisan dalam katalog galeri seni. Di beberapa halaman ada 4 lukisan, dan di beberapa 6. Berapa halaman dari setiap jenis yang ada di katalog?
Larutan. Biarkan x menjadi jumlah halaman dengan empat gambar,
y adalah jumlah halaman dengan enam gambar,
Kami memecahkan persamaan ini sehubungan dengan yang tidak diketahui yang koefisien terkecil (modulo). Dalam kasus kami, ini adalah 4x, yaitu:
Kami membagi seluruh persamaan dengan faktor ini:
4x=96-6th | : empat;
Sisanya bila dibagi 4:1,2,3. Substitusikan angka-angka ini untuk y.
Jika y=1, maka x=(96-6∙1):4=90:4 - Tidak berhasil, solusinya bukan bilangan bulat.
Jika y=2, maka x=(96-6∙2):4=21 - Sesuai.
Jika y=3, maka x=(96-6∙3):4=78:4 - Tidak berhasil, solusinya bukan bilangan bulat.
Jadi, solusi tertentu adalah pasangan (21;2), yang berarti ada 4 gambar pada 21 halaman, dan 6 gambar pada 2 halaman.
Mari kita menganalisis metode solusi menggunakan algoritma Euclid.
Soal 4. Toko menjual dua jenis cokelat: susu dan pahit. Semua cokelat disimpan dalam kotak. Ada 7 kotak coklat susu di gudang, dan 4 coklat hitam, diketahui masih ada satu batang coklat hitam lagi. Berapa banyak batang cokelat di setiap jenis kotak?
Larutan. Biarkan x menjadi jumlah batang cokelat susu dalam satu kotak,
y adalah jumlah batang cokelat hitam dalam satu kotak,
Kemudian, sesuai dengan kondisi masalah ini, kita dapat menulis persamaan:
Mari selesaikan persamaan ini menggunakan algoritma Euclid.
Ekspres 7=4∙1+3, => 3=7-4∙1.
Ekspres 4=3∙1+1, => 1=4-3∙1=4-(7-4∙1)=4-7+4∙1=4∙ 2 -7∙1 =1.
Jadi, ternyata x=1; y=2.
Dan ini berarti cokelat susu ada dalam kotak 1 buah, dan pahit ada 2 buah.
Mari kita menganalisis metode untuk menemukan solusi tertentu dan rumus umum solusi.
Masalah 5. Di suku Afrika Tumbe-Yumbe, dua penduduk asli Tumba dan Yumba bekerja sebagai penata rambut, dan Tumba selalu mengepang 7 kepang untuk kliennya, dan Yumba 4 kepang masing-masing. Berapa banyak klien yang dilayani secara individu oleh master selama shift, jika diketahui bahwa mereka bersama-sama menjalin 53 kuncir?
Larutan. Misalkan x adalah jumlah pelanggan Tumba,
y adalah jumlah klien Yumba,
maka 7x+4y=53 (1).
Sekarang, untuk menemukan solusi tertentu dari persamaan (,), kita mengganti jumlah angka yang diberikan kepada kita dengan 1. Ini akan sangat menyederhanakan pencarian angka yang sesuai. Kita mendapatkan:
Selesaikan persamaan ini dengan metode substitusi.
4th \u003d 1-7x : 4;
Sisanya jika dibagi 4:1, 2, 3. Gantikan bilangan-bilangan ini sebagai ganti x:
Jika x=1, maka y=(1-7):4 tidak sesuai, karena penyelesaiannya tidak dalam bilangan bulat.
Jika x=2, maka y=(1-7∙2):4 tidak sesuai, karena penyelesaiannya tidak dalam bilangan bulat.
Jika x=3, maka y=(1-7∙3):4=-5 baik-baik saja.
Kemudian kami mengalikan nilai yang dihasilkan dengan nilai awal jumlah, yang kami ganti dengan 1, mis.
x=x 0 53=3∙53=159;
y=y 0 53=-5∙53=-265.
Kami telah menemukan solusi khusus dari persamaan (1). Mari kita periksa dengan mengganti persamaan awal:
7∙159+4∙(-265)=53; (3)
Jawabannya datang bersamaan. Jika kita memecahkan persamaan abstrak, kita bisa berhenti di situ. Namun, kami memecahkan masalah, dan karena Tumba tidak dapat mengepang kepang dalam jumlah negatif, kami perlu melanjutkan solusinya. Sekarang kita akan menulis rumus untuk solusi umum. Untuk melakukan ini, kita kurangi dari persamaan awal (1) persamaan dengan nilai tersubstitusi (3). Kita mendapatkan:
Mari kita keluarkan faktor-faktor umum dari tanda kurung:
7(x-159)+4(y+265)=0.
Mari kita pindahkan salah satu suku dari satu bagian persamaan ke bagian lain:
7(x-159)=-4(y+265).
Sekarang menjadi jelas bahwa agar persamaan yang akan diselesaikan (x-159) harus habis dibagi -4, dan (y + 265) harus habis dibagi 7. Mari kita perkenalkan variabel n, yang akan menampilkan pengamatan kita ini:
Mari kita pindahkan suku-suku dari satu sisi persamaan ke sisi yang lain:
Kami telah memperoleh solusi umum untuk persamaan ini, sekarang kami dapat mengganti berbagai angka ke dalamnya dan mendapatkan jawaban yang sesuai.
Misal n=39, maka
Dan ini berarti bahwa Tumba mengepang kuncir untuk 3 klien, dan Yumba untuk 8 klien.
Memecahkan masalah dengan berbagai cara.
Tugas 6: Vovochka membeli pena seharga 8 rubel dan pensil seharga 5 rubel. Selain itu, dia membayar 19 rubel lebih banyak untuk semua pensil daripada untuk semua pena. Berapa banyak pulpen dan berapa pensil yang dibeli Little Johnny? (metode mencari solusi umum, solusi untuk satu yang tidak diketahui, menggunakan algoritma Euclidean).
Soal 7. Pulpen flanel dibeli seharga 7 rubel dan pensil masing-masing seharga 4 rubel, dengan total 53 rubel. Berapa banyak spidol dan pensil yang dibeli?
Soal 8. (Tur kota VOSH 2014-2015): di planet C, ada dua jenis koin: masing-masing 16 tugriks dan 27 tugriks. Apakah mungkin untuk membeli barang dengan harga 1 tugrik dengan bantuan mereka?
Masalah 9. Scheherazade menceritakan kisahnya kepada penguasa besar. Secara total, dia harus menceritakan 1001 dongeng. Berapa malam yang dibutuhkan Scheherazade untuk menceritakan semua kisahnya, jika pada suatu malam dia menceritakan 3 kisah, dan pada beberapa malam lainnya? Dalam berapa malam Scheherazade akan menceritakan semua kisahnya jika dia ingin melakukannya secepat mungkin? Berapa malam yang dibutuhkan Scheherazade jika dia membosankan untuk menceritakan lima cerita semalam, jadi seharusnya ada malam seperti itu sesedikit mungkin?
Tugas 10. (ingat "Aquarius") Bagaimana cara menuangkan 3 liter air, memiliki wadah 9 liter dan 5 liter?
Soal 11. Johnny kecil pandai matematika. Dalam buku hariannya, dia hanya memiliki balita dan empat, dan masih ada balita lagi. Jumlah semua nilai Vovochka dalam matematika adalah 47. Berapa banyak Vovochka yang mendapat angka lima dan berapa angka empat?
Soal 12. Koschey the Immortal mendirikan pembibitan untuk membiakkan Gorynych Serpents. Pada tandu terakhir, ia memiliki Ular berkepala 17 dan Ular berkepala 19. Secara total, induk ini memiliki 339 gol. Berapa banyak Ular berkepala 17 dan berapa banyak Ular berkepala 19 yang dikembangbiakkan Koshchei?
Jawaban: Diophantus hidup selama 84 tahun;
tugas 2: 4 kotak 17 kg dan 2 kotak 16 kg;
tugas 6: 7 pensil dan 8 pena dibeli, yaitu (7,2) adalah solusi khusus dan y = 2 + 5n, x = 7 + 8n, di mana nє Z adalah solusi umum;
tugas 7: (-53; 106) - solusi khusus, x=4n-53, y=-7n+106 - solusi umum, dengan n=14, x=3, y=8, yaitu, 3 felt-tip pena dan 8 pensil dibeli;
tugas 8: misalnya, membayar 3 koin dari 27 tugriks dan mendapatkan kembalian 5 koin dari 16 tugriks;
tugas 9: (2002; -1001) - solusi tertentu, x=-5 n+2002, y=3n-1001 - solusi umum, dengan n=350, y=49, x=252, yaitu 252 malam, 3 dongeng masing-masing dan 49 malam dari 5 dongeng - total 301 malam; opsi tercepat: 2 malam dari tiga cerita dan 199 malam dari 5 cerita - total 201 malam; opsi terpanjang: 332 malam dari 3 dongeng dan 1 malam dari 5 dongeng - total 333 malam.
tugas 10: misalnya, tuangkan air 2 kali dengan toples 9 liter dan ambil 3 kali dengan toples 5 liter;
tugas 11: Johnny kecil mendapat 7 balita dan 4 merangkak;
Soal 12: 11 Ular dengan 17 kepala dan 8 Ular dengan 19 kepala.
Pertidaksamaan aljabar atau sistemnya dengan koefisien rasional yang solusinya dicari dalam bilangan integral atau bilangan bulat. Sebagai aturan, jumlah yang tidak diketahui dalam persamaan Diophantine lebih besar. Dengan demikian, mereka juga dikenal sebagai pertidaksamaan tak tentu. Dalam matematika modern, konsep di atas diterapkan pada persamaan aljabar, yang solusinya dicari dalam bilangan bulat aljabar dari beberapa perluasan bidang variabel Q-rasional, bidang variabel p-adik, dll.
Asal usul ketidaksetaraan ini
Studi tentang persamaan Diophantine berada di batas antara teori bilangan dan geometri aljabar. Menemukan solusi dalam variabel integer adalah salah satu masalah matematika tertua. Sudah di awal milenium kedua SM. orang Babilonia kuno berhasil memecahkan sistem persamaan dengan dua yang tidak diketahui. Cabang matematika ini paling berkembang di Yunani kuno. Aritmatika Diophantus (sekitar abad ke-3 M) adalah sumber penting dan utama yang berisi jenis yang berbeda dan sistem persamaan.
Dalam buku ini, Diophantus meramalkan sejumlah metode untuk mempelajari ketidaksetaraan tingkat kedua dan ketiga yang dikembangkan sepenuhnya pada abad ke-19. Penciptaan teori bilangan rasional oleh peneliti Yunani kuno ini mengarah pada analisis solusi logis untuk sistem tak tentu, yang secara sistematis diikuti dalam bukunya. Meskipun karyanya berisi solusi untuk persamaan Diophantine tertentu, ada alasan untuk percaya bahwa ia juga akrab dengan beberapa metode umum.
Studi tentang ketidaksetaraan ini biasanya dikaitkan dengan kesulitan yang serius. Karena fakta bahwa mereka mengandung polinomial dengan koefisien bilangan bulat F (x, y1,…, y n). Atas dasar ini, ditarik kesimpulan bahwa tidak ada algoritma tunggal yang memungkinkan setiap x yang diberikan untuk menentukan apakah persamaan F (x, y 1 ,…., y n) terpenuhi. Situasi ini dapat diselesaikan untuk y 1 , …, y n . Contoh polinomial tersebut dapat dituliskan.
Pertidaksamaan paling sederhana
ax + by = 1, di mana a dan b relatif bilangan bulat dan bilangan prima, ada sejumlah besar eksekusi untuk itu (jika x 0, y 0 hasilnya terbentuk, maka pasangan variabel x = x 0 + b n dan y = y 0 -an , di mana n sembarang, juga akan dianggap memenuhi pertidaksamaan). Contoh lain dari persamaan Diophantine adalah x 2 + y 2 = z 2 . Solusi integral positif dari pertidaksamaan ini adalah panjang sisi kecil x, y dan segitiga siku-siku, serta sisi miring z dengan dimensi lateral bilangan bulat. Angka-angka ini dikenal sebagai bilangan Pythagoras. Semua kembar tiga sehubungan dengan variabel sederhana yang disebutkan di atas diberikan oleh rumus x=m 2 - n 2 , y = 2mn, z = m 2 + n 2 , di mana m dan n adalah bilangan bulat dan bilangan prima (m>n>0 ).

Diophantus, dalam Arithmetic-nya, mencari solusi rasional (tidak harus integral) dari tipe khusus ketidaksetaraannya. Sebuah teori umum untuk memecahkan persamaan diophantine tingkat pertama dikembangkan oleh C. G. Baschet pada abad ke-17. Ilmuwan lain di awal XIX abad, terutama mempelajari ketidaksetaraan seperti jenis ax 2 +bxy + cy 2 + dx +ey +f = 0, di mana a, b, c, d, e, dan f adalah umum, tidak homogen, dengan dua yang tidak diketahui dari tingkat dua. Lagrange menggunakan pecahan lanjutan dalam studinya. Gauss untuk bentuk kuadrat dikembangkan teori umum mendasari beberapa jenis solusi.
Dalam studi tentang ketidaksetaraan tingkat kedua ini, kemajuan signifikan hanya dibuat pada abad ke-20. A. Ditemukan bahwa persamaan Diophantine a 0 x n + a 1 x n-1 y +…+a n y n =c, di mana n≥3, a 0 ,…,a n ,c adalah bilangan bulat, dan a 0 t n + … + a n tidak dapat memiliki jumlah tak terbatas dari solusi bilangan bulat. Namun, metode Thue tidak dikembangkan dengan benar. A. Baker menciptakan teorema efektif yang memberikan perkiraan kinerja beberapa persamaan semacam ini. BN Delaunay mengusulkan metode investigasi lain yang dapat diterapkan pada kelas yang lebih sempit dari ketidaksetaraan ini. Secara khusus, bentuk ax 3 + y 3 = 1 dapat diselesaikan sepenuhnya dengan cara ini.
Persamaan Diophantine: Metode Solusi
Teori Diophantus memiliki banyak arah. Jadi, masalah yang terkenal dalam sistem ini adalah dugaan bahwa tidak ada solusi non-sepele untuk persamaan Diophantine x n + y n = z n jika n 3 (pertanyaan Fermat). Studi tentang pemenuhan bilangan bulat dari ketidaksetaraan adalah generalisasi alami dari masalah triplet Pythagoras. Euler memperoleh solusi positif dari masalah Fermat untuk n = 4. Berdasarkan hasil ini, ini mengacu pada bukti bilangan bulat yang hilang, studi bukan-nol dari persamaan jika n adalah bilangan prima ganjil.
Kajian mengenai keputusan tersebut belum selesai. Kesulitan dengan implementasinya terkait dengan fakta bahwa faktorisasi sederhana dalam ring bilangan bulat aljabar tidak unik. Teori pembagi dalam sistem ini untuk banyak kelas eksponen prima n memungkinkan untuk mengkonfirmasi validitas teorema Fermat. Lewat sini, metode yang ada dan metode, persamaan Diophantine linier dengan dua yang tidak diketahui terpenuhi.

Jenis dan jenis tugas yang dijelaskan
Aritmatika cincin bilangan bulat aljabar juga digunakan dalam banyak masalah dan solusi persamaan Diophantine lainnya. Misalnya, metode tersebut diterapkan ketika memenuhi pertidaksamaan bentuk N(a 1 x 1 +…+ a n x n) = m, di mana N(a) adalah norma dari a, dan x 1 , …, x n variabel rasional integral ditemukan . Kelas ini mencakup persamaan Pell x 2- dy 2 =1.
Nilai-nilai a 1, ..., a n yang muncul, persamaan ini dibagi menjadi dua jenis. Jenis pertama - yang disebut bentuk lengkap - termasuk persamaan di mana di antara a ada m bilangan bebas linier di atas bidang variabel rasional Q, di mana m = , di mana ada derajat eksponen aljabar Q (a1,…, a n) di atas Q. Spesies tidak lengkap adalah spesies yang jumlah maksimum a i kurang dari m.
Bentuk lengkapnya lebih sederhana, studinya selesai, dan semua solusi dapat dijelaskan. Tipe kedua - spesies yang tidak lengkap - lebih rumit, dan pengembangan teori semacam itu belum selesai. Persamaan tersebut dipelajari dengan menggunakan pendekatan Diophantine, yang mencakup pertidaksamaan F(x,y)=C, di mana F (x,y) - polinomial dengan derajat n≥3 tidak dapat direduksi, homogen. Dengan demikian, kita dapat mengasumsikan bahwa y i → . Dengan demikian, jika y i cukup besar, maka pertidaksamaan akan bertentangan dengan teorema Thue, Siegel dan Roth, dari mana dapat disimpulkan bahwa F(x,y)=C, di mana F adalah bentuk derajat ketiga atau lebih tinggi, tidak dapat direduksi memiliki jumlah solusi yang tak terbatas.
Contoh ini adalah kelas yang agak sempit di antara semuanya. Misalnya, meskipun sederhana, x 3 + y 3 + z 3 = N, serta x 2 + y 2 + z 2 + u 2 = N tidak termasuk dalam kelas ini. Studi tentang solusi adalah cabang persamaan Diophantine yang dipelajari dengan hati-hati, di mana basisnya adalah representasi dengan bentuk bilangan kuadrat. Lagrange menciptakan teorema yang mengatakan bahwa pemenuhan ada untuk semua N alami. Setiap bilangan asli dapat direpresentasikan sebagai jumlah dari tiga kuadrat (Teorema Gauss), tetapi tidak boleh dalam bentuk 4 a (8K-1), di mana a dan k adalah skor bilangan bulat non-negatif.
Solusi rasional atau integral dari sistem persamaan Diophantine tipe F (x 1 , …, x n) = a, di mana F (x 1 , …, x n) adalah bentuk kuadrat dengan koefisien bilangan bulat. Jadi, menurut teorema Minkowski-Hasse, pertidaksamaan a ij x i x j = b di mana a ij dan b rasional, memiliki solusi integral dalam bilangan real dan p-adik untuk setiap bilangan prima p hanya jika dapat diselesaikan dalam struktur ini .
Karena kesulitan yang melekat, studi angka dengan bentuk arbitrer dari tingkat ketiga dan di atas telah dipelajari pada tingkat yang lebih rendah. Metode eksekusi utama adalah metode penjumlahan trigonometri. Dalam hal ini, jumlah solusi persamaan ditulis secara eksplisit dalam integral Fourier. Setelah itu, metode lingkungan digunakan untuk menyatakan banyaknya pemenuhan pertidaksamaan dari kongruensi yang bersesuaian. Metode jumlah trigonometri tergantung pada fitur aljabar dari pertidaksamaan. Ada sejumlah besar metode dasar untuk memecahkan persamaan Diophantine linier.

Analisis diophantine
Cabang matematika, yang subjeknya adalah studi tentang solusi integral dan rasional dari sistem persamaan aljabar dengan metode geometri, dari bidang yang sama. Pada paruh kedua abad ke-19, munculnya teori bilangan ini mengarah pada studi persamaan Diophantine dari bidang arbitrer dengan koefisien, dan solusi dipertimbangkan baik di dalamnya atau di dalam cincinnya. Sistem fungsi aljabar dikembangkan secara paralel dengan angka. Analogi dasar antara keduanya, yang ditekankan oleh D. Hilbert dan, khususnya, L. Kronecker, menyebabkan konstruksi seragam berbagai konsep aritmatika, yang biasanya disebut global.
Hal ini terutama terlihat jika fungsi aljabar yang dipelajari pada bidang konstanta yang terbatas adalah satu variabel. Konsep seperti teori medan kelas, pembagi, dan percabangan dan hasil adalah ilustrasi yang baik dari hal di atas. Sudut pandang ini diadopsi dalam sistem ketidaksetaraan Diophantine hanya kemudian, dan penelitian sistematis tidak hanya dengan koefisien numerik, tetapi juga dengan koefisien yang merupakan fungsi, baru dimulai pada 1950-an. Salah satu faktor penentu dalam pendekatan ini adalah pengembangan geometri aljabar. Studi simultan bidang bilangan dan fungsi, yang muncul sebagai dua aspek yang sama pentingnya dari subjek yang sama, tidak hanya memberikan hasil yang elegan dan meyakinkan, tetapi juga mengarah pada pengayaan timbal balik dari kedua topik tersebut.
Dalam geometri aljabar, gagasan variasi digunakan untuk menggantikan himpunan pertidaksamaan non-invarian pada bidang K yang diberikan, dan solusinya digantikan oleh titik rasional dengan nilai dalam K atau dalam ekstensi terbatasnya. Oleh karena itu, seseorang dapat mengatakan bahwa masalah mendasar dari geometri Diophantine adalah mempelajari titik-titik rasional dari himpunan aljabar X(K), di mana X adalah bilangan-bilangan tertentu dalam bidang K. Eksekusi bilangan bulat memiliki pengertian geometris dalam persamaan Diophantine linier.
Studi dan Pilihan Ketimpangan
Dalam studi poin rasional (atau integral) pada varietas aljabar, masalah pertama muncul, yaitu keberadaannya. Masalah kesepuluh Hilbert dirumuskan sebagai masalah menemukan metode umum untuk memecahkan masalah ini. Dalam proses membuat definisi algoritma yang tepat, dan setelah terbukti bahwa eksekusi serupa untuk jumlah yang besar tugas tidak ada, masalahnya telah memperoleh hasil negatif yang jelas, dan sebagian besar pertanyaan menarik adalah definisi kelas persamaan Diophantine yang sistem di atas ada. Pendekatan yang paling alami, dari sudut pandang aljabar, adalah apa yang disebut prinsip Hasse: bidang awal K dipelajari bersama dengan penyelesaiannya K v untuk semua perkiraan yang mungkin. Karena X(K) = X(K v) adalah kondisi yang diperlukan untuk keberadaan, dan titik K memperhitungkan bahwa himpunan X(K v) tidak kosong untuk semua v.
Pentingnya terletak pada kenyataan bahwa ia menyatukan dua masalah. Yang kedua jauh lebih sederhana, dapat dipecahkan dengan algoritma yang dikenal. Dalam kasus tertentu di mana varietas X adalah proyektif, lemma Hansel dan generalisasinya memungkinkan reduksi lebih lanjut: masalahnya dapat direduksi menjadi studi titik-titik rasional di atas bidang terbatas. Dia kemudian memutuskan untuk membangun konsep, baik melalui penelitian yang konsisten atau metode yang lebih efisien.
Pertimbangan penting terakhir adalah bahwa himpunan X(Kv) tidak kosong untuk semua kecuali sejumlah terbatas v, sehingga jumlah kondisi selalu terbatas dan dapat diuji secara efektif. Namun, prinsip Hasse tidak berlaku untuk kurva derajat. Misalnya, 3x 3 + 4y 3 =5 memiliki titik di semua bidang bilangan p-adik dan dalam sistem tetapi tidak memiliki titik rasional.
Metode ini berfungsi sebagai titik awal untuk membangun konsep yang menggambarkan kelas ruang homogen utama varietas Abelian untuk melakukan "penyimpangan" dari prinsip Hasse. Ini dijelaskan dalam kerangka struktur khusus yang dapat dikaitkan dengan masing-masing manifold (kelompok Tate-Shafarevich). Kesulitan utama dari teori ini terletak pada kenyataan bahwa metode untuk menghitung kelompok sulit diperoleh. Konsep ini juga telah diperluas ke kelas lain dari varietas aljabar.

Cari algoritma untuk memenuhi ketidaksetaraan
Ide heuristik lain yang digunakan dalam studi persamaan Diophantine adalah bahwa jika jumlah variabel yang terlibat dalam himpunan pertidaksamaan besar, maka sistem biasanya memiliki solusi. Namun, ini sangat sulit dibuktikan untuk kasus tertentu. Pendekatan umum untuk masalah jenis ini menggunakan teori bilangan analitik dan didasarkan pada perkiraan untuk jumlah trigonometri. Metode ini awalnya diterapkan pada jenis persamaan khusus.
Namun, kemudian dibuktikan dengan bantuannya bahwa jika bentuk derajat ganjil adalah F, dalam variabel d dan n dan dengan koefisien rasional, maka n cukup besar dibandingkan dengan d, sehingga hipersurface proyektif F = 0 memiliki titik rasional Menurut Artin dugaan, hasil ini benar bahkan jika n > d 2 . Ini hanya terbukti untuk bentuk kuadrat. Masalah serupa dapat ditanyakan untuk bidang lain juga. Masalah utama geometri Diophantine adalah struktur himpunan bilangan bulat atau titik rasional dan studinya, dan pertanyaan pertama yang harus diklarifikasi adalah apakah himpunan ini berhingga. Dalam masalah ini, situasi biasanya memiliki jumlah eksekusi yang terbatas jika derajat sistem jauh lebih besar daripada jumlah variabel. Ini adalah asumsi utama.
Pertidaksamaan pada garis dan kurva
Grup X(K) dapat direpresentasikan sebagai jumlah langsung dari struktur bebas pangkat r dan grup berhingga orde n. Sejak tahun 1930-an, pertanyaan apakah bilangan-bilangan ini terbatas pada himpunan semua kurva eliptik pada bidang tertentu K telah dipelajari.Keterbatasan torsi n ditunjukkan pada tahun tujuh puluhan. Ada kurva peringkat tinggi sewenang-wenang dalam kasus fungsional. Dalam kasus numerik, masih belum ada jawaban untuk pertanyaan ini.
Akhirnya, dugaan Mordell menyatakan bahwa jumlah titik integral adalah terbatas untuk kurva genus g>1. Secara fungsional, konsep ini didemonstrasikan oleh Yu.I. Manin pada tahun 1963. Alat utama yang digunakan dalam membuktikan teorema finiteness dalam geometri Diophantine adalah ketinggian. Dari varietas aljabar berdimensi lebih besar dari satu, varietas Abelian, yang merupakan analog multidimensi dari kurva eliptik, telah dipelajari paling menyeluruh.
A. Weyl menggeneralisasi teorema tentang keterbatasan jumlah generator dari kelompok titik rasional ke varietas Abelian dari dimensi apa pun (konsep Mordell-Weil), memperluasnya. Pada 1960-an, dugaan Birch dan Swinnerton-Dyer muncul, meningkatkan ini dan fungsi grup dan zeta dari manifold. Bukti numerik mendukung hipotesis ini.

Masalah decidability
Masalahnya adalah menemukan algoritma yang dapat digunakan untuk menentukan apakah persamaan Diophantine memiliki solusi. Fitur penting dari masalah yang diajukan adalah pencarian metode universal yang cocok untuk setiap ketidaksetaraan. Metode seperti itu juga akan memungkinkan penyelesaian sistem di atas, karena setara dengan P21+⋯+P2k=0.p1= 0 , ... , PK= 0p = 0,...,pK = 0 atau p21+ + P2K= 0 . n12+⋯+pK2=0. Masalah menemukan cara universal untuk menemukan solusi untuk ketidaksetaraan linier dalam bilangan bulat ditempatkan oleh D. Gilbert.
Pada awal 1950-an, studi pertama muncul bertujuan untuk membuktikan tidak adanya algoritma untuk memecahkan persamaan Diophantine. Pada saat ini, dugaan Davis muncul, yang mengatakan bahwa setiap himpunan enumerable juga milik ilmuwan Yunani. Karena contoh himpunan yang tidak dapat diputuskan secara algoritmik diketahui, tetapi dapat dihitung secara rekursif. Oleh karena itu dugaan Davis benar dan masalah solvabilitas persamaan ini memiliki pemenuhan negatif.
Setelah itu, untuk dugaan Davis, masih harus dibuktikan bahwa ada metode untuk mengubah pertidaksamaan yang juga (atau tidak) pada saat yang sama memiliki solusi. Ditunjukkan bahwa perubahan persamaan Diophantine seperti itu dimungkinkan jika memiliki dua sifat yang ditunjukkan: 1) dalam setiap larutan jenis ini v≤uu; 2) untuk apa saja k ada eksekusi di mana ada pertumbuhan eksponensial.

Contoh persamaan linear Diophantine kelas ini melengkapi pembuktiannya. Masalah keberadaan algoritma untuk solvabilitas dan pengenalan ketidaksetaraan ini dalam bilangan rasional masih dianggap sebagai pertanyaan penting dan terbuka yang belum dipelajari secara memadai.