Класифікація подій на можливі, ймовірні та випадкові. Поняття простої та складної елементарної події. Операції над подіями. Класичне визначення ймовірності випадкової події та її властивості. Елементи комбінаторики теоретично ймовірностей. Геометрична можливість. Аксіоми теорії ймовірностей.

Одним із основних понять теорії ймовірностей є поняття події. Під подією розуміють будь-який факт, який може статися внаслідок досвіду чи випробування. Під досвідом , або випробуванням , Зрозуміло здійснення певного комплексу умов.

Приклади подій:

• - Потрапляння в ціль при пострілі з зброї (досвід - добуток пострілу; подія - попадання в ціль);
• - випадання двох гербів при триразовому киданні монети (досвід - триразове кидання монети; подія - випадання двох гербів);
• - Поява помилки виміру в заданих межах при вимірі дальності до мети (досвід - вимір дальності; подія - помилка виміру).

Можна навести безліч подібних прикладів. Події позначаються великими літерами латинського алфавіту A, B, C тощо.

Розрізняють події спільні і несумісні . Події називаються спільними, якщо наступ однієї з них виключає наступу іншого. Інакше події називаються несумісними. Наприклад, підкидаються дві гральні кістки. Подія AA - випадання трьох очок на першій гральній кістці, подія B - випадання трьох очок на другій кістці. A і В - спільні події.

Нехай до магазину надійшла партія взуття одного фасону та розміру, але різного кольору. Подія A - навмання взята коробка виявиться із взуттям чорного кольору, подія B - коробка виявиться із взуттям коричневого кольору, A і B - несумісні події.

Подія називається достовірним якщо воно обов'язково відбудеться в умовах даного досвіду.

Подія називається неможливим, якщо вона може статися за умов даного досвіду. Наприклад, подія, що полягає в тому, що з партії стандартних деталей буде взято стандартну деталь, є достовірною, а нестандартна - неможливою.

Подія називається можливим , або випадковим якщо в результаті досвіду воно може з'явитися, але може і не з'явитися. Прикладом випадкової події може бути виявлення дефектів вироби під час контролю партії готової продукції, невідповідність розміру оброблюваного вироби заданому, відмова однієї з ланок автоматизованої системи управління.

Події називаються рівноможливими , якщо за умовами випробування жодна з цих подій не є більш можливим, ніж інші. Наприклад, нехай магазину постачають електролампочки (причому в рівних кількостях) кілька заводів-виробників. Події, які перебувають у купівлі лампочки будь-якого з цих заводів, можливі.

Важливим поняттям є повна група подій . Декілька подій у цьому досвіді утворюють повну групу, якщо в результаті досвіду обов'язково з'явиться хоча б одне з них. Наприклад, в урні знаходиться десять куль, з них шість куль червоних, чотири білі, причому п'ять куль мають номери.

A - поява червоної кулі при одному витягу,

B - поява білої кулі,

C – поява кулі з номером. Події A,B,C утворюють повну групу спільних подій.

Введемо поняття протилежної, або додаткової, події. Під протилежним подією

AЇ розуміється подія, яка обов'язково має відбутися, якщо не настала деяка подія

A. Протилежні події несумісні та єдино можливі. Вони утворюють повну групу подій.

План.

1. Випадкова величина (СВ) та ймовірність події.

2. Закон розподілу СВ.

3. Біноміальний розподіл (розподіл Бернуллі).

4. Розподіл Пуассона.

5. Нормальний (гауссівський) розподіл.

6. Рівномірний розподіл.

7. Розподіл Стьюдента.

2.1 Випадкова величина та ймовірність події

Математична статистика тісно пов'язана з іншою математичною наукою – теорією ймовірності та базується на її математичному апараті.

Теорія ймовірності - Це наука, яка вивчає закономірності, породжені випадковими подіями.

Педагогічні явища ставляться до масових: вони охоплюють великі сукупності людей, повторюються рік у рік, відбуваються безперервно. Показники (параметри, результати) педагогічного процесу мають імовірнісний характер: той самий педагогічний вплив може призводити до різних наслідків (випадкові події, випадкових величин). Проте, при багаторазовому відтворенні умов певні наслідки з'являються найчастіше, - і є прояв про статистичних закономірностей (вивченням яких займаються теорія ймовірностей і математична статистика).

Випадкова величина (СВ) - Це чисельна характеристика, що вимірюється по ходу досвіду і залежить від випадкового результату. СВ реалізована під час досвіду і сама є випадковою. Кожна СВ визначає розподіл ймовірностей.

Основною властивістю педагогічних процесів, явищ служить їхній імовірнісний характер (за цих умов вони можуть статися, реалізуватися, але можуть і не відбутися). Для таких явищ істотну роль грає поняття ймовірності.

Імовірність (Р) показує ступінь можливості здійснення цієї події, явища, результату. Імовірність неможливої ​​події дорівнює нулю p = 0, достовірного – одиниці p = 1 (100%). Імовірність будь-якої події лежить у межах від 0 до 1, залежно від того, наскільки ця подія є випадковою.

Якщо ми цікавимося подією A, то, швидше за все, можемо спостерігати фіксувати факти його появи. Потреба у понятті ймовірності та її обчислення виникне, зрозуміло, лише тоді, коли ми спостерігаємо цю подію щоразу, або усвідомлюємо, що може статися, і може статися. І в тому й іншому випадку корисно використовувати поняття частоти появи події f(A) - як відношення числа випадків його появи (сприятливих наслідків) до загального числа спостережень. Частота настання випадкової події залежить не тільки від ступеня випадковості самої події, а й від числа (кількості) спостережень за цією СВ.

Існує два види вибірок СВ: залежніі незалежні. Якщо результати вимірювання певної якості об'єктів першої вибірки не впливають на результати вимірювання цієї властивості об'єктів другої вибірки, такі вибірки вважаються незалежними. У тих випадках, коли результати однієї вибірки впливають на результати іншої вибірки, вибірки вважають залежними. Класичний спосіб отримання залежних вимірів – це дворазове вимір однієї й тієї ж властивості (чи різних властивостей) в членів однієї й тієї групи.

Подія А не залежить від події, якщо ймовірність події А не залежить від того сталася чи ні подія В. Події А і В незалежні, якщо Р(АВ)=Р(А)Р(В). Насправді незалежність події встановлюється з умов досвіду, інтуїції дослідника і практики.

СВ буває дискретною (ми можемо пронумерувати її можливі значення), наприклад, випадання гральної кістки = 4, 6, 2 і безперервної (її функція розподілу F(x) – безперервна), наприклад, час служби лампочки.

Математичне очікування – числова характеристика СВ, приблизно дорівнює середньому значенню СВ:

M(x)=x 1 p 1 +x 2 p 2 +…+x n p n

2.2 Закон розподілу СВ

Чи підпорядковуються будь-яким законам явища, що мають випадковий характер? Так, але ці закони відрізняються від звичних для нас фізичних законів. Значення СВ неможливо передбачити навіть за відомих умов експерименту, ми можемо лише вказати ймовірність того, що СВ прийме те чи інше значення. Зате знаючи розподіл ймовірностей СВ, ми можемо робити висновки про події, у яких беруть участь ці випадкові величини. Щоправда, ці висновки також носитимуть імовірнісний характер.

Нехай деяка СВ дискретна, тобто. може приймати лише фіксовані значення X i. І тут ряд значень ймовірностей P(X i) всім (i=1…n) допустимих значень цієї величини називають її законом розподілу.

Закон розподілу СВ – це відношення, що встановлює зв'язок між можливими значеннями СВ та ймовірностями, з якими приймаються ці значення. Закон розподілу повністю характеризує СВ.

При побудові математичної моделі для перевірки статистичної гіпотези необхідно запровадити математичне припущення закон розподілу СВ (параметричний шлях побудови моделі).

Непараметричний підхід до опису математичної моделі (СВ не має параметричного закону розподілу) менш точний, але має більш широку сферу застосування.

Так само, як і для ймовірності випадкової події, для закону розподілу СВ є лише два шляхи його відшукання. Або ми будуємо схему випадкової події і знаходимо аналітичний вираз (формулу) обчислення ймовірності (можливо, хтось вже зробив або зробить це до вас!), або доведеться використовувати експеримент і за частотами спостережень робити якісь припущення (висувати гіпотези) про закон розподілу.

Звичайно ж, для кожного з "класичних" розподілів вже давно ця робота зроблена – широко відомими і дуже часто використовуваними в прикладній статистиці є біноміальний та поліноміальний розподіл, геометричний та гіпергеометричний, розподіл Паскаля та Пуассона та багато інших.

Багато класичних розподілів негайно будувалися і публікувалися спеціальні статистичні таблиці, уточнювані зі збільшенням точності розрахунків. Без використання багатьох томів цих таблиць, без навчання правилам користування ними останніх два століття практичне використання статистики було неможливо.

Сьогодні становище змінилося – немає потреби зберігати дані розрахунків за формулами (як би останні не були складними!), час на використання закону розподілу для практики зведено до хвилин, а то й секунд. Вже зараз існує достатньо різноманітних пакетів прикладних комп'ютерних програм для цих цілей.

Серед усіх ймовірнісних розподілів є такі, що використовуються практично особливо часто. Ці розподіли детально вивчені та властивості їх добре відомі. Багато з цих розподілів лежать в основі цілих областей знань – таких як теорія масового обслуговування, теорія надійності, контроль якості, теорія ігор тощо.

2.3 Біноміальний розподіл (розподіл Бернуллі)

Виникає в тих випадках, коли ставиться питання: скільки разів відбувається певна подія в серії з певної кількості незалежних спостережень (дослідів), що виконуються в однакових умовах.

Для зручності і наочності будемо вважати, що нам відома величина p - ймовірність того, що відвідувач, що увійшов до магазину, виявиться покупцем і (1 - p) = q - ймовірність того, що відвідувач, що увійшов до магазину, не виявиться покупцем.

Якщо X - число покупців із загальної кількості n відвідувачів, то ймовірність того, що серед n відвідувачів виявилося k покупців дорівнює

P(X= k) = де k=0,1,…n (1)

Формулу (1) називають формулою Бернуллі. При великій кількості випробувань биномиальное розподіл йти до нормальному.

2.4 Розподіл Пуассона

Відіграє важливу роль у низці питань фізики, теорії зв'язку, теорії надійності, теорії масового обслуговування тощо. Усюди, де протягом певного часу може відбуватися випадкова кількість якихось подій (радіоактивних розпадів, телефонних викликів, відмов обладнання, нещасних випадках тощо).

Розглянемо найбільш типову ситуацію, де виникає розподіл Пуассона. Нехай деякі події (покупки у магазині) можуть відбуватися у випадкові моменти часу. Визначимо кількість появ таких подій у проміжку часу від 0 до Т.

Випадкове число подій, що відбулися за час від 0 до Т, розподілено за законом Пуассона з параметром l = АТ, де а> 0 - параметр завдання, що відображає середню частоту подій. Імовірність k покупок протягом великого інтервалу часу (наприклад, – дня) становитиме

P(Z=k) =

(2)

2.5 Нормальний (гауссівський) розподіл

Нормальний (гауссівський) розподіл займає центральне місце в теорії та практиці імовірнісно-статистичних досліджень. Як безперервну апроксимацію до біноміального розподілу його вперше розглядав А.Муавр в 1733 р. Через деякий час нормальний розподіл знову відкрили і вивчили К.Гаусс (1809 р.) і П.Лаплас, які прийшли до нормальної функції у зв'язку з роботою з теорії помилок спостережень.

Безперервна випадкова величина Хназивається розподіленою за нормальним закономякщо її щільність розподілу дорівнює

де

збігається з математичним очікуванням величини Х:
=М(Х), параметр s збігається із середнім квадратичним відхиленням величини Х: s =s(Х). Графік функції нормального розподілу, як видно з малюнка, має вигляд куполоподібної кривої, яка називається Гауссовою, точка максимуму має координати (а;

Ця крива при μ=0, σ=1 набула статусу стандарту, її називають одиничною нормальною кривою, тобто будь-які зібрані дані прагнуть перетворити так, щоб крива їх розподілу була максимально близька до цієї стандартної кривої.

Нормалізовану криву винайшли на вирішення завдань теорії ймовірності, але виявилося практично, що вона добре апроксимує розподіл частот при великому числі спостережень для безлічі змінних. Можна припустити, що не маючи матеріальних обмежень на кількість об'єктів та час проведення експерименту, статистичне дослідження наводиться до нормальної кривої.

2.6 Рівномірний розподіл

Поступово розподіл ймовірностей є найпростішим і може бути як дискретним, так і безперервним. Дискретний рівномірний розподіл – це такий розподіл, для якого ймовірність кожного зі значень СВ одна й та сама, тобто:

де N - кількість можливих значень СВ.

Розподіл ймовірностей безперервної CВ Х, що приймають всі свої значення з відрізка [а;

(5)

2.7 Розподіл Стьюдента

Цей розподіл пов'язаний із нормальним. Якщо СВ x 1 , x 2 , … x n – незалежні, і кожна з них має стандартний нормальний розподіл N(0,1), то СВ має розподіл, що називається розподілом Стьюдента:

Багато хто, зіткнувшись з поняттям «теорія ймовірності», лякається, думаючи, що це непосильне, дуже складне. Але все насправді не таке трагічно. Сьогодні ми розглянемо основне поняття теорії ймовірності, навчимося вирішувати завдання на конкретних прикладах.

Наука

Що ж вивчає такий розділ математики, як теорія ймовірності? Вона відзначає закономірності та величин. Вперше цим питанням зацікавилися вчені ще у вісімнадцятому столітті, коли вивчали азартні ігри. Основне поняття теорії ймовірності – подія. Це будь-який факт, який констатується досвідом чи спостереженням. Але що таке досвід? Ще одне основне поняття теорії ймовірності. Воно означає, що це склад обставин створено невипадково, і з певною метою. Щодо спостереження, то тут дослідник сам не бере участі в досвіді, а просто є свідком цих подій, він ніяк не впливає на те, що відбувається.

Події

Ми дізналися, що основне поняття теорії ймовірності – це подія, але не розглянули класифікацію. Усі вони поділяються на такі категорії:

• Достовірні.
• Неможливі.
• Випадкові.

Незалежно від того, які це події, за якими спостерігають або створюють у ході досвіду, всі вони схильні до даної класифікації. Пропонуємо з кожним із видів познайомитися окремо.

Достовірна подія

Це така обставина, перед якою зроблено необхідний комплекс заходів. Для того, щоб краще вникнути в суть, краще навести кілька прикладів. Цьому закону підпорядковані і фізика, і хімія, і економіка, і математика. Теорія ймовірності включає таке важливе поняття як достовірне подія. Наведемо приклади:

• Ми працюємо та отримуємо винагороду у вигляді заробітної плати.
• Здали добре іспити, пройшли конкурс, за це отримуємо винагороду у вигляді вступу до навчального закладу.
• Ми вклали гроші в банк, за необхідності отримаємо їх назад.

Такі події є достовірними. Якщо ми виконали всі необхідні умови, обов'язково отримаємо очікуваний результат.

Неможливі події

Наразі ми розглядаємо елементи теорії ймовірності. Пропонуємо перейти до пояснення наступного виду події, а саме неможливого. Для початку обмовимо найважливіше правило – ймовірність неможливої ​​події дорівнює нулю.

Від цього формулювання не можна відступати під час вирішення завдань. Для пояснення наведемо приклади таких подій:

• Вода стала при температурі плюс десять (це неможливо).
• Відсутність електроенергії ніяк не впливає на виробництво (так само неможливо, як і в попередньому прикладі).

Більше прикладів наводити не варто, тому що описані вище дуже яскраво відображають суть цієї категорії. Неможлива подія ніколи не станеться під час досвіду за жодних обставин.

Випадкові події

Вивчаючи елементи особливу увагу варто приділити саме цьому виду події. Саме їх і вивчає ця наука. В результаті досвіду може щось статися чи ні. Крім цього, випробування може проводитися необмежену кількість разів. Яскравими прикладами можуть бути:

• Кидок монети – це досвід, або випробування, випадання орла – це подія.
• Витягування м'ячика з мішка наосліп - випробування, попалася червона куля - це подія і таке інше.

Таких прикладів може бути необмежену кількість, але, загалом, суть має бути зрозумілою. Для узагальнення та систематизування отриманих знань про події наведено таблицю. Теорія ймовірності вивчає лише останній вид із усіх представлених.

Закони

Теорія ймовірності - це наука, що вивчає можливість випадання будь-якої події. Як і інші, вона має певні правила. Існують такі закони теорії ймовірності:

• Схожість послідовностей випадкових величин.
• Закон великих чисел.

При розрахунку можливості складного можна використовувати комплекс простих подій для досягнення результату більш легким та швидким шляхом. Зазначимо, закони теорії ймовірності легко доводяться з допомогою деяких теорем. Пропонуємо спочатку познайомитися з першим законом.

Схожість послідовностей випадкових величин

Відзначимо, що видів збіжності кілька:

• Послідовність випадкових величин схожа на ймовірність.
• Майже неможливе.
• Середньоквадратична збіжність.
• Збіжність із розподілу.

Так, з льоту дуже важко вникнути в суть. Наведемо визначення, які допоможуть розібратися у цій темі. Спочатку перший вид. Послідовність називають схожій ймовірно, якщо дотримано така умова: n прагне нескінченності, число, якого прагне послідовність, більше нуля і наближена до одиниці.

Переходимо до наступного виду, майже напевно. Говорять, що послідовність сходиться майже напевнодо випадкової величини при n, що прагне нескінченності, і Р, що прагне величини, наближеної до одиниці.

Наступний тип - це збіжність середньоквадратична. З використанням СК-сходимости вивчення векторних випадкових процесів зводиться до вивчення їх координатних випадкових процесів.

Залишився останній тип, давайте розберемо коротко і його, щоб переходити безпосередньо до вирішення завдань. Збіжність за розподілом має ще одну назву - «слабке», далі пояснимо, чому. Слабка збіжність- Це збіжність функцій розподілу у всіх точках безперервності граничної функції розподілу.

Обов'язково виконаємо обіцянку: слабка збіжність відрізняється від усіх перелічених вище тим, що випадкова величина не визначена на ймовірнісному просторі. Це можливо тому, що умова формується виключно за допомогою функцій розподілу.

Закон великих чисел

Відмінними помічниками при доведенні цього закону стануть теореми теорії ймовірності, такі як:

• Нерівність Чебишева.
• Теорема Чебишева.
• Узагальнена теорема Чебишева.
• Теорема Маркова.

Якщо будемо розглядати всі ці теореми, то це питання може затягнутися на кілька десятків аркушів. А в нас основне завдання - це застосування теорії ймовірності на практиці. Пропонуємо вам зараз цим і зайнятися. Але перед цим розглянемо аксіоми теорії ймовірностей, вони будуть основними помічниками під час вирішення завдань.

Аксіоми

З першою ми вже познайомилися, коли говорили про неможливу подію. Давайте згадувати: ймовірність неможливої ​​події дорівнює нулю. Приклад ми наводили дуже яскравий і незабутній: випав сніг при температурі повітря тридцять градусів за Цельсієм.

Друга звучить так: достовірна подія відбувається з ймовірністю, що дорівнює одиниці. Тепер покажемо, як це записати з допомогою математичної мови: Р(В)=1.

Третя: Випадкова подія може статися чи ні, але можливість завжди варіюється в межах від нуля до одиниці. Чим ближче значення до одиниці, тим більше шансів; якщо значення наближається до нуля, можливість дуже мала. Запишемо це математичною мовою: 0<Р(С)<1.

Розглянемо останню, четверту аксіому, яка звучить так: ймовірність суми двох подій дорівнює сумі ймовірностей. Записуємо математичною мовою: Р (А + В) = Р (А) + Р (В).

Аксіоми теорії ймовірностей - це найпростіші правила, які не важко запам'ятати. Спробуймо вирішити деякі завдання, спираючись на вже отримані знання.

Лотерейний квиток

Для початку розглянемо найпростіший приклад – лотерея. Уявіть, що ви придбали один лотерейний квиток на удачу. Яка ймовірність, що ви виграєте щонайменше двадцять рублів? Загалом у тиражі бере участь тисяча квитків, один із яких має приз у п'ятсот рублів, десять по сто рублів, п'ятдесят по двадцять рублів, а сто – по п'ять. Завдання з теорії ймовірності засновані на тому, щоб знайти можливість удачі. Зараз разом розберемо рішення вище за представлене завдання.

Якщо ми буквою А позначимо виграш у п'ятсот рублів, то ймовірність випадання А дорівнюватиме 0,001. Як ми це здобули? Просто необхідно кількість "щасливих" квитків розділити на їх загальне число (в даному випадку: 1/1000).

В - це виграш у сто рублів, ймовірність дорівнюватиме 0,01. Зараз ми діяли за тим же принципом, що й у минулому (10/1000)

С – виграш дорівнює двадцяти рублям. Знаходимо можливість, вона дорівнює 0,05.

Інші квитки нас не цікавлять, тому що їхній призовий фонд менший за заданий за умови. Застосуємо четверту аксіому: Ймовірність виграти щонайменше двадцяти рублів становить Р(А)+Р(В)+Р(С). Буквою Р позначається ймовірність походження цієї події, ми в попередніх діях вже їх знайшли. Залишилося лише скласти необхідні дані, у відповіді ми отримуємо 0,061. Це і буде відповіддю питання завдання.

Карткова колода

Завдання з теорії ймовірності бувають і складнішими, наприклад візьмемо наступне завдання. Перед вами колода із тридцяти шести карт. Ваше завдання - витягнути дві карти поспіль, не перемішуючи стос, перша та друга карти повинні бути тузами, масть значення не має.

Для початку знайдемо можливість, що перша карта буде тузом, для цього чотири ділимо на тридцять шість. Відклали його убік. Дістаємо другу карту, це буде туз із ймовірністю три тридцять п'ятих. Імовірність другої події залежить від того, яку карту ми витягли першою, нам цікаво, був це туз чи ні. З цього випливає, що подія залежить від події А.

Наступною дією знаходимо ймовірність одночасного здійснення, тобто перемножуємо А і В. Їх твір перебуває таким чином: ймовірність однієї події множимо на умовну ймовірність іншої, яку ми обчислюємо, припускаючи, що перша подія відбулася, тобто першою картою ми витягли туз.

Щоб стало зрозуміло, дамо позначення такому елементу, як події. Обчислюється вона, припускаючи, що А сталося. Розраховується так: Р(В/А).

Продовжимо розв'язання нашого завдання: Р(А*В)=Р(А)*Р(В/А) або Р(А*В)=Р(В)*Р(А/В). Імовірність дорівнює (4/36) * ((3/35)/(4/36). Обчислюємо, округляючи до сотих. Ми маємо: 0,11 * (0,09/0,11) = 0,11 * 0, 82 = 0,09 Імовірність того, що ми витягнемо два тузи поспіль, дорівнює дев'яти сотим.

Забутий номер

Пропонуємо розібрати ще кілька варіантів завдань, які вивчає теорія ймовірності. Приклади вирішення деяких з них ви вже бачили в даній статті, спробуємо вирішити таке завдання: хлопчик забув останню цифру номера свого друга, але оскільки дзвінок був дуже важливий, то почав набирати все по черзі. Нам необхідно обчислити ймовірність того, що він зателефонує трохи більше трьох разів. Розв'язання задачі найпростіше, якщо відомі правила, закони та аксіоми теорії ймовірності.

Перед тим, як дивитися рішення, спробуйте вирішити самостійно. Нам відомо, що остання цифра може бути від нуля до дев'яти, тобто лише десять значень. Можливість набрати необхідну становить 1/10.

Далі нам потрібно розглядати варіанти походження події, припустимо, що хлопчик вгадав і одразу набрав потрібну, ймовірність такої події дорівнює 1/10. Другий варіант: перший дзвінок промах, а другий - ціль. Розрахуємо можливість такої події: 9/10 множимо на 1/9, в результаті отримуємо також 1/10. Третій варіант: перший і другий дзвінок виявилися не за адресою, тільки з третього хлопчик потрапив туди, куди хотів. Обчислюємо можливість такої події: 9/10 множимо на 8/9 і на 1/8, отримуємо в результаті 1/10. Інші варіанти за умовою завдання нас не цікавлять, тому нам залишилося скласти отримані результати, в результаті ми маємо 3/10. Відповідь: ймовірність того, що хлопчик зателефонує трохи більше трьох разів, дорівнює 0,3.

Картки з числами

Перед вами дев'ять карток, кожної з яких написано число від однієї до дев'яти, цифри не повторюються. Їх поклали в коробку та ретельно перемішали. Вам необхідно розрахувати ймовірність того, що

• випаде парне число;
• двоцифрове.

Перед тим як переходити до рішення, зауважимо, що m – це кількість вдалих випадків, а n – це загальна кількість варіантів. Знайдемо ймовірність того, що число буде парним. Не важко порахувати, що парних чисел чотири, це буде наша m, всього можливо дев'ять варіантів, тобто m=9. Тоді ймовірність дорівнює 0,44 чи 4/9.

Розглядаємо другий випадок: кількість варіантів дев'ять, а вдалих результатів взагалі бути не може, тобто m дорівнює нулю. Імовірність того, що витягнута картка міститиме двозначне число, так само дорівнює нулю.

ймовірність подія комбінаторика статистика

Теорія ймовірностей – це розділ математики, що вивчає моделі випадкових явищ. Випадковими явищами називаються явища з невизначеним результатом, що відбуваються при неодноразовому відтворенні певного комплексу умов. Становлення та розвитку теорії ймовірностей пов'язані з іменами таких великих учених, як: Кардано, Паскаль, Ферма, Бернуллі, Гаусса, Чебишева, Калмогорова та інших. Закономірності випадкових явищ вперше було виявлено в16 - 17 ст. на прикладі азартних ігор, подібних до гри в кістки. Дуже давно відомі також закономірності народження і смерті. Наприклад, відомо, що можливість новонародженому бути хлопчиком? 0,515. У 19-20 ст. було відкрито велику кількість закономірностей у фізиці, хімії, біології і т. д. В даний час методи теорії ймовірностей широко застосовуються в різних галузях природознавства та техніки: в теорії надійності, теорії масового обслуговування, в теоретичній фізиці, геодезії, астрономії, теорії стрільби, теорії помилок спостережень, теорії автоматичного управління, загальної теорії зв'язку та у багатьох інших теоретичних та прикладних науках. Теорія ймовірностей служить також для обґрунтування математичної та прикладної статистики, яка у свою чергу використовується при плануванні та організації виробництва, при аналізі технологічних процесів, запобіжному та приймальному контролі якості продукції та для багатьох інших цілей. В останні роки методи теорії ймовірностей все ширше і ширше проникають у різні галузі науки і техніки, сприяючи їхньому прогресу.

Випробування. Подія. Класифікація подій

Випробування - це багаторазове відтворення однієї й тієї ж комплексу умов, у якому проводиться спостереження. Якісний результат випробування – подія. Приклад 1: У скриньці є кольорові кулі. Зі урни на удачу беруть одну кулю. Випробування - вилучення кулі з урни; Подія – поява кулі певного кольору. О. 2: Багато взаємовиключних результатів одного випробування називається безліччю елементарних подій або елементарних результатів. Приклад 2: Гральна кістка підкидається один раз. Випробування – підкидання кістки; Подія - випадання певної кількості очок. Багато елементарних результатів - (1,2,3,4,5,6). Події позначаються великими літерами латинського алфавіту: А 1, А 2 ,…,А,В,С,… Події (явлення), що спостерігаються, можна поділити на наступні три види: достовірні, неможливі, випадкові. О. 3: Подія називається достовірною, якщо в результаті випробування вона обов'язково відбудеться. О. 4: Подія називається неможливою, якщо в результаті випробування вона ніколи не станеться. О. 5: Подія називається випадковою, якщо в результаті випробування вона може або відбутися або не відбутися. Приклад 3: Випробування – м'яч підкидається вгору. Подія A = (м'яч впаде) – достовірна; Подія B=(м'яч зависне у повітрі) - неможлива; Подія C=(м'яч впаде на голову, що кидав) - випадкова. Випадкові події (яви) можна поділити на такі види: спільні, несумісні, протилежні, рівноможливі. О. 6: Дві події називаються спільними, якщо при одному випробуванні поява одного з них не виключає поява іншого. О. 7: Дві події називаються несумісними, якщо при одному випробуванні поява одного з них виключає появу іншого. Приклад 4: Монета підкидається двічі. Подія A - (Вперше випав герб); Подія B - (Вдруге випав герб); Подія C - (Вперше випав орел). Події A та B – спільні, A та C – несумісні. О. 8: Декілька подій утворюють повну групу в даному випробуванні, якщо вони попарно несумісні і в результаті випробування одна з цих подій обов'язково з'явиться. Приклад 5: Хлопчик кидає монету в гральний автомат. Подія A = (хлопчик виграє); Подія B = (хлопчик не виграє); A та B - утворюють повну групу подій. О. 9: Дві несумісні події, що утворюють повну групу, називаються протилежними. Подія протилежна до події A позначається. Приклад 6. Робиться один постріл з мішені. Подія A – влучення; Подія – промах.

Класифікація подій на можливі, ймовірні та випадкові. Поняття простої та складної елементарної події. Операції над подіями. Класичне визначення ймовірності випадкової події та її властивості. Елементи комбінаторики теоретично ймовірностей. Геометрична можливість. Аксіоми теорії ймовірностей.

Класифікація подій

Одним із основних понять теорії ймовірностей є поняття події. Під подієюрозуміють будь-який факт, який може статися внаслідок досвіду чи випробування. Під досвідом, або випробуванням, Зрозуміло здійснення певного комплексу умов.

Приклади подій:

- Потрапляння в ціль при пострілі з зброї (досвід - добуток пострілу; подія - попадання в ціль);
- Випадання двох гербів при триразовому киданні монети (досвід - триразове кидання монети; подія - випадання двох гербів);
- Поява помилки вимірювання в заданих межах при вимірюванні дальності до мети (досвід - вимірювання дальності; подія - помилка вимірювання).

Можна навести безліч подібних прикладів. Події позначаються великими літерами латинського алфавіту тощо.

Розрізняють події спільніі несумісні. Події називаються спільними, якщо наступ однієї з них виключає наступу іншого. Інакше події називаються несумісними. Наприклад, підкидаються дві гральні кістки. Подія - випадання трьох очок на першій гральній кістці, подія - випадання трьох очок на другій кістці. та - спільні події. Нехай до магазину надійшла партія взуття одного фасону та розміру, але різного кольору. Подія - навмання взята коробка опиниться із взуттям чорного кольору, подія - коробка опиниться із взуттям коричневого кольору, та - несумісні події.

Подія називається достовірнимякщо воно обов'язково відбудеться в умовах даного досвіду.

Подія називається неможливим, якщо вона може статися за умов даного досвіду. Наприклад, подія, що полягає в тому, що з партії стандартних деталей буде взято стандартну деталь, є достовірною, а нестандартна - неможливою.

Подія називається можливим, або випадковимякщо в результаті досвіду воно може з'явитися, але може і не з'явитися. Прикладом випадкової події може бути виявлення дефектів вироби під час контролю партії готової продукції, невідповідність розміру оброблюваного вироби заданому, відмова однієї з ланок автоматизованої системи управління.

Події називаються рівноможливими, якщо за умовами випробування жодна з цих подій не є більш можливим, ніж інші. Наприклад, нехай магазину постачають електролампочки (причому в рівних кількостях) кілька заводів-виробників. Події, які перебувають у купівлі лампочки будь-якого з цих заводів, можливі.

Важливим поняттям є повна група подій. Декілька подій у цьому досвіді утворюють повну групу, якщо в результаті досвіду обов'язково з'явиться хоча б одне з них. Наприклад, в урні знаходиться десять куль, з них шість куль червоних, чотири білі, причому п'ять куль мають номери. - поява червоної кулі при одному видобутку; - поява білої кулі; - поява кулі з номером. Події утворюють повну групу спільних подій.

Введемо поняття протилежної, або додаткової, події. Під протилежнимподією розуміється подія, яка обов'язково має відбутися, якщо не настала деяка подія. Протилежні події несумісні та єдино можливі. Вони утворюють повну групу подій. Наприклад, якщо партія виготовлених виробів складається з придатних та бракованих, то при витягуванні одного виробу воно може виявитися або придатним - подія або бракованим - подія .

Операції над подіями

При розробці апарату та методики дослідження випадкових подій у теорії ймовірностей дуже важливим є поняття суми та добутку подій.

Сумою, або об'єднанням, кількох подій називається подія, що полягає у настанні хоча б однієї з цих подій.

Сума подій позначається так:

Наприклад, якщо подія є попадання в ціль при першому пострілі, подія - при другому, то подія є попадання в ціль взагалі, байдуже, при якому пострілі - першому, другому або за обох разом.

Твором, або перетином, кількох подій називається подія, що полягає у спільній появі всіх цих подій.

Твір подій позначається

Наприклад, якщо подія є попадання в ціль при першому пострілі, подія - при другому, то подія полягає в тому, що ціль потрапили при обох пострілах.

Поняття суми та твори подій мають наочну геометричну інтерпретацію. Нехай подія полягає в попаданні точки в область, подія - в попаданні в область, тоді подія полягає в попаданні точки в область, заштриховану на рис. 1 і подія - в попаданні точки в область, заштриховану на рис. 2.

Класичне визначення ймовірності випадкової події

Для кількісного порівняння подій за ступенем можливості їх появи вводиться числова міра, що називається ймовірністю події.

Імовірністю події називається число, яке є виразом міри об'єктивної можливості появи події.

Імовірність події позначатимемо символом.

Імовірність події дорівнює відношенню числа випадків , що сприяють йому, із загального числа можливих, рівноможливих і несумісних випадків до ,тобто.

Це класичне визначення ймовірності. Отже, знаходження ймовірності події необхідно, розглянувши різні результати випробування, знайти сукупність єдино можливих, рівноможливих і несумісних випадків, підрахувати загальне їх число , число випадків , сприятливих даному події, і потім виконати розрахунок за формулою (1.1).

З формули (1.1) випливає, що ймовірність події є невід'ємним числом і може змінюватися в межах від нуля до одиниці, залежно від того, яку частку становить сприятливе число випадків від загальної кількості випадків:

Властивості ймовірності

Властивість 1. Якщо всі випадки є сприятливими для цієї події, то ця подія обов'язково відбудеться. Отже, подія, що розглядається, є достовірною, а ймовірність її появи, тому що в цьому випадку

Властивість 2. Якщо немає жодного випадку, сприятливого даному події , це подія в результаті досвіду відбутися неспроможна. Отже, подія, що розглядається, є неможливим, а ймовірність його появи, тому що в цьому випадку:

Властивість 3. Імовірність настання подій, що утворюють повну групу, дорівнює одиниці.

Властивість 4. Імовірність наступу протилежної події визначається так само, як і ймовірність наступу, події:

де - число випадків, що сприяють появі протилежної події. Звідси ймовірність настання протилежної події дорівнює різниці між одиницею та ймовірністю настання події.

Важливе достоїнство класичного визначення ймовірності події у тому, що з його допомогою ймовірність події можна визначити, не вдаючись до досвіду, а з логічних міркувань.

Приклад 1. Набираючи номер телефону, абонент забув одну цифру та набрав її навмання. Знайти ймовірність того, що набрано потрібну цифру.

Рішення. Позначимо подію, яка полягає в тому, що набрано необхідну цифру. Абонент міг набрати будь-яку з 10 цифр, тому загальна кількість можливих результатів дорівнює 10. Ці результати єдино можливі (одна з цифр набрано обов'язково) і рівноможливі (цифра набрана навмання). Сприяє події лише один результат (потрібна цифра лише одна). Шукана ймовірність дорівнює відношенню числа результатів, що сприяють події, до всіх результатів:

Елементи комбінаторики

Теоретично ймовірностей часто використовують розміщення, перестановки та поєднання. Якщо дано безліч, то розміщенням (поєднанням)з елементів називається будь-яке впорядковане (невпорядковане) підмножина елементів множини . При розміщенні називається перестановкоюз елементів.

Нехай, наприклад, дано безліч. Розміщеннями із трьох елементів цієї множини по два є , , , , , ; поєднаннями - , , .

Два поєднання розрізняються хоча б одним елементом, а розміщення розрізняються або самими елементами, або порядком їхнього прямування. Число поєднань з елементів обчислюється за формулою

є число розміщень з елементів ; - Число перестановок з елементів.

Приклад 2. У партії із 10 деталей є 7 стандартних. Знайти ймовірність того, що серед взятих навмання 6 деталей рівно 4 стандартних.

Рішення. Загальна кількість можливих результатів випробування дорівнює числу способів, якими можна отримати 6 деталей з 10, тобто рівно - числу поєднань з 10 елементів по 6. Число результатів, сприятливих події (серед 6 взятих деталей рівно 4 стандартних), визначаємо так: 4 стандартні деталі можна взяти із 7 стандартних деталей способами; при цьому інші деталі мають бути нестандартними; взяти 2 нестандартні деталі з нестандартних деталей можна способами. Отже, число сприятливих результатів дорівнює . Вихідна ймовірність дорівнює відношенню числа результатів, що сприяють події, до всіх результатів:

Статистичне визначення ймовірності

Формулу (1.1) використовують для безпосереднього обчислення ймовірностей подій лише тоді, коли досвід зводиться до схеми випадків. Насправді часто класичне визначення ймовірності не застосовується з двох причин: по-перше, класичне визначення ймовірності передбачає, що загальна кількість випадків має бути звичайно. Насправді воно часто не обмежене. По-друге, часто неможливо уявити результати досвіду як рівноможливих і несумісних подій.

Частота появи подій при багаторазово повторюваних Дослідах має тенденцію стабілізуватися при якійсь постійної величини. Таким чином, з подією, що розглядається, можна пов'язати деяку постійну величину, біля якої групуються частоти і яка є характеристикою об'єктивного зв'язку між комплексом умов, за яких проводяться досліди, і подією.

Імовірністю випадкової події називається число, біля якого групуються частоти цієї події зі збільшенням числа випробувань.

Це визначення ймовірності називається статистичним.

Перевага статистичного способу визначення ймовірності у тому, що він спирається реальний експеримент. Однак його істотний недолік полягає в тому, що для визначення ймовірності необхідно виконати велику кількість дослідів, які часто пов'язані з матеріальними витратами. Статистичне визначення ймовірності події хоч і досить повно розкриває зміст цього поняття, але це не дає можливості фактичного обчислення ймовірності.

У традиційному визначенні ймовірності розглядається повна група кінцевого числа рівноможливих подій. Насправді дуже часто кількість можливих результатів випробувань нескінченно. У разі класичне визначення ймовірності неприменимо. Однак іноді у подібних випадках можна скористатися іншим методом обчислення ймовірності. Для певності обмежимося двовимірним випадком.

Нехай на площині задана деяка область площею , де міститься інша область площею (рис. 3). В область навмання кидається крапка. Чому дорівнює можливість того, що точка потрапить в область ? При цьому передбачається, що наудачу покинута точка може потрапити в будь-яку точку області, і ймовірність потрапити в будь-яку частину області пропорційна площі частини і не залежить від її розташування та форми. У такому разі ймовірність попадання в область при киданні навмання точки в область

Таким чином, у загальному випадку, якщо можливість випадкової появи точки всередині деякої області на прямій, площині або в просторі визначається не положенням цієї області та її межами, а лише її розміром, тобто довжиною, площею або об'ємом, то ймовірність попадання випадкової точки всередину певної області визначається як відношення розміру цієї області до розміру всієї області, де може з'являтися дана точка. Це геометричне визначення ймовірності.

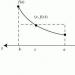
Приклад 3. Кругла мета обертається з постійною кутовою швидкістю. П'ята частина мішені забарвлена ​​у зелений колір, а решта – у білий (рис. 4). По мішені проводиться постріл так, що попадання в ціль - подія достовірна. Потрібно визначити можливість попадання в сектор мішені, пофарбований у зелений колір.

Рішення. Позначимо - "постріл потрапив у сектор, пофарбований у зелений колір". Тоді. Імовірність отримана як відношення площі частини мішені, пофарбованої в зелений колір, до всієї площі мішені, оскільки попадання будь-які частини мішені рівноможливі.

Аксіоми теорії ймовірностей

Зі статистичного визначення ймовірності випадкової події випливає, що ймовірність події є число, біля якого групуються частоти цієї події, що спостерігаються на досвіді. Тому аксіоми теорії ймовірностей вводяться так, щоб ймовірність події мала основні властивості частоти.

Аксіома 1. Кожній події відповідає певна кількість, що задовольняє умові і називається його ймовірністю.