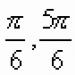Тригонометрия. Обратные тригонометрические функции. Выразим через все обратные тригонометрические функции Обратные тригонометрические формулы таблица

Задания, связанные с обратными тригонометрическими функциями, часто предлагаются на школьных выпускных экзаменах и на вступительных экзаменах в некоторых ВУЗах. Подробное изучение этой темы может быть достигнуто только на факультативных занятиях или на элективных курсах. Предлагаемый курс призван как можно полнее развить способности каждого ученика, повысить его математическую подготовку.

Курс рассчитан на 10 часов:

1.Функции arcsin x, arccos x, arctg x, arcctg x (4 ч.).

2.Операции над обратными тригонометрическими функциями (4 ч.).

3.Обратные тригонометрические операции над тригонометрическими функциями (2 ч.).

Урок 1 (2 ч.) Тема: Функции y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.

Цель: полное освещение данного вопроса.

1.Функция y = arcsin х.

а) Для функции y = sin x на отрезке существует обратная (однозначная) функция, которую условились называть арксинусом и обозначать так: y = arcsin x. График обратной функции симметричен с графиком основной функции относительно биссектрисы I - III координатных углов.

Свойства функции y = arcsin x .

1)Область определения: отрезок [-1; 1];

2)Область изменения: отрезок ;

3)Функция y = arcsin x нечетная: arcsin (-x) = - arcsin x;

4)Функция y = arcsin x монотонно возрастающая;

5)График пересекает оси Ох, Оу в начале координат.

Пример 1. Найти a = arcsin . Данный пример подробно можно сформулировать так: найти такой аргумент a , лежащий в пределах от до , синус которого равен .

Решение. Существует бесчисленное множество аргументов, синус которых равен , например: и т.д. Но нас интересует только тот аргумент, который находится на отрезке . Таким аргументом будет . Итак, .

Пример 2. Найти .Решение. Рассуждая так же, как и в примере 1, получим .

б) устные упражнения. Найти: arcsin 1, arcsin (-1), arcsin , arcsin (), arcsin , arcsin (), arcsin , arcsin (), arcsin 0. Образец ответа: , т.к. . Имеют ли смысл выражения: ; arcsin 1,5; ?

в) Расположите в порядке возрастания: arcsin, arcsin (-0,3), arcsin 0,9.

II. Функции y = arccos x, y = arctg x, y = arcctg x (аналогично).

Урок 2 (2 ч) Тема: Обратные тригонометрические функции, их графики.

Цель: на данном уроке необходимо отработать навыки в определении значений тригонометрических функций, в построении графиков обратных тригонометрических функций с использованием Д (у), Е (у) и необходимых преобразований.

На данном уроке выполнить упражнения, включающие нахождение области определения, области значения функций типа: y = arcsin , y = arccos (x-2), y = arctg (tg x), y = arccos .

Следует построить графики функций: а) y = arcsin 2x; б) y = 2 arcsin 2x; в) y = arcsin ;

г) y = arcsin ; д) y = arcsin ; е) y = arcsin ; ж) y = | arcsin | .

Пример. Построим график y = arccos

В домашнее задание можно включить следующие упражнения: построить графики функций: y = arccos , y = 2 arcctg x, y = arccos | x | .

Графики обратных функций

Урок № 3 (2 ч.) Тема:
Операции над обратными тригонометрическими функциями.

Цель: расширить математические познания (это важно для поступающих на специальности с повышенными требованиями к математической подготовке) путем введения основных соотношений для обратных тригонометрических функций.

Материал для урока.

Некоторые простейшие тригонометрические операции над обратными тригонометрическими функциями: sin (arcsin x) = x , i xi ? 1; cos (arсcos x) = x , i xi ? 1; tg (arctg x)= x , x I R; ctg (arcctg x) = x , x I R.

Упражнения.

а) tg (1,5 + arctg 5) = - ctg (arctg 5) = .

ctg (arctg x) = ; tg (arcctg x) = .

б) cos ( + arcsin 0,6) = - cos (arcsin 0,6). Пусть arcsin 0,6 = a , sin a = 0,6;

cos (arcsin x) = ; sin (arccos x) = .

Замечание: берем перед корнем знак “+” потому, что a = arcsin x удовлетворяет .

в) sin (1,5 + arcsin ).Ответ: ;

г) ctg ( + arctg 3).Ответ: ;

д) tg ( – arcctg 4).Ответ: .

е) cos (0,5 + arccos ) . Ответ: .

Вычислить:

a) sin (2 arctg 5) .

Пусть arctg 5 = a , тогда sin 2 a = или sin (2 arctg 5) = ;

б) cos ( + 2 arcsin 0,8).Ответ: 0,28.

в) arctg + arctg .

Пусть a = arctg , b = arctg ,

тогда tg (a + b) = .

г) sin (arcsin + arcsin ).

д) Доказать, что для всех x I [-1; 1] верно arcsin x + arccos x = .

Доказательство:

arcsin x = – arccos x

sin (arcsin x) = sin ( – arccos x)

x = cos (arccos x)

Для самостоятельного решения: sin (arccos ), cos (arcsin ) , cos (arcsin ()), sin (arctg (- 3)), tg (arccos ) , ctg (arccos ).

Для домашнего решения: 1) sin (arcsin 0,6 + arctg 0); 2) arcsin + arcsin ; 3) ctg ( – arccos 0,6); 4) cos (2 arcctg 5) ; 5) sin (1,5 – arcsin 0,8); 6) arctg 0,5 – arctg 3.

Урок № 4 (2ч.) Тема: Операции над обратными тригонометрическими функциями.

Цель: на данном уроке показать использование соотношений в преобразовании более сложных выражений.

Материал для урока.

УСТНО:

а) sin (arccos 0,6), cos (arcsin 0,8);

б) tg (arcсtg 5), ctg (arctg 5);

в) sin (arctg -3), cos (arcсtg());

г) tg (arccos ), ctg (arccos()).

ПИСЬМЕННО:

1) cos (arcsin + arcsin + arcsin ).

2) cos (arctg 5–arccos 0,8) = cos (arctg 5) cos (arccos 0,8) + sin (arctg 5) sin (arccos 0,8) =

3) tg ( - arcsin 0,6) = - tg (arcsin 0,6) =

Самостоятельная работа поможет выявить уровень усвоения материала

1) tg (arctg 2 – arctg )

2) cos( - arctg2)

3) arcsin + arccos

1) cos (arcsin + arcsin )

2) sin (1,5 - arctg 3)

3) arcctg3 – arctg 2

Для домашнего задания можно предложить:

1) ctg (arctg + arctg + arctg ); 2) sin 2 (arctg 2 – arcctg ()); 3) sin (2 arctg + tg ( arcsin )); 4) sin (2 arctg ); 5) tg ( (arcsin ))

Урок № 5 (2ч) Тема: Обратные тригонометрические операции над тригонометрическими функциями.

Цель: сформировать представление учащихся об обратных тригонометрических операциях над тригонометрическими функциями, основное внимание уделить повышению осмысленности изучаемой теории.

При изучении данной темы предполагается ограничение объема теоретического материала, подлежащего запоминанию.

Материал для урока:

Изучение нового материала можно начать с исследования функции y = arcsin (sin x) и построения ее графика.

3. Каждому x I R ставится в соответствие y I , т.е. <= y <= такое, что sin y = sin x.

4. Функция нечетна: sin(-x) = - sin x ; arcsin(sin(-x)) = - arcsin(sin x).

6. График y = arcsin (sin x) на :

a) 0 <= x <= имеем y = arcsin(sin x) = x, ибо sin y = sin x и <= y <= .

б) <= x <= получим y = arcsin (sin x) = arcsin ( - x) = - x, ибо

sin y = sin ( – x) = sinx , 0 <= - x <= .

Итак,

Построив y = arcsin (sin x) на , продолжим симметрично относительно начала координат на [- ; 0], учитывая нечетность этой функции. Используя периодичность, продолжим на всю числовую ось.

Затем записать некоторые соотношения: arcsin (sin a) = a , если <= a <= ; arccos (cos a ) = a , если 0 <= a <= ; arctg (tg a) = a , если < a < ; arcctg (ctg a) = a , если 0 < a < .

И выполнить следующие упражнения:a) arccos(sin 2).Ответ: 2 - ; б) arcsin (cos 0,6).Ответ: - 0,1 ; в) arctg (tg 2).Ответ: 2 - ;

г) arcctg(tg 0,6).Ответ: 0,9 ; д) arccos (cos ( - 2)).Ответ:2 - ; е) аrcsin (sin ( - 0,6)). Ответ: - 0,6; ж) аrctg (tg 2) = arctg (tg (2 - )). Ответ:2 - ; з) аrcctg (tg 0,6). Ответ: - 0,6; - arctg x; д) arccos + arccos

К обратным тригонометрическим функциям относятся следующие 6 функций: арксинус , арккосинус , арктангенс , арккотангенс , арксеканс и арккосеканс .

Поскольку исходные тригонометрические функции периодические, то обратные функции, вообще говоря, являются многозначными . Чтобы обеспечить однозначное соответствие между двумя переменными, области определения исходных тригонометрических функций ограничивают, рассматривая лишь их главные ветви . Например, функция \(y = \sin x\) рассматривается лишь в промежутке \(x \in \left[ { - \pi /2,\pi /2} \right]\). На этом интервале обратная функция арксинус определена однозначно.

Функция арксинус
Арксинусом числа \(a\) (обозначается \(\arcsin a\)) называется значение угла \(x\) в интервале \(\left[ { - \pi /2,\pi /2} \right]\), при котором \(\sin x = a\). Обратная функция \(y = \arcsin x\) определена при \(x \in \left[ { -1,1} \right]\), область ее значений равна \(y \in \left[ { - \pi /2,\pi /2} \right]\).

Функция арккосинус
Арккосинусом числа \(a\) (обозначается \(\arccos a\)) называется значение угла \(x\) в интервале \(\left[ {0,\pi} \right]\), при котором \(\cos x = a\). Обратная функция \(y = \arccos x\) определена при \(x \in \left[ { -1,1} \right]\), область ее значений принадлежит отрезку \(y \in \left[ {0,\pi} \right]\).

Функция арктангенс
Арктангенсом числа a (обозначается \(\arctan a\)) называется значение угла \(x\) в открытом интервале \(\left({-\pi/2, \pi/2} \right)\), при котором \(\tan x = a\). Обратная функция \(y = \arctan x\) определена при всех \(x \in \mathbb{R}\), область значений арктангенса равна \(y \in \left({-\pi/2, \pi/2} \right)\).

Функция арккотангенс
Арккотангенсом числа \(a\) (обозначается \(\text{arccot } a\)) называется значение угла \(x\) в открытом интервале \(\left[ {0,\pi} \right]\), при котором \(\cot x = a\). Обратная функция \(y = \text{arccot } x\) определена при всех \(x \in \mathbb{R}\), область ее значений находится в интервале \(y \in \left[ {0,\pi} \right]\).

Функция арксеканс
Арксекансом числа \(a\) (обозначается \(\text{arcsec } a\)) называется значение угла \(x\), при котором \(\sec x = a\). Обратная функция \(y = \text{arcsec } x\) определена при \(x \in \left({ - \infty , - 1} \right] \cup \left[ {1,\infty } \right)\), область ее значений принадлежит множеству \(y \in \left[ {0,\pi /2} \right) \cup \left({\pi /2,\pi } \right]\).

Функция арккосеканс
Арккосекансом числа \(a\) (обозначается \(\text{arccsc } a\) или \(\text{arccosec } a\)) называется значение угла \(x\), при котором \(\csc x = a\). Обратная функция \(y = \text{arccsc } x\) определена при \(x \in \left({ - \infty , - 1} \right] \cup \left[ {1,\infty } \right)\), область ее значений принадлежит множеству \(y \in \left[ { - \pi /2,0} \right) \cup \left({0,\pi /2} \right]\).

Главные значения функций арксинус и арккосинус (в градусах)

\(x\)	\(-1\)	\(-\sqrt 3/2\)	\(-\sqrt 2/2\)	\(-1/2\)	\(0\)	\(1/2\)	\(\sqrt 2/2\)	\(\sqrt 3/2\)	\(1\)
\(\arcsin x\)	\(-90^\circ\)	\(-60^\circ\)	\(-45^\circ\)	\(-30^\circ\)	\(0^\circ\)	\(30^\circ\)	\(45^\circ\)	\(60^\circ\)	\(90^\circ\)
\(\arccos x\)	\(180^\circ\)	\(150^\circ\)	\(135^\circ\)	\(120^\circ\)	\(90^\circ\)	\(60^\circ\)	\(45^\circ\)	\(30^\circ\)	\(0^\circ\)

Главные значения функций арктангенс и арккотангенс (в градусах)

\(x\)	\(-\sqrt 3\)	\(-1\)	\(-\sqrt 3/3\)	\(0\)	\(\sqrt 3/3\)	\(1\)	\(\sqrt 3\)
\(\arctan x\)	\(-60^\circ\)	\(-45^\circ\)	\(-30^\circ\)	\(0^\circ\)	\(30^\circ\)	\(45^\circ\)	\(60^\circ\)
\(\text{arccot } x\)	\(150^\circ\)	\(135^\circ\)	\(120^\circ\)	\(90^\circ\)	\(60^\circ\)	\(45^\circ\)	\(30^\circ\)

Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x , при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x . Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y .

Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.

Арксинус (y = arcsin x ) - это функция, обратная к синусу (x = sin y
Арккосинус (y = arccos x ) - это функция, обратная к косинусу (x = cos y ), имеющая область определения и множество значений .
Арктангенс (y = arctg x ) - это функция, обратная к тангенсу (x = tg y ), имеющая область определения и множество значений .
Арккотангенс (y = arcctg x ) - это функция, обратная к котангенсу (x = ctg y ), имеющая область определения и множество значений .

Графики обратных тригонометрических функций

Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус , Тангенс, котангенс .

y = arcsin x

y = arccos x

y = arctg x

y = arcctg x

Основные формулы

Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.

arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = x

arctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = x

Формулы, связывающие обратные тригонометрические функции

См. также: Вывод формул обратных тригонометрических функций

Формулы суммы и разности

при или

при и

при и

при

при

при

при

при

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Определение и обозначения

Арксинус (y = arcsin x ) - это функция, обратная к синусу (x = sin y -1 ≤ x ≤ 1 и множество значений -π/2 ≤ y ≤ π/2 .
sin(arcsin x) = x ;
arcsin(sin x) = x .

Арксинус иногда обозначают так:
.

График функции арксинус

График функции y = arcsin x

График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.

Арккосинус, arccos

Определение и обозначения

Арккосинус (y = arccos x ) - это функция, обратная к косинусу (x = cos y ). Он имеет область определения -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π .
cos(arccos x) = x ;
arccos(cos x) = x .

Арккосинус иногда обозначают так:
.

График функции арккосинус

График функции y = arccos x

График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.

Четность

Функция арксинус является нечетной:
arcsin(- x) = arcsin(-sin arcsin x) = arcsin(sin(-arcsin x)) = - arcsin x

Функция арккосинус не является четной или нечетной:
arccos(- x) = arccos(-cos arccos x) = arccos(cos(π-arccos x)) = π - arccos x ≠ ± arccos x

Свойства - экстремумы, возрастание, убывание

Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.

	y = arcsin x	y = arccos x
Область определения и непрерывность	- 1 ≤ x ≤ 1	- 1 ≤ x ≤ 1
Область значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы
Минимумы
Нули, y = 0	x = 0	x = 1
Точки пересечения с осью ординат, x = 0	y = 0	y = π/2

Таблица арксинусов и арккосинусов

В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.

x	arcsin x		arccos x
	град.	рад.	град.	рад.
- 1	- 90°	-	180°	π
-	- 60°	-	150°
-	- 45°	-	135°
-	- 30°	-	120°
0	0°	0	90°
	30°		60°
	45°		45°
	60°		30°
1	90°		0°	0

≈ 0,7071067811865476
≈ 0,8660254037844386

Формулы

См. также: Вывод формул обратных тригонометрических функций

Формулы суммы и разности

при или

при и

при и

при

при

Выражения через логарифм, комплексные числа

См. также: Вывод формул

Выражения через гиперболические функции

Производные

;
.
См. Вывод производных арксинуса и арккосинуса > > >

Производные высших порядков :
,
где - многочлен степени . Он определяется по формулам:
;
;
.

См. Вывод производных высших порядков арксинуса и арккосинуса > > >

Интегралы

Делаем подстановку x = sin t . Интегрируем по частям, учитывая что -π/2 ≤ t ≤ π/2 , cos t ≥ 0 :
.

Выразим арккосинус через арксинус:
.

Разложение в ряд

При |x| < 1 имеет место следующее разложение:
;
.

Обратные функции

Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.

Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .

Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .

См. также:

Уроки 32-33. Обратные тригонометрические функции

09.07.2015 8495 0

Цель: рассмотреть обратные тригонометрические функции, их использование для записи решений тригонометрических уравнений.

I. Сообщение темы и цели уроков

II. Изучение нового материала

1. Обратные тригонометрические функции

Рассмотрение этой темы начнем со следующего примера.

Пример 1

Решим уравнение: a ) sin x = 1/2; б) sin x = а.

а) На оси ординат отложим значение 1/2 и построим углы x 1 и х2, для которых sin x = 1/2. При этом х1 + х2 = π, откуда х2 = π – x 1 . По таблице значений тригонометрических функций найдем величину х1 = π/6, тогда Учтем периодичность функции синуса и запишем решения данного уравнения: где k ∈ Z .

б) Очевидно, что алгоритм решения уравнения sin х = а такой же, как и в предыдущем пункте. Разумеется, теперь по оси ординат откладывается величина а. Возникает необходимость каким-то образом обозначить угол х1. Условились такой угол обозначать символом arcsin а. Тогда решения данного уравнения можно записать в виде Эти две формулы можно объединить в одну: при этом

Аналогичным образом вводятся и остальные обратные тригонометрические функции.

Очень часто бывает необходимо определить величину угла по известному значению его тригонометрической функции. Такая задача является многозначной - существует бесчисленное множество углов, тригонометрические функции которых равны одному и тому же значению. Поэтому, исходя из монотонности тригонометрических функций, для однозначного определения углов вводят следующие обратные тригонометрические функции.

Арксинус числа a (arcsin , синус которого равен а, т. е.

Арккосинус числа a (arccos а) - такой угол а из промежутка , косинус которого равен а, т. е.

Арктангенс числа a (arctg а) - такой угол а из промежутка тангенс которого равен а, т. е. tg а = а.

Арккотангенс числа a (arcctg а) - такой угол а из промежутка (0; π), котангенс которого равен а, т. е. ctg а = а.

Пример 2

Найдем:

Учитывая определения обратных тригонометрических функций получим:

Пример 3

Вычислим

Пусть угол а = arcsin 3/5, тогда по определению sin a = 3/5 и . Следовательно, надо найти cos а. Используя основное тригонометрическое тождество, получим: Учтено, что и cos a ≥ 0. Итак,

Свойства функции	Функция
Свойства функции	у = arcsin х	у = arccos х	у = arctg х	у = arcctg х
Область определения	х ∈ [-1; 1]	х ∈ [-1; 1]	х ∈ (-∞; +∞)	х ∈ (-∞ +∞)
Область значений	y ∈ [ -π/2 ; π /2 ]	y ∈	y ∈ (-π/2 ; π /2 )	y ∈ (0; π)
Четность	Нечетная	Ни четная, ни нечетная	Нечетная	Ни четная, ни нечетная
Нули функции (y = 0)	При х = 0	При х = 1	При х = 0	у ≠ 0
Промежутки знакопостоянства	у > 0 при х ∈ (0; 1], у < 0 при х ∈ [-1; 0)	у > 0 при х ∈ [-1; 1)	у > 0 при х ∈ (0; +∞), у < 0 при х ∈ (-∞; 0)	у > 0 при x ∈ (-∞; +∞)
Монотонность	Возрастает	Убывает	Возрастает	Убывает
Связь с тригонометрической функцией	sin у = х	cos у = х	tg у = х	ctg у = х
График

Приведем еще ряд типичных примеров, связанных с определениями и основными свойствами обратных тригонометрических функций.

Пример 4

Найдем область определения функции

Для того чтобы функция у была определена, необходимо выполнение неравенства которое эквивалентно системе неравенств Решением первого неравенства является промежуток х ∈ (-∞; +∞), второго - Этот промежуток и является решением системы неравенств, а следовательно, и областью определения функции

Пример 5

Найдем область изменения функции

Рассмотрим поведение функции z = 2х - х2 (см. рисунок).

Видно, что z ∈ (-∞; 1]. Учитывая, что аргумент z функции арккотангенса меняется в указанных пределах, из данных таблицы получим, что Таким образом, область изменения

Пример 6

Докажем, что функция у = arctg х нечетная. Пусть Тогда tg а = -х или х = - tg а = tg (- a ), причем Следовательно, - a = arctg х или а = - arctg х. Таким образом, видим, что т. е. у(х) - функция нечетная.

Пример 7

Выразим через все обратные тригонометрические функции

Пусть Очевидно, что Тогда Так как

Введем угол Так как то

Аналогично поэтому и

Итак,

Пример 8

Построим график функции у = cos (arcsin х).

Обозначим а = arcsin x , тогда Учтем, что х = sin а и у = cos а, т. е. x 2 + у2 = 1, и ограничения на х (х ∈ [-1; 1]) и у (у ≥ 0). Тогда графиком функции у = cos (arcsin х) является полуокружность.

Пример 9

Построим график функции у = arccos (cos x ).

Так как функция cos х изменяется на отрезке [-1; 1], то функция у определена на всей числовой оси и изменяется на отрезке . Будем иметь в виду, что у = arccos (cos x ) = х на отрезке ; функция у является четной и периодической с периодом 2π. Учитывая, что этими свойствами обладает функция cos x , теперь легко построить график.

Отметим некоторые полезные равенства:

Пример 10

Найдем наименьшее и наибольшее значения функции Обозначим тогда Получим функцию Эта функция имеет минимум в точке z = π/4, и он равен Наибольшее значение функции достигается в точке z = -π/2, и оно равно Таким образом, и

Пример 11

Решим уравнение

Учтем, что Тогда уравнение имеет вид: или откуда По определению арктангенса получим:

2. Решение простейших тригонометрических уравнений

Аналогично примеру 1 можно получить решения простейших тригонометрических уравнений.

Уравнение	Решение


tgx = а
ctg х = а

Пример 12

Решим уравнение

Так как функция синус нечетная, то запишем уравнение в виде Решения этого уравнения: откуда находим

Пример 13

Решим уравнение

По приведенной формуле запишем решения уравнения: и найдем

Заметим, что в частных случаях (а = 0; ±1) при решении уравнений sin х = а и cos х = а проще и удобнее использовать не общие формулы, а записывать решения на основании единичной окружности:

для уравнения sin х = 1 решения

для уравнения sin х = 0 решения х = π k ;

для уравнения sin х = -1 решения