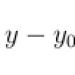ПЛОСКАЯ ВОЛНА
ПЛОСКАЯ ВОЛНА
Волна, у к-рой направление распространения одинаково во всех точках пространства. Простейший пример - однородная монохроматич. незатухающая П. в.:
и(z, t)=Aeiwt±ikz, (1)
где А - амплитуда, j= wt±kz - , w=2p/Т - круговая частота, Т -период колебаний, k - . Поверхности постоянной фазы (фазовые фронты) j=const П. в. являются плоскостями.
При отсутствии дисперсии, когда vф и vгр одинаковы и постоянны (vгр=vф= v), существуют стационарные (т. е. перемещающиеся как целое) бегущие П. в., к-рые допускают общее представление вида:
u(z, t)=f(z±vt), (2)
где f - произвольная функция. В нелинейных средах с дисперсией также возможны стационарные бегущие П. в. типа (2), но их форма уже не произвольна, а зависит как от параметров системы, так и от характера движения . В поглощающих (диссипативных) средах П. в. уменьшают свою амплитуду по мере распространения; при линейном затухании это может быть учтено путём замены в (1) k на комплексное волновое число kд ± ikм, где kм - коэфф. затухания П. в.
Однородная П. в., занимающая всё бесконечное , является идеализацией, однако любое волновое , сосредоточенное в конечной области (напр., направляемое линиями передачи или волноводами), можно представить как суперпозицию П. в. с тем или иным пространств. спектром k. При этом волна может по-прежнему иметь плоский фазовый фронт, но неоднородное амплитуды. Такие П. в. наз. плоскими неоднородными волнами. Отдельные участки сферич. и цилиндрич. волн, малые по сравнению с радиусом кривизны фазового фронта, приближённо ведут себя как П. в.
Физический энциклопедический словарь. - М.: Советская энциклопедия . . 1983 .
ПЛОСКАЯ ВОЛНА
- волна, ук-рой направление распространения одинаково во всех точках пространства.
где А -
амплитуда,- фаза,- круговая частота, Т -
период колебаний, k -
волновое число. = const П. в. являются плоскостями.
При отсутствии дисперсии, когда фазоваяскорость v
ф и групповая v
гр одинаковы и постоянны (v
гр = v
ф = v
) существуют стационарные (т. е. перемещающиеся как целое) бегущиеП. в., к-рые можно представить в общем виде
где f - произвольная ф-ция. В нелинейныхсредах с дисперсией также возможны стационарные бегущие П. в. типа (2),но их форма уже не произвольна, а зависит как от параметров системы, таки от характера движения волны. В поглощающих (диссипативных) средах П. k на комплексное волновоечисло k д ik м,где k м - коэф. затухания П. в. Однородная П. в., занимающаявсё бесконечное , является идеализацией, однако любое волновоеполе, сосредоточенное в конечной области (напр., направляемое линиямипередачи или волноводами), можно представить как суперпозициюП. в. с тем или иным пространственным спектром k. При этом волнаможет no-прежнему иметь плоский фазовый фронт, во неоднородное распределениеамплитуды. Такие П. в. наз. плоскими неоднородными волнами. Отд. участкисферич. или цилиндрич. волн, малые по сравнению с радиусом кривизны фазовогофронта, приближённо ведут себя как П. в.
Лит. см. при ст. Волны.
М. А. Миллер, Л. А. Островский.
Физическая энциклопедия. В 5-ти томах. - М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .
Уравнение волны – это уравнение, выражающее зависимость смещения колеблющейся частицы, участвующей в волновом процессе, от координаты ее равновесного положения и времени:
Эта функция должна быть периодической как относительно времени , так и относительно координат . Кроме того, точки, отстоящие на расстоянии l друг от друга, колеблются одинаковым образом.
Найдём вид функции x в случае плоской волны.
Рассмотрим плоскую гармоническую волну, распространяющуюся вдоль положительного направления оси в среде, не поглощающей энергию. В этом случае волновые поверхности будут перпендикулярны оси . Все величины, характеризующие колебательное движение частиц среды, зависят только от времени и координаты . Смещение будет зависеть только от и : 
. Пусть колебание точки с координатой (источник колебаний) задается функцией . Задача
: найти вид колебания точек в плоскости, соответствующей произвольному значению . Для того, чтобы пройти путь от плоскости до этой плоскости, волне требуется время . Следовательно, колебания частиц, лежащих в плоскости , будут отставать по фазе на время от колебаний частиц в плоскости . Тогда уравнение колебаний частиц в плоскости будет иметь вид:
В итоге получили уравнение плоской волны распространяющейся в направлении возрастания :
. (3)
В этом уравнении – амплитуда волны; – циклическая частота; – начальная фаза, которая определяется выбором начала отсчета и ; 
– фаза плоской волны.
Пусть фаза волны будет величиной постоянной (зафиксируем значение фазы в уравнении волны):
Сократим это выражение на и продифференцируем. В итоге получим:
или .
Таким образом, скорость распространения волны в уравнении плоской волны есть не что иное, как скорость распространения фиксированной фазы волны. Такую скорость называют фазовой скоростью .
Для синусоидальной волны скорость переноса энергии равна фазовой скорости. Но синусоидальная волна не несёт никакой информации, а любой сигнал это модулированная волна, т.е. не синусоидальная (не гармоническая). При решении некоторых задач получается, что фазовая скорость больше скорости света. Здесь нет парадокса, т.к. скорость перемещения фазы не есть скорость передачи (распространения) энергии. Энергия, масса не могут двигаться со скоростью больше чем скорость света c .
Обычно уравнению плоской волны придают симметричный относительно и вид. Для этого вводится величина 
, которая называется волновым числом
. Преобразуем выражение для волнового числа. Запишем его в виде 
(
). Подставим это выражение в уравнение плоской волны:
Окончательно получим
Это уравнение плоской волны, распространяющейся в сторону возрастания . Противоположное направление распространения волны будет характеризоваться уравнением, в котором поменяется знак перед членом .
Удобна запись уравнения плоской волны в следующем виде.
Обычно знак Re опускают, подразумевая, что берётся только вещественная часть соответствующего выражения. Кроме этого вводится комплексное число.
Это число называется комплексной амплитудой. Модуль этого числа даёт амплитуду, а аргумент – начальную фазу волны.
Таким образом, уравнение плоской незатухающей волны можно представить в следующем виде.
Всё рассмотренное выше относилось к среде, где отсутствовало затухание волны. В случае затухания волны, в соответствии с законом Бугера (Пьер Бугер, французский учёный (1698 – 1758)), амплитуда волны будет уменьшаться при её распространении. Тогда уравнение плоской волны будет иметь следующий вид.
a – коэффициент затухания волна. A 0 – амплитуда колебаний в точке с координатами . Это величина обратная расстоянию, при котором амплитуда волны уменьшается в e раз.
Найдем уравнение сферической волны . Будем считать источник колебаний точечным. Это возможно, если ограничиться рассмотрением волны на расстоянии, много большем размеров источника. Волна от такого источника в изотропной и однородной среде будет сферической . Точки лежащие на волновой поверхности радиуса , будут колебаться с фазой
Амплитуда колебаний в этом случае, даже если энергия волны не поглощается средой, не будет оставаться постоянной. Она убывает с расстоянием от источника по закону . Следовательно, уравнение сферической волны имеет вид:
или
В силу сделанных предположений уравнение справедливо только при , значительно превышающих размеры источника волн. Уравнение (6) неприменимо для малых значений , т.к. амплитуда устремилась бы к бесконечности, а это абсурд.
При наличии затухания в среде уравнение сферической волны запишется следующим образом.
Групповая скорость
Строго монохроматическая волна представляет собой бесконечную во времени и пространстве последовательность "горбов" и "впадин".
Фазовая скорость этой волны или 
(2)
С помощью такой волны нельзя передать сигнал, т.к. в любой точке волны все "горбы" одинаковы. Сигнал должен отличаться. Быть знаком (меткой) на волне. Но тогда волна уже не будет гармонической, и не будет описываться уравнением (1). Сигнал (импульс) можно представить согласно теореме Фурье в виде суперпозиции гармонических волн с частотами, заключёнными в некотором интервале Dw . Суперпозиция волн, мало отличающихся друг от друга по частоте,
 |
называется волновым пакетом или группой волн .
Выражение для группы волн может быть записано следующим образом.
(3)
Значок w подчеркивает, что эти величины зависят от частоты.
Этот волновой пакет может быть суммой волн с мало отличающимися частотами. Там, где фазы волн совпадают, наблюдается усиление амплитуды, а там, где фазы противоположны, наблюдается гашение амплитуды (результат интерференции). Такая картина представлена на рисунке. Чтобы суперпозицию волн можно было считать группой волн необходимо выполнение следующего условия Dw << w 0 .
В недиспергирующей среде все плоские волны, образующие волновой пакет, распространяются с одинаковой фазовой скоростью v . Дисперсия это зависимость фазовой скорости синусоидальной волны в среде от частоты. Явление дисперсии мы рассмотрим позже в разделе "Волновая оптика". В отсутствии дисперсии скорость перемещения волнового пакета совпадает с фазовой скорость v . В диспергирующей среде каждая волна диспергирует со своей скоростью. Поэтому волновой пакет с течением времени расплывается, его ширина увеличивается.
Если дисперсия невелика, то расплывание волнового пакета происходит не слишком быстро. Поэтому движению всего пакета можно приписать некоторую скорость U
.
Скорость, с которой перемещается центр волнового пакета (точка с максимальным значением амплитуды) называется групповой скоростью .
В диспергирующей среде v¹ U . Вместе с движением самого волнового пакета происходит движение "горбов" внутри самого пакета. "Горбы" перемещаются в пространстве со скоростью v , а пакет в целом со скоростью U .
Рассмотрим подробнее движение волнового пакета на примере суперпозиции двух волн с одинаковой амплитудой и разными частотами w (разными длинами волн l ).
Запишем уравнения двух волн. Примем для простоты начальные фазы j 0 = 0.
Здесь 
Пусть Dw << w , соответственно Dk << k .
Сложим колебания и проведём преобразования с помощью тригонометрической формулой для суммы косинусов:
В первом косинусе пренебрежём Dwt и Dkx , которые много меньше других величин. Учтём, что cos(–a) = cosa . Окончательно запишем.
(4)
Множитель в квадратных скобках изменяется от времени и координаты значительно медленнее, чем второй множитель. Следовательно, выражение (4) можно рассматривать как уравнение плоской волны с амплитудой, описываемой первым сомножителем. Графически волна, описываемая выражением (4) представлена на рисунке, изображённом выше.
Результирующая амплитуда получается в результате сложения волн, следовательно, будут наблюдаться максимумы и минимумы амплитуды.
Максимум амплитуды будет определяться следующим условием.
(5)
m = 0, 1, 2…
x max – координата максимальной амплитуды.
Косинус принимает максимальное значение по модулю через p .
Каждый из этих максимумов можно рассматривать как центр соответствующей группы волн.
Разрешив (5) относительно x max получим.
Так как фазовая скорость , то 
называется групповой скоростью. С такой скоростью перемещается максимум амплитуды волнового пакета. В пределе, выражение для групповой скорости будет иметь следующий вид.
(6)
Это выражение справедливо для центра группы произвольного числа волн.
Следует отметить, что при точном учёте всех членов разложения (для произвольного числа волн), выражение для амплитуды получается таким, что из него следует, что волновой пакет со временем расплывается.
Выражению для групповой скорости можно придать другой вид.
В отсутствии дисперсии 
Максимум интенсивности приходится на центр группы волн. Поэтому скорость переноса энергии равна групповой скорости.
Понятие групповой скорости применимо только при условии, что поглощение волны в среде невелико. При значительном затухании волн понятие групповой скорости утрачивает смысл. Этот случай наблюдается в области аномальной дисперсии. Это мы будем рассматривать в разделе "Волновая оптика".
Установим связь между смещением колеблющейся частицы среды (точки) от положения равновесия и временем, отсчитанным от момента начала колебания источника, который находится на расстоянии х от «нашей» частицы в начале координат.
Пусть колебания источника S гармонические, т.е. описываются уравнением ξ (t ) = A sinωt . С течением времени все частицы среды также будут совершать синусоидальные колебания с той же частотой и амплитудой, но с различными фазами. В среде возникнет гармоническая бегущая волна.
Частица среды, находящаяся на оси ОХ на расстоянии х от источника S (рис. 1.2), начнёт колебаться позже, чем источник, на время, необходимое, чтобы волна, распространяющаяся от источника со скоростью V , преодолела расстояние х до частицы. Очевидно, что если источник колеблется уже в течение времени t , то частица среды колеблется еще только в течение времени (t – t), где t - время распространения колебаний от источника до частицы.
Тогда уравнение колебания для этой частицы будет
ξ (x,t ) =A sinω(t- τ),
но t =x /V , где V – модуль cкорости распространения волны. Тогда
ξ (x,t ) =A sinω(t-x/V )
– уравнение волны.
С учётом того, что и , уравнению можно придать вид
ξ (x,t )=A sin2 (t/T-x/λ ) = A sin2 (νt -x/λ ) = A sin (ωt -2πx/λ ) = A sin (ωt -kx ),(1.1)
где k = 2p/l – волновое число.Здесь (1.1) – уравнение плоской гармонической монохроматической волны (рис. 1.3), распространяющейся в направлении оси ОХ . График волны внешне похож на график гармонического колебания, но по существу они различны.
 |
График колебания – зависимость смещения данной частицы от времени. График волны – смещение всех частиц среды в данный момент времени на всем расстоянии от источника колебаний до волнового фронта. График волны является как бы моментальной фотографией волны.
Уравнение бегущей волны, распространяющейся в произвольном направлении, имеет вид:
ξ (x,y,z,t ) = A sin = A sin(ωt – k x x – k y y – k z z ), (1.2)
где ξ – мгновенное смещение колеблющегося элемента среды (точки) с координатами x, y, z ; А – амплитуда смещения; ω – круговая частота колебаний;
– волновой вектор, равный ( – единичный вектор, указывающий направление распространения волны); 
; - орты;
λ – длинна волны (рис. 1.3), т.е. расстояние, на которое распространяется волна за время, равное периоду колебаний частиц среды; – радиус-вектор, проведённый в рассматриваемую точку, 
;
– фаза волны, где 
.
Здесь – углы, составленные волновым вектором с соответствующими осями координат.
Если волна распространяется в среде, не поглащающей энергию, то амплитуда волны не изменяется, т.е. А = const.
Скорость распространения волнового движения является скоростью распространения фазы волны (фазовая скорость). В однородной среде скорость волны постоянна. Если фазовая скорость волны в среде зависит от частоты, то такое явление называется дисперсией волн, а среда – дисперсирующей средой.
При переходе из одной среды в другую может меняться скорость распространения волн, так как меняются упругие свойства среды, однако частота колебаний, как показывает опыт, остается неизменной. Это значит, что припереходе из одной среды в другую будет меняться длина волны l.
Если мы возбудили колебания в какой-либо точке среды, то колебания передадутся всем окружающим ее точкам, т.е. колебаться будет совокупность частиц, заключенных в некотором объеме. Распространяясь от источника колебаний волновой процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к некоторому моменту времени t, называется фронтом волны.
Таким образом, фронт волны является той поверхностью, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут быть различной формы. Простейшие из них имеют форму сферы или плоскости. Волны, имеющие такие поверхности, называются соответственно сферическими или плоскими.
Часто при решении задач о распространении волн надо строить волновой фронт для некоторого момента времени по волновому фронту, заданному для начального момента времени. Это можно сделать, используя принцип Гюйгенса , сущность которого в следующем.
Пусть волновой фронт, перемещающийся в однородной среде, занимает в данный момент времени положение 1 (рис. 1.4). Требуется найти его положение через промежуток времени Dt .
 |
В соответствии с принципом Гюйгенса, каждая точка среды, до которой дошла волна, сама становится источником вторичных волн (первое положение принципа Гюйгенса).
Это значит, что от нее, как из центра, начинает распространяться сферическая волна. Чтобы построить вторичные волны, вокруг каждой точки исходного фронта опишем сферы радиусом Dx = V Dt , где V – скорость волны. На рис. 1.4 показаны такие сферы. Здесь кружочки – сечения сферических поверхностей плоскостью чертежа.
Вторичные волны взаимно гасятся во всех направлениях, кроме направлений исходного фронта (второе положение принципа Гюйгенса), то есть, колебания сохраняются только на внешней огибающей вторичных волн. Построив эту огибающую, получим исходное положение 2 волнового фронта (штриховая линия). Положения 1 и 2 волнового фронта
− в нашем случае плоскости.
Принцип Гюйгенса применим и к неоднородной среде. В этом случае значения V, а, следовательно, и Dх неодинаковы в различных направлениях.
Так как прохождение волны сопровождается колебанием частиц среды, то вместе с волной перемещается в пространстве и энергия колебаний.
Бегущими волнами называются волны, которые переносят в пространстве энергию и импульс. Перенос энергии волнами характеризуется вектором плотности потока энергии. Направление этого вектора совпадает с направлением переноса энергии, а его модуль называется интенсивностью волны (или плотностью потока энергии) и представляет собой отношение энергии W , переносимой волною сквозь площадь S ┴ , перпендикулярную лучу, к продолжительности времени переноса ∆t и размеру площади:
I = W/ (∆t∙S ┴),
откуда численно I=W , если ∆t =1 и S ┴ =1. Единица интенсивности: ватт на метр в квадрате (Вт /м 2 ).
Получим выражение для интенсивности волны. При концентрации n 0 частиц среды, каждая из которых имеет массу m , объемная плотность w 0 энергии складывается из кинетической энергии движения частиц среды и потенциальной энергии, являющейся энергией деформированного объема. Объемная плотность энергии определяется выражением:
w 0 = n 0 mw 2 A 2 / 2 = rw 2 A 2 / 2,
где r =n 0 m . Подробный вывод выражения для объемной плотности энергии упругих волн приведен в учебном пособии . Очевидно, за 1с сквозь площадку в 1 м 2 переносится энергия, содержащаяся в объеме прямоугольного параллелепипеда с основанием 1 м 2 и высотой, численно равной скорости V (рис. 1.5), следовательно интенсивность волны
I = w 0 V = rVw 2 A 2 / 2. (1.3)
Таким образом, интенсивность волны пропорциональна плотности среды, скорости, квадрату круговой частоты и квадратуамплитуды волны
.
Вектор , модуль которого равен интенсивности волны, а направление совпадает с направлением распространения волны (и переноса энергии), определяется выражением.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом.
Уравнение плоской волны
Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер.
Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x . Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t : . Пусть колебание точек, лежащих в плоскости , имеет вид (при начальной фазе )
| (5.2.2) |
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x . Чтобы пройти путь x , необходимо время .
Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости , т.е.
 ,
| (5.2.3) |
– это уравнение плоской волны.
Таким образом, x есть смещение любой из точек с координатой x в момент времени t . При выводе мы предполагали, что амплитуда колебания . Это будет, если энергия волны не поглощается средой.
Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z .
В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны .
Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x . Волна, распространяющаяся в противоположном направлении, имеет вид:
.
Уравнение волны можно записать и в другом виде.
Введем волновое число , или в векторной форме:
| , | (5.2.5) |
где – волновой вектор, – нормаль к волновой поверхности.
Так как , то 
. Отсюда . Тогда уравнение плоской волны
запишется так:
 .
| (5.2.6) |
Уравнение сферической волны
Указание по мерам безопасности
При выполнении лабораторной работы
Внутри используемых в работе электроизмерительных приборов имеется переменное сетевое напряжение 220 В, 50 Гц, представляющее опасность для жизни.
Наиболее опасными местами являются сетевой выключатель, гнезда предохранителей, шнур сетевого питания приборов, соединительные провода, находящиеся под напряжением.
К выполнению лабораторных работ в учебной лаборатории допускаются обучающиеся прошедшие обучение по мерам безопасности при проведении лабораторных работ с обязательным оформлением в журнале протоколов проверки знаний по мерам безопасности при проведении лабораторных работ.
Перед выполнением лабораторной работы обучающимся
необходимо:
Усвоить методику выполнения лабораторной работы, правила ее безопасного выполнения;
Ознакомиться с экспериментальной установкой; знать безопасные методы и приемы обращения с приборами и оборудованием при выполнении данной лабораторной работы;
Проверить качество сетевых шнуров; убедиться, что все токоведущие части приборов закрыты и недоступны для прикосновения;
Проверить надежность соединения клемм на корпусе прибора с шиной заземления;
В случае обнаружения неисправности немедленно доложить преподавателю или инженеру;
Получить у преподавателя допуск к ее выполнению, подтверждая этим усвоение теоретического материала. Обучающийся не получивший допуск к выполнению лабораторной работы не допускается.
Включение приборов производит преподаватель или инженер. Только после того, как он убедится в исправности приборов и правильности их сборки можно приступать к выполнению лабораторной работы.
При выполнении лабораторной работы обучающиеся должны:
Не оставлять без присмотра включенные приборы;
Не наклоняться к ним близко, не передавать через них какие-либо предметы и не опираться на них;
При работе с грузиками надежно закреплять их крепежными винтами на осях.
замену любого элемента установки, присоединение или разъединение разъемных соединений производить только при отключенном электропитании под четким наблюдением преподавателя или инженера.
Обо всех недостатках, обнаруженных во время выполнения лабораторной работы, сообщить преподавателю или инженеру
По окончании работы отключение аппаратуры и приборов от электросети производит преподаватель или инженер.
Лабораторная работа № 5
ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ МЕТОДОМ СТОЯЧЕЙ ВОЛНЫ
Цель работы:
ознакомиться с основными характеристиками волновых процессов;
изучить условия образования и особенности стоячей волны.
Задачи работы
определить скорость звука в воздухе методом стоячей волны;
определить для воздуха отношение изобарической теплоемкости к изохорической.
Понятие о волнах.
Тело, совершающее механические колебания, передает в окружающую среду за счет сил трения или сопротивления теплоту, что усиливает беспорядочное движение частиц среды. Однако во многих случаях за счет энергии колебательной системы возникает упорядоченное движение соседних частиц окружающей среды – они начинают совершать вынужденные колебания относительно своего исходного положения под действием упругих сил, связывающих частицы друг с другом. Объем пространства, в котором происходят эти колебания, возрастает с течением времени. Такой процесс распространения колебаний в среде называется волновым движением или просто в о л н о й.
В общем случае наличие упругих свойств в среде не является обязательным для распространения в ней волн. Например, электромагнитные и гравитационные волны распространяются и в вакууме. Поэтому в физике в о л н а м и называют всякие распространяющиеся в пространстве возмущения состояния вещества или поля. Под возмущением понимают отклонение физических величин от их равновесных состояний.
В твердых телах под возмущением понимают периодически изменяющуюся деформацию, порожденную действием периодической силы и вызывающую отклонение частиц среды от положения равновесия – их вынужденные колебания. При рассмотрении процессов распространения волн в телах обычно отвлекаются от молекулярного строения этих тел и рассматривают тела как сплошную среду, непрерывно распределенную в пространстве. Под частицей среды, совершающей вынужденные колебания, понимают малый элемент объема среды, размеры которого в то же время во много раз больше межмолекулярных расстояний. Вследствие действия упругих сил деформация будет распространяться в среде с определенной скоростью, называемой скоростью волны.
Важно отметить, что частицы среды не увлекаются движущейся волной. Скорость их колебательного движения отличается от скорости волны. Траектория частиц представляет собой замкнутую кривую, а их суммарное отклонение за период равно нулю. Поэтому распространение волн не вызывает переноса вещества, хотя при этом переносится энергия от источника колебаний в окружающее пространство.
В зависимости от того, в каком направлении происходят колебания частиц, говорят о волнах продольной или поперечной поляризации.
Волны называются продольными, если смещение частиц среды происходит вдоль направления распространения волны (например, при периодическом упругом сжатии или растяжении тонкого стержня вдоль его оси). Продольные волны распространяются в средах, в которых силы упругости возникают при сжатии или растяжении (т. е. в твердых, жидких и газообразных).
Если частицы колеблются в направлении, перпендикулярном к направлению распространения волны, то волны называются поперечными. Они распространяются только в средах, в которых возможна деформация сдвига (только в твердых телах). Кроме того, поперечные волны распространяются на свободной поверхности жидкости (например, волны на поверхности воды) или на границе раздела двух несмешивающихся жидкостей (например, на границе пресной и соленой воды).
В газовой среде волны представляют собой чередующиеся области более высокого и более низкого давления и плотности. Они возникают в результате вынужденных колебаний частиц газа, происходящих с различной фазой в различных точках. Под действием изменяющегося давления барабанная перепонка уха совершает вынужденные колебания, которые через уникальную сложную систему слухового аппарата вызывают биотоки, протекающие к мозгу.
Уравнение плоской волны. Фазовая скорость
Волновой поверхностью называют геометрическое место точек, колеблющихся в одинаковой фазе. В простейших случаях они имеет форму плоскости или сферы, а соответствующая волна называется плоской или сферической. Фронтом волны называется геометрическое место точек, до которых в данный момент времени доходят колебания. Фронт волны разделяет области пространства, уже вовлеченную в волновой процесс и еще не вовлеченную. Волновых поверхностей существует бесконечное множество и они неподвижны, а фронт волны один и он перемещается с течением времени.
Рассмотрим плоскую волну, распространяющуюся вдоль оси х. Пусть частицы среды, лежащие в плоскости x = 0 , начинают в момент t =0 совершать колебания по гармоническому закону относительно исходного положения равновесия. Это значит, что смещение частиц от их исходного положения f изменяется во времени по закону синуса или косинуса, например:
где f - смещение данных частиц от их исходного положения равновесия в момент времени t , А -максимальное значение смещения (амплитуда); ω - циклическая частота.
Пренебрегая затуханием в среде, получим уравнение колебания частиц, расположенных в плоскости, соответствующей произвольному значению x >0). Пусть волна распространяется в направлении возрастания координаты х . Чтобы пройти путь от плоскости x =0 до указанной плоскости, волне требуется время
где v -скорость перемещения поверхности постоянной фазы (фазовая скорость).
Поэтому колебания частиц, лежащих в плоскости х , начнутся в момент t = τ и будут происходить по такому же закону, что и в плоскости х=0, но с отставанием по времени на величину τ , а именно:
(3)
Иначе говоря, смещение частиц, находившихся в момент t =0 в плоскости х, в момент t будут такими же, как в плоскости х =0, но в более ранний момент времени
t 1 = (4)
С учетом (4), выражение (3) преобразуется:
(5)
Уравнение (5) представляет собой уравнение плоской бегущей волны, распространяющейся вдоль положительного направления оси х . Из него можно определить отклонение частиц среды от равновесия в любой точке пространства с координатой х и в любой момент времени t при распространении указанной волны. Уравнение (5) соответствует случаю, когда частицам в начальный момент была сообщена начальная скорость. Если же в начальный момент частицам сообщено отклонение от положения равновесия без сообщения скорости, в (5) вместо синуса нужно поставить косинус. Аргумент косинуса или синуса называют фазой колебания. Фаза определяет состояние колебательного процесса в данный момент времени (знак и абсолютную величину относительного отклонения частиц от их положения равновесия). Из (5) видно, что фаза колебаний частиц, расположенных в плоскости х , меньше соответствующей величины для частиц, расположенных в плоскости х =0, на величину, равную .
Если плоская волна распространяется в направлении убывания х (налево), то уравнение (5) преобразуется к виду:
(6)
Учитывая, что
запишем (6) в виде:
(8)
где Т - периодколебания, ν - частота.
Расстояние λ, на которое волна распространяется за период Т , называется длиной волны.
Можно также определить длину волны и как расстояние между двумя ближайшими точками, фазы колебаний которых отличаются на 2π (рис.1).
Как отмечено выше, упругие волны в газах представляют собой чередующиеся области с более высоким и более низким давлением и плотностью. Это иллюстрируется рис 1, на котором представлены для некоторого момента времени смещение частиц (а), их скорости (б), давление или плотность (в) в различных точках пространства. Частицы среды движутся со скоростью 
(не путать с фазовой скоростью v
). Слева и справа от точек A 1
, A 3
, A 5
и др. скорости частиц направлены к этим точкам. Поэтому в данных точках образуются максимумы плотности (давления). Справа и слева от точек A 2
, A 4
, A 6
и др. скорости частиц направлены от данных точек и в них образуются минимумы плотности (давления).
Смещение частиц среды при распространении в ней бегущей волны в различные моменты времени представлены на рис. 2. Как видно, имеется аналогия с волнами на поверхности жидкости. Максимумы и минимумы отклонений от положения равновесия перемещаются в пространстве с течением времени с фазовой скоростью v . С такой же скоростью перемещаются максимумы и минимумы плотности (давления).
Фазовая скорость волны зависит от упругих свойств и плотности среды. Предположим, что имеется длинный упругий стержень (рис. 3) с площадью поперечного сечения, равной S , в котором распространяется продольное возмущение вдоль оси х с плоским волновым фронтом Пусть за промежуток времени от t 0 до t 0 +Δt фронт переместится от точки А до точки В на расстояние АВ = v Δt , где v – фазовая скорость упругой волны. Длительность промежутка Δt возьмем настолько малой, что скорость движения частиц во всем объеме (т.е. между сечениями, проходящими перпендикулярно оси х через точки А и В ) будет одинаковой и равной u . Частицы из точки А за указанный промежуток времени переместятся на расстояние u Δt . Частицы же, расположенные в точке В , в момент t 0 +Δt только начнут движение и их перемещение к данному моменту времени будет равно нулю. Пусть первоначальная длина участка АВ равна l . К моменту t 0 +Δt она изменится на величину u Δt , которая и будет величиной деформации Δl . Масса участка стержня между точками А и В равна Δm = ρSvΔt. Изменение импульса этой массы за промежуток времени от t 0 до t 0 +Δt равно
Δр = ρSvuΔt (10).
Силу, действующую на массу Δm , можно определить из закона Гука:
По второму закону Ньютона , или . Приравни
вая правые части последнего выражения и выражения (10), получим:
откуда следует:
Скорость распространения поперечной волны
где G - модуль сдвига.
Звуковые волны в воздухе являются продольными. Для жидкостей и газов вместо модуля Юнга в формулу (1) входит отношение отклонения давления ΔΡ к относительному изменению объема
(13)
Знак минус означает, что увеличению давления (процессу сжатия среды) соответствует уменьшение объема и наоборот. Полагаяизменения объема и давления бесконечно малыми, можно записать
(14)
При распространении волн в газах давление и плотность периодически повышаются и понижаются (соответственно, при сжатии и разрежении), в результате чего происходит изменение температуры различных участков среды. Сжатие и разрежение происходят так быстро, что смежные участки не успевают обменяться энергией. Процессы, происходящие в системе без теплообмена с окружающей средой, называются адиабатическими. При адиабатическом процессе изменение состояния газа описывается уравнением Пуассона
(15)
Параметр γ называют показателем адиабаты. Он равен отношению молярных теплоемкостей газа при постоянном давлении C p и постоянном объеме C v:
Взяв дифференциал от обеих частей равенства (15), получаем
,
откуда следует:
Подставив (6) в (4), получим для модуля упругости газа
Подставив (7) в (1), найдем скорость упругих волн в газах:
Из уравнения Менделеева-Клапейрона 
можно выразить плотность газа
, (19)
где - молярная масса.
Подставляя (9) в (8), получим конечную формулу для нахождения скорости звука в газе:
где R - универсальная газовая постоянная, Т - температура газа.
Измерение скорости звука - один из наиболее точных методов определения показателя адиабаты.
Преобразуя формулу (10), получим:
Таким образом, для определения показателя адиабаты достаточно измерить температуру газа и скорость распространения звука.
В дальнейшем более удобно использовать в уравнении волны косинус. Учитывая (19 и 20), уравнение бегущей волны можно представить в виде:
(22)
где - волновое число, показывающее, сколько длин волн укладывается на расстоянии, равном 2π метров.
Для бегущей волны, распространяющейся против положительного направления оси х, получим:
(23)
Особую роль играют гармоническиеволны (см., например, уравнения (5, 6, 22, 23)). Это связано с тем,чтолюбое распространяющееся колебание, какова бы ни была его форма, всегда можно рассматривать как результат суперпозиции (сложения) гармонических волн с соответственно подобранными частотами, амплитудами и фазами.
Стоячие волны.
Особый интерес представляет собой результат интерференции двух волн с одинаковой амплитудой и частотой, распространяющихся навстречу друг другу. На опыте это можно осуществить, если на пути бегущей волны перпендикулярно к направлению распространения поставить хорошо отражающую преграду. В результате сложения (интерференции) падающей и отраженной волн возникнет так называемая стоячая волна.
Пусть падающая волна описывается уравнением (22), а отраженная – уравнением (23). По принципу суперпозиции суммарное смещение равно сумме смещений, создаваемых обеими волнами. Сложение выражений (22) и (23) дает
Это уравнение, называемое уравнением стоячей волны, удобно в дальнейшем анализировать в виде:
, (25)
где множитель
(26)
является амплитудой стоячей волны. Как видноиз выражения (26), амплитуда стоячей волны зависит от координаты точки, но не зависит от времени. У бегущей плоской волны амплитуда не зависит ни от координаты, ни от времени (при отсутствии затухания).
Из (27) и (28) следует, что расстояние между соседними узлами, как и расстояние между соседними пучностями равно , а расстояние между соседними узлом и пучностью равно .
Из уравнения (25) следует, что все точки среды, расположенные между двумя соседними узлами, колеблются в одной фазе, причем значение фазы определяется только временем. В частности, они достигают максимального отклонения в один и тот же момент времени. Для бегущей волны как следует из (16), фаза определяется как временем, так и пространственной координатой. В этом еще одно отличие между стоячими и бегущими волнами. При переходе через узел фаза стоячей волны скачкообразно изменяется на 180 о.
Смещение от положения равновесия для различных моментов времени в стоячей волне приведено на рис. 4. За начальный момент времени принят момент, когда частицы среды максимально отклонены от исходного положения равновесия (кривая 1).
И , представленные кривыми 6, 7, 8 и 9, совпадают с отклонениями в соответствующие моменты первого полупериода (т. е. кривая 6 совпадает с кривой 4 и т.д.). Как видно, с момента смещение частиц снова изменяет знак.
При отражении волн на границе двух сред возникает либо узел, либо пучность (в зависимости от так называемых акустических сопротивлений сред). Акустическим сопротивлением среды называют величину , где . – плотность среды, - скорость упругих волн в среде. Если среда, от которой отражается волна, обладает более высоким акустическим сопротивлением, чем та, в которой эта волна возбуждается, то на границе раздела образуется узел (рис. 5). В этом случае фаза волны при отражении меняется на противоположную (на 180°). При отражении волны от среды с меньшим акустическим сопротивлением изменение фазы колебаний не происходит.
В отличие от бегущей волны, которая переносит энергию, в стоячей волне никакого переноса энергии нет. Бегущая волна может двигаться вправо или влево, а у стоячей волны нет направления распространения. Под термином "стоячая волна" нужно понимать особое колебательное состояние среды, образованное интерферирующими волнами.
В момент, когда частицы среды проходят положение равновесия, полная энергия частиц, захваченных колебанием, равна кинетической. Она сосредоточена в окрестностях пучностей. Напротив, в момент, когда отклонение частиц от положения равновесия максимально, их полная энергия является уже потенциальной. Она сосредоточена вблизи узлов. Таким образом, два раза за период происходит переход энергии от пучностей к соседним узлам и наоборот. В результате средний по времени поток энергии в любом сечении стоячей волны равен нулю.
