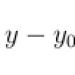Глава 6. Непрерывные случайные величины.
§ 1. Плотность и функция распределения непрерывной случайной величины.
Множество значений непрерывной случайной величины несчетно и обычно представляет собой некоторый промежуток конечный или бесконечный.
Случайная величина x(w),заданная в вероятностном пространстве {W, S,P}, называется непрерывной (абсолютно непрерывной) W, если существует неотрицательная функция такая, что при любых х функцию распределения Fx(x) можно представить в виде интеграла
Функция называется функцией плотности распределения вероятностей .
Из определения вытекают свойства функции плотности распределения :
1..gif" width="97" height="51">
3. В точках непрерывности плотность распределения равна производной функции распределения: .
4. Плотность распределения определяет закон распределения случайной величины, т. к. определяет вероятность попадания случайной величины на интервал :
5.Вероятность того, что непрерывная случайная величина примет конкретное значение равна нулю: . Поэтому справедливы следующие равенства:
График функции плотности распределения называется кривой распределения , и площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Тогда геометрически значение функции распределения Fx(x) в точке х0 есть площадь, ограниченная кривой распределения и осью абсцисс и лежащая левее точки х0.
Задача 1. Функция плотности непрерывной случайной величины имеет вид:
Определить константу C, построить функцию распределения Fx(x) и вычислить вероятность .
Решение. Константа C находится из условия Имеем:
откуда C=3/8.
Чтобы построить функцию распределения Fx(x), отметим, что интервал делит область значений аргумента x (числовую ось) на три части: https://pandia.ru/text/78/107/images/image017_17.gif" width="264" height="49">
так как плотность x на полуоси равна нулю. Во втором случае
Наконец, в последнем случае, когда x>2,
Так как плотность обращается в нуль на полуоси . Итак, получена функция распределения
Вероятность вычислим по формуле . Таким образом,
§ 2. Числовые характеристики непрерывной случайной величины
Математическое ожидание для непрерывно распределенных случайных величин определяется по формуле https://pandia.ru/text/78/107/images/image028_11.gif" width="205" height="56 src=">,
если интеграл, стоящий справа, абсолютно сходится.
Дисперсия
x может быть вычислена по формуле 
, а также, как и в дискретном случае, по формуле https://pandia.ru/text/78/107/images/image031_11.gif" width="123" height="49 src=">.
Все свойства математического ожидания и дисперсии , приведенные в главе 5 для дискретных случайных величин, справедливы и для непрерывных случайных величин.
Задача 2 . Для случайной величины x из задачи 1 вычислить математическое ожидание и дисперсию.
Решение.
И значит,
https://pandia.ru/text/78/107/images/image035_9.gif" width="184" height="69 src=">
График плотности равномерного распределения см. на рис. .
Рис.6.2. Функция распределения и плотность распределения. равномерного закона
Функция распределения Fx(x) равномерно распределенной случайной величины равна
Fx(x)= 
Математическое ожидание и дисперсия ; .
Показательное (экспоненециальное) распределение. Непрерывная случайная величина x, принимающая неотрицательные значения, имеет показательное распределение с параметром l>0, если плотность распределения вероятностей случайной величины равна
рx(x)=
Рис. 6.3. Функция распределения и плотность распределения показательного закона.
Функция распределения показательного распределения имеет вид
Fx(x)=https://pandia.ru/text/78/107/images/image041_8.gif" width="17" height="41">.gif" width="13" height="15"> и , если ее плотность распределения равна
.
Через обозначается множество всех случайных величин, распределенных по нормальному закону с параметрами параметрами и .
Функция распределения нормально распределенной случайной величины равна
.
Рис. 6.4. Функция распределения и плотность распределения нормального закона
Параметры нормального распределения суть математическое ожидание https://pandia.ru/text/78/107/images/image048_6.gif" width="64 height=24" height="24">
В частном случае, когда https://pandia.ru/text/78/107/images/image050_6.gif" width="44" height="21 src="> нормальное распределение называется стандартным , и класс таких распределений обозначается https://pandia.ru/text/78/107/images/image052_6.gif" width="119" height="49">,
а функция распределения
Такой интеграл не вычислим аналитически (не берется в «квадратурах»), и потому для функции составлены таблицы. Функция связана с введенной в главе 4 функцией Лапласа
,
следующим соотношением 
. В случае же произвольных значений параметров https://pandia.ru/text/78/107/images/image043_5.gif" width="21" height="21 src="> функция распределения случайной величины связана с функцией Лапласа с помощью соотношения:
.
Поэтому вероятность попадания нормально распределенной случайной величины на интервал можно вычислять по формуле
.
Неотрицательная случайная величина x называется логарифмически нормально распределенной, если ее логарифм h=lnx подчинен нормальному закону. Математическое ожидание и дисперсия логарифмически нормально распределенной случайной величины равны Мx= и Dx=.
Задача 3. Пусть задана случайная величина https://pandia.ru/text/78/107/images/image065_5.gif" width="81" height="23">.
Решение. Здесь и https://pandia.ru/text/78/107/images/image068_5.gif" width="573" height="45">
Распределение Лапласа задается функцией fx(x)=https://pandia.ru/text/78/107/images/image070_5.gif" width="23" height="41"> и эксцесс равен gx=3.
Рис.6.5. Функция плотности распределения Лапласа.
Случайная величина x распределена по закону Вейбулла , если она имеет функцию плотности распределения, равную https://pandia.ru/text/78/107/images/image072_5.gif" width="189" height="53">
Распределению Вейбулла подчиняются времена безотказной работы многих технических устройств. В задачах данного профиля важной характеристикой является интенсивность отказа (коэффициент смертности) l(t) исследуемых элементов возраста t, определяемый соотношением l(t)=. Если a=1, то распределение Вейбулла превращается в экспоненциальное распределение, а если a=2 - в так называемое распределение Рэлея.
Математическое ожидание распределения Вейбулла: -https://pandia.ru/text/78/107/images/image075_4.gif" width="219" height="45 src=">, где Г(а) - функция Эйлера. .
В различных задачах прикладной статистики часто встречаются так называемые «усеченные» распределения. Например, налоговые органы интересуются распределением доходов тех лиц, годовой доход которых превосходит некоторый порог с0, установленный законами о налогообложении. Эти распределения оказываются приближенно совпадающими с распределением Парето. Распределение Парето задается функциями
Fx(x)=P(x
Здесь https://pandia.ru/text/78/107/images/image081_4.gif" width="60" height="21 src=">.
Задача 4. Случайная величина равномерно распределена на отрезке . Найти плотность случайной величины .
Решение. Из условия задачи следует, что
Далее, функция является монотонной и дифференцируемой функцией на отрезке и имеет обратную функцию 
, производная которой равна Следовательно,
§ 5. Пара непрерывных случайных величин
Пусть заданы две непрерывные случайные величины x и h. Тогда пара (x, h) определяет «случайную» точку на плоскости. Пару (x, h) называют случайным вектором или двумерной случайной величиной.
Совместной функцией распределения
случайных величин x и h и называется функция F(x, y)=Phttps://pandia.ru/text/78/107/images/image093_3.gif" width="173" height="25">. Совместной плотностью
распределения вероятностей случайных величин x и h называется функция такая, что 
.
Смысл такого определения совместной плотности распределения заключается в следующем. Вероятность того, что «случайная точка» (x, h) попадет в область на плоскости, вычисляется как объем трехмерной фигуры – «криволинейного» цилиндра, ограниченного поверхностью https://pandia.ru/text/78/107/images/image098_3.gif" width="211" height="39 src=">
Простейшим примером совместного распределения двух случайных величин является двумерное равномерное распределение на множестве A . Пусть задано ограниченное множество М с площадью Оно определяется как распределение пары (x, h), задаваемое с помощью следующей совместной плотности:
Задача 5. Пусть двумерный случайный вектор (x, h) равномерно распределен внутри треугольника . Вычислить вероятность неравенства x>h.
Решение. Площадь указанного треугольника равна (см. рис. № ?). В силу определения двумерного равномерного распределения совместная плотность случайных величин x, h равна
Событие соответствует множеству 
на плоскости, т. е. полуплоскости. Тогда вероятность
На полуплоскости B совместная плотность равна нулю вне множества https://pandia.ru/text/78/107/images/image102_2.gif" width="15" height="17">. Таким образом, полуплоскость B разбивается на два множества и https://pandia.ru/text/78/107/images/image110_1.gif" width="17" height="23"> и , причем второй интеграл равен нулю, так как там совместная плотность равна нулю. Поэтому
Если задана совместная плотность распределения для пары (x, h), то плотности и составляющих x и h называются частными плотностями и вычисляются по формулам:
https://pandia.ru/text/78/107/images/image116_1.gif" width="224" height="23 src=">
Для непрерывно распределенных случайных величин с плотностями рx(х), рh(у) независимость означает, что
Задача 6. В условиях предыдущей задачи определить, независимы ли составляющие случайного вектора x и h?
Решение . Вычислим частные плотности и . Имеем:
https://pandia.ru/text/78/107/images/image119_1.gif" width="283" height="61 src=">
Очевидно, что в нашем случае https://pandia.ru/text/78/107/images/image121_1.gif" width="64" height="25"> - совместная плотность величин x и h, а j(х, у) - функция двух аргументов, тогда
https://pandia.ru/text/78/107/images/image123_1.gif" width="184" height="152 src=">
Задача 7. В условиях предыдущей задачи вычислить .
Решение. Согласно указанной выше формуле имеем:
.
Представив треугольник в виде
https://pandia.ru/text/78/107/images/image127_1.gif" width="479" height="59">
§ 5. Плотность суммы двух непрерывных случайных величин
Пусть x и h - независимые случайные величины с плотностями https://pandia.ru/text/78/107/images/image128_1.gif" width="43" height="25">. Плотность случайной величины x + h вычисляется по формуле свертки
https://pandia.ru/text/78/107/images/image130_0.gif" width="39" height="19 src=">. Вычислить плотность суммы .
Решение. Так как x и h распределены по показательному закону с параметром , то их плотности равны
Следовательно,
https://pandia.ru/text/78/107/images/image134_0.gif" width="339 height=51" height="51">
Если x<0, то в этой формуле аргумент https://pandia.ru/text/78/107/images/image136_0.gif" width="65" height="25">отрицателен, и потому . Поэтому Если же https://pandia.ru/text/78/107/images/image140_0.gif" width="359 height=101" height="101">
Таким образом, мы получили ответ:
https://pandia.ru/text/78/107/images/image142_0.gif" width="40" height="41 "> нормально распределена с параметрами 0 и 1. Случайные величины x1 и x2 независимы и имеют нормальные распределения с параметрами а1, и а2, соответственно. Доказать, что x1 + x2 имеет нормальное распределение. Случайные величины x1, x2, ... xn распределены и независимы и имеют одинаковую функцию плотности распределения
.
Найти функцию распределения и плотность распределения величин:
а) h1 = min {x1 , x2, ...xn} ; б) h(2) = max {x1,x2, ... xn }
Случайные величины x1, x2, ... xn независимы и равномерно распределены на отрезке [а, b]. Найти функции распределения и функции плотности распределения величин
x(1) = min {x1,x2, ... xn} и x(2)= max{x1, x2, ...xn}.
Доказать, что Мhttps://pandia.ru/text/78/107/images/image147_0.gif" width="176" height="47">.
Случайная величина распределена по закону Коши Найти: а) коэффициент а; б) функцию распределения; в) вероятность попадания на интервал (-1, 1). Показать, что математическое ожидание x не существует. Случайная величина подчинена закону Лапласа с параметром l (l>0): Найти коэффициент а; построить графики плотности распределения и функции распределения; найти Mx и Dx; найти вероятности событий {|x|< и {çxç<}. Случайная величина x подчинена закону Симпсона на отрезке [-а, а], т. е. график её плотности распределения имеет вид:
Написать формулу для плотности распределения, найти Мx и Dx.
Вычислительные задачи.
Случайная точка А имеет в круге радиуса R равномерное распределение. Найти математическое ожидание и дисперсию расстояния r точки до центра круга. Показать, что величина r2 равномерно распределена на отрезке . 
Плотность распределения случайной величины имеет вид:
Вычислить константу C, функцию распределения F(x), и вероятность 
Плотность распределения случайной величины имеет вид:
Вычислить константу C, функцию распределения F(x), и вероятность 
Плотность распределения случайной величины имеет вид: 
Вычислить константу C, функцию распределения F(x), , дисперсию и вероятность Случайная величина имеет функцию распределения
Вычислить плотность случайной величины, математическое ожидание, дисперсию и вероятность Проверить, что функция =
может быть функцией распределения случайной величины. Найти числовые характеристики этой величины: Mx и Dx. Случайная величина равномерно распределена не отрезке . Выписать плотность распределения. Найти функцию распределения. Найти вероятность попадания случайной величины на отрезок и на отрезок . Плотность распределения x равна
.
Найти постоянную с, плотность распределения h = и вероятность
Р (0,25 Время безотказной работы ЭВМ распределено по показательному закону с параметром l = 0,05 (отказа в час), т. е. имеет функцию плотности р(х) = Решение определенной задачи требует безотказной работы машины в течение 15 минут. Если за время решения задачи произошел сбой, то ошибка обнаруживается только по окончании решения, и задача решается заново. Найти: а) вероятность того, что за время решения задачи не произойдет ни одного сбоя; б) среднее время, за которое будет решена задача. Стержень длины 24 см ломают на две части; будем считать, что точка излома распределена равномерно по всей длине стержня. Чему равна средняя длина большей части стержня? Отрезок длины 12 см случайным образом разрезается на две части. Точка разреза равномерно распределена по всей длине отрезка. Чему равна средняя длина малой части отрезка? Случайная величина равномерно распределена на отрезке . Найти плотность распределения случайной величины а) h1 = 2x + 1; б) h2 =-ln(1-x); в) h3 = . Показать, что если x имеет непрерывную функцию распределения F(x) = P(x Найти функцию плотности и функцию распределения суммы двух независимых величин x и h c равномерными законами распределения на отрезках и соответственно. Случайные величины x и h независимы и равномерно распределены на отрезках и соответственно. Вычислить плотность суммы x+h. Случайные величины x и h независимы и равномерно распределены на отрезках и соответственно. Вычислить плотность суммы x+h. Случайные величины x и h независимы и равномерно распределены на отрезках и соответственно. Вычислить плотность суммы x+h. Случайные величины независимы и имеют показательное распределение с плотностью Как известно, случайной величиной
называется переменная величина, которая может
принимать те или иные значения в зависимости от случая. Случайные величины обозначают
заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными
буквами (x, y, z). Случайные величины делятся на прерывные (дискретные) и непрерывные. Дискретной случайной величиной
называется случайная величина, принимающая лишь
конечное или бесконечное (счетное) множество значений с определенными ненулевыми вероятностями. Законом распределения дискретной случайной величины
называется
функция, связывающая значения случайной величины с соответствующими им вероятностями. Закон распределения может быть
задан одним из следующих способов. 1
. Закон распределения может быть задан таблицей:
где λ>0, k = 0, 1, 2, … . в)
с помощью функции распределения F(x)
, определяющей для каждого значения x
вероятность того, что случайная величина X примет значение, меньшее x, т.е. F(x) = P(X < x). Свойства функции F(x) 3
. Закон распределения может быть задан графически
– многоугольником
(полигоном) распределения (смотри задачу 3). Отметим, что для решения некоторых задач не обязательно знать закон распределения. В некоторых случаях достаточно знать
одно или несколько чисел, отражающих наиболее важные особенности закона распределения. Это
может быть число, имеющее смысл «среднего значения» случайной величины, или же число,
показывающее средний размер отклонения случайной величины от своего среднего значения.
Числа такого рода называют числовыми характеристиками случайной величины. Основные числовые характеристики дискретной случайной величины
: Выпущено 1000 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на
10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить
закон распределения вероятностей случайной величины X – выигрыша на один билет. Решение.
По условию задачи возможны следующие значения случайной
величины X: 0, 10, 50, 100 и 500. Число билетов без выигрыша равно 1000 – (5+10+20+50) = 915, тогда P(X=0) = 915/1000 = 0,915. Аналогично находим все другие вероятности: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01,
P(X=500) = 5/1000=0,005. Полученный закон представим в виде таблицы: Найдем математическое ожидание величины Х:
М(Х) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2+3+4+5+6)/6 = 21/6 = 3,5 Устройство состоит из трех независимо работающих элементов.
Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа
отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения
F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое
отклонение дискретной случайной величины. Решение.
1.
Дискретная случайная величина X={число отказавших элементов в
одном опыте} имеет следующие возможные значения: х 1 =0 (ни один из элементов устройства не
отказал), х 2 =1 (отказал один элемент), х 3 =2 (отказало два элемента) и х 4 =3 (отказали три
элемента). Отказы элементов независимы друг от друга, вероятности отказа каждого элемента равны между собой,
поэтому применима формула
Бернулли
. Учитывая, что, по условию, n=3, р=0,1, q=1-р=0,9, определим
вероятности значений: Таким образом, искомый биномиальный закон распределения Х имеет вид: По оси абсцисс откладываем возможные значения х i , а по оси ординат –
соответствующие им вероятности р i . Построим точки М 1 (0; 0,729), М 2 (1; 0,243),
М 3 (2; 0,027), М 4 (3; 0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения. 3.
Найдем функцию распределения F(x) = Р(Х График функции F(x) 4.
Для биномиального распределения Х: Случайная величина Х
имеет нормальное распределение (или распределение по закону Гаусса), если ее плотность вероятности имеет вид: Рис. 2.13 Рис. 2.14 Функцией распределения случайной величины X называется функция F(x), выражающая для каждого х вероятность того, что случайная величина X примет значение
, меньшее х
Пример 2.5. Дан ряд распределения случайной величины Найти и изобразить графически ее функцию распределения. Решение. В соответствии с определением F(jc) = 0 при х
х
F(x) =
0,4 + 0,1 = 0,5 при 4 F{x) = 0,5 + 0,5 = 1 при х
> 5. Итак (см. рис. 2.1): Свойства функции распределения: 1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. при х
2
>х
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности - равна единице, т.е. 4. Вероятность попадания случайной величины X
в интервал
равна определенному интегралу от ее плотности вероятности в пределах от а
до b
(см. рис. 2.2), т.е.
Рис. 2.2 3. Функция распределения непрерывной случайной величины (см. рис. 2.3) может быть выражена через плотность вероятности по формуле: F(x)=
Jp (*)*. (2.10) 4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: Геометрически свойства / и 4
плотности вероятности означают, что ее график - кривая распределения
- лежит не ниже оси абсцисс
, и полная площадь фигуры
, ограниченной кривой распределения и осью абсцисс
, равна единице.
Для непрерывной случайной величины X
математическое ожидание М(Х)
и дисперсия D(X)
определяются по формулам: (если интеграл абсолютно сходится); или
(если приведенные интегралы сходятся). Наряду с отмеченными выше числовыми характеристиками для описания случайной величины используется понятие квантилей и процентных точек. Квантилем уровня q
(или q-квантилем) называется такое значение
x q
случайной величины
, при котором функция ее распределения принимает значение
, равное q,
т. е. По данным примера 2.6 найти квантиль xqj и 30%-ную точку случайной величины X.
Решение. По определению (2.16) F(xo t3)= 0,3, т. е. ~Y~ =
0,3, откуда квантиль х 0
3 = 0,6. 30%-ная точка случайной величины X
, или квантиль Х)_о,з = xoj
» находится аналогично из уравнения ^ = 0,7 . откуда *,= 1,4. ? Среди числовых характеристик случайной величины выделяют начальные
v* и центральные
р* моменты к-го порядка
, определяемые для дискретных и непрерывных случайных величин по формулам: ЗАКОН РАСПРЕДЕЛЕНИЯ И ХАРАКТЕРИСТИКИ
СЛУЧАЙНЫХ ВЕЛИЧИН
Случайные величины, их классификация и способы описания.
Случайной называется величина, которая в результате опыта может принимать то или иное значение, но какое именно заранее не известно. Для случайной величины, таким образом, можно указать только значения, одно из которых она обязательно примет в результате опыта. Эти значения в дальнейшем будем называть возможными значениями случайной величины. Так как случайная величина количественно характеризует случайный результат опыта, она может рассматриваться как количественная характеристика случайного события. Случайные величины обычно обозначаются заглавными буквами латинского алфавита, например, X..Y..Z, а их возможные значения- соответствующими малыми буквами. Различают три типа случайных величин: Дискретные; Непрерывные; Смешанные. Дискретной
называется такая случайная величина, число возможных значений которой образует счетное множество. В свою очередь, счетным называется множество, элементы которого можно пронумеровать. Слово «дискретный» происходит от латинского discretus , что означает «прерывистый, состоящий из отдельных частей» . Пример 1. Дискретной случайной величиной является число бракованных деталей Х в партии из nтук. Действительно, возможными значениями этой случайной величины является ряд целых чисел от 0 до n. Пример 2. Дискретной случайной величиной является число выстрелов до первого попадания в цель. Здесь, как и в примере 1, возможные значения можно пронумеровать, хотя в предельном случае возможное значение является бесконечно большим числом. Непрерывной
называется случайная величина, возможные значения которой непрерывно заполняют некоторый интервал числовой оси, называемый иногда интервалом существования этой случайной величины. Таким образом, на любом конечном интервале существования число возможных значений непрерывной случайной величины бесконечно велико. Пример 3. Непрерывной случайной величиной является расход электроэнергии на предприятии за месяц. Пример 4. Непрерывной случайной величиной является ошибка измерения высоты с помощью высотомера. Пусть из принципа работы высотомера известно, что ошибка лежит в пределах от 0 до 2 м. Поэтому интервалом существования данной случайной величины является интервал от 0 до 2 м. Закон распределения случайных величин.
Случайная величина считается полностью заданной, если на числовой оси указаны ее возможные значения и установлен закон распределения. Законом распределения случайной величины
называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.
Про случайную величину говорят, что она распределена по данному закону, или подчинена данному закону распределения. В качестве законов распределения используются ряд вероятностей, функция распределения, плотность вероятности, характеристическая функция. Закон распределения дает полное вероятное описание случайной величины. По закону распределения можно судить до опыта о том какие возможные значения случайной величины будут появляться чаще, а какие – реже. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Простейшей формой задания закона распределения дискретной случайной величины является таблица (матрица), в которой перечислены в порядке возрастания все возможные значения случайной величины и соответствующие их вероятности, т.е. Такая таблица называется рядом распределения дискретной случайной величины. 1 События Х 1 , Х 2 ,..., Х n , состоящие в том, что в результате испытания случайная величина X примет соответственно значения х 1 , x 2 ,...х n являются несовместными и единственно возможными (ибо в таблице перечислены все возможные значения случайной величины), т.е. образуют полную группу. Следовательно, сумма их вероятностей равна 1. Таким образом, для любой дискретной случайной величины (Эта единица как-то распределена между значениями случайной величины, отсюда и термин «распределение»). Ряд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а по оси ординат - соответствующие их вероятности. Соединение полученных точек образует ломаную, называемую многоугольником или полигоном распределения вероятностей (рис. 1). Пример
В лотерее разыгрывается: автомобиль стоимостью 5000 ден. ед., 4 телевизора стоимостью 250 ден. ед., 5 видеомагнитофонов стоимостью 200 ден. ед. Всего продается 1000 билетов по 7 ден. ед. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет. Решение
. Возможные значения случайной величины X - чистого выигрыша на один билет - равны 0-7 = -7 ден. ед. (если билет не выиграл), 200-7 = 193, 250-7 = 243, 5000-7 = 4993 ден. ед. (если на билет выпал выигрыш соответственно видеомагнитофона, телевизора или автомобиля). Учитывая, что из 1000 билетов число невыигравших составляет 990, а указанных выигрышей соответственно 5, 4 и 1, и используя классическое определение вероятности, получим.
.
. Найти плотность распределения их суммы. Найти распределение суммы независимых случайных величин x и h, где x имеет равномерное на отрезке распределение, а h имеет показательное распределение с параметром l. Найти Р
, если x имеет: а) нормальное распределение с параметрами а и s2 ; б) показательное распределение с параметром l; в) равномерное распределение на отрезке [-1;1]. Совместное распределение x, h является равномерным в квадрате
К ={х, у): |х| +|у|£ 2}. Найти вероятность
. Являются ли x и h независимыми? Пара случайных величин x и h равномерно распределена внутри треугольника K=. Вычислить плотность x и h. Являются ли эти случайные величины независимыми? Найти вероятность . Случайные величины x и h независимы и равномерно распределены на отрезках и [-1,1]. Найти вероятность . Двумерная случайная величина (x, h) равномерно распределена в квадрате с вершинами (2,0), (0,2), (-2, 0), (0,-2). Найти значение совместной функции распределения в точке (1, -1). Случайный вектор (x, h) равномерно распределен внутри круга радиуса 3 с центром в начале координат. Написать выражение для совместной плотности распределения. Определить, зависимы ли эти случайные величины. Вычислить вероятность . Пара случайных величин x и h равномерно распределена внутри трапеции с вершинами в точках (-6,0), (-3,4), (3,4), (6,0). Найти совместную плотность распределения для этой пары случайных величин и плотности составляющих. Зависимы ли x и h? Случайная пара (x, h) равномерно распределена внутри полукруга . Найти плотности x и h, исследовать вопрос об их зависимости. Совместная плотность двух случайных величин x и h равна 
.
Найти плотности x, h. Исследовать вопрос о зависимости x и h. Случайная пара (x, h) равномерно распределена на множестве . Найти плотности x и h, исследовать вопрос об их зависимости. Найти М(xh). Случайные величины x и h независимы и распределены по показательному закону с параметром Найти
Для биномиального распределения M(X)=np, для распределения Пуассона M(X)=λ
Для биномиального распределения D(X)=npq, для распределения Пуассона D(X)=λПримеры решения задач по теме «Закон распределения дискретной
случайной величины»
Задача 1.
Задача 3.
P 3 (0) = С 3 0 p 0 q 3-0 = q 3 = 0,9 3 = 0,729;
P 3 (1) = С 3 1 p 1 q 3-1 = 3*0,1*0,9 2 = 0,243;
P 3 (2) = С 3 2 p 2 q 3-2 = 3*0,1 2 *0,9 = 0,027;
P 3 (3) = С 3 3 p 3 q 3-3 = р 3 =0,1 3 = 0,001;
Проверка: ∑p i = 0,729+0,243+0,027+0,001=1.
для 0 < x ≤1 имеем F(x) = Р(Х<1) = Р(Х = 0) = 0,729;
для 1< x ≤ 2 F(x) = Р(Х<2) = Р(Х=0) + Р(Х=1) =0,729+ 0,243 = 0,972;
для 2 < x ≤ 3 F(x) = Р(Х<3) = Р(Х = 0) + Р(Х = 1) + Р(Х = 2) = 0,972+0,027 = 0,999;
для х > 3 будет F(x) = 1, т.к. событие достоверно.
- математическое ожидание М(X) = np = 3*0,1 = 0,3;
- дисперсия D(X) = npq = 3*0,1*0,9 = 0,27;
- среднее квадратическое отклонение σ(X) = √D(X) = √0,27 ≈ 0,52.
,
где параметры а
– любое действительное число и σ >0.
График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса). Нормальная кривая (рис. 2.12) симметрична относительно прямой х
=а
, имеет максимальную ординату , а в точках х
= а
± σ – перегиб.
Рис. 2.12
Доказано, что параметр а
является математическим ожиданием (также модой и медианой), а σ – средним квадратическим отклонением. Коэффициенты асимметрии и эксцесса для нормального распределения равны нулю:As
= Ex
= 0.
Установим теперь, как влияет изменение параметров а
и σ на вид нормальной кривой. При изменении параметра а
форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а
) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо (рис. 2.13).
При изменении параметра σ изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение функции убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох
, должна быть постоянной и равной 1, то с увеличением параметра σ кривая приближается к оси Ох
и растягивается вдоль нее, а с уменьшением σ кривая стягивается к прямой х
= а
(рис. 2.14).
Функция плотности нормального распределения φ(х
) с параметрами а
= 0, σ = 1 называется плотностью стандартной нормальной случайной величины
, а ее график – стандартной кривой Гаусса.
Функция плотности нормальной стандартной величины определяется формулой , а ее график изображен на рис. 2.15.
Из свойств математического ожидания и дисперсии следует, что для величины , D(U
)=1, M
(U
) = 0. Поэтому стандартную нор мальную кривую можно рассматривать как кривую распределения случайной величины , где Х
– случайная величина, подчиненная нормальному закону распределения с параметрами а
и σ.
Нормальный закон распределения случайной величины в интегральной форме имеет вид
(2.10)
Полагая в интеграле (3.10) , получим
,
где . Первое слагаемое равно 1/2 (половине площади криволинейной трапеции, изображенной на рис. 3.15). Второе слагаемое
(2.11)
называется функцией Лапласа
, а также интегралом вероятности.
Поскольку интеграл в формуле (2.11) не выражается через элементарные функции, для удобства расчетов составлена для z
≥ 0 таблица функции Лапласа. Чтобы вычислить функцию Лапласа для отрицательных значений z
, необходимо воспользоваться нечетностью функции Лапласа: Ф(–z
) = – Ф(z
). Окончательно получаем расчетную формулу
Отсюда получаем, что для случайной величины Х
, подчиняющейся нормальному закону, вероятность ее попадания на отрезок [ α, β] есть
(2.12)
С помощью формулы (2.12) найдем вероятность того, что модуль отклонения нормального распределения величины Х
от ее центра распределения а
меньше 3σ. Имеем
Р(|x
– a
| < 3 s) =P(а
–3 s< X
< а
+3 s)= Ф(3) – Ф(–3) = 2Ф(3) »0,9973.
Значение Ф(3) получено по таблице функции Лапласа.
Принято считать событие практически достоверным
, если его вероятность близка к единице, и практически невозможным, если его вероятность близка к нулю.
Мы получили так называемое правило трех сигм
: для нормального распределения событие (|x
–a
| < 3σ) практически достоверно.
Правило трех сигм можно сформулировать иначе: хотя нормальная случайная величина распределена на всей оси х
, интервал ее практически возможных значений есть
(a
–3σ, a
+3σ)
.
Нормальное распределение имеет ряд свойств, делающих его одним из самых употребительных в статистике распределений.
Если предоставляется возможность рассматривать некоторую случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения. Суммируемые случайные величины могут подчиняться каким угодно распределениям, но при этом должно выполняться условие их независимости (или слабой независимости). Также ни одна из суммируемых случайных величин не должна резко отличаться от других, т.е. каждая из них должна играть в общей сумме примерно одинаковую роль и не иметь исключительно большую по сравнению с другими величинами дисперсию.
Этим и объясняется широкая распространенность нормального распределения. Оно возникает во всех явлениях, процессах, где рассеяния случайной изучаемой величины вызывается большим количеством случайных причин, влияние каждой из которых в отдельности на рассеяние ничтожно мало.
Большинство встречающихся на практике случайных величин (таких, например, как количества продаж некоторого товара, ошибка измерения; отклонение снарядов от цели по дальности или по направлению; отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров и т.д.) может быть представлено как сумма большого числа независимых случайных величин, оказывающих равномерно малое влияние на рассеяние суммы. Такие случайные величины принято считать нормально распределенными. Гипотеза о нормальности подобных величин находит свое теоретическое обоснование в центральной предельной теореме и получила многочисленные практические подтверждения.
Представим себе, что некоторый товар реализуется в нескольких торговых точках. Из–за случайного влияния различных факторов количества продаж товара в каждой точке будут несколько различаться, но среднее всех значений будет приближаться к истинному среднему числу продаж.
Отклонения числа продаж в каждой торговой точке от среднего образуют симметричную кривую распределения, близкую к кривой нормального распределения. Любое систематическое влияние какого-либо фактора проявится в асимметрии распределения.
Задача
. Случайная величина распределена нормально с параметрами а
= 8, σ = 3.Найти вероятность того, что случайная величина в результате опыта примет значение, заключенной в интервале (12,5; 14).
Решение
. Воспользуемся формулой (2.12). Имеем
Задача
. Число проданного за неделю товара определенного вида Х
можно считать распределенной нормально. Математическое ожидание числа продаж
тыс. шт. Среднее квадратическое отклонение этой случайной величины σ = 0,8 тыс. шт. Найти вероятность того, что за неделю будет продано от 15 до 17 тыс. шт. товара.
Решение.
Случайная величина Х
распределена нормально с параметрами а
= М(Х
) = 15,7; σ = 0,8. Требуется вычислить вероятность неравенства 15 ≤ X
≤ 17. По формуле (2.12) получаем
