Моделі, які описуються системами двох автономних диференціальних рівнянь.
Фазова площина. Фазовий портрет. Метод ізоклін. Головні ізокліни. Стійкість стаціонарного стану. Лінійні системи. Типи особливих точок: вузол, сідло, центр, фокус. Приклад: хімічні реакціїпершого порядку.
Найбільш цікаві результати щодо якісного моделювання властивостей біологічних систем отримані на моделях із двох диференціальних рівнянь, які допускають якісне дослідження за допомогою методу фазової площини. Розглянемо систему двох автономних звичайних диференціальних рівнянь загального вигляду
(4.1)
P(x,y), Q(x,y)- безперервні функції, визначені у певній області Gевклідової площини ( x,y ‑ декартові координати) і мають у цій галузі безперервні похідні порядку не нижче першого.
Область Gможе бути як необмеженою, і обмеженою. Якщо змінні x, yмають конкретний біологічний зміст (концентрації речовин, чисельності видів). Gє позитивним квадрантом правої напівплощини:
0 £ x< ¥ ,0 £ y< ¥ .
Концентрації речовин або чисельності видів можуть бути обмежені зверху обсягом судини або площею ареалу проживання. Тоді область значень змінних має вигляд:
0 £ x< x 0 , 0 £ y< y 0 .
Змінні x, yу часі змінюються відповідно до системи рівнянь (4.1), тому кожному стану системи відповідає пара значень змінних ( x, y).
|
|
Назад, кожній парі змінних ( x, y) відповідає певний стан системи.
Розглянемо площину з осями координат, на яких відкладено значення змінних x,y. Кожна точка Мцій площині відповідає певному стану системи. Така площина зветься фазової площини і зображує сукупність усіх станів системи. Точка М(x,y) називається зображувальною або точкою, що представляє.
Нехай у початковий момент часу t=t 0 координати зображувальної точки М 0 (x(t 0), y(t 0)). Кожного наступного моменту часу tточка, що зображає, буде зміщуватися відповідно до змін значень змінних x(t), y(t). Сукупність точок М(x(t), y(t)) на фазовій площині, положення яких відповідає станам системи у процесі зміни у часі змінних x(t), y(t)згідно з рівняннями (4.1), називається фазовою траєкторією.
Сукупність фазових траєкторій при різних початкових значеннях змінних дає легко доступний для огляду "портрет" системи. Побудова фазового портретадозволяє зробити висновки про характер змін змінних x, yбез знання аналітичних рішень вихідної системи рівнянь(4.1).
Для зображення фазового портрета необхідно побудувати векторне поле напрямків траєкторій системи у кожній точці фазової площини. Задаючи прирістD t>0,отримаємо відповідні прирощення D xі D yз виразів:
D x = P (x, y)D t,
D y=Q(x,y)D t.
Напрямок вектора dy/dxу точці ( x, y) залежить від знака функцій P(x, y), Q(x, y)і може бути задано таблицею:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Вирішення цього рівняння y = y(x, c), або в неявному вигляді F(x,y)=c,де з- Постійна інтегрування, дає сімейство інтегральних кривих рівняння (4.2) - фазових траєкторійсистеми (4.1) на площині x, y.
Метод ізоклін
Для побудови фазового портрета користуються методом ізоклін –на фазовій площині наносять лінії, які перетинають інтегральні криві під певним кутом. Рівняння ізоклін легко отримати (4.2). Покладемо
де А– певна стала величина. Значення Аявляє собою тангенс кута нахилу дотичної фазової траєкторії і може приймати значення від –¥ до + ¥ . Підставляючи замість dy/dxв (4.2) величину Аотримаємо рівняння ізоклін:
.(4.3)
Рівняння (4.3) визначає у кожній точці площини єдину дотичну до відповідної інтегральної кривої за винятком точки, де P (x, y)= 0, Q (x,y) = 0 , в якій напрям дотичної стає невизначеним, тому що при цьому стає невизначеним значення похідної:
.
Ця точка є точкою перетину всіх ізоклін – особливою точкою.У ній одночасно перетворюються на нуль похідні за часом змінних xі y.
Таким чином, в особливій точці швидкості зміни змінних дорівнюють нулю. Отже, особлива точкадиференціальних рівнянь фазових траєкторій (4.2) відповідає стаціонарного стану системи(4.1), а її координати – суть стаціонарні значення змінних x, y.
Особливий інтерес представляють головні ізокліни:
dy/dx=0, P(x,y)=0 – ізокліна горизонтальних дотичних і
dy/dx=¥ , Q(x,y)=0 – ізокліна вертикальних дотичних.
Побудувавши головні ізокліни і знайшовши точку їх перетину (x, y), координати якої задовольняють умовам:
ми знайдемо тим самим точку перетину всіх ізоклін фазової площини, в якій напрямок дотичних до фазових траєкторій невизначений. Це – особлива точка, яка відповідає стаціонарного стану системи(Рис. 4.2).
Система (4.1) має стільки стаціонарними станами, скільки точок перетину головних ізоклін є на фазовій площині.
Кожна фазова траєкторія відповідає сукупності рухів динамічної системи, що проходять через одні й ті ж стани і відрізняються один від одного лише початком часу.
 |
|
Якщо умови теореми Коші виконані, то через кожну точку простору x, y, tпроходить єдина інтегральна крива. Те саме справедливо завдяки автономності для фазових траєкторій: через кожну точку фазової площини проходить єдина фазова траєкторія.
Стійкість стаціонарного стану
Нехай система перебуває у стані рівноваги.
Тоді зображувальна точка знаходиться в одній з особливих точок системи, в яких за визначенням:
.
Стійка чи ні особлива точка, визначається тим, чи піде ні зображувальна точка при малому відхиленні від стаціонарного стану. Щодо системи з двох рівнянь визначення стійкості мовоюe, dвиглядає наступним чином.
Стан рівноваги стійкий, якщо для будь-якої заданої області відхилень від стану рівноваги (e )можна вказати область d (e ), що оточує стан рівноваги і має ту властивість, що жодна траєкторія, яка починається всередині області d , ніколи не досягне кордону e . (Рис. 4.4)
 |
|
Для великого класу систем – грубих систем – характер поведінки яких не змінюється при малій зміні виду рівнянь, інформацію про тип поведінки на околиці стаціонарного стану можна отримати, досліджуючи не вихідну, а спрощену лінеаризованусистему.
Лінійні системи.
Розглянемо систему двох лінійних рівнянь:
.(4.4)
Тут a, b, c, d- Константи, x, y- Декартові координати на фазовій площині.
Загальне рішення шукатимемо у вигляді:
.(4.5)
Підставимо ці вирази в (4.4) і скоротимо на e l t:
(4.6)
Алгебраїчна система рівнянь (4.6) з невідомими A, Bмає ненульове рішення лише в тому випадку, якщо її визначник, складений з коефіцієнтів за невідомих, дорівнює нулю:
.
Розкриваючи цей визначник, отримаємо характеристичне рівняння системи:
.(4.7)
Вирішення цього рівняння дає значення показникаl 1,2 , при яких можливі ненульові для Aі Bрішення рівняння (4.6). Ці значення суть
.(4.8)
Якщо підкорене вираз негативне, тоl 1,2 комплексно пов'язані числа. Припустимо, що обидва корені рівняння (4.7) мають відмінні від нуля дійсні частини і що немає кратного коріння. Тоді загальне рішення системи (4.4) можна подати у вигляді лінійної комбінації експонент з показникамиl 1 , l 2 :
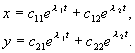(4.9)
Для аналізу характеру можливих траєкторій системи на фазовій площині використовуємо лінійне однорідне перетворення координат,яке дозволить привести систему до канонічного вигляду:
,(4.10)
що дозволяє більш зручне уявлення на фазовій площині порівняно з вихідною системою (4.4). Введемо нові координатиξ , η за формулами:
(4.1)
З курсу лінійної алгебри відомо, що у разі нерівності нулю дійсних частинl 1 , l 2 вихідну систему (4.4) за допомогою перетворень (4.11) завжди можна перетворити до канонічного виду (4.10) та вивчати її поведінку на фазовій площиніξ , η . Розглянемо різні випадки, які тут можуть представитися.
Коріння λ 1 , λ 2 – дійсні та одного знака
У цьому випадку коефіцієнти перетворення є дійсними, ми переходимо від дійсної площини.x,yдо дійсної площини ξ, η. Розділивши друге із рівнянь (4.10) на перше, отримаємо:
.(4.12)
Інтегруючи це рівняння, знаходимо:
Де. (4.13)
Умовимося розуміти під λ 2 корінь характеристичного рівняння з великим модулем, що порушує спільності нашого міркування. Тоді, оскільки в даному випадку коріння λ 1 , λ 2 - дійсні й одного знака,a>1 , і ми маємо справу з інтегральними кривими параболічного типу.
Усі інтегральні криві (крім осі η , якій відповідає ) стосуються на початку координат осі ξ, яка також є інтегральною кривою рівняння (4.11). Початок координат є особливою точкою.
З'ясуємо тепер напрямок рухів зображувальної точки вздовж фазових траєкторій. Якщо λ 1 , λ 2 – негативні, те, як очевидно з рівнянь (4.10), |ξ|, |η| спадають з часом. Точка, що зображає, наближається до початку координат, ніколи, однак, не досягаючи його. В іншому випадку це суперечило б теоремі Коші, яка стверджує, що через кожну точку фазової площини проходить лише одна фазова траєкторія.
Така особлива точка, через яку проходять інтегральні криві, подібно до того, як сімейство парабол 
проходить через початок координат, зветься вузла (рис. 4.5)
Стан рівноваги типу вузол при λ 1 , λ 2 < 0 стійко по Ляпунову, оскільки зображуюча точка по всіх інтегральних кривих рухається до початку координат. Це стійкий вузол. Якщо ж λ 1 , λ 2 > 0, то |ξ|, |η| зростають з часом і зображуюча точка віддаляється від початку координат. У цьому випадку особлива точка– нестійкий вузол .
На фазовій площині x, y загальний якісний характер поведінки інтегральних кривих збережеться, але дотичні до інтегральних кривих нічого очікувати збігатися з осями координат. Кут нахилу цих дотичних визначатиметься співвідношенням коефіцієнтів α , β , γ , δ у рівняннях (4.11).
Коріння λ 1 , λ 2 – дійсні та різних знаків.
Перетворення відкоординат x,y до координат ξ, η знову дійсне. Рівняння для канонічних змінних знову мають вигляд (4.10), але тепер знаки λ 1 , λ 2 різні. Рівняння фазових траєкторій має вигляд:
Де ,(4.14)
Інтегруючи (4.14), знаходимо
(4.15)
Це рівняння визначає сімейство кривих гіперболічного типу, де обидві осі координат- асимптоти (при a=1 ми мали б сімейство рівнобічних гіпербол). Осі координат і в цьому випадку є інтегральними кривими– це будуть єдині інтегральні криві, які проходять через початок координат. Кожнаїх складається з трьох фазових траєкторій: з двох рухів до стану рівноваги (або стану рівноваги) і зі стану рівноваги. Всі інші інтегральні криві– суть гіперболи, які проходять через початок координат (рис. 4.6) Така особлива точка має назву «сідло ». Лінії рівня поблизу гірської сідловини поводяться подібно до фазових траєкторій в околиці сідла.
Розглянемо характер руху зображувальної точки фазовим траєкторіям поблизу стану рівноваги. Нехай, наприклад,λ 1 >0 , λ 2<0 . Тоді зображуюча точка, поміщена на осі ξ , буде віддалятися від початку координат, а поміщена на осі η – буде необмежено наближатися до початку координат, не досягаючи його за кінцевий час. Де б не знаходилася зображувальна точка в початковий момент (за винятком особливої точки та точок на асимптоті η =0), вона в кінцевому рахунку буде віддалятися від стану рівноваги, навіть якщо на початку вона рухається однією з інтегральних кривих у напрямку до особливої точки.
Очевидно, що особлива точка типу сідла завжди нестійка . Тільки за спеціально обраних початкових умов на асимптотіη =0 система наближатиметься до стану рівноваги. Однак це не суперечить твердженню про нестійкість системи. Якщо рахувати, що всі початкові стани системи на фазовій площині рівноймовірні, то ймовірність такого початкового стану, що відповідає руху за напрямкомдо особливій точці, що дорівнює нулю. Тому всякий реальний рух видалятиме систему стану рівноваги.Переходячи назад до координатx,y,ми отримаємо ту саму якісну картину характеру руху траєкторій навколо початку координат.
Прикордонним між розглянутими випадками вузла та сідла є випадок,коли один із характеристичних показників, наприклад λ 1 , звертається в нуль, що має місце, коли визначник системи- Вираз ad-bc=0(див. формулу 4.8 ). У цьому випадку коефіцієнти правих частин рівнянь (4.4) є пропорційними один одному:
і система має своїми станами рівноваги всі точки прямої:
Інші інтегральні криві є сімейством паралельних прямих з кутовим коефіцієнтом , за якими зображувальні точки або наближаються до стану рівноваги, або віддаляються від нього залежно від знака другого кореня характеристичного рівняння 2 = a+d.(Рис.4. 7 ) У разі координати стану рівноваги залежить від початкового значення змінних.
Коріння λ 1 , λ 2 – комплексніпов'язані
У цьому випадку за дійснихxі yми будемо мати комплексні пов'язані ξ , η (4.10) . Однак, вводячи ще одне проміжне перетворення, можна і в цьому випадку звести розгляд до дійсного однорідного однорідного перетворення. Покладемо:
(4.16)
де a,b,і u,v – дійсні величини. Можна показати, що перетворення відx,yдо u,v є за наших припущень дійсним, лінійним, однорідним з детермінантом, відмінним від нуля. У силу рівнянь(4.10, 4.16) маємо:
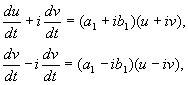
звідки
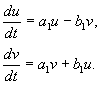(4.17)
Розділивши друге із рівнянь на перше, отримаємо :
яке легше інтегрується, якщо перейти до полярної системи координат (r, φ ) . Після підстановкиотримаємо, звідки:
.(4.18)
Таким чином, на фазовій площиніu, vми маємо справу із сімейством логарифмічних спіралей, кожна з яких маєасимптотичну точку на початку координат.Особлива точка, яка є асимптотичною точкою всіх інтегральних кривих, що мають вигляд спіралей., вкладених один вдруга, називається фокусом ( рис.4.8 ) .
Розглянемо характер руху зображувальної точки фазовими траєкторіями. Помножуючи перше з рівнянь (4.17) наu, а друге на vі складаючи, отримуємо:
Де
Нехай a 1 < 0 (a 1 = Reλ ) . Зображуюча точка безперервно наближається до початку координат, не досягаючи його в кінцевий час. Це означає, що фазові траєкторії являють собою спіралі, що скручуються, і відповідають загасаючим коливаннямзмінних. Це – стійкий фокус .
У разі стійкого фокусу, як і у разі стійкого вузла, виконано не лише умову Ляпунова, а й жорсткішу вимогу. Саме, при будь-яких початкових відхиленнях система з часом повернеться як завгодно близько до положення рівноваги. Така стійкість, при якій початкові відхилення не тільки не наростають, але згасають, прагнучи нуля, називають абсолютною стійкістю .
Якщо у формулі (4.18) a 1 >0 , то зображуюча точка віддаляється від початку координат, і ми маємо справу з нестійким фокусом . При переході від площиниu,vдо фазової площиниx, yспіралі також залишаться спіралями, проте деформовані.
Розглянемо тепер випадок, колиa 1
=0
. Фазовими траєкторіями на площиніu, vбудуть кола 
яким на площиніx,yвідповідають еліпси:
Таким чином, приa 1=0 через особливу точкуx= 0, y= 0 не проходить жодна інтегральна крива. Така ізольована особлива точка, поблизу якої інтегральні криві являють собою замкнуті криві, зокрема, еліпси, вкладені одна в одну і які охоплюють особливу точку, називається центром.
Отже, можливі шість типів стану рівноваги залежно від характеру коренів характеристичного рівняння (4.7). Вид фазових траєкторій на площині x, yдля цих шести випадків зображено на рис. 4.9.
Мал. 4.9.Типи фазових портретів на околиці стаціонарного стану системи лінійних рівнянь (4.4).
П'ять типів стану рівноваги грубі, їх характер не змінюється за досить малих змін правих частин рівнянь (4.4). При цьому малими мають бути зміни не лише правих частин, а й їх похідних першого порядку. Шостий стан рівноваги – центр – негрубий. При малих змінах параметрів правої частини рівнянь він перетворюється на стійкий чи нестійкий фокус.
Біфуркаційна діаграма
Введемо позначення:
.
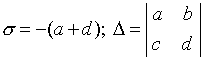(4.11)
Тоді характеристичне рівняння запишеться як:
.
(4.12)
Розглянемо площину із прямокутними декартовими координатами s , D та відзначимо на ній області, що відповідають тому чи іншому типу стану рівноваги, що визначається характером коренів характеристичного рівняння
.(4.13)
Умовою стійкості стану рівноваги буде наявність негативної дійсної частини уl 1 та l 2 . Необхідна та достатня умова цього – виконання нерівностейs > 0, D > 0 . На діаграмі (4.15) цій умові відповідають точки, розташовані в першій чверті площини параметрів. Особлива точка буде фокусом, якщоl 1 та l 2 комплексні. Цій умові відповідають ті точки площини, для яких , тобто. точки між двома гілками параболиs 2 = 4 D. Крапки півосі s = 0, D>0, відповідають станам рівноваги типу центр. Аналогічно,l 1 та l 2 - дійсні, але різних символів, тобто. особлива точка буде сідлом, якщо D<0, і т.д. У результаті ми отримаємо діаграму розбиття площини параметрів s, D, на області, що відповідають різним типам стану рівноваги
Мал. 4.10.Біфуркаційна діаграма
для системи лінійних рівнянь 4.4
Якщо коефіцієнти лінійної системи a, b, c, dзалежать від деякого параметра, то при зміні цього параметра змінюватимуться і величиниs , D . При переході через кордон характер фазового портрета якісно змінюється. Тому такі межі називаються біфуркаційними – по різні боки від кордону система має два топологічно різні фазові портрети і, відповідно два різні типи поведінки.
На діаграмі видно, як можуть відбуватись такі зміни. Якщо виключити особливі випадки - початок координат, то легко бачити, що сідло може переходити у вузол, стійкий або нестійкий при перетині осі ординат. Стійкий вузол може перейти або в сідло, або стійкий фокус, і т.д. Зазначимо, що переходи стійкий вузол – стійкий фокус і нестійкий вузол – нестійкий фокус є біфуркационными, оскільки топологія фазового простору у своїй не змінюється. Більш детально ми поговоримо про топологію фазового простору та біфуркаційні переходи в лекції 6.
При біфуркаційних переходах змінюється характер сталості особливої точки. Наприклад, стійкий фокус через центр може переходити у нестійкий фокус. Ця біфуркація називається біфуркацією Андронова-Хопфаза іменами вчених, що її досліджували. При цій біфуркації в нелінійних системах відбувається народження граничного циклу, і система стає автоколивальної (див. лекцію 8).
приклад. Система лінійних хімічних реакцій
Речовина Хпритікає ззовні з постійною швидкістю, перетворюється на речовину Y та зі швидкістю, пропорційної концентрації речовини Y, Виводиться зі сфери реакції. Усі реакції мають перший порядок, крім припливу речовини ззовні, що має нульовий порядок. Схема реакцій має вигляд:
(4.14)
та описується системою рівнянь:
(4.15)
Стаціонарні концентрації отримаємо, прирівнявши праві частини нулю:
.(4.16)
Розглянемо фазовий портрет системи. Розділимо друге рівняння системи (4.16) на перше. Отримаємо:
.(4.17)
Рівняння (4.17) визначає поведінку змінних фазової площині. Побудуємо фазовий портрет цієї системи. Спочатку намалюємо головні ізокліни на фазовій площині. Рівняння ізоклин вертикальних дотичних:
Рівняння ізоклін горизонтальних дотичних:
Особлива точка (стаціонарний стан) лежить на перетині головних ізоклін.
Тепер визначимо під яким кутом перетинаються координатні осі інтегральними кривими.
Якщо x= 0, то .
Таким чином, тангенс кута нахилу дотичної до інтегральних кривих. y=y(x),перетинає вісь ординат x=0, від'ємний у верхній напівплощині (згадаємо, що змінні x, yмають значення концентрацій і тому нас цікавить тільки правий верхній квадрант фазової площини). При цьому величина тангенса кута нахилу дотичної збільшується з віддаленням від початку координат.
Розглянемо вісь y= 0. У місці перетину цієї осі інтегральними кривими вони описуються рівнянням
При тангенс кута нахилу інтегральних кривих, що перетинають вісь абсцис, позитивний і збільшується від нуля до нескінченності зі збільшенням x.
При .
Потім при подальшому збільшенні тангенс кута нахилу зменшується по абсолютній величині, залишаючись негативним і прагне -1 при x ® ¥ . Знаючи напрямок дотичних до інтегральних кривих на головних ізоклінах і на осях координат, легко побудувати всю картину фазових траєкторій.
 |
|
Характер стійкості особливої точки встановимо, користуючись методом Ляпунова. Характеристичний визначник системи має вигляд:
.
Розкриваючи визначник, отримаємо характеристичне рівняння системи: , тобто. коріння характеристичного рівняння обидва негативні. Отже, стаціонарне стан системи є стійкий вузол. При цьому концентрація речовини Xпрагне стаціонарного стану завжди монотонно, концентрація речовини Y може проходити через min або max. Коливальні режими в такій системі неможливі.
Основні поняття та визначення:
Нулем аналітичної функції f(z) називається точка “a”, на яку f(a)=0.
Нулем порядку “n” функції f(z) називається точка «а», якщо fn(a)¹0.
Особлива точка "a" називається ізольованою особливою точкою функції f(z), якщо існує околиця цієї точки, в якій немає особливих точок, крім "a".
Ізольовані спеціальні точки бувають трьох типів: .
1 усунуті спеціальні точки;
3 значно особливі точки.
Тип особливої точки може бути визначений виходячи з поведінки даної функції в знайденій особливій точці, а також виду ряду Лорана, отриманого для функції в околиці знайденої особливої точки.
Визначення типу особливої точки щодо поведінки функції у ній.
1. Усунуті спеціальні точки.
Ізольована особлива точка a функції f(z) називається усувною, якщо існує кінцева межа .
2. Полюси.
Ізольована особлива точка a функції f(z) називається полюсом, якщо 
.
3.Суттєво особливі точки.
Ізольована особлива точка a функції f(z) називається істотно особливою точкою, якщо не існує кінцевий, ні нескінченний .
Між нулями та полюсами функції має місце наступний зв'язок.
Для того щоб точка a була полюсом порядку n функції f(Z), необхідно і достатньо, щоб ця точка була нулем порядку n функції .
Якщо n=1 полюс називається простим.
Визначення:Ізольована особлива точка однозначного характеру називається:
а) усувною, якщо головна частина розкладання відсутня;
б) полюсом, якщо головна частина містить кінцеве число членів;
в) суттєво особливою точкою, якщо головна частина містить нескінченну кількість членів.
а) Таким чином, в околиці особливої точки розкладання має вигляд:
воно виражає функцію у всіх точках кола | z-a | У центрі z=a рівність не так, т.к. функція при z=a має розрив, а права частина безперервна. Якщо в центрі значення функції змінити, прийнявши його рівним значенню правої частини, то розрив буде усунений-звідси і назва – усунутий. б) В околиці полюса порядку m розкладання до ряду Лорана має вигляд: в) На околиці простого полюса Відрахування та формули для їх обчислення. Вирахуванням аналітичної функції f(z) в ізольованій особливій точці z 0 називається комплексне число, що дорівнює значенню інтеграла Позначається віднімання функції f(z) в ізольованій особливій точці z 0 символом Res f(z 0) або Res (f(z); z 0). Таким чином, Res f(z 0)= Якщо формулі (22.15.1) покласти n=-1, то отримаємо: C -1 = або Res f (z 0) = C -1 тобто. відрахування функції f(z) щодо особливої точки z 0 дорівнює коефіцієнту при першому члені з негативним показником розкладання функції f(z) в ряд Лорана. Обчислення відрахувань. Правильні або усувні спеціальні точки. Очевидно, якщо z = z 0 є правильна або усувна особлива точка функції f (z), Res f (z 0) = 0 (у розкладі Лорана в цих випадках відсутня головна частина, тому c-1 = 0). Полюс. Нехай точка z0 є простим полюсом функції f(z). Тоді ряд Лоран для функції f(z) в околиці точки z 0 має вигляд: Звідси Тому, переходячи в цій рівності до межі при z --z 0 , отримуємо Res f(z0)= Істотно особлива точка. Якщо точка z 0 - істотно особлива точка функції f(z), то обчислення відрахування функції у цій точці зазвичай безпосередньо визначають коефіцієнт c-1 у розкладанні функції до ряду Лорана. Класифікація подій. Сума, добуток подій, їх властивості, графічна вистава. Події поділяються на: 1. Випадкові 2. Достовірні 3. Неможливі Достовірне - це така подія, яка настає обов'язково в цих умовах (за ніч слідує ранок). Випадкове – це така подія, яка може статися, а може і не відбутися (складання іспиту). Неможливе – це така подія, яка в цих умовах не настане (дістати зелений олівець із коробки тільки з червоними). Визначення.Особлива точка функції називається ізольовані,
якщо в деякій околиці цієї точки - аналітична функція (тобто аналітична в кільці). Класифікація ізольованих особливих точок функції пов'язані з поведінкою цієї функції на околиці особливої точки. Визначення.Крапка називається усувається
особливою точкою функції, якщо існує кінцева межа цієї функції. Приклад 5.Показати, що функція має в точці особливість. Рішення.Згадуючи першу чудову межу, обчислимо Значить, у точці задана функція має особливість. Завдання 4.Показати, що точка усувається для . Визначення.Крапка називається полюсом
функції, якщо ця функція необмежено зростає при, тобто. Звернімо увагу на зв'язок між поняттями нуля та полюса аналітичної функції. Представимо функцію як . Якщо точка є простим нулем функції, то функція має у простий полюс Якщо точка - нуль порядку для функції, то для функції це полюс порядку.
Приклад 6.Показати, що функція має у точці полюс третього порядку. Рішення.Вважаючи, отримаємо. При прагненні до нуля за будь-яким законом маємо. Тоді, а з ним і сама функція необмежено зростає. Отже, тобто особлива точка є полюсом. Для функції ця точка, очевидно, є триразовим нулем. Отже, для цієї функції точка є полюсом третього порядку. Завдання 5.Показати, що у точці має простий полюс. Визначення.Крапка називається істотно особливою
точкою функції , якщо у цій точці немає ні кінцевого, ні нескінченного межі функції (поведінка функції не визначено). Нехай є суттєво особливою точкою функції. Тоді для будь-якого наперед заданого комплексного числа знайдеться така послідовність точок, що сходить до, вздовж якої значення прагнуть до: ( теорема Сохоцького).
Приклад 7.Показати, що функція у точці має суттєву особливість. Рішення.Розглянемо поведінку заданої функції на околиці точки. При вздовж позитивної частини дійсної осі (тобто) маємо і; якщо ж вздовж негативної частини дійсної осі (тобто), то й. Отже, немає межі при . За визначенням, у точці функція має суттєву особливість. Розглянемо поведінку функції на нулі з погляду теореми Сохоцького. Нехай - будь-яке комплексне число, відмінне від нуля та нескінченності. З рівності знаходимо. Вважаючи, отримаємо послідовність точок. Вочевидь, . У кожній точці цієї послідовності функція дорівнює , тому і Завдання 6.Показати, що функція має у точці суттєву особливість. Нескінченно віддалена точка завжди вважається особливою для функції. Точка називається ізольованою особливою точкою функції , якщо ця функція поза деяким колом з центром на початку координат немає інших особливих точок. Класифікацію ізольованих особливих точок можна поширити і на випадок. Приклад 8.Показати, що функція має на нескінченності двократний полюс. Рішення.Розглянемо функцію, де - аналітична функція в околиці точки, причому. Значить, функція має на нескінченності дворазовий нуль, але для функції точка є дворазовим полюсом. Приклад 9.Показати, що функція має на нескінченності суттєву особливість. Рішення.Аналогічне завдання розглянуто у пр.7. Розглянемо поведінку функції на околиці нескінченно віддаленої точки. При вздовж позитивної частини дійсної осі, а при вздовж негативної частини дійсної осі. Отже, немає межі функції у точці і з визначення ця точка - істотно особлива. Про характер особливості функції в точці можна судити з головної частини
лоранівського розкладання на околиці цієї точки. Теорема 1.Для того щоб крапка була усувається
особливою точкою функції необхідно і достатньо, щоб відповідне лоранівське розкладання не містило головної частини.
Завдання 6.Користуючись тейлорівським розкладанням функції в околиці точки, показати, що має в нулі особливість. Теорема 2.Для того щоб крапка була полюсом
функції , необхідно і достатньо, щоб Головна частина
відповідного лоранівського розкладання містила кінцеве число членів
: Номер старшого негативного члена визначає порядок полюса. У цьому випадку функцію можна подати у вигляді де - аналітична в точці функція, - порядок полюса. приклад 10.Показати, що функція має у точках і прості полюси. Рішення.Розглянемо точку. Скористаємося лоранівським розкладанням цієї функції на околиці цієї точки, отриманим у прикладі 2: Так як у головній частині цього розкладання старша (і єдина) негативна ступінь дорівнює одиниці, то точка - простий полюс цієї функції. Можна було одержати цей результат іншим шляхом. Представимо у вигляді і покладемо – це функція, аналітична в точці та . Отже, і з (8) у точці дана функція має простий полюс. Ще один спосіб: розглянемо функцію, яка в точці має простий нуль. Значить, у цій точці має простий полюс. Аналогічно, якщо записати функцію у вигляді , де - функція, аналітична в точці і , то відразу ясно, що точка - простий полюс функції. Завдання 7.Показати, що функція має полюс 2-го порядку в точці та полюс 4-го порядку в точці . Теорема 3.Для того щоб крапка була істотно особливою
точкою функції , необхідно і достатньо, щоб Головна частина
лоранівського розкладання на околиці точки містила нескінченну кількість членів
. Приклад 11.Визначити характер особливості у точці функції Рішення.У відомому розкладанні косинуса покладемо замість: Значить, лоранівське розкладання на околиці точки має вигляд Тут правильна частина - один доданок. А головна частина містить нескінченну кількість доданків, тому точка - суттєво особлива. Завдання 8.Показати, що у точці функція має суттєву особливість. Розглянемо деяку функцію і запишемо її лоранівське розкладання в точці: Зробимо заміну , у своїй точка перетворюється на точку . Тепер на околиці нескінченно віддаленої точки маємо Залишилося запровадити нове позначення. Отримуємо де - головна частина, а - правильна частина лоранівського розкладання функції на околиці нескінченно віддаленої точки. Таким чином, у лоранівському розкладі функції на околиці точки головна частина - це ряд за позитивними ступенями, а правильна частина - ряд за негативними ступенями. З урахуванням цього заступника Наведені критерії для визначення характеру особливості залишаються в силі і для нескінченно віддаленої точки. приклад 12.З'ясувати характер особливості функції у точці. , то в точці може виявитися неізольованою. приклад 15.Функція у нескінченно віддаленій точці має суттєву особливість. Показати, що точка функції не є ізольованою особливою точкою. Рішення.Функція має безліч полюсів в нулях знаменника, тобто в точках , . Так як точка, в будь-якій околиці якої є полюси, є граничною для полюсів. Ряди Тейлора служать ефективним засобом для вивчення функцій, аналітичних у колі zol Для дослідження функцій, аналітичних в кільцевій ділянці, виявляється можливим побудова розкладів за позитивними та негативними ступенями (z - zq) виду узагальнюючим тейлорівські розкладання. Ряд (1), який розуміється як сума двох рядів називається поруч Лорана. Зрозуміло, що областю збіжності ряду (1) є загальна частина областей збіжності кожного ряду (2). Знайдемо її. Областью збіжності першого ряду є коло радіус якого визначається за формулою Коші-Адамара. Другий ряд є степеневим рядом щодо змінного Ряд (5) сходиться всередині свого кола збіжності до аналітичної функції комплексного змінного m-*oo причому в будь-якому колі меншого радіуса він сходиться абсолютно і рівномірно, ^го означає, що областю збіжності ряду (4) є Зовнішність кола - Якщо існує загальна область збіжності рядів (3) і (4) - кругове кільце в якому ряд (1) сходить до аналітичної функції. Причому в будь-якому кільці він сходиться абсолютно і рівномірно. Приклад 1. Визначити область збіжності рада Ряди Лорана Ізольовані особливі точки та їх класифікація М Область сходи першого ряду - зовнішність кола а область з ходи другого ряду - нутро кола Тим самим, даний ряд сходиться в коли» f Теорема 15. Будь-яку фун (z), однозначну і аполітичну в круговому кітці можна представити в цьому кільці у вигляді суми ряду, що сходить, коефіцієнти Сп якого визначені однозначно і обчислюються за формулами де 7р - окружність радіуса м Зафіксуємо всередині кільця Я довільну точку z. Побудуємо кола центрами в точці го, радіуси яких задовольняють нерівностям і розглянемо нове кільце По інтегральній теоремі Коші для багатозв'язкової області маємо Перетворимо окремо кожен з інтегралів у сумі (8). Для всіх точок £ по колу 7д* виконується співвідношення де суми ряду, що рівномірно сходить, 1 1 Тому дріб ^ можна представити у ви- /" / Помножуючи обидві частини на безперервну функцію (Про і проводячи почленное інтегрування вздовж кола, отримаємо, що Перетворення другого інтеграла Для всіх точок £ на колі ir> виконано співвідношення Тому дріб ^ можна представити у вигляді суми рівномірно східного ряду (Множучи обидві частини на безперервну функцію) і інтегруючи почленно вздовж кола 7/, отримаємо, що зауважимо, що підінтегральні функції у формулах (10) та (12) є аналітичними функціями у круговому кільці. Тому через теорему Коші значення відповідних інтегралів не зміняться, якщо замінити кола 7/г і 7г/ будь-яким колом. Це дозволяє об'єднати формули (10) і (12), замінюючи інтеграли у правій частині формули (8) їх виразами (9) і (11) відповідно, отримаємо потрібне розкладання Так як z - довільна точка кільця, то звідси випливає, що ряд ( 14) сходить до функції f(z) всюди в цьому кільці, причому в будь-якому кільці ряд сходить до цієї функції абсолютно і рівномірно. Доведемо тепер, що розкладання виду (6) єдине. Припустимо, що має місце ще одне розкладання Тоді всюди всередині кільця R матимемо На колі ряди (15) сходяться рівномірно. Помножимо обидві частини рівності (де т - фіксоване ціле число, і проінтегруємо обидва ряди почленно. В результаті отримаємо в лівій частині, а в правій - Сщ. Таким чином, (4, = Ст. Так як m - довільне число, то остання рівність) Ряд (6), коефіцієнти якого обчислюються поформулам (7), називається поруч Лорану функції f(z) у кільці Сукупність членів цього ряду з невід'ємними ступенями називається правильною частиною ряду Лорану, а з негативними - його головною частиною. 7) для коефіцієнтів ряду Лорана на практиці застосовуються рідко, бо, як правило, вимагають громіздких обчислень.Зазвичай, якщо це можливо, використовуються готові тейлорівські розкладання елементарних функцій. Розглянути розкладання в ряд Лорана функції різних областях, прийнявши Фуісція /(г) має дві особливі точки: Отже, є три кільцеві області, з центром в точці го = 0. у кожній з яких функція /(г) є аналітичною: а. ) коло кільце зовнішність кола (рис.27). Знайдемо лоранівські розкладання функції /(z) у кожній із цих областей. Представимо /(z) у вигляді суми елементарних дробів а) Коло Перетворимо співвідношення (16) наступним чином. б) Кільце для функції -г залишається схожим у цьому кільці, оскільки Ряд (19) для функції j^j при | z | > 1 розходиться. Тому перетворимо функцію /(z) наступним чином: знову застосовуючи формулу (19), отримаємо, що цей ряд сходить для. Підставляючи розкладання (18) і (21) співвідношення (20), отримаємо в) Зовнішність кола для функції -г при |z| > 2 розходиться, а ряд (21) для функ- Представимо функцію /(z) у такому вигляді: /<*> Використовуючи формули (18) і (19), отримаємо АБО 1 Егот приклад показує, що для однієї і тієї ж функції f(z) лоранівське розкладання, взагалі кажучи, має різний вид для різних кілець. Приклад 3. Знайти розкладання 8 ряд Лорана функції Ряди Лорана Ізольовані особливі точки та їх класифікація а кільцевої області А Скористаємося поданням функції f(z) у наступному вигляді: і перетворимо другий доданок Використовуючи формулу для суми членів геометричної прогресії, отримаємо (22), маємо Приклад 4. Розкласти в ряд Лорана функцію в окреслюванні тонкі zq = 0. Для будь-якого комплексного маємо Покладемо Це розкладання справедливе для будь-якої точки z Ф 0. У даному випадку кільцева область являє собою всю комплексну площину з однією викинутою точкою z - 0. Цю область можна визначити таким співвідношенням: Дана функція є аналітичною в області З формул (13) для коефіцієнтів ряду Лорана такими ж міркуваннями, що й у попередньому параграфі, можна отримати нерівності Kouiw. якщо функція f(z) обмежена на колі, де М - постійна), то ізольовані особливі точки Точка zo називається ізольованою особливою точкою функції / (z), якщо існує кільцева околиця точки (це безліч іноді називають також проколотою околицею точки 2о), в якою функція f(z) однозначна та аналітична. У самій точці zo функція або визначена, або є однозначної і аналітичної. Залежно від поведінки функції / (г) при наближенні до точки zo розрізняються три типи спеціальних точок. Ізольована особлива точка називається: 1) усуненою, якщо існує кінцевий 2) пмюсач, якщо 3) істотно особливою точкою, якщо функція f(z) не має межі при Тип ізольованої особливої точки тісно пов'язаний з характером лоранівського розкладання функції виколотим центром го. Теорема 16. Ізольована особлива точка z0 функції f(z) є усувною особливою точкою в тому і тільки в тач випадку, коли лоранівське розкладання функції f(z) в околиці точки zo не містить головної частини, тобто має вигляд Нехай zo - усувна особлива точка. Тоді існує кінцевий, отже, функція f(z) обмежена впрокологой околиці точки го, Покладемо В силу нерівностей Коші Так як р мимо вибрати хоч який малий, то всі коефіцієнти при негативних ступенях (z - 20) рівні нулю: Назад, нехай лоранівське розкладання функції /(г) на околиці точки zq містить тільки правильну частину, тобто має вигляд (23) і, отже, є тейлорівським. Неважко бачити, що при z -* z0 У функції /(г) існує граничне значення: Теорема 17. Ізольована особлива точка zq функції f(z) є усувною тоді і тільки тоді, коли функція J(z) обмежена в деякій проколотій околиці точки zq, Згмечаи не. Нехай го - особлива точка функції, що усувається, / (г). Вважаючи ми отримаємо, що функція / (г) аналітична в деякому колі з центром у точці го. Це визначає назву точки – усувна. Теорема 18. Ізольована особлива точка zq функції f(z) є полюсом в тому і тільки в тому випадку, коли головна частина лоранівського розкладання функції f (z) в околиці точки містить кінцеве (і позитивне) число відмінних від нуля членів, тобто має вигляд 4 Нехай z0 – полюс. Оскільки існує проколота околиця точки z0, у якій функція f(z) аналітична і відмінна від нуля. Тоді в цій околиці визначена аналітична функція причому, отже, точка zq є усувною особливою точкою (нулем) функції або де h(z) - аналітична функція, h(z0) Ф 0. Тоді аналітична і h(zo) ф 0, то функція щ аналітична в околиці точки zq, і отже, звідки отримуємо, що Припустимо тепер, що функція f(z) має в проколотий околиці точки z розкладання виду (24). Це означає, що у цій околиці функція f(z) аналітична разом із функцією. Для функції g(z) справедливе розкладання з якого видно, що zq - особлива точка функції g(z) і існує Тоді функція при 0 прагне - полюс функції Має місце ще один простий факт. Точка Zq - полюс функції f(z) у тому й лише у тому випадку, коли функцію g(z) = ущ можна довизначити до аналітичної функції в околиці точки zq, поклавши g(z0) = 0. Порядком полюса функції f(z) називається порядок нуля функції jfa. З теорем 16 та 18 випливає наступне твердження. Теорема 19. Ізольована особлива тонка є суттєво особливою в тому і тільки в тому випадку, коли головна частина лоранівського розкладання в проколоті околиці цієї точки містить нескінченно багато відмінних від нуля членів. Приклад 5. Особливою точкою функції є zo = 0. Маємо ряди Лорана Ізольовані особливі точки та їх класифікація Отже, zo = О - особлива точка. Розкладання функції /(z) у ряд Лорана в околиці нульової точки містить лише правильну частину: Приклад7. /(г) = Особлива точка функції f(z) є zq = 0. Розглянемо поведінку цієї функції на дійсній і уявній осях: на дійсній осі при х 0, на уявній осі Отже, ні кінцевої, ні нескінченної межі f(z) при z -* 0 не існує. Отже, точка го = 0 - значно особлива точка функції f(z). Знайдемо лоранівське розкладання функції f(z) на околиці нульової точки. Для будь-якого комплексного маємо Покладемо. Тоді Лоранівське розкладання містить нескінченну кількість членів із негативними ступенями z.
, взятого в позитивному напрямку по колу L з центром у точці z 0 , що лежить в області аналітичності функції f(z) (тобто в кільці 0<|z-z0| . (22.15.1)
