Якщо задачі необхідно провести повне дослідження функції f (x) = x 2 4 x 2 - 1 з побудовою його графіка, тоді розглянемо цей принцип докладно.

Для вирішення завдання даного типу слід використовувати властивості та графіки основних елементарних функцій. Алгоритм дослідження включає кроки:

Знаходження області визначення

Оскільки дослідження проводяться області визначення функції, необхідно починати з цього кроку.

Приклад 1

Заданий приклад передбачає знаходження нулів знаменника у тому, щоб виключити їх із ОДЗ.

4 x 2 - 1 = 0 x = ± 1 2 ⇒ x ∈ - ∞; - 1 2 ∪ - 1 2; 1 2 ∪ 1 2; + ∞

В результаті можна отримати коріння, логарифми, і таке інше. Тоді ОДЗ можна шукати для кореня парного ступенятипу g (x) 4 за нерівністю g (x) ≥ 0 для логарифму log a g (x) за нерівністю g (x) > 0 .

Дослідження меж ОДЗ та знаходження вертикальних асимптот

На межах функції є вертикальні асимптоти, коли односторонні межі таких точках нескінченні.

Приклад 2

Наприклад розглянемо прикордонні точки, рівні x = ± 1 2 .

Тоді необхідно проводити дослідження функції перебування одностороннього межі. Тоді отримуємо, що: lim x → - 1 2 - 0 f (x) = lim x → - 1 2 - 0 x 2 4 x 2 - 1 = = lim x → - 1 2 - 0 x 2 (2 x - 1 ) (2 x + 1) = 1 4 (-2) · - 0 = + ∞ lim x → - 1 2 + 0 f (x) = lim x → - 1 2 + 0 x 2 4 x - 1 = = lim x → - 1 2 + 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 2) · (+ 0) = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 0) · 2 = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 ( + 0) · 2 = + ∞

Звідси видно, що односторонні межі є нескінченними, отже, прямі x = ± 1 2 - вертикальні асимптоти графіка.

Дослідження функції та парність чи непарність

Коли виконується умова y(-x) = y(x), функція вважається парною. Це говорить про те, що графік розташовується симетрично щодо У. Коли виконується умова y(-x) = -y(x), функція вважається непарною. Отже, симетрія йде щодо початку координат. При невиконанні хоча б однієї нерівності отримуємо функцію загального виду.

Виконання рівності y(-x) = y(x) говорить про те, що функція парна. При побудові необхідно врахувати, що буде симетричність щодо У.

Для розв'язання нерівності застосовуються проміжки зростання та спадання з умовами f" (x) ≥ 0 і f "(x) ≤ 0 відповідно.

Визначення 1

Стаціонарні точки- Це такі точки, які звертають похідну в нуль.

Критичні точки- це внутрішні точки з області визначення, де похідна функції дорівнює нулю чи немає.

При вирішенні необхідно враховувати такі зауваження:

при наявних проміжках зростання та зменшення нерівності виду f "(x) > 0 критичні точки до рішення не включаються;
точки, в яких функція визначена без кінцевої похідної, необхідно включати в проміжки зростання та зменшення (наприклад, y = x 3 , де точка х = 0 робить функцію певною, похідна має значення нескінченності у цій точці, y " = 1 3 · x 2 3 , y "(0) = 10 = ∞, х = 0 включається в проміжок зростання);
щоб уникнути розбіжностей рекомендовано користуватися математичною літературою, яка рекомендована міністерством освіти.

Включення критичних точок у проміжки зростання та зменшення у тому випадку, якщо вони задовольняють області визначення функції.

Визначення 2

Для визначення проміжків зростання та зменшення функції необхідно знайти:

похідну;
критичні точки;
розбити область визначення за допомогою критичних точок на інтервали;
визначити знак похідної кожному з проміжків, де + є зростанням, а - є спаданням.

Приклад 3

Знайти похідну на області визначення f "(x) = x 2 "(4 x 2 - 1) - x 2 4 x 2 - 1" (4 x 2 - 1) 2 = - 2 x (4 x 2 - 1) 2 .

Рішення

Для вирішення необхідно:

знайти стаціонарні точки, даний приклад має в своєму розпорядженні х = 0;
знайти нулі знаменника, приклад набуває значення нуль при x = ± 1 2 .

Виставляємо точки на числовій осі для визначення похідної кожного проміжку. Для цього достатньо взяти будь-яку точку з проміжку та зробити обчислення. При позитивному результаті графіку зображаємо + , що означає зростання функції, а - означає її спадання.

Наприклад, f "(- 1) = - 2 · (- 1) 4 - 1 2 - 1 2 = 2 9 > 0 , отже, перший інтервал зліва має знак +. Розглянемо на числовий прямий.

Відповідь:

відбувається зростання функції на проміжку - ∞; - 1 2 і (- 1 2; 0];
відбувається зменшення на проміжку [ 0 ; 1 2) та 1 2 ; + ∞.

На схемі з допомогою + і - зображується позитивність і негативність функції, а стрілочки – спадання і зростання.

Точки екстремуму функції – точки, де функція визначена і якими похідна змінює знак.

Приклад 4

Якщо розглянути приклад, де х = 0 тоді значення функції в ній дорівнює f (0) = 0 2 4 · 0 2 - 1 = 0 . При зміні знака похідної з + на - і проходженні через точку х = 0 тоді точка з координатами (0 ; 0) вважається точкою максимуму. При зміні знака з – на + отримуємо точку мінімуму.

Випуклість і увігнутість визначається при розв'язанні нерівностей виду f "" (x) ≥ 0 і f "" (x) ≤ 0 . Рідше використовують назву опуклість вниз замість увігнутості, а опуклість вгору замість опуклості.

Визначення 3

Для визначення проміжків увігнутості та опуклостінеобхідно:

знайти другу похідну;
знайти нулі функції другої похідної;
розбити область визначення точками, що з'явилися, на інтервали;
визначити знак проміжку.

Приклад 5

Знайти другу похідну з області визначення.

Рішення

f "" (x) = - 2 x (4 x 2 - 1) 2 " = = (- 2 x) "(4 x 2 - 1) 2 - - 2 x 4 x 2 - 1 2 "(4 x 2 - 1) 4 = 24 x 2 + 2 (4 x 2 - 1) 3

Знаходимо нулі чисельника та знаменника, де на прикладі нашого прикладу маємо, що нулі знаменника x = ± 1 2

Тепер необхідно нанести крапки на числову вісь та визначити знак другої похідної з кожного проміжку. Отримаємо, що

Відповідь:

функція є опуклою з проміжку - 1 2; 1 2;
функція є увігнутою з проміжків - ∞; - 1 2 та 1 2 ; + ∞.

Визначення 4

Крапка перегину- Це точка виду x 0; f(x0) . Коли у ній є дотична до графіка функції, то її проходженні через x 0 функція змінює знак на протилежний.

Інакше висловлюючись, це така точка, якою проходить друга похідна і змінює знак, а самих точках дорівнює нулю чи немає. Усі точки вважаються областю визначення функції.

У прикладі було видно, що точки перегину відсутні, оскільки друга похідна змінює знак під час проходження через точки x = ± 12. Вони, своєю чергою, до області визначення не входять.

Знаходження горизонтальних та похилих асимптот

При визначенні функції на нескінченності потрібно шукати горизонтальні та похилі асимптоти.

Визначення 5

Похилі асимптотизображуються за допомогою прямих, заданих рівнянням y = k x + b , де k = lim x → f (x) x і b = lim x → f (x) - k x .

При k = 0 і b не рівному нескінченності, отримуємо, що похила асимптота стає горизонтальною.

Інакше висловлюючись, асимптотами вважають лінії, яких наближається графік функції на нескінченності. Це сприяє швидкій побудові графіка функції.

Якщо асимптоти відсутні, але функція визначається на обох нескінченностях, необхідно порахувати межу функції на цих нескінченностях, щоб зрозуміти, як поводитиметься графік функції.

Приклад 6

На прикладі розглянемо, що

k = lim x → ∞ f (x) x = lim x → ∞ x 2 4 x 2 - 1 x = 0 b = lim x → ∞ (f (x) - k x) = lim x → ∞ x 2 4 x 2 - 1 = 1 4 ⇒ y = 1 4

є горизонтальною асимптотою. Після дослідження функції можна приступати до її побудови.

Обчислення значення функції у проміжних точках

Щоб побудова графіка була найточнішою, рекомендовано знаходити кілька значень функції у проміжних точках.

Приклад 7

З розглянутого нами прикладу необхідно знайти значення функції в точках х = - 2, х = - 1, х = - 34, х = -14. Так як функція парна, отримаємо, що значення співпадуть зі значеннями в цих точках, тобто отримаємо х = 2 х = 1 х = 3 4 х = 1 4 .

Запишемо і вирішимо:

F (- 2) = f (2) = 2 2 4 · 2 2 - 1 = 4 15 ≈ 0 , 27 f (- 1) - f (1) = 1 2 4 · 1 2 - 1 = 1 3 ≈ 0 , 33 f - 3 4 = f 3 4 = 3 4 2 4 3 4 2 - 1 = 9 20 = 0 , 45 f - 1 4 = f 1 4 = 1 4 2 4 · 1 4 2 - 1 = - 1 12 ≈ - 0 , 08

Для визначення максимумів та мінімумів функції, точок перегину, проміжних точок необхідно будувати асимптоти. Для зручного позначення фіксуються проміжки зростання, спадання, опуклість, увігнутість. Розглянемо малюнку, зображеному нижче.

Необхідно через зазначені точки проводити лінії графіка, що дозволить наблизити до асимптотів, слідуючи стрілочкам.

У цьому закінчується повне дослідження функції. Трапляються випадки побудови деяких елементарних функцій, для яких застосовують геометричні перетворення.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Як досліджувати функцію та побудувати її графік?

Схоже, я починаю розуміти одухотворено-проникливе обличчя вождя світового пролетаріату, автора зібрання творів у 55 томах. Нескорий шлях почався елементарними відомостями про функціях та графіках, і ось зараз робота над трудомісткою темою закінчується закономірним результатом – статтею про повне дослідження функції. Довгоочікуване завдання формулюється так:

Дослідити функцію методами диференціального обчислення та на підставі результатів дослідження побудувати її графік

Або коротше: досліджувати функцію та побудувати графік.

Навіщо досліджувати?У простих випадках нам не важко розібратися з елементарними функціями, накреслити графік, отриманий за допомогою елементарних геометричних перетвореньі т.п. Однак властивості і графічні зображеннябільше складних функційдалеко не очевидні, саме тому й потрібне ціле дослідження.

Основні етапи рішення зведені у довідковому матеріалі Схема дослідження функціїце ваш путівник по розділу. Чайникам потрібне покрокове пояснення теми, деякі читачі не знають з чого почати і як організувати дослідження, а просунуті студенти, можливо, будуть цікаві лише деякі моменти. Але ким би ви не були, шановний відвідувачу, запропонований конспект з вказівниками на різні уроки в найкоротший термін зорієнтує та направить Вас у напрямку, що цікавить. Роботи розплакалися =) Керівництво зверстано у вигляді pdf-файлу і зайняло заслужене місце на сторінці Математичні формули та таблиці.

Дослідження функції я звик розбивати на 5-6 пунктів:

6) Додаткові точки та графік за результатами дослідження.

На рахунок заключної дії, думаю, всім все зрозуміло - буде дуже прикро, якщо за лічені секунди його перекреслять і повернуть завдання на доопрацювання. ПРАВИЛЬНИЙ І АКУРАТНИЙ КРЕСЛЕННЯ – це основний результат рішення! Він з великою ймовірністю «прикриє» аналітичні помилки, тоді як некоректний та/або недбалий графік завдасть проблем навіть при ідеально проведеному дослідженні.

Слід зазначити, що в інших джерелах кількість пунктів дослідження, порядок їх виконання та стиль оформлення можуть суттєво відрізнятися від запропонованої мною схеми, але здебільшого її цілком достатньо. Найпростіша версія завдання складається всього з 2-3 етапів і формулюється приблизно так: «дослідити функцію за допомогою похідної та побудувати графік» або «дослідити функцію за допомогою 1-ї та 2-ї похідної, побудувати графік».

Природно – якщо у вашій методичці докладно розібраний інший алгоритм або ваш викладач суворо вимагає дотримуватись його лекцій, то доведеться внести деякі корективи у вирішення. Не складніше, ніж замінити вилку бензопилою ложкою.

Перевіримо функцію на парність/непарність:

Після чого слідує шаблонна відписка:
, отже, дана функція не є парною чи непарною.

Оскільки функція безперервна на , вертикальні асимптоти відсутні.

Немає і похилих асимптотів.

Примітка : нагадую, що вищого порядку зростання, чим , тому підсумкова межа дорівнює саме « плюснескінченності».

З'ясуємо, як поводиться функція на нескінченності:

Іншими словами, якщо йдемо вправо, то графік йде нескінченно далеко вгору, якщо вліво – нескінченно далеко вниз. Так, тут теж дві межі під єдиним записом. Якщо у вас виникли труднощі з розшифровкою знаків, будь ласка, відвідайте урок про нескінченно малих функціях.

Таким чином, функція не обмежена зверхуі не обмежена знизу. Враховуючи, що у нас немає точок розриву, стає зрозумілою і область значень функції: - теж будь-яке дійсне число

КОРИСНИЙ ТЕХНІЧНИЙ ПРИЙОМ

Кожен етап завдання приносить нову інформацію про графік функціїТому в ході рішення зручно використовувати своєрідний Макет. Зобразимо на чернетці декартову систему координат. Що вже достеменно відомо? По-перше, у графіка немає асимптот, отже, прямі креслити не потрібно. По-друге, ми знаємо, як функція поводиться на нескінченності. Згідно з проведеним аналізом, намалюємо перше наближення:

Зауважте, що в силу безперервностіФункції і того факту, що , графік повинен, щонайменше, один раз перетнути вісь . А може бути точок перетину кілька?

3) Нулі функції та інтервали знаковості.

Спочатку знайдемо точку перетину графіка з віссю ординат. Це просто. Необхідно обчислити значення функції при:

Півтора над рівнем моря.

Щоб знайти точки перетину з віссю (нулі функції) потрібно вирішити рівняння , і тут на нас чекає неприємний сюрприз:

Наприкінці причаївся вільний член, який суттєво ускладнює завдання.

Таке рівняння має, як мінімум, один дійсний корінь, і найчастіше цей корінь ірраціональний. У гіршій же казці нас чекають три порося. Рівняння можна за допомогою так званих формул Кардано, Але псування паперу можна порівняти майже з усім дослідженням. У цьому розумніше усно або на чернетці спробувати підібрати хоча б один цілийкорінь. Перевіримо, чи не є ними числа :
- не підходить;
- Є!

Тут пощастило. У разі невдачі можна протестувати ще й, а якщо ці цифри не підійшли, то шансів на вигідне рішення рівняння, боюся, дуже мало. Тоді пункт дослідження краще повністю пропустити - може станеться що-небудь зрозуміліше на завершальному кроці, коли пробиватимуться додаткові точки. І якщо корінь (коріння) вочевидь «нехороші», то про інтервали знакопостійності краще взагалі скромно промовчати і акуратніше виконати креслення.

Однак у нас є гарний корінь, тому ділимо багаточлен на без залишку:

Алгоритм поділу багаточлена на багаточлен детально розібраний у першому прикладі уроку Складні межі.

У результаті ліва частина вихідного рівняння розкладається у твір:

А тепер трохи про здоровий спосіб життя. Я, звичайно ж, розумію, що квадратні рівнянняпотрібно вирішувати кожен день, але сьогодні зробимо виняток: рівняння має два дійсних кореня.

На числовій прямій відкладемо знайдені значення і методом інтерваліввизначимо знаки функції:

ог Таким чином, на інтервалах графік розташований
нижче осі абсцис, а на інтервалах - Више цієї осі .

Отримані висновки дозволяють деталізувати наш макет, і друге наближення графіка виглядає так:

Зверніть увагу, що на інтервалі функція обов'язково повинна мати хоча б один максимум, а на інтервалі – хоча б один мінімум. Але скільки разів, де і коли «петлятиме» графік, ми поки що не знаємо. До речі, функція може мати і багато екстремумів.

4) Зростання, спадання та екстремуми функції.

Знайдемо критичні точки:

Дане рівняння має два дійсні корені. Відкладемо їх на числовій прямій та визначимо знаки похідної:

Отже, функція зростає на і зменшується на .
У точці функція досягає максимуму: .
У точці функція досягає мінімуму: .

Встановлені факти заганяють наш шаблон у досить жорсткі рамки:

Що й казати, диференціальне числення – штука потужна. Давайте остаточно розберемося з формою графіка:

5) Випуклість, увігнутість та точки перегину.

Знайдемо критичні точки другої похідної:

Визначимо знаки:

Графік функції є опуклим і увігнутим на . Обчислимо ординату точки перегину: .

Майже все прояснилося.

6) Залишилося знайти додаткові точки, які допоможуть точніше побудувати графік та виконати самоперевірку. В даному випадку їх мало, але нехтуватимемо не:

Виконаємо креслення:

Зеленим кольором відзначено точку перегину, хрестиками – додаткові точки. Графік кубічної функції симетричний щодо своєї точки перегину, яка завжди розташована посередині між максимумом і мінімумом.

Під час виконання завдання я навів три гіпотетичні проміжні креслення. Насправді ж досить намалювати систему координат, відзначати знайдені точки і після кожного пункту дослідження подумки прикидати, як виглядатиме графік функції. Студентам з хорошим рівнем підготовки не важко провести такий аналіз виключно в розумі без залучення чернетки.

Для самостійного рішення:

Приклад 2

Дослідити функцію та побудувати графік.

Тут все швидше і веселіше, зразок чистового оформлення наприкінці уроку.

Чимало секретів розкриває дослідження дрібно-раціональних функцій:

Приклад 3

Методами диференціального обчислення досліджувати функцію і виходячи з результатів дослідження побудувати її графік.

Рішення: перший етап дослідження не відрізняється чимось примітним, за винятком дірки в області визначення:

1) Функція визначена і безперервна на всій числовій прямій крім точки , область визначення: .

Отже, дана функція не є парною або непарною.

Вочевидь, що функція неперіодична.

Графік функції є дві безперервні гілки, розташовані в лівій і правій півплощині - це, мабуть, найважливіший висновок 1-го пункту.

2) Асимптоти, поведінка функції на нескінченності.

а) За допомогою односторонніх меж досліджуємо поведінку функції поблизу підозрілої точки, де явно має бути вертикальна асимптота:

Справді, функції терпить нескінченний розриву точці ,
а пряма (вісь ) є вертикальною асимптотоюграфіка.

б) Перевіримо, чи існують похилі асимптоти:

Так, пряма є похилою асимптотоюграфіка, якщо.

Межі аналізувати сенсу не має, оскільки і так зрозуміло, що функція в обіймах зі своєю похилою асимптотою не обмежена зверхуі не обмежена знизу.

Другий пункт дослідження приніс багато важливої інформації про функцію. Виконаємо чорновий малюнок:

Висновок №1 стосується інтервалів знаковості. На «мінус нескінченності» графік функції однозначно розташований нижче за осю абсцис, а на «плюс нескінченності» – вище за цю осю. Крім того, односторонні межі повідомили нам, що і зліва і праворуч від точки функція теж більша за нуль. Зверніть увагу, що в лівій півплощині графік щонайменше один раз повинен перетнути вісь абсцис. У правій напівплощині нулів функції може бути.

Висновок №2 у тому, що функція зростає і зліва від точки (йде «знизу нагору»). Справа ж від цієї точки - функція зменшується (йде «зверху вниз»). У правої гілки графіка обов'язково має бути хоча б один мінімум. Ліворуч екстремуми не гарантовані.

Висновок №3 дає достовірну інформацію про увігнутість графіка на околиці точки. Про опуклість/увігнутість на нескінченності ми поки що нічого сказати не можемо, оскільки лінія може притискатися до своєї асимптоти як зверху, так і знизу. Взагалі кажучи, є аналітичний спосіб з'ясувати це зараз, але форма графіка «дарма» проясниться на пізніших етапах.

Навіщо стільки слів? Щоб контролювати наступні пункти дослідження та не допустити помилок! Подальші викладки нічого не винні суперечити зробленим висновкам.

3) Точки перетину графіка з координатними осями, інтервали знаковості функції.

Графік функції не перетинає вісь.

Методом інтервалів визначимо знаки:

, якщо;
, якщо .

Результати пункту повністю відповідають Висновку №1. Після кожного етапу дивіться на чернетку, подумки звіряйтеся з дослідженням та домальовуйте графік функції.

У прикладі чисельник почленно ділиться на знаменник, що дуже вигідно для диференціювання:

Власне, це вже робилося при знаходженні асимптоту.

- Критична точка.

Визначимо знаки:

зростає на і зменшується на

У точці функція досягає мінімуму: .

Різночитань із Висновком №2 також не виявилося, і, найімовірніше, ми на правильному шляху.

Отже, графік функції є увігнутим по всій області визначення.

Чудово - і креслити нічого не треба.

Точки перегину відсутні.

Увігнутість узгоджується з Висновком №3, більше, вказує, що у нескінченності (і там і там) графік функції розташований вищесвоєї похилої асимптоти.

6) Добросовісно приколоти завдання додатковими точками. Ось тут доведеться добряче попрацювати, оскільки з дослідження нам відомі лише дві точки.

І картинка, яку, напевно, багато хто давно представив:

У ході виконання завдання потрібно ретельно стежити за тим, щоб не виникало протиріч між етапами дослідження, але іноді ситуація буває екстреною або навіть відчайдушно-тупиковою. Ось "не сходиться" аналітика - і все тут. У цьому випадку рекомендую аварійний прийом: знаходимо якнайбільше точок, що належать графіку (скільки вистачить терпіння), і відзначаємо їх на координатній площині. Графічний аналіз знайдених значень у більшості випадків підкаже, де правда, а де брехня. Крім того, графік можна заздалегідь побудувати за допомогою якоїсь програми, наприклад, у тому ж Екселі (зрозуміло, для цього потрібні навички).

Приклад 4

Методами диференціального обчислення досліджувати функцію та побудувати її графік.

Це приклад самостійного рішення. У ньому самоконтроль посилюється парністю функції – графік симетричний щодо осі , і якщо у вашому дослідженні щось суперечить цьому факту, шукайте помилку.

парну або непарну функцію можна досліджувати тільки при , а потім користуватися симетрією графіка. Таке рішення оптимальне, проте виглядає, на мою думку, дуже незвично. Особисто я розглядаю всю числову вісь, але додаткові точки знаходжу все ж таки лише праворуч:

Приклад 5

Провести повне дослідження функції та побудувати її графік.

Рішення: понеслася нелегка:

1) Функція визначена і безперервна на всій числовій прямій: .

Отже, ця функція є непарною, її графік симетричний щодо початку координат.

Вочевидь, що функція неперіодична.

2) Асимптоти, поведінка функції на нескінченності.

Оскільки функція безперервна на , то вертикальні асимптоти відсутні

Для функції, що містить експоненту, типово роздільнедослідження «плюс» і «мінус нескінченності», проте наше життя полегшує саме симетрія графіка – або ліворуч і праворуч є асимптота, або її немає. Тому обидва нескінченні межі можна оформити під єдиним записом. У ході рішення використовуємо правило Лопіталя:

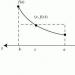
Пряма (вісь) є горизонтальною асимптотою графіка при .

Зверніть увагу, як я хитро уникнув повного алгоритму знаходження похилої асимптоти: межа цілком легальна і проясняє поведінку функції на нескінченності, а горизонтальна асимптота виявилася «начебто заодно».

З безперервності і існування горизонтальної асимптоти випливає той факт, що функція обмежена зверхуі обмежена знизу.

3) Точки перетину графіка з координатними осями, інтервали знакопостійності.

Тут також скорочуємо рішення:
Графік відбувається через початок координат.

Інших точок перетину з координатними осями немає. Більше того, інтервали знаковості очевидні, і вісь можна не креслити: , а значить, знак функції залежить тільки від «ікса»:
, якщо;
якщо .

4) Зростання, спадання, екстремуми функції.

- Критичні точки.

Крапки симетричні щодо нуля, як і має бути.

Визначимо знаки похідної:

Функція зростає на інтервалі та зменшується на інтервалах

У точці функція досягає максимуму: .

З огляду на властивості (непарності функції) мінімум можна не обчислювати:

Оскільки функція зменшується на інтервалі, то, очевидно, на «мінус нескінченності» графік розташований підсвоєю асимптотою. На інтервалі функція теж зменшується, але тут навпаки – після переходу через точку максимуму лінія наближається до осі вже зверху.

З вищесказаного також випливає, що графік функції є опуклим на мінус нескінченності і увігнутим на плюс нескінченності.

Після цього пункту дослідження промалювалася і область значень функції:

Якщо у вас виникло непорозуміння будь-яких моментів, ще раз закликаю накреслити у зошиті координатні осі та з олівцем у руках наново проаналізувати кожен висновок завдання.

5) Випуклість, увігнутість, перегини графіка.

- Критичні точки.

Симетрія точок зберігається, і, швидше за все, ми не помиляємось.

Визначимо знаки:

Графік функції є опуклим на і увігнутим на .

Випуклість/увігнутість на крайніх інтервалах підтвердилася.

У всіх критичних точках є перегини графіка. Знайдемо ординати точок перегину, при цьому знову скоротимо кількість обчислень, використовуючи непарність функції:

Решник Кузнєцова.
III Графіки

Завдання 7. Провести повне дослідження функції та побудувати її графік.

Перш ніж Ви почнете завантажувати свої варіанти, спробуйте вирішити задачу за зразком, наведеним нижче для варіанта 3. Частина варіантів заархівована у форматі.rar

7.3 Провести повне дослідження функції та побудувати її графік

Рішення.

1) Область визначення: або , тобто .
.
Таким чином: .

2) Точек перетину з віссю Ox немає. Справді, рівняння не має рішень.
Крапок перетину з віссю Oy немає, оскільки .

3) Функціяні парна, ні непарна. Симетрії щодо осі ординат немає. Симетрії щодо початку координат також немає. Так як
.
Бачимо, що .

4) Функція безперервна в області визначення
.

; .

; .
Отже, точка є точкою розриву другого роду (нескінченний розрив).

5) Вертикальні асимптоти:

Знайдемо похилу асимптоту nbsp nbsp nbsp nbsp. Тут

;
.
Отже, маємо горизонтальну асимптоту: y=0. Похилих асимптотів немає.

6) Знайдемо першу похідну. Перша похідна:
.
І ось чому
.
Знайдемо стаціонарні точки, де похідна дорівнює нулю, тобто
.

7) Знайдемо другу похідну. Друга похідна:
.
І це легко переконається, оскільки

Стоїть завдання: провести повне дослідження функції та побудувати її графік.

Кожен студент пройшов через такі завдання.

Подальший виклад передбачає хороше знання. Рекомендуємо звертатися до цього розділу у разі виникнення запитань.

Алгоритм дослідження функції складається з наступних кроків.

Знаходження області визначення функції.

Це дуже важливий крок дослідження функції, тому що всі подальші дії будуть проводитись на області визначення.

У нашому прикладі потрібно знайти нулі знаменника і виключити їх із дійсних чисел.

(В інших прикладах можуть бути коріння, логарифми тощо. Нагадаємо, що в цих випадках область визначення шукається таким чином:
для кореня парного ступеня, наприклад, - область визначення перебуває з нерівності;
для логарифму - область визначення перебуває з нерівності ).

Дослідження поведінки функції межі області визначення, перебування вертикальних асимптот.

На межах області визначення функція має вертикальні асимптотиякщо в цих граничних точках нескінченні.

У прикладі граничними точками області визначення є .

Досліджуємо поведінку функції при наближенні до цих точок ліворуч та праворуч, для чого знайдемо односторонні межі:

Оскільки односторонні межі нескінченні, то прямі є вертикальними асимптотами графіка.

Дослідження функції на парність чи непарність.

Функція є парнийякщо . Четність функції свідчить про симетрію графіка щодо осі ординат.

Функція є непарною, якщо . Непарність функції вказує на симетрію графіка щодо початку координат.

Якщо жодна з рівностей не виконується, то маємо функція загального виду.

У прикладі виконується рівність , отже, наша функція парна. Враховуватимемо це при побудові графіка - він буде симетричний щодо осі oy.

Знаходження проміжків зростання та зменшення функції, точок екстремуму.

Проміжки зростання та зменшення є рішеннями нерівностей і відповідно.

Крапки, у яких похідна звертається у нуль, називають стаціонарними.

Критичними точками функціїназивають внутрішні точки області визначення, у яких похідна функції дорівнює нулю чи немає.

ЗАУВАЖЕННЯ(Чи включати критичні точки в проміжки зростання і спадання).

Ми будемо включати критичні точки у проміжки зростання та спадання, якщо вони належать області визначення функції.

Таким чином, щоб визначити проміжки зростання та зменшення функції

по-перше, знаходимо похідну;
по-друге, знаходимо критичні точки;
по-третє, розбиваємо область визначення критичними точками на інтервали;
по-четверте, визначаємо знак похідної кожному з проміжків. Знак «плюс» відповідатиме проміжку зростання, знак «мінус» - проміжку зменшення.

Поїхали!

Знаходимо похідну області визначення (при виникненні складнощів, дивіться розділ ).

Знаходимо критичні точки, для цього:

Наносимо ці точки на числову вісь і визначаємо знак похідної всередині кожного отриманого проміжку. Як варіант, можна взяти будь-яку точку з проміжку та обчислити значення похідної у цій точці. Якщо значення позитивне, ставимо плюсик над цим проміжком і переходимо до наступного, якщо негативне, то ставимо мінус і т.д. Наприклад, Отже, над першим зліва інтервалом ставимо плюс.

Робимо висновок:

Схематично плюсами/мінусами відзначені проміжки де похідна позитивна/негативна. Зростаючі / спадні стрілочки показують напрямок зростання / спадання.

Точками екстремуму функціїє точки, в яких функція визначена та проходячи через які похідна змінює знак.

У прикладі точкою екстремуму є точка х=0 . Значення функції у цій точці одно . Оскільки похідна змінює знак із плюса на мінус під час проходження через точку х=0 , то (0; 0) є точкою локального максимуму. (Якби похідна міняла знак з мінусу на плюс, ми мали б точку локального мінімуму).

Знаходження проміжків опуклості та увігнутості функції та точок перегину.

Проміжки увігнутості та опуклості функції знаходяться при розв'язках нерівностей та відповідно.

Іноді увігнутість називають опуклістю вниз, а опуклість – опуклістю вгору.

Тут також справедливі зауваження, подібні до зауважень з пункту про проміжки зростання і спадання.

Таким чином, щоб визначити проміжки увігнутості та опуклості функції:

по-перше, знаходимо другу похідну;
по-друге, знаходимо нулі чисельника та знаменника другої похідної;
по-третє, розбиваємо область визначення одержаними точками на інтервали;
по-четверте, визначаємо знак другої похідної кожному з проміжків. Знак «плюс» відповідатиме проміжку увігнутості, знак «мінус» - проміжку опуклості.

Поїхали!

Знаходимо другу похідну області визначення.

У прикладі нулів чисельника немає, нулі знаменника .

Наносимо ці точки на числову вісь і визначаємо знак другої похідної всередині кожного отриманого проміжку.

Робимо висновок:

Крапка називається точкою перегину, якщо у цій точці існує дотична до графіка функції та друга похідна функції змінює знак під час проходження через .

Іншими словами, точками перегину можуть бути точки, проходячи через які друга похідна змінює знак, у самих точках або дорівнює нулю, або немає, але ці точки входять у область визначення функції.

У прикладі точок перегину немає, оскільки друга похідна змінює знак проходячи через точки , що вони входять у область визначення функції.

Знаходження горизонтальних та похилих асимптот.

Горизонтальні чи похилі асимптоти слід шукати лише тоді, коли функція визначена на нескінченності.

Похилі асимптотишукаються у вигляді прямих , де і .

Якщо k=0 і b не дорівнює нескінченності, то похила асимптота стане горизонтальною.

Хто такі взагалі ці асимптоти?

Це такі лінії, яких наближається графік функції на нескінченності. Таким чином вони дуже допомагають при побудові графіка функції.

Якщо горизонтальних або похилих асимптот немає, але функція визначена на плюс нескінченності та (або) мінус нескінченності, слід обчислити межу функції на плюс нескінченності та (або) мінус нескінченності, щоб мати уявлення про поведінку графіка функції.

Для нашого прикладу

- Горизонтальна асимптота.

На цьому дослідження функції завершується, переходимо до побудови графіка.

Обчислюємо значення функції у проміжних точках.

Для більш точної побудови графіка рекомендуємо знайти кілька значень функції у проміжних точках (тобто у будь-яких точках з області визначення функції).

Для нашого прикладу знайдемо значення функції в точках х=-2, х=-1, х=-3/4, х=-1/4. У силу парності функції, ці значення співпадатимуть зі значеннями в точках х=2, х=1, х=3/4, х=1/4.

Побудова графіка.

Спочатку будуємо асимптоти, наносимо точки локальних максимумів та мінімумів функції, точки перегину та проміжні точки. Для зручності побудови графіка можна нанести і схематичне позначення проміжків зростання, спадання, опуклості та увігнутості, не дарма ж ми проводили дослідження функції =).