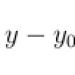Похідна функції. Правила обчислення похідних Похідна функція fx

(\large\bf Похідна функції)

Розглянемо функцію y=f(x), задану на інтервалі (a, b). Нехай x- будь-яка фіксована точка інтервалу (a, b), а Δx- довільне число, таке, що значення x+Δxтакож належить інтервалу (a, b). Це число Δxназивають збільшенням аргументу.

Визначення. Збільшенням функції y=f(x)у точці x, що відповідає прирощенню аргументу Δx, назвемо число

Δy = f(x+Δx) - f(x).

Вважаємо, що Δx ≠ 0. Розглянемо у цій фіксованій точці xвідношення збільшення функції в цій точці до відповідного збільшення аргументу Δx

Це ставлення називатимемо різницевим ставленням. Оскільки значення xми вважаємо фіксованим, різницеве ​​ставлення є функцією аргументу Δx. Ця функція визначена для всіх значень аргументу Δx, Що належать деякої досить малої околиці точки Δx=0, за винятком самої точки Δx=0. Таким чином, ми маємо право розглядати питання про існування межі зазначеної функції при Δx → 0.

Визначення. Похідної функції y=f(x)у цій фіксованій точці xназивається межа при Δx → 0різницевих відносин, тобто

За умови, що ця межа існує.

Позначення. y′(x)або f′(x).

Геометричний зміст похідної: Похідна від функції f(x)у цій точці xдорівнює тангенсу кута між віссю Oxі щодо графіку цієї функції у відповідній точці:

f′(x 0) = \tgα.

Механічний сенс похідної: Похідна від шляху за часом дорівнює швидкості прямолінійного руху точки:

Рівняння дотичної до лінії y=f(x)у точці M 0 (x 0, y 0)набуває вигляду

y-y 0 = f′(x 0) (x-x 0).

Нормаллю до кривої в деякій її точці називається перпендикуляр до дотичної в тій же точці. Якщо f′(x 0)≠ 0, то рівняння нормалі до лінії y=f(x)у точці M 0 (x 0, y 0)записується так:

Поняття диференційованості функції

Нехай функція y=f(x)визначено на деякому інтервалі (a, b), x- деяке фіксоване значення аргументу цього інтервалу, Δx- будь-яке приріст аргументу, таке, що значення аргументу x+Δx ∈ (a, b).

Визначення. Функція y=f(x)називається диференційованою в даній точці x, якщо збільшення Δyцієї функції у точці x, що відповідає збільшенню аргументу Δx, може бути представимо у вигляді

Δy = A Δx +αΔx,

де A- деяке число, що не залежить від Δx, а α - функція аргументу Δx, що є нескінченно малою при Δx→ 0.

Так як добуток двох нескінченно малих функцій αΔxє нескінченно малою вищого порядку, ніж Δx(властивість 3 нескінченно малих функцій), то можемо записати:

Δy = A Δx +o(Δx).

Теорема. Для того, щоб функція y=f(x)була диференційованою в даній точці xнеобхідно, і достатньо, щоб вона мала в цій точці кінцеву похідну. При цьому A=f′(x), тобто

Δy = f′(x) Δx +o(Δx).

Операцію знаходження похідної зазвичай називають диференціюванням.

Теорема. Якщо функція y=f(x) x, то вона безперервна у цій точці.

Зауваження. З безперервності функції y=f(x)у цій точці xвзагалі кажучи, не випливає диференційованість функції f(x)у цій точці. Наприклад, функція y=|x|- безперервна у точці x=0але не має похідної.

Поняття диференціала функції

Визначення. Диференціалом функції y=f(x)називається твір похідної цієї функції на збільшення незалежної змінної x:

dy = y′ Δx, df(x) = f′(x) Δx.

Для функції y=xотримуємо dy=dx=x′Δx = 1· Δx= Δx, тобто dx=Δx- диференціал незалежної змінної дорівнює приросту цієї змінної.

Таким чином, можемо записати

dy = y′ dx, df(x) = f′(x) dx

Диференціал dyта приріст Δyфункції y=f(x)у цій точці x, обидва відповідають одному й тому збільшенню аргументу Δx, Загалом кажучи, не рівні один одному.

Геометричний зміст диференціала: Диференціал функції дорівнює приросту ординати щодо графіку даної функції, коли аргумент отримує прирощення Δx.

Правила диференціювання

Теорема. Якщо кожна з функцій u(x)і v(x)диференційована в даній точці x, то сума, різниця, добуток і приватне виконання цих функцій (приватне за умови, що v(x)≠ 0) також диференційовані в цій точці, причому мають місце формули:

Розглянемо складну функцію y=f(φ(x))≡ F(x), де y=f(u), u=φ(x). В цьому випадку uназивають проміжним аргументом, x - незалежної змінної.

Теорема. Якщо y=f(u)і u=φ(x)- диференційовані функції своїх аргументів, то похідна складної функції y=f(φ(x))Існує і дорівнює добутку цієї функції по проміжному аргументу на похідну проміжного аргументу незалежної змінної, тобто.

Зауваження. Для складної функції, яка є суперпозицією трьох функцій y=F(f(φ(x))), правило диференціювання має вигляд

y′ x = y′ u u′ v v′ x,

де функції v=φ(x), u=f(v)і y=F(u)- функції своїх аргументів, що диференціюються.

Теорема. Нехай функція y=f(x)зростає (або зменшується) і безперервна в деякій околиці точки x 0. Нехай, крім того, ця функція диференційована у вказаній точці x 0та її похідна у цій точці f′(x 0) ≠ 0. Тоді в деякій околиці відповідної точки y 0 = f(x 0)визначено зворотну для y=f(x)функція x=f -1 (y), причому зазначена зворотна функція диференційована у відповідній точці y 0 = f(x 0)і для її похідної у цій точці yсправедлива формула

Таблиця похідних

Інваріантність форми першого диференціалу

Розглянемо диференціал складної функції. Якщо y=f(x), x=φ(t)- диференційовані функції своїх аргументів, то похідна функції y=f(φ(t))виражається формулою

y′ t = y′ x x′ t.

За визначенням dy=y′ t dtтоді отримаємо

dy = y′t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,

dy = y′ x dx.

Отже, довели,

Властивість інваріантності форми першого диференціалу функції: як у випадку, коли аргумент xє незалежною змінною, так і у випадку, коли аргумент xсам є диференційованою функцією нової змінної, диференціал dyфункції y=f(x)дорівнює похідної цієї функції, помноженої на диференціал аргументу dx.

Застосування диференціала у наближених обчисленнях

Ми показали, що диференціал dyфункції y=f(x), взагалі кажучи, не дорівнює прирощенню Δyцієї функції. Проте з точністю до нескінченно малої функції вищого порядку малості, ніж Δx, справедливо наближена рівність

Δy ≈ dy.

Ставлення називають відносною похибкою рівності цієї рівності. Так як Δy-dy=o(Δx), то відносна похибка даної рівності стає як завгодно малою при зменшенні |Δх|.

Враховуючи що Δy=f(x+δ x)-f(x), dy=f′(x)Δx, отримаємо f(x+δ x)-f(x) ≈ f′(x)Δxабо

f(x+δ x) ≈ f(x) + f′(x)Δx.

Ця наближена рівність дозволяє з помилкою o(Δx)замінити функцію f(x)в малій околиці точки x(тобто для малих значень Δx) лінійною функцією аргументу Δx, що стоїть у правій частині.

Похідні вищих порядків

Визначення. Другий похідний (або похідний другого порядку) функції y=f(x)називається похідна від першої похідної.

Позначення другої похідної функції y=f(x):

Механічний зміст другої похідної. Якщо функція y=f(x)описує закон руху матеріальної точки по прямій лінії, то друга похідна f″(x)дорівнює прискоренню точки, що рухається в момент часу x.

Аналогічно визначається третя, четверта похідна.

Визначення. n-ї похідної (або похідної n-го порядку) функції y=f(x)називається похідна від неї n-1-ї похідної:

y (n) = (y (n-1)) ', f (n) (x) = (f (n-1) (x)) '.

Позначення: y″′, y IV, y Vі т.д.

Процес знаходження похідної функції називається диференціюванням.Похідну доводиться знаходити у низці завдань курсу математичного аналізу. Наприклад, при знайденні точок екстремуму та перегину графіка функції.

Як знайти?

Щоб знайти похідну функції потрібно знати таблицю похідних елементарних функцій та застосовувати основні правила диференціювання:

1. Винесення константи за знак похідної: $$ (Cu)" = C(u)" $$
2. Похідна суми / різниці функцій: $$ (u \pm v)" = (u)" \pm (v)" $$
3. Похідна робота двох функцій: $$ (u \cdot v)" = u"v + uv" $$
4. Похідна дробу : $$ \bigg (\frac(u)(v) \bigg)" = \frac(u"v - uv")(v^2) $$
5. Похідна складної функції: $$ (f(g(x)))" = f"(g(x)) \cdot g"(x) $$

Приклади рішення

Приклад 1

Знайти похідну функції $ y = x^3 - 2x^2 + 7x - 1$

Рішення

Похідна суми / різниці функцій дорівнює сумі / різниці похідних: $$ y" = (x^3 - 2x^2 + 7x - 1)" = (x^3)" - (2x^2)" + (7x)" - (1)" = $$ Використовуючи правило похідної статечної функції $ (x^p)" = px^(p-1) $ маємо: $$ y" = 3x^(3-1) - 2 \cdot 2 x^(2-1) + 7 - 0 = 3x^2 - 4x + 7 $$ Також було враховано, що похідна від константи дорівнює нулю. Якщо не вдається вирішити своє завдання, то надсилайте його до нас. Ми надамо детальне рішення. Ви зможете ознайомитися з ходом обчислення та отримати інформацію. Це допоможе вчасно отримати залік у викладача!

Відповідь

$$ y" = 3x^2 - 4x + 7 $$

На цьому занятті ми будемо вчитися застосовувати формули та правила диференціювання.

приклади. Знайти похідні функції.

1. y=x7+x5-x4+x3-x2+x-9. Застосовуємо правило I, формули 4, 2 та 1. Отримуємо:

y'=7x6+5x4-4x3+3x2-2x+1.

2. y=3x6-2x+5. Вирішуємо аналогічно, використовуючи ті ж формули та формулу 3.

y'=3∙6x 5 -2=18x 5 -2.

Застосовуємо правило I, формули 3, 5 і 6 і 1.

Застосовуємо правило IV, формули 5 і 1 .

У п'ятому прикладі за правилом Iпохідна суми дорівнює сумі похідних, а похідну 1-го доданку ми щойно знаходили (приклад 4 ), тому, знаходимо похідні 2-гоі 3-гододанків, а для одногододанку можемо відразу писати результат.

Диференціюємо Другеі 3-тєдоданки за формулою 4 . Для цього перетворимо коріння третього та четвертого ступенів у знаменниках до ступенів з негативними показниками, а потім, за 4 формулі, знаходимо похідні ступенів.

Подивіться цей приклад і отриманий результат. Вловили закономірність? Добре. Це означає, що ми отримали нову формулу і можемо додати її до таблиці похідних.

Вирішимо шостий приклад і виведемо ще одну формулу.

Використовуємо правило IVта формулу 4 . Дріб, що вийшло, скоротимо.

Дивимося на цю функцію та її похідну. Ви, звичайно, зрозуміли закономірність і готові назвати формулу:

Вчимо нові формули!

приклади.

1. Знайти збільшення аргументу та збільшення функції y= x 2, якщо початкове значення аргументу дорівнювало 4 , а нове - 4,01 .

Рішення.

Нове значення аргументу х = х 0 +Δx. Підставимо дані: 4,01 = 4 + Δх, звідси збільшення аргументу Δх=4,01-4=0,01. Приріст функції, за визначенням, дорівнює різниці між новим і колишнім значеннями функції, тобто. Δy = f (х 0 + Δх) - f (x 0). Так як у нас функція y=x 2, то Δу=(х 0 +Δx) 2 - (х 0) 2 = (х 0) 2 +2x 0 · Δx+(Δx) 2 - (х 0) 2 = 2x 0 · Δx+(Δx) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

Відповідь: приріст аргументу Δх=0,01; збільшення функції Δу=0,0801.

Можна було збільшення функції знайти по-іншому: Δy= y (x 0 +Δx) -y (x 0) = у (4,01) - у (4) = 4,01 2 -4 2 = 16,0801-16 = 0,0801.

2. Знайти кут нахилу щодо графіку функції y=f(x)у точці х 0, якщо f" (х 0) = 1.

Рішення.

Значення похідної у точці торкання х 0і є значення тангенса кута нахилу дотичної (геометричний зміст похідної). Маємо: f "(х 0) = tgα = 1 → α = 45°,так як tg45 ° = 1.

Відповідь: дотична до графіка цієї функції утворює з позитивним напрямом осі Ох кут, рівний 45°.

3. Вивести формулу похідної функції y=x n.

Диференціювання- Це дія знаходження похідної функції.

При знаходженні похідних застосовують формули, які були виведені на підставі визначення похідної так само, як ми вивели формулу похідного ступеня: (x n)" = nx n-1.

Ось ці формули.

Таблицю похіднихлегше буде завчити, промовляючи словесні формулювання:

1. Похідна постійної величини дорівнює нулю.

2. Ікс штрих дорівнює одиниці.

3. Постійний множник можна винести за похідний знак.

4. Похідна ступеня дорівнює добутку показника цього ступеня на ступінь з тією самою основою, але показником на одиницю менше.

5. Похідна кореня дорівнює одиниці, поділеній на два такі ж корені.

6. Похідна одиниці, поділеної на ікс дорівнює мінус одиниці, поділеної на ікс у квадраті.

7. Похідна синуса дорівнює косінусу.

8. Похідна косинуса дорівнює мінус синусу.

9. Похідна тангенса дорівнює одиниці, поділеній на квадрат косинуса.

10. Похідна котангенса дорівнює мінус одиниці, поділеної на квадрат синуса.

Вчимо правила диференціювання.

1. Похідна суми алгебри дорівнює алгебраїчній сумі похідних доданків.

2. Похідна твори дорівнює добутку похідної першого множника на другий плюс добуток першого множника на похідну другого.

3. Похідна «у», поділеного на «ве» дорівнює дробу, в чисельнику якого "у штрих помножений на "ве" мінус "у, помножений на ве штрих", а в знаменнику - "ве в квадраті".

4. Окремий випадок формули 3.

Вчимо разом!

Сторінка 1 з 1 1

Операція відшукання похідної називається диференціюванням.

В результаті вирішення завдань про відшукання похідних у найпростіших (і не дуже простих) функцій визначення похідної як межі відношення прирощення до прирощення аргументу з'явилися таблиця похідних і точно визначені правила диференціювання. Першими на ниві знаходження похідних попрацювали Ісаак Ньютон (1643-1727) та Готфрід Вільгельм Лейбніц (1646-1716).

Тому в наш час, щоб знайти похідну будь-якої функції, не треба обчислювати згадану вище межу відношення збільшення функції до збільшення аргументу, а потрібно лише скористатися таблицею похідних та правилами диференціювання. Для знаходження похідної підходить наступний алгоритм.

Щоб знайти похідну, треба вираз під знаком штриха розібрати на складові прості функціїта визначити, якими діями (твір, сума, приватна)пов'язані ці функції. Далі похідні елементарних функцій знаходимо у таблиці похідних, а формули похідних твору, суми та частки - у правилах диференціювання. Таблиця похідних та правила диференціювання дані після перших двох прикладів.

приклад 1.Знайти похідну функції

Рішення. З правил диференціювання з'ясовуємо, що похідна суми функцій є сума похідних функцій, тобто.

З таблиці похідних з'ясовуємо, що похідна "ікса" дорівнює одиниці, а похідна синуса - косінус. Підставляємо ці значення у суму похідних і знаходимо необхідну умовою завдання похідну:

приклад 2.Знайти похідну функції

Рішення. Диференціюємо як похідну суми, в якій другий доданок з постійним множником, його можна винести за знак похідної:

Якщо поки що виникають питання, звідки береться, вони, як правило, прояснюються після ознайомлення з таблицею похідних та найпростішими правилами диференціювання. До них ми і переходимо зараз.

Таблиця похідних простих функцій

1. Похідна константи (числа). Будь-якого числа (1, 2, 5, 200 ...), яке є у виразі функції. Завжди дорівнює нулю. Це дуже важливо пам'ятати, тому що потрібно дуже часто
2. Похідна незалежною змінною. Найчастіше "ікса". Завжди дорівнює одиниці. Це також важливо запам'ятати надовго
3. Похідна ступеня. У ступінь під час вирішення завдань необхідно перетворювати неквадратні коріння.
4. Похідна змінної у ступені -1
5. Похідна квадратного кореня
6. Похідна синуса
7. Похідна косинуса
8. Похідна тангенса
9. Похідна котангенсу
10. Похідна арксинусу
11. Похідна арккосинусу
12. Похідна арктангенса
13. Похідна арккотангенса
14. Похідна натурального логарифму
15. Похідна логарифмічна функція
16. Похідна експоненти
17. Похідна показової функції

Правила диференціювання

1. Похідна суми чи різниці
2. Похідна твори
2a. Похідна вирази, помноженого на постійний множник
3. Похідна приватного
4. Похідна складної функції

Правило 1.Якщо функції

диференційовані в деякій точці, то в тій же точці диференційовані і функції

причому

тобто. похідна суми алгебраїчної функцій дорівнює сумі алгебри похідних цих функцій.

Слідство. Якщо дві функції, що диференціюються, відрізняються на постійний доданок, то їх похідні рівні, тобто.

Правило 2Якщо функції

диференційовані в деякій точці, то в тій же точці диференційовано та їх добуток

причому

тобто. похідна твори двох функцій дорівнює сумі творів кожної з цих функцій похідну інший.

Наслідок 1. Постійний множник можна виносити за знак похідної:

Наслідок 2. Похідна твори кількох функцій, що диференціюються, дорівнює сумі творів похідної кожного з співмножників на всі інші.

Наприклад, для трьох множників:

Правило 3Якщо функції

диференційовані в деякій точці і , то в цій точці диференційовано та їх приватнеu/v , причому

тобто. похідна приватного двох функцій дорівнює дробу, чисельник якого є різниця творів знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадрат колишнього чисельника.

Де що шукати на інших сторінках

При знаходженні похідної твори і частки у реальних завданнях завжди потрібно застосовувати відразу кілька правил диференціювання, тому більше прикладів на ці похідні - у статті"Виробничі твори та приватні функції".

Зауваження.Слід не плутати константу (тобто число) як доданок у сумі і як постійний множник! У разі доданку її похідна дорівнює нулю, а у разі постійного множника вона виноситься за знак похідних. Це типова помилка, яка зустрічається на початковому етапі вивчення похідних, але в міру вирішення вже кількох одно-двоскладових прикладів середній студент цієї помилки вже не робить.

А якщо при диференціюванні твору чи приватного у вас з'явився доданок u"v, в котрому u- число, наприклад, 2 або 5, тобто константа, то похідна цього числа дорівнюватиме нулю і, отже, все доданок буде дорівнює нулю (такий випадок розібраний у прикладі 10).

Інша часта помилка - механічне рішення похідної складної функції як похідної простий функції. Тому похідної складної функціїприсвячено окрему статтю. Але спочатку вчитимемося знаходити похідні простих функцій.

По ходу не обійтися без перетворень виразів. Для цього може знадобитися відкрити у нових вікнах посібники Дії зі ступенями та коріннямі Дії з дробами .

Якщо Ви шукаєте рішення похідних дробів зі ступенями та корінням, тобто, коли функція має вигляд начебто , то слідуйте на заняття "Похідна суми дробів зі ступенями та корінням".

Якщо ж перед Вами завдання начебто , то Вам на заняття "Виробні простих тригонометричних функцій".

Покрокові приклади - як знайти похідну

приклад 3.Знайти похідну функції

Рішення. Визначаємо частини виразу функції: весь вираз представляє твір, яке співмножники - суми, у другий у тому числі одне з доданків містить постійний множник. Застосовуємо правило диференціювання твору: похідна твори двох функцій дорівнює сумі творів кожної з цих функцій на похідну інший:

Далі застосовуємо правило диференціювання суми: похідна суми алгебраїчної функцій дорівнює сумі алгебри похідних цих функцій. У нашому випадку в кожній сумі другий доданок зі знаком мінус. У кожній сумі бачимо і незалежну змінну, похідна якої дорівнює одиниці, і константу (число), похідна якої дорівнює нулю. Отже, "ікс" у нас перетворюється на одиницю, а мінус 5 - на нуль. У другому виразі "ікс" помножено на 2, так що двійку множимо на ту ж одиницю як похідну "ікса". Отримуємо такі значення похідних:

Підставляємо знайдені похідні у суму творів і отримуємо необхідну умовою завдання похідну всієї функції:

А перевірити розв'язання задачі на похідну можна на .

приклад 4.Знайти похідну функції

Рішення. Від нас потрібно знайти похідну приватного. Застосовуємо формулу диференціювання частки: похідна частки двох функцій дорівнює дробу, чисельник якого є різниця творів знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадрат колишнього чисельника. Отримуємо:

Похідну співмножників у чисельнику ми вже знайшли у прикладі 2. Не забудемо також, що твір, що є другим співмножником у чисельнику в поточному прикладі береться зі знаком мінус:

Якщо Ви шукаєте вирішення таких завдань, в яких треба знайти похідну функції, де суцільне нагромадження коренів та ступенів, як, наприклад, , то ласкаво просимо на заняття "Виробна суми дробів зі ступенями і корінням" .

Якщо ж Вам потрібно дізнатися більше про похідні синуси, косінуси, тангенси та інші тригонометричні функції, тобто, коли функція має вигляд начебто , то Вам на урок "Виробні простих тригонометричних функцій" .

Приклад 5.Знайти похідну функції

Рішення. У цій функції бачимо твір, один із співмножників яких - квадратний корінь із незалежної змінної, з похідною якого ми ознайомились у таблиці похідних. За правилом диференціювання твору та табличного значення похідної квадратного кореня отримуємо:

Перевірити рішення задачі на похідну можна на калькуляторі похідних онлайн .

Приклад 6.Знайти похідну функції

Рішення. У цій функції бачимо приватне, ділене якого - квадратний корінь із незалежної змінної. За правилом диференціювання приватного, яке ми повторили і застосували в прикладі 4, та табличного значення похідної квадратного кореня отримуємо:

Щоб позбутися дробу в чисельнику, множимо чисельник і знаменник на .

Вирішувати фізичні завдання або приклади з математики неможливо без знань про похідну і методи її обчислення. Похідна – одне з найважливіших понять математичного аналізу. Цій фундаментальній темі ми вирішили присвятити сьогоднішню статтю. Що таке похідна, який її фізичний та геометричний зміст, як порахувати похідну функції? Всі ці питання можна поєднати в одне: як зрозуміти похідну?

Геометричний та фізичний зміст похідної

Нехай є функція f(x) , задана в певному інтервалі (a, b) . Точки х і х0 належать до цього інтервалу. При зміні х змінюється сама функція. Зміна аргументу – різниця його значень х-х0 . Ця різниця записується як дельта ікс і називається збільшенням аргументу. Зміною або збільшенням функції називається різниця значень функції у двох точках. Визначення похідної:

Похідна функції у точці – межа відношення збільшення функції у цій точці до збільшення аргументу, коли останнє прагне нулю.

Інакше це можна записати так:

Який сенс у знаходженні такої межі? А ось який:

похідна від функції в точці дорівнює тангенсу кута між віссю OX і щодо графіку функції в даній точці.

Фізичний зміст похідної: похідна шляхи за часом дорівнює швидкості прямолінійного руху.

Дійсно, ще зі шкільних часів усім відомо, що швидкість – це приватна дорога. x=f(t) та часу t . Середня швидкість за деякий проміжок часу:

Щоб дізнатися швидкість руху в момент часу t0 потрібно обчислити межу:

Правило перше: виносимо константу

Константу можна винести за знак похідної. Більше того – це потрібно робити. При вирішенні прикладів математики візьміть за правило - якщо можете спростити вираз, обов'язково спрощуйте .

приклад. Обчислимо похідну:

Правило друге: похідна суми функцій

Похідна суми двох функцій дорівнює сумі похідних цих функцій. Те саме справедливо і для похідної різниці функцій.

Не наводитимемо доказ цієї теореми, а краще розглянемо практичний приклад.

Знайти похідну функції:

Правило третє: похідна робота функцій

Похідна твори двох функцій, що диференціюються, обчислюється за формулою:

Приклад: знайти похідну функції:

Рішення:

Тут важливо сказати про обчислення похідних складних функцій. Похідна складної функції дорівнює добутку похідної цієї функції за проміжним аргументом на похідну проміжного аргументу за незалежною змінною.

У наведеному вище прикладі ми зустрічаємо вираз:

В даному випадку проміжний аргумент - 8х у п'ятому ступені. Для того, щоб обчислити похідну такого виразу спочатку вважаємо похідну зовнішньої функції за проміжним аргументом, а потім множимо на похідну безпосередньо проміжного аргументу незалежної змінної.

Правило четверте: похідна приватного двох функцій

Формула для визначення похідної від частки двох функцій:

Ми постаралися розповісти про похідні для чайників з нуля. Ця тема не така проста, як здається, тому попереджаємо: у прикладах часто зустрічаються пастки, так що будьте уважні при обчисленні похідних.

З будь - яким питанням з цієї та інших тем ви можете звернутися до студентського сервісу . За короткий термін ми допоможемо вирішити найскладнішу контрольну та розібратися із завданнями, навіть якщо ви ніколи раніше не займалися обчисленням похідних.