Стандартними методами, але зайшли в глухий кут з черговим прикладом.
У чому полягає труднощі і де можливо загвоздка? Відкладемо убік намилену мотузку, спокійно проаналізуємо причини та ознайомимося з практичними прийомами рішення.
Перше, і найголовніше: у переважній більшості випадків для дослідження збіжності ряду необхідно застосувати якийсь знайомий спосіб, але загальний член ряду набитий настільки хитрою начинкою, що зовсім не очевидно, що з нею робити. І ви ходите по колу: не спрацьовує перша ознака, не годиться друга, не виходить третім, четвертим, п'ятим методом, потім чернетки відкидаються убік і все починається наново. Зазвичай це пов'язано з нестачею досвіду або пробілами в інших розділах математичного аналізу. Зокрема, якщо запущено межі послідовностейта поверхнево розібрані межі функцій, то доведеться туго.
Іншими словами, людина просто не бачить потрібний прийом рішення через брак знань чи досвіду.
Буває винне і «затемнення», коли, наприклад, елементарно не виконаний необхідний ознака збіжності низки, але з незнання, неуважності чи недбалості це випадає з поля зору. І виходить як у тій байці, де професор математики вирішив дитяче завдання за допомогою диких рекурентних послідовностей та числових рядів =)
У найкращих традиціях одразу живі приклади: ряди 
та його родичі – розходяться, оскільки у теорії доведено межі послідовностей. Швидше за все, у першому семестрі з вас витрясуть душу за доказ на 1-2-3 сторінки, але зараз цілком достатньо показати невиконання необхідної умови збіжності низки, пославшись на відомі факти. Відомі? Якщо студент не знає, що корінь енного ступеня – штука надзвичайно потужна, то, скажімо, лави 
поставлять його в безвихідь. Хоча рішення, як двічі два: , тобто. зі зрозумілої причини обидва ряди розходяться. Скромного коментаря «дані межі доведені в теорії» (або навіть зовсім його відсутності) цілком вистачить для заліку, все-таки викладки досить важкі і ставляться вони не до розділу числових рядів.
А вивчивши найближчі приклади, ви тільки дивуватиметеся стислості та прозорості багатьох рішень:
Приклад 1
Дослідити збіжність ряду
Рішення: перш за все, перевіряємо виконання необхідної ознаки збіжності. Це не формальність, а чудовий шанс розправитися з прикладом «малою кров'ю».
«Огляд місця події» наводить на думку про ряд, що розходиться (випадок узагальненого гармонійного ряду), але знову ж таки виникає питання, як врахувати логарифм у чисельнику?
Зразки оформлення завдань наприкінці уроку.
Не рідкість, коли доводиться проводити двоходове (а то й триходове) міркування:
Приклад 6
Дослідити збіжність ряду 
Рішення: спочатку акуратно розуміємось з тарабарщиною чисельника. Послідовність – обмежена: . Тоді: 
Порівняємо наш ряд із поруч. В силу щойно отриманого подвійної нерівності, для всіх «ен» буде виконано: 
Тепер порівняємо ряд з гармонійним рядом, що розходиться.
Знаменник дробу меншезнаменника дробу сам дріб – більшедроби (розпишіть кілька перших членів, якщо не зрозуміло). Таким чином, для будь-якого «ен»: 
Отже, за ознакою порівняння ряд 
розходитьсяразом із гармонійним рядом.
Якщо трохи видозмінити знаменник: 
, то перша частина міркувань буде аналогічна: 
. Але для доказу розбіжності низки вже застосуємо лише граничний ознака порівняння, оскільки нерівність неправильно.
Ситуація з рядами, що сходяться, «дзеркальна», тобто, наприклад, для ряду можна використовувати обидві ознаки порівняння (нерівність справедлива), а для ряду – тільки гранична ознака (нерівність невірна).
Продовжуємо наше сафарі за дикою природою, де на горизонті замаячило стадо граціозних та соковитих антилоп:
Приклад 7
Дослідити збіжність ряду
Рішення: необхідна ознака збіжності виконується, і ми знову ставимося до класичного питання: що робити? Перед нами щось нагадує низку, що сходить, однак, чіткого правила тут немає - такі асоціації часто оманливі.
Найчастіше, та не цього разу. За допомогою граничної ознаки порівнянняпорівняємо наш ряд зі схожим рядом. Під час обчислення межі використовуємо чудова межа 
, де як нескінченно малої величинивиступає: 
сходитьсяразом із поруч.
Замість застосування стандартного штучного прийому домноження і розподілу на «трійку», можна було спочатку провести порівняння з рядом, що сходить.
Але тут бажане застереження, що константа-множник загального члена не впливає на збіжність низки. І саме в такому стилі оформлено рішення наступного прикладу:
Приклад 8
Дослідити збіжність ряду
Зразок наприкінці уроку.
Приклад 9
Дослідити збіжність ряду
Рішення: у попередніх прикладах ми користувалися обмеженістю синуса, але зараз ця властивість виявляється поза грою. Знаменник дробу вищого порядку зростання, Чим чисельник, тому при аргумент синуса і весь спільний член нескінченно мали. Необхідна умова збіжності, як розумієте, виконано, що не дозволяє нам ухилятися від роботи.
Проведемо розвідку: відповідно до чудовою еквівалентністю 
, подумки відкинемо синус і отримаємо ряд . Ну а вже таке….
Оформляємо рішення:
Порівняємо досліджуваний ряд із розбіжним рядом. Використовуємо граничну ознаку порівняння: 
Замінимо нескінченно малу еквівалентну: при 
.
Отримано кінцеве число, відмінне від нуля, отже, досліджуваний ряд розходитьсяразом із гармонійним рядом.
Приклад 10
Дослідити збіжність ряду
Це приклад самостійного рішення.
Для планування подальших дій у подібних прикладах здорово допомагає уявне відкидання синуса, арксинусу, тангенсу, арктангенсу. Але пам'ятайте, така можливість існує лише за нескінченно маломуаргументі, нещодавно мені трапився провокаційний ряд:
Приклад 11
Дослідити збіжність ряду 
.
Рішення: тут марно використовувати обмеженість арктангенса, і еквівалентність також не працює. Вихід несподівано простий: 
Досліджуваний ряд розходиться, тому що не виконано необхідну ознаку збіжності ряду.
Друга причина«Затику на завданні» полягає в пристойній навароченості загального члена, що спричиняє складнощі вже технічного характеру. Грубо кажучи, якщо розглянуті вище ряди відносяться до розряду «фіг здогадаєшся», то ці – категорії «хрін вирішиш». Власне, це і називають складністю у «звичайному» розумінні. Далеко не кожен правильно розрулить кілька факторіалів, ступенів, коріння та інших мешканців савани. Найбільше проблем завдають, звичайно ж, факторіали:
Приклад 12
Дослідити збіжність ряду
Як звести факторіал у ступінь? Легко. За правилом дій зі ступенями, необхідно звести в ступінь кожен множник твору:
І, звичайно ж, увага і ще раз увага, сама по собі ознака Даламбера працює традиційно: 
Таким чином, досліджуваний ряд сходиться.
Нагадую раціональну методику усунення невизначеності: коли зрозумілий порядок зростаннячисельника та знаменника – зовсім не обов'язково мучитися та розкривати дужки.
Приклад 13
Дослідити збіжність ряду
Звір дуже рідкісний, але трапляється, і було б несправедливим обійти його об'єктивом камери.
Що таке факторіал з подвійним знаком оклику? Факторіал «накручує» добуток позитивних парних чисел:
Аналогічно, факторіал «накручує» добуток позитивних непарних чисел: 
Проаналізуйте, у чому полягає відмінність від і
Приклад 14
Дослідити збіжність ряду
А в цьому завданні постарайтеся не заплутатися зі ступенями, чудовими еквівалентностямиі чудовими межами.
Зразки рішень та відповіді наприкінці уроку.
Але студент дістається на корм не лише тиграм – свою здобич вистежують і хитрі леопарди:
Приклад 15
Дослідити збіжність ряду 
Рішення: практично миттєво відпадають необхідну ознаку збіжності, граничну ознаку, ознаки Даламбера та Коші. Але найгірше, що безсила неодноразово рятувала нас ознака з нерівностями. Справді, порівняння з розбіжним поруч неможливо, оскільки нерівність 
неправильно - множник-логарифм тільки збільшує знаменник, зменшуючи саму дріб 
по відношенню до дробу. І інше глобальне питання: а чому ми взагалі спочатку впевнені, що наш ряд 
Обов'язково повинен розходитися та її треба порівнювати з будь-яким розбіжним поруч? Раптом він узагалі сходиться?
Інтегральна ознака? Невласний інтеграл 
навіює жалобний настрій. От якби у нас був ряд 
… тоді так. Стоп! Так народжуються ідеї. Оформляємо рішення у два кроки:
1) Спочатку досліджуємо збіжність ряду 
. Використовуємо інтегральна ознака:
Підінтегральна функція безперервнана
Таким чином, ряд 
розходиться разом із відповідним невласним інтегралом.
2) Порівняємо наш ряд з розбіжним рядом 
. Використовуємо граничну ознаку порівняння:
Отримано кінцеве число, відмінне від нуля, отже, досліджуваний ряд розходитьсяразом з поруч 
.
І у такому рішенні немає нічого незвичайного чи творчого – так і треба вирішувати!
Пропоную самостійно оформити наступну двоходівку:
Приклад 16
Дослідити збіжність ряду 
Студент з деяким досвідом у більшості випадків відразу бачить, сходиться ряд або розходиться, але буває, що хижак вправно маскується в кущах:
Приклад 17
Дослідити збіжність ряду 
Рішення: на перший погляд взагалі не зрозуміло, як поводиться цей ряд А якщо перед нами туман, то логічно розпочати з чорнової перевірки необхідної умови збіжності низки. З метою усунення невизначеності використовуємо непотоплюваний метод множення та поділу на сполучене вираження:
Потрібна ознака збіжності не спрацювала, але вивів на чисту воду нашого тамбовського товариша. В результаті виконаних перетворень отримано еквівалентний ряд 
, який у свою чергу сильно нагадує ряд , що сходить .
Записуємо чистове рішення:
Порівняємо даний ряд з рядом, що збігається. Використовуємо граничну ознаку порівняння:
Помножимо і розділимо на сполучене вираз:
Отримано кінцеве число, відмінне від нуля, отже, досліджуваний ряд сходитьсяразом із поруч.
Можливо, у деяких виникло питання, звідки на нашому африканському сафарі з'явилися вовки? Не знаю. Завезли, мабуть. Наступну трофейну шкуру добувати вам:
Приклад 18
Дослідити збіжність ряду 
Зразковий рішення наприкінці уроку
І, нарешті, ще одна думка, яка у відчаї відвідує багатьох студентів: а чи не використовувати більш рідкісну ознаку збіжності ряду? Ознака Раабе, ознака Абеля, ознака Гауса, ознака Діріхле та інші невідомі звірятка. Ідея робоча, але в реальні прикладиздійснюється дуже рідко. Особисто я за всі роки практики лише 2-3 рази вдався до ознакою Раабеколи дійсно нічого не допомогло зі стандартного арсеналу. Повністю відтворюю хід свого екстремального квесту:
Приклад 19
Дослідити збіжність ряду
Рішення: Без жодних сумнівів ознака Даламбера Під час обчислень активно використовую властивості ступенів, а також друга чудова межа:
Ось тобі й раз. Ознака Даламбера не дала відповіді, хоча нічого не віщувало такого результату.
Пошерстивши довідник, я знайшов доведену в теорії маловідому межу і застосував сильнішу радикальну ознаку Коші:
Ось тобі й два. І, головне, зовсім не зрозуміло, сходиться ряд або розходиться (вкрай рідкісна для мене ситуація). Потрібна ознака порівняння? Без особливих надій - навіть якщо немислимим чином розберуся з порядком зростання чисельника і знаменника, це ще не гарантує винагороди.
Повний даламбер, але найгірше, що ряд потрібно вирішити. Потрібно. Це буде перший випадок, коли я здамся. І тут мені згадалося, що начебто існують ще якісь сильніші ознаки. Переді мною вже не вовк, не леопард і не тигр. Це був величезний слон, який розмахував великим хоботом. Довелося взяти до рук гранатомет:
Ознака Раабе
Розглянемо позитивний числовий ряд.
Якщо існує межа 
, то:
а) При ряд розходиться. Причому отримане значення може бути нульовим чи негативним
б) При ряд сходиться. Зокрема, ряд сходиться за .
в при ознака Раабе не дає відповіді.
Складаємо межу і дбайливо-акуратно спрощуємо дріб: 
Так, картина, м'яко кажучи, неприємна, але я вже не здивувався. Подібні межі розколюються за допомогою правила Лопіталя, І перша думка, як потім з'ясувалося, виявилося правильною. Але спочатку я десь годину крутив-крутив межу «звичайними» методами, проте невизначеність не хотіла усуватися. А ходьба по колу, як нагадує досвід – типова ознака того, що обрано неправильний спосіб вирішення.
Довелося звернутися до російської народної мудрості: Якщо нічого не допомагає, прочитайте інструкцію. І коли я відкрив 2-й том Фіхтенгольця, то на превелику радість виявив дослідження ідентичного ряду. І далі пішло рішення на зразок.
У ряді випадків, досліджуючи коефіцієнти рядів виду (С) або можна встановити, що ці ряди сходяться (виключаючи, можливо, окремі точки) і є рядами Фур'є для своїх сум (див., наприклад, попередній п°), але у всіх цих випадках природно виникає питання,
як знайти суми цих рядів або - точніше - як висловити їх у кінцевому вигляді через елементарні функції, якщо вони взагалі в такому вигляді виражаються. Ще Ейлер (а також Лагранж) з успіхом застосовував для підсумовування тригонометричних рядів у кінцевому вигляді аналітичні функції комплексної змінної. Ідея методу Ейлера полягає у наступному.
Припустимо, що з деякому наборі коефіцієнтів ряди (З) і сходяться до функцій всюди у проміжку виключаючи хіба що окремі точки. Розглянемо тепер статечний ряд з тими ж коефіцієнтами, розташований за ступенями комплексної змінної
На колі одиничного кола т. е. за цей ряд за припущенням сходиться, крім окремих точок:
У такому разі, за відомою властивістю статечних рядів ряд (5) свідомо сходиться при т. е. всередині одиничного кола, визначаючи там деяку функцію комплексної змінної. Використовуючи відомі нам [див. § 5 глави XII] розкладання елементарних функцій комплексної змінної, часто вдається звести до них і функцію.
і за теоремою Абеля , як тільки ряд (6) сходиться, його сума виходить як межа
Зазвичай ця межа дорівнює просто що і дозволяє обчислити в кінцевому вигляді функції
Нехай, наприклад, запропоновані ряди
Доведені в попередньому п° твердження приводять до висновку, що обидва ці ряди сходяться (перший - виключаючи точки 0 і
служать рядами Фур'є для функцій, що визначаються ними Але що це за функції? Для відповіді це питання складемо ряд
За подібністю до логарифмічного ряду легко встановлюється його сума:
отже,
Тепер легке обчислення дає:
так що модуль цього виразу є, а аргумент.
і, таким чином, остаточно
Ці результати нам знайомі і навіть були одного разу отримані за допомогою «комплексних» міркувань; Але в першому випадку ми виходили з функцій і, а в другому - з аналітичної функції. Тут же вперше нам відправною точкою послужили самі лави. Подальші приклади такого роду читач знайде в наступному п°.
Підкреслимо ще раз, що потрібно наперед бути впевненим у сході та рядах (С) та щоб мати право визначити їх суми за допомогою граничної рівності (7). Одне існування межі у правій частині цієї рівності ще дозволяє зробити висновок про збіжності згаданих рядів. Щоб показати це на прикладі, розглянемо ряди
Умова Гельдера.Будемо говорити, що функція $f(x)$ задовольняє в точці $x_0$ умови Гельдера, якщо є односторонні кінцеві межі $f(x_0 \pm 0)$ і такі числа $\delta > 0$, $\alpha \in ( 0,1]$ і $c_0 > 0$, що всім $t \in (0,\delta)$ виконані нерівності: $|f(x_0+t)-f(x_0+0)|\leq c_0t^( \alpha )$, $|f(x_0-t)-f(x_0-0)|\leq c_0t^(\alpha )$.
Формула Діріхле.Перетвореною формулою Діріхле називають формулу виду:
$$S_n(x_0)= \frac(1)(\pi)\int\limits_(0)^(\pi)(f(x_0+t)+f(x_0-t))D_n(t)dt \quad (1),$$ де $D_n(t)=\frac(1)(2)+ \cos t + \ldots+ \cos nt = \frac(\sin(n+\frac(1)(2))t) (2\sin\frac(t)(2)) (2)$ - .
Використовуючи формули $(1)$ і $(2)$, запишемо часткову суму низки Фур'є у такому вигляді:
$$S_n(x_0)= \frac(1)(\pi)\int\limits_(0)^(\pi)\frac(f(x_0+t)+f(x_0-t))(2\sin\) frac(t)(2))\sin \left (n+\frac(1)(2) \right) t dt$$
$$\Rightarrow \lim\limits_(n \to \infty )S_n(x_0) — \frac(1)(\pi)\int\limits_(0)^(\pi)\frac(f(x_0+t) +f(x_0-t))(2\sin\frac(t)(2)) \cdot \\ \cdot \sin \left (n+\frac(1)(2) \right)t dt = 0 \quad (3)$$
Для $f \equiv \frac(1)(2)$ формула $(3)$ приймає наступний вид: $$ \lim\limits_(n \to \infty )\frac(1)(\delta)\frac(\sin(n+\frac(1)(2))t)(2\sin\frac(t) (2))dt=\frac(1)(2), 0
Схожість ряду Фур'є в точці
Теорема.Нехай $f(x)$ — $2\pi$-періодична абсолютно інтегрована на $[-\pi,\pi]$ функція і в точці $x_0$ задовольняє умову Гельдера. Тоді ряд Фур'є функції $f(x)$ у точці $x_0$ сходиться до $$\frac(f(x_0+0)+f(x_0-0))(2).$$
Якщо в точці $x_0$ функція $f(x)$ безперервна, то в цій точці сума ряду дорівнює $f(x_0)$.
Доведення
Оскільки функція $f(x)$ задовольняє в точці $x_0$ умові Гельдера, то за $\alpha > 0$ і $0< t$ $ < \delta$ выполнены неравенства (1), (2).
Запишемо при заданому $\delta > 0$ рівності $(3)$ і $(4)$. Помножуючи рівність $(4)$ на $f(x_0+0)+f(x_0-0)$ і віднімаючи результат із рівності $(3)$, отримуємо $$ \lim\limits_(n \to \infty) (S_n (x_0) - \frac(f(x_0+0)+f(x_0-0))(2) - \\ - \frac(1)(\pi)\int\limits_(0)^(\delta)\ frac(f(x_0+t)+f(x_0-t)-f(x_0+0)-f(x_0-0))(2\sin \frac(t)(2)) \cdot \\ \cdot \ sin \left (n + \frac(1)(2) \right)t \, dt) = 0. \quad (5)$$
З умови Гельдера випливає, що функція $$\Phi(t)= \frac(f(x_0+t)+f(x_0-t)-f(x_0+0)-f(x_0-0))(2\sin \frac(t)(2)).$$ абсолютно інтегрована на відрізку $$. Насправді, застосовуючи нерівність Гельдера, отримуємо, що для функції $\Phi(t)$ справедлива така нерівність: $|\Phi(t)| \leq \frac(2c_0t^(\alpha ))(\frac(2)(\pi)t) = \pi c_0t^(\alpha — 1) (6)$, де $\alpha \in (0,1 ]$.
З огляду на ознаки порівняння для невласних інтегралів з нерівності $(6)$ слід, що $\Phi(t)$ абсолютно интергрируема на $.$
В силу леми Рімана $$\lim\limits_(n \to\infty)\int\limits_(0)^(\delta)\Phi(t)\sin \left (n + \frac(1)(2) \ right)t\cdot dt = 0.$$
З формули $(5)$ тепер випливає, що $$\lim\limits_(n \to \infty)S_n(x_0) = \frac(f(x_0+0)+f(x_0-0))(2) . $$
[згорнути]
Наслідок 1.Якщо $2\pi$-періодична та абсолютно інтегрована на $[-\pi,\pi]$ функція $f(x)$ має у точці $x_0$ похідну, то її ряд Фур'є сходить у цій точці до $f(x_0) $.
Наслідок 2.Якщо $2\pi$-періодична і абсолютно інтегрована на $[-\pi,\pi]$ функція $f(x)$ має в точці $x_0$ обидві односторонні похідні, то її ряд Фур'є сходиться в цій точці до $\frac (f(x_0+0)+f(x_0-0))(2).$
Наслідок 3.Якщо $2\pi$-періодична і абсолютно інтегрована на $[-\pi,\pi]$ функція $f(x)$ задовольняє в точках $-\pi$ і $\pi$ умові Гельдера, то через періодичність сума ряду Фур'є в точках $-\pi$ і $\pi$ дорівнює $$\frac(f(\pi-0)+ f(-\pi+0))(2).$$
Ознака Діні
Визначення.Нехай $f(x)$ — $2\pi$-періодична функція, точка $x_0$ буде регулярною точкою функції $f(x)$, якщо
- 1) існують кінцеві лівий і правий межі $\lim\limits_(x \to x_0+0 )f(x)= \lim\limits_(x \to x_0-0 )f(x)= f(x_0+0)= f(x_0-0),$
- 2) $f(x_0)=\frac(f(x_0+0)+f(x_0-0))(2).$
Теорема.Нехай $f(x)$ — $2\pi$-періодична абсолютно інтегрована на $[-\pi,\pi]$ функція та точка $x_0 \in \mathbb(R)$ — регулярна точка функції $f(x)$ . Нехай функція $f(x)$ задовольняє в точці $x_0$ умовам Діні: існують невласні інтеграли $$\int\limits_(0)^(h)\frac(|f(x_0+t)-f(x_0+0) |)(t)dt, \\ \int\limits_(0)^(h)\frac(|f(x_0-t)-f(x_0-0)|)(t)dt,$$
тоді ряд Фур'є функції $f(x)$ у точці $x_0$ має суму $f(x_0)$, тобто. $$ \lim\limits_(n \to \infty )S_n(x_0)=f(x_0)=\frac(f(x_0+0)+f(x_0-0))(2).$$
Доведення
Для часткової суми $S_n(x)$ низки Фур'є має місце інтегральне уявлення $(1)$. І з рівності $\frac(2)(\pi )\int\limits_(0)^(\pi )D_n(t) \, dt=1,$
$$ f(x_0)= \frac(1)(\pi )\int\limits_(0)^(\pi )f(x_0+0)+f(x_0-0)D_n(t) \, dt$$
Тоді маємо $$S_n(x_0)-f(x_0) = \frac(1)(\pi)\int\limits_(0)^(\pi)(f(x_0+t)-f(x_0+0)) D_n(t) \, dt + $$ $$+\frac(1)(\pi)\int\limits_(0)^(\pi)(f(x_0-t)-f(x_0-0))D_n (t) \, dt. \quad(7)$$
Очевидно, що теорема буде доведена, якщо доведемо, що обидва інтеграли у формулі $(7)$ мають межі при $n \to \infty $ рівні $0$. Розглянемо перший інтеграл: $$I_n(x_0)=\int\limits_(0)^(\pi)(f(x_0+t)-f(x_0+0))D_n(t)dt. $$
У точці $x_0$ виконується умова Діні: сходиться невласний інтеграл $$\int\limits_(0)^(h)\frac(|f(x_0+t)-f(x_0+0)|)(t) \, dt .$$
Тому для будь-якого $\varepsilon > 0$ існує $\delta \in (0, h)$ таке, що $$\int\limits_(0)^(\delta )\frac(\left | f(x_0+t) -f(x_0+0) \right |)(t)dt
За вибраним $\varepsilon > 0$ і $\delta > 0$ інтеграл $I_n(x_0)$ представимо у вигляді $I_n(x_0)=A_n(x_0)+B_n(x_0)$, де
$$A_n(x_0)=\int\limits_(0)^(\delta )(f(x_0+t)-f(x_0+0))D_n(t)dt ,$$ $$B_n(x_0)=\ int\limits_(\delta)^(\pi )(f(x_0+t)-f(x_0+0))D_n(t)dt .$$
Розглянемо спочатку $A_n(x_0)$. Використовуючи оцінку $ \ left | D_n(t) \right |
для всіх $t\in(0,\delta)$.
Тому $$A_n(x_0) \leq \frac(\pi)(2) \int\limits_(0)^(\delta ) \frac(|f(x_0+t)-f(x_0+0)|)( t)dt
Перейдемо до оцінки інтеграла $B_n(x_0)$ за $n \to \infty $. Для цього введемо функцію $$ \Phi(t)=\left\(\begin(matrix)
\frac(f(x_0+t)-f(x_0+0))(2\sin \frac(t)(2)), 0
$$B_n(x_0)=\int\limits_(-\pi)^(\pi)\Phi(t) \sin \left (n+\frac(1)(2) \right)t\,dt.$$ Отримуємо, що $\lim\limits_(n \to \infty )B_n(x_0)=0$, а це означає, що для обраного раніше довільного $\varepsilon > 0$ існує таке $N$, що для всіх $n> N$ виконується нерівність $|I_n(x_0)|\leq |A_n(x_0)| + | B_n (x_0) |
Абсолютно аналогічно доводиться, що і другий інтеграл формули $(7)$ має рівний нулюмежа при $n\to\infty$.
[згорнути]
СлідствоЯкщо $2\pi$ періодична функція $f(x)$ шматково диференційована на $[-\pi,\pi]$, то її ряд Фур'є в будь-якій точці $x \in [-\pi,\pi]$ сходиться до числа $$\frac(f(x_0+0)+f(x_0-0))(2).$$
На відрізку $[-\pi,\pi]$ знайти тригонометричний ряд Фур'є функції $f(x)=\left\(\begin(matrix)
1, x \in (0,\pi), -1, x \in (-\pi,0),
0, x=0.
\end(matrix)\right.$
Дослідити збіжність одержаного ряду.
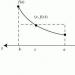
Продовжуючи періодично $f(x)$ на всю речову вісь, отримаємо функцію $\widetilde(f)(x)$, графік якої зображений на малюнку.
Оскільки функція $f(x)$ непарна, то $$a_k=\frac(1)(\pi)\int\limits_(-\pi)^(\pi)f(x)\cos kx dx =0; $$
$$b_k=\frac(1)(\pi)\int\limits_(-\pi)^(\pi)f(x)\sin kx \, dx = $$ $$=\frac(2)(\ pi)\int\limits_(0)^(\pi)f(x)\sin kx \, dx =$$ $$=-\frac(2)(\pi k)(1- \cos k\pi) $$
$$b_(2n)=0, b_(2n+1) = \frac(4)(\pi(2n+1)).$$
Отже, $\tilde(f)(x)\sim \frac(4)(\pi)\sum_(n=0)^(\infty)\frac(\sin(2n+1)x)(2n+1 ).$
Оскільки $(f)"(x)$ існує при $x\neq k \pi$, то $\tilde(f)(x)=\frac(4)(\pi)\sum_(n=0)^ (\infty)\frac(\sin(2n+1)x)(2n+1)$, $x\neq k \pi$, $k \in \mathbb(Z).$
У точках $x=k \pi$, $k \in \mathbb(Z)$, функція $\widetilde(f)(x)$ не визначена, а сума ряду Фур'є дорівнює нулю.
Вважаючи $x=\frac(\pi)(2)$, отримуємо рівність $1 - \frac(1)(3) + \frac(1)(5)- \ldots + \frac((-1)^n) (2n+1)+ \ldots = \frac(\pi)(4)$.
[згорнути]
Знайти ряд Фур'є наступної $2\pi$-періодичної та абсолютно інтегрованої на $[-\pi,\pi]$ функції:
$f(x)=-\ln |
\sin \frac(x)(2)|$, $x \neq 2k\pi$, $k \in \mathbb(Z)$, і досліджувати збіжність отриманого ряду.
Оскільки $(f)"(x)$ існує при $ x \neq 2k \pi$, то ряд Фур'є функції $f(x)$ буде сходитися у всіх точках $ x \neq 2k \pi$ до значення функції. Очевидно , що $f(x)$ парна функція і тому її розкладання в ряд Фур'є має містити косинуси.Знайдемо коефіцієнт $a_0$. \sin \frac(x)(2)dx = $$ $$= -2 \int\limits_(0)^(\frac(\pi)(2))\ln \sin \frac(x)(2) dx \,- \, 2\int\limits_(\frac(\pi)(2))^(\pi)\ln \sin \frac(x)(2)dx =$$ $$= -2 \int \limits_(0)^(\frac(\pi)(2))\ln \sin \frac(x)(2)dx \, - \, 2\int\limits_(0)^(\frac(\pi) )(2))\ln\cos \frac(x)(2)dx=$$ $$= -2 \int\limits_(0)^(\frac(\pi)(2))\ln (\frac (1)(2)\sin x)dx =$$ $$= \pi \ln 2 \, - \, 2 \int\limits_(0)^(\frac(\pi)(2))\ln \ sin x dx =$$ $$= \pi \ln 2 \, - \, \int\limits_(0)^(\pi)\ln \sin \frac(t)(2)dt = \pi\ln 2 + \frac(\pi a_0)(2),$$ звідки $a_0= \pi \ln 2$.
Знайдемо тепер $a_n$ за $n \neq 0$. Маємо $$\pi a_n = -2 \int\limits_(0)^(\pi)\cos nx \ln \sin \frac(x)(2)dx = $$ $$ = \int\limits_(0) ^(\pi) \frac(\sin(n+\frac(1)(2))x+\sin (n-\frac(1)(2))x)(2n \sin\frac(x)(2) )dx=$$ $$= \frac(1)(2n) \int\limits_(-\pi)^(\pi) \begin(bmatrix)
D_n(x)+D_(n-1)(x)\\end(bmatrix)dx.$$
Тут $D_n(x)$- ядро Діріхле, яке визначається формулою (2) і отримуємо, що $\pi a_n = \frac(\pi)(n)$ і, отже, $a_n = \frac(1)(n) $. Таким чином $$-\ln |
\sin \frac(x)(2)| = \ln 2 + \sum_(n=1)^(\infty ) \frac(\cos nx)(n), x \neq 2k\pi, k \in \mathbb(Z).$$
[згорнути]
Література
- Лисенко З.М., конспект лекцій з математичного аналізу, 2015-2016 рр.
- Тер-Крікор А.М. та Шабунін М.І. Курс математичного аналізу, стор 581-587
- Демидович Б.П., Збірник завдань та вправ з математичного аналізу, видання 13, виправлене, Видавництво ЧеРо, 1997, стор 259-267
Ліміт часу: 0
Навігація (тільки номери завдань)
0 із 5 завдань закінчено
Інформація
Тест з матеріалу цієї теми:
Ви вже проходили тест раніше. Ви не можете запустити його знову.
Тест завантажується...
Ви повинні увійти або зареєструватися, щоб почати тест.
Ви повинні закінчити наступні тести, щоб почати цей:
Результати
Правильних відповідей: 0 з 5
Ваш час:
Час вийшов
Ви набрали 0 з 0 балів (0 )
Ваш результат було записано до таблиці лідерів
- З відповіддю
- З позначкою про перегляд
Завдання 1 з 5
1 .
Кількість балів: 1Якщо $2\pi$ -періодична і абсолютно інтегрована на $[−\pi,\pi]$ функція $f(x)$ має у точці $x_0$ похідну, то чого буде сходиться її ряд Фур'є в цій точці?
Завдання 2 з 5
2 .
Кількість балів: 1Якщо виконані всі умови ознаки Діні, то якого числа сходиться ряд Фур'є функції $f$ у точці $x_0$?
У науці та техніці нерідко доводиться мати справу з періодичними явищами, тобто. такими, що відтворюються через певний проміжок часу T, називається періодом. Найпростішою з періодичних функцій (якщо не вважати постійною) є синусоїдальна величина: Asin(x+ ), гармонійне коливання, де є «частота», що з періодом співвідношенням: . З таких найпростіших періодичних функцій може бути складено складніші. Очевидно, що складові синусоїдальні величини повинні бути різних частот, оскільки додавання синусоїдальних величин однієї і тієї ж частоти призводить до синусоїдальної величини тієї ж частоти. Якщо скласти кілька величин виду
Наприклад ми відтворюємо тут додавання трьох синусоїдальних величин: . Розглянемо графік цієї функції
Цей графік значно відрізняється від синусоїди. Ще більшою мірою це має місце для суми нескінченного ряду, складеного з доданків цього виду. Поставимо питання: чи можна цю періодичну функцію періоду Тпредставити у вигляді суми кінцевої або хоча б нескінченної множини синусоїдальних величин? Виявляється, по відношенню до великого класу функцій на це питання можна дати ствердну відповідь, але це тільки якщо залучити всю нескінченну послідовність таких доданків. Геометрично це означає, що графік періодичної функції утворюється шляхом накладання ряду синусоїд. Якщо ж розглядати кожну синусоїдальну величину як деякий гармонійний коливальний рух, то можна сказати, що це складне коливання, яке характеризується функцією або просто її гармоніками (першою, другою тощо). Процес розкладання періодичної функції на гармоніки зветься гармонійного аналізу
Важливо відзначити, що подібні розкладання часто виявляються корисними і при дослідженні функцій, заданих лише в певному кінцевому проміжку і не породжених ніякими коливальними явищами.
Визначення.Тригонометричним рядом називається ряд виду:
Або 
(1).
Справжні числаназиваються коефіцієнтами тригонометричного ряду. Цей ряд можна записати і так:
Якщо ряд представленого вище типу сходиться, його сума є періодичною функцією з періодом 2p.
Визначення.Коефіцієнтами Фур'є тригонометричного ряду називаються: 
(2)
(3)
(4)
Визначення.Поруч Фур'є для функції f(x)називається тригонометричний ряд, коефіцієнти якого є коефіцієнтами Фур'є.
Якщо ряд Фур'є функції f(x)сходиться до неї у всіх її точках безперервності, то кажуть, що функція f(x)розкладається у ряд Фур'є.
Теорема.(Теорема Діріхле) Якщо функція має період 2p і на відрізку безперервна або має кінцеву кількість точок розриву першого роду, відрізок можна розбити на кінцеве число відрізків так, що всередині кожного з них функція монотонна, то ряд Фур'є для функції сходить при всіх значеннях х, причому у точках безперервності функції його сума S(x)дорівнює, а точках розриву його сума дорівнює, тобто. середнього арифметичного граничних значень ліворуч і праворуч.
При цьому ряд Фур'є функції f(x)сходиться поступово будь-якому відрізку, який належить інтервалу безперервності функції .
Функція, що задовольняє умов цієї теореми, називається шматково - гладкою на відрізку .
Розглянемо приклади на розкладання функції ряд Фур'є.
Приклад 1. Розкласти в ряд Фур'є функцію f(x)=1-x, що має період 2pта задану на відрізку.
Рішення. Побудуємо графік цієї функції
Ця функція безперервна на відрізку , тобто на відрізку довжиною в період, тому допускає розкладання ряд Фур'є, що сходить до неї в кожній точці цього відрізка. За формулою (2) знайдемо коефіцієнт цього ряду: .
Застосуємо формулу інтегрування частинами і знайдемо і за формулами (3) і (4) відповідно:
Підставляючи коефіцієнти у формулу (1), отримуємо 
або .
Ця рівність має місце у всіх точках, крім точок (точки склеювання графіків). У кожній із цих точок сума ряду дорівнює середньому арифметичному її граничних значень праворуч і ліворуч, тобто .
Наведемо алгоритм розкладання функціїдо ряду Фур'є.
Загальний порядок вирішення поставленого завдання зводиться до наступного.
Рішення Навье придатне лише розрахунку пластинок, шарнірно опертих по контуру. Більш загальним є рішення Леві. Воно дозволяє виконати розрахунок платівки, шарнірно опертої з двох паралельних сторін, з довільними граничними умовами на кожній з двох інших сторін.
У прямокутній платівці, зображеній на рис. 5.11, (a), шарнірно опертими є краї, паралельні осі y. Граничні умови на цих краях мають вигляд
 |
Рис. 5.11
Очевидно, що кожен член нескінченного тригонометричного ряду
https://pandia.ru/text/78/068/images/image004_89.gif" width="99" height="49">; другі приватні похідні функції прогинів
(5.45)
при x = 0 та x = aтакож рівні нулю, оскільки містять https://pandia.ru/text/78/068/images/image006_60.gif" width="279" height="201 src="> (5.46)
Підстановка (5.46) у (5.18) дає
Помножуючи обидві частини отриманого рівняння на , інтегруючи в межах від 0 до aі пам'ятаючи, що
,
отримуємо для визначення функції Ymтаке лінійне диференціальне рівняння із постійними коефіцієнтами
. (5.48)
Якщо для скорочення запису позначити
рівняння (5.48) набуде вигляду
. (5.50)
Загальне рішення неоднорідного рівняння (5.50), як відомо з курсу диференціальних рівнянь, має вигляд
Ym(y) = jm (y)+ Fm(y), (5.51)
де jm (y) - приватне вирішення неоднорідного рівняння (5.50); його вид залежить від правої частини рівняння (5.50), тобто фактично від виду навантаження q (x, y);
Fm(y)= Am shamy + Bm chamy + y(Cm shamy + Dm chamy), (5.52)
загальне вирішення однорідного рівняння
Чотири довільні постійні Am,Вm ,Cmі Dmповинні бути визначені з чотирьох умов закріплення країв пластинки, паралельних осі , що додається до пластинки постійна q (x, y) = qправа частина рівняння (5.50) набуває вигляду
https://pandia.ru/text/78/068/images/image014_29.gif" width="324" height="55 src=">. (5.55)
Оскільки права частина рівняння (5.55) стала, то постійна і ліва його частина; тому всі похідні jm (y) рівні нулю, і
, (5.56)
, (5.57)
де зазначено: .
Розглянемо платівку, защемленууздовж країв, паралельних осі х(Рис. 5.11, (в)).
Граничні умови з обох боків y = ± b/2
. (5.59)
Внаслідок симетрії прогину пластинки щодо осі Проx, У загальному рішенні (5.52) слід зберегти лише члени, що містять парні функції. Оскільки sh amy- функція непарна, а сh am y– парна та, при прийнятому положенні осі Ох, y sh amy- парно, в у ch am y- непарно, то загальний інтеграл (5.51) у даному випадку можна уявити так
. (5.60)
Оскільки (5.44) не залежить від значення аргументу y, другу пару граничних умов (5.58), (5.59) можна записати у вигляді:
Ym = 0, (5.61)
Y¢ m = = 0. (5.62)
amBm sh amy + Cm(sh amy + yam ch amy)
З (5.60) – (5.63) слід
https://pandia.ru/text/78/068/images/image025_20.gif" width="364" height="55 src=">. (5.65)
Домноживши рівняння (5.64) на , а рівняння (5..gif" width="191" height="79 src=">. (5.66)
Підстановка (5.66) рівняння (5.64) дозволяє отримати Bm
https://pandia.ru/text/78/068/images/image030_13.gif" width="511" height="103">. (5.68)
При такому вираженні функції Ym. , формула (5.44) для визначення функції прогинів набуває вигляду
(5.69)
Ряд (5.69) швидко сходиться. Наприклад, для квадратної платівки у її центрі, тобто при x =a/2, y = 0
(5.70)
Утримавши в (5.70) лише один член ряду, тобто прийнявши 
, Отримаємо величину прогину, завищену менш ніж на 2,47% Врахувавши, що p 5 =
306,02, знайдемо Варіація" варіаційний метод В..Рітца - базується на сформульованому в п. 2 варіаційному принципі Лагран-жа.
Розглянемо цей метод стосовно задачі вигину пластинок. Представимо вигнуту поверхню платівки у вигляді ряду
, (5.71)
де fi(x, y) безперервні координатні функції, кожна з яких повинна задовольняти кінематичним граничним умовам; Ci– невідомі параметри, що визначаються рівнянням Лагранжа. Це рівняння
(5.72)
призводить до системи з n алгебраїчних рівняньщодо параметрів Ci.
У загальному випадку енергія деформації пластинки складається з згинальної U та мембранної U mчастин
, (5.73)
, (5.74)
де Мх.,Мy. ,Мxy- Згинальні зусилля; Nх., Ny. , Nxy– мембранні зусилля. Відповідна поперечним силам частина енергії невелика і її можна знехтувати.
Якщо u, vі w– складові дійсного переміщення, px. , pyі pz– складові інтенсивності поверхневого навантаження, Рi- Зосереджена сила, D iвідповідне їй лінійне переміщення, Мj- Зосереджений момент, qj– відповідний йому кут повороту (рис. 5.12), то потенційну енергію зовнішніх сил можна представити так:
Якщо краї пластинки допускають переміщення, то крайові сили vn. , mn. , mnt(рис. 5.12, (а)) збільшують потенціал зовнішніх сил
 |
|
 |
|
Рис. 5.12
Тут nі t– нормаль та дотична до елементу краю ds.
В декартових координатах, з урахуванням відомих виразів для зусиль та кривизн
, (5.78)
повна потенційна енергія Е прямокутної платівки розміром a ´ b, при дії тільки вертикального навантаження pz
(5.79)
Як приклад розглянемо прямокутну пластинку зі ставленням сторін 2 a´ 2 b(Рис. 5.13).
Платівка защемлена за контуром і навантажена рівномірним навантаженням
pz = q = const. І тут вираз (5.79) для енергії Е спрощується
. (5.80)
Приймемо для w(x, y) ряд
який задовольняє контурним умовам
 |  |
Рис. 5.13
Утримаємо лише перший член ряду
.
Тоді згідно (5.80)
.
Мінімізуючи енергію Е згідно (5..gif".
.
Прогин центру квадратної платівки розміром 2 а´ 2 а
,
що на 2,5% більше точного рішення 0,0202 qa 4/D. Зазначимо, що прогин центру платівки, опертої з чотирьох сторін, у 3,22 рази більше.
Цей приклад ілюструє переваги методу: простоту та можливість отримання хорошого результату. Платівка може мати різні контури, змінну товщину. Труднощі в цьому методі, як, втім, і в інших енергетичних методах, виникають при виборі відповідних координатних функцій.
5.8. Метод ортогоналізації
Метод ортогоналізації, запропонований і заснований на наступній властивості ортогональних функцій ji. , jj
. (5.82)
Прикладом ортогональних функцій на інтервалі ( – p, p) можуть служити тригонометричні функції cos nxі sin nxдля яких
Якщо одна з функцій, наприклад, функція ji (x) тотожно дорівнює нулю, то умова (5.82) виконується для довільної функції jj (x).
Для вирішення задачі про вигин пластинки рівняння –
можна уявити так
, (5.83)
де F- Площа, обмежена контуром платівки; jij– функції, що задаються так, щоб вони задовольняли кінематичні та силові граничні умови завдання.
Представимо наближене рішення рівняння вигину платівки (5.18) у вигляді ряду
. (5.84)
Якби рішення (5.84) було точним, то рівняння (5.83) виконувалося б тотожно для будь-якої системи координатних функцій. jij. , оскільки в цьому випадку DÑ2Ñ2 wn – q = 0. Вимагаємо, щоб рівняння DÑ2Ñ2 wn – qбуло ортогональним до сімейства функцій jij, та вимогу це використовуємо для визначення коефіцієнтів Cij. . Підставляючи (5.84) у (5.83) отримаємо
. (5.85)
Після виконання деяких перетворень отримаємо наступну систему рівнянь алгебри для визначення Cij
, (5.86)
причому hij = hji.
Методу Бубнова-Галеркіна можна дати таке тлумачення. Функція DÑ2Ñ2 wn – q = 0 є по суті рівнянням рівноваги і є проекцією зовнішніх і внутрішніх сил, що діють на малий елемент пластинки в напрямку вертикальної осі z. Функція прогинів wnє переміщення у напрямі тієї ж осі, а функції jijможна вважати за можливі переміщення. Отже, рівняння (5.83) приблизно виражає рівність нулю роботи всіх зовнішніх і внутрішніх сил на можливих переміщеннях jij. . Таким чином, метод Бубнова-Галеркіна по суті своїй є варіаційним.
Як приклад розглянемо прямокутну пластинку, защемлену по контуру і навантажену рівномірно розподіленим навантаженням. Розміри платівки та розташування координатних осей такі ж, як на рис. 5.6.
Граничні умови
при x = 0, x= а: w = 0, ,
при y = 0, y = b: w = 0, .
Наближений вираз для функції прогинів виберемо у вигляді ряду (5.84), де функція jij
задовольняє граничним умовам; Cij- Шукані коефіцієнти. Обмежившись одним членом ряду
отримаємо наступне рівняння
Після інтегрування
Звідки обчислимо коефіцієнт З 11
,
який повністю відповідає коефіцієнту З 11., отриманому методом
В. Рітца -.
У першому наближенні функція прогинів така
.
Максимальний прогин у центрі квадратної платівки розміром а ´ а
.
5.9. Застосування методу кінцевих різниць
Розглянемо застосування методу кінцевих різницьдля прямокутних пластин зі складними контурними умовами. Різнистий оператор – аналог диференціального рівняння вигнутої поверхні пластинки (5.18), для квадратної сітки, при D x = D y = D набуває вигляду (3.54)
20 wi, j + 8 (wi, j+ 1 + wi, j– 1 + wi– 1, j + wi+ 1, j) + 2 (wi– 1, j– 1 + wi– 1, j+ 1 +
Рис. 5.14
З урахуванням наявності трьох осей симетрії навантаження та деформацій пластинки, можна обмежитися розглядом її восьмушки та визначати величини прогинів лише у вузлах 1...10 (рис. 5.14, (б)). На рис. 5.14, (б) представлені сітка та нумерація вузлів (D = а/4).
Оскільки краї пластинки защемлені, то записавши контурні умови (5.25), (5.26) у кінцевих різницях
