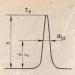
Розглянемо поняття кінцевих різниць.
Нехай задана функція у = f (x)на відрізку [х 0, х„], який розбитий на поднакових відрізків (випадок рівновіддалених значень аргументу): Ax = h = const. Для кожного вузла х 0х, =х 0 + /г, ...,х„ =х ()+ п hвизначено значення функції у вигляді
Введемо поняття кінцевих різниць.
Кінцеві різниціпершого порядку

Кінцеві різниці другого порядку  Аналогічно визначаються кінцеві різниці вищих порядків:
Аналогічно визначаються кінцеві різниці вищих порядків: 
Кінцеві різниці функцій зручно розташовувати в таблицях, які можуть бути діагональними (табл. 5.1) або горизонтальними (табл. 5.2).
Діагональна таблиця
Таблиця 5.1
Горизонтальна таблиця
Таблиця 5.2
|
а 5 у, |
||||||
|
А 5 Уо |
||||||
|
а 4 у. |
||||||
Перша інтерполяційна формула Ньютона
Нехай для функції у=/(х) задані значення у, =/(х,) для рівноважних значень незалежних змінних:
![]()
де h- крок інтерполяції.
Необхідно знайти поліном Р„(х)ступеня нс вище п,приймає в точках (вузлах) х, значення:
Інтерполюючий поліном шукається у вигляді:
Завдання побудови багаточлена зводиться до визначення коефіцієнтів а,із умов:

Вважаємо в (5.13) х=х 0 , тому що друге, третє та інші доданки рівні 0, то ![]()
Знайдемо коефіцієнт а ( .
Приес=Х1 отримаємо:

Для визначення а 2складемо кінцеву різницю другого порядку. При х = х 2отримаємо:

Аналогічно можна знайти інші коефіцієнти. Загальна формуламає вигляд:
Підставляючи ці вирази у формулу (5.13), отримуємо:

де х„ у х- вузли інтерполяції; х- поточна змінна; h- різницю між двома вузлами інтерполяції; h- величина стала, т. е. вузли інтерполяції одно відстоять друг від друга.
Цей багаточлен називають інтерполяційним поліномом Ньютонадля інтерполяції на початку таблиці (інтерполіювання «вперед»), або першим поліном Ньютона.
Для практичного використання цей поліном записують у перетвореному вигляді, вводячи позначення t=(х - x 0)/h,тоді

Ця формула застосовна для обчислення значень функції значення аргументів, близьких до початку інтервалу інтерполування.
Блок-схема алгоритму методу Ньютона для інтерполювання «наперед» наведено на рис. 5.3, програма – у додатку.
Приклад 5.3. Дано таблицю значень теплоємності речовини в залежності від температури C p = f(T)(Табл. 5.3).
Таблиця 5.3
Скористаємося формулою (5.16):



Рис. 5.3.
Після виконання перетворень отримаємо інтерполяційний багаточлен виду:
Поліном має третій ступінь і дозволяє обчислення за допомогою знайденої формули значення удля невідомого х.
Приклад 5.4.У табл. 5.3.1 наведено значення теплоємності залежно від температури. Визначити значення теплоємності у точці Г=450 К.
Скористайтеся першою інтерполяційною формулою Ньютона. Кінцеві різниці розраховані в попередньому прикладі (табл. 5.3.2), запишемо інтерполяційний багаточлен при х = 450 К:

Таким чином, теплоємність при температурі 450 К буде
Значення теплоємності при Г = 450 К отримали таке саме, що і розраховане за формулою Лагранжа.
Друга інтерполяційна формула Ньютона
Для знаходження значень функцій у точках, розташованих наприкінці інтервалу інтерполування, використовують другий поліполіном інтерполяційний Ньютона. Запишемо інтерполяційний багаточлен у вигляді
Коефіцієнти а 0 , а ь..., а„визначаємо з умови:
![]()
Вважаємо (5.18) х=х„,тоді

Вважаємо х=х„_|, тоді отже, 
Якщо x = x n - 2 iто

Аналогічно можна знайти інші коефіцієнти багаточлена (5.18):

Підставляючи ці вирази у формулу (5.18), отримаємо другу інтерполяційну формулу Ньютона,або багаточлен Ньютона для інтерполювання "назад":

Введемо позначення: 
Зробивши заміну в (5.19), отримаємо:

Це друга формула Ньютона для інтерполювання "назад".
Приклад 5.5. Обчислити теплоємність (див. табл. 5.3) для температури Г = 550 К.
Скористаємося другою формулою Ньютона (5.19) та відповідними кінцевими різницями (див. табл. 5.4):

Отже, значення теплоємності при температурі 550 К дорівнює
ІНТЕРПОЛЮВАННЯ
Нехай функція у = f(x) задана на сітці рівновіддалених вузлів x i=x 0 +ih,де i = 0,1, ..., п,та для неї побудовано таблицю кінцевих різниць § 16.3.
Відповідно до того, що було сказано про направлення модифікації інтерполяційної формули Лагранжа на початку попереднього параграфу, будуватимемо інтерполяційний багаточлен Р п(х) в формі
Р n(х)= а 0 +а 1 (х-х 0)+ а 2 (х-х 0)(х-х 1)+... + а n(х-х 0)(х-х 1) … (х-х n - 1). (17.1)
Його п+ 1 коефіцієнт а 0 , а 1 , ..., а nбудемо знаходити послідовно з п+1 інтерполяційних рівностей
Р n(х i)=y i, i = 0,1, ..., п.
А саме, вважаючи i= 0, тобто. х = х 0у (1.23) маємо Р n(х 0)= а 0 , отже, а 0 = у 0 .
а 0 +а 1 (х-х 0)=y 1 ,
у яке підставляємо вже знайдене значення а 0 = у 0 . Дозволяючи цю рівність щодо а 1 і використовуючи позначення кінцевої різниці, отримуємо
Повною індукцією можна показати справедливість висловлювання
Підставляючи знайдені коефіцієнти а 0 , а 1 ,..., а nв (17.1), отримуємо багаточлен
який називають першим інтерполяційним багаточленом Ньютона.
Враховуючи, що кожен доданок багаточлена (17.2), починаючи з другого, містить множник х-х 0 , Звичайно припустити, що цей многочлен найбільш пристосований для інтерполування в околиці вузла х 0 . Будемо називати вузол х 0 базовим для багаточлена (17.2) та спростимо (17.2) запровадженням нової змінної qрайенством або (що те саме) рівністю x = x 0 +qh.Так як
x - x i =x 0 + qh - x 0 - ih = h (q-i),
то в результаті підстановки цих різниць (17.2) приходимо до першої інтерполяційної формули Ньютона у вигляді
де позначення Р n(x 0 + qh) вказує не тільки на n-ю ступінь многочлена, а й на базовий вузол x 0 та зв'язок змінних хі q.
Перша формула Ньютона (17.3) зазвичай застосовується за значеннях | q| < 1, а саме, для інтерполювання вперед(при х Î ( х 0 , x 1), тобто. при qÎ (0, 1)) та екстраполювання назад(при х< х 0 тобто. при q < 0).
Оскільки реально ступеня інтерполяційних многочленів бувають негаразд великі, тоді як таблиці значень функцій досить великі, і оскільки у реальної числової таблиці жодних індексів - номерів вузлів немає, то базовий для формули (17.3) вузол х 0 можна приймати вузол, найближчий до заданої фіксованої точки х,якщо за ним є достатньо вузлів для побудови необхідних різниць. Оскільки в першій формулі Ньютона використовуються низхідні діагоналі таблиці кінцевих різниць, то таке зміщення вузла, що приймається за базовий, наприкінці таблиці буде неприйнятним.
Облік цієї обставини призводить до потреби у симетричній, у певному сенсі, для (17.3) формули, яка була б придатною для інтерполювання наприкінці таблиці. Для цього, на відміну (17.1), форма інтерполяційного багаточлена Р n(х) береться така, що передбачає почергове підключення вузлів у зворотному порядку: спочатку останній, потім передостанній тощо, тобто.
Р(х)= а 0 +а 1 (х-х n)+ а 2 (х-х n)(х-х n - 1)+... + а n(х-х n)(х-х n - 1)…(х-х 1).
Коефіцієнти а 0 , а 1 ,..., а nцього многочлена знаходяться аналогічно тому, як вони знаходилися для многочлена (17.1), тільки тут підстановка вузлових точок замість хта розгляд інтерполяційних рівностей проводиться також у зворотному порядку.
Таким чином, отримуємо другий інтерполяційний багаточлен Ньютона
в якому базовим є вузол х nі коефіцієнти якого визначаються кінцевими різницями, розташованими на висхідній від у nдіагоналі.
Покладемо в (17.4) x = x n +qh,інакше, введемо нову змін і перетворимо до неї різні (17.4) різниці:
x - x i =x n + qh - x 0 - ih = x 0 + nh + qh - x 0 - ih = h (q+n-i)
В результаті приходимо до другий інтерполяційній формулі Ньютона виду
Її також доцільно використовувати за значеннях | q| < 1, т.е. в окрестности узла х п для інтерполювання назад(при qÎ (-1, 0)) та екстраполювання вперед(при q >В).
Поряд з виведеними спеціально для початку та кінця таблиці першої та другої інтерполяційними формулами Ньютона є ще кілька формул, розрахованих на їх застосування в центральній частині таблиці і тому званих центральними інтерполяційними формулами. Перш ніж визначати ці формули, введемо поняття центральних різниць.
Вважатимемо, що вузол x 0 розташований у середині таблиці, і нумерація інших вузлів проводиться, починаючи з х 0 , з використанням як позитивних, і негативних індексів, тобто. рахуємо x i=x 0 +ih,де i= 0, ±1, ±2,... . Тоді центральна частина таблиці кінцевих різниць буде проіндексована так, як показано в табл. 1.7. Всі підкреслені в ній кінцеві різниці (що знаходяться з XQ,y Qв одному рядку і на піврядки вище і нижче) називаються центральними різницями.
x - 3 y- 3D y - 3
x - 2 y- 3D y- 2 D 2 y- 3 D 3 y - 3
x - 1 y - 1 Dy - 1 D 2 y - 2 D 3y - 2 D 4 y - 3 D 5y - 3
x 0 y 0 Dy 0 D 2y - 1 D 3y - 1 D 4y - 2 D 5y - 2 D 6y - 3
x 1 y 1 D y 1 D 2 y 0 D 3 y 0 D 4 y - 1
x 2 y 2D y 2 D 2 y 1
x 3 y 3
Інтерполяційний багаточлен шукаємо у формі
Р(х)= а 0 +а 1 (х-х 0)+ а 2 (х-х 0)(х-х 1)+ а 3 (х-х - 1) (х-х 0)(х-х 1)+
+а 4 (х-х - 1) (х-х 0)(х-х 1)(х-х 2)+… .
Коефіцієнти шукаємо, як і раніше. Ввівши нову змінну та висловивши через неї різниці x - x i =h (q-i) для всіх i= 0, ±1, ±2, ..., в результаті підстановки цих різниць та виразів коефіцієнтів після перетворень призводить до формули
званою інтерполяційною формулою Стірлінга.
Розглянемо питання у тому, як може бути трансформовані залишковий член та її оцінки при конечноразностной інтерполяції.
Відомо, що це побудовані тут конечноразностные інтерполяційні багаточлени Ньютона і Стірлінга - це лише різні форми уявлення інтерполяційного многочлена Лагранжа. Отже, всім цих форм справедливе вираз залишкового члена (16.7).
Для першого інтерполяційного багаточлена Ньютона у формі (17.3) похибка може бути записана таким чином
Для другого інтерполяційного багаточлена Ньютона у формі (17.5) похибка може бути записана таким чином
Вибірка експериментальних даних є масивом даних, який характеризує процес зміни вимірюваного сигналу протягом заданого часу (або щодо іншої змінної). Для виконання теоретичного аналізу вимірюваного сигналу необхідно знайти апроксимуючу функцію, яка зв'яже дискретний набір експериментальних даних з безперервною функцією - поліномом інтерполяції n -ступеня. Цей інтерполяційний поліном n-ступеня може бути записаний, наприклад, у формі Ньютона (один із способів уявлення).
Інтерполяційний багаточлен
у формі Ньютона– це математична функція, що дозволяє записати поліном n -ступеня, який з'єднуватиме всі задані точки з набору значень, отриманих дослідним шляхом або методом випадкової вибірки з постійним/змінним тимчасовим кроком вимірювань.
1. Інтерполяційна формула Ньютона для нерівновіддалених значень аргументу
В загальному виглядіінтерполяційний багаточлену формі Ньютона записується у такому вигляді:
де n – дійсне число, Який вказує ступінь полінома;
![]() – змінна, яка є розділеною різницеюk-го порядку, що обчислюється за такою формулою:
– змінна, яка є розділеною різницеюk-го порядку, що обчислюється за такою формулою:
Розділена різниця є симетричною функцією своїх аргументів, тобто за будь-якої їх перестановці її значення не змінюється. Слід зазначити, що з розділеної різниці k-го порядку справедлива така формула:

Як приклад, розглянемо побудову полінома у формі Ньютона за представленою вибіркою даних, що складається з трьох заданих точок. Інтерполяційний багаточлену формі Ньютона, який проходить через три заданих точки, буде записуватися в наступному вигляді:
Розділена різницю 1-го порядку визначається наступним виразом


Розділена різницю 2-го порядку визначається наступним виразом
Слід зазначити, що цей вираз може бути переписаний в іншому вигляді:
Форма Ньютона є зручною формою представлення інтерполяційного полінома n-ступеня, так як при додаванні додаткового вузла всі обчислені раніше доданки залишаються без зміни, а до виразу додається тільки один новий доданок. Варто зазначити, щоінтерполяційний поліном у формі Ньютона тільки формою відрізняється від інтерполяційного полінома у формі Лагранжа, являючи собою на заданій сітці один і той же інтерполяційний поліном.
Слід зазначити, що поліном у формі Ньютона може бути представлений більш компактному вигляді (за схемою Горнера), яка виходить шляхом послідовного винесення за дужки множників
2. Інтерполяційна формула Ньютона для рівновіддалених значень аргументу
Якщо значення функції задані для рівновіддалених значень аргументу, які мають постійний крок вимірювань![]() то використовують іншу форму запису інтерполяційного багаточлена за формулою Ньютона.
то використовують іншу форму запису інтерполяційного багаточлена за формулою Ньютона.
Для інтерполування функції в кінці інтервалу ( інтерполювання назад та екстраполювання вперед

де кінцеві різниці k
Кінцеві різниці, що отримуються, зручно представляти в табличній формі запису, у вигляді горизонтальної таблиці кінцевих різниць. У цій формулі з таблиці кінцевих різниць використовуютьсяверхній діагоналі.

Для інтерполування функції на початку розглянутого інтервалу ( інтерполювання вперед та екстраполювання назад) використовують інтерполяційний поліном у формі Ньютона у наступному записі:

де кінцеві різниці k -порядку визначаються за таким виразом
Кінцеві різниці, що отримуються, зручно представляти в табличній формі запису, у вигляді горизонтальної таблиці кінцевих різниць. У формулі з таблиці кінцевих різниць використовуютьсянижньої діагоналі.

3. Похибка інтерполяційного полінома у формі Ньютона
Розглянемо функцію f (x ), яка безперервна і диференційована на аналізованому відрізку . Інтерполяційний поліном P (x) у формі Ньютона приймає у точкахзадані значення функції. В інших точках інтерполяційний поліном P(x) відрізняється від значення функції f(x) на величину залишкового члена , Який визначає абсолютну похибку інтерполяційної формули Ньютона:
![]()
Абсолютну похибку інтерполяційної формули Ньютона визначають так:

Змінна являє собою верхню межу значення модуля (n+1)-ї похідної функції f(x) на заданому інтервалі
![]()
У разі рівновіддалених вузлівабсолютна похибка інтерполяційної формули Ньютона визначають наступним чином:
Вираз записано з урахуванням наступної формули:
Вибір вузлів інтерполяції
За допомогою коректного вибору вузлів можна мінімізувати значення в оцінці похибки, тим самим підвищити точність інтерполяції. Це завдання може бути вирішено за допомогою багаточлена Чебишева:
Як вузли слід взяти коріння цього багаточлена, тобто точки:

4. Методика обчислення полінома у формі Ньютона (прямий спосіб)
Алгоритм обчислення полінома у формі Ньютона дозволяє розділити завдання визначення коефіцієнтів та обчислення значень полінома при різних значеннях аргументу:
1. Як вихідні дані задається вибірка з n -точок, яка включає значення функції і значення аргументу функції.
2. Виконується обчислення розділених різниць n-порядку, які будуть використовуватися для побудови полінома у формі Ньютона.
3. Виконується обчислення полінома n-ступеня у формі Ньютона за такою формулою:
Алгоритм обчислення полінома у формі Ньютонапредставлений малюнку 1.

Анотація
Пояснювальна записка курсової роботи "Інтерполяція функції однієї змінної методом Ньютона" містить у собі вступ, аналіз завдання описом вхідних та вихідних даних, огляд літературних джерел, опис математичної моделі та методів обчислювальної математики, пояснення до алгоритму, текст програми, інструкцію. При вивченні дисципліни "Інформатика" для написання курсової роботи використовувалися різні літературні джерела, які перелічені у цьому документі. У цій роботі наведена програма, яка застосовується для інтерполяції таблично заданої функціїметодом Ньютона. У ній був використаний метод структурного програмування для полегшення написання та налагодження програми, а також підвищення її наочності та читання. Метою написання даної роботи було отримання та закріплення практичних навичок розробки алгоритмів у різний спосіб. Подана програма реалізована мовою програмування Pascal. Пояснювальна записка містить 25 аркушів, на яких розміщено два малюнки, текст програми та опис програми та алгоритму.
Вступ
Аналіз завдання
Математична модель завдання
Програмування функції формули Ньютона
Огляд літературних джерел
Розробка програми за схемою алгоритму
Інструкція користування програмою
Текст програми
Вихідні дані та результат вирішення контрольного прикладу
Висновок
Список використаних джерел
Вступ
Сучасний розвитокфізики та техніки тісно пов'язано з використанням електронних обчислювальних машин (ЕОМ). В даний час ЕОМ стали звичайним обладнанням багатьох інститутів та конструкторських бюро. Це дозволило від найпростіших розрахунків та оцінок різних конструкцій чи процесів перейти до нової стадії роботи – детального математичного моделювання(обчислювальному експерименту), яке суттєво скорочує потребу в натурних експериментах, а в ряді випадків може їх замінити.
Складні обчислювальні завдання, що виникають щодо фізичних і технічних проблем, можна розбити на ряд елементарних -таких як обчислення інтеграла, розв'язання диференціального рівняння і т. п. Багато елементарних завдань є нескладними і добре вивчені. Для цих завдань вже розроблені методи чисельного рішення, і нерідко є стандартні програми їх вирішення на ЕОМ. Є досить складні елементарні завдання; Методи вирішення таких завдань зараз інтенсивно розробляються.
У зв'язку з цим сучасний фахівець з вищою освітоюповинен мати не тільки високим рівнемпідготовки за профілем своєї спеціальності, а й добре знати математичні методи вирішення інженерних завдань, орієнтуватися використання обчислювальної техніки, практично освоїти принципи роботи на ЕОМ.
Аналіз завдання
Як вхідні дані використані:
1. Кількість вузлів.
2. Табличні значення функції.
Вихідними даними, тобто. результатом програми є:
1. Значення таблично заданої функції у проміжних значеннях.
2. Графік полінома.
Математична модель завдання
При виконанні курсової роботи було обрано наступну математичну модель:
Інтерполяція та наближення функцій.
1. Постановка задачі.
Одним із основних завдань чисельного аналізу є завдання про інтерполяцію функцій. Часто потрібно відновити функцію
для всіх значень на відрізку, якщо відомі її значення в певному кінцевому числі точок цього відрізка. Ці значення можуть бути знайдені в результаті спостережень (вимірювань) у якомусь натурному експерименті або в результаті обчислень. Крім того, може виявитися, що функція задається формулою і обчислення її значень за цією формулою дуже трудомісткі, тому бажано мати для функції простішу (менш трудомістку для обчислення) формулу, яка дозволяла б знаходити наближене значення функції з необхідною точністю в будь-якій точці відрізка . У результаті виникає таке математичне завдання.Нехай і» відрізку
задана сітка зіта у її вузлах задані значення функції
, рівні.Потрібно побудувати інтерполянту – функцію
, що з функцією у вузлах сітки: .Основна мета інтерполяції – отримати швидкий (економічний) алгоритм обчислення значень
для значень , які у таблиці даних.2. Інтерполяція за Ньютоном
Дана таблична функція:
| i | ||
| 0 | ||
| 1 | ||
| 2 | ||
| .. | .. | .. |
| n |
Крапки з координатами
називаються вузловими точками чи вузлами.Кількість вузлів у табличній функції дорівнює N=n+1.
Необхідно знайти значення цієї функції в проміжній точці, наприклад,
, Причому . Для вирішення задачі використовується інтерполяційний багаточлен.Інтерполяційний багаточлен за формулою Ньютона має вигляд:
де n - ступінь многочлена,
Інтерполяційна формула Ньютона формула дозволяє висловити інтерполяційний багаточлен
через значення одному з вузлів і через розділені різниці функції, побудовані вузлами.Спочатку наведемо необхідні відомості про розділені різниці.
Нехай у вузлах
,відомі значення функції
. Припустимо, що серед точок , , немає збігаються. Розділеними різницями першого порядку називаються відносини,,,.Розглянемо розділені різниці, складені по сусіднім вузлам, тобто висловлювання
Нехай задана функція y=f(x) на відрізку , який розбитий на n однакових відрізків (випадок рівновіддалених значень аргументу). x = h = const. Для кожного вузла x 0, x 1 =x 0 +h,..., x n =x 0 +n h визначено значення функції у вигляді: f(x 0)=y 0, f(x 1)=y 1,. ., f(x n)=y n.
Кінцеві різниці першого порядку y 0 = y 1 - y 0 y 1 = y 2 - y y n-1 = y n - y n-1. Кінцеві різниці другого порядку 2 y 0 = y 1 – y 0 2 y 1 = y 2 – y y n-2 = y n-1 – y n-2 Аналогічно визначаються кінцеві різниці вищих порядків: k y 0 = k-1 y 1 – k-1 y 0 k y 1 = k-1 y 2 – k-1 y k y i = k-1 y i+1 – k-1 y i, i = 0,1,...,n-k.




Нехай для функції y = f(x) задані значення y i = f(x i) для рівноважних значень незалежних змінних: x n = x 0 +nh де h - крок інтерполяції. Необхідно знайти поліном P n (x) ступеня не вище n, що приймає в точках (вузлах) x i значення: P n (xi) = y i, i = 0, ..., n. Запишемо інтерполюючий поліном у вигляді:

Завдання побудови многочлена зводиться до визначення коефіцієнтів а з умов: P n (x 0) = y 0 P n (x 1) = y P n (x n) = y n



Аналогічно можна знайти інші коефіцієнти. Загальна формула має вигляд. Підставляючи ці висловлювання формулу полінома, отримуємо: де x i,y i – вузли інтерполяції; x - поточна змінна; h – різниця між двома вузлами інтерполяції h – величина стала, тобто. вузли інтерполяції рівновідстоять один від одного.

















Особливістю інтерполяції було те, що інтерполююча функція суворо проходить через вузлові точки таблиці, тобто розраховані значення співпадали з табличними: y i = f (x i). Ця особливість обумовлювалася тим, що кількість коефіцієнтів в інтерполюючій функції (m) дорівнювала кількості табличних значень (n)







4. Інтерполюючою функцією неможливо описати табличні дані, в яких є кілька точок однаковим значеннямаргументу. Така ситуація можлива, якщо той самий експеримент проводиться кілька разів при одних і тих же вихідних даних. Однак це не є обмеженням для використання апроксимації, де не ставиться умова проходження графіка функції через кожну точку.