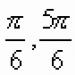Част 1. Основи на приложната статистика
1.2.3. Същността на вероятностно-статистическите методи за вземане на решения
Как се използват подходите, идеите и резултатите от теорията на вероятностите и математическата статистика при вземането на решения?
Основата е вероятностен модел на реално явление или процес, т.е. математически модел, в който обективните връзки са изразени от гледна точка на теорията на вероятностите. Вероятностите се използват предимно за описание на несигурностите, които трябва да се вземат предвид при вземането на решения. Това се отнася както за нежелани възможности (рискове), така и за привлекателни („щастлив шанс”). Понякога произволността се въвежда умишлено в ситуация, например при теглене на жребий, произволен избор на единици за контрол, провеждане на лотарии или провеждане на потребителски проучвания.
Теорията на вероятностите позволява една вероятност да се използва за изчисляване на други, които представляват интерес за изследователя. Например, като използвате вероятността да получите герб, можете да изчислите вероятността при 10 хвърляния на монети да получите поне 3 герба. Такова изчисление се основава на вероятностен модел, според който хвърлянията на монети се описват чрез модел на независими опити, освен това гербът и хеш-знаците са еднакво възможни и следователно вероятността за всяко от тези събития е еднаква; до ½. По-сложен модел е този, който обмисля проверка на качеството на единица продукция вместо хвърляне на монета. Съответният вероятностен модел се основава на предположението, че контролът на качеството на различни производствени единици е описан от независима схема за тестване. За разлика от модела за хвърляне на монета е необходимо да се въведе нов параметър - вероятност Рче продуктът е дефектен. Моделът ще бъде напълно описан, ако приемем, че всички производствени единици имат еднаква вероятност да бъдат дефектни. Ако последното предположение е неправилно, тогава броят на параметрите на модела се увеличава. Например, можете да предположите, че всяка производствена единица има своя собствена вероятност да бъде дефектна.
Нека обсъдим модел за контрол на качеството с вероятност за дефектност, обща за всички производствени единици Р. За да се „стигне до числото“ при анализ на модела, е необходимо да се замени Рдо някаква конкретна стойност. За да направите това, е необходимо да преминете отвъд вероятностния модел и да се обърнете към данните, получени по време на контрола на качеството. Математическата статистика решава обратния проблем по отношение на теорията на вероятностите. Неговата цел е въз основа на резултатите от наблюдения (измервания, анализи, тестове, експерименти) да се получат заключения относно вероятностите, залегнали в основата на вероятностния модел. Например, въз основа на честотата на поява на дефектни продукти по време на инспекция, могат да се направят заключения относно вероятността от дефект (вижте теоремата на Бернули по-горе). Въз основа на неравенството на Чебишев бяха направени изводи за съответствието на честотата на поява на дефектни продукти на хипотезата, че вероятността за дефектност приема определена стойност.
По този начин приложението на математическата статистика се основава на вероятностен модел на явление или процес. Използват се две паралелни серии от понятия – тези, свързани с теорията (вероятностен модел) и тези, свързани с практиката (извадка от резултатите от наблюдението). Например, теоретичната вероятност съответства на честотата, намерена от извадката. Математическото очакване (теоретична серия) съответства на средноаритметичното извадково (практическа серия). По правило характеристиките на извадката са оценки на теоретичните. В същото време количествата, свързани с теоретичните серии, „са в главите на изследователите“, се отнасят до света на идеите (според древногръцкия философ Платон) и не са достъпни за директно измерване. Изследователите разполагат само с примерни данни, с които се опитват да установят свойствата на теоретичен вероятностен модел, който ги интересува.
Защо се нуждаем от вероятностен модел? Факт е, че само с негова помощ свойствата, установени от анализа на конкретна проба, могат да бъдат пренесени върху други проби, както и върху цялата така наречена генерална съвкупност. Терминът "популация" се използва, когато се говори за голяма, но ограничена колекция от изследвани единици. Например за съвкупността от всички жители на Русия или за съвкупността от всички потребители на разтворимо кафе в Москва. Целта на маркетинговите или социологическите проучвания е да прехвърлят твърдения, получени от извадка от стотици или хиляди хора, към популации от няколко милиона души. При контрола на качеството партида от продукти действа като обща съвкупност.
За да се прехвърлят заключения от извадка към по-голяма популация, са необходими някои допускания относно връзката на характеристиките на извадката с характеристиките на тази по-голяма популация. Тези предположения се основават на подходящ вероятностен модел.
Разбира се, възможно е да се обработват примерни данни, без да се използва един или друг вероятностен модел. Например, можете да изчислите примерно средно аритметично, да преброите честотата на изпълнение на определени условия и т.н. Резултатите от изчислението обаче ще се отнасят само до конкретна извадка; прехвърлянето на заключенията, получени с тяхна помощ, към всяка друга популация е неправилно. Тази дейност понякога се нарича „анализ на данни“. В сравнение с вероятностно-статистическите методи, анализът на данни има ограничена образователна стойност.
Така че използването на вероятностни модели, базирани на оценка и тестване на хипотези, използвайки характеристики на извадка, е същността на вероятностно-статистическите методи за вземане на решения.
Подчертаваме, че логиката на използване на примерни характеристики за вземане на решения въз основа на теоретични модели включва едновременното използване на две паралелни серии от концепции, едната от които съответства на вероятностни модели, а втората - на примерни данни. За съжаление, в редица литературни източници, обикновено остарели или написани в рецептурен дух, не се прави разлика между извадкови и теоретични характеристики, което води читателите до объркване и грешки при практическото използване на статистическите методи.
| Предишен |
При провеждането на психологически и педагогически изследвания важна роля се дава на математическите методи за моделиране на процеси и обработка на експериментални данни. Тези методи включват на първо място така наречените вероятностно-статистически методи на изследване. Това се дължи на факта, че поведението както на индивида в процеса на неговата дейност, така и на човек в екип е значително повлияно от много случайни фактори. Случайността не ни позволява да описваме явления в рамките на детерминистични модели, тъй като се проявява като недостатъчна редовност в масовите явления и следователно не позволява надеждно прогнозиране на настъпването на определени събития. Въпреки това, когато се изучават такива явления, се откриват определени закономерности. Неравномерността, присъща на случайни събития, с голям брой тестове, обикновено се компенсира от появата на статистически модел, стабилизиране на честотата на възникване на случайни събития. Следователно тези случайни събития имат определена вероятност. Има два фундаментално различни вероятностно-статистически метода на психологическо и педагогическо изследване: класически и некласически. Нека направим сравнителен анализ на тези методи.
Класически вероятностно-статистически метод. Класическият вероятностно-статистически метод на изследване се основава на теорията на вероятностите и математическата статистика. Този метод се използва при изследване на масови явления със случаен характер, включва няколко етапа, основните от които са следните.
1. Изграждане на вероятностен модел на реалността въз основа на анализ на статистически данни (определяне на закона за разпределение на случайна променлива). Естествено, закономерностите на масовите случайни явления се изразяват толкова по-ясно, колкото по-голям е обемът на статистическия материал. Примерните данни, получени по време на експеримент, винаги са ограничени и, строго погледнато, от случаен характер. В това отношение важна роля се отдава на обобщаването на моделите, получени от извадката, и разширяването им към цялата съвкупност от обекти. За да се реши този проблем, се приема определена хипотеза за естеството на статистическия модел, който се проявява в изследваното явление, например хипотезата, че изследваното явление се подчинява на закона за нормалното разпределение. Тази хипотеза се нарича нулева хипотеза, която може да се окаже невярна, следователно заедно с нулевата хипотеза се излага и алтернативна или конкурентна хипотеза. Проверката доколко получените експериментални данни съответстват на определена статистическа хипотеза се извършва с помощта на така наречените непараметрични статистически тестове или тестове за добро съответствие. Понастоящем широко се използват критериите за съответствие на Колмогоров, Смирнов, омега-квадрат и др. Основната идея на тези тестове е да се измери разстоянието между емпиричната функция на разпределение и напълно известната теоретична функция на разпределение. Методологията за тестване на статистическа хипотеза е строго разработена и очертана в голям брой трудове по математическа статистика.
2. Извършване на необходимите изчисления с помощта на математически средства в рамките на вероятностен модел. В съответствие с установения вероятностен модел на явлението се извършват изчисления на характерни параметри, например като математическо очакване или средна стойност, дисперсия, стандартно отклонение, мода, медиана, индекс на асиметрия и др.
3. Интерпретация на вероятностни и статистически изводи спрямо реалната ситуация.
В момента класическият вероятностно-статистически метод е добре развит и широко използван в изследванията в различни области на природните, техническите и социалните науки. Подробно описание на същността на този метод и приложението му за решаване на конкретни проблеми може да се намери в голям брой литературни източници, например в.
Некласически вероятностно-статистически метод. Некласическият вероятностно-статистически метод на изследване се различава от класическия по това, че се прилага не само към масови събития, но и към индивидуални събития, които са фундаментално случайни по природа. Този метод може ефективно да се използва при анализиране на поведението на индивида в процеса на извършване на определена дейност, например в процеса на усвояване на знания от ученик. Ще разгледаме характеристиките на некласическия вероятностно-статистически метод на психолого-педагогическо изследване на примера на поведението на учениците в процеса на придобиване на знания.
За първи път в работата е предложен вероятностно-статистически модел на поведението на учениците в процеса на усвояване на знания. По-нататъшното развитие на този модел беше направено в работата. Обучението като вид дейност, чиято цел е придобиването на знания, умения и способности от човек, зависи от нивото на развитие на съзнанието на ученика. Структурата на съзнанието включва такива когнитивни процеси като усещане, възприятие, памет, мислене, въображение. Анализът на тези процеси показва, че те се характеризират с елементи на случайност, дължащи се на случайния характер на психичните и соматични състояния на индивида, както и на физиологични, психологически и информационни шумове по време на работата на мозъка. Последното доведе, когато се описват мисловните процеси, до изоставяне на използването на детерминиран динамичен системен модел в полза на произволен динамичен системен модел. Това означава, че детерминизмът на съзнанието се осъществява чрез случайността. От това можем да заключим, че човешкото знание, което всъщност е продукт на съзнанието, също има случаен характер и следователно може да се използва вероятностно-статистически метод за описание на поведението на всеки отделен ученик в процеса на придобиване на знания.
В съответствие с този метод ученикът се идентифицира чрез функция на разпределение (плътност на вероятността), която определя вероятността да бъде намерен в един регион на информационното пространство. По време на учебния процес разпределителната функция, с която се идентифицира ученикът, се движи в информационното пространство, докато се развива. Всеки студент има индивидуални свойства и е разрешена независима локализация (пространствена и кинематична) на индивидите един спрямо друг.
Въз основа на закона за запазване на вероятността е написана система от диференциални уравнения, които са уравнения за непрекъснатост, които свързват промяната в плътността на вероятността за единица време във фазовото пространство (пространството на координати, скорости и ускорения от различни порядъци) с дивергенцията на потока на вероятностната плътност в разглежданото фазово пространство. Извършен е анализ на аналитични решения на редица уравнения на непрекъснатостта (функции на разпределение), характеризиращи поведението на отделните ученици в процеса на обучение.
При провеждане на експериментални изследвания на поведението на учениците в процеса на придобиване на знания се използва вероятностно-статистическо скалиране, според което скалата за измерване е подредена система
1. Намиране на експериментални функции на разпределение въз основа на резултатите от контролно събитие, например изпит. Типична форма на отделни функции на разпределение, намерени с помощта на двадесетобална скала, е представена на фиг. 1. Методът за намиране на такива функции е описан в.
2. Картографиране на функции на разпределение върху числово пространство. За целта се изчисляват моментите на отделните функции на разпределение. На практика, като правило, е достатъчно да се ограничим до определяне на моментите от първи ред (математическо очакване), втори ред (дисперсия) и трети ред, характеризиращи асиметрията на функцията на разпределение.
3. Класиране на учениците по ниво на знания въз основа на сравнение на моменти от различен ред на техните индивидуални функции на разпределение.
Ориз. 1. Типична форма на индивидуалните функции на разпределение на учениците, получили различни оценки на общия изпит по физика: 1 - традиционна оценка "2"; 2 - традиционна оценка "3"; 3 - традиционна оценка "4"; 4 - традиционна оценка "5"
Въз основа на адитивността на отделните функции на разпределение са намерени експериментални функции на разпределение за потока от ученици (фиг. 2).

Ориз. 2. Еволюция на пълната функция на разпределение на студентския поток, апроксимирана с плавни линии: 1 - след първата година; 2 - след втората година; 3 - след третата година; 4 - след четвъртата година; 5 - след петата година
Анализ на данните, представени на фиг. 2 показва, че докато се движим през информационното пространство, разпределителните функции се размиват. Това се дължи на факта, че математическите очаквания на функциите на разпределение на индивидите се движат с различни скорости, а самите функции се размиват поради дисперсия. Допълнителен анализ на тези функции на разпределение може да се извърши в рамките на класическия вероятностно-статистически метод.
Обсъждане на резултатите. Анализът на класическите и некласическите вероятностно-статистически методи на психолого-педагогически изследвания показа, че между тях има съществена разлика. Както може да се разбере от горното, класическият метод е приложим само за анализ на масови събития, а некласическият метод е приложим както за анализ на масови, така и за единични събития. В тази връзка класическият метод може условно да се нарече масов вероятностно-статистически метод (МПСМ), а некласическият метод - индивидуален вероятностно-статистически метод (ИПСМ). В 4] е показано, че нито един от класическите методи за оценка на знанията на учениците в рамките на вероятностно-статистически модел на индивида не може да бъде приложен за тези цели.
Нека разгледаме отличителните черти на методите MVSM и IVSM, като използваме примера за измерване на пълнотата на знанията на учениците. За тази цел нека проведем мисловен експеримент. Нека приемем, че има голям брой ученици, които са абсолютно идентични по умствени и физически характеристики и имат еднакъв произход, и нека те, без да взаимодействат помежду си, едновременно участват в един и същ познавателен процес, преживявайки абсолютно едни и същи строго определени влияние. Тогава, в съответствие с класическите представи за обектите на измерване, всички ученици трябва да получат еднакви оценки за пълнотата на знанията с всяка дадена точност на измерване. В действителност обаче при достатъчно висока точност на измерване оценките за пълнотата на знанията на учениците ще се различават. Не е възможно да се обясни този резултат от измерването в рамките на MVSM, тъй като първоначално се предполага, че въздействието върху абсолютно идентични ученици, които не взаимодействат помежду си, е от строго детерминистичен характер. Класическият вероятностно-статистически метод не отчита факта, че детерминизмът на процеса на познаване се осъществява чрез случайността, която е присъща на всеки индивид, който познава света около себе си.
Случайният характер на поведението на учениците в процеса на усвояване на знания отчита IVSM. Използването на индивидуален вероятностно-статистически метод за анализ на поведението на разглежданата идеализирана група студенти би показало, че е невъзможно да се посочи точната позиция на всеки ученик в информационното пространство; може да се каже само вероятността да бъде намерен в него една или друга област на информационното пространство. Всъщност всеки ученик се идентифицира чрез индивидуална функция на разпределение, като нейните параметри, като математическо очакване, дисперсия и др., са индивидуални за всеки ученик. Това означава, че отделните разпределителни функции ще бъдат разположени в различни области на информационното пространство. Причината за това поведение на учениците се крие в случайния характер на учебния процес.
Въпреки това, в редица случаи резултатите от изследванията, получени в рамките на IVSM, могат да бъдат интерпретирани в рамките на IVSM. Да приемем, че учителят използва петобална скала за измерване, когато оценява знанията на ученика. В този случай грешката при оценката на знанията е ±0,5 точки. Следователно, когато на ученик се постави оценка например 4 точки, това означава, че знанията му са в диапазона от 3,5 точки до 4,5 точки. Всъщност позицията на индивида в информационното пространство в този случай се определя от правоъгълна функция на разпределение, чиято ширина е равна на грешката на измерване от ±0,5 точки, а оценката е математическото очакване. Тази грешка е толкова голяма, че не ни позволява да наблюдаваме истинската форма на функцията на разпределение. Въпреки това, въпреки такова грубо приближение на функцията на разпределение, изследването на нейната еволюция ни позволява да получим важна информация както за поведението на индивида, така и за група ученици като цяло.
Резултатът от измерването на пълнотата на знанията на ученика се влияе пряко или косвено от съзнанието на учителя (измерителя), който също се характеризира с произволност. В процеса на педагогически измервания всъщност има взаимодействие между две произволни динамични системи, които идентифицират поведението на ученика и учителя в този процес. Разгледано е взаимодействието на подсистемата ученик с подсистемата обучение и е показано, че скоростта на движение на математическото очакване на отделните разпределителни функции на студентите в информационното пространство е пропорционална на функцията на влияние на преподавателския състав и е обратно пропорционална на пропорционална на инерционната функция, която характеризира неподатливостта на промяна на положението на математическото очакване в пространството (аналог на закона на Аристотел в механиката).
В момента, въпреки значителните постижения в развитието на теоретичните и практическите основи на измерванията при провеждане на психологически и педагогически изследвания, проблемът с измерването като цяло все още е далеч от решение. Това се дължи преди всичко на факта, че все още няма достатъчно информация за влиянието на съзнанието върху процеса на измерване. Подобна ситуация възникна при решаването на проблема с измерването в квантовата механика. Така в работата, когато се разглеждат концептуалните проблеми на квантовата теория на измерванията, се казва, че разрешаването на някои парадокси на измерванията в квантовата механика „... едва ли е възможно без директно включване на съзнанието на наблюдателя в теоретичното описание на квантово измерване." По-нататък се казва, че „... последователно е да се приеме, че съзнанието може да направи някое събитие вероятно, дори ако според законите на физиката (квантовата механика) вероятността за това събитие е малка. Нека направим важно пояснение на формулировката: съзнанието на даден наблюдател може да направи вероятно той да види това събитие.
3. Същност на вероятностно-статистическите методи
Как се използват подходите, идеите и резултатите от теорията на вероятностите и математическата статистика при обработката на данни – резултатите от наблюдения, измервания, тестове, анализи, експерименти с цел вземане на практически важни решения?
Основата е вероятностен модел на реално явление или процес, т.е. математически модел, в който обективните връзки са изразени от гледна точка на теорията на вероятностите. Вероятностите се използват предимно за описание на несигурностите, които трябва да се вземат предвид при вземането на решения. Това се отнася както за нежелани възможности (рискове), така и за привлекателни („щастлив шанс”). Понякога произволността се въвежда умишлено в ситуация, например при теглене на жребий, произволен избор на единици за контрол, провеждане на лотарии или провеждане на потребителски проучвания.
Теорията на вероятностите позволява една вероятност да се използва за изчисляване на други, които представляват интерес за изследователя. Например, като използвате вероятността да получите герб, можете да изчислите вероятността при 10 хвърляния на монети да получите поне 3 герба. Такова изчисление се основава на вероятностен модел, според който хвърлянията на монети се описват чрез модел на независими опити, освен това гербът и хеш-знаците са еднакво възможни и следователно вероятността за всяко от тези събития е еднаква; до ½. По-сложен модел е този, който обмисля проверка на качеството на единица продукция вместо хвърляне на монета. Съответният вероятностен модел се основава на предположението, че контролът на качеството на различни производствени единици е описан от независима схема за тестване. За разлика от модела за хвърляне на монета е необходимо да се въведе нов параметър - вероятност Рче продуктът е дефектен. Моделът ще бъде напълно описан, ако приемем, че всички производствени единици имат еднаква вероятност да бъдат дефектни. Ако последното предположение е неправилно, тогава броят на параметрите на модела се увеличава. Например, можете да предположите, че всяка производствена единица има своя собствена вероятност да бъде дефектна.
Нека обсъдим модел за контрол на качеството с вероятност за дефектност, обща за всички производствени единици Р. За да се „стигне до числото“ при анализ на модела, е необходимо да се замени Рдо някаква конкретна стойност. За да направите това, е необходимо да преминете отвъд вероятностния модел и да се обърнете към данните, получени по време на контрола на качеството. Математическата статистика решава обратния проблем по отношение на теорията на вероятностите. Неговата цел е въз основа на резултатите от наблюдения (измервания, анализи, тестове, експерименти) да се получат заключения относно вероятностите, залегнали в основата на вероятностния модел. Например, въз основа на честотата на поява на дефектни продукти по време на инспекция, могат да се направят заключения относно вероятността от дефект (вижте дискусията по-горе, използвайки теоремата на Бернули). Въз основа на неравенството на Чебишев бяха направени изводи за съответствието на честотата на поява на дефектни продукти на хипотезата, че вероятността за дефектност приема определена стойност.
По този начин приложението на математическата статистика се основава на вероятностен модел на явление или процес. Използват се две паралелни серии от понятия – тези, свързани с теорията (вероятностен модел) и тези, свързани с практиката (извадка от резултатите от наблюдението). Например, теоретичната вероятност съответства на честотата, намерена от извадката. Математическото очакване (теоретична серия) съответства на средноаритметичното извадково (практическа серия). По правило характеристиките на извадката са оценки на теоретичните. В същото време количествата, свързани с теоретичните серии, „са в главите на изследователите“, се отнасят до света на идеите (според древногръцкия философ Платон) и не са достъпни за директно измерване. Изследователите разполагат само с примерни данни, с които се опитват да установят свойствата на теоретичен вероятностен модел, който ги интересува.
Защо се нуждаем от вероятностен модел? Факт е, че само с негова помощ свойствата, установени от анализа на конкретна проба, могат да бъдат пренесени върху други проби, както и върху цялата така наречена генерална съвкупност. Терминът "популация" се използва, когато се говори за голяма, но ограничена колекция от изследвани единици. Например за съвкупността от всички жители на Русия или за съвкупността от всички потребители на разтворимо кафе в Москва. Целта на маркетинговите или социологическите проучвания е да прехвърлят твърдения, получени от извадка от стотици или хиляди хора, към популации от няколко милиона души. При контрола на качеството партида от продукти действа като обща съвкупност.
За да се прехвърлят заключения от извадка към по-голяма популация, са необходими някои допускания относно връзката на характеристиките на извадката с характеристиките на тази по-голяма популация. Тези предположения се основават на подходящ вероятностен модел.
Разбира се, възможно е да се обработват примерни данни, без да се използва един или друг вероятностен модел. Например, можете да изчислите примерно средно аритметично, да преброите честотата на изпълнение на определени условия и т.н. Резултатите от изчислението обаче ще се отнасят само до конкретна извадка; прехвърлянето на заключенията, получени с тяхна помощ, към всяка друга популация е неправилно. Тази дейност понякога се нарича „анализ на данни“. В сравнение с вероятностно-статистическите методи, анализът на данни има ограничена образователна стойност.
Така че използването на вероятностни модели, базирани на оценка и тестване на хипотези, използвайки характеристики на извадка, е същността на вероятностно-статистическите методи за вземане на решения.
Подчертаваме, че логиката на използване на примерни характеристики за вземане на решения въз основа на теоретични модели включва едновременното използване на две паралелни серии от концепции, едната от които съответства на вероятностни модели, а втората - на примерни данни. За съжаление, в редица литературни източници, обикновено остарели или написани в рецептурен дух, не се прави разлика между извадкови и теоретични характеристики, което води читателите до объркване и грешки при практическото използване на статистическите методи.
| Предишен |
Особен интерес представлява количествената оценка на бизнес риска с помощта на методите на математическата статистика. Основните инструменти на този метод за оценка са:
§ вероятност за възникване на случайна променлива,
§ математическо очакване или средна стойност на изследваната случайна променлива,
§ дисперсия,
§ стандартно (средно квадратично) отклонение,
§ коефициентът на вариация,
§ вероятностно разпределение на изследваната случайна променлива.
За да вземете решение, трябва да знаете големината (степента) на риска, който се измерва по два критерия:
1) средна очаквана стойност (математическо очакване),
2) колебания (променливост) на възможния резултат.
Средна очаквана стойност ![]() това е среднопретеглената стойност на случайна променлива, която е свързана с несигурността на ситуацията:
това е среднопретеглената стойност на случайна променлива, която е свързана с несигурността на ситуацията:
![]() ,
,
където е стойността на случайната променлива.
Средната очаквана стойност измерва резултата, който очакваме средно.
Средната стойност е обобщена качествена характеристика и не позволява да се вземе решение в полза на някаква конкретна стойност на случайна величина.
За да вземете решение, е необходимо да измерите колебанията в показателите, тоест да определите мярката за променливост на възможен резултат.
Вариацията във възможния резултат е степента, до която очакваната стойност се отклонява от средната стойност.
За тази цел в практиката обикновено се използват два тясно свързани критерия: “дисперсия” и “стандартно отклонение”.
дисперсия – среднопретеглена стойност на квадратите на действителните резултати спрямо очакваната средна стойност:
Стандартно отклонение е корен квадратен от дисперсията. Това е размерна величина и се измерва в същите единици, в които се измерва изследваната случайна променлива:
![]() .
.
Дисперсията и стандартното отклонение осигуряват мярка за абсолютна вариация. Коефициентът на вариация обикновено се използва за анализ.
Коефициентът на вариация представлява отношението на стандартното отклонение към средната очаквана стойност, умножено по 100%
![]() или
или  .
.
Коефициентът на вариация не се влияе от абсолютните стойности на изследвания показател.
Използвайки коефициента на вариация, можете дори да сравните колебанията в характеристиките, изразени в различни мерни единици. Коефициентът на вариация може да варира от 0 до 100%. Колкото по-висок е коефициентът, толкова по-голяма е флуктуацията.
В икономическата статистика се установява следната оценка на различни стойности на коефициента на вариация:
до 10% - слаба флуктуация, 10 - 25% - умерена, над 25% - висока.
Съответно, колкото по-големи са колебанията, толкова по-голям е рискът.
Пример.Собственикът на малък магазин в началото на всеки ден купува някакъв нетраен продукт за продажба. Една единица от този продукт струва 200 UAH. Продажна цена - 300 UAH. за единица. От наблюденията е известно, че търсенето на този продукт през деня може да бъде 4, 5, 6 или 7 единици със съответните вероятности от 0,1; 0,3; 0,5; 0,1. Ако продуктът не се продава през деня, тогава в края на деня той винаги ще бъде закупен на цена от 150 UAH. за единица. Колко единици от този продукт трябва да закупи собственикът на магазина в началото на деня?
Решение. Нека изградим матрица на печалбата за собственика на магазина. Нека изчислим печалбата, която собственикът ще получи, ако например закупи 7 единици от даден продукт и продаде една единица през ден 6 и в края на деня. Всяка единица продукт, продаден през деня, дава печалба от 100 UAH, а в края на деня - загуба от 200 - 150 = 50 UAH. По този начин печалбата в този случай ще бъде:
Изчисленията се извършват по подобен начин за други комбинации от търсене и предлагане.
Очакваната печалба се изчислява като математическото очакване на възможните стойности на печалбата за всеки ред от изградената матрица, като се вземат предвид съответните вероятности. Както можете да видите, сред очакваните печалби най-голямата е 525 UAH. Съответства на закупуване на въпросния продукт в размер на 6 бр.
За да оправдаем крайната препоръка за закупуване на необходимия брой единици от продукта, ние изчисляваме дисперсията, стандартното отклонение и коефициента на вариация за всяка възможна комбинация от търсене и предлагане на продукта (всеки ред от матрицата на печалбата):
| 400 | 0,1 | 40 | 16000 |
| 400 | 0,3 | 120 | 48000 |
| 400 | 0,5 | 200 | 80000 |
| 400 | 0,1 | 40 | 16000 |
| 1,0 | 400 | 160000 |
| 350 | 0,1 | 35 | 12250 |
| 500 | 0,3 | 150 | 75000 |
| 500 | 0,5 | 250 | 125000 |
| 500 | 0,1 | 50 | 25000 |
| 1,0 | 485 | 2372500 |
| 300 | 0,1 | 30 | 9000 |
| 450 | 0,3 | 135 | 60750 |
| 600 | 0,5 | 300 | 180000 |
| 600 | 0,1 | 60 | 36000 |
| 1,0 | 525 | 285750 |
Що се отнася до собственика на магазина, който закупува 6 единици продукт в сравнение с 5 и 4 единици, това не е очевидно, тъй като рискът при закупуване на 6 единици продукт (19,2%) е по-голям, отколкото при закупуване на 5 единици (9,3%) и дори повече отколкото при закупуване на 4 единици (0%).
Така имаме цялата информация за очакваните печалби и рискове. И собственикът на магазина решава колко единици от продукта трябва да купува всяка сутрин, като взема предвид неговия опит и склонност към риск.
Според нас собственикът на магазина трябва да бъде препоръчан да закупува 5 единици от продукта всяка сутрин и неговата средна очаквана печалба ще бъде равна на 485 UAH. и ако сравните това с покупката на 6 единици продукт, при което средната очаквана печалба е 525 UAH, което е 40 UAH. повече, но рискът в този случай ще бъде 2,06 пъти по-голям.
Изпратете добрата си работа в базата знания е лесно. Използвайте формата по-долу
Студенти, докторанти, млади учени, които използват базата от знания в обучението и работата си, ще ви бъдат много благодарни.
публикувано на http://www.allbest.ru/
публикувано на http://www.allbest.ru/
Въведение
1. Хи-квадрат разпределение
Заключение
Приложение
Въведение
Как се използват подходите, идеите и резултатите от теорията на вероятностите в живота ни? математическа квадратна теория
Основата е вероятностен модел на реално явление или процес, т.е. математически модел, в който обективните връзки са изразени от гледна точка на теорията на вероятностите. Вероятностите се използват предимно за описание на несигурностите, които трябва да се вземат предвид при вземането на решения. Това се отнася както за нежелани възможности (рискове), така и за привлекателни („щастлив шанс”). Понякога произволността се въвежда умишлено в ситуация, например при теглене на жребий, произволен избор на единици за контрол, провеждане на лотарии или провеждане на потребителски проучвания.
Теорията на вероятностите позволява една вероятност да се използва за изчисляване на други, които представляват интерес за изследователя.
Вероятностният модел на явление или процес е в основата на математическата статистика. Използват се две паралелни серии от понятия – тези, свързани с теорията (вероятностен модел) и тези, свързани с практиката (извадка от резултатите от наблюдението). Например, теоретичната вероятност съответства на честотата, намерена от извадката. Математическото очакване (теоретична серия) съответства на средноаритметичното извадково (практическа серия). По правило характеристиките на извадката са оценки на теоретичните. В същото време количествата, свързани с теоретичните серии, „са в главите на изследователите“, се отнасят до света на идеите (според древногръцкия философ Платон) и не са достъпни за директно измерване. Изследователите разполагат само с примерни данни, с които се опитват да установят свойствата на теоретичен вероятностен модел, който ги интересува.
Защо се нуждаем от вероятностен модел? Факт е, че само с негова помощ свойствата, установени от анализа на конкретна проба, могат да бъдат пренесени върху други проби, както и върху цялата така наречена генерална съвкупност. Терминът "популация" се използва, когато се говори за голяма, но ограничена колекция от изследвани единици. Например за съвкупността от всички жители на Русия или за съвкупността от всички потребители на разтворимо кафе в Москва. Целта на маркетинговите или социологическите проучвания е да прехвърлят твърдения, получени от извадка от стотици или хиляди хора, към популации от няколко милиона души. При контрола на качеството партида от продукти действа като обща съвкупност.
За да се прехвърлят заключения от извадка към по-голяма популация, са необходими някои допускания относно връзката на характеристиките на извадката с характеристиките на тази по-голяма популация. Тези предположения се основават на подходящ вероятностен модел.
Разбира се, възможно е да се обработват примерни данни, без да се използва един или друг вероятностен модел. Например, можете да изчислите примерно средно аритметично, да преброите честотата на изпълнение на определени условия и т.н. Резултатите от изчислението обаче ще се отнасят само до конкретна извадка; прехвърлянето на заключенията, получени с тяхна помощ, към всяка друга популация е неправилно. Тази дейност понякога се нарича „анализ на данни“. В сравнение с вероятностно-статистическите методи, анализът на данни има ограничена образователна стойност.
Така че използването на вероятностни модели, базирани на оценка и тестване на хипотези, използвайки характеристики на извадка, е същността на вероятностно-статистическите методи за вземане на решения.
1. Хи-квадрат разпределение
С помощта на нормалното разпределение се дефинират три разпределения, които сега често се използват в статистическата обработка на данни. Това са разпределенията на Пиърсън („хи-квадрат“), Студент и Фишер.
Ще се съсредоточим върху разпределението („хи-квадрат“). Това разпределение е изследвано за първи път от астронома Ф. Хелмерт през 1876 г. Във връзка с теорията на грешките на Гаус той изучава сумите от квадратите на n независими стандартно нормално разпределени случайни променливи. По-късно Карл Пиърсън дава името "хи-квадрат" на тази функция на разпределение. И сега разпределението носи неговото име.
Поради тясната си връзка с нормалното разпределение, разпределението h2 играе важна роля в теорията на вероятностите и математическата статистика. Разпределението h2 и много други разпределения, които се определят от разпределението h2 (например разпределението на Стюдънт), описват примерни разпределения на различни функции от нормално разпределени резултати от наблюдение и се използват за конструиране на доверителни интервали и статистически тестове.
Разпределение на Пиърсън (хи - квадрат) - разпределение на случайна променлива, където X1, X2,..., Xn са нормални независими случайни променливи, като математическото очакване на всяка от тях е нула, а стандартното отклонение е единица.
Сбор на квадрати
разпределени според закона (“хи - квадрат”).
В този случай броят на термините, т.е. n се нарича "брой степени на свобода" на разпределението хи-квадрат. С увеличаването на броя на степените на свобода разпределението бавно се доближава до нормалното.
Плътността на това разпределение
И така, разпределението h2 зависи от един параметър n - броя на степените на свобода.
Функцията на разпределение h2 има формата:
ако h2?0. (2.7.)
Фигура 1 показва графика на функциите на плътността на вероятността и разпределението h2 за различни степени на свобода.
Фигура 1 Зависимост на плътността на вероятността q (x) в разпределението h2 (chi - квадрат) за различен брой степени на свобода
Моменти на разпределението хи-квадрат:
Разпределението хи-квадрат се използва при оценяване на дисперсията (използване на доверителен интервал), тестване на хипотези за съгласие, хомогенност, независимост, предимно за качествени (категоризирани) променливи, които приемат краен брой стойности, и в много други задачи на анализ на статистически данни .
2. "Хи-квадрат" в задачите на статистическия анализ на данни
Статистическите методи за анализ на данни се използват в почти всички области на човешката дейност. Те се използват винаги, когато е необходимо да се получат и обосноват някакви преценки за група (обекти или субекти) с някаква вътрешна хетерогенност.
Съвременният етап на развитие на статистическите методи може да се брои от 1900 г., когато англичанинът К. Пиърсън основава списанието "Биометрика". Първата третина на ХХ век. премина под знака на параметричната статистика. Методите са изследвани въз основа на анализ на данни от параметрични семейства от разпределения, описани от криви на семейство Пиърсън. Най-популярното беше нормалното разпределение. За проверка на хипотезите са използвани тестовете на Pearson, Student и Fisher. Предложени са методът на максималната вероятност и дисперсионният анализ и са формулирани основните идеи за планиране на експеримента.
Разпределението хи-квадрат е едно от най-широко използваните в статистиката за тестване на статистически хипотези. Въз основа на разпределението хи-квадрат е конструиран един от най-мощните тестове за добро съответствие - хи-квадрат тестът на Pearson.
Критерият за съгласие е критерият за проверка на хипотезата за приетия закон на неизвестно разпределение.
Тестът h2 ("хи-квадрат") се използва за проверка на хипотезата за различни разпределения. Това е неговото достойнство.
Формулата за изчисление на критерия е равна на
където m и m" са съответно емпирични и теоретични честоти
въпросното разпределение;
n е броят на степените на свобода.
За да проверим, трябва да сравним емпиричните (наблюдавани) и теоретичните (изчислени при предположението за нормално разпределение) честоти.
Ако емпиричните честоти напълно съвпадат с изчислените или очаквани честоти, S (E - T) = 0 и критерият h2 също ще бъде равен на нула. Ако S (E - T) не е равно на нула, това ще означава несъответствие между изчислените честоти и емпиричните честоти на серията. В такива случаи е необходимо да се оцени значимостта на критерия h2, който теоретично може да варира от нула до безкрайност. Това се прави чрез сравняване на действителната стойност на h2f с нейната критична стойност (h2st). Нулевата хипотеза, т.е. предположението, че несъответствието между емпиричните и теоретичните или очакваните честоти е случайно, се опровергава, ако h2f е по-голямо или равно на h2st. за приетото ниво на значимост (a) и броя на степените на свобода (n).
Разпределението на вероятните стойности на случайната променлива h2 е непрекъснато и асиметрично. Зависи от броя на степените на свобода (n) и се доближава до нормално разпределение с увеличаване на броя на наблюденията. Следователно прилагането на критерия h2 за оценка на дискретни разпределения е свързано с някои грешки, които влияят на неговата стойност, особено при малки извадки. За да се получат по-точни оценки, извадката, разпределена в серията вариации, трябва да има поне 50 опции. Правилното прилагане на критерия h2 също изисква честотите на вариантите в екстремните класове да не са по-малки от 5; ако има по-малко от 5 от тях, тогава те се комбинират с честотите на съседни класове, така че общата сума да е по-голяма или равна на 5. Според комбинацията от честоти броят на класовете (N) намалява. Броят на степените на свобода се определя от вторичния брой класове, като се вземе предвид броят на ограниченията на свободата на вариация.
Тъй като точността на определяне на критерия h2 до голяма степен зависи от точността на изчисляване на теоретичните честоти (T), трябва да се използват незакръглени теоретични честоти, за да се получи разликата между емпиричните и изчислените честоти.
Като пример, нека вземем проучване, публикувано на уебсайт, посветен на приложението на статистически методи в хуманитарните науки.
Хи-квадрат тестът ви позволява да сравнявате честотните разпределения, независимо дали те са нормално разпределени или не.
Честотата се отнася до броя на случванията на дадено събитие. Обикновено честотата на възникване на събитията се разглежда, когато променливите се измерват по скала от имена и другите им характеристики, освен честотата, са невъзможни или проблематични за избор. С други думи, когато една променлива има качествени характеристики. Освен това много изследователи са склонни да преобразуват резултатите от тестовете в нива (високо, средно, ниско) и да съставят таблици с разпределение на резултатите, за да открият броя на хората на тези нива. За да се докаже, че в едно от нивата (в една от категориите) броят на хората наистина е по-голям (по-малък) също се използва коефициентът Хи-квадрат.
Нека да разгледаме най-простия пример.
Беше проведен тест сред по-младите юноши за идентифициране на самочувствието. Резултатите от теста бяха преобразувани в три нива: високо, средно, ниско. Честотите бяха разпределени както следва:
Висока (B) 27 души.
Средно (C) 12 души.
Ниска (L) 11 души
Очевидно е, че по-голямата част от децата имат високо самочувствие, но това трябва да бъде доказано статистически. За целта използваме теста Хи-квадрат.
Нашата задача е да проверим дали получените емпирични данни се различават от теоретично еднакво вероятните. За да направите това, трябва да намерите теоретичните честоти. В нашия случай теоретичните честоти са еднакво вероятни честоти, които се намират чрез добавяне на всички честоти и разделяне на броя на категориите.
В нашия случай:
(B + C + H)/3 = (27+12+11)/3 = 16,6
Формула за изчисляване на хи-квадрат теста:
h2 = ?(E - T)I / T
Изграждаме масата:
|
Емпиричен (E) |
Теоретичен (T) |
(E - T)I / T |
||
Намерете сумата от последната колона:
Сега трябва да намерите критичната стойност на критерия, като използвате таблицата с критични стойности (Таблица 1 в Приложението). За да направим това, имаме нужда от броя на степените на свобода (n).
n = (R - 1) * (C - 1)
където R е броят на редовете в таблицата, C е броят на колоните.
В нашия случай има само една колона (което означава оригиналните емпирични честоти) и три реда (категории), така че формулата се променя - изключваме колоните.
n = (R - 1) = 3-1 = 2
За вероятността за грешка p?0,05 и n = 2, критичната стойност е h2 = 5,99.
Получената емпирична стойност е по-голяма от критичната – разликите в честотите са значими (h2 = 9.64; p? 0.05).
Както можете да видите, изчисляването на критерия е много просто и не отнема много време. Практическата стойност на хи-квадрат теста е огромна. Този метод е най-ценен, когато се анализират отговорите на въпросниците.
Нека да разгледаме по-сложен пример.
Например, един психолог иска да знае дали е вярно, че учителите са по-предубедени към момчетата, отколкото към момичетата. Тези. по-вероятно е да хвали момичета. За да направи това, психологът анализира характеристиките на учениците, написани от учителите, за честотата на срещане на три думи: „активен“, „усърден“, „дисциплиниран“ и също бяха преброени синонимите на думите.
Данните за честотата на срещане на думите бяха въведени в таблицата:
За обработка на получените данни използваме теста хи-квадрат.
За да направим това, ще изградим таблица на разпределението на емпиричните честоти, т.е. тези честоти, които наблюдаваме:
Теоретично очакваме, че честотите ще бъдат равномерно разпределени, т.е. честотата ще бъде разпределена пропорционално между момчета и момичета. Нека изградим таблица с теоретични честоти. За да направите това, умножете сумата на реда по сумата на колоната и разделете полученото число на общата сума (s).
Финалната таблица за изчисления ще изглежда така:
|
Емпиричен (E) |
Теоретичен (T) |
(E - T)I / T |
|||
|
Момчета |
"Активен" |
||||
|
"прилежен" |
|||||
|
"Дисциплиниран" |
|||||
|
"Активен" |
|||||
|
"прилежен" |
|||||
|
"Дисциплиниран" |
|||||
|
Сума: 4.21 |
h2 = ?(E - T)I / T
където R е броят на редовете в таблицата.
В нашия случай хи-квадрат = 4,21; n = 2.
Използвайки таблицата с критични стойности на критерия, намираме: с n = 2 и ниво на грешка от 0,05, критичната стойност h2 = 5,99.
Получената стойност е по-малка от критичната стойност, което означава, че нулевата хипотеза е приета.
Извод: учителите не отдават значение на пола на детето, когато пишат характеристики за него.
Заключение
Студентите от почти всички специалности изучават раздела „Теория на вероятностите и математическа статистика” в края на курса по висша математика, в действителност те се запознават само с някои основни понятия и резултати, които очевидно не са достатъчни за практическа работа. Студентите се запознават с някои математически изследователски методи в специални курсове (например „Прогнозиране и технико-икономическо планиране“, „Технико-икономически анализ“, „Контрол на качеството на продуктите“, „Маркетинг“, „Контрол“, „Математически методи за прогнозиране“ ”), „Статистика“ и др. – при студенти от икономически специалности), но представянето в повечето случаи е много съкратено и шаблонно. В резултат на това знанията на специалистите по приложна статистика са недостатъчни.
Ето защо курсът „Приложна статистика” в техническите университети е от голямо значение, а курсът „Иконометрия” в икономическите университети, тъй като иконометрията, както е известно, е статистически анализ на конкретни икономически данни.
Теорията на вероятностите и математическата статистика предоставят фундаментални знания за приложна статистика и иконометрия.
Те са необходими на специалистите за практическа работа.
Разгледах непрекъснатия вероятностен модел и се опитах да покажа използването му с примери.
И в края на работата си стигнах до извода, че компетентното прилагане на основните процедури за математическо-статически анализ на данни и статично тестване на хипотези е невъзможно без познаване на модела хи-квадрат, както и способността да се използва неговият маса.
Библиография
1. Орлов А.И. Приложна статистика. М .: Издателство "Изпит", 2004 г.
2. Гмурман В.Е. Теория на вероятностите и математическа статистика. М .: Висше училище, 1999. - 479 с.
3. Айвозян С.А. Теория на вероятностите и приложна статистика, том 1. М .: Единство, 2001. - 656 с.
4. Хамитов Г.П., Ведерникова Т.И. Вероятности и статистики. Иркутск: BGUEP, 2006 - 272 с.
5. Ежова Л.Н. Иконометрия. Иркутск: BGUEP, 2002. - 314 с.
6. Мостелер Ф. Петдесет забавни вероятностни задачи с решения. М.: Наука, 1975. - 111 с.
7. Мостелер Ф. Вероятност. М.: Мир, 1969. - 428 с.
8. Яглом А.М. Вероятност и информация. М.: Наука, 1973. - 511 с.
9. Чистяков В.П. Курс по теория на вероятностите. М.: Наука, 1982. - 256 с.
10. Кремер Н.Ш. Теория на вероятностите и математическа статистика. М.: ЕДИНСТВО, 2000. - 543 с.
11. Математическа енциклопедия, кн.1. М.: Съветска енциклопедия, 1976. - 655 с.
12. http://psystat.at.ua/ - Статистика в психологията и педагогиката. Статия Хи-квадрат тест.
Приложение
Критични точки на разпространение h2
маса 1
Публикувано на Allbest.ru
...Подобни документи
Вероятностен модел и аксиоматика на A.N. Колмогоров. Случайни променливи и вектори, класическа гранична задача на теорията на вероятностите. Първична обработка на статистически данни. Точкови оценки на числови характеристики. Статистическа проверка на хипотези.
ръководство, добавено на 03/02/2010
Правила за изпълнение и попълване на тестове за кореспондентския отдел. Задачи и примери за решаване на задачи по математическа статистика и теория на вероятностите. Таблици с референтни данни на разпределенията, плътност на стандартното нормално разпределение.
ръководство за обучение, добавено на 29.11.2009 г
Основни методи за формализирано описание и анализ на случайни явления, обработка и анализ на резултатите от физични и числени експерименти в теорията на вероятностите. Основни понятия и аксиоми на теорията на вероятностите. Основни понятия на математическата статистика.
курс от лекции, добавен на 08.04.2011 г
Определяне на закона за вероятностно разпределение на резултатите от измерванията в математическата статистика. Проверка на съответствието на емпиричното разпределение с теоретичното. Определяне на доверителния интервал, в който се намира стойността на измерената величина.
курсова работа, добавена на 11.02.2012 г
Конвергенция на последователности от случайни променливи и вероятностни разпределения. Метод на характеристичните функции. Тестване на статистически хипотези и изпълнение на централната гранична теорема за дадени последователности от независими случайни променливи.
курсова работа, добавена на 13.11.2012 г
Основните етапи на обработка на данни от естествени наблюдения с помощта на метода на математическата статистика. Оценка на получените резултати, използването им при вземане на управленски решения в областта на опазването на природата и управлението на околната среда. Тестване на статистически хипотези.
практическа работа, добавена на 24.05.2013 г
Същност на закона за разпределение и практическото му приложение за решаване на статистически задачи. Определяне на дисперсията на случайна величина, математическо очакване и стандартно отклонение. Характеристики на еднопосочния дисперсионен анализ.
тест, добавен на 12/07/2013
Вероятност и нейното общо определение. Теореми за събиране и умножение на вероятностите. Дискретни случайни величини и техните числени характеристики. Закон за големите числа. Статистическо разпределение на извадката. Елементи на корелационен и регресионен анализ.
курс от лекции, добавен на 13.06.2015 г
Програма на курса, основни понятия и формули на теорията на вероятностите, тяхната обосновка и значение. Мястото и ролята на математическата статистика в дисциплината. Примери и обяснения за решаване на най-често срещаните задачи по различни теми от тези учебни дисциплини.
ръководство за обучение, добавено на 15.01.2010 г
Теорията на вероятностите и математическата статистика са науки за методите за количествен анализ на масови случайни явления. Наборът от стойности на случайна променлива се нарича извадка, а елементите на набора се наричат примерни стойности на случайна променлива.