Prikazane su osnovne trigonometrijske formule i osnovne supstitucije. Opisane su metode integriranja trigonometrijskih funkcija - integracija racionalnih funkcija, umnožak potencijskih funkcija sin x i cos x, umnožak polinoma, eksponenta i sinusa ili kosinusa, integracija inverznih trigonometrijskih funkcija. Zahvaćene su nestandardne metode.

Sadržaj

Standardne metode integriranja trigonometrijskih funkcija

Opći pristup

Prvo, ako je potrebno, integrand se mora transformirati tako da trigonometrijske funkcije ovise o jednom argumentu, koji bi se podudarao s integracijskom varijablom.

Na primjer, ako integrand ovisi o sin(x+a) i cos(x+b), tada biste trebali izvršiti transformaciju:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + sin(x+a) sin(b-a).
Zatim napravite promjenu z = x+a. Kao rezultat toga, trigonometrijske funkcije ovisit će samo o integracijskoj varijabli z.

Kada trigonometrijske funkcije ovise o jednom argumentu, koji se poklapa s integracijskom varijablom (recimo da je ovo z ), to jest, integrand se sastoji samo od funkcija tipa grijeh z, jer z, tgz, ctgz, tada morate izvršiti zamjenu
.
Takva zamjena dovodi do integracije racionalnih ili iracionalnih funkcija (ako postoje korijeni) i omogućuje izračun integrala ako je integriran u elementarne funkcije.

Međutim, često možete pronaći druge metode koje vam omogućuju izračunavanje integrala na kraći način, na temelju specifičnosti integranda. U nastavku je sažetak glavnih takvih metoda.

Metode integriranja racionalnih funkcija sin x i cos x

Racionalne funkcije iz grijeh x i cos x su funkcije izvedene iz grijeh x, cos x i sve konstante koje koriste operacije zbrajanja, oduzimanja, množenja, dijeljenja i dizanja na cjelobrojnu potenciju. Označavaju se na sljedeći način: R (sinx, cosx). To također može uključivati ​​tangente i kotangense, budući da nastaju dijeljenjem sinusa s kosinusom i obrnuto.
Integrali racionalnih funkcija imaju oblik:
.

Metode za integriranje racionalnih trigonometrijskih funkcija su sljedeće.
1) Supstitucija uvijek vodi do integrala racionalnog razlomka. Međutim, u nekim slučajevima postoje zamjene (vidi dolje) koje rezultiraju kraćim izračunima.
2) Ako je R (sinx, cosx) cos x → - cos x grijeh x.
3) Ako je R (sinx, cosx) pomnoženo s -1 prilikom zamjene sin x → - sin x, tada je supstitucija t = cos x.
4) Ako je R (sinx, cosx) ne mijenja kao kod istodobne zamjene cos x → - cos x, i sin x → - sin x, tada je supstitucija t = tg x ili t= ctg x.

Primjeri:
, , .

Umnožak funkcija potencije cos x i sin x

Integrali oblika

su integrali racionalnih trigonometrijskih funkcija. Stoga se na njih mogu primijeniti metode navedene u prethodnom odjeljku. U nastavku razmatramo metode koje se temelje na specifičnostima takvih integrala.

Ako su m i n racionalni brojevi, tada je jedna od permutacija t = grijeh x ili t= cos x integral se svodi na integral diferencijalnog binoma.

Ako su m i n cijeli brojevi, tada se integracija izvodi pomoću redukcijskih formula:

;
;
;
.

Primjer:
.

Integrali umnoška polinoma i sinusa ili kosinusa

Integrali oblika:
, ,
gdje je P(x) polinom od x integriraju se po dijelovima. To rezultira sljedećim formulama:

;
.

Primjeri:
, .

Integrali iz umnoška polinoma, eksponenta i sinusa ili kosinusa

Integrali oblika:
, ,
gdje je P(x) polinom od x, integriraju se pomoću Eulerove formule
e iax = cos sjekira + isin sjekira(gdje je i 2 = - 1 ).
Za to, metoda opisana u prethodnom paragrafu izračunava integral
.
Odvajanjem realnog i imaginarnog dijela od rezultata dobivaju se izvorni integrali.

Primjer:
.

Nestandardne metode integriranja trigonometrijskih funkcija

Dolje je niz nestandardnih metoda koje vam omogućuju izvođenje ili pojednostavljenje integracije trigonometrijskih funkcija.

Ovisnost o (a sin x + b cos x)

Ako integrand ovisi samo o a sin x + b cos x, korisno je primijeniti formulu:
,
gdje .

Na primjer

Rastavljanje razlomaka iz sinusa i kosinusa na jednostavnije razlomke

Razmotrimo integral
.
Najlakši način integracije je rastavljanje razlomka na jednostavnije, primjenom transformacije:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Integracija razlomaka prvog stupnja

Pri računanju integrala
,
zgodno je odabrati cjelobrojni dio razlomka i derivaciju nazivnika
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)' .
Konstante A i B nalaze se usporedbom lijeve i desne strane.

Reference:
N.M. Gunther, R.O. Kuzmin, Zbirka zadataka iz više matematike, Lan, 2003.

Vidi također:

Bit će tu i zadataka za samostalno rješavanje, na koje možete vidjeti odgovore.

Integrand se može pretvoriti iz umnoška trigonometrijskih funkcija u zbroj

Razmotrimo integrale u kojima je integrand umnožak sinusa i kosinusa prvog stupnja x pomnoženih različitim faktorima, to jest integrale oblika

Koristeći poznate trigonometrijske formule

(2)
(3)
(4)
svaki umnožak u integralima oblika (31) može se transformirati u algebarski zbroj i integrirati formulama

(5)

(6)

Primjer 1 Pronaći

Riješenje. Prema formuli (2) na

Primjer 2 Pronaći integral trigonometrijske funkcije

Riješenje. Prema formuli (3) na

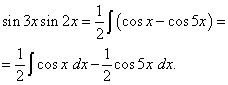
Primjer 3 Pronaći integral trigonometrijske funkcije

Riješenje. Prema formuli (4) na dobivamo sljedeću transformaciju integranda:

Primjenom formule (6) dobivamo

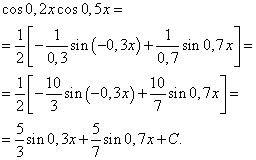
Integral umnoška potencija sinusa i kosinusa istog argumenta

Razmotrimo sada integrale funkcija koje su umnožak potencija sinusa i kosinusa istog argumenta, tj.

(7)

U posebnim slučajevima, jedan od pokazatelja ( m ili n) može biti nula.

Pri integriranju takvih funkcija koristi se da se parna potencija kosinusa može izraziti preko sinusa, a diferencijal sinusa jednak je cos x dx(ili se parna potencija sinusa može izraziti preko kosinusa, a kosinusni diferencijal je - sin x dx ) .

Treba razlikovati dva slučaja: 1) barem jedan od pokazatelja m i n neparan; 2) oba indikatora su parna.

Neka se dogodi prvi slučaj, odnosno eksponent n = 2k+ 1 - neparno. Zatim, s obzirom na to

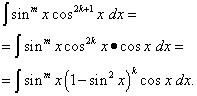
Integrand je prikazan na način da je jedan njegov dio funkcija samo sinusa, a drugi je diferencijal sinusa. Sada s promjenom varijable t= grijeh x rješenje se svodi na integriranje polinoma s obzirom na t. Kad bi samo diploma m je neparan, onda učinite isto, odvajajući faktor sin x, izražavajući ostatak integranda u smislu cos x i pod pretpostavkom t= cos x. Ovaj se pristup također može koristiti kada integracija parcijalnih potencija sinusa i kosinusa , kada barem jedan od pokazatelja je neparan . Cijela poanta je u tome kvocijent potencija sinusa i kosinusa poseban je slučaj njihovog umnoška : kada je trigonometrijska funkcija u nazivniku integranda, njen stupanj je negativan. Ali postoje i slučajevi parcijalnih trigonometrijskih funkcija, kada su njihovi stupnjevi samo parni. O njima - sljedeći paragraf.

Ako oba pokazatelja m i n su parni, a zatim pomoću trigonometrijskih formula

smanjiti eksponente sinusa i kosinusa, nakon čega će se dobiti integral istog tipa kao gore. Stoga integraciju treba nastaviti na isti način. Ako je jedan od parnih pokazatelja negativan, odnosno, razmatra se kvocijent parnih potencija sinusa i kosinusa, tada ova shema nije prikladna . Zatim se koristi promjena varijable, ovisno o tome kako se integrand može transformirati. Takav slučaj ćemo razmotriti u sljedećem odjeljku.

Primjer 4 Pronaći integral trigonometrijske funkcije

Riješenje. Eksponent kosinusa je neparan. Stoga, zamislite

t= grijeh x(zatim dt= cos x dx ). Onda dobivamo

Vraćajući se na staru varijablu, konačno nalazimo

Primjer 5 Pronaći integral trigonometrijske funkcije

.

Riješenje. Eksponent kosinusa, kao u prethodnom primjeru, je čudan, ali više. Zamisliti

i napravite promjenu varijable t= grijeh x(zatim dt= cos x dx ). Onda dobivamo

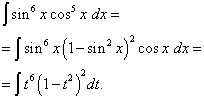
Otvorimo zagrade

i dobiti

Vraćajući se na staru varijablu, dobivamo rješenje

Primjer 6 Pronaći integral trigonometrijske funkcije

Riješenje. Eksponenti sinusa i kosinusa su parni. Stoga transformiramo integrand na sljedeći način:

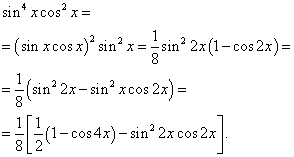
Onda dobivamo

U drugom integralu vršimo promjenu varijable, postavke t= grijeh2 x. Zatim (1/2)dt= cos2 x dx . Posljedično,

Napokon dobivamo

Korištenje metode zamjene varijable

Metoda zamjene varijable pri integraciji trigonometrijskih funkcija, može se koristiti u slučajevima kada je samo sinus ili samo kosinus prisutan u integrandu, umnošku sinusa i kosinusa, u kojem je ili sinus ili kosinus na prvom stupnju, tangens ili kotangens, također kao kvocijent parnih potencija sinusa i kosinusa jednog te istog argumenta. U ovom slučaju, moguće je izvršiti permutacije ne samo grijeh x = t i grijeh x = t, ali i tg x = t i ctg x = t .

Primjer 8 Pronaći integral trigonometrijske funkcije

.

Riješenje. Promijenimo varijablu: , zatim . Dobiveni integrand lako se integrira preko tablice integrala:

.

Primjer 9 Pronaći integral trigonometrijske funkcije

Riješenje. Pretvorimo tangens u omjer sinusa i kosinusa:

Promijenimo varijablu: , zatim . Rezultirajući integrand je stolni integral sa znakom minus:

.

Vraćajući se na izvornu varijablu, konačno dobivamo:

.

Primjer 10 Pronaći integral trigonometrijske funkcije

Riješenje. Promijenimo varijablu: , zatim .

Transformiramo integrand da primijenimo trigonometrijski identitet :

Mijenjamo varijablu, ne zaboravljajući staviti znak minus ispred integrala (vidi gore, što je jednako dt). Zatim rastavljamo integrand na faktore i integriramo prema tablici:

Vraćajući se na izvornu varijablu, konačno dobivamo:

.

Pronađite sami integral trigonometrijske funkcije, a zatim pogledajte rješenje

Univerzalna trigonometrijska supstitucija

Univerzalna trigonometrijska supstitucija može se koristiti u slučajevima kada integrand ne spada u slučajeve razmotrene u prethodnim paragrafima. Uglavnom kada je sinus ili kosinus (ili oboje) u nazivniku razlomka. Dokazano je da se sinus i kosinus mogu zamijeniti drugim izrazom koji sadrži tangens polovice izvornog kuta kako slijedi:

Ali imajte na umu da univerzalna trigonometrijska supstitucija često uključuje prilično složene algebarske transformacije, tako da je najbolje koristiti kada nijedna druga metoda ne radi. Pogledajmo primjere kada se uz univerzalnu trigonometrijsku zamjenu koristi zamjena pod predznakom diferencijala i metoda neodređenih koeficijenata.

Primjer 12. Pronaći integral trigonometrijske funkcije

.

Riješenje. Riješenje. Iskoristimo univerzalna trigonometrijska supstitucija. Zatim
.

Razlomke u brojniku i nazivniku pomnožimo sa , a dvojku izvadimo i stavimo ispred znaka integrala. Zatim

Detaljno se razmatraju primjeri rješenja integrala po dijelovima čiji je integrand umnožak polinoma i eksponenta (e na potenciju x) ili sinusa (sin x) ili kosinusa (cos x).

Sadržaj

Vidi također: Metoda integracije po dijelovima
Tablica neodređenih integrala
Metode izračunavanja neodređenih integrala
Osnovne elementarne funkcije i njihova svojstva

Formula za integraciju po dijelovima

Pri rješavanju primjera u ovom dijelu koristi se formula za integraciju po dijelovima:
;
.

Primjeri integrala koji sadrže umnožak polinoma i sin x, cos x ili e x

Evo primjera takvih integrala:
, , .

Da bi se integrirali takvi integrali, polinom se označava s u, a ostatak s v dx. Zatim se primjenjuje formula integracije po dijelovima.

Ispod je detaljno rješenje ovih primjera.

Primjeri rješavanja integrala

Primjer s eksponentom, e na potenciju x

Definirajte integral:
.

Uvodimo eksponent ispod predznaka diferencijala:
e - x dx = - e - x d(-x) = - d(e - x).

Integriramo po dijelovima.

ovdje
.
Preostali integral također je integrabilan po dijelovima.
.
.
.
Konačno imamo:
.

Primjer definiranja integrala sa sinusom

Izračunaj integral:
.

Uvodimo sinus ispod predznaka diferencijala:

Integriramo po dijelovima.

ovdje je u = x 2 , v = cos(2x+3), du = ( x2 )′ dx

Preostali integral također je integrabilan po dijelovima. Da bismo to učinili, uvodimo kosinus ispod znaka diferencijala.


ovdje u = x, v = grijeh(2x+3), du = dx

Konačno imamo:

Primjer umnoška polinoma i kosinusa

Izračunaj integral:
.

Uvodimo kosinus ispod predznaka diferencijala:

Integriramo po dijelovima.

ovdje je u = x 2+3x+5, v = grijeh2x, du = ( x 2 + 3 x + 5 )′ dx

Integrali trigonometrijskih funkcija.
Primjeri rješenja

U ovoj lekciji ćemo razmatrati integrale trigonometrijskih funkcija, odnosno popuna integrala će biti sinusi, kosinusi, tangensi i kotangensi u raznim kombinacijama. Svi primjeri će biti detaljno analizirani, dostupni i razumljivi čak i za čajnik.

Da biste uspješno proučavali integrale trigonometrijskih funkcija, morate dobro poznavati najjednostavnije integrale, kao i ovladati nekim tehnikama integracije. S ovim materijalima možete se upoznati na predavanjima. Neodređeni integral. Primjeri rješenja i .

A sada nam treba: Tablica integrala, Tablica izvedenica i Priručnik trigonometrijskih formula. Sve priručnike možete pronaći na stranici Matematičke formule i tablice. Preporučam ispisati sve. Posebno se fokusiram na trigonometrijske formule, trebaju vam biti pred očima– bez njega će se učinkovitost rada značajno smanjiti.

Ali prvo o kojim integralima u ovom članku Ne. Ovdje nema integrala oblika , - kosinus, sinus pomnožen nekim polinomom (rjeđe nešto s tangensom ili kotangensom). Takvi se integrali integriraju po dijelovima, a za učenje metode posjetite lekciju Integracija po dijelovima. Primjeri rješenja.Također, nema integrala s "lukovima" - arc tangens, arc sinus itd., također se najčešće integriraju po dijelovima.

Za pronalaženje integrala trigonometrijskih funkcija koriste se brojne metode:

(4) Koristite tabličnu formulu , jedina razlika je u tome što umjesto "x" imamo složen izraz.

Primjer 2

Primjer 3

Nađi neodređeni integral.

Klasik žanra za one koji se dave u poretku. Kao što ste vjerojatno primijetili, u tablici integrala nema integrala tangensa i kotangensa, ali se ipak mogu pronaći takvi integrali.

(1) Koristimo trigonometrijsku formulu

(2) Funkciju dovodimo pod predznak diferencijala.

(3) Koristite tablični integral .

Primjer 4

Nađi neodređeni integral.

Ovo je primjer za samostalno rješavanje, potpuno rješenje i odgovor su na kraju lekcije.

Primjer 5

Nađi neodređeni integral.

Naše će razine postupno rasti =).
Prvo rješenje:

(1) Koristimo formulu

(2) Koristimo osnovni trigonometrijski identitet , iz čega proizlazi da .

(3) Podijelite brojnik s nazivnikom pojam po pojam.

(4) Koristimo svojstvo linearnosti neodređenog integrala.

(5) Integriramo pomoću tablice.

Primjer 6

Nađi neodređeni integral.

Ovo je primjer za samostalno rješavanje, potpuno rješenje i odgovor su na kraju lekcije.

Postoje i integrali tangensa i kotangenata, koji su u višim potencijama. U lekciji se razmatra integral tangente u kocki Kako izračunati površinu figure u ravnini? Integrale tangensa (kotangensa) na četvrtoj i petoj potenciji možete dobiti na stranici Kompleksni integrali.

Smanjenje stupnja integranda

Ova tehnika funkcionira kada su integrandi napunjeni sinusima i kosinusima čak stupnjeva. Za smanjenje stupnja koriste se trigonometrijske formule , i , a posljednja formula se češće koristi u suprotnom smjeru: .

Primjer 7

Nađi neodređeni integral.

Riješenje:

U principu, nema tu ništa novo, osim što smo primijenili formulu (snižavanje stupnja integranda). Imajte na umu da sam skratio rješenje. Kako se stječe iskustvo, integral se može naći i usmeno, što štedi vrijeme i sasvim je prihvatljivo pri izradi zadataka. U ovom slučaju, preporučljivo je ne napisati pravilo , prvo usmeno uzimamo integral od 1, zatim - od .

Primjer 8

Nađi neodređeni integral.

Ovo je primjer za samostalno rješavanje, potpuno rješenje i odgovor su na kraju lekcije.

Obećano povećanje diplome:

Primjer 9

Nađi neodređeni integral.

Prvo rješenje, zatim komentari:

(1) Pripremite integrand za primjenu formule .

(2) Zapravo primjenjujemo formulu.

(3) Kvadriramo nazivnik i izuzimamo konstantu iz predznaka integrala. Moglo bi se učiniti malo drugačije, ali, po mom mišljenju, prikladnije je.

(4) Koristimo formulu

(5) U trećem članu ponovno spuštamo stupanj, ali koristeći formulu .

(6) Dajemo slične termine (ovdje sam podijelio termin po termin i izvršio zbrajanje).

(7) Mi zapravo uzimamo integral, pravilo linearnosti a način dovođenja funkcije pod znak diferencijala izvodi se usmeno.

(8) Češljamo odgovor.

! U neodređenom integralu odgovor se često može napisati na više načina.

U primjeru koji smo upravo razmotrili, konačni odgovor mogao bi se napisati drugačije - otvorite zagrade i čak to učinite prije integriranja izraza, odnosno sljedeći završetak primjera sasvim je prihvatljiv:

Moguće je da je ova opcija čak i praktičnija, samo sam objasnio kako sam i sam odlučio). Evo još jednog tipičnog primjera neovisnog rješenja:

Primjer 10

Nađi neodređeni integral.

Ovaj primjer je riješen na dva načina, a možete dobiti dva potpuno različita odgovora.(točnije, izgledat će potpuno drugačije, ali će s matematičke strane biti ekvivalentni). Najvjerojatnije nećete vidjeti najracionalniji način i patit ćete s otvaranjem zagrada, koristeći druge trigonometrijske formule. Najučinkovitije rješenje daje se na kraju lekcije.

Sumirajući odlomak, zaključujemo da svaki integral oblika , gdje i - čak broj, rješava se snižavanjem stupnja integranda.
U praksi sam se susreo s integralima s 8 i 10 stupnjeva, njihove strašne hemoroide morao sam rješavati snižavanjem stupnja nekoliko puta, što je rezultiralo dugim, dugim odgovorima.

Metoda zamjene varijable

Kao što je navedeno u članku Metoda promjene varijable u neodređenom integralu, glavni preduvjet za korištenje metode zamjene je činjenica da integrand sadrži neku funkciju i njezinu derivaciju:
(funkcije nisu nužno u proizvodu)

Primjer 11

Nađi neodređeni integral.

Gledamo tablicu izvedenica i uočavamo formule, , odnosno u našem integrandu postoji funkcija i njezina derivacija. Međutim, vidimo da se kod diferenciranja kosinus i sinus međusobno pretvaraju jedan u drugi, te se postavlja pitanje kako izvršiti promjenu varijable i što označiti za - sinus ili kosinus?! Pitanje se može riješiti metodom znanstvenog bockanja: ako zamjenu izvršimo pogrešno, onda od toga neće biti ništa dobro.

Opća smjernica: u sličnim slučajevima trebate označiti funkciju koja je u nazivniku.

Prekidamo rješenje i vršimo zamjenu

U nazivniku je kod nas sve u redu, sve ovisi samo o , sad ostaje vidjeti u što će se pretvoriti.
Da bismo to učinili, nalazimo diferencijal:

Ili, ukratko:
Iz dobivene jednakosti, prema pravilu proporcije, izražavamo izraz koji nam je potreban:

Tako:

Sada cijeli integrand ovisi samo o i možemo nastaviti rješenje

Spreman. Podsjećam vas da je svrha zamjene pojednostaviti integrand, u ovom slučaju sve se svodi na integraciju funkcije potencije preko tablice.

Nisam slučajno naslikao ovaj primjer tako detaljno, to je učinjeno kako bih ponovio i konsolidirao materijale lekcije. Metoda promjene varijable u neodređenom integralu.

A sada dva primjera za neovisno rješenje:

Primjer 12

Nađi neodređeni integral.

Primjer 13

Nađi neodređeni integral.

Potpuna rješenja i odgovori na kraju lekcije.

Primjer 14

Nađi neodređeni integral.

I ovdje se u integrandu nalazi sinus s kosinusom (funkcija s izvodom), ali već u umnošku i postavlja se dilema - za što označiti, sinus ili kosinus?

Možete pokušati napraviti zamjenu koristeći znanstvenu metodu bockanja, a ako ništa ne uspije, označite je kao drugu funkciju, ali postoji:

Opća smjernica: jer trebate označiti funkciju koja je, slikovito rečeno, u "neudobnom položaju".

Vidimo da u ovom primjeru studentski kosinus "pati" od stupnja, a sinus slobodno sjedi tako, sam za sebe.

Pa napravimo zamjenu:

Ako netko još uvijek ima poteškoća s algoritmom promjene varijable i pronalaženjem diferencijala, trebao bi se vratiti na lekciju Metoda promjene varijable u neodređenom integralu.

Primjer 15

Nađi neodređeni integral.

Analiziramo integrand, što treba označiti s ?
Pogledajmo naše smjernice:
1) Funkcija je najvjerojatnije u nazivniku;
2) Funkcija je u "neudobnom položaju".

Usput, ove smjernice vrijede ne samo za trigonometrijske funkcije.

Pod oba kriterija (osobito pod drugi) sinus odgovara, pa se zamjena nameće sama od sebe. U principu, zamjena se već može izvršiti, ali prvo bi bilo lijepo shvatiti što učiniti? Prvo, "odkačimo" jedan kosinus:

Rezerviramo za naš "budući" diferencijal

I izražavamo kroz sinus koristeći osnovni trigonometrijski identitet:

Sada je zamjena:

Opće pravilo: Ako je u integrandu jedna od trigonometrijskih funkcija (sinus ili kosinus). neparan stupnja, tada trebate od neparnog stupnja “odgristi” jednu funkciju, a iza nje označiti drugu funkciju. Govorimo samo o integralima, gdje postoje kosinusi i sinusi.

U razmatranom primjeru imali smo kosinus u neparnom stupnju, pa smo jedan kosinus odvojili od stupnja i označili sinus.

Primjer 16

Nađi neodređeni integral.

Razine rastu =).
Ovo je primjer "uradi sam". Potpuno rješenje i odgovor na kraju lekcije.

Univerzalna trigonometrijska supstitucija

Univerzalna trigonometrijska supstitucija je čest slučaj promjene metode varijable. Možete ga pokušati primijeniti kada "ne znate što učiniti". Ali zapravo postoje neke smjernice za njegovu primjenu. Tipični integrali kod kojih treba primijeniti univerzalnu trigonometrijsku zamjenu su sljedeći integrali: , , , itd.

Primjer 17

Nađi neodređeni integral.

Univerzalna trigonometrijska supstitucija u ovom slučaju provodi se na sljedeći način. Zamijenimo: . Ne koristim slovo, nego slovo, nije to nekakvo pravilo, samo opet, tako sam navikao odlučivati.

Ovdje je prikladnije pronaći diferencijal, jer to, iz jednakosti, izražavam:
Visim na oba dijela arc tangente:

Arktangens i tangens se poništavaju:

Na ovaj način:

U praksi ne možete slikati tako detaljno, već jednostavno koristiti gotov rezultat:

! Izraz vrijedi samo ako ispod sinusa i kosinusa imamo samo “xes”, za integral (o čemu ćemo kasnije) sve će biti malo drugačije!

Prilikom zamjene sinusa i kosinusa pretvaramo se u sljedeće razlomke:
, , te se jednakosti temelje na dobro poznatim trigonometrijskim formulama: ,

Dakle, čišćenje bi moglo izgledati ovako:

Provedimo univerzalnu trigonometrijsku zamjenu:

Za integraciju racionalnih funkcija oblika R(sin x, cos x) koristi se supstitucija, koja se naziva univerzalna trigonometrijska supstitucija. Zatim . Univerzalna trigonometrijska supstitucija često rezultira velikim izračunima. Stoga, kad god je moguće, koristite sljedeće zamjene.

Integracija funkcija racionalno ovisnih o trigonometrijskim funkcijama

1. Integrali oblika ∫ sin n xdx , ∫ cos n xdx , n>0
a) Ako je n neparan, tada jednu potenciju sinx (ili cosx) treba staviti pod predznak diferencijala, a od preostale parne potence prijeći na suprotnu funkciju.
b) Ako je n paran, koristimo se redukcijskim formulama
2. Integrali oblika ∫ tg n xdx , ∫ ctg n xdx , gdje je n cijeli broj.
Moraju se koristiti formule

3. Integrali oblika ∫ sin n x cos m x dx
a) Neka su m i n različite parnosti. Primjenjujemo zamjenu t=sin x ako je n neparan ili t=cos x ako je m neparan.
b) Ako su m i n parni, koristimo formule za redukciju
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Integrali oblika
Ako brojevi m i n imaju isti paritet, tada koristimo zamjenu t=tg x . Često je zgodno primijeniti tehniku ​​trigonometrijske jedinice.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

Upotrijebimo formule za pretvaranje umnoška trigonometrijskih funkcija u njihov zbroj:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Primjeri
1. Izračunajte integral ∫ cos 4 x sin 3 xdx .
Napravimo zamjenu cos(x)=t . Tada je ∫ cos 4 x sin 3 xdx =
2. Izračunajte integral.
Zamjenom sin x=t dobivamo

3. Nađi integral.
Vršimo zamjenu tg(x)=t . Zamjenom, dobivamo

Integracija izraza oblika R(sinx, cosx)

Primjer #1. Izračunaj integrale:

Riješenje.
a) Integracija izraza oblika R(sinx, cosx) , gdje je R racionalna funkcija od sin x i cos x , pretvara se u integrale racionalnih funkcija korištenjem univerzalne trigonometrijske supstitucije tg(x/2) = t .
Onda imamo

Univerzalna trigonometrijska zamjena omogućuje prijelaz s integrala oblika ∫ R(sinx, cosx) dx na integral racionalno-frakcijske funkcije, ali takva zamjena često dovodi do glomaznih izraza. Pod određenim uvjetima, jednostavnije zamjene pokazuju se učinkovitima:

• Ako je jednakost R(-sin x, cos x) = -R(sin x, cos x)dx točna, tada se primjenjuje zamjena cos x = t.
• Ako je R(sin x, -cos x) = -R(sin x, cos x)dx istinito, tada je supstitucija sin x = t .
• Ako je R(-sin x, -cos x) = R(sin x, cos x)dx istinito, tada je zamjena tgx = t ili ctg x = t.

U ovom slučaju, za pronalaženje integrala
primjenjujemo univerzalnu trigonometrijsku zamjenu tg(x/2) = t .
Onda odgovori: