У вигляді програми ми можемо тепер зайнятися вирішенням однієї вже раніше порушеної популярної математичної проблеми, - а саме, завдання про розподіл будь-якого кута на рівних частин, зокрема для - задачі про трисекцію кута. Завдання полягає в тому, щоб знайти точну побудову за допомогою циркуля та лінійки, яке давало б розподіл будь-якого кута на три рівні частини. Для цілого ряду спеціальних значень кута легко можна знайти такі побудови. Я хочу познайомити вас з перебігом думок у доказі неможливості трисекції кута у зазначеному сенсі; при цьому я прошу вас згадати доказ неможливості побудови правильного семикутника за допомогою циркуля та лінійки. Як і в тому доказі, ми зведемо завдання до неприводимого кубічного рівняння і потім покажемо, що його неможливо вирішити за допомогою лише вилучення квадратного кореня. Але тепер у рівняння входитиме параметр - кут - тоді як раніше коефіцієнти були цілими числами; відповідно до цього тепер замість числової має бути функціональна неприводимость.

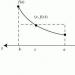
Щоб отримати рівняння, що дає запис нашої проблеми, уявімо, що на позитивній півосі дійсних чиселпобудований кут (рис. 41); тоді його друга сторона перетне коло радіуса 1 у точці

Наше завдання зводиться до того, щоб знайти таку незалежну від величини кута побудову, що складається з кінцевої кількості операцій з циркулем і лінійкою, яке щоразу давало б точку перетину цього кола зі стороною кута, тобто точку.

Це значення z відповідає рівнянню

і аналітичний еквівалент нашої геометричної задачі полягає в тому, щоб вирішити це рівняння за допомогою кінцевої кількості витягів квадратних коренів з раціональних функцій від бо це суть координати точки w, з яких ми повинні виходити при нашому побудові.

Насамперед треба переконатися, що рівняння (3) неприводимо з погляду теорії функцій. Щоправда, це рівняння не цілком підходить під той тип рівнянь, який ми мали на увазі в попередніх загальних міркуваннях: замість раціонально вхідного комплексного параметра w тут раціонально входять дві функції - косинус і синус - дійсного параметра. Розпадається на багаточлени щодо , коефіцієнти яких теж є раціональними функціями від дати критерій розуміється в цьому сенсі приводності, цілком подібний до колишнього. А саме, якщо в рівності (3) пробігає всі дійсні значення, то пробігає в той же час коло радіуса 1 у площині w, якій через стереографічну проекцію відповідає екватор на сфері w. Лінія, що лежить над цим колом на ріманової поверхні рівняння і одночасно пробігає всі три листи, за допомогою (3) взаємно однозначно відображається на коло радіусу 1 сфери і тому може бути певною мірою названа його «одномірним римановим зображенням». Ясно, що подібним чином можна для будь-якого рівняння виду побудувати таке риманове зображення; для цього потрібно взяти стільки екземплярів кіл з радіусом 1 і з довжиною дуги скільки коренів має рівняння, і скріпити їх відповідно до зв'язності коренів.

Далі укладаємо абсолютно подібно до колишнього, що рівняння тільки тоді могло б бути наведеним, якби його одномірне риманове зображення розпадалося на окремі частини, але в даному випадку це не має місця, і тому непривідність нашого рівняння (3) доведена.

Колишній доказ того, що будь-яке кубічне рівняння з раціональними чисельними коефіцієнтами, дозволене за допомогою ряду витягів квадратного кореня, є наведеним, може бути перенесено на справжній випадок неприведеного в функціональному сенсі рівняння (3); варто тільки замість слів «раціональні числа» говорити щоразу «раціональні функції». , Що займаються трисекцією кута, приречені на вічну безплідність!

Тепер перейдемо до розгляду дещо складнішого прикладу.

Завдання на побудову циркулем та лінійкою і сьогодні вважаються математично дуже цікавими. Вже понад сто років це традиційний матеріал шкільного курсугеометрії. Однією з найцінніших сторін таких завдань є те, що вони розвивають пошукові навички вирішення практичних проблем, залучають до самостійних досліджень, сприяють виробленню конкретних геометричних уявлень. Завдання на побудову викликають інтерес, сприяють активізації розумової та пізнавальної діяльності. При вирішенні їх активно використовуються знання про властивості фігур, удосконалюються навички геометричних побудов. В результаті розвиваються конструктивні здібності, що є однією із цілей вивчення геометрії.

Коло завдань, що розглядаються в геометрії, дуже широке. Серед них особливе місце займають завдання на побудову, які сприяють розвитку визначеності, послідовності та обґрунтованості мислення. На цих завданнях можна навчитися таким методам пізнання, як аналіз та синтез.

Тема урока:Поділ кута циркулем та лінійкою.

Клас: 7 (поглиблене вивчення)

Тип уроку:урок вивчення нового матеріалу. Методи та прийоми ведення уроку:

• фронтальна робота із класом;
• закріплення: робота учнів у парах за картками.

Цілі уроку:

Навчальна: забезпечити засвоєння нового матеріалу, перевірка знання учнями фактичного матеріалу на тему «Завдання на побудову циркулем та лінійкою»; умінь учнів самостійно застосовувати знання у змінених нестандартних умовах.

Розвиваюча: Розвивати мислення учнів під час вирішення завдань, які виходять за рамки шкільного курсу; розвивати вміння аналізувати, порівнювати, робити висновки; розвивати пам'ять учнів.

Виховна: виховання в учнів інтересу до предмета, доброзичливості, вміння працювати у колективі й у парах.

Обладнання:

• інтерактивна дошка чи проектор;
• робоча картка для кожного учня (Додаток);
• Поділ кута циркулем і лінійкою.

Завдання уроку:

1. повторити основні побудови циркулем та лінійкою;
2. розглянути можливість поділу кута на рівних кутів;
3. відпрацювати навичку побудови бісектриси кута, рівностороннього трикутника.

Хід уроку

I. Організаційний момент

ІІ. Постановка мети та завдань уроку.

Хлопці повинні

знати: стандартні побудови циркулем та лінійкою,

вміти: 1) будувати бісектрису кута, рівносторонній трикутник; 2) застосовувати стандартні побудови при вирішенні задач на розподіл кута циркулем та лінійкою.

ІІІ. Актуалізація опорних знань

На екрані з'являються слайди, у яких послідовність кроків. Учням необхідно визначити яке завдання побудова описує дана послідовність кроків.

Завдання 1:

1. АВ – пряма.
2. Проведемо окр. (А; АВ) С - точка перетину кола і прямий АВ.
3. Проведемо окр. (С; R) і окр. (В; R) Р - точка перетину кіл.
4. Проведемо СР.

Відповідь: побудова прямого кута

Завдання 2:

1. АВ – відрізок.
2. Проведемо окр. (А; R) і окр. (В; R) Р, Н - точки перетину кіл.
3. Проведемо РН, отримаємо точку на АВ.

Відповідь: побудова серединного перпендикуляра РН до АВ

Завдання 3:

1. Проведемо окр. (А; R) Р, Н - точки перетину кола і сторін кута.
2. Проведемо окр. (Р; РН) і окр. (Н; РН) К - точка перетину кіл.
3. Проведемо АК.

Відповідь: побудова бісектриси кута

Завдання 4:

1. АВ – відрізок.
2. Проведемо окр. (А; АВ) і окр. (В; АВ) С - точка перетину кіл.
3. Проведемо АС та ПС

Відповідь: побудова рівностороннього трикутника

IV. Вивчення нового матеріалу

Вчитель: Сьогодні нам необхідно визначити, чи завжди можна здійснити «Ділення даного кута на рівних кутів».

Вчитель: Як ви вважаєте, яка стандартна побудова дозволить нам виконати розподіл кута на 2, 4, 8, 16, … рівних кута?

Відповідь: Побудова бісектриси кута дозволяє розділити будь-який кут на 2, 4, 8, … 2n рівних кутів. У кожному випадку завдання зводиться до побудови бісектрис отриманих кутів, що здійснено завжди циркулем та лінійкою. Наприклад, розділити кут АВС на 4 рівні кути. Будуємо бісектрису ВК кута АВС, отримуємо кут АВК = куту СВК = кут АВС:2. Будуємо бісектриси ВР та ВМ кутів АВК та CDR відповідно. Отримуємо: кути АВР = РВК = МВК = СВМ = АВК: 2 = АВС: 4.

Вчитель: Чи можна розділити довільний кут на 3 рівні кути?

Історична довідка.Можна дати завдання учням підготувати невелику доповідь на тему трисекції кута. Трисекція кута. Мистецтво побудови геометричних фігур за допомогою циркуля та лінійки було в високого ступенярозвинене в Стародавню Грецію. Знаменитою була в давнину задача про трисекцію кута (про поділ кута на три рівні частини за допомогою циркуля та лінійки). Будь-який кут неможливо розділити на три рівні частини за допомогою тільки циркуля та лінійки. Спроби розв'язання задачі за допомогою інструментів та засобів були здійснені ще у V ст. до н.е. Французький математик П. Ванцель у 1837р. першим суворо довів, що неможливо здійснити трисекцію циркулем та лінійкою.

Завдання про трисекції кута стає вирішальним і загальному випадку, якщо не обмежуватися в геометричних побудовах одними тільки класичними інструментами, циркулем та лінійкою. Так, наприклад, Гіппій Елідський, знаменитий софіст, який жив близько 420 р. е., користувався для трисекції кута квадратрисою. Олександрійський математик Нікомед (II ст. до н.е.) вирішив завдання про трисекцію кута за допомогою однієї кривої, названої конхоїдою Нікомеда, і дав опис приладу для креслення цієї кривої. Цікаве вирішення завдання про трисекцію кута дав Архімед у своїй книзі «Лемми».

Завдання про трисекції кута виявляється розв'язним і за деяких інших приватних значеннях кута: 90, 45, 135 (у градусах). Розподіл прямого кута на три рівні частини вміли виробляти ще піфагорійці, ґрунтуючись на тому, що в рівносторонньому трикутнику кожен кут дорівнює 60 градусів.

Вчитель: На інтерактивній дошці наведено розв'язання задачі.

1. Розгляньте розв'язання цієї задачі.
2. Визначте основні побудови.
3. Доведіть, що ці кроки призведуть до необхідного результату.

Завдання 1:Трисекція прямого кута.

Нехай потрібно розділити на три рівні частини прямий кут MAN. Відкладаємо на промені АN довільний відрізок АК, у якому будуємо рівносторонній трикутник AКB. Оскільки кут КAB дорівнює 60 градусів, то кут МАВ = 30 градусів. Побудуємо бісектрису кута КАВ, отримуємо шукане розподіл прямого кута MAN на три рівні кути.

Відповіді:

2. Побудова рівностороннього трикутника, побудова бісектриси кута.

3. Доказ: кут MAN = 90 градусів. Трикутник AКB – рівносторонній, кут КAB = 60 градусів. Отже, кут МАВ = кут MAN - кут КAB = 30 градусів. АР - бісектриса кута КАВ, значить кут КАР = куті РАВ = 30 градусів. Отримуємо, що кут КАР = кут РАВ = кут МАВ = 30 градусів, тобто. шукане розподіл прямого кута MAN на три рівні кути.

Вчитель: В робочого зошитавиконайте побудову трисекції прямого кута, описав всі етапи «Побудови». Обов'язково написати "Доказ".

Вчитель: Які кути завжди можна побудувати за допомогою циркуля та лінійки?

Відповідь: кути: 60 градусів - кут в рівносторонньому трикутнику, 30 градусів - бісектриса кута в рівносторонньому трикутнику, 45 градусів - бісектриса прямого кута, 15 градусів - бісектриса кута 30 градусів, 90 градусів - перпендикуляр до прямої, 180

Вчитель: Чи можна розділити довільний кут на 5, 7, 11, рівних кутів?

Вчитель: Це завдання виявляється розв'язаною за деяких приватних значеннях кута. Наприклад: циркулем і лінійкою можна виконати таку побудову (за умови, що задані кути вже побудовані та їхня величина відома):

Завдання 2:Розділити кут 66 градусів на 11 рівних частин (за умови, що цей кут побудований та його величина відома).

Рішення:Т.к. 66 градусів: 11 = 6 градусів, то для вирішення цього завдання знову скористаємося кутом 60 градусів – рівностороннім трикутником. При побудові рівностороннього трикутника отримуємо 66 градусів-60 градусів = 6 градусів, будуємо двічі по куту 6 градусів (60-6-6 = 48 градусів), потім ділимо кут 48 градусів на 8 рівних кутів (тобто проводимо бісектриси). При цьому отримуємо 11 кутів по 6 градусів.

При розгляді цього завдання вчитель ставить наводящие питання і підводить хлопців до розв'язання завдання. Розв'язання задачі записується в робочий зошит.

V. ФізкультхвилинкаВчитель проводить із учнями вправи для розслаблення очей.

V. Закріплення вивченого матеріалу – самостійна роботау парах

Вчитель: Кожен учень отримує картку із завданнями (Додаток). Учні, які сидять за однією партою, мають однаковий варіант завдань. Роботу учні виконують у парі, але кожен оформляє рішення на картці.

Оцінка за роботу на картці (вчитель озвучує перед початком роботи):

«5» - за 3 правильно виконані та оформлені завдання.

«4» - за 2 правильно виконані та оформлені завдання або за 3 завдання з недоліками в оформленні.

«3» - за 1 правильно виконану та оформлену задачу або за 2 завдання з недоліками в оформленні.

Розв'язання задач самостійної роботи:

Завдання 1:Трисекція кута 45 градусів.

Рішенняцієї задачі зводиться до побудови рівностороннього трикутника. Нехай потрібно розділити на три рівні частини кут MAN = 45 градусів. Відкладаємо на промені АN довільний відрізок АК, на якому будуємо рівносторонній трикутник AКB в одній півплощині з точкою М щодо прямої АК. Будуємо бісектрису АР кута КАВ, потім бісектрису АС кута РАК і отримуємо шукане розподіл кута MAN на три рівні кути кути МАР=РАС=САК=15 градусів.

Доведення:Т.к. трикутник АКВ - рівносторонній, то кут КАВ = 60 градусів. АР - бісектриса кута КАВ, значить кути ВАР = РАК = 30 градусів і кут МАР = кут МАК - кут РАК = 45 градусів - 30 градусів = 15 градусів. АС - бісектриса кута РАК, значить кути РАС = САК = 15 градусів. Значить, кути МАР = РАС = САК = 15 градусів.

Завдання 2 (1 варіант):Розділити кут 50 градусів на 10 рівних кутів.

Рішення:Т.к. 50: 5 = 10, то для вирішення цього завдання скористаємося кутом 60 градусів - рівностороннім трикутником. Отримуємо 1) 60-50 = 10, 2) 50-10 = 40, 3) 40: 4 = 10 (у градусах).

Завдання 2 (2 варіант):Розділити кут 720 на 6 рівних кутів.

Рішення:Т.к. 72: 6 = 12, то для вирішення цього завдання скористаємося кутом 60 - рівностороннім трикутником. Отримуємо 1) 72-60 = 12, 2) 60-12 = 48, 3) 48: 4 = 12 (у градусах).

Завдання 3:Розділити кут на 4 рівні кути.

Рішення:Розділити кут АВС на 4 рівні кути. Будуємо бісектрису ВК кута АВС, отримуємо кути АВК = СВК = кут АВС:2. Будуємо бісектриси ВР та ВМ кутів АВК та CDR відповідно. Отримуємо: кути АВР = РВК = МВК = СВМ = кут АВК: 2 = кут АВС: 4.

VI. Домашня робота

Будинки. Розв'язати задачі:

1.Трисекція кута в 135 градусів.

2.Побудувати кут 53 градуси, якщо побудований кут 104 градуси.

VII. Підсумок уроку

Відповісти на питання:

1.Завжди здійсненна трисекція кута?

Лише у окремих випадках: 450, 900.

2.Що нового дізналися на уроці?

Завжди можна побудувати циркулем та лінійкою:

1) кута в n разів більше від даного кута.

2) розділити будь-який кут на 2, 4, 8, … 2n рівних кутів.

3) кути: 60, 30, 45, 15, 90, 180 (у градусах).

4) можна розділити деякі задані кути на цю кількість рівних кутів або побудувати кут необхідної величини.

3. Чи можна розділити довільний кут на 5, 7, 11, … рівних кутів?

Ні. Тільки у деяких окремих випадках.

Домашня робота:

Завдання 1:Трисекція кута 135 градусів.

Нехай потрібно розділити на три рівні частини кут MAN = 135 градусів. Т.к. 135:3 = 45, то з точки А будуємо перпендикуляр АК до прямої АМ. Потім будуємо бісектрису АР кута КАМ. При цьому отримуємо поділ кута MAN на три рівні кути кути КАN=КАР=РАМ=45 градусів.

Доведення:Т.к. АК - перпендикуляр до прямої АМ, то кут КАМ = 90 градусів, кут NАК = 135 градусів - 90 градусів = 45 градусів. АР - бісектриса кута КАМ, значить кут ВАР = куті РАК = 45 градусів. Значить, кути МАР = РАС = САК = 45 градусів.

Завдання 2:Побудувати кут 53 градуси, якщо збудований кут 104 градуси.

При вирішенні використовуємо побудови прямого кута, бісектриси кута та кута 60 градусів.

Побудова: 1) 104 градуси-90 градусів = 14 градусів, 2) 14 градусів: 2 = 7 градусів, 3) будуємо 60 градусів і 60 градусів -7 градусів = 53 градуси.

Додаток:

Список літератури:

1. Атанасян Л.С. Геометрія 7-9. М.: Просвітництво, 2005. – 335 с.
2. Далінгер В.А. Планиметричні завдання на побудову. Омськ: Вид-во ОГПИ, 1999. – 78 с.
3. Ільїна Н.І. Геометричні побудовина площині. М.: Школа – прес, 1997. – 172 с.
4. Манін І.Ю. Про розв'язання задач на побудову за допомогою циркуля та лінійки // Енциклопедія елементарної математики. М.: Фізматгіз, 1963. Т. 4: Геометрія. З. 205-227.
5. Погорєлов А.В. Геометрія, 7-11. М: Просвітництво, 1992
6. Прасолов В.В. Три класичні завдання на шикування. М: Наука, 1992. 80 с.
7. Енциклопедія для дітей. Т. 11. Математика/Ред. колегія: М. Аксенова, В. Володін та ін - М.: Аванта +, 2005.

Виникнення задачі про трисекцію кута (тобто розподілу кута на три рівні частини) обумовлюється необхідністю розв'язання задачі про побудову правильних багатокутників. Побудова правильного п'ятикутника циркулем і лінійкою мала справити на піфагорійців велике враження, бо правильна п'ятикутна зірка була їхньою розпізнавальним знаком (вона символізувала здоров'я). Відома така легенда.

Один піфагорієць помирав на чужині і не міг заплатити людині, яка його доглядала. Перед смертю він наказав йому зобразити на своєму житлі п'ятикутну зірку: якщо колись мимо йтиме піфагорієць, він обов'язково запитає про неї. І справді, через кілька років якийсь піфагорієць побачив цей знак і винагородив господаря будинку.

Походження завдання про трисекції кута також пов'язане з практичною діяльністю, зокрема, вміти ділити коло на рівні частини потрібно було при виготовленні колеса зі спицями, розподіл кута або дуги кола на кілька рівних частин необхідно було і в архітектурі, у створенні орнаментів, у будівельній техніці та в астрономії.

За допомогою циркуля та лінійки для n=6 та 8 правильні n-кутники побудувати можна, а для n=7 та 9 не можна. Побудова правильного семикутника – цікаве завдання: його можна вирішити за допомогою способу «вставок». Побудову правильного семикутника запропонував Архімед. А ось спроби побудувати правильний дев'ятикутник якраз і повинні були привести до завдання трисекції кута, тому що для побудови правильного дев'ятикутника потрібно було побудувати кут 360 ° / 9 = 120 / 3, тобто розділити кут 120 ° на три рівні частини.

Чому греки віддавали перевагу циркулю та лінійці іншим інструментам?

Відповісти на це питання однозначно і достатньо переконливо вчені не можуть. Чи циркуль і лінійка є найпростішими інструментами? Може бути і так. Однак можна вказати безліч інших інструментів, настільки ж простих, як циркуль і лінійка, або майже простих. З допомогою деяких їх вирішуються і сформульовані завдання.

У відповідній літературі можна знайти спроби пояснення такої незвичайної симпатії греків саме до циркулю та лінійки. Будь-яка геометрична фігураскладається з двох видів ліній – прямий чи кривий. А будь-яка крива складається з частин кіл різного діаметра. При цьому пряме і коло - єдині лінії постійної кривизни на площині.

Розподіл прямого кута на три рівні частини.

У окремих випадках легко вдається виконати розподіл кута. Так, розподіл прямого кута на три рівні частини вміли виробляти ще піфагорійці, виходячи з того, що в рівносторонньому трикутнику кожен кут дорівнює 60º.

Нехай потрібно розділити на три рівні частини прямої (MAN).

Відкладаємо на промені AN довільний відрізок АС, на якому будуємо рівносторонній трикутник АСВ. Так як (САВ дорівнює 60 º, то (ВАМ дорівнює 30 º. Побудуємо бісектрису АD кута САВ, отримуємо шукане розподіл прямого) (МАN на три рівні кути: (NAD, (DAB, (ВАМ)).

Завдання про трисекції кута виявляється розв'язним і за деяких інших приватних значеннях кута (наприклад, для кутів 90о / 2n, де n – натуральне число). Те, що будь-який кут неможливо розділити на три рівні частини за допомогою лише циркуля та лінійки, було доведено лише в першій половині XIX століття.

Рішення способом «вставок»

Деякі способи трисекції кута, які розглядають греки, використовували так званий метод вставки. Він полягав у тому, щоб знайти положення прямої, що проходить через цю точку O, де дві задані прямі (або пряма і окружність) висікали б відрізок даної довжини a. Таку побудову можна здійснити за допомогою циркуля та лінійки з двома поділами, відстань між якими дорівнює a.

За допомогою вставок розділити кут на три рівні частини дуже легко. Візьмемо на стороні кута з вершиною довільну точку А і опустимо з неї перпендикуляр АС на інший бік.

Проведемо через точку А промінь, спрямований з променем ВС. Вставимо тепер між променями АС і l відрізок DE довжиною 2АВ так, щоб його продовження проходило через точку В. Тоді (ЕВС = (ABC/3. Нехай G - середина відрізка DE. Точка А лежить на колі з діаметром DE, тому AG = GE = DE/2 = AB. Трикутники BAG і AGE рівнобедрені, тому (ABG = (AGB = 2 (AEG = 2 (EBC)).

Папп Олександрійський показав, що завдання "вставлення" відрізка між даними перпендикулярними прямими l1 і l2 зводиться до побудови точки перетину кола та гіперболи. Розглянемо прямокутник ABCD, продовження сторін ВС та CD якого є даними прямими, а вершина А є даною точкою, через яку потрібно провести пряму, що перетинає прямі l1 та l2 у таких точках Е та F, що відрізок EF має дану довжину.

Добудуємо трикутник DEF до паралелограма DEFG. Для побудови шуканої прямої достатньо побудувати точку G, а потім через точку А провести пряму, паралельну до прямої DG. Точка G віддалена від точки D на дану відстань DG = EF, тому точка G лежить на колі, яке можна побудувати.

З іншого боку, з подоби трикутників ABF та EDA отримуємо АВ: ED = BF: AD, тобто ED*BF=AB*AD. Отже, FG*BF=AB*AD = SABCD, тобто точка G лежить на гіперболі (якщо направити осі Ох та Оу з променів BF та ВА, то ця гіпербола задається рівнянням xy = SABCD)

Рішення за допомогою квадратири

До «граматичних» завдань відноситься завдання про розподіл кута в будь-якому відношенні. Першу криву для вирішення такої задачі винайшов Гіппій Елідський. В подальшому (починаючи з Динострату) цю криву також використовували і для вирішення квадратури кола. Лейбніц назвав цю криву квадратирою.

Вона виходить в такий спосіб. Нехай у квадраті ABCD кінці відрізка B′C′ рівномірно рухаються по сторонах, відповідно, BA і CD, a відрізок AN рівномірно обертається навколо точки A. Відрізок B′C′ у початковий момент збігається з відрізком BC, a ; обидва відрізки одночасно досягають свого кінцевого положення AD. Квадратрісою називається крива, яку при цьому описує точка перетину відрізків B′C′ та AN.

Для того щоб розділити гострий кут φ в деякому відношенні, треба на наведеному вище кресленні відкласти кут DAL = φ, де L лежить на квадратрисі. Опустимо перпендикуляр LH на відрізок AD. Поділимо цей перпендикуляр у потрібному відношенніточкою P. Проведемо через P відрізок, паралельний AD, до перетину з квадратрисою в точці Q; промінь AQ ділить кут LAD у необхідному відношенні, оскільки, за визначенням квадратриси, (LAQ: (QAD = (LP: (LH)).

Практична робота з побудови трисектрис кута

Способом "вставок"

За допомогою квадратирів

Рішення за допомогою теореми Морлея

Оскільки будь-який кут не можна розділити втричі рівні, ми можемо вирішити завдання про трисекції кута у зворотному порядку, використовуючи теорему Морлея.

Теорема. Нехай найближчі до сторони ВС трисектриси кутів B і перетинаються в точці A1; точки В1 та С1 визначаються аналогічно. Тоді трикутник А1В1С1 є рівностороннім, а відрізок С1С є перпендикуляром до основи правильного трикутника.

Розв'яжемо наступне завдання: побудуємо трикутник, з усіх кутів якого проведено трисектриси.

План побудови.

1) Побудуємо два довільні кути (BAC1 і (АВС1), одна сторона яких є спільною.

Побудовані кути повинні задовольняти нерівності:

2) Нехай промінь АС1 – вісь симетрії. Відобразимо (ВАС1 щодо осі АС1. Аналогічно, відобразимо щодо осі ВС1 (АВС1).

3) Нехай промінь АС2 – вісь симетрії. Відобразимо (C1АC2 щодо осі АС2. Аналогічно, відобразимо щодо осі ВС2 (C1ВC2).

4) З'єднаємо точки перетину трисектрис С1 та С2 відрізком С1С2.

5) У теоремі Морлі сказано, що при перетині трисектрис трикутника виходить правильний трикутник, а відрізок С1С2 є перпендикуляром до основи правильного трикутника і проходить через вершину цього трикутника. Для того, щоб побудувати правильний трикутник, знаючи його висоту, необхідно: а) побудувати промені, що виходять із точки С1 під кутом 30º щодо відрізка С1С2; б) відзначити точки перетину побудованих променів із трисектрисами літерами В1 та А1; в) поєднати точки А1, В1, С1. Отримаємо рівносторонній трикутник А1В1С1.

6) Проведемо промені з точки С, що проходять через вершини правильного трикутника В1 та А1.

Залишимо на малюнку відрізки трисектрис трикутника.

Ми побудували трикутник АВС, з усіх кутів якого проведено трисектриси.

Нерозв'язність трисекції кута за допомогою циркуля та лінійки

Для доказу неможливості розділити будь-який кут на три рівні частини за допомогою циркуля та лінійки достатньо довести, що не можна розділити певний конкретний кут. Ми доведемо, що за допомогою циркуля та лінійки не можна зробити трисекцію кута 30°. Введемо систему координат Оху, обравши як початок координат вершину даного кута АОВ і направивши вісь Ох за ОА. Можна вважати, що точки А і віддалені від точки Про на відстань 1. Тоді в задачі трисекції кута потрібно по точці з координатами (cos Зφ, sin Зφ) побудувати точку (cosφ, sinφ). У разі коли φ=10°, вихідна точка має координати. Обидві її координати виражаються у квадратних радикалах. Тому достатньо довести, що число sin 10 ° не виявляється у квадратних радикалах.

Оскільки sin3φ = sin(φ + 2φ) =

sin(α + β) = sinα cosβ + cosα sinβ

Sinφ cos2φ + cosφ sin2φ =

cos2α = cos2α - sin2α

sin2α = 2sinα cosα

Sinφ(cos2φ - sin2φ) + cosφ(2sinφ cosφ) =

sin2α + cos2α = 1 cos2α = 1 - sin2α

Sinφ(1 - sin2φ - sin2φ) + 2sinφ cos2φ =

Sinφ(1 - 2sin2φ) + 2sinφ(1 - sin2φ) =

Sinφ(1 - 2sin2φ + 2 - 2sin2φ) =

Sinφ(3 - 4sin2φ) =

3sinφ - 4sin3φ sin3φ = 3sinφ - 4sin3φ, то число х = sin 10° задовольняє кубічне рівняння

3x - 4x3 = ½ (φ =10°, 3φ =30°, sin3φ = ½)

8x3 – 6x + 1 = 0

(2x)3 -3*2x + 1 = 0

Досить довести, що це рівняння немає раціонального коріння. Припустимо, що 2x=p/q, де р і q - цілі числа, які мають спільних дільників. Тоді p3 - 3pq2 + q3 = 0, тобто q3 = p (3q2-p2). Отже, число q поділяється на р, отже р=±1. Тому ±13q2 + q3 = 0, тобто q2(q±3) = ±1. Число 1 ділиться на q тому q=±1. Через війну отримуємо, що x=±1/2. Легко перевірити, що значення ±1/2 є корінням рівняння. Отримано протиріччя, тому рівняння немає раціонального коріння, отже, число sin10° виявляється у квадратних радикалах.

Застосування

Трисекція кута потрібна при побудові правильних багатокутників. Ми розглянемо процес побудови з прикладу правильного дев'ятикутника, вписаного в окружність.

Будуємо прямокутний трикутникАВС. Будуємо трисектриси ВС1 та ВС2. Вийшли кути по 30 º. Ділимо один з кутів, що утворилися, на два по 15º бісектрисою. До прямому куту«додаємо» по 15 º з кожного боку. Знов будуємо трисектриси кута DBE, що вийшов. Повторюємо так ще двічі, повертаючи трикутник у точці так, щоб DB збіглася з попереднім положенням ВЕ. З'єднуємо отримані точки.

Нам вдалося побудувати правильний дев'ятикутник, використовуючи побудову трисектрису.

Трисектор

Завдання про трисекції кута в загальному випадку не можна розв'язати за допомогою циркуля і лінійки, але це зовсім не означає, що це завдання не можна вирішити іншими допоміжними засобами.

Досягнення зазначеної мети придумано багато механічних приладів, які називаються трисекторами. Найпростіший трисектор легко виготовити із щільного паперу, картону або тонкої жерсті. Він послужить підсобним креслярським інструментом.

Трисектор та схема його застосування.

Смужка АВ, що примикає до півкола, дорівнює по довжині радіусу півкола. Край смужки ВD становить прямий кут із прямою АС; він стосується півкола в точці; довжина цієї смужки є довільною. На тому ж малюнку показано застосування трисектора. Нехай, наприклад, потрібно розділити на три рівні частини кут КSМ

Трисектор поміщають так, щоб вершина кута S знаходилася на лінії ВD, одна сторона кута пройшла через точку А, а інша сторона торкнулася півкола. Потім проводять прямі SВ і SО, і розподіл цього кута на три рівні частини закінчено. Для доказу з'єднаємо відрізком прямий центр півкола О з точкою дотику N. Легко переконатися в тому, що трикутник АSВ дорівнює трикутнику SВО, а трикутник SВО дорівнює трикутнику OSN. З рівності цих трьох трикутників слід, що кути АSВ, ВS0 і 0SN рівні між собою, що потрібно було довести.

Такий спосіб трисекції кута не є чисто геометричним; його скоріше можна назвати механічним.

Годинник-трисектор

(Інструкція із застосування)

Обладнання: циркуль, лінійка, годинник зі стрілками, олівець, прозорий папір.

Хід роботи:

Переведіть фігуру даного кута на прозорий папір і в той момент, коли обидві стрілки годинника поєднуються, накладіть креслення на циферблат так, щоб вершина кута збіглася з центром обертання стрілок і одна сторона кута пішла вздовж стрілок.

У той момент, коли хвилинна стрілка годинника пересунеться до збігу з напрямком другої сторони даного кута, проведіть з вершини кута промінь у напрямку годинникової стрілки. Утворюється кут, що дорівнює куту повороту годинникової стрілки. Тепер за допомогою циркуля та лінійки цей кут подвайте і подвоєний кут знову подвайте. Отриманий таким чином кут і складатиме ⅓даного.

Справді, щоразу, коли хвилинна стрілка описує якийсь кут, годинна стрілка цей час пересувається на кут, в 12 разів менший, а після збільшення цього кута вчетверо виходить кут (a/12)*4=⅓ a.

Висновок

Отже, нерозв'язні завдання побудова зіграли особливу роль історії математики. Зрештою, було доведено, що ці завдання неможливо вирішити, користуючись лише циркулем та лінійкою. Але сама постановка завдання - «довести нерозв'язність» - була сміливим кроком вперед.

Натомість пропонувалося безліч рішень за допомогою нетрадиційних інструментів. Все це призвело до виникнення та розвитку абсолютно нових ідей у ​​геометрії та алгебрі.

Закінчивши та проаналізувавши свою дослідницьку роботу, я зробила такі висновки:

✓ виникнення подібних завдань зумовлювалося їхньою практичною значимістю (зокрема, побудова правильних багатокутників);

✓ подібні завдання викликають розвиток нових методів та теорій (спосіб «вставок», поява квадратриси, теореми Морлі);

✓ нерозв'язні завдання привертають більше уваги до наук: знайти рішення чи довести неможливість – велика шана.

А також я дізналася:

✓ про математиків, які вивчали це завдання;

✓ нові поняття, терміни (трисекція, трисектор, квадратриса) та теореми (Морлея) та навчилася:

✓ ефективно знаходити та відбирати необхідний матеріал;

✓ систематизувати отримані знання;

✓ правильно оформляти науково-дослідну роботу.

Поділ кута на три рівні частини за допомогою циркуля та лінійки (трисекція кута).

Жарков В'ячеслав Сергійович

Відсутнє

Інтернет

Анотація:

Пропонується загальний підхід до вирішення задач про розподіл кута на рівні частини за допомогою циркуля та лінійки. Як приклад показано розподіл кута на три рівні частини (Трисекція кута).

Це відповідає за те, що загальна відповідь на проблему-відповідь до dividen angle into equal parts by using a compass and ruler. Як an example, angle shows the Division in three equal parts (Trisection of the angle).

Ключові слова:

кут; розподіл кута; трисекція кута.

angle; divide angle; trisection of an angle.

УДК 51

Вступ.

Трисекція кута — задача поділу заданого кута на три рівні частини побудовою циркулем і лінійкою. Інакше кажучи, необхідно побудувати трисектриси кута - промені, що ділять кут на три рівні частини. Поряд із завданнями про квадратуру кола та подвоєння куба є одним із класичних нерозв'язних завдань на побудову, відомих з часів Стародавньої Греції.

Метоюцієї статті є доказ хибності вище за наведене твердження про нерозв'язність, у всякому разі, стосовно завдання про трисекцію кута.

Пропоноване рішення не вимагає складних побудов, практично універсально і дозволяє ділити кути на будь-яку кількість рівних частинщо дозволяє будувати будь-які правильні багатокутники.

Вступна частина.

Проведемо пряму лінію aта побудуємо на ній ∆CDE. Умовно назвемо його "базовим" (Рис.1).

Виберемо на лінії aдовільну точку F і проведемо ще одну пряму лінію bчерез т.F та вершину D трикутника. На лінії bвізьмемо дві довільні точки G та H і з'єднаємо їх з точками C та E як показано на Рис.1. Аналіз малюнка дозволяє записати такі очевидні співвідношення між кутами:

1. α 1 -α 3 = y 1; α 3 -α 5 = y 3; α 1 -α 5 = y 1 + y 3;

2. α 2 -α 4 = y 2; α 4 -α 6 = y 4; α 2 -α 6 = y 2 + y 4;

3. y 1 / y 2 = y 3 / y 4;

Пояснення1.до п.3: Нехай кути – ∟C,∟ D,∟ Eє кутами за відповідними вершинами базового трикутника ∆CDE. Тоді можна записати:

∟ C+∟ D+∟ E=180 0 - сума кутів ∆CDE;

∟ C+ y 2 +∟ D-(y 2 + y 1 )+∟ E+ y 1 =180 0 - сума кутів ∆CGE;

Нехайy 1 / y 2 = nабоy 1 = n* y 2 тоді,

∟ C+ y 2 +∟ D-(y 2 + y 1 )+∟ E+ n* y 2 =180 0

Сума кутів ∆CHE:

∟ C+(y 2 + y 4 )+∟ D-(y 2 + y 4 + y 1 + y 3 )+∟ E+ n*(y 2 + y 4 ) = 180 0, звідки

y 1 + y 3 = n*(y 2 + y 4 ) абоy 1 + y 3 = n* y 2 + n* y 4 , і тому щоy 1 = n* y 2 ,то

y 3 = n* y 4 і, отже y 1 / y 2 = y 3 / y 4 = n.

Далі, візьмемо дві довільні точки на лінії a- N та M, і проведемо через них дві лінії cі dяк показано на Рис.2. Очевидно, у тому числі з раніше сказаного, що відношення змін відповідних кутів на лініях c і d величина постійна, тобто: (β 1 -β 3)/(β 3 -β 5) = (β 2 -β 4) /(β 4 -β 6)= y 1 / y 3 = y 2 / y 4;

Розподіл кута на три рівні частини.

На колі з центром у точці A відкладемо кут E 1 AE 2 =β (див. мал. 3.1). На протилежному боці кола відкладемо симетрично три кути - CAC 1 , C 1 AC 2 , C 2 AC 3 кожен рівний β. Розділимо кут E 1 AE 2 , у точках K 1 ,K 3 , на три рівні кути - ∟E 1 AK 1 , ∟K 1 AK 3 , ∟K 3 AE 2 рівних β/3. Проведемо прямі лінії через точки на колі як показано на Рис. 3.1. З'єднаємо прямими лініями точки C,E 1 і C 2 E. (Див. Рис. 3.2)

Через точку K - перетину ліній, і точку K 1 проведемо пряму лінію. Виберемо на цій лінії довільну точку K 2 і проведемо через неї дві прямі з точок C та C 2 .

Не важко помітити, що Рис. 3.2, якщо усунути лінію кола, практично ідентичний Рис. 2. (Для наочності додано штрихову лінію CC 2). Значить і всі співвідношення, про які говорилося вище, застосовні і тут, а саме для кутів, які необхідно розділити на три рівні частини, справедливе співвідношення y 1 /y 2 =y 3 /y 4 =1/2 (див. Пояснення 1. у вступній частини). З малюнка 3.2 стає ясно, як поділити кут на три рівні частини.

Розглянемо, як приклад, розподіл на три рівні частини кута β=50 0 .

Варіант 1.

На колі з центром A відкладаємо циркулем симетрично відносно один одного та діаметра CB (див. Рис 4.1) дуги C 1 C 2 =B 1 B 2 =B 2 B 3 =B 1 B 4 рівні β=50 0 - щодо центру кола. Половину дуги C 1 C 2 - CC 1 ділимо навпіл (точка D). Проводимо прямі через точки B 1 і D і точки B 3 і C. З'єднуємо між собою точки B 1 і C, B 3 і C 1 . З'єднуємо точки перетину - F та E, раніше проведених ліній, між собою. Отриманий кут = C 1 AG, ​​де G точка перетину лінії FE з колом, дорівнює β/3.

Варіант 2.

На колі з центром A відкладаємо циркулем симетрично відносно один одного та діаметра CB (див. Рис 4.2) дуги C 1 C 2 =B 1 B 2 =B 2 B 3 =B 1 B 4 =β=50 0 - щодо центру кола. З'єднуємо між собою точки B1 і C, B3 і C1. Відкладемо кути y 2 =2y 1 (див. Рис 4.2) від ліній B 1 C і B 3 C 1 і проведемо прямі лінії відповідно до цих кутів. З'єднуємо точки перетину - F та E, раніше проведених ліній, між собою. Отриманий кут α=C 1 AG≈16.67 0 де G точка перетину лінії FE з колом, дорівнює β/3.

Повна побудова розподілу кута на три рівні частини (на прикладі кута β=50 0) показано на Рис.5

Розподіл кута на непарну кількість (>3-х) рівних кутів.

Як приклад розглянемо розподіл кута β=35 0 п'ять рівних між собою кутів.

Спосіб №1.

На колі з центром A відкладаємо циркулем симетрично відносно один одного та діаметра CB кути C 2 AC 1 =B 1 AB 2 =B 2 AB 3 =B 3 AB 4 =B 4 AB 5 =B 5 AB 6 =β=35 0 . (див. мал.6)

Ділимо кут C 2 AC рівний половинікута C 2 AC 1 навпіл у точці E. З'єднуємо точки

E,C 2 ,B 1 ,B 2 ,B 3 між собою як показано на малюнку 6. Далі, для поділу кута, використовуємо Варіант 2 з наведеного прикладу, т. К. Варіант 1 для поділу кутів на непарну кількість >3- х рівних кутів явно не застосовується. Від ліній B 3 E та B 1 C 2 у точках B 3 та B 1 відповідно, відкладемо кути y 1 та y 2 у співвідношенні 1:4. З точок B 3 і B 1 проведемо прямі відповідно до цих кутів, до перетину в точці N. Кут C 2 AK=α=7 0 буде шуканим.

Спосіб №2.

Цей спосіб (див. рис.7) аналогічний першому з тією лише різницею, що для побудов використовується кут кута C2AC1 - кут EAC прилеглий до середньої лінії кола BC. Перевага даного способу в тому, що він полегшує розподіл кута на велику кількість кутів – 7, 9, 11 і т.д.

Побудова правильного семикутника.

Приймемо, що n - число розбиття (кількість секторів, на яке ділиться кут).

Тоді якщо n-1=2 k(1), де k- будь-яке ціле число, то кут ділиться на один етап, що було показано раніше. Якщо n-1 ≠ 2 k(2) - то кут ділиться на два етапи, спочатку на n-1 , а потім вже на n. При цьому у всіх випадках дотримується співвідношення: y 1 / y 2 = 1/ n-1 (3).

Пояснимо це з прикладу побудови правильного семикутника.

Для того щоб побудувати семикутник треба знайти 1/7-ю частину кута 60 0, помножити її на шість, і відкласти отриманий кут сім разів по колу (це один із можливих варіантів). Так як 7-1=6 то відповідно до формули (2) кут 60 0 ділитимемо в два етапи. На першому етапі розділимо на шість, а потім, на другому етапі, на сім. З цією метою розділимо кут 30 0 на три рівні сектори по 10 0 (див. Рис.8), використовуючи, як найпростіший, Варіант 1 описаний на початку статті. Отриманий кут ECL=10 0 відкладемо від середньої лінії кола (див. мал.9). Вважатимемо, що кут ECL належить симетрично відкладеному щодо середньої лінії куту 60 0 .

Далі, щоб знайти 1/7-ю частину кута 60 0 використовуємо Спосіб №2 описаний раніше. З цією метою відкладемо кут D 1 CD 2 =60 0 симетрично до середньої лінії та кут D 2 CD 3 =60 0 примикає до нього. У точках D 1 і D 3 побудуємо кути y 1 і y 2 до ліній D 1 E і D 3 L відповідно, дотримуючись пропорцій відповідно до формули (3) - тобто 1 до 6.

Проведемо прямі лінії під кутами y1 та y2. З'єднаємо точки перетину G та F відповідних ліній. Кут LCH=60 0/7. Відкладемо цей кут шість разів від точки L до точки B. Відкладемо отриманий кут BCL ще шість разів, і в результаті отримаємо семикутник LBKFMNA.

Висновок.

Спосіб розподілу кута на рівні частини, пропонований у цій статті має обмеження - неможливість його застосування безпосередньо для кутів > 60 0 , що, втім, не таке істотне з точки зору принципової вирішуваності завдання.

Бібліографічний список:

1. Метельський Н. В. Математика. Курс середньої школидля вступників до вузів та технікумів. Вид. 3-тє, стереотип. Мн., «Вишийш. Школа», 1975 688 с. з ілл.

Рецензії:

20.03.2016, 14:39 Назарова Ольга Петрівна
Рецензія: Цікаві викладки, рекомендується до друку

22.03.2016, 11:09 Мирмович-Тихомиров Едуард Григорович
Рецензія: Цікаво, пізнавально, лаконічно Видно інженерний підхід. Але цей матеріал слід публікувати не тут, а у будь-якому освітньому журналі. Якщо він вже був опублікований автором в іншому виданні, то тим більше. Крім того, дана платформа є дуже дискомфортною до формул. Рецензент не хотів би, щоб тут публікувалися будь-які навчально-дидактичні та методичні матеріали. Але сперечатися з шановною Ольгою Петрівною не стану. Може, редакція ще сама щось вирішує!? Чіткої рекомендації да-ні дати важко.

22.03.2016 16:16 Відповідь на рецензію автора Жарков Вячеслав Сергійович:
Наведене рішення, що очевидно, не передбачає приблизності рішення задачі! Воно неправильне лише в одному випадку, що теж досить очевидно, якщо сума кутів трикутника на площині ≠1800. Що – нонсенс. Деякі основи, зокрема й у математиці, іноді вимагають коригування. І дидактика тут ні до чого.