Представени са основни тригонометрични формули и основни замествания. Описани са методи за интегриране на тригонометрични функции - интегриране на рационални функции, произведение на степенни функции на sin x и cos x, произведение на полином, експонента и синус или косинус, интегриране на обратни тригонометрични функции. Засегнати нестандартни методи.

Съдържание

Стандартни методи за интегриране на тригонометрични функции

Общ подход

Първо, ако е необходимо, интегралната функция трябва да се трансформира така, че тригонометричните функции да зависят от един аргумент, който да съвпада с интегралната променлива.

Например, ако интегралната функция зависи от грях(x+a)и cos(x+b), тогава трябва да извършите трансформацията:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + sin(x+a) sin(b-a).
След това направете промяната z = x+a. В резултат на това тригонометричните функции ще зависят само от интегриращата променлива z.

Когато тригонометричните функции зависят от един аргумент, съвпадащ с интеграционната променлива (да кажем, че това е z ), т.е. интегралната функция се състои само от функции от типа грях z, защото z, tgz, ctgz, тогава трябва да направите замяна
.
Такова заместване води до интегриране на рационални или ирационални функции (ако има корени) и позволява да се изчисли интегралът, ако е интегриран в елементарни функции.

Въпреки това, често можете да намерите други методи, които ви позволяват да изчислите интеграла по по-кратък начин, въз основа на спецификата на интегранта. По-долу е представено обобщение на основните такива методи.

Методи за интегриране на рационални функции на sin x и cos x

Рационални функции от грях хи cos xса функции, получени от грях х, cos xи всякакви константи, използващи операциите събиране, изваждане, умножение, деление и повишаване на цяло число. Те се обозначават по следния начин: R (sinx, cosx). Това може също да включва тангенси и котангенси, тъй като те се образуват чрез разделяне на синус на косинус и обратно.
Интегралите на рационалните функции имат формата:
.

Методите за интегриране на рационални тригонометрични функции са както следва.
1) Заместването винаги води до интеграл на рационална дроб. В някои случаи обаче има замествания (вижте по-долу), които водят до по-кратки изчисления.
2) Ако Р (sinx, cosx) cos x → - cos x грях х.
3) Ако Р (sinx, cosx)умножено по -1 при замяна sin x → - sin x, тогава заместването t = cos x.
4) Ако R (sinx, cosx)не се променя както при едновременна подмяна cos x → - cos x, и sin x → - sin x, тогава заместването t = tg xили t= ctg x.

Примери:
, , .

Произведение на степенни функции на cos x и sin x

Интеграли на формата

са интеграли на рационални тригонометрични функции. Следователно методите, описани в предишния раздел, могат да бъдат приложени към тях. По-долу разглеждаме методи, базирани на спецификата на такива интеграли.

Ако m и n са рационални числа, тогава една от пермутациите t = грях хили t= cos xинтегралът се редуцира до интеграла на диференциалния бином.

Ако m и n са цели числа, тогава интегрирането се извършва с помощта на формулите за редукция:

;
;
;
.

Пример:
.

Интеграли от произведението на полином и синус или косинус

Интеграли от формата:
, ,
където P(x) е полином от x, се интегрират по части. Това води до следните формули:

;
.

Примери:
, .

Интеграли от произведението на полином, експонента и синус или косинус

Интеграли от формата:
, ,
където P(x) е полином от x, се интегрират с помощта на формулата на Ойлер
e iax = cos брадва + isin брадва(където i 2 = - 1 ).
За целта методът, описан в предишния параграф, изчислява интеграла
.
След като се отделят реалните и имагинерните части от резултата, се получават оригиналните интеграли.

Пример:
.

Нестандартни методи за интегриране на тригонометрични функции

По-долу са дадени редица нестандартни методи, които ви позволяват да изпълнявате или опростявате интегрирането на тригонометрични функции.

Зависимост от (a sin x + b cos x)

Ако интегралната функция зависи само от a sin x + b cos x, е полезно да се приложи формулата:
,
където .

Например

Разлагане на дроби от синуси и косинуси на по-прости дроби

Разгледайте интеграла
.
Най-лесният начин за интегриране е да разложите дробта на по-прости, като приложите трансформацията:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Интегриране на дроби от първа степен

При изчисляване на интеграла
,
удобно е да изберете цялата част от дробта и производната на знаменателя
а 1 sin x + b 1 cos x =А (a sin x + b cos x) +б (a sin x + b cos x)' .
Константите A и B се намират чрез сравняване на лявата и дясната страна.

Препратки:
Н.М. Гюнтер, Р.О. Кузмин, Сборник задачи по висша математика, Lan, 2003.

Вижте също:

Ще има и задачи за самостоятелно решение, на които можете да видите отговорите.

Интегрантът може да се преобразува от произведение на тригонометрични функции в сума

Разгледайте интеграли, в които интегралната функция е произведение на синуси и косинуси от първа степен на x, умножени по различни множители, тоест интеграли от вида

Използвайки добре познатите тригонометрични формули

(2)
(3)
(4)
всеки от продуктите в интеграли от формата (31) може да се трансформира в алгебрична сума и да се интегрира по формулите

(5)

(6)

Пример 1намирам

Решение. Съгласно формула (2) при

Пример 2намирам интеграл на тригонометричната функция

Решение. Съгласно формула (3) при

Пример 3намирам интеграл на тригонометричната функция

Решение. Съгласно формула (4) при получаваме следната трансформация на интегранта:

Прилагайки формула (6), получаваме

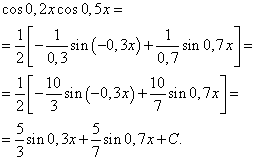
Интеграл от произведението на степени на синус и косинус от същия аргумент

Нека сега разгледаме интегралите на функции, които са произведение на степените на синуса и косинуса на същия аргумент, т.е.

(7)

В конкретни случаи един от индикаторите ( мили н) може да бъде нула.

При интегрирането на такива функции се използва, че четната степен на косинуса може да бъде изразена чрез синуса, а диференциалът на синуса е равен на cos x dx(или четна степен на синуса може да бъде изразена чрез косинус, а косинусният диференциал е - sin x dx ) .

Трябва да се разграничат два случая: 1) поне един от показателите ми нстранно; 2) двата показателя са четни.

Нека се случи първият случай, а именно показателят н = 2к+ 1 - странно. Тогава, като се има предвид това

Интеграндът е представен по такъв начин, че едната му част е функция само на синуса, а другата е диференциала на синуса. Сега с промяната на променливата T= грях хрешението се свежда до интегриране на полинома по отношение на T. Ако само степента ме странно, тогава направете същото, като отделите фактора sin х, изразяваща остатъка от интегранта по отношение на cos хи приемайки T= cos х. Този подход може да се използва и когато интегриране на частични степени на синус и косинус , кога поне един от показателите е нечетен . Цялата работа е в това частното на степените на синус и косинус е частен случай на тяхното произведение : когато тригонометричната функция е в знаменателя на интегранта, нейната степен е отрицателна. Но има и случаи на частични тригонометрични функции, когато техните степени са само четни. За тях - следващия параграф.

Ако и двата показателя ми нса четни, след което се използват тригонометрични формули

намалете показателите на синуса и косинуса, след което ще се получи интеграл от същия тип като горния. Следователно интеграцията трябва да продължи по същия начин. Ако един от четните показатели е отрицателен, т.е. се взема предвид коефициентът на четните степени на синус и косинус, тогава тази схема не е подходяща . След това се използва промяна на променлива, в зависимост от това как може да се трансформира интеграндът. Такъв случай ще бъде разгледан в следващия раздел.

Пример 4намирам интеграл на тригонометричната функция

Решение. Показателят на косинуса е нечетен. Ето защо, представете си

T= грях х(тогава дт= cos х dx ). Тогава получаваме

Връщайки се към старата променлива, най-накрая намираме

Пример 5намирам интеграл на тригонометричната функция

.

Решение. Показателят на косинуса, както в предишния пример, е странно, но повече. Представете си

и направете промяната на променливата T= грях х(тогава дт= cos х dx ). Тогава получаваме

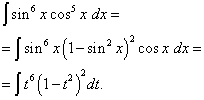
Нека отворим скобите

и получи

Връщайки се към старата променлива, получаваме решението

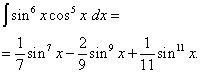
Пример 6намирам интеграл на тригонометричната функция

Решение. Показателите на синус и косинус са четни. Следователно трансформираме интегралната функция, както следва:

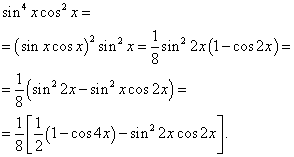
Тогава получаваме

Във втория интеграл правим промяна на променлива, настройка T= грях2 х. Тогава (1/2)дт= cos2 х dx . Следователно,

Накрая получаваме

Използване на метода за замяна на променливи

Метод на променлива замянапри интегриране на тригонометрични функции може да се използва в случаите, когато само синус или само косинус присъства в интегранта, произведението на синус и косинус, в който синус или косинус е на първа степен, тангенс или котангенс, както и като частно на четни степени на синус и косинус от един и същи аргумент. В този случай е възможно да се извършват пермутации не само грях х = Tи грях х = T, но също и tg х = Tи ctg х = T .

Пример 8намирам интеграл на тригонометричната функция

.

Решение. Нека променим променливата: , тогава . Полученият интеграл лесно се интегрира върху таблицата с интеграли:

.

Пример 9намирам интеграл на тригонометричната функция

Решение. Нека преобразуваме тангенса в отношението на синус и косинус:

Нека променим променливата: , тогава . Полученият интегрант е табличен интегралсъс знак минус:

.

Връщайки се към оригиналната променлива, най-накрая получаваме:

.

Пример 10намирам интеграл на тригонометричната функция

Решение. Нека променим променливата: , тогава .

Трансформираме интегранта, за да приложим тригонометричната идентичност :

Правим промяна на променлива, като не забравяме да поставим знак минус пред интеграла (вижте по-горе, какво е равно на дт). След това разлагаме интегранта на фактори и интегрираме според таблицата:

Връщайки се към оригиналната променлива, най-накрая получаваме:

.

Намерете сами интеграла на тригонометричната функция и след това вижте решението

Универсално тригонометрично заместване

Универсално тригонометрично заместване може да се използва в случаите, когато интегралната функция не попада в случаите, разгледани в предходните параграфи. По принцип, когато синусът или косинусът (или и двете) е в знаменателя на дроб. Доказано е, че синусът и косинусът могат да бъдат заменени с друг израз, съдържащ тангенса на половината от първоначалния ъгъл, както следва:

Но имайте предвид, че универсалното тригонометрично заместване често включва доста сложни алгебрични трансформации, така че е най-добре да се използва, когато никой друг метод не работи. Нека разгледаме примери, когато заедно с универсалното тригонометрично заместване се използва заместване под знака на диференциала и метода на неопределените коефициенти.

Пример 12.намирам интеграл на тригонометричната функция

.

Решение. Решение. Да използваме универсално тригонометрично заместване. Тогава
.

Умножаваме дробите в числителя и знаменателя по , изваждаме двойката и я поставяме пред знака за интеграл. Тогава

Подробно са разгледани примери за решения на интеграли по части, чиято интегрална функция е произведение на полином и експонента (e на степен x) или синус (sin x) или косинус (cos x).

Съдържание

Вижте също: Метод на интегриране по части
Таблица на неопределените интеграли
Методи за изчисляване на неопределени интеграли
Основни елементарни функции и техните свойства

Формула за интегриране по части

При решаване на примерите в този раздел се използва формулата за интегриране по части:
;
.

Примери за интеграли, съдържащи произведението на полином и sin x, cos x или e x

Ето примери за такива интеграли:
, , .

За да се интегрират такива интеграли, полиномът се означава с u, а остатъкът с v dx. След това се прилага формулата за интегриране по части.

По-долу е дадено подробно решение на тези примери.

Примери за решаване на интеграли

Пример с показател, e на степен x

Определете интеграла:
.

Въвеждаме експонентата под диференциалния знак:
e - x dx = - e - x d(-x) = - d(e - x).

Интегрираме по части.

тук
.
Останалият интеграл също е интегрируем по части.
.
.
.
Накрая имаме:
.

Пример за определяне на интеграл със синус

Изчислете интеграл:
.

Въвеждаме синуса под знака на диференциала:

Интегрираме по части.

тук u = x 2 , v = cos(2x+3), du = ( x2 )′ dx

Останалият интеграл също е интегрируем по части. За да направим това, въвеждаме косинуса под знака на диференциала.


тук u = x, v = грях (2x+3), du = dx

Накрая имаме:

Пример за произведение на полином и косинус

Изчислете интеграл:
.

Въвеждаме косинуса под знака на диференциала:

Интегрираме по части.

тук u = x 2+3x+5, v = sin2x, du = ( x 2 + 3 x + 5 )′ dx

Интеграли на тригонометрични функции.
Примери за решения

В този урок ще разгледаме интегралите на тригонометричните функции, тоест запълването на интегралите ще бъде синуси, косинуси, тангенси и котангенси в различни комбинации. Всички примери ще бъдат анализирани подробно, достъпни и разбираеми дори за чайник.

За да изучавате успешно интеграли на тригонометрични функции, трябва да сте добре запознати с най-простите интеграли, както и да владеете някои техники за интегриране. Можете да се запознаете с тези материали на лекциите. Неопределен интеграл. Примери за решенияи .

И сега имаме нужда от: Таблица на интегралите, Производна таблицаи Справочник с тригонометрични формули. Всички ръководства могат да бъдат намерени на страницата Математически формули и таблици. Препоръчвам да отпечатате всичко. Особено се фокусирам върху тригонометричните формули, те трябва да са пред очите ви– без него ефективността на работа ще намалее значително.

Но първо, за кои интеграли в тази статия Не. Тук няма интеграли от формата , - косинус, синус, умножен по някакъв многочлен (по-рядко, нещо с тангенс или котангенс). Такива интеграли се интегрират по части и за да научите метода, посетете урока Интегриране по части. Примери за решения Също така няма интеграли с "арки" - арктангенс, арксинус и т.н., те също най-често се интегрират по части.

При намиране на интеграли на тригонометрични функции се използват редица методи:

(4) Използвайте табличната формула , единствената разлика е, че вместо "х" имаме сложен израз.

Пример 2

Пример 3

Намерете неопределения интеграл.

Класика в жанра за тези, които се давят в класирането. Както вероятно сте забелязали, в таблицата на интегралите няма интеграл от тангенс и котангенс, но въпреки това такива интеграли могат да бъдат намерени.

(1) Използваме тригонометричната формула

(2) Подвеждаме функцията под знака на диференциала.

(3) Използвайте табличния интеграл .

Пример 4

Намерете неопределения интеграл.

Това е пример за самостоятелно решаване, пълното решение и отговор са в края на урока.

Пример 5

Намерете неопределения интеграл.

Нивата ни постепенно ще се повишават =).
Първо решение:

(1) Използваме формулата

(2) Използваме основното тригонометрично тъждество , от което следва, че .

(3) Разделете числителя на знаменателя термин по термин.

(4) Използваме свойството за линейност на неопределения интеграл.

(5) Интегрираме с помощта на таблицата.

Пример 6

Намерете неопределения интеграл.

Това е пример за самостоятелно решаване, пълното решение и отговор са в края на урока.

Има и интеграли от тангенси и котангенси, които са на по-високи степени. В урока се разглежда интегралът на тангентата в куба Как да изчислим площта на равнинна фигура?Интеграли на тангенса (котангенса) на четвърта и пета степен можете да получите на страницата Комплексни интеграли.

Намаляване на степента на интегранта

Тази техника работи, когато интеграндите са пълни със синуси и косинуси дористепени. За намаляване на степента се използват тригонометрични формули , и , а последната формула се използва по-често в обратна посока: .

Пример 7

Намерете неопределения интеграл.

решение:

По принцип тук няма нищо ново, освен че сме приложили формулата (понижаване степента на интегранта). Моля, обърнете внимание, че съкратих решението. С натрупването на опит интегралът на може да се намери устно, това спестява време и е доста приемливо при завършване на задачи. В този случай е препоръчително да не пишете правилото , първо устно вземаме интеграла от 1, след това - от .

Пример 8

Намерете неопределения интеграл.

Това е пример за самостоятелно решаване, пълното решение и отговор са в края на урока.

Обещаното увеличение на степента:

Пример 9

Намерете неопределения интеграл.

Първо решение, коментари по-късно:

(1) Подгответе интегранта за прилагане на формулата .

(2) Всъщност прилагаме формулата.

(3) Поставяме на квадрат знаменателя и изваждаме константата от знака за интеграл. Може да се направи малко по-различно, но според мен е по-удобно.

(4) Използваме формулата

(5) В третия член отново намаляваме степента, но използвайки формулата .

(6) Даваме подобни условия (тук разделих термин по термин и направи добавянето).

(7) Всъщност вземаме интеграла, правилото за линейност а методът за привеждане на функцията под знака на диференциала се извършва устно.

(8) Разресваме отговора.

! В неопределения интеграл отговорът често може да бъде написан по няколко начина.

В току-що разгледания пример крайният отговор може да бъде написан по различен начин - отворете скобите и дори направете това, преди да интегрирате израза, тоест следният завършек на примера е напълно приемлив:

Възможно е тази опция да е още по-удобна, просто го обясних по начина, по който сам реших). Ето още един типичен пример за самостоятелно решение:

Пример 10

Намерете неопределения интеграл.

Този пример е решен по два начина и можете да получите два напълно различни отговора.(по-точно ще изглеждат съвсем различно, но от математическа гледна точка ще са еквивалентни). Най-вероятно няма да видите най-рационалния начин и ще страдате от отваряне на скоби, като използвате други тригонометрични формули. Най-ефективното решение е дадено в края на урока.

Обобщавайки параграфа, заключаваме, че всеки интеграл на формата , където и - доричисло, се решава чрез понижаване на степента на интегранта.
На практика срещнах интеграли с 8 и 10 градуса, трябваше да разреша ужасните им хемороиди, като намалих степента няколко пъти, което доведе до дълги, дълги отговори.

Метод на променлива замяна

Както се споменава в статията Метод на промяна на променлива в неопределен интеграл, основната предпоставка за използване на метода на заместване е фактът, че интеграндът съдържа някаква функция и нейната производна:
(функциите не са непременно в продукта)

Пример 11

Намерете неопределения интеграл.

Разглеждаме таблицата с производни и забелязваме формулите, , тоест в нашия интегранд има функция и нейната производна. Виждаме обаче, че при диференциране косинусът и синусът взаимно се трансформират един в друг и възниква въпросът: как да направим промяна на променливата и за какво да обозначим - синус или косинус ?! Въпросът може да бъде решен чрез метода на научното мушкане: ако направим замяната неправилно, тогава нищо добро няма да излезе от това.

Обща насока: в подобни случаи трябва да обозначите функцията, която е в знаменателя.

Прекъсваме решението и извършваме подмяна

В знаменателя всичко ни е наред, всичко зависи само от , сега остава да разберем в какво ще се превърне.
За да направим това, намираме диференциала:

Или накратко:
От полученото равенство, съгласно правилото за пропорцията, изразяваме израза, от който се нуждаем:

Така:

Сега целият интегранд зависи само от и можем да продължим решението

Готов. Напомням ви, че целта на замяната е да опрости интегранта, в този случай всичко се свежда до интегриране на степенната функция върху таблицата.

Не случайно нарисувах този пример толкова подробно, това беше направено с цел повторение и консолидиране на материалите от урока. Метод на промяна на променлива в неопределен интеграл.

А сега два примера за независимо решение:

Пример 12

Намерете неопределения интеграл.

Пример 13

Намерете неопределения интеграл.

Пълни решения и отговори в края на урока.

Пример 14

Намерете неопределения интеграл.

Тук отново в подинтегралната функция има синус с косинус (функция с производна), но вече в произведението и възниква дилемата - за какво да обозначим синус или косинус?

Можете да опитате да направите замяна с помощта на научния метод на мушкане и ако нищо не работи, тогава го определете като друга функция, но има:

Обща насока: защото трябва да посочите функцията, която, образно казано, е в "неудобно положение".

Виждаме, че в този пример ученическият косинус "страда" от степента, а синусът си стои свободно така, сам по себе си.

Така че нека направим заместване:

Ако някой все още има затруднения с алгоритъма за промяна на променливата и намирането на диференциала, тогава трябва да се върнете към урока Метод на промяна на променлива в неопределен интеграл.

Пример 15

Намерете неопределения интеграл.

Анализираме интегранта, какво трябва да се обозначи с ?
Нека да разгледаме нашите насоки:
1) Функцията най-вероятно е в знаменателя;
2) Функцията е в "неудобно положение".

Между другото, тези указания са валидни не само за тригонометрични функции.

И при двата критерия (особено при втория) синусът пасва, така че замяната се предполага. По принцип подмяната вече може да се извърши, но първо би било хубаво да разберете какво да правите? Първо, ние "защипваме" един косинус:

Запазваме за нашия "бъдещ" диференциал

И ние изразяваме чрез синуса, използвайки основната тригонометрична идентичност:

Ето го замяната:

Общо правило: Ако в интегранта една от тригонометричните функции (синус или косинус) е в странностепен, тогава трябва да „отхапете“ една функция от нечетната степен и да посочите друга функция отзад.Говорим само за интеграли, където има косинуси и синуси.

В разглеждания пример имахме косинус в нечетна степен, така че откъснахме един косинус от степента и обозначихме синуса.

Пример 16

Намерете неопределения интеграл.

Нивата се покачват =).
Това е пример за „направи си сам“. Пълно решение и отговор в края на урока.

Универсално тригонометрично заместване

Универсалното тригонометрично заместване е често срещан случай на промяна на метода на променливата. Можете да опитате да го приложите, когато „не знаете какво да правите“. Но всъщност има някои насоки за прилагането му. Типичните интеграли, при които трябва да се приложи универсалното тригонометрично заместване, са следните интеграли: , , , и т.н.

Пример 17

Намерете неопределения интеграл.

Универсалното тригонометрично заместване в този случай се осъществява по следния начин. Да заменим: . Аз не използвам буквата, но буквата, това не е някакво правило, просто отново, толкова съм свикнал да решавам.

Тук е по-удобно да се намери диференциала, за това, от равенството, изразявам:
Вися на двете части на аркутангентата:

Арктангенс и тангенс взаимно се компенсират:

Поради това:

На практика не можете да рисувате толкова подробно, а просто да използвате готовия резултат:

! Изразът е валиден само ако под синусите и косинусите имаме просто “xes” за интеграла (за което ще говорим по-късно) всичко ще бъде малко по-различно!

Когато заместваме синусите и косинусите, ние се превръщаме в следните дроби:
, , тези равенства се основават на добре известни тригонометрични формули: ,

Така че почистването може да изглежда така:

Нека извършим универсално тригонометрично заместване:

За интегриране на рационални функции от формата R(sin x, cos x) се използва заместване, което се нарича универсално тригонометрично заместване. Тогава . Универсалното тригонометрично заместване често води до големи изчисления. Затова, когато е възможно, използвайте следните замествания.

Интегриране на функции, рационално зависими от тригонометрични функции

1. Интеграли от вида ∫ sin n xdx , ∫ cos n xdx , n>0
а) Ако n е нечетно, тогава една степен на sinx (или cosx) трябва да се постави под знака на диференциала, а от останалата четна степен трябва да се премине към противоположната функция.
б) Ако n е четно, тогава използваме формулите за редукция
2. Интеграли от вида ∫ tg n xdx , ∫ ctg n xdx , където n е цяло число.
Трябва да се използват формули

3. Интеграли от вида ∫ sin n x cos m x dx
а) Нека m и n са с различна четност. Прилагаме заместването t=sin x, ако n е нечетно, или t=cos x, ако m е нечетно.
б) Ако m и n са четни, тогава използваме формулите за редукция
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Интеграли на формата
Ако числата m и n имат еднаква четност, тогава използваме заместването t=tg x . Често е удобно да се прилага техниката на тригонометричната единица.
5. ∫ sin(nx) cos(mx)dx, ∫ cos(mx) cos(nx)dx, ∫ sin(mx) sin(nx)dx

Нека използваме формулите за преобразуване на произведението на тригонометричните функции в тяхната сума:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Примери
1. Изчислете интеграла ∫ cos 4 x sin 3 xdx .
Правим заместването cos(x)=t. Тогава ∫ cos 4 x sin 3 xdx =
2. Изчислете интеграла.
Правейки заместването sin x=t, получаваме

3. Намерете интеграла.
Правим замяната tg(x)=t. Замествайки, получаваме

Интегриране на изрази от формата R(sinx, cosx)

Пример #1. Изчислете интеграли:

Решение.
а) Интегрирането на изрази от формата R(sinx, cosx) , където R е рационална функция на sin x и cos x , се преобразуват в интеграли на рационални функции с помощта на универсалното тригонометрично заместване tg(x/2) = t .
Тогава имаме

Универсалното тригонометрично заместване прави възможно преминаването от интеграл на формата ∫ R(sinx, cosx) dx към интеграл на рационално-дробна функция, но такова заместване често води до тромави изрази. При определени условия по-простите замествания се оказват ефективни:

• Ако равенството R(-sin x, cos x) = -R(sin x, cos x)dx е вярно, тогава се прилага заместването cos x = t.
• Ако R(sin x, -cos x) = -R(sin x, cos x)dx е вярно, тогава заместването sin x = t.
• Ако R(-sin x, -cos x) = R(sin x, cos x)dx е вярно, тогава заместването е tgx = t или ctg x = t.

В този случай, за да намерите интеграла
прилагаме универсалното тригонометрично заместване tg(x/2) = t .
Тогава отговори: