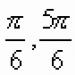Trigonometrija. Inverzne trigonometrijske funkcije. Izrazimo kroz sve inverzne trigonometrijske funkcije Tablica inverznih trigonometrijskih formula

Zadaci vezani uz inverzne trigonometrijske funkcije često se nude na završnim ispitima u školi i na prijamnim ispitima na nekim sveučilištima. Detaljno proučavanje ove teme moguće je ostvariti samo u okviru izborne nastave ili izbornih kolegija. Predloženi tečaj osmišljen je tako da što potpunije razvije sposobnosti svakog učenika i poboljša njegovu matematičku pripremu.

Tečaj traje 10 sati:

1. Funkcije arcsin x, arccos x, arctg x, arcctg x (4 sata).

2.Operacije na inverznim trigonometrijskim funkcijama (4 sata).

3. Inverzne trigonometrijske operacije na trigonometrijskim funkcijama (2 sata).

Lekcija 1 (2 sata) Tema: Funkcije y = arcsin x, y = arccos x, y = arctan x, y = arcctg x.

Cilj: cjelovito pokrivanje ove problematike.

1. Funkcija y = arcsin x.

a) Za funkciju y = sin x na segmentu postoji inverzna (jednoznačna) funkcija koju smo se dogovorili nazvati arcsinus i označiti je na sljedeći način: y = arcsin x. Graf inverzne funkcije je simetričan grafu glavne funkcije u odnosu na simetralu I - III koordinatnih kutova.

Svojstva funkcije y = arcsin x.

1) Domena definicije: segment [-1; 1];

2) Područje promjene: segment;

3) Funkcija y = arcsin x neparan: arcsin (-x) = - arcsin x;

4) Funkcija y = arcsin x je monotono rastuća;

5) Graf siječe osi Ox, Oy u ishodištu.

Primjer 1. Nađi a = arcsin. Ovaj se primjer može detaljno formulirati na sljedeći način: pronađite argument a, koji leži u rasponu od do, čiji je sinus jednak.

Riješenje. Postoji bezbroj argumenata čiji je sinus jednak , na primjer: itd. Ali nas zanima samo argument koji je na segmentu. Ovo bi bio argument. Dakle, .

Primjer 2. Pronađite .Riješenje. Raspravljajući na isti način kao u primjeru 1, dobivamo .

b) usmene vježbe. Pronađite: arcsin 1, arcsin (-1), arcsin, arcsin(), arcsin, arcsin(), arcsin, arcsin(), arcsin 0. Primjer odgovora: , jer . Imaju li smisla izrazi: ; arcsin 1,5; ?

c) Poredajte uzlaznim redoslijedom: arcsin, arcsin (-0,3), arcsin 0,9.

II. Funkcije y = arccos x, y = arctg x, y = arcctg x (slično).

Lekcija 2 (2 sata) Tema: Inverzne trigonometrijske funkcije, njihovi grafovi.

Svrha: u ovoj lekciji potrebno je razviti vještine određivanja vrijednosti trigonometrijskih funkcija, konstruirati grafove inverznih trigonometrijskih funkcija pomoću D (y), E (y) i potrebne transformacije.

U ovoj lekciji dovršite vježbe koje uključuju pronalaženje domene definicije, domene vrijednosti funkcija tipa: y = arcsin, y = arccos (x-2), y = arctg (tg x), y = arccos.

Treba konstruirati grafove funkcija: a) y = arcsin 2x; b) y = 2 arcsin 2x; c) y = arcsin;

d) y = arcsin; e) y = arcsin; e) y = arcsin; g) y = | arcsin | .

Primjer. Nacrtajmo y = arccos

U svoju domaću zadaću možete uključiti sljedeće vježbe: izgraditi grafove funkcija: y = arccos, y = 2 arcctg x, y = arccos | x | .

Grafovi inverznih funkcija

Lekcija br. 3 (2 sata) Tema:
Operacije na inverznim trigonometrijskim funkcijama.

Cilj: proširiti matematičko znanje (ovo je važno za one koji upisuju specijalnosti s povećanim zahtjevima za matematičko obrazovanje) uvođenjem osnovnih odnosa za inverzne trigonometrijske funkcije.

Materijal za lekciju.

Neke jednostavne trigonometrijske operacije na inverznim trigonometrijskim funkcijama: sin (arcsin x) = x, i xi? 1; cos (arcos x) = x, i xi? 1; tg (arctg x)= x , x I R; ctg (arcctg x) = x , x I R.

Vježbe.

a) tg (1,5 + arctg 5) = - ctg (arctg 5) = .

ctg (arctg x) = ; tg (arcctg x) = .

b) cos ( + arcsin 0,6) = - cos (arcsin 0,6). Neka je arcsin 0,6 = a, sin a = 0,6;

cos (arcsin x) = ; sin (arccos x) = .

Napomena: uzimamo znak “+” ispred korijena jer a = arcsin x zadovoljava .

c) sin (1,5 + arcsin) Odgovor: ;

d) ctg ( + arctg 3) Odgovor: ;

e) tg ( – arcctg 4).

e) cos (0,5 + arccos). Odgovor: .

Izračunati:

a) grijeh (2 arctan 5) .

Neka je arctan 5 = a, tada je sin 2 a = ili grijeh (2 arctan 5) = ;

b) cos ( + 2 arcsin 0,8).

c) arctg + arctg.

Neka je a = arctan, b = arctan,

tada je tg(a + b) = .

d) sin(arcsin + arcsin).

e) Dokažite da je za sve x I [-1; 1] pravi arcsin x + arccos x = .

Dokaz:

arcsin x = – arccos x

sin (arcsin x) = sin ( – arccos x)

x = cos (arccos x)

Da biste to sami riješili: sin (arccos), cos (arcsin), cos (arcsin ()), sin (arctg (- 3)), tg (arccos), ctg (arccos).

Za kućno rješenje: 1) sin (arcsin 0,6 + arctan 0); 2) arcsin + arcsin ; 3) ctg ( – arccos 0,6); 4) cos (2 arcctg 5) ; 5) sin (1,5 – arcsin 0,8); 6) arctg 0,5 – arctg 3.

Lekcija br. 4 (2 sata) Tema: Operacije nad inverznim trigonometrijskim funkcijama.

Cilj: U ovoj lekciji pokazati korištenje omjera u transformaciji složenijih izraza.

Materijal za lekciju.

ORALNO:

a) sin (arccos 0,6), cos (arcsin 0,8);

b) tg (luk 5), ctg (luk 5);

c) sin (arctg -3), cos (arcstg());

d) tg (arccos), ctg (arccos()).

PISANO:

1) cos (arcsin + arcsin + arcsin).

2) cos (arctg 5–arccos 0,8) = cos (arctg 5) cos (arctg 0,8) + sin (arctg 5) sin (arctg 0,8) =

3) tg ( - arcsin 0,6) = - tg (arcsin 0,6) =

Samostalni rad pomoći će u utvrđivanju razine ovladanosti gradivom.

1) tg (luk 2 – luk g)

2) cos( - arctan2)

3) arcsin + arccos

1) cos (arcsin + arcsin)

2) sin (1.5 - arctan 3)

3) arcctg3 – arcctg 2

Za domaću zadaću možete predložiti:

1) ctg (luk + luk + luk + luk); 2) sin 2 (arctg 2 – arcctg ()); 3) sin (2 arctg + tan ( arcsin )); 4) sin(2 arctan); 5) tg ( (arcsin ))

Lekcija br. 5 (2 sata) Tema: Inverzne trigonometrijske operacije na trigonometrijskim funkcijama.

Cilj: formirati razumijevanje učenika o inverznim trigonometrijskim operacijama na trigonometrijskim funkcijama, s fokusom na povećanje razumijevanja teorije koja se proučava.

Pri proučavanju ove teme pretpostavlja se da je opseg teorijskog materijala koji treba zapamtiti ograničen.

Materijal za lekciju:

Možete početi učiti novi materijal proučavanjem funkcije y = arcsin (sin x) i iscrtavanjem njezina grafikona.

3. Svaki x I R je pridružen y I, tj.<= y <= такое, что sin y = sin x.

4. Funkcija je neparna: sin(-x) = - sin x; arcsin(sin(-x)) = - arcsin(sin x).

6. Graf y = arcsin (sin x) na:

a) 0<= x <= имеем y = arcsin(sin x) = x, ибо sin y = sin x и <= y <= .

b)<= x <= получим y = arcsin (sin x) = arcsin ( - x) = - x, ибо

sin y = sin ( – x) = sin x , 0<= - x <= .

Tako,

Nakon što smo konstruirali y = arcsin (sin x) na , nastavljamo simetrično oko ishodišta na [- ; 0], s obzirom na neparnost ove funkcije. Koristeći periodičnost, nastavljamo duž cijelog brojevnog pravca.

Zatim zapišite neke odnose: arcsin (sin a) = a if<= a <= ; arccos (cos a ) = a ako je 0<= a <= ; arctg (tg a) = a ako< a < ; arcctg (ctg a) = a , если 0 < a < .

I napravite sljedeće vježbe:a) arccos(sin 2).Odgovor: 2 - ; b) arcsin (cos 0,6) Odgovor: - 0,1; c) arctg (tg 2) Odgovor: 2 - ;

d) arcctg(tg 0,6).Odgovor: 0,9; e) arccos (cos ( - 2)) Odgovor: 2 - ; e) arcsin (sin ( - 0,6)). Odgovor: - 0,6; g) arctg (tg 2) = arctg (tg (2 - )). Odgovor: 2 - ; h) arcctg (tg 0,6). Odgovor: - 0,6; - arctan x; e) arccos + arccos

DO inverzne trigonometrijske funkcije Sljedećih 6 funkcija uključuje: arcsinus , arkosinus , arktangens , arkotangens , arcsekant I arkokosekant .

Budući da su izvorne trigonometrijske funkcije periodične, onda su inverzne funkcije, općenito govoreći, periodične polisemantičan . Kako bi se osigurala korespondencija jedan-na-jedan između dviju varijabli, domene definicije izvornih trigonometrijskih funkcija ograničene su uzimajući u obzir samo njih glavne grane . Na primjer, funkcija \(y = \sin x\) razmatra se samo u intervalu \(x \in \lijevo[ ( - \pi /2,\pi /2) \desno]\). Na tom je intervalu funkcija inverznog arkusina jednoznačno definirana.

Arkusinus funkcija
Arkus sinus broja \(a\) (označen s \(\arcsin a\)) je vrijednost kuta \(x\) u intervalu \(\left[ ( - \pi /2,\pi / 2) \desno]\), za koje je \(\sin x = a\). Inverzna funkcija \(y = \arcsin x\) definirana je na \(x \in \left[ ( -1,1) \desno]\), njezin raspon vrijednosti je \(y \in \left[ ( - \pi / 2,\pi /2) \desno]\).

Arkus kosinusna funkcija
Arkosinus broja \(a\) (označen s \(\arccos a\)) vrijednost je kuta \(x\) u intervalu \(\lijevo[ (0,\pi) \desno]\ ), pri čemu \(\cos x = a\). Inverzna funkcija \(y = \arccos x\) definirana je na \(x \in \lijevo[ ( -1,1) \desno]\), njezin raspon vrijednosti pripada segmentu \(y \in \lijevo[ (0,\pi)\desno]\).

Arktangens funkcija
Arktangens broja a(označeno s \(\arctan a\)) vrijednost je kuta \(x\) u otvorenom intervalu \(\lijevo((-\pi/2, \pi/2) \desno)\), na koji \(\tan x = a\). Inverzna funkcija \(y = \arctan x\) definirana je za sve \(x \in \mathbb(R)\), raspon arktangensa jednak je \(y \in \left((-\pi/2, \pi/2 )\desno)\).

Arkus tangens funkcija
Arcotangens broja \(a\) (označen s \(\text(arccot ) a\)) je vrijednost kuta \(x\) u otvorenom intervalu \(\left[ (0,\ pi) \desno]\), pri čemu \(\cot x = a\). Inverzna funkcija \(y = \text(arccot ) x\) je definirana za sve \(x \in \mathbb(R)\), njen raspon vrijednosti je u intervalu \(y \in \ lijevo[ (0,\pi) \desno]\).

Funkcija arsekansa
Arkuseksant broja \(a\) (označen s \(\text(arcsec ) a\)) je vrijednost kuta \(x\) pod kojim \(\sec x = a\). Inverzna funkcija \(y = \text(arcsec ) x\) definirana je na \(x \in \left(( - \infty , - 1) \right] \cup \left[ (1,\infty ) \right )\ ), njegov raspon vrijednosti pripada skupu \(y \in \left[ (0,\pi /2) \right) \cup \left((\pi /2,\pi ) \right] \).

Funkcija arkosekansa
Arkusosekant broja \(a\) (označen kao \(\text(arccsc ) a\) ili \(\text(arccosec ) a\)) vrijednost je kuta \(x\) pod kojim \(\ csc x = a\ ). Inverzna funkcija \(y = \text(arccsc ) x\) definirana je na \(x \in \left(( - \infty , - 1) \right] \cup \left[ (1,\infty ) \right )\ ), raspon njegovih vrijednosti pripada skupu \(y \in \left[ ( - \pi /2,0) \right) \cup \left((0,\pi /2) \right ]\).

Glavne vrijednosti funkcija arksinusa i arkkosinusa (u stupnjevima)

\(x\)	\(-1\)	\(-\sqrt 3/2\)	\(-\sqrt 2/2\)	\(-1/2\)	\(0\)	\(1/2\)	\(\sqrt 2/2\)	\(\sqrt 3/2\)	\(1\)
\(\arcsin x\)	\(-90^\circ\)	\(-60^\circ\)	\(-45^\circ\)	\(-30^\circ\)	\(0^\circ\)	\(30^\krug\)	\(45^\krug\)	\(60^\krug\)	\(90^\krug\)
\(\arccos x\)	\(180^\krug\)	\(150^\krug\)	\(135^\krug\)	\(120^\krug\)	\(90^\krug\)	\(60^\krug\)	\(45^\krug\)	\(30^\krug\)	\(0^\circ\)

Glavne vrijednosti funkcija arktangensa i arkotangensa (u stupnjevima)

\(x\)	\(-\sqrt 3\)	\(-1\)	\(-\sqrt 3/3\)	\(0\)	\(\sqrt 3/3\)	\(1\)	\(\sqrt 3\)
\(\arctan x\)	\(-60^\circ\)	\(-45^\circ\)	\(-30^\circ\)	\(0^\circ\)	\(30^\krug\)	\(45^\krug\)	\(60^\krug\)
\(\text(arccot ) x\)	\(150^\krug\)	\(135^\krug\)	\(120^\krug\)	\(90^\krug\)	\(60^\krug\)	\(45^\krug\)	\(30^\krug\)

Budući da su trigonometrijske funkcije periodične, njihove inverzne funkcije nisu jedinstvene. Dakle, jednadžba y = grijeh x, za zadano , ima beskonačno mnogo korijena. Doista, zbog periodičnosti sinusa, ako je x takav korijen, onda je i takav x + 2πn(gdje je n cijeli broj) također će biti korijen jednadžbe. Tako, inverzne trigonometrijske funkcije su višeznačne. Radi lakšeg rada s njima, uvodi se pojam njihovih glavnih značenja. Razmotrimo, na primjer, sinus: y = grijeh x. Ograničimo li argument x na interval , tada je funkcija y = grijeh x monotono raste. Stoga ima jedinstvenu inverznu funkciju, koja se naziva arcsinus: x = arcsin y.

Ako nije drugačije navedeno, pod inverznim trigonometrijskim funkcijama podrazumijevamo njihove glavne vrijednosti, koje su određene sljedećim definicijama.

arkusinus ( y= arcsin x) je inverzna funkcija sinusa ( x = siny
Arkus kosinus ( y= arccos x) je inverzna funkcija kosinusa ( x = jer y), ima domenu definicije i skup vrijednosti.
Arktangens ( y= arctan x) je inverzna funkcija tangensa ( x = tg y), ima domenu definicije i skup vrijednosti.
Arkotangens ( y= arcctg x) je inverzna funkcija kotangensa ( x = ctg y), ima domenu definicije i skup vrijednosti.

Grafovi inverznih trigonometrijskih funkcija

Grafovi inverznih trigonometrijskih funkcija dobivaju se iz grafova trigonometrijskih funkcija zrcalnom refleksijom u odnosu na pravac y = x. Pogledajte odjeljke Sinus, kosinus, Tangens, kotangens.

y= arcsin x

y= arccos x

y= arctan x

y= arcctg x

Osnovne formule

Ovdje posebnu pozornost treba obratiti na intervale za koje formule vrijede.

arcsin(sin x) = x na
sin(arcsin x) = x
arccos(cos x) = x na
cos(arccos x) = x

arctan(tg x) = x na
tg(arctg x) = x
arcctg(ctg x) = x na
ctg(arcctg x) = x

Formule koje povezuju inverzne trigonometrijske funkcije

Vidi također: Derivacija formula za inverzne trigonometrijske funkcije

Formule zbroja i razlike

kod ili

kod i

kod i

na

na

na

na

na

Reference:
U. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente, “Lan”, 2009.

Definicija i zapis

Arkusinus (y = arcsin x) je inverzna funkcija sinusa (x = siny -1 ≤ x ≤ 1 a skup vrijednosti -π /2 ≤ y ≤ π/2.
sin(arcsin x) = x ;
arcsin(sin x) = x .

Arksinus se ponekad označava na sljedeći način:
.

Graf funkcije arkusina

Graf funkcije y = arcsin x

Arkusinusni graf se dobiva iz sinusnog grafa ako se apscisna i ordinatna os zamijene. Kako bi se uklonila dvosmislenost, raspon vrijednosti ograničen je na interval u kojem je funkcija monotona. Ova se definicija naziva glavnom vrijednošću arkusina.

Arkosinus, arkos

Definicija i zapis

Arkus kosinus (y = arccos x) je inverzna funkcija kosinusa (x = jer y). Ima opseg -1 ≤ x ≤ 1 i mnogo značenja 0 ≤ y ≤ π.
cos(arccos x) = x ;
arccos(cos x) = x .

Arkosinus se ponekad označava na sljedeći način:
.

Graf ark kosinusne funkcije

Graf funkcije y = arccos x

Arkus kosinusni graf dobiva se iz kosinusnog grafa ako se apscisna i ordinatna os zamijene. Kako bi se uklonila dvosmislenost, raspon vrijednosti ograničen je na interval u kojem je funkcija monotona. Ova se definicija naziva glavnom vrijednošću ark kosinusa.

Paritet

Funkcija arkusina je neparna:
arcsin(- x) = arcsin(-sin arcsin x) = arcsin(sin(-arcsin x)) = - arcsin x

Arkus kosinus funkcija nije paran ili neparan:
arccos(- x) = arccos(-cos arccos x) = arccos(cos(π-arccos x)) = π - arccos x ≠ ± arccos x

Svojstva - ekstremi, porast, pad

Funkcije arksinus i arkosinus su kontinuirane u svojoj domeni definicije (vidi dokaz kontinuiteta). Glavna svojstva arksinusa i arkkosinusa prikazana su u tablici.

	y= arcsin x	y= arccos x
Opseg i kontinuitet	- 1 ≤ x ≤ 1	- 1 ≤ x ≤ 1
Raspon vrijednosti
Uzlazno, silazno	monotono raste	monotono opada
Visoki
minimalci
Nule, y = 0	x = 0	x = 1
Točke presjeka s osi ordinata, x = 0	y= 0	y = π/ 2

Tablica arksinusa i arkkosinusa

Ova tablica predstavlja vrijednosti arksinusa i arkkosinusa, u stupnjevima i radijanima, za određene vrijednosti argumenta.

x	arcsin x		arccos x
	tuča	radostan.	tuča	radostan.
- 1	- 90°	-	180°	π
-	- 60°	-	150°
-	- 45°	-	135°
-	- 30°	-	120°
0	0°	0	90°
	30°		60°
	45°		45°
	60°		30°
1	90°		0°	0

≈ 0,7071067811865476
≈ 0,8660254037844386

Formule

Vidi također: Derivacija formula za inverzne trigonometrijske funkcije

Formule zbroja i razlike

kod ili

kod i

kod i

na

na

Izrazi kroz logaritme, kompleksni brojevi

Vidi također: Izvođenje formula

Izrazi preko hiperboličkih funkcija

Derivati

;
.
Vidi Derivacija arksinusa i arkkosinusa > > >

Izvodnice višeg reda:
,
gdje je polinom stupnja . Određuje se formulama:
;
;
.

Vidi Derivacija višeg reda izvoda arksinusa i arkkosinusa > > >

Integrali

Vršimo zamjenu x = grijeh t. Integriramo po dijelovima, vodeći računa da je -π/ 2 ≤ t ≤ π/2, cos t ≥ 0:
.

Izrazimo ark kosinus kroz ark sinus:
.

Proširenje serije

Kada |x|< 1 odvija se sljedeća dekompozicija:
;
.

Inverzne funkcije

Inverzi arkusina i arkosinusa su sinus i kosinus.

Sljedeće formule vrijede u cijeloj domeni definicije:
sin(arcsin x) = x
cos(arccos x) = x .

Sljedeće formule vrijede samo za skup vrijednosti arksinusa i arkkosinusa:
arcsin(sin x) = x na
arccos(cos x) = x u .

Reference:
U. Bronstein, K.A. Semendjajev, Priručnik iz matematike za inženjere i studente, “Lan”, 2009.

Vidi također:

Lekcije 32-33. Inverzne trigonometrijske funkcije

09.07.2015 8495 0

Cilj: razmatrati inverzne trigonometrijske funkcije i njihovu upotrebu za pisanje rješenja trigonometrijskih jednadžbi.

I. Priopćavanje teme i svrhe lekcija

II. Učenje novog gradiva

1. Inverzne trigonometrijske funkcije

Započnimo našu raspravu o ovoj temi sa sljedećim primjerom.

Primjer 1

Riješimo jednadžbu: a) sin x = 1/2; b) sin x = a.

a) Na os ordinata nanesemo vrijednost 1/2 i konstruiramo kutove x 1 i x2, za koje grijeh x = 1/2. U ovom slučaju x1 + x2 = π, odakle je x2 = π – x 1 . Koristeći tablicu vrijednosti trigonometrijskih funkcija, nalazimo vrijednost x1 = π/6, zatimUzmimo u obzir periodičnost funkcije sinusa i zapišimo rješenja ove jednadžbe:gdje je k ∈ Z.

b) Očigledno, algoritam za rješavanje jednadžbe grijeh x = a je isti kao u prethodnom paragrafu. Naravno, sada je vrijednost a iscrtana duž ordinatne osi. Postoji potreba da se nekako označi kut x1. Dogovorili smo se da taj kut označimo simbolom arcsin A. Tada se rješenja te jednadžbe mogu napisati u oblikuOve dvije formule mogu se kombinirati u jednu: pri čemu

Preostale inverzne trigonometrijske funkcije uvode se na sličan način.

Vrlo često je potrebno odrediti veličinu kuta iz poznate vrijednosti njegove trigonometrijske funkcije. Takav problem je višeznačan - postoji bezbroj kutova čije su trigonometrijske funkcije jednake istoj vrijednosti. Stoga, na temelju monotonosti trigonometrijskih funkcija, uvode se sljedeće inverzne trigonometrijske funkcije za jedinstveno određivanje kutova.

Arksinus broja a (arcsin , čiji je sinus jednak a, tj.

Arkus kosinus broja a(arccos a) je kut a iz intervala čiji je kosinus jednak a, tj.

Arktangens broja a(arctg a) - takav kut a iz intervalačiji je tangens jednak a, tj.tg a = a.

Arkotangens broja a(arcctg a) je kut a iz intervala (0; π), čiji je kotangens jednak a, tj. ctg a = a.

Primjer 2

Pronađimo:

Uzimajući u obzir definicije inverznih trigonometrijskih funkcija, dobivamo:

Primjer 3

Izračunajmo

Neka je kut a = arcsin 3/5, onda po definiciji sin a = 3/5 i . Stoga, moramo pronaći cos A. Koristeći osnovni trigonometrijski identitet, dobivamo:Uzima se u obzir da je cos a ≥ 0. Dakle,

Svojstva funkcija	Funkcija
Svojstva funkcija	y = arcsin x	y = arccos x	y = arctan x	y = arcctg x
Domena	x ∈ [-1; 1]	x ∈ [-1; 1]	x ∈ (-∞; +∞)	x ∈ (-∞ +∞)
Raspon vrijednosti	y ∈ [-π/2; π /2]	y ∈	y ∈ (-π/2; π/2)	y ∈ (0;π)
Paritet	Neparan	Ni par ni nepar	Neparan	Ni par ni nepar
Funkcijske nule (y = 0)	Na x = 0	Na x = 1	Na x = 0	y ≠ 0
Intervali predznaka	y > 0 za x ∈ (0; 1], na< 0 при х ∈ [-1; 0)	y > 0 za x ∈ [-1; 1)	y > 0 za x ∈ (0; +∞), na< 0 при х ∈ (-∞; 0)	y > 0 za x ∈ (-∞; +∞)
Monotonija	Povećavajući se	Silazni	Povećavajući se	Silazni
Veza s trigonometrijskom funkcijom	sin y = x	cos y = x	tg y = x	ctg y = x
Raspored

Navedimo još nekoliko tipičnih primjera vezanih uz definicije i osnovna svojstva inverznih trigonometrijskih funkcija.

Primjer 4

Nađimo domenu definicije funkcije

Da bi funkcija y bila definirana potrebno je zadovoljiti nejednakostšto je ekvivalentno sustavu nejednakostiRješenje prve nejednadžbe je interval x∈ (-∞; +∞), drugi - Ovaj interval i rješenje je sustava nejednadžbi, a time i domena definiranja funkcije

Primjer 5

Nađimo područje promjene funkcije

Razmotrimo ponašanje funkcije z = 2x - x2 (vidi sliku).

Jasno je da je z ∈ (-∞; 1]. S obzirom na to da argument z funkcija arc kotangensa varira unutar navedenih granica, to dobivamo iz podataka u tabliciDakle, područje promjene

Primjer 6

Dokažimo da je funkcija y = arctg x neparan. NekaTada je tg a = -x ili x = - tg a = tg (- a), i Prema tome, - a = arctg x ili a = - arctg X. Dakle, vidimo datj. y(x) je neparna funkcija.

Primjer 7

Izrazimo kroz sve inverzne trigonometrijske funkcije

Neka Očito je da Tada od

Predstavimo kut Jer Da

Slično dakle I

Tako,

Primjer 8

Izgradimo graf funkcije y = cos(arcsin x).

Označimo tada a = arcsin x Uzmimo u obzir da je x = sin a i y = cos a, tj. x 2 + y2 = 1, i ograničenja na x (x∈ [-1; 1]) i y (y ≥ 0). Tada je graf funkcije y = cos(arcsin x) je polukrug.

Primjer 9

Izgradimo graf funkcije y = arccos (cos x ).

Budući da funkcija cos x promjene na intervalu [-1; 1], tada je funkcija y definirana na cijeloj numeričkoj osi i varira na segmentu . Imajmo na umu da je y = arccos(cosx) = x na segmentu; funkcija y je parna i periodična s periodom 2π. S obzirom da funkcija ima ova svojstva cos x Sada je lako izraditi grafikon.

Zabilježimo neke korisne jednakosti:

Primjer 10

Nađimo najmanju i najveću vrijednost funkcije Označimo Zatim Idemo dobiti funkciju Ova funkcija ima minimum u točki z = π/4, a jednak je Najveća vrijednost funkcije postiže se u točki z = -π/2, i jednak je Dakle, i

Primjer 11

Riješimo jednadžbu

Uzmimo to u obzir Tada jednadžba izgleda ovako:ili gdje Po definiciji arktangensa dobivamo:

2. Rješavanje jednostavnih trigonometrijskih jednadžbi

Slično primjeru 1, možete dobiti rješenja najjednostavnijih trigonometrijskih jednadžbi.

Jednadžba	Riješenje


tgx = a
ctg x = a

Primjer 12

Riješimo jednadžbu

Budući da je funkcija sinus neparna, jednadžbu zapisujemo u oblikuRješenja ove jednadžbe:odakle to nalazimo?

Primjer 13

Riješimo jednadžbu

Koristeći zadanu formulu, zapisujemo rješenja jednadžbe:i naći ćemo

Imajte na umu da u posebnim slučajevima (a = 0; ±1) pri rješavanju jednadžbi sin x = a i cos x = i lakše je i praktičnije koristiti ne općenite formule, već zapisivati rješenja temeljena na jediničnom krugu:

za jednadžbu sin x = 1 rješenje

za jednadžbu sin x = 0 rješenja x = π k;

za jednadžbu sin x = -1 rješenje