Pitanja.

1. Koje se formule koriste za izračunavanje projekcije i modula vektora pomaka tijela tijekom njegova jednoliko ubrzanog kretanja iz stanja mirovanja?

2. Koliko će se puta povećati modul vektora pomaka tijela s povećanjem vremena njegovog gibanja iz mirovanja za n puta?

3. Zapišite kako su moduli vektora pomaka tijela koje se kreće jednoliko ubrzano iz stanja mirovanja međusobno povezane s povećanjem vremena njegova kretanja za cijeli broj puta u odnosu na t 1.

4. Napišite kako su moduli vektora pomaka koje tijelo izvodi u uzastopnim jednakim vremenskim intervalima međusobno povezani ako se ovo tijelo giba jednoliko ubrzano iz stanja mirovanja.

5. U koju svrhu se mogu koristiti pravilnosti (3) i (4)?

Pravilnosti (3) i (4) se koriste za određivanje je li kretanje jednoliko ubrzano ili ne (vidi str.33).

Vježbe.

1. Vlak koji polazi s kolodvora tijekom prvih 20 s kreće se pravocrtno i jednoliko ubrzano. Poznato je da je u trećoj sekundi od početka kretanja vlak prešao 2 m. Odredite modul vektora pomaka koji je vlak napravio u prvoj sekundi i modul vektora ubrzanja s kojim se kretao.

Stranica 8 od 12

§ 7. Kretanje s jednoliko ubrzanim
pravolinijsko gibanje

1. Koristeći graf brzine u odnosu na vrijeme, možete dobiti formulu za pomicanje tijela jednoličnim pravolinijskim gibanjem.

Na slici 30. prikazan je graf projekcije brzine jednolikog kretanja na os x s vremena. Ako u nekoj točki postavimo okomicu na vremensku os C, tada dobivamo pravokutnik OABC. Površina ovog pravokutnika jednaka je umnošku stranica OA i OC. Ali bočna duljina OA jednako je v x, i duljina strane OC - t, stoga S = v x t. Umnožak projekcije brzine na os x a vrijeme je jednako projekciji pomaka, t.j. s x = v x t.

Tako, projekcija pomaka za jednoliko pravolinijsko gibanje brojčano je jednaka površini pravokutnika omeđenog koordinatnim osi, grafom brzine i okomicom podignutom na vremensku os.

2. Na sličan način dobivamo formulu za projekciju pomaka u pravocrtnom jednoliko ubrzanom gibanju. Da bismo to učinili, koristimo graf ovisnosti projekcije brzine na os x od vremena (slika 31). Odaberite malo područje na grafikonu ab i ispusti okomice iz točaka a i b na vremenskoj osi. Ako je vremenski interval D t, što odgovara odjeljku CD na vremenskoj osi mala, onda možemo pretpostaviti da se brzina tijekom tog vremenskog razdoblja ne mijenja i da se tijelo giba jednoliko. U ovom slučaju lik cabd malo se razlikuje od pravokutnika i njegova je površina brojčano jednaka projekciji kretanja tijela u vremenu koje odgovara segmentu CD.

Možete razbiti cijelu figuru u takve trake OABC, a njegova površina bit će jednaka zbroju površina svih traka. Dakle, projekcija kretanja tijela tijekom vremena t brojčano jednak površini trapeza OABC. Iz kolegija geometrije znate da je površina trapeza jednaka umnošku polovice zbroja njegovih baza i visine: S= (OA + PRIJE KRISTA)OC.

Kao što se može vidjeti sa slike 31, OA = v 0x , PRIJE KRISTA = v x, OC = t. Slijedi da se projekcija pomaka izražava formulom: s x= (v x + v 0x)t.

Kod jednoliko ubrzanog pravocrtnog gibanja brzina tijela u svakom trenutku jednaka je v x = v 0x + a x t, stoga, s x = (2v 0x + a x t)t.

Odavde:

Da bismo dobili jednadžbu gibanja tijela, u formulu projekcije pomaka zamjenjujemo njegov izraz kroz razliku koordinata s x = x – x 0 .

dobivamo: x – x 0 = v 0x t+ , ili

x = x 0 + v 0x t + .

Prema jednadžbi gibanja moguće je u svakom trenutku odrediti koordinatu tijela, ako su poznate početna koordinata, početna brzina i akceleracija tijela.

3. U praksi se često javljaju problemi u kojima je potrebno pronaći pomak tijela tijekom jednoliko ubrzanog pravocrtnog gibanja, ali je vrijeme gibanja nepoznato. U tim se slučajevima koristi drugačija formula za projekciju pomaka. Nabavimo to.

Iz formule za projekciju brzine jednoliko ubrzanog pravocrtnog gibanja v x = v 0x + a x t izrazimo vrijeme:

t = .

Zamjenom ovog izraza u formulu projekcije pomaka, dobivamo:

s x = v 0x + .

Odavde:

s x = , ili
–= 2a x s x.

Ako je početna brzina tijela nula, tada:

2a x s x.

4. Primjer rješenja problema

Skijaš se kreće niz planinsku padinu iz stanja mirovanja s ubrzanjem od 0,5 m/s 2 za 20 s, a zatim se kreće duž horizontalne dionice, prešavši do zaustavljanja od 40 m. S kojim se ubrzanjem skijaš kretao duž vodoravna površina? Kolika je duljina padine planine?

S obzirom na to:	Odluka
v 01 = 0 a 1 = 0,5 m/s 2 t 1 = 20 s s 2 = 40 m v 2 = 0	Kretanje skijaša sastoji se od dvije etape: u prvom stupnju, spuštajući se s padine planine, skijaš se kreće sve većom brzinom u apsolutnoj vrijednosti; u drugoj fazi, kada se kreće duž vodoravne površine, njegova se brzina smanjuje. Vrijednosti koje se odnose na prvu fazu pokreta bit će zapisane indeksom 1, a one vezane za drugu fazu indeksom 2.
a 2? s 1?

Spojit ćemo referentni sustav sa Zemljom, osi x usmjerimo u smjeru brzine skijaša u svakoj fazi njegova kretanja (slika 32).

Napišimo jednadžbu za brzinu skijaša na kraju spuštanja s planine:

v 1 = v 01 + a 1 t 1 .

U projekcijama na os x dobivamo: v 1x = a 1x t. Budući da su projekcije brzine i ubrzanja na os x su pozitivni, modul brzine skijaša je: v 1 = a 1 t 1 .

Napišimo jednadžbu koja povezuje projekcije brzine, ubrzanja i kretanja skijaša u drugoj fazi kretanja:

–= 2a 2x s 2x .

S obzirom da je početna brzina skijaša u ovoj fazi kretanja jednaka njegovoj konačnoj brzini u prvoj fazi

v 02 = v 1 , v 2x= 0 dobivamo

– = –2a 2 s 2 ; (a 1 t 1) 2 = 2a 2 s 2 .

Odavde a 2 = ;

a 2 == 0,125 m/s 2.

Modul kretanja skijaša u prvoj fazi kretanja jednak je duljini planinske padine. Napišimo jednadžbu za pomak:

s 1x = v 01x t + .

Stoga je duljina planinske padine s 1 = ;

s 1 == 100 m.

Odgovor: a 2 \u003d 0,125 m / s 2; s 1 = 100 m.

Pitanja za samoispitivanje

1. Kao prema dijagramu projekcije brzine ravnomjernog pravocrtnog gibanja na os x

2. Kao prema grafu projekcije brzine jednoliko ubrzanog pravocrtnog gibanja na os x od vremena odrediti projekciju pomaka tijela?

3. Koja se formula koristi za izračunavanje projekcije pomaka tijela tijekom jednoliko ubrzanog pravocrtnog gibanja?

4. Kojom se formulom izračunava projekcija pomaka tijela koje se giba jednoliko ubrzano i pravocrtno ako je početna brzina tijela nula?

Zadatak 7

1. Koliki je modul pomaka automobila za 2 minute ako se za to vrijeme njegova brzina promijenila od 0 do 72 km/h? Koja je koordinata automobila u tom trenutku t= 2 min? Pretpostavlja se da je početna koordinata nula.

2. Vlak se kreće početnom brzinom od 36 km/h i ubrzanjem od 0,5 m/s 2 . Koliki je pomak vlaka za 20 s i njegova koordinata u trenutku vremena t= 20 s ako je početna koordinata vlaka 20 m?

3. Koliko se kretao biciklist 5 s nakon početka kočenja, ako je njegova početna brzina pri kočenju 10 m/s, a ubrzanje 1,2 m/s 2? Kolika je koordinata biciklista u vremenu t= 5 s, ako je u početnom trenutku vremena bilo u ishodištu?

4. Automobil koji se kreće brzinom od 54 km/h zaustavlja se pri kočenju na 15 sekundi. Koliki je modul pomaka automobila pri kočenju?

5. Dva automobila se kreću jedan prema drugom iz dva naselja koja se nalaze na udaljenosti od 2 km jedno od drugog. Početna brzina jednog automobila je 10 m/s i akceleracija je 0,2 m/s 2 , početna brzina drugog je 15 m/s, a ubrzanje je 0,2 m/s 2 . Odredite vrijeme i koordinate mjesta susreta automobila.

Laboratorij broj 1

Proučavanje jednoliko ubrzanog
pravolinijsko gibanje

Cilj:

naučiti kako mjeriti ubrzanje u jednoliko ubrzanom pravocrtnom gibanju; eksperimentalno utvrditi omjer putova koje tijelo prijeđe tijekom jednoliko ubrzanog pravocrtnog gibanja u uzastopnim jednakim vremenskim intervalima.

Uređaji i materijali:

padobran, tronožac, metalna kugla, štoperica, mjerna traka, metalni cilindar.

Radni nalog

1. Pričvrstite jedan kraj žlijeba u podnožje stativa tako da tvori mali kut s površinom stola, a na drugi kraj žlijeba stavite metalni cilindar u njega.

2. Izmjerite putanje koje je loptica prešla u 3 uzastopna vremenska intervala jednaka po 1 s. To se može učiniti na različite načine. Možete staviti oznake na padobran s kredom, fiksirajući položaj lopte u vremenskim točkama jednakim 1 s, 2 s, 3 s, i mjeriti udaljenosti s_ između ovih oznaka. Moguće je, svaki put puštajući loptu s iste visine, izmjeriti putanju s, prošao pored njega prvo za 1 s, zatim za 2 s i za 3 s, a zatim izračunaj put koji je lopta prešla u drugoj i trećoj sekundi. Zabilježite rezultate mjerenja u tablicu 1.

3. Nađi omjer prijeđenog puta u drugoj sekundi i puta prijeđenog u prvoj sekundi, te puta prijeđenog u trećoj sekundi i puta prijeđenog u prvoj sekundi. Donesite zaključak.

4. Izmjerite vrijeme koje je lopta putovala duž žlijeba i udaljenost koju je prešla. Izračunajte njegovu akceleraciju pomoću formule s = .

5. Koristeći eksperimentalno dobivenu vrijednost akceleracije izračunaj putove koje lopta mora proći u prvoj, drugoj i trećoj sekundi svog kretanja. Donesite zaključak.

stol 1

broj iskustva	Eksperimentalni podaci					Teorijski rezultati
	Vrijeme t , s	Put s , cm	Vrijeme t , s	Put s, cm	Ubrzanje a, cm/s2	Vrijemet, s	Put s , cm
1	1		1

Brzina (v) je fizička veličina, brojčano jednaka putu (s) koji tijelo prijeđe u jedinici vremena (t).

Put

Put (S) - duljina putanje po kojoj se tijelo kretalo, brojčano je jednaka umnošku brzine (v) tijela i vremena (t) kretanja.

Vrijeme putovanja

Vrijeme kretanja (t) jednako je omjeru puta (S) koji je prešlo tijelo i brzine (v) kretanja.

Prosječna brzina

Prosječna brzina (vav) jednaka je omjeru zbroja dionica puta (s 1 s 2, s 3, ...) koje pređe tijelo i vremenskog intervala (t 1 + t 2 + t 3 + ...) za koji je ovaj put pređen .

Prosječna brzina je omjer duljine puta koji je prešlo tijelo i vremena za koje je ovaj put prešao.

Prosječna brzina kada se krećete neravnomjerno u pravoj liniji: ovo je omjer cijelog puta prema ukupnom vremenu.

Dvije uzastopne etape s različitim brzinama: gdje

Prilikom rješavanja problema - koliko će faza kretanja biti toliko komponenti:

Projekcije vektora pomaka na koordinatne osi

Projekcija vektora pomaka na os OX:

Projekcija vektora pomaka na os OY:

Projekcija vektora na os je nula ako je vektor okomit na os.

Znakovi projekcija pomaka: projekcija se smatra pozitivnom ako se kretanje od projekcije početka vektora do projekcije kraja događa u smjeru osi, a negativnom ako je prema osi. U ovom primjeru

Modul za kretanje je duljina vektora pomaka:

Prema Pitagorinoj teoremi:

Projekcije kretanja i kut nagiba

U ovom primjeru:

Koordinatna jednadžba (općenito):

Radijus vektor- vektor, čiji se početak podudara s ishodištem koordinata, a kraj - s položajem tijela u danom trenutku. Projekcije radijus vektora na koordinatne osi određuju koordinate tijela u danom trenutku.

Radijus vektor vam omogućuje da postavite položaj materijalne točke u danom referentni sustav:

Ravnomjerno pravolinijsko gibanje - definicija

Ravnomjerno pravolinijsko gibanje- kretanje u kojem tijelo za bilo koje jednake vremenske intervale čini jednake pomake.

Brzina u ravnomjernom pravocrtnom kretanju. Brzina je vektorska fizička veličina koja pokazuje koliko se kretalo tijelo u jedinici vremena.

U vektorskom obliku:

U projekcijama na os OX:

Dodatne jedinice brzine:

1 km/h = 1000 m/3600 s,

1 km/s = 1000 m/s,

1 cm/s = 0,01 m/s,

1 m/min = 1 m/60 s.

Mjerni uređaj - brzinomjer - pokazuje modul brzine.

Predznak projekcije brzine ovisi o smjeru vektora brzine i koordinatnoj osi:

Graf projekcije brzine je ovisnost projekcije brzine o vremenu:

Grafikon brzine za jednoliko pravocrtno gibanje- ravna linija paralelna s vremenskom osi (1, 2, 3).

Ako graf leži iznad vremenske osi (.1), tada se tijelo pomiče u smjeru osi OX. Ako se graf nalazi ispod vremenske osi, tada se tijelo pomiče prema osi OX (2, 3).

Geometrijsko značenje kretanja.

Kod ravnomjernog pravolinijskog gibanja, pomak se određuje formulom. Isti rezultat dobivamo ako izračunamo površinu figure ispod grafa brzine u osi. Dakle, za određivanje putanje i modula pomaka tijekom pravocrtnog gibanja, potrebno je izračunati površinu figure ispod grafikona brzine u osi:

Pločica projekcije pomaka- ovisnost projekcije pomaka o vremenu.

Grafikon projekcije pomaka za jednoliko pravolinijsko gibanje- ravna crta koja izlazi iz ishodišta (1, 2, 3).

Ako pravac (1) leži iznad vremenske osi, tada se tijelo giba u smjeru osi OX, a ako ispod osi (2, 3), onda prema osi OX.

Što je veća tangenta nagiba (1) grafa, to je veći modul brzine.

Koordinata parcele- ovisnost koordinata tijela o vremenu:

Koordinate grafa za ravnomjerno pravocrtno gibanje - ravne linije (1, 2, 3).

Ako se tijekom vremena koordinata poveća (1, 2), tada se tijelo pomiče u smjeru osi OX; ako se koordinata smanji (3), tada se tijelo pomiče protiv smjera osi OX.

Što je veća tangenta nagiba (1), to je veći modul brzine.

Ako se grafovi koordinata dvaju tijela sijeku, tada iz točke presjeka treba spustiti okomice na vremensku os i koordinatnu os.

Relativnost mehaničkog gibanja

Pod relativnošću podrazumijevamo ovisnost nečega o izboru referentnog okvira. Na primjer, mir je relativan; relativno kretanje i relativni položaj tijela.

Pravilo zbrajanja pomaka. Vektorski zbroj pomaka

gdje je pomak tijela u odnosu na pokretni referentni okvir (RFR); - kretanje PSO-a u odnosu na fiksni referentni okvir (FRS); - kretanje tijela u odnosu na fiksni referentni okvir (FRS).

Vektorski dodatak:

Zbrajanje vektora usmjerenih duž jedne ravne linije:

Zbrajanje vektora okomitih jedan na drugi

Prema Pitagorinoj teoremi

Izvedimo formulu kojom se može izračunati projekcija vektora pomaka tijela koje se kreće pravocrtno i jednoliko ubrzano za bilo koji vremenski period. Da bismo to učinili, okrenimo se slici 14. I na slici 14, a i na slici 14, b, segment AC je graf projekcije vektora brzine tijela koje se kreće konstantnom akceleracijom a (početnom brzinom v 0).

Riža. 14. Projekcija vektora pomaka tijela koje se kreće pravocrtno i jednoliko ubrzano brojčano je jednaka površini S ispod grafa

Podsjetimo da je kod pravocrtnog jednolikog gibanja tijela projekcija vektora pomaka koju je napravilo ovo tijelo određena istom formulom kao i površina pravokutnika zatvorenog ispod grafa projekcije vektora brzine (vidi sliku 6). Stoga je projekcija vektora pomaka numerički jednaka površini ovog pravokutnika.

Dokažimo da se u slučaju pravocrtnog jednoliko ubrzanog gibanja projekcija vektora pomaka s x može odrediti istom formulom kao i površina lika zatvorene između grafa AC, osi Ot i odsječaka OA i BC , tj. u ovom slučaju, projekcija vektora pomaka numerički jednaka površini figure ispod grafa brzine. Da bismo to učinili, na osi Ot (vidi sliku 14, a) odabiremo mali vremenski interval db. Iz točaka d i b povlačimo okomice na os Ot dok se ne sijeku s grafom projekcije vektora brzine u točkama a i c.

Dakle, za vrijeme koje odgovara segmentu db, brzina tijela se mijenja od v ax do v cx.

Za dovoljno kratko vrijeme projekcija vektora brzine se vrlo malo mijenja. Stoga se kretanje tijela u tom vremenskom razdoblju malo razlikuje od jednolikog, odnosno od kretanja konstantnom brzinom.

Moguće je podijeliti cijelo područje figure OASV, koja je trapez, na takve trake. Stoga je projekcija vektora pomaka sx za vremenski interval koji odgovara segmentu OB brojčano jednaka površini S trapeza OASV i određena je istom formulom kao i ovo područje.

Prema pravilu danom u školskim kolegijima geometrije, površina trapeza jednaka je umnošku polovice zbroja njegovih baza i visine. Slika 14, b pokazuje da su osnovice trapeza OASV odsjeci OA = v 0x i BC = v x, a visina je odsječak OB = t. Stoga,

Budući da v x \u003d v 0x + a x t, a S \u003d s x, onda možemo napisati:

Tako smo dobili formulu za izračun projekcije vektora pomaka tijekom jednoliko ubrzanog gibanja.

Po istoj formuli izračunava se i projekcija vektora pomaka kada se tijelo kreće sa opadajućim modulom brzine, samo će u tom slučaju vektori brzine i ubrzanja biti usmjereni u suprotnim smjerovima, pa će njihove projekcije imati različite predznake.

Pitanja

1. Pomoću slike 14, a dokazati da je projekcija vektora pomaka tijekom jednoliko ubrzanog gibanja brojčano jednaka površini OASV figure.
2. Zapišite jednadžbu za određivanje projekcije vektora pomaka tijela tijekom njegovog pravocrtnog jednoliko ubrzanog gibanja.

Vježba 7

Stranica 8 od 12

§ 7. Kretanje s jednoliko ubrzanim
pravolinijsko gibanje

1. Koristeći graf brzine u odnosu na vrijeme, možete dobiti formulu za pomicanje tijela jednoličnim pravolinijskim gibanjem.

Na slici 30. prikazan je graf projekcije brzine jednolikog kretanja na os x s vremena. Ako u nekoj točki postavimo okomicu na vremensku os C, tada dobivamo pravokutnik OABC. Površina ovog pravokutnika jednaka je umnošku stranica OA i OC. Ali bočna duljina OA jednako je v x, i duljina strane OC - t, stoga S = v x t. Umnožak projekcije brzine na os x a vrijeme je jednako projekciji pomaka, t.j. s x = v x t.

Tako, projekcija pomaka za jednoliko pravolinijsko gibanje brojčano je jednaka površini pravokutnika omeđenog koordinatnim osi, grafom brzine i okomicom podignutom na vremensku os.

2. Na sličan način dobivamo formulu za projekciju pomaka u pravocrtnom jednoliko ubrzanom gibanju. Da bismo to učinili, koristimo graf ovisnosti projekcije brzine na os x od vremena (slika 31). Odaberite malo područje na grafikonu ab i ispusti okomice iz točaka a i b na vremenskoj osi. Ako je vremenski interval D t, što odgovara odjeljku CD na vremenskoj osi mala, onda možemo pretpostaviti da se brzina tijekom tog vremenskog razdoblja ne mijenja i da se tijelo giba jednoliko. U ovom slučaju lik cabd malo se razlikuje od pravokutnika i njegova je površina brojčano jednaka projekciji kretanja tijela u vremenu koje odgovara segmentu CD.

Možete razbiti cijelu figuru u takve trake OABC, a njegova površina bit će jednaka zbroju površina svih traka. Dakle, projekcija kretanja tijela tijekom vremena t brojčano jednak površini trapeza OABC. Iz kolegija geometrije znate da je površina trapeza jednaka umnošku polovice zbroja njegovih baza i visine: S= (OA + PRIJE KRISTA)OC.

Kao što se može vidjeti sa slike 31, OA = v 0x , PRIJE KRISTA = v x, OC = t. Slijedi da se projekcija pomaka izražava formulom: s x= (v x + v 0x)t.

Kod jednoliko ubrzanog pravocrtnog gibanja brzina tijela u svakom trenutku jednaka je v x = v 0x + a x t, stoga, s x = (2v 0x + a x t)t.

Da bismo dobili jednadžbu gibanja tijela, u formulu projekcije pomaka zamjenjujemo njegov izraz kroz razliku koordinata s x = x – x 0 .

dobivamo: x – x 0 = v 0x t+ , ili

x = x 0 + v 0x t + .

Prema jednadžbi gibanja moguće je u svakom trenutku odrediti koordinatu tijela, ako su poznate početna koordinata, početna brzina i akceleracija tijela.

3. U praksi se često javljaju problemi u kojima je potrebno pronaći pomak tijela tijekom jednoliko ubrzanog pravocrtnog gibanja, ali je vrijeme gibanja nepoznato. U tim se slučajevima koristi drugačija formula za projekciju pomaka. Nabavimo to.

Iz formule za projekciju brzine jednoliko ubrzanog pravocrtnog gibanja v x = v 0x + a x t izrazimo vrijeme:

Zamjenom ovog izraza u formulu projekcije pomaka, dobivamo:

s x = v 0x + .

s x = , ili
–= 2a x s x.

Ako je početna brzina tijela nula, tada:

2a x s x.

4. Primjer rješenja problema

Skijaš se kreće niz planinsku padinu iz stanja mirovanja s ubrzanjem od 0,5 m/s 2 za 20 s, a zatim se kreće duž horizontalne dionice, prešavši do zaustavljanja od 40 m. S kojim se ubrzanjem skijaš kretao duž vodoravna površina? Kolika je duljina padine planine?

S obzirom na to:
v 01 = 0 a 1 = 0,5 m/s 2 t 1 = 20 s s 2 = 40 m v 2 = 0	Kretanje skijaša sastoji se od dvije etape: u prvom stupnju, spuštajući se s padine planine, skijaš se kreće sve većom brzinom u apsolutnoj vrijednosti; u drugoj fazi, kada se kreće duž vodoravne površine, njegova se brzina smanjuje. Vrijednosti koje se odnose na prvu fazu pokreta bit će zapisane indeksom 1, a one vezane za drugu fazu indeksom 2.
a 2? s 1?

Spojit ćemo referentni sustav sa Zemljom, osi x usmjerimo u smjeru brzine skijaša u svakoj fazi njegova kretanja (slika 32).

Napišimo jednadžbu za brzinu skijaša na kraju spuštanja s planine:

v 1 = v 01 + a 1 t 1 .

U projekcijama na os x dobivamo: v 1x = a 1x t. Budući da su projekcije brzine i ubrzanja na os x su pozitivni, modul brzine skijaša je: v 1 = a 1 t 1 .

Napišimo jednadžbu koja povezuje projekcije brzine, ubrzanja i kretanja skijaša u drugoj fazi kretanja:

–= 2a 2x s 2x .

S obzirom da je početna brzina skijaša u ovoj fazi kretanja jednaka njegovoj konačnoj brzini u prvoj fazi

v 02 = v 1 , v 2x= 0 dobivamo

– = –2a 2 s 2 ; (a 1 t 1) 2 = 2a 2 s 2 .

Odavde a 2 = ;

a 2 == 0,125 m/s 2.

Modul kretanja skijaša u prvoj fazi kretanja jednak je duljini planinske padine. Napišimo jednadžbu za pomak:

s 1x = v 01x t + .

Stoga je duljina planinske padine s 1 = ;

s 1 == 100 m.

Odgovor: a 2 \u003d 0,125 m / s 2; s 1 = 100 m.

Pitanja za samoispitivanje

1. Kao prema dijagramu projekcije brzine ravnomjernog pravocrtnog gibanja na os x

2. Kao prema grafu projekcije brzine jednoliko ubrzanog pravocrtnog gibanja na os x od vremena odrediti projekciju pomaka tijela?

3. Koja se formula koristi za izračunavanje projekcije pomaka tijela tijekom jednoliko ubrzanog pravocrtnog gibanja?

4. Kojom se formulom izračunava projekcija pomaka tijela koje se giba jednoliko ubrzano i pravocrtno ako je početna brzina tijela nula?

Zadatak 7

1. Koliki je modul pomaka automobila za 2 minute ako se za to vrijeme njegova brzina promijenila od 0 do 72 km/h? Koja je koordinata automobila u tom trenutku t= 2 min? Pretpostavlja se da je početna koordinata nula.

2. Vlak se kreće početnom brzinom od 36 km/h i ubrzanjem od 0,5 m/s 2 . Koliki je pomak vlaka za 20 s i njegova koordinata u trenutku vremena t= 20 s ako je početna koordinata vlaka 20 m?

3. Koliko se kretao biciklist 5 s nakon početka kočenja, ako je njegova početna brzina pri kočenju 10 m/s, a ubrzanje 1,2 m/s 2? Kolika je koordinata biciklista u vremenu t= 5 s, ako je u početnom trenutku vremena bilo u ishodištu?

4. Automobil koji se kreće brzinom od 54 km/h zaustavlja se pri kočenju na 15 sekundi. Koliki je modul pomaka automobila pri kočenju?

5. Dva automobila se kreću jedan prema drugom iz dva naselja koja se nalaze na udaljenosti od 2 km jedno od drugog. Početna brzina jednog automobila je 10 m/s i akceleracija je 0,2 m/s 2 , početna brzina drugog je 15 m/s, a ubrzanje je 0,2 m/s 2 . Odredite vrijeme i koordinate mjesta susreta automobila.

Laboratorij broj 1

Proučavanje jednoliko ubrzanog
pravolinijsko gibanje

Cilj:

naučiti kako mjeriti ubrzanje u jednoliko ubrzanom pravocrtnom gibanju; eksperimentalno utvrditi omjer putova koje tijelo prijeđe tijekom jednoliko ubrzanog pravocrtnog gibanja u uzastopnim jednakim vremenskim intervalima.

Uređaji i materijali:

padobran, tronožac, metalna kugla, štoperica, mjerna traka, metalni cilindar.

Radni nalog

1. Pričvrstite jedan kraj žlijeba u podnožje stativa tako da tvori mali kut s površinom stola, a na drugi kraj žlijeba stavite metalni cilindar u njega.

2. Izmjerite putanje koje je loptica prešla u 3 uzastopna vremenska intervala jednaka po 1 s. To se može učiniti na različite načine. Možete staviti oznake na padobran s kredom, fiksirajući položaj lopte u vremenskim točkama jednakim 1 s, 2 s, 3 s, i mjeriti udaljenosti s_ između ovih oznaka. Moguće je, svaki put puštajući loptu s iste visine, izmjeriti putanju s, prošao pored njega prvo za 1 s, zatim za 2 s i za 3 s, a zatim izračunaj put koji je lopta prešla u drugoj i trećoj sekundi. Zabilježite rezultate mjerenja u tablicu 1.

3. Nađi omjer prijeđenog puta u drugoj sekundi i puta prijeđenog u prvoj sekundi, te puta prijeđenog u trećoj sekundi i puta prijeđenog u prvoj sekundi. Donesite zaključak.

4. Izmjerite vrijeme koje je lopta putovala duž žlijeba i udaljenost koju je prešla. Izračunajte njegovu akceleraciju pomoću formule s = .

5. Koristeći eksperimentalno dobivenu vrijednost akceleracije izračunaj putove koje lopta mora proći u prvoj, drugoj i trećoj sekundi svog kretanja. Donesite zaključak.

stol 1

broj iskustva	Eksperimentalni podaci					Teorijski rezultati
	Vrijeme t , s	Put s , cm	Vrijeme t , s	Put s, cm	Ubrzanje a, cm/s2	Vrijemet, s	Put s , cm
1	1		1

Kako, poznavajući zaustavni put, odrediti početnu brzinu automobila i kako, poznavajući karakteristike kretanja, kao što su početna brzina, ubrzanje, vrijeme, odrediti kretanje automobila? Odgovore ćemo dobiti nakon što se upoznamo s temom današnje lekcije: "Pomak pri jednoliko ubrzanom kretanju, ovisnost koordinata o vremenu uz jednoliko ubrzano kretanje"

Uz jednoliko ubrzano kretanje, graf izgleda kao ravna crta koja ide prema gore, budući da je njegova projekcija ubrzanja veća od nule.

Kod ravnomjernog pravolinijskog gibanja, površina će biti brojčano jednaka modulu projekcije pomaka tijela. Ispada da se ta činjenica može generalizirati za slučaj ne samo jednolikog gibanja, već i za bilo koje gibanje, odnosno pokazati da je površina ispod grafa brojčano jednaka modulu projekcije pomaka. To se radi strogo matematički, ali ćemo koristiti grafičku metodu.

Riža. 2. Grafikon ovisnosti brzine o vremenu kod jednoliko ubrzanog kretanja ()

Podijelimo graf projekcije brzine od vremena za jednoliko ubrzano gibanje na male vremenske intervale Δt. Pretpostavimo da su toliko mali da se tijekom njihove duljine brzina praktički nije promijenila, odnosno uvjetno ćemo graf linearne ovisnosti na slici pretvoriti u ljestve. Na svakom njegovom koraku vjerujemo da se brzina nije puno promijenila. Zamislimo da vremenske intervale Δt činimo beskonačno malima. U matematici kažu: pravimo prolaz do granice. U ovom slučaju, površina takve ljestve će se neograničeno usko podudarati s površinom trapeza, koja je ograničena grafom V x (t). A to znači da za slučaj jednoliko ubrzanog gibanja možemo reći da je modul projekcije pomaka numerički jednak površini omeđenoj grafom V x (t): apscisa i ordinatna os i okomica spuštena na os apscise, odnosno površina trapeza OABS, koju vidimo na slici 2.

Problem se iz fizičkog pretvara u matematički - pronalaženje površine trapeza. To je standardna situacija kada fizičari naprave model koji opisuje određenu pojavu, a onda na scenu stupa matematika koja ovaj model obogaćuje jednadžbama, zakonima – koji model pretvaraju u teoriju.

Nalazimo područje trapeza: trapez je pravokutan, budući da je kut između osi 90 0, trapez dijelimo na dva oblika - pravokutnik i trokut. Očito će ukupna površina biti jednaka zbroju površina ovih figura (slika 3). Nađimo njihova područja: površina pravokutnika jednaka je umnošku stranica, odnosno V 0x t, površina pravokutnog trokuta bit će jednaka polovici umnoška nogu - 1/2AD BD, zamjenom vrijednosti projekcije, dobivamo: 1/2t (V x - V 0x), a, prisjetimo se zakona promjene brzine iz vremena s jednoliko ubrzanim gibanjem: V x (t) = V 0x + a x t, to je sasvim očito da je razlika u projekcijama brzina jednaka umnošku projekcije akceleracije a x po vremenu t, odnosno V x - V 0x = a x t.

Riža. 3. Određivanje površine trapeza ( Izvor)

Uzimajući u obzir činjenicu da je površina trapeza numerički jednaka modulu projekcije pomaka, dobivamo:

S x (t) \u003d V 0 x t + a x t 2 / 2

Dobili smo zakon ovisnosti projekcije pomaka o vremenu s jednoliko ubrzanim gibanjem u skalarnom obliku, u vektorskom obliku će izgledati ovako:

(t) = t + t 2 / 2

Izvedimo još jednu formulu za projekciju pomaka, koja neće uključivati ​​vrijeme kao varijablu. Rješavamo sustav jednadžbi, isključujući vrijeme iz njega:

S x (t) \u003d V 0 x + a x t 2 / 2

V x (t) \u003d V 0 x + a x t

Zamislite da ne znamo vrijeme, tada ćemo vrijeme izraziti iz druge jednadžbe:

t \u003d V x - V 0x / a x

Zamijenite rezultirajuću vrijednost u prvu jednadžbu:

Dobivamo tako glomazan izraz, kvadriramo ga i dajemo slične:

Dobili smo vrlo zgodan izraz za projekciju pomaka za slučaj kada ne znamo vrijeme gibanja.

Neka nam je početna brzina automobila, kada je počelo kočenje, V 0 \u003d 72 km / h, konačna brzina V = 0, ubrzanje a = 4 m / s 2. Saznajte duljinu puta kočenja. Pretvaranjem kilometara u metre i zamjenom vrijednosti u formulu, dobivamo da će zaustavni put biti:

S x \u003d 0 - 400 (m / s) 2 / -2 4 m / s 2 = 50 m

Analizirajmo sljedeću formulu:

S x \u003d (V 0 x + V x) / 2 t

Projekcija kretanja je polovica zbroja projekcija početne i konačne brzine, pomnožene s vremenom kretanja. Prisjetite se formule pomaka za prosječnu brzinu

S x \u003d V usp t

U slučaju ravnomjerno ubrzanog kretanja, prosječna brzina će biti:

V cf \u003d (V 0 + V k) / 2

Približili smo se rješavanju glavnog problema mehanike jednoliko ubrzanog gibanja, odnosno dobivanju zakona prema kojem se koordinata mijenja s vremenom:

x(t) \u003d x 0 + V 0 x t + a x t 2 / 2

Kako bismo naučili kako koristiti ovaj zakon, analizirat ćemo tipičan problem.

Automobil, krećući se iz stanja mirovanja, postiže ubrzanje od 2 m / s 2. Pronađite put koji je automobil prešao za 3 sekunde i za treću sekundu.

Zadano: V 0 x = 0

Zapišimo zakon prema kojem se pomak mijenja s vremenom u

jednoliko ubrzano gibanje: S x \u003d V 0 x t + a x t 2 /2. 2 c

Na prvo pitanje problema možemo odgovoriti dodavanjem podataka:

t 1 \u003d 3 c S 1x \u003d a x t 2 / 2 \u003d 2 3 2 / 2 \u003d 9 (m) - ovo je put koji je otišao

c auto za 3 sekunde.

Saznajte koliko je daleko prešao u 2 sekunde:

S x (2 s) \u003d a x t 2 / 2 \u003d 2 2 2 / 2 \u003d 4 (m)

Dakle, ti i ja znamo da je auto u dvije sekunde prešao 4 metra.

Sada, znajući ove dvije udaljenosti, možemo pronaći put koji je prešao u trećoj sekundi:

S 2x = S 1x + S x (2 s) = 9 - 4 \u003d 5 (m)

Ravnomjerno ubrzano kretanje naziva se takvo kretanje u kojem vektor ubrzanja ostaje nepromijenjen po veličini i smjeru. Primjer takvog kretanja je pomicanje kamena bačenog pod određenim kutom prema horizontu (zanemarujući otpor zraka). U bilo kojoj točki putanje, ubrzanje kamena jednako je ubrzanju slobodnog pada. Dakle, proučavanje jednoliko ubrzanog gibanja svodi se na proučavanje pravocrtnog jednoliko ubrzanog gibanja. U slučaju pravocrtnog gibanja, vektori brzine i ubrzanja usmjereni su duž ravne linije gibanja. Stoga se brzina i ubrzanje u projekcijama na smjer gibanja mogu smatrati algebarskim veličinama. Kod jednoliko ubrzanog pravolinijskog gibanja brzina tijela određena je formulom (1)

U ovoj formuli, brzina tijela na t = 0 (početna brzina ), = const – ubrzanje. U projekciji na odabranu x-os, jednadžba (1) će biti zapisana u obliku: (2). Na grafu projekcije brzine υ x ( t), ova ovisnost ima oblik ravne linije.

Nagib grafa brzine može se koristiti za određivanje ubrzanja a tijelo. Odgovarajuće konstrukcije izrađene su na sl. za graf I Ubrzanje je brojčano jednako omjeru stranica trokuta ABC: .

Što je veći kut β koji formira graf brzine s vremenskom osi, to je veći nagib grafa ( strmina), što je veće ubrzanje tijela.

Za grafikon I: υ 0 \u003d -2 m / s, a\u003d 1/2 m / s 2. Za grafikon II: υ 0 \u003d 3 m / s, a\u003d -1/3 m / s 2.

Grafikon brzine također vam omogućuje da odredite projekciju pomaka s tijela za neko vrijeme t. Dodijelimo na vremenskoj osi neki mali vremenski interval Δt. Ako je ovaj vremenski period dovoljno mali, tada je promjena brzine u tom razdoblju mala, odnosno kretanje tijekom tog vremenskog razdoblja može se smatrati jednoličnim uz određenu prosječnu brzinu, koja je jednaka trenutnoj brzini υ tijelo u sredini intervala Δt. Stoga će pomak Δs tijekom vremena Δt biti jednak Δs = υΔt. Ovaj pomak je jednak površini zasjenjenoj na Sl. pruge. Dijeljenjem vremenskog intervala od 0 do određenog trenutka t na male intervale Δt, možemo dobiti da je pomak s za dano vrijeme t tijekom jednoliko ubrzanog pravolinijskog gibanja jednak površini ODEF trapeza. Odgovarajuće konstrukcije izrađene su na sl. za raspored II. Vrijeme t uzima se jednakim 5,5 s.

(3) - rezultirajuća formula omogućuje određivanje pomaka s jednoliko ubrzanim gibanjem ako ubrzanje nije poznato.

Zamijenimo li izraz za brzinu (2) u jednadžbu (3), dobivamo (4) - ova formula se koristi za pisanje jednadžbe gibanja tijela: (5).

Izrazimo li iz jednadžbe (2) vrijeme gibanja (6) i zamijenimo u jednakost (3), tada

Ova formula vam omogućuje da odredite kretanje u nepoznato vrijeme kretanja.

Razmotrimo kako se izračunava projekcija vektora pomaka tijela koje se kreće jednoliko ubrzano ako je njegova početna brzina v 0 jednaka nuli. U ovom slučaju, jednadžba

izgledat će ovako:

Prepišimo ovu jednadžbu zamjenom u nju, umjesto projekcija s x i a x, modula s i a vektora

pomak i ubrzanje. Budući da su u ovom slučaju vektori sua usmjereni u istom smjeru, njihove projekcije imaju iste predznake. Stoga se jednadžba za module vektora može napisati:

Iz ove formule proizlazi da je kod pravocrtnog jednoliko ubrzanog kretanja bez početne brzine modul vektora pomaka izravno proporcionalan kvadratu vremenskog intervala tijekom kojeg je to kretanje napravljeno. To znači da se s povećanjem vremena kretanja za n puta (računajući od trenutka početka gibanja) kretanje povećava za n 2 puta.

Na primjer, ako se u proizvoljnom vremenskom razdoblju t 1 od početka kretanja tijelo kretalo

tada će se za vrijeme t 2 = 2t 1 (računajući od istog trenutka kada i t 1) kretati

za vremenski period t n \u003d nt l - pomak s n = n 2 s l (gdje je n prirodni broj).

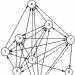
Ova ovisnost modula vektora pomaka o vremenu tijekom pravocrtnog jednoliko ubrzanog kretanja bez početne brzine jasno se odražava na slici 15, gdje su segmenti OA, OB, OS, OD i OE moduli vektora pomaka (s 1, s 2, s 3, s 4 i s 5), koje je tijelo počinilo za vremenske intervale t 1 , t 2 = 2t 1 , t 3 = 3t 1 , t 4 = 4t 1 i t 5 = 5t 1 .

Riža. 15. Obrasci jednoliko ubrzanog gibanja: OA:OB:OS:OD:0E = 1:4:9:16:25; OA:AB:BC:CD:DE = 1:3:5:7:9

Iz ove brojke je jasno da

OA:OB:OS:OD:OE = 1:4:9:16:25, (1)

tj. s povećanjem vremenskih intervala koji se računaju od početka kretanja, za cijeli broj puta u usporedbi s t 1, moduli odgovarajućih vektora pomaka rastu kao niz kvadrata uzastopnih prirodnih brojeva.

Slika 15 prikazuje još jedan uzorak:

OA:AB:BC:CD:DE = 1:3:5:7:9, (2)

tj. moduli vektora pomaka koje tijelo izvodi u uzastopnim jednakim vremenskim razdobljima (od kojih je svaki jednak t 1) povezani su kao niz uzastopnih neparnih brojeva.

Pravilnosti (1) i (2) svojstvene su samo jednoliko ubrzanom gibanju. Stoga se mogu koristiti ako je potrebno utvrditi je li kretanje jednoliko ubrzano ili ne.

Utvrdimo, na primjer, je li jednoliko ubrzano kretanje pužnice, koja se u prvih 20 sekundi kretanja pomaknula 0,5 cm, u drugih 20 sekundi 1,5 cm, a u trećih 20 sekundi 2,5 cm.

Da bismo to učinili, pronađimo koliko su puta pokreti napravljeni u drugom i trećem vremenskom intervalu veći nego u prvom:

To znači da je 0,5 cm: 1,5 cm: 2,5 cm = 1: 3: 5. Budući da su ti omjeri niz uzastopnih neparnih brojeva, kretanje tijela je jednoliko ubrzano.

U ovom slučaju je na temelju pravilnosti (2) otkrivena jednoliko ubrzana priroda kretanja.

Pitanja

1. Koje se formule koriste za izračunavanje projekcije i modula vektora pomaka tijela tijekom njegova jednoliko ubrzanog kretanja iz stanja mirovanja?
2. Koliko će se puta povećati modul vektora pomaka tijela s povećanjem vremena njegovog kretanja iz mirovanja za n puta?
3. Zapišite kako su moduli vektora pomaka tijela koje se giba jednoliko ubrzano iz stanja mirovanja međusobno povezane s povećanjem vremena njegova kretanja za cijeli broj puta u odnosu na t 1.
4. Zapišite kako su moduli vektora pomaka koje tijelo izvodi u uzastopnim jednakim vremenskim intervalima međusobno povezani ako se ovo tijelo giba jednoliko ubrzano iz stanja mirovanja.
5. Koja je svrha korištenja pravilnosti (1) i (2)?

Vježba 8

1. Vlak koji polazi s kolodvora tijekom prvih 20 s kreće se pravocrtno i jednoliko ubrzano. Poznato je da je u trećoj sekundi od početka kretanja vlak prešao 2 m. Odredite modul vektora pomaka koji je vlak napravio u prvoj sekundi i modul vektora ubrzanja s kojim se kretao.
2. Automobil koji se giba jednoliko ubrzan iz stanja mirovanja, u petoj sekundi ubrzanja prijeđe 6,3 m. Koju brzinu je automobil razvio do kraja pete sekunde od početka kretanja?
3. Neko tijelo u prvih 0,03 s kretanja bez početne brzine pomaknulo se 2 mm, u prvih 0,06 s - 8 mm, u prvih 0,09 s - 18 mm. Na temelju pravilnosti (1) dokazati da se tijekom svih 0,09 s tijelo kretalo jednoliko ubrzano.