В однорідному електричному полі сила, що діє на заряджену частинку, постійна як за величиною, так і за напрямком. Тому рух такої частки повністю аналогічний до руху тіла в полі тяжкості землі без урахування опору повітря. Траєкторія частинки в цьому випадку є плоскою, лежить у площині, що містить вектори початкової швидкостічастки та напруженості електричного поля
Потенціал електростатичного поля. Загальний вираз, що пов'язує потенціал із напруженістю.
Потенціал у будь-якій точці електростатичного поля є фізична величина, що визначається потенційною енергією одиничного позитивного заряду, поміщеного в цю точку. Потенціал поля, створюваного точковим зарядом Q, дорівнює
Потенціал - фізична величина, яка визначається роботою по переміщенню одиничного позитивного електричного зарядупри видаленні його з цієї точки поля в нескінченність. Ця робота чисельно дорівнює роботі, яку здійснюють зовнішні сили (проти сил електростатичного поля) з переміщення одиничного позитивного заряду з нескінченності в цю точкуполя.
Одиниця потенціалу - вольт (В): 1 В дорівнює потенціалу такої точки поля, в якій заряд в 1 Кл має потенційну енергію 1 Дж (1 В = 1 Дж/Кл). Враховуючи розмірність вольта, можна показати, що введена раніше одиниця напруженості електростатичного поля дійсно дорівнює 1 В/м: 1 Н/Кл=1 Н м/(Кл м)=1 Дж/(Кл м)=1 В/м.
З формул (3) і (4) слід, що й поле створюється кількома зарядами, то потенціал даного поля системи зарядів дорівнює алгебраїчній суміпотенціалів полів усіх цих зарядів:
Напруженість у будь-якій точці електричного поля дорівнює градієнту потенціалу у цій точці, взятому зі зворотним знаком. Знак «мінус» показує, що напруженість E спрямована у бік зменшення потенціалу.
E = - grad фі = - N фі.
Для встановлення зв'язку між силовою характеристикою електричного поля - напруженістю та його енергетичною характеристикою - потенціалом розглянемо елементарну роботу сил електричного поля на нескінченно малому переміщенні точкового заряду q: dA = q E dl, ця ж робота дорівнює втраті потенційної енергії заряду q: dA = - dWп = - q dфі, де d фі - Зміна потенціалу електричного поля на довжині переміщення dl. Прирівнюючи праві частини виразів, отримуємо: E dl = -d фі або декартовій системікоординат
Ex dx + Ey dy + Ez dz = -d фі
де Ex, Ey, Ez – проекції вектора напруженості на осі системи координат. Оскільки вираз є повний диференціал, то для проекцій вектора напруженості маємо
Вираз, що стоїть у дужках, є градієнтом потенціалу фі.
Принцип суперпозиції як фундаментальне властивість полів. Загальні висловлювання для напруженості та потенціалу поля, створюваного в точці з радіус-вектором системою точкових зарядів, що знаходяться в точках з координатами.
Якщо розглянути принцип суперпозиції у найзагальнішому сенсі, то відповідно до нього, сума впливу зовнішніх сил, що діють на частинку, складатиметься з окремих значень кожної з них. Цей принцип застосовується до різних лінійним системам, тобто. таких систем, поведінка яких можна описати лінійними співвідношеннями. Прикладом може бути проста ситуація, коли лінійна хвиля поширюється у певному середовищі, у разі її властивості зберігатимуться навіть під впливом обурень, що виникають через самої хвилі. Ці властивості визначаються як конкретна сума ефектів кожної гармонійних складових.
Принцип суперпозиції може приймати й інші формулювання, які повністю еквівалентні наведеній вище:
· Взаємодія між двома частинками не змінюється при внесенні третьої частки, що також взаємодіє з першими двома.
· Енергія взаємодії всіх частинок у багаточастинній системі є просто сума енергій парних взаємодій між усіма можливими парами частинок. У системі немає багаточасткових взаємодій.
· Рівняння, що описують поведінку багаточасткової системи, є лінійними за кількістю частинок.
6 Циркуляцією вектора напруженості називається робота, яку здійснюють електричні сили при переміщенні одиничного позитивного заряду замкненим шляхом L
Оскільки робота сил електростатичного поля по замкнутому контуру дорівнює нулю (робота сил потенційного поля), отже циркуляція напруженості електростатичного поля по замкнутому контуру дорівнює нулю.
Потенціал сфери. Робота будь-якого електростатичного поля при переміщенні в ньому зарядженого тіла з однієї точки в іншу також не залежить від форми траєкторії, як робота однорідного поля. На замкнутій траєкторії робота електростатичного поля завжди дорівнює нулю. Поля, що мають таку властивість, називають потенційними. Потенційний характер, зокрема, має електростатичне поле точкового заряду.
Роботу потенційного поля можна виразити через зміну потенційної енергії. Формула справедлива для будь-якого електростатичного поля.
7-11Якщо силові лінії однорідного електричного поля напруженістю пронизують деяку площадку S, то потік вектора напруженості (раніше ми називали число силових ліній через майданчик) визначатиметься формулою:
де En - добуток вектора на нормаль до даного майданчика (рис. 2.5).
Рис. 2.5
Повне число силових ліній, що проходять через поверхню S, називається потоком вектора напруженості ФЕ через цю поверхню.
У векторній формі можна записати - скалярне твір двох векторів, де вектор .
Таким чином, потік вектора є скаляр, який залежно від величини кута може бути як позитивним, так і негативним.
Розглянемо приклади, зображені на рисунках 2.6 та 2.7.
 | |||
| Рис. 2.6 | Рис. 2.7 | ||
Для малюнка 2.6 – поверхня А1 оточує позитивний заряд і тут потік спрямований назовні, тобто. Поверхня А2 - оточує негативний заряд, тут і спрямований усередину. Загальний потік через поверхню А дорівнює нулю.
Для малюнку 2.7 – потік не дорівнює нулю, якщо сумарний заряд усередині поверхні не дорівнює нулю. Для цієї конфігурації потік через поверхню А є негативним (підрахуйте число силових ліній).
Таким чином, потік вектора напруги залежить від заряду. У цьому сенсі теореми Остроградського-Гаусса.
Теорема Гауса
Експериментально встановлені закон Кулона та принцип суперпозиції дозволяють повністю описати електростатичне поле заданої системи зарядів у вакуумі. Однак, властивості електростатичного поля можна виразити в іншій, більш загальній формі, не вдаючись до уявлення про кулонівське поле точкового заряду.
Введемо нову фізичну величину, що характеризує електричне поле – потік Φ вектор напруженості електричного поля. Нехай у просторі, де створено електричне поле, розташований деякий досить малий майданчик ΔS. Добуток модуля вектора на площу ΔS та на косинус кута α між вектором та нормаллю до майданчика називається елементарним потоком вектора напруженості через майданчик ΔS (рис. 1.3.1):
Розглянемо тепер деяку довільну замкнуту поверхню S. Якщо розбити цю поверхню на малі майданчики ΔSi, визначити елементарні потоки ΔΦi поля через ці малі майданчики, а потім підсумувати, то в результаті ми отримаємо потік Φ вектора через замкнуту поверхню S (рис. 1.3.2 ):
Теорема Гауса стверджує:
Потік вектора напруженості електростатичного поля через довільну замкнуту поверхню дорівнює сумі алгебри зарядів, розташованих усередині цієї поверхні, поділеної на електричну постійну ε0.
де R - Радіус сфери. Потік Φ через сферичну поверхню буде дорівнює твору E на площу сфери 4πR2. Отже,
Оточимо тепер точковий заряд довільною замкненою поверхнею S і розглянемо допоміжну сферу радіусу R0 (рис. 1.3.3).
Розглянемо конус із малим тілесним кутом ΔΩ при вершині. Цей конус виділить на сфері малий майданчик ΔS0, а на поверхні S – майданчик ΔS. Елементарні потоки ΔΦ0 та ΔΦ через ці майданчики однакові. Справді,
Аналогічним чином можна показати, що якщо замкнута поверхня S не охоплює точкового заряду q, то потік Φ = 0. Такий випадок зображений на рис. 1.3.2. Усі силові лінії електричного поля точкового заряду пронизують замкнуту поверхню S наскрізь. Всередині поверхні S зарядів немає, тому в цій області силові лінії не обриваються та не зароджуються.
Узагальнення теореми Гауса на випадок довільного розподілу зарядів випливає із принципу суперпозиції. Поле будь-якого розподілу зарядів можна як векторну суму електричних полів точкових зарядів. Потік Φ системи зарядів через довільну замкнуту поверхню S складатиметься з потоків Φi електричних полів окремих зарядів. Якщо заряд qi виявився всередині поверхні S, то він дає внесок у потік, рівний якщо цей заряд виявився зовні поверхні, то внесок його електричного поля в потік буде дорівнює нулю.
Таким чином, теорема Гауса доведена.
Теорема Гауса є наслідком закону Кулона та принципу суперпозиції. Але якщо прийняти твердження, що міститься в цій теоремі, за початкову аксіому, її наслідком виявиться закон Кулона. Тому теорему Гауса іноді називають альтернативним формулюванням закону Кулона.
Використовуючи теорему Гауса, можна у ряді випадків легко обчислити напруженість електричного поля навколо зарядженого тіла, якщо заданий розподіл зарядів має будь-яку симетрію і загальну структуру поля можна заздалегідь вгадати.
Прикладом може бути завдання обчислення поля тонкостінного порожнистого однорідно зарядженого довгого циліндра радіуса R. Це має осьову симетрію. З міркувань симетрії електричне поле має бути спрямоване радіусом. Тому для застосування теореми Гауса доцільно вибрати замкнуту поверхню S у вигляді співвісного циліндра деякого радіусу r та довжини l, закритого з обох торців (рис. 1.3.4).
За r ≥ R весь потік вектора напруженості буде проходити через бічну поверхнюциліндра, площа якої дорівнює 2πrl, так як потік через обидва підстави дорівнює нулю. Застосування теореми Гауса дає:
Цей результат не залежить від радіусу R зарядженого циліндра, тому він застосовний і до поля довгої однорідно зарядженої нитки.
Для визначення напруженості поля всередині зарядженого циліндра необхідно побудувати замкнуту поверхню для випадку r< R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.
Аналогічним чином можна застосувати теорему Гауса для визначення електричного поля в ряді інших випадків, коли розподіл зарядів має будь-яку симетрію, наприклад, симетрію щодо центру, площини або осі. У кожному з таких випадків потрібно вибирати замкнуту поверхню гаусса доцільної форми. Наприклад, у випадку центральної симетріїГаусову поверхню зручно вибирати у вигляді сфери з центром у точці симетрії. При осьовий симетріїзамкнуту поверхню потрібно вибирати у вигляді співвісного циліндра, замкненого з обох торців (як у розглянутому вище прикладі). Якщо розподіл зарядів не має будь-якої симетрії і загальну структуру електричного поля вгадати неможливо, застосування теореми Гауса не може спростити завдання визначення напруженості поля.
Розглянемо ще один приклад симетричного розподілу зарядів – визначення поля рівномірно зарядженої площини (рис. 1.3.5).
В цьому випадку гаусову поверхню S доцільно вибрати у вигляді циліндра деякої довжини, закритого з обох торців. Вісь циліндра спрямована перпендикулярно до зарядженої площини, а його торці розташовані на однаковій відстані від неї. У силу симетрії поле рівномірно зарядженої площини має бути скрізь спрямоване за нормаллю. Застосування теореми Гауса дає:
|
де σ - Поверхнева щільність заряду, тобто заряд, що припадає на одиницю площі.
Отриманий вираз для електричного поля однорідно зарядженої площини застосовується і у разі заряджених плоских майданчиків кінцевого розміру. У цьому випадку відстань від точки, в якій визначається напруженість поля, до зарядженого майданчика має бути значно меншою за розміри майданчика.
І графіки до 7 – 11
1. Напруженість електростатичного поля, що створюється рівномірно зарядженою сферичною поверхнею.
Нехай сферична поверхня радіуса R (рис. 13.7) несе рівномірно розподілений заряд q, тобто. поверхнева густина заряду в будь-якій точці сфери буде однакова.
a. Заключимо нашу сферичну поверхню симетричну поверхню S з радіусом r>R. Потік вектора напруженості через поверхню S дорівнюватиме
По теоремі Гауса
Отже
с. Проведемо через точку, що знаходиться всередині зарядженої сферичної поверхні, сферу S радіусом г 2. Електростатичне поле кулі. Нехай маємо шар радіусу R, рівномірно заряджений з об'ємною щільністю. У будь-якій точці А, що лежить поза кулею на відстані r від його центру (r>R), його поле аналогічне до поля точкового заряду, розташованого в центрі кулі. Тоді поза кулею але в його поверхні (r=R) У точці, що лежить всередині кулі на відстаней r від його центру (r>R), поле визначається лише зарядом, укладеним всередині сфери радіусом r. Потік вектора напруженості через цю сферу дорівнює з іншого боку, відповідно до теореми Гауса По теоремі Гауса З останніх двох виразів визначаємо напруженість поля, що створюється рівномірно зарядженою ниткою: Нехай площина має нескінченну протяжність та заряд на одиницю площі дорівнює σ. З законів симетрії випливає, що поле спрямоване всюди перпендикулярно до площини, і якщо не існує жодних інших зовнішніх зарядів, то поля по обидва боки площини повинні бути однакові. Обмежимо частину зарядженої площини уявним циліндричним ящиком, таким чином, щоб ящик розсікався навпіл і його утворюють перпендикулярні, а дві основи, що мають площу S кожна, паралельні зарядженої площини (рис 1.10). 12. Поле рівномірно зарядженої сфери. Нехай електричне поле створюється зарядом Q, рівномірно розподіленим по поверхні сфери радіусу R(Мал. 190). Для обчислення потенціалу поля у довільній точці, що знаходиться на відстані rвід центру сфери, необхідно обчислити роботу, яку виконує поле при переміщенні одиничного позитивного заряду від даної точки до нескінченності. Раніше ми довели, що напруженість поля рівномірно зарядженої сфери поза її еквівалентним полем точкового заряду, розташованого в центрі сфери. Отже, поза сферою потенціал поля сфери збігатиметься з потенціалом поля точкового заряду φ
(r)=Q 4πε
0r . (1) Зокрема, на поверхні сфери потенціал дорівнює φ
0=Q 4πε
0R. Всередині сфери електростатичне поле відсутнє, тому робота з переміщення заряду з довільної точки, що знаходиться всередині сфери, на її поверхню дорівнює нулю A= 0, тому й різниця потенціалів між цими точками також дорівнює нулю Δ φ
= -A= 0. Отже, всі точки всередині сфери мають той самий потенціал, що збігається з потенціалом її поверхні φ
0=Q 4πε
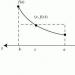
0R . Отже, розподіл потенціалу поля рівномірно зарядженої сфери має вигляд (Рис. 191) φ
(r)=⎧⎩⎨Q 4πε
0R, npu r<RQ 4πε
0r, npu r>R . (2) Зверніть увагу, що поле всередині сфери відсутнє, а потенціал відмінний від нуля! Цей приклад є яскравою ілюстрацією, що потенціал визначається значенням поля від даної точки до нескінченності. Приклад 1 . Тонка, нескінченно довга нитка заряджена однорідно з лінійною щільністю заряду λ
. Знайти напруженість електростатичного поля Е(r) на довільній відстані rвід нитки. Зробимо малюнок: Аналіз: Т.к. нитка несе не точковий заряд, застосуємо метод ДІ. Виділимо нескінченно малий елемент довжини провідника dl, який міститиме заряд dq=dlλ. Розрахуємо напруженість поля, створеного кожним елементом провідника у довільній точці А, що знаходиться від нитки на відстані а. Вектор буде направлено вздовж прямої, що з'єднує точковий заряд із точкою спостереження. Результуюче поле отримаємо за нормаллю до нитки вздовж осі х. Необхідно знайти величину dE x:
dE x =dE cosα. За визначенням: Величина dl, r, змінюються узгоджено при зміні положення елемента dl. Виразимо їх через величину α: де dα– нескінченно мале збільшення кута α в результаті повороту радіуса-вектора щодо точки А при переміщенні по нитці на dl. Тоді dl=r 2 dα/ а. При переміщенні dlвід до точки О кут змінюється від 00 до π/2. Отже Перевірка розмірності: [Е] = В / м = кгм / мфм = КлВ / Клм = В / м; Відповідь: Спосіб 2. З огляду на аксіальної симетрії розподілу заряду, всі точки, розташовані рівному відстані від нитки, еквівалентні і напруженість поля у яких однакова, тобто. Е(r)=const, де r- Відстань від точки спостереження до нитки. Напрямок Еу цих точках завжди збігається з напрямком нормалі до нитки. По теоремі Гауса; де Q-заряд, охоплений поверхнею – S' через яку обчислюється потік, виберемо у вигляді циліндра радіусом а і утворює з ниткою. Враховуючи, що нормальна бічна поверхня циліндра, отримаємо для потоку: Т.к. Е= Const. Sбок.пов. = На 2π
. З іншого боку Е 2πаН=Q/ε 0 , де λН=q. Відповідь:Е=λ
/4πε
0 а. Приклад 2. Розрахувати напруженість рівномірно зарядженої нескінченної площини з поверхневою щільністю зарядів σ
. Лінії напруженості перпендикулярні та направлені в обидві сторони від площини. Як замкнуту поверхню виберемо поверхню циліндра, основи якого паралельні площині, а вісь циліндра перпендикулярна площині. Т.к. утворюють циліндри паралельні лініям напруженості (α=0, cos α=1 ),
то потік вектора напруженості крізь бічну поверхню дорівнює нулю, а повний потік крізь замкнуту циліндричну поверхню дорівнює суміпотоків крізь його основу. Заряд, укладений усередині замкнутої поверхні, дорівнює σ Sосн. тоді: ФЕ = 2 ЕSосн або Ф Е = = тоді E = = Відповідь: E = не залежить від довжини циліндра і на будь-яких відстанях від площини однакова за модулем. Поле рівномірно зарядженої площини однорідне. Приклад 3. Розрахувати поле двох нескінченно заряджених площин з поверхневою щільністю +σ і –σ відповідно. E = E = 0; E = E + + E - =. Відповідь:Результуюча напруженість поля в області між площинами дорівнює E =, а поза обсягом, обмеженим площинами дорівнює нулю. Приклад 4. Розрахувати напруженість поля рівномірно зарядженої з поверхневою щільністю заряду +σ сферичної поверхні радіусу R. Те , і , якщо r< R
, то внутри замкнутой поверхности нет зарядов и электростатическое поле отсутствует (Е=0). Відповідь:. Приклад 5. Розрахувати напруженість об'ємно зарядженої з об'ємною щільністю ρ
, кулі радіусів R. Як замкнутої поверхні візьмемо сферу. Якщо r ≥R, = 4πr 2 E ; E = якщо r< R
, то сфера радиусом r, охоплює заряд q" рівний q"= (оскільки заряди відносяться як об'єми, а об'єми, як куби радіусів) Тоді по т. Гаусса Відповідь:; всередині рівномірно зарядженої кулі напруженість зростає лінійно з відстанню rвід його центру, а поза - убуває назад пропорційно r 2 . Приклад №6. Розрахувати напруженість поля нескінченного, круглого циліндра, зарядженого з лінійною щільністю заряду λ
, радіуса R. Потік вектора напруженості крізь торці циліндра дорівнює 0, а крізь бічну поверхню: Т.к. , або , тоді якщо λ > 0, Е > 0 , вектор спрямований від циліндра, якщо λ< 0, Е < 0 , вектор Ē направлен к цилиндру. Якщо r< R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0 Відповідь:(R> R); E = 0 (R>r). Усередині рівномірно зарядженого по поверхні нескінченного, круглого циліндра поля немає. Приклад 7. Електричне поле створено двома нескінченно довгими паралельними площинами з поверхневими площинами зарядів 2 нКл/м2 та 4нКл/м2. Визначити напруженість поля в областях І, ІІ, ІІІ. Побудувати графік залежності Ē
(r) . Площини ділять простір на 3 області Напрямок Ē результуючого поля у бік більшого. У проекції на r: ; «–»; ; «–»; ; «+»; Графік Ē
(r) Вибір масштабу: Е 2 =2 Е 1 Е 1 = 1; Е 2 = 2 Відповідь:ЕІ = -345 В/м; ЕІ I = -172 В/м; ЕІ II = 345 В/м. Приклад №8. Ебонітова суцільна куля радіусом R= 5 см несе заряд, рівномірно розподілений з об'ємною щільністю ρ
=10 нКл/м3. Визначити напруженість електричного поля у точках: 1) на відстані r 1 = 3 див від центру сфери; 2) на поверхні сфери; 3) на відстані r 2=10 см від центру сфери. Жидкевич В. І. Електричне поле площини // Фізіка: проблеми викладання. – 2009. – № 6. – С. 19-23. Завдання з електростатики можна розділити на дві групи: задачі про точкові заряди та задачі про заряджені тіла, розміри яких не можна не враховувати. Вирішення завдань з розрахунку електричних полів та взаємодій точкових зарядів засноване на застосуванні закону Кулона і не викликає особливих труднощів. Більш складним є визначення напруженості поля та взаємодії заряджених тіл кінцевих розмірів: сфери, циліндра, площини. При обчисленні напруженості електростатичних полів різної конфігурації слід підкреслити важливість принципу суперпозиції та використовувати його при розгляді полів, створених не тільки точковими зарядами, а й зарядами, розподіленими по поверхні та об'єму. При розгляді впливу поля на заряд формула F=qE в загальному випадку справедлива для точкових заряджених тіл і тільки в однорідному полі застосовна для тіл будь-яких розмірів та форми, що несуть заряд q. Електричне поле конденсатора утворюється в результаті накладання двох полів, створених кожною пластиною. У плоскому конденсаторі можна розглядати одну пластину як тіло із зарядомq 1поміщене в електричне поле напруженістюЕ 2 , створене іншою пластиною. Розглянемо кілька завдань. 1.
Нескінченна площина заряджена з поверхневою щільністю σ
>0. Знайдіть напруженість поля Ета потенціал ϕ
з обох боків площини, вважаючи потенціал площини рівним нулю. Побудуйте графіки залежностейЕ(х), ϕ
(х). Ось х перпендикулярна до площини, точка х=0 лежить на площині. Рішення. Електричне поле нескінченної площини є однорідним та симетричним щодо площини. Йогонапруженість Зв'язок між на пряженістю та різницею потенціалів між двома точками однорідного електростатичного поля виражається формулоюде х - відстань між точками, виміряна вздовж силової лінії.Тоді ϕ
2 =
ϕ
1 -Ех. При х<0
при х>0 Залежності Е(х) та ϕ
(х) представлені малюнку 1. 2.
Дві плоскопаралельні тонкі пластини, розташовані на малій відстані d один від одного, рівномірно заряджені зарядом поверхневою щільністюσ 1 та σ 2 . Знайдіть напруженості поля в точках, що лежать між пластинами та із зовнішнього боку. Побудуйте графік залежності напруженостіЕ(х) та потенціалу ϕ
(х), вважаючи ϕ
(0) = 0. Розгляньте випадки, коли: a)σ 1 =-σ 2; б) σ 1 = σ 2; в) σ 1 =3 σ 2 - Рішення.Так як відстань між пластинами мало, їх можна розглядати як нескінченні площини. Напруженість поля позитивно зарядженої площини дорівнюєі спрямована від неї; напруга поля негативно зарядженої площини спрямована до неї. Відповідно до принципу суперпозиції поле в будь-якій точці, що розглядається, буде створюватися кожним із зарядів окремо. а) Поля двох площин, заряджених рівними та протилежними за знаком зарядами (плоский конденсатор), складаються в області між площинами та взаємно знищуються у зовнішніх областях (рис. 2,а). При х<0
Е=
0,
ϕ
=0; при 0 Якщо площини кінцевих розмірів, то поле між площинами не буде однорідним, а поле поза площинами не буде точно дорівнює нулю. б) Поля площин, заряджених рівними за величиною та знаком зарядами (σ 1 = σ 2 ), компенсують один одного у просторі між площинами та складаються у зовнішніх областях (рис. 3,а). При х<0
при 0 Скориставшись графікомЕ(х) (рис. 3, б), побудуємо якісно графік залежності ϕ
(х) (рис. 3, в). в) Якщо σ 1 = σ 2 , то, враховуючи напрямки полів і вибираючи напрямок праворуч за позитивне, знаходимо: Залежність напруженості Е від відстані показана малюнку 4. 3.
На одній із пластин плоского конденсатора ємністюЗ знаходиться зарядq 1=+3q, а на інший q 2
=+
q.
Визначте різницю потенціалів між пластинами конденсатора. Рішення. 1-й спосіб. Нехай площа пластини конденсатора S, а відстань між ними d. Поле всередині конденсатора однорідне, тому різницю потенціалів (напруження) на конденсаторі можна визначити за формулою U=E*d, де Е - Напруженість поля всередині конденсатора. де Е 1 , Е 2 - Напруженості поля, створюваного пластинами конденсатора. Тоді 2-й спосіб. Додамо на кожну пластину зарядТоді пластини конден сатора матимуть заряди +
qта -q. Поля однакових зарядів пластини всередині конденсатора компенсують один одного. Додані заряди не змінили поле між пластинами, а значить, і різниця потенціалівконденсатор. U= q/C
.
4.
У простір між обкладинками незарядженого плоского конденсатора вносять тонку металеву пластину, що має заряд + q. Визначте різницю потенціалів між обкладинками конденсатора. Рішення.Оскільки конденсатор не заряджений, то електричне поле створюється лише пластиною, що має заряд. q (Рис. 5). Це поле однорідне, симетричне щодо пластини, та його напруженістьНехай потенціал металевої пластини дорівнює ϕ
. Тоді потенціали обкладень АіВ конденсатора будуть рівні ϕ-
ϕ А
=
ϕ
El 1; ϕ А
=
ϕ-El 1
;
ϕ-
ϕ B
=
ϕ-El 2
;
ϕ B
=
ϕ-El 2
.
Різниця потенціалів між обкладинками конденсатора 5.
В однорідне електричне поле напруженістюЕ 0 перпендикулярно силовим лініям поміщають заряджену металеву пластину із щільністю заряду на поверхні кожної сторони пластини σ
(Рис. 6). Визначте напруженість поля Е"всередині та зовні пластини та поверхневу щільність зарядівσ 1 та σ 2 , Що виникне на лівій та правій сторонах пластини. Рішення.Поле всередині пластини дорівнює нулю і є суперпозицією трьох полів: зовнішнього поляЕ 0 , поля, створюваного зарядами лівої сторони пластини, та поля, створюваного зарядами правої сторони пластини. Отже, 6.
У плоскому повітряному конденсаторі напруженість поля Е = 104 В/м. Відстань між обкладками d= 2 см. Чому дорівнюватиме різниця потенціалів, якщо між пластинами паралельно їм помістити металевий лист товщиноюd 0=0,5 див (рис. 7)? Рішення.Оскільки електричне поле між пластинами однорідне, то U = Ed, U = 200 Ст. Якщо між пластинами помітити металевий лист, виходить система з двох послідовно з'єднаних конденсаторів з відстанню між пластинамиd 1і d 2 . Ємності цих конденсаторівЇхня загальна ємність Оскільки конденсатор відключено від джерела струму, то заряд конденсатора при внесенні металевого листа не змінюється: q"=CU=С"U 1 ; де ємність конден сатора до внесення до нього металевого листа. Отримуємо: U 1=
150 Ст. 7.
На пластинахА та С, розташованих паралельно на відстані d= 8 см один від одного, підтримуються потенціали ϕ 1= 60 В та ϕ 2
=-
60 відповідно. Між ними помістили заземлену пластину D з відривом d 1 = 2 див від пластини А. Наскільки змінилася напруженість поля на ділянках AD та CD? Побудуйте графіки залежностей ϕ
(x) та Е(х). Для розрахунку полів, створених зарядами, рівномірно розподіленими по сферичних, циліндричних або плоских поверхнях, застосовують теорему Остроградського – Гауса (розділ 2.2). Методика розрахунку полів за допомогою теореми Остроградського - Гауса. 1) Вибираємо довільну замкнуту поверхню, що охоплює заряджене тіло. 2) Обчислюємо потік вектора напруги крізь цю поверхню. 3) Обчислюємо сумарний заряд, охоплений цією поверхнею. 4) Підставляємо в теорему Гауса обчислені величини та виражаємо напруженість електростатичного поля. Поле рівномірно зарядженого нескінченного циліндра (нитки).
Нехай нескінченний циліндр радіусом R
рівномірно заряджений з лінійною щільністю заряду +
τ
(Рис. 16). З міркувань симетрії випливає, що лінії напруженості поля в будь-якій точці будуть спрямовані вздовж прямих радіальних, перпендикулярних осі циліндра. Як замкнута поверхня виберемо коаксіальний з даними (із загальною віссю симетрії) циліндр радіусом
r
та заввишки ℓ
. Розрахуємо потік вектора
де S
осн ,
S
бік– площі основ та бічної поверхні. Потік вектора напруженості крізь площі основ дорівнює нулю, тому Сумарний заряд, що охоплюється обраною поверхнею: Підставивши все в теорему Гауса, з огляду на те, що ε
= 1, отримаємо: Напруженість електростатичного поля, створеного нескінченно довгим рівномірно зарядженим циліндром або нескінченно довгою рівномірно зарядженою ниткою в точках, розташованих поза нею: де r
- Відстань від осі
циліндра до заданої точки ( r
≥ R
); τ
- лінійна щільність заряду .
Якщо r
< R
, то аналізована замкнута поверхня зарядів усередині не містить, тому в цій галузі Е
= 0, тобто. всередині циліндра, поля немає
. Поле рівномірно зарядженої нескінченної площини П Як замкнута поверхня виберемо циліндр, основи якого паралельні зарядженій площині, а вісь перпендикулярна їй (рис. 17). Оскільки лінії, що утворюють бічну поверхню циліндра, паралельні лініям напруги, то потік вектора напруги крізь бічну поверхню дорівнює нулю. Потік вектора напруженості через дві площі основи Сумарний заряд, що охоплюється обраною поверхнею: Підставивши все в теорему Гауса, отримаємо: Напруженість електростатичного поля нескінченної рівномірно зарядженої площини З цієї формули випливає, що Е
не залежить від довжини циліндра, тобто напруга поля однакова у всіх точках. Іншими словами, поле рівномірно зарядженої площини однорідно.
Поле двох нескінченних паралельних різноіменно заряджених площин П Відповідно до принципу суперпозиції, З малюнка видно, що в області між площинами силові лінії спрямовані, тому результативна напруженість Поза обсягом, обмеженого площинами, поля, що складаються, мають протилежні напрямки, так що результуюча напруженість дорівнює нулю. Таким чином, поле виявляється зосередженим між площинами. Отриманий результат приблизно справедливий і для площин кінцевих розмірів, якщо відстань між площинами набагато менша за їх площу (плоский конденсатор). Якщо на площинах розподілені заряди одного знака з однаковою поверхневою щільністю, то поле відсутнє між пластинами, а поза пластинами обчислюється за формулою (2.7). Напруженість поля рівномірно зарядженої сфери Поле, що створюється сферичною поверхнею радіусу
R
, зарядженої з поверхневою щільністю заряду
σ
, буде центрально симетричним, тому лінії напруженості спрямовані вздовж радіусів сфери (рис. 19 а). Як замкнута поверхня виберемо сферу радіусу r
, що має загальний центр із зарядженою сферою. Якщо r
>
R
, то всередину поверхні потрапляє весь заряд Q
.
Потік вектора напруженості крізь поверхню сфери Підставивши цей вислів у теорему Гауса, отримаємо: Напруженість електростатичного поля поза рівномірно зарядженою сферою: де r
- Відстань від центру
сфери. Звідси видно, що поле тотожне з полем точкового заряду тієї самої величини, поміщеного центр сфери. Якщо r
<
R
, то замкнута поверхня не містить усередині зарядів, тому всередині зарядженої сфери поле відсутнє
(Рис.19, б). Напруженість поля об'ємно зарядженої кулі П Поле в цьому випадку має центральну симетрію. Для напруженості поля поза кулею виходить той самий результат, що у разі поверхнево зарядженої сфери (2.8). Для точок усередині кулі напруженість буде іншою (рис. 20). Сферична поверхня охоплює заряд Тому, відповідно до теореми Гауса Враховуючи що Напруженість електростатичного поля, всередині об'ємно зарядженої кулі Завдання 2.3
. У полі нескінченно довгої площини з поверхневою щільністю заряду σ
підвішений на нитки маленька кулька масою m
, що має заряд того ж знака, що й площину. Знайти заряд кульки, якщо нитка утворює з вертикаллю кут α
Рішення.
Повернемося до розв'язання задачі 1.4. Різниця полягає в тому, що в задачі 1.4 сила П Зверніть увагу
, що для знаходження сили, що діє на заряд, поміщений у полі розподіленого заряду, необхідно використати формулу а напруженість поля, створеного декількома розподіленими набоями, знаходити за принципом суперпозиції. Тому наступні завдання присвячені знаходженню напруженості електростатичного поля розподілених набоїв з використанням теореми Остроградського-Гаусса. Завдання 2.4.
Випередити напруженість поля всередині і поза рівномірно зарядженої пластинки завтовшки d
об'ємна щільність заряду всередині пластинки ρ
. Побудувати графік залежності Е
(х
). Рішення.
Початок координат помістимо в середній площині пластинки, а вісь ОХнаправимо перпендикулярно до неї (рис. 22, а). Застосуємо теорему Остроградського-Гаус для розрахунку напруженості електростатичного поля зарядженої нескінченної площини, тоді З визначення об'ємної щільності заряду тоді для напруженості отримаємо Звідси видно, що поле всередині платівки залежить від х
. Поле поза платівкою розраховується аналогічно: Звідси видно, що поле поза платівкою однорідне. Графік залежності напруженості Е
від х
на рис. 22, б. Завдання 2.5.
Поле створено двома нескінченно довгими нитками, зарядженими з лінійними щільностями зарядів –
τ
1
та + τ
2
. Нитки розташовані перпендикулярно одна одній (рис. 23). Знайти напруженість поля в точці, що знаходиться на відстані r
1
і r
2
від ниток. Р За принципом суперпозиції За теоремою Піфагора Завдання 2.6
. Поле створене двома зарядженими нескінченно довгими порожніми коаксіальними циліндрами радіусами.
R
1
і R
2
>
R
1
. Поверхневі густини зарядів рівні –
σ
1
і +
σ
2
. Знайти напруженість електростатичного поля в наступних точках: а) точка А
розташована на відстані d
1
<
R
1
; б) точка В
розташована на відстані R
1
<
d
2
<
R
2
; в) точка З
розташована на відстані d
3
>
R
1
>
R
2
. Відстань відлічується від осі циліндрів. Рішення.
Коаксіальні циліндри – це циліндри, що мають спільну вісь симетрії. Зробимо малюнок та покажемо на ньому точки (рис. 24). Е
А
= 0. крапка В
розташована всередині більшого циліндра, тому в цій точці поле створюється тільки меншим циліндром: Виразимо лінійну густину заряду через поверхневу густину заряду. Для цього скористаємося формулами (1.4) та (1.5), з яких висловимо заряд: Прирівняємо праві частини та отримаємо: де S
1
- Площа поверхні першого циліндра. З урахуванням того що крапка З
розташована зовні обох циліндрів, тому поле створюється обома циліндрами. За принципом суперпозиції: З урахуванням напрямків та розрахунків, отриманих вище, отримаємо: Завдання 2.7
. Поле створене двома зарядженими нескінченно довгими паралельними площинами. Поверхневі густини зарядів рівні σ
1
і σ
2
> σ
1
. Знайти напруженість електростатичного поля в точках, що знаходяться між пластинами та поза пластинами. Розв'язати задачу для двох випадків: а) пластини однойменно заряджені; б) пластини різноіменно заряджені. Рішення.
У векторному вигляді напруженість результуючого поля записується однаково. Відповідно до принципу суперпозиції: Модулі векторів а) Якщо площини заряджені однойменно, то між площинами напруженості спрямовані у різні боки (рис. 26, а). Модуль результуючої напруженості Поза площинами напруженості .
б) Якщо площини заряджені різноіменно, то, навпаки, між площинами напруженості спрямовані в один бік (рис. 26, б), а поза площинами – у різні. 8. Електростатичне поле створюється рівномірно зарядженою нескінченною площиною. Покажіть, що це поле є однорідним. Нехай поверхнева густина заряду дорівнює s. Очевидно, що вектор Е може бути тільки перпендикулярним зарядженій площині. Крім того, очевидно, що в симетричних щодо цієї площині точках вектор Е однаковий за модулем і протилежний у напрямку. Така конфігурація поля підказує, що як замкнута поверхня слід вибрати прямий циліндр, де передбачається що s більше нуля. Потік крізь бічну поверхню цього циліндра дорівнює нулю, тому повний потік через всю поверхню циліндра буде рівним 2*Е*DS, де DS – площа кожного торця. Відповідно до теореми Гауса де s*DS – заряд ув'язнений усередині циліндра. Точніше цей вираз слід записати так: де Еn – проекція вектора Е на нормаль n до зарядженої площини, причому вектор n від цієї площини. Той факт, що не залежить від відстані до площини, означає, що відповідне електричне поле є однорідним. 9. З мідного дроту виготовлено чверть кола радіусом 56 см. По дроті рівномірно розподілено заряд з лінійною щільністю 0,36 нКл/м. Знайдіть потенціал у центрі кола. Так як заряд лінійно розподілений по дроту для знаходження потенціалу в центрі, скористаємося формулою: Де s – лінійна щільність заряду, dL – елемент дроту. 10. В електричному полі, створеному точковим зарядом Q, по силовій лінії з точки розташованої на відстані r 1 від заряду Q в точку, розташовану на відстані r 2 переміщується негативний заряд -q. Знайдіть збільшення потенційної енергії заряду -q на цьому переміщенні. За визначенням потенціал – це величина, чисельно рівна потенційної енергії одиничного позитивного заряду у цій точці поля. Отже, потенційна енергія заряду q 2: 11. Два однакові елементи з е.р.с. 1,2 і внутрішнім опором 0,5 Ом з'єднані паралельно. Отримана батарея замкнена на зовнішнє опір 3,5 Ом. Знайдіть силу струму у зовнішньому ланцюзі. Відповідно до закону Ома для всього ланцюга сила струму у зовнішньому ланцюгу: Де E` - ЕРС батареї елементів, r` - внутрішній опір батареї, який дорівнює: ЕРС батареї дорівнює сумі ЕРС трьох послідовно з'єднаних елементів: Отже: Розглянемо дріт довжиною L і діаметром d, виготовлену з матеріалу з питомим опіром p. Опір дроту R можна знайти за формулою Де s = - Площа поперечного перерізу дроту. При силі струму I протягом t у провіднику виділяється кількість теплоти Q: При цьому, падіння напруги на дроті одно: Питомий опір міді: p1 = 0.017 мкОм * м = 1.7 * 10 -8 Ом * м питомий опір сталі: p2 = 10 -7 Ом * м так як дроти включені послідовно, то сили струму в них однакові і за час t виділяються в кількості теплоти Q1 і Q2: 12. В однорідному магнітному полі знаходиться круговий виток із струмом. Площина витка перпендикулярна до силових ліній поля. Доведіть, що результуюча сила, що діє з боку магнітного поля на контур, дорівнює нулю. Оскільки круговий виток із струмом перебуває у однорідному магнітному полі, нею діє сила Ампера. Відповідно до формули dF=I результуюча амперова сила, що діє на виток із струмом визначається: Де інтегрування проводиться за даним контуром зі струмом I. Оскільки магнітне поле однорідне, то вектор можна винести з-під інтеграла і завдання звільниться до обчислення векторного інтеграла . Цей інтеграл є замкнутим ланцюжком елементарних векторів dL, тому він дорівнює нулю. Значить і F=0, тобто результуюча амперова сила дорівнює нулю однорідному магнітному полі. 13. По короткій котушці, що містить 90 витків діаметром 3 см, йде струм. Напруженість магнітного поля, створеного струмом на осі котушки на відстані 3 см від неї дорівнює 40 А/м. Визначте силу струму в котушці. Вважаючи, що магнітна індукція в точці А є суперпозиція магнітних індукцій, створюваних кожним витком котушки окремо: Для знаходження у витка скористаємося законом Біо-Савара-Лапласа. Де, dBвитка – магнітна індукція поля, створювана елементом струму IDL у точці, яка визначається радіус-вектором r Виділимо на кінці елемент dL і від нього в точку А проведемо радіус-вектор r. Вектор dBвитка направимо у відповідність до правила буравчика. Відповідно до принципу суперпозиції: Де інтегрування ведеться по всіх елементах dLвитка. Розкладемо dBвитка на дві складові dBвитка(II) - паралельну площині кільця і dBвитка(I) - перпендикулярну площині кільця. Тоді Помітивши, що Де dBвитка(I) =dBвитка*cosb і Оскільки dl перпендикулярний r Скоротимо на 2p і замінимо cosb на R/r1 Виразимо звідси I знаючи що R=D/2 згідно з формулою, що зв'язує магнітну індукцію і напруженість магнітного поля: тоді за теоремою Піфагора з креслення: 14. В однорідне магнітне поле в напрямку перпендикулярному силовим лініям влітає електрон зі швидкістю 10?10 6 м/с і рухається по дузі кола радіусом 2,1 см. Знайдіть індукцію магнітного поля. На електрон, що рухається в однорідному магнітному полі, діятиме сила Лоренца, перпендикулярна швидкості електрона і відтак спрямована до центру кола: Оскільки кут між v та І дорівнює 90 0: Оскільки сила Fл спрямовано центру окружності, і електрон рухається по колу під впливом цієї сили, то Виразимо магнітну індукцію: 15. Квадратна рамка зі стороною 12 см, виготовлена з мідного дроту, поміщена в магнітне поле, магнітна індукція якого змінюється за законом В=В 0 ·Sin(ωt), де В 0 =0,01 Тл, ω=2·π/ Т та Т=0,02 с. Площина рамки перпендикулярна напряму магнітного поля. Знайдіть найбільше значення е.р.с. індукції, що у рамці. Площа квадратної рамки S = a2. Зміна магнітного потоку dj при перпендикулярності площини рамки dj=SdB ЕРС індукції визначається Е буде максимальною при cos(wt)=1
(13.10)
(13.11)
(13.13)
.
.
.
.
(якщо r > R)
;
;
.
Якщо пластина знаходиться на однаковій відстані від обкладок конденсатора, різниця потенціалів між обкладками дорівнює нулю.
де σ 1 та σ 2 - поверхнева щільність заряду на лівій та правій сторонах пластини, яка виникає після внесення пластини в поліЕ 0 . Сумарний заряд пластини не зміниться, томуσ 1 + σ 2 =2 σ , звідки σ 1 = σ- ε 0 E 0
, σ 2 = σ + ε 0 E 0
. Поле зовні пластини є суперпозицією поляЕ 0 та поля зарядженої пластини Е. Зліва відпластини Праворуч від пластини
Приклади розрахунку деяких полів
через дану поверхню:
,
.
.
, (2.5)
усть нескінченна площина заряджена з постійною поверхневою щільністю +
σ
.
.
.
. (2.6)
усть площини рівномірно заряджені з однаковими за величиною поверхневими густинами + σ
і – σ
(Рис. 18).
.
. (2.7)
.
, (2.8)
усть шар радіуса R
заряджений з постійною об'ємною щільністю заряду ρ
.
, отримаємо:
(r
≤
R
). (2.9)
.
обчислюється за законом Кулона (1.2), а задачі 2.3 – з визначення напруженості електростатичного поля (2.1) 
. Напруженість електростатичного поля нескінченної рівномірно зарядженої площини виведена за допомогою теореми Остроградського-Гаусса (2.4).
оле площині однорідно і залежить від відстані до площині. З рис. 21:
.
,
.
,
.
ешение.
Покажемо малюнку напруженість поля, створеного кожною ниткою окремо. Вектор 
спрямований до
першої нитки, оскільки вона заряджена негативно. Вектор 
спрямований від
другий нитки, оскільки вона заряджена позитивно. Вектори 
і 
взаємно перпендикулярні, тому результуючий вектор 
буде гіпотенузою прямокутного трикутника. Модулі векторів 
і 
визначаються за формулою (2.5).
.
.
,
, остаточно отримаємо:
.
.
.
і 
обчислюються за формулою (2.6).
і 
спрямовані в один бік. Так як поле нескінченних заряджених площин однорідно, тобто не залежить від відстані до площин, то в будь-якій точці ліворуч і праворуч від площин поле буде однаково:
12 В електричний ланцюг включені послідовно мідний та сталевий дроти рівної довжини та діаметра. Знайдіть відношення кількостей тепла, що виділяється в цих дротах.
з міркувань симетрії і що вектори dBвитка(I) спрямовані, замінимо векторне інтегрування скалярним:
