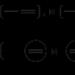а. Ми знову говоритимемо лише про функції двох змінних (але міркування придатні і для функцій будь-якого числа змінних).

Нехай маємо функцію

та - її приватні похідні. Останні, очевидно, також є функціями х і у, а тому також можна знаходити їх приватні похідні з х та у.

Приватна похідна за приватною похідною називається приватною похідною другого порядку і позначається так:

Аналогічно визначаємо і приватну похідну другого порядку:

Приватна похідна по у приватної похідної по називається змішаною другою приватною похідною по і по:

Аналогічно визначаємо другу приватну похідну, взяту спочатку за у, а потім за

Можна довести, що для багатьох функцій змішана похідна залежить від порядку диференціювання, тобто що

Ми не будемо наводити (через складність) докази цієї важливої ​​властивості, а продемонструємо його на якомусь прикладі.

Нехай, наприклад, дана функція

Диференціюємо її спочатку по х, а потім по

Тепер продиференціюємо цю функцію спочатку у, а потім по

Як бачимо, результат обох випадках вийшов однаковим.

Якщо ми братимемо приватні похідні по і по приватних похідних другого порядку, то отримаємо приватні похідні третього порядку

Аналогічно визначаємо приватні похідні четвертого, п'ятого порядків тощо.

b. Подібно до того, як ми брали приватні похідні приватних похідних, ми можемо брати повний диференціал повного диференціалу. Результат називається другим повним диференціалом і позначається як і, як другий диференціал функції однієї змінної, т. е. так:

Третім повним диференціалом називається повний диференціал другого повного диференціалу тощо.

с. Покажемо тепер, як виражається другий повний диференціал через приватні похідні другого порядку. Для спільності ми припустимо, що вони можуть залежати від будь-яких інших змінних. Позначимо для стислості

Щоб знайти другий повний диференціал, ми маємо взяти перший повний диференціал першого повного диференціала. Помічаючи при цьому, що, як показано в пункті «е» § 3 цього розділу, правило для диференціювання суми та добутку застосовне до повного диференціала, ми можемо написати

Оскільки p і q самі є функціями двох змінних х і у, то

Зауважимо, що

Підставляючи їх в останню формулу, після розкриття дужок остаточно отримаємо

Якщо х і у є незалежними змінними або лінійними функціямиінших будь-яких змінних, їх другі диференціали рівні нулю;

та формула (8) спрощується:

Ми бачимо, що закон інваріантності застосуємо до другого диференціалу лише з дуже великими обмеженнями: він буде вірний тільки в тому випадку, якщо х і є лінійними функціями інших змінних, у всіх інших випадках він не застосовний. Розглядаючи формулу (9), бачимо, що вона дуже нагадує формулу квадрата суми двох чисел. Ця аналогія навела на думку записувати другий диференціал у наступній символічній формі:

Нехай задано функцію двох змінних. Дамо аргументу збільшення, а аргумент залишимо незмінним. Тоді функція отримає збільшення, яке називається приватним збільшенням змінної і позначається:

Аналогічно, фіксуючи аргумент і надаючи аргументу прирощення, отримаємо приватне збільшення функції за змінною:

Величина називається повним збільшенням функції в точці.

Визначення 4. Приватної похідної функції двох змінних однією з цих змінних називається межа відношення відповідного приватного збільшення функції до збільшення даної змінної, коли останнє прагне нуля (якщо ця межа існує). Позначається приватна похідна так: або, або.

Таким чином, за визначенням маємо:

Приватні похідні функції обчислюються за тими самими правилами і формулами, як і функція однієї змінної, у своїй враховується, що з диференціюванні по змінної, вважається постійної, а при диференціюванні по змінної постійної вважається.

Приклад 3. Знайти приватні похідні функції:

Рішення. а) Щоб знайти рахуємо постійною величиноюі диференціюємо як функцію однієї змінної:

Аналогічно, вважаючи постійною величиною, знаходимо:

Визначення 5. Повним диференціалом функції називається сума творів приватних похідних цієї функції на збільшення відповідних незалежних змінних, тобто.

З огляду на, що диференціали незалежних змінних збігаються зі своїми приростами, тобто. , формулу повного диференціала можна записати у вигляді

Приклад 4. Визначити повний диференціал функції.

Рішення. Оскільки за формулою повного диференціалу знаходимо

Приватні похідні найвищих порядків

Приватні похідні називають приватними похідними першого порядку або першими приватними похідними.

Визначення 6. Приватними похідними другого порядку функції називаються приватні похідні від приватних похідних першого порядку.

Приватних похідних другого порядку чотири. Вони позначаються так:

Аналогічно визначаються приватні похідні 3-го, 4-го та більш високих порядків. Наприклад, для функції маємо:

Приватні похідні другого або вищого порядку, взяті з різних змінних, називаються змішаними приватними похідними. Для функції є похідні. Зауважимо, що у випадку, коли змішані похідні безперервні, має місце рівність.

Приклад 5. Визначити приватні похідні другого порядку функції

Рішення. Приватні похідні першого порядку цієї функції знайдено у прикладі 3:

Диференціюючи і змінними х і y, отримаємо

4. Приватні похідні найвищих порядків

Приватні похідні називають приватними похідними першого порядку або першими приватними похідними.

Визначення 6. Приватними похідними другого порядку функції називаються приватні похідні від приватних похідних першого порядку.

Приватних похідних другого порядку чотири. Вони позначаються так:

Або ; або ;

Або ; або .

Аналогічно визначаються приватні похідні 3-го, 4-го та більш високих порядків. Наприклад, для функції маємо:

, і т.д.

Приватні похідні другого або вищого порядку, взяті з різних змінних, називаються змішаними приватними похідними. Для функції такими є похідні. Зауважимо, що у випадку, коли змішані похідні безперервні, має місце рівність .

Приклад 5. Визначити приватні похідні другого порядку функції

Рішення. Приватні похідні першого порядку цієї функції знайдено у прикладі 3:

Диференціюючи і змінними х і y, отримаємо

5. Екстремум функції кількох змінних. Необхідні та достатні умови існування екстремуму

Визначення 7. Точка називається точкою мінімуму (максимуму) функції, якщо існує така околиця точки, що для всіх точок з цієї околиці виконується нерівність , ().

Точки мінімуму та максимуму функції називаються точками екстремуму, а значення функції у цих точках – екстремумами функції (мінімумом та максимумом відповідно).

Зауважимо, що мінімум і максимум функції мають локальний характер, тому що значення функції в точці порівнюється з її значеннями в точках досить близьких до .

Теорема 1 (необхідні умови екстремуму). Якщо - точка екстремуму функції, що диференціюється , то її приватні похідні і в цій точці рівні нулю: .

Крапки, у яких приватні похідні першого порядку дорівнюють нулю, називаються критичними або стаціонарними. У критичних точках функція може мати екстремум, а може не мати.

Теорема 2 (достатня умова екстремуму). Нехай функція: а) визначена в деякій околиці критичної точки, в якій і ; б) має безперервні приватні похідні другого порядку . Тоді, якщо , то функція в точці має екстремум: максимум, якщо А<0; минимум, если А>0; якщо , то функція в точці екстремуму немає. В разі питання наявності екстремуму залишається відкритим.

При дослідженні функції двох змінних на екстремум рекомендується використовувати таку схему:

1. Визначити приватні похідні першого порядку: і .

2. Вирішити систему рівнянь та знайти критичні точки функції.

3. Визначити приватні похідні другого порядку: , , .

4. Обчислити значення приватних похідних другого порядку у кожній критичній точці та, використовуючи достатні умови, зробити висновок про наявність екстремуму.

5. Знайти екстремуми функції.

Приклад 6. Знайти екстремуми функції .

Рішення. 1. Знаходимо приватні похідні та:

, .

І градієнт функції обчислюється у меншому числі точок. Опис програми Програма призначена для знаходження точок мінімуму функцій кількох змінних - тобто для мінімізації цих функцій. У програмі реалізований один із методів спуску – Градієнтний метод спуску з вибором кроку. Початковий крок задається. Зміна кроку здійснюється за схемою якщо; якщо Обчислення...

Межа функції: Рішення. Скористаємося першою чудовою межею Приклад 3. Знайти межу функції: Рішення. Скористаємося другою чудовою межею Тоді Безперервність функції кількох змінних За визначенням функція f (x, y) безперервна в точці (х0, у0), якщо вона визначена в деякій її околиці, у тому числі в самій точці (х0, у0) і якщо межа f (x, y) у цій...

Приватні похідні та диференціали вищих порядків.

Вступ.

Так само як і у разі функцій однієї змінної, можна для функцій декількох змінних обчислювати диференціали порядку вище за перший.

Причому для складних функцій диференціали порядку вище першого не мають постійної формою і вирази для них більш громіздкі. У цій лекції належить розглянути так само геометричний зміст повного диференціала функції декількох змінних, який вводиться за аналогією з геометричним змістом функції однієї дійсної змінної.

1. Диференціювання неявної функції.

а) Нехай дано рівняння, яке зв'язує дві змінні хі у. Якщо всі члени цього рівняння перенести до лівої частини, то воно матиме вигляд

Рівняння (1) взагалі кажучи, визначає одну чи кілька функцій
. Наприклад, рівняння
визначає одну функцію
, а рівняння визначає дві функції
і
.

Якщо у розглянуті рівняння замість упідставити знайдені функції, вони обернуться на тотожності.

Визначення:Будь-яка безперервна функція, що обертає рівняння в тотожність, називається неявною функцією, що визначається рівнянням.

Не всяке рівняння визначає неявну функцію. Так рівняння
не задовольняє жодній парі дійсних чисел
і, отже, не визначає неявну функцію. Сформулюємо умови, у яких рівняння визначає неявну функцію .

Нехай дано рівняння (1)

б) Теорема існування неявної функції.

Якщо функція
та її приватні похідні
і
визначені і безперервні в околиці точки
і при цьому
, а
, то рівняння визначає в цій околиці точки
єдину неявну функцію , безперервну та диференційовану в деякому інтервалі, що містить точку , причому
.

Геометрично це означає, що в околиці точки крива є графіком безперервної і диференційованої функції .

в) Похідна неявна функція.

Нехай ліва частина рівняння задовольняє умовам, зазначеним у теоремі, тоді це рівняння визначає неявну функцію , для якої в околиці точки має місце тотожність щодо х:
. Тоді
, за будь-якого хз околиці х 0 .

За правилом диференціювання складної функції

і, отже,
.

або
(2)

За цією формулою знаходиться похідна неявної функції (однієї змінної).

Приклад: х 3 +у 3 -3ху = 0

Маємо
х 3 +у 3 -3ху, =3х 2 -3у =3у 2 -3х

= -
.

Узагальним поняття неявно заданої функції у разі функції кількох змінних.

Рівняння (3) визначає неявно задану функцію , якщо ця функція безперервна і звертає рівняння тотожність, тобто.
(4).

Умови існування та єдиності неявно заданої функції формулюються аналогічно.

Знайдемо і :

= -

= -

Приклад:

2х

2у

= -
; = -
.

2. Приватні похідні найвищих порядків.

Нехай функція має приватні похідні

Ці похідні, взагалі кажучи, є функціями незалежних змінних. хі у.

Приватні похідні від приватних похідних
і
називаються приватними похідними другого порядку функції.

Кожна приватна похідна першого порядку та має дві приватні похідні. Таким чином, отримуємо чотири приватні похідні другого порядку

1. Похідні
і
називаються змішаними похідними другого порядку.

2. Виникає питання, чи залежить результат диференціювання функції

Від порядку диференціювання з різних змінних, тобто. будуть

чи тотожно рівні і .

Справедлива теорема:

Теорема:Якщо похідні та визначені та безперервні точці М(х,у)і деякою її околиці, то в цій точці

Приклад:

Похідні другого порядку можна знову диференціювати

як по х, так і по у. Отримаємо приватні похідні третього порядку.

Приватна похідна п-го порядку є приватною похідною від

похідної (п-1)-го порядку.

3. Повні диференціали вищих систем.

Нехай - функція, що диференціюється, отже, будемо називати диференціалом першого порядку.

Нехай і - функції, що диференціюються в точці М(х,у),
і
розглядатимемо як постійні множники. Тоді
є функцією 2-х змінних хі у, що диференціюється в точці М(х,у). Її диференціал має вигляд:

Диференціал від диференціалу у точці М(х,у)називається диференціалом другого порядку в цій точці та позначається
.

За визначенням Помилка! Об'єкт не може бути створений із кодів полів редагування.=

Помилка! Об'єкт не може бути створений із кодів полів редагування.=

Диференціал від диференціалу (п-1)-го порядку називається диференціалом п-го порядку функції

Вираз для символічно можна записати у вигляді

Помилка! Об'єкт не може бути створений із кодів полів редагування.=
=

Приклад:

4. Дотична площина та нормаль до поверхні.

нормаль

дотична площина

Нехай N та N 0 – точки даної поверхні. Проведемо пряму NN0. Площина, яка проходить через точку N 0 називається дотичної площиноюдо поверхні, якщо кут між січною NN 0 і цією площиною прагне нуля, коли прагне нуля відстань NN 0 .

Визначення. Нормаллюдо поверхні у точці N 0 називається пряма, що проходить через точку N 0 перпендикулярно дотичної площині до цієї поверхні.

У якій – або точці поверхня має, або лише одну дотичну площину, або її зовсім.

Якщо поверхня задана рівнянням z = f(x, y), де f(x, y) – функція, що диференціюється в точці М 0 (х 0, у 0), дотична площина в точці N 0 (x 0, y 0, ( x 0 ,y 0)) існує і має рівняння:

Рівняння нормалі до поверхні цієї точки:

Геометричним змістомповного диференціала функції двох змінних f(x, y) у точці (х 0 , у 0) є збільшення аплікати (координати z) дотичної площини до поверхні при переході від точки (х 0 , у 0) до точки (х 0 +х , У 0 +у).

Як видно, геометричний сенс повного диференціалу функції двох змінних є просторовим аналогом геометричного сенсу диференціалу функції однієї змінної.

приклад.Знайти рівняння дотичної площини та нормалі до поверхні

у точці М(1, 1, 1).

Рівняння дотичної площини:

Рівняння нормалі:

Висновок.

Визначення та позначення, пов'язані з приватними похідними вищих порядків, залишаються чинними і для функцій, що залежать від трьох і більше змінних. Залишається справедливою і можливість зміни порядку вироблених диференцій за умови безперервності порівнюваних між собою похідних.

Кожна приватна похідна (по xі по y) функції двох змінних є звичайну похідну функції однієї змінної при фіксованому значенні іншої змінної:

(де y= const),

(де x= const).

Тому приватні похідні обчислюють за формулам та правилам обчислення похідних функцій однієї змінної, Вважаючи при цьому іншу змінну постійною (константою).

Якщо Вам не потрібен розбір прикладів та необхідного для цього мінімуму теорії, а потрібне лише вирішення Вашого завдання, то переходьте до калькулятору приватних похідних онлайн .

Якщо важко зосередитися, щоб відстежувати, де функції константа, то можна в чорновому рішенні прикладу замість змінної з фіксованим значенням підставити будь-яке число - тоді можна буде швидше обчислити приватну похідну як звичайну похідну функції однієї змінної. Треба не забути при чистовому оформленні повернути місце константу (змінну з фіксованим значенням).

Описане вище властивість приватних похідних випливає з визначення приватної похідної, що може потрапити у екзаменаційних питаннях. Тож ознайомлення з визначенням нижче можна відкрити теоретичну довідку.

Поняття безперервності функції z= f(x, y) у точці визначається аналогічно до цього поняття для функції однієї змінної.

Функція z = f(x, y) називається безперервною в точці якщо

Різниця (2) називається повним збільшенням функції z(Воно у результаті прирощень обох аргументів).

Нехай задані функції z= f(x, y) і крапка

Якщо зміна функції zвідбувається при зміні лише одного з аргументів, наприклад, x, при фіксованому значенні іншого аргументу y, то функція отримає приріст

зване приватним збільшенням функції f(x, y) за x.

Розглядаючи зміну функції zЗалежно від зміни лише одного з аргументів, ми фактично переходимо до функції однієї змінної.

Якщо існує кінцева межа

то він називається приватною похідною функції f(x, y) за аргументом xі позначається одним із символів

(4)

Аналогічно визначаються приватне збільшення zпо y:

та приватна похідна f(x, y) за y:

(6)

приклад 1.

Рішення. Знаходимо приватну похідну за змінною "ікс":

(yфіксовано);

Знаходимо приватну похідну за змінною "гравець":

(xфіксовано).

Як видно, не має значення, якою мірою змінна, яка фіксована: в даному випадку це просто деяке число, що є множником (як у випадку звичайної похідної) при змінній, за якою знаходимо приватну похідну. Якщо ж фіксована змінна не помножена на змінну, за якою знаходимо приватну похідну, то ця самотня константа, байдуже, якою мірою, як і у випадку звичайної похідної, звертається в нуль.

приклад 2.Дана функція

Знайти приватні похідні

(за іксом) і (за гріком) і обчислити їх значення в точці А (1; 2).

Рішення. При фіксованому yпохідна першого доданка знаходиться як похідна статечної функції ( таблиця похідних функцій однієї змінної):

.

При фіксованому xпохідна першого доданка перебуває як похідна показової функції, а другого – як похідна постійної:

Тепер обчислимо значення цих приватних похідних у точці А (1; 2):

Перевірити розв'язання задач з приватними похідними можна на калькулятор приватних похідних онлайн .

Приклад 3.Знайти приватні похідні функції

Рішення. В один крок знаходимо

(y xяк би аргументом синуса було 5 x: так само 5 опиняється перед знаком функції);

(xфіксовано і є в даному випадку множником при y).

Перевірити розв'язання задач з приватними похідними можна на калькулятор приватних похідних онлайн .

Аналогічно визначаються приватні похідні функції трьох і більше змінних.

Якщо кожному набору значень ( x; y; ...; t) незалежних змінних з множини Dвідповідає одне певне значення uз множини E, то uназивають функцією змінних x, y, ..., tі позначають u= f(x, y, ..., t).

Для функцій трьох і більше змінних геометричної інтерпретації немає.

Приватні похідні функції кількох змінних визначаються і обчислюються також у припущенні, що змінюється лише одне із незалежних змінних, інші при цьому фіксовані.

Приклад 4.Знайти приватні похідні функції

.

Рішення. yі zфіксовані:

xі zфіксовані:

xі yфіксовані:

Знайти приватні похідні самостійно, а потім переглянути рішення

Приклад 5.

Приклад 6.Знайти приватні похідні функції.

Приватна похідна функції кількох змінних має той самий механічний сенс, як і похідна функції однієї змінної, - це швидкість зміни функції щодо зміни одного з аргументів.

Приклад 8.Кількісна величина потоку Ппасажирів залізницьможе бути виражена функцією

де П- кількість пасажирів, N– кількість жителів кореспондуючих пунктів, R- Відстань між пунктами.

Приватна похідна функції Ппо R, рівна

показує, що зменшення потоку пасажирів обернено пропорційно квадрату відстані між кореспондуючими пунктами за однієї і тієї ж чисельності жителів у пунктах.

Приватна похідна Ппо N, рівна

показує, що збільшення потоку пасажирів пропорційно до подвоєного числа жителів населених пунктівпри тому самому відстані між пунктами.

Перевірити розв'язання задач з приватними похідними можна на калькулятор приватних похідних онлайн .

Повний диференціал

Твір приватної похідної на збільшення відповідної незалежної змінної називається приватним диференціалом. Приватні диференціали позначаються так:

Сума приватних диференціалів за всіма незалежними змінними дає повний диференціал. Для функції двох незалежних змінних повний диференціал виражається рівністю

(7)

Приклад 9.Знайти повний диференціал функції

Рішення. Результат використання формули (7):

Функція, що має повний диференціал у кожній точці деякої області, називається диференційованою в цій галузі.

Знайти повний диференціал самостійно, а потім переглянути рішення

Так само як і у випадку функції однієї змінної, з диференційованості функції в деякій області випливає її безперервність у цій галузі, але не навпаки.

Сформулюємо без доказів достатню умову диференційності функції.

Теорема.Якщо функція z= f(x, y) має безперервні приватні похідні

у цій галузі, вона диференційована у цій галузі та її диференціал виражається формулою (7).

Можна показати, що подібно до того, як у випадку функції однієї змінної диференціал функції є головною лінійною частиною прирощення функції , так і у випадку декількох змінних повний диференціал є головною, лінійною щодо прирощень незалежних змінних частиною повного прирощення функції.

Для функції двох змінних повне збільшення функції має вигляд

(8)

де α і β - нескінченно малі при і.

Приватні похідні найвищих порядків

Приватні похідні та функції f(x, y) самі є деякими функціями тих самих змінних і, у свою чергу, можуть мати похідні за різними змінними, які називаються приватними похідними вищих порядків.