1. Производна и диференциал. Дефинициите на производната и диференциала на функция на комплексна променлива буквално съвпадат със съответните дефиниции за функции на единична реална променлива.

Нека функцията w = f(z) = и + ivопределени в някакъв квартал Uточки зо.Нека дадем независимата променлива z = x + гуувеличение А z= A.g + гау,не води извън околността U.След това функцията w = f(z)ще получи съответното увеличение Aw = = f(z 0 + Dg) - f(z 0).

Производна на функцията w = f(z) в точката zqсе нарича граница на коефициента на увеличение на функцията ахкъм увеличението на аргумент А zдокато се стремим аздо нула (по произволен начин).

Производната е означена f"(z Q), wили y-. Определението за производна може да бъде написано като

Границата в (6.1) може да не съществува; тогава те казват, че функцията w = f(z)няма производна в точката zq.

функция w = f(z)Наречен диференцируема относно точката Zq, ако е дефиниран в някакъв квартал Uточки zq и неговото нарастване ахмогат да бъдат представени във формата

където е комплексно число Лне зависи от A g, а функцията a(Ag) е безкрайно малка при аз-» 0, т.е. Pm a(Ag) = 0.

Точно както при функции на реална променлива, доказано е, че функцията f(z)диференцируеми в точката zq тогава и само ако има производна в зо. и A = f"(zo).Изразяване f"(zo)AzНаречен диференциал на функцията f(z) в точката Zqи е обозначен dwили df(zo).В този случай увеличението азна независимата променлива -r се нарича още диференциал на променливата r и

обозначен с дз.По този начин,

Диференциалът е основната линейна част от нарастването на функцията.

Пример 6.1. Проучете дали функцията има w= /(r) = R езпроизводна в произволна точка Zq.

Решение. По условие w = Rea = Х.Поради дефиницията на производната, границата (C.1) не трябва да зависи от това кой път

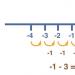
точка z = Zq + Azприближава thпри А z-? 0. Нека първо вземем A z - Ах(Фиг. 15, а). защото Aw = Ах.тогава = 1. Ако

вземете А z = да(фиг. 15, b), Че о= 0 и следователно ах = 0.

Това означава u = 0. Следователно връзката ще издаде кога аз-> 0 не А zА z

съществува и следователно функцията w= Re g = хняма производна в нито една точка.

В същото време функцията w = z = х + iy,очевидно има производна във всяка точка r и /"(th) = 1. От тук става ясно, че реалната и имагинерната част на диференцируемата функция f(r) не могат да бъдат произволни; те трябва да бъдат свързани с някои допълнителни отношения. Тези отношения възникват, защото условието за съществуване на производната /"(0) е значително по-рестриктивно от условието за съществуване на производната на функции на една реална променлива или частични производни на функции на няколко реални променливи: изисква се, че границата в (6.1) съществува и не зависи от пътя, според който точката r = r + Ar се доближава до r като Ar 0. За да изведем тези отношения, припомнете дефиницията за диференцируемост на функция от две променливи.

Реална функция u = u(x,y)реални променливи хИ принаречена диференцируема в точка Ро (хо, о),ако е дефиниран в някаква околност на точка D> и общото му увеличение е A И = техено + Ох ох+ А y) - и (хо, Uo)представим във формата

Където INИ СЪС- реални числа, независими от J , да,А {3 оИ да,клоняща към нула при о -» 0, да-> 0.

Ако функцията Ие диференцируема в точка Po, тогава има a

G, " ди(P 0)^ ди(ро) gt ,

ny производни в Po, и IN= ---, C = ---. Но (различен

Ох ох

от функции на една променлива) от съществуването на частни производни на функцията u(x,y)неговата диференцируемост все още не следва.

2. Условия на Коши-Риман.

Теорема 6.1. Нека функцията w = f(z) на комплексна променлива z= (f, y) се определя в околността на точката, zq= (джо, y o) и f(z) = u(x,y) +iv(x, y). За да бъде f(z) диференцируема в точката Zq, е необходимо и достатъчно функциите u(x, y) XI v(x, y) да бъдат диференцируеми в точката(джо, oo) и че в този момент условията са изпълнени

Равенствата (6.4) се наричат Условия на Коши-Риман .

Доказателство. Необходимост. Нека функцията w = f(z)е диференцируема в точката zq, т.е.

Нека обозначим f"(zo) = a + ib a(Dg) = fi(Ax, Ау)+ g7(J, Ay); Аз = Ах + (Да,Където /3 и 7 - реални функции на променливи ах, о,клоняща към нула като J -> 0, Au -> 0. Замествайки тези равенства в (6.5) и разделяйки реалната и имагинерната част, получаваме:

Тъй като равенството на комплексните числа е еквивалентно на равенството на техните реални и имагинерни части, тогава (6.6) е еквивалентно на системата от равенства

Равенствата (6.7) означават, че функциите u(x,y), v(x,y)отговарят на условие (6.3) и следователно са диференцируеми. Тъй като коефициентите за J и даса равни на частните производни по отношение на w и присъответно, тогава от (6.7) получаваме

откъдето следват условия (6.4).

Адекватност. Нека сега приемем, че функциите u(x, y)И v(x,y)диференцируеми в точка (хо.оо)И u(x,y)и условията (6.4) са изпълнени.

Означавайки a = ^, 6 = -^ и прилагайки (6.4), стигаме до равенства (6.8). От (6.8) и условието за диференцируемост на функциите u(x,y), v(x,y)ние имаме

където ft, 7i, ft, д-2 - функции, клонящи към нула като Ах -> 0, Au ->-> 0. Оттук

Ан + iAv= (o + ib) (Ах + i.Ay)+ (ft + ift)Ax + (71 + *72) да(6.9) Нека дефинираме функцията a(Dr) чрез равенството

и сложи А = А 4- ib.Тогава (6.9) ще бъде пренаписано като равенството

което съвпада с (6.2). Ден на доказателство за диференцируемост

функции f(z)Остава да се покаже, че lim a(Az) = 0. От равенството

следва това о^ |Dg|, да^ |Dg|. Ето защо

Ако аз-? 0, тогава о-? 0, да-> 0, което означава, че функциите ft, ft, 71, 72 клонят към нула. Следователно a(Dr) -> 0 at аз-> 0 и доказателството на теорема 6.1 е завършено.

Пример 6.2. Разберете дали дадена функция е w = z 2 диференцируеми; ако да, в кои точки?

Решение, w = u + iv = (x + iy) 2 = x 2 - y 2 + 2ixy,където и = = x 2 - y 2, V = 2xy.следователно

По този начин условията на Коши-Риман (6.4) са изпълнени във всяка точка; това означава функцията w = g 2 ще бъде диференцируемо в C.

Пример 6.3. Изследвайте диференцируемостта на функция w = - z - x - iy.

Решение. w = u + iv = x - iy,където u = x, v = -yИ

По този начин условията на Коши-Риман не са изпълнени в нито една точка и следователно функцията w = zне се диференцира никъде.

Можете да проверите диференцируемостта на функция и да намерите производни директно, като използвате формула (6.1).

Пример 6.4. Използвайки формула (6.1), изследвайте диференцируемостта на функцията IV = z 2.

Решение. А т- (zq + A з) 2- Zq = 2 zqAz -I- (A z) 2,където

Следователно функцията w = zrе диференцируема във всяка точка 2o и нейната производна f"(zo) =2 зо-

Тъй като основните теореми за границите са запазени за функции на комплексна променлива и дефиницията на производната на функция на комплексна променлива също не се различава от съответната дефиниция за функции на реална променлива, тогава добре известните правила за диференцирането на сумата, разликата, произведението, частното и комплексната функция остават валидни за функции на комплексна променлива. По същия начин може да се докаже, че ако функцията f(z)диференцируеми в точката зо.тогава тя е непрекъсната в тази точка; обратното не е вярно.

3. Аналитични функции. функция w= /(^диференцируем само в самата точка zq, но също така и в някои околности на тази точка, се нарича аналитичен в точка zq.Ако f(z)е аналитичен във всяка точка на региона Д,тогава се нарича аналитичен (правилен, холоморфен) в област D.

От свойствата на производните веднага следва, че ако f(z)И g(z)- аналитични функции в областта Д,след това функциите f(z) + g(z), f(z) - g(z), f(z) g(z)също аналитичен в областта Д,и частното f(z)/g(z)аналитична функция във всички точки на региона Д.в който g(z) f 0. Например функция

е аналитичен в равнината C с отпаднали точки z= = 1 и z - i.

От теоремата за производната на сложна функция следва следното твърдение: ако функцията И = u(z) е аналитичен в домейна ди дисплеи дкъм региона Д"променлива и, и функция w = е(ф)аналитичен в областта Д", тогава сложна функция w = f(u(z))променлива zаналитичен в Д.

Нека въведем концепцията за функция, която е аналитична в затворена област Д.Разликата от отворения регион тук е, че се добавят гранични точки, към които не принадлежи квартал Д;следователно производната в тези точки не е дефинирана. функция f(z)Наречен аналитичен (редовен, холоморфен) в затворен регион D, ако тази функция може да бъде разширена в някаква по-широка област даз, съдържащ Д,към аналитичен дфункции.

• Условията (6.4) са изследвани още през 18 век. д'Аламбер и Ойлер. Поради това понякога се наричат ​​също условия на д'Аламберт-Ойлер, което е по-правилно от историческа гледна точка.

Функции на комплексна променлива.
Диференциране на функции на комплексна променлива.

Тази статия отваря поредица от уроци, в които ще разгледам типични проблеми, свързани с теорията на функциите на комплексна променлива. За да усвоите успешно примерите, трябва да имате основни познания за комплексните числа. За да консолидирате и повторите материала, просто посетете страницата. Ще ви трябват и умения за намиране частични производни от втори ред. Ето ги тези частични производни... даже сега бях малко изненадан колко често се срещат...

Темата, която започваме да разглеждаме, не представлява особени трудности и във функциите на сложна променлива по принцип всичко е ясно и достъпно. Основното нещо е да се придържате към основното правило, което извадих експериментално. Прочетете!

Понятие за функция на комплексна променлива

Първо, нека опресним знанията си за училищната функция на една променлива:

Функция с единична променливае правило, според което на всяка стойност на независимата променлива (от областта на дефиниране) съответства една и само една стойност на функцията. Естествено, "x" и "y" са реални числа.

В сложния случай функционалната зависимост се определя по подобен начин:

Еднозначна функция на комплексна променлива- това е правилото, според което всеки изчерпателенстойността на независимата променлива (от областта на дефиницията) съответства на една и само една изчерпателенстойност на функцията. Теорията също така разглежда многозначни и някои други видове функции, но за простота ще се съсредоточа върху една дефиниция.

Каква е разликата между функция на сложна променлива?

Основната разлика: комплексни числа. Не съм ироничен. Такива въпроси често оставят хората в ступор; в края на статията ще ви разкажа една забавна история. На урока Комплексни числа за манекениразгледахме комплексно число във формата . От сега буквата "z" стана променлива, тогава ще го обозначим по следния начин: , докато „x“ и „y“ могат да приемат различни валидензначения. Грубо казано, функцията на комплексна променлива зависи от променливите и , които приемат „обикновени“ стойности. От този факт логично следва следното:

Функцията на комплексна променлива може да бъде записана като:
, където и са две функции на две валиденпроменливи.

Функцията се извиква реална частфункции
Функцията се извиква въображаема частфункции

Тоест функцията на комплексна променлива зависи от две реални функции и . За да изясним най-накрая всичко, нека да разгледаме практически примери:

Пример 1

Решение:Независимата променлива „zet“, както си спомняте, е написана във формата , следователно:

(1) Заменихме .

(2) За първия член е използвана формулата за съкратено умножение. В термина скобите са отворени.

(3) Внимателно квадрат, без да забравяме това

(4) Пренареждане на термини: първо пренаписваме термините , в който няма имагинерна единица(първа група), след това термините, където има (втора група). Трябва да се отбележи, че разбъркването на термините не е необходимо и тази стъпка може да се пропусне (като всъщност се направи устно).

(5) За втората група я изваждаме от скоби.

В резултат на това нашата функция се оказа представена във формата

Отговор:
– реална част от функцията.
– имагинерна част от функцията.

Какви функции се оказаха? Най-често срещаните функции на две променливи, от които можете да намерите такива популярни частични производни. Без милост ще го намерим. Но малко по-късно.

Накратко, алгоритъмът за решаваната задача може да се напише по следния начин: заместваме , в оригиналната функция, извършваме опростявания и разделяме всички термини на две групи - без въображаема единица (реална част) и с имагинерна единица (въображаема част) .

Пример 2

Намерете реалната и имагинерната част на функцията

Това е пример, който можете да решите сами. Преди да се впуснете в битка на сложната равнина с теглени пулове, нека ви дам най-важния съвет по темата:

БЪДИ ВНИМАТЕЛЕН!Трябва да внимавате, разбира се, навсякъде, но в сложните числа трябва да сте по-внимателни от всякога! Не забравяйте, че внимателно отворете скобите, не губете нищо. По мои наблюдения най-честата грешка е загубата на знак. Не бързай!

Пълно решение и отговор в края на урока.

Сега кубът. Използвайки формулата за съкратено умножение, извличаме:
.

Формулите са много удобни за използване на практика, тъй като значително ускоряват процеса на решаване.

Диференциране на функции на комплексна променлива.

Имам две новини: добра и лоша. Ще започна с добрия. За функция на комплексна променлива са валидни правилата за диференциране и таблицата с производни на елементарни функции. По този начин производната се взема точно по същия начин, както в случай на функция на реална променлива.

Лошата новина е, че за много сложни функции на променлива изобщо няма производна и вие трябва да разберете диференцируема ли еедна или друга функция. А „разбирането“ как се чувства сърцето ви е свързано с допълнителни проблеми.

Нека разгледаме функцията на комплексна променлива. За да бъде тази функция диференцируема е необходимо и достатъчно:

1) Така че съществуват частни производни от първи ред. Забравете за тези нотации веднага, тъй като в теорията на функциите на комплексна променлива традиционно се използва различна нотация: .

2) Да се ​​извърши т.нар Условия на Коши-Риман:

Само в този случай производното ще съществува!

Пример 3

Решениесе разделя на три последователни етапа:

1) Нека намерим реалната и имагинерната част на функцията. Тази задача беше обсъдена в предишни примери, така че ще я запиша без коментар:

От тогава:

По този начин:

– имагинерна част от функцията.

Нека засегна още една техническа точка: в какъв реднапишете условията в реалната и имагинерната част? Да, по принцип няма значение. Например реалната част може да бъде написана така: , а въображаемата – така: .

2) Нека проверим изпълнението на условията на Коши-Риман. Двама са.

Нека започнем с проверка на състоянието. Намираме частични производни:

Така условието е изпълнено.

Разбира се, добрата новина е, че частичните производни почти винаги са много прости.

Проверяваме изпълнението на второто условие:

Резултатът е същият, но с противоположни знаци, тоест условието също е изпълнено.

Условията на Коши-Риман са изпълнени, следователно функцията е диференцируема.

3) Да намерим производната на функцията. Производната също е много проста и се намира по обичайните правила:

Въображаемата единица се счита за константа по време на диференциацията.

Отговор: – реална част, – въображаема част.
Условията на Коши-Риман са изпълнени, .

Има още два начина за намиране на производната, те, разбира се, се използват по-рядко, но информацията ще бъде полезна за разбирането на втория урок - Как да намерим функция на комплексна променлива?

Производната може да се намери по формулата:

В такъв случай:

По този начин

Трябва да решим обратната задача - в получения израз трябва да изолираме . За да направите това, е необходимо в условията и извън скобите:

Обратното действие, както мнозина са забелязали, е малко по-трудно за проверка, винаги е по-добре да вземете израза на чернова или устно да отворите скобите обратно, като се уверите, че резултатът е точен;

Огледална формула за намиране на производната:

В такъв случай: , Ето защо:

Пример 4

Определяне на реалните и въображаемите части на функция . Проверете изпълнението на условията на Коши-Риман. Ако са изпълнени условията на Коши-Риман, намерете производната на функцията.

Кратко решение и приблизителен образец на окончателния дизайн в края на урока.

Винаги ли са изпълнени условията на Коши-Риман? Теоретично те не се изпълняват по-често, отколкото се изпълняват. Но в практически примери не си спомням случай, в който те не са били изпълнени =) По този начин, ако вашите частични производни „не се сближават“, тогава с много голяма вероятност можете да кажете, че сте направили грешка някъде.

Нека усложним нашите функции:

Пример 5

Определяне на реалните и въображаемите части на функция . Проверете изпълнението на условията на Коши-Риман. Изчисли

Решение:Алгоритъмът за решение е напълно запазен, но в края ще бъде добавена нова точка: намиране на производната в точка. За куба необходимата формула вече е изведена:

Нека дефинираме реалните и въображаемите части на тази функция:

Внимание и пак внимание!

От тогава:


По този начин:
– реална част от функцията;
– имагинерна част от функцията.

Проверка на второто условие:

Резултатът е същият, но с противоположни знаци, тоест условието също е изпълнено.

Условията на Коши-Риман са изпълнени, следователно функцията е диференцируема:

Нека изчислим стойността на производната в исканата точка:

Отговор:, , условията на Коши-Риман са изпълнени,

Функциите с кубчета са често срещани, така че ето пример за засилване:

Пример 6

Определяне на реалните и въображаемите части на функция . Проверете изпълнението на условията на Коши-Риман. Изчисли.

Решение и пример за завършване в края на урока.

В теорията на комплексния анализ се дефинират и други функции на комплексен аргумент: експонента, синус, косинус и др. Тези функции имат необичайни и дори странни свойства - и това е наистина интересно! Наистина искам да ви кажа, но тук, както се случва, не е справочник или учебник, а книга с решения, така че ще разгледам същия проблем с някои общи функции.

Първо за т.нар Формули на Ойлер:

За всеки валиденчисла, валидни са следните формули:

Можете също да го копирате в бележника си като справочен материал.

Строго погледнато, има само една формула, но обикновено за удобство пишат и специален случай с минус в степента. Параметърът не трябва да бъде една буква; той може да бъде сложен израз или функция, важно е само те да приемат само валидензначения. Всъщност ще видим това точно сега:

Пример 7

Намерете производната.

Решение:Генералната линия на партията остава непоклатима - необходимо е да се разграничат реалната и мнимата част на функцията. Ще дам подробно решение и ще коментирам всяка стъпка по-долу:

От тогава:

(1) Вместо това заменете „z“.

(2) След заместването трябва да изберете реалните и въображаемите части първи в индикатораизложители. За да направите това, отворете скобите.

(3) Групираме имагинерната част на индикатора, като поставяме имагинерната единица извън скоби.

(4) Използваме училищното действие със степени.

(5) За множителя използваме формулата на Ойлер и .

(6) Отворете скобите, което води до:

– реална част от функцията;
– имагинерна част от функцията.

По-нататъшните действия са стандартни, нека проверим изпълнението на условията на Коши-Риман:

Пример 9

Определяне на реалните и въображаемите части на функция . Проверете изпълнението на условията на Коши-Риман. Така да бъде, няма да намерим производното.

Решение:Алгоритъмът за решение е много подобен на предишните два примера, но има много важни точки, така че отново ще коментирам началния етап стъпка по стъпка:

От тогава:

1) Заменете „z“ вместо това.

(2) Първо избираме реалните и въображаемите части вътре в синуса. За тези цели отваряме скобите.

(3) Използваме формулата и .

(4) Използвайте четност на хиперболичен косинус: И странност на хиперболичен синус: . Хиперболите, макар и извън този свят, в много отношения напомнят подобни тригонометрични функции.

В крайна сметка:
– реална част от функцията;
– имагинерна част от функцията.

внимание!Знакът минус се отнася за имагинерната част и в никакъв случай не трябва да я губим! За ясна илюстрация полученият по-горе резултат може да се пренапише, както следва:

Нека проверим изпълнението на условията на Коши-Риман:

Условията на Коши-Риман са изпълнени.

Отговор:, , условията на Коши-Риман са изпълнени.

Дами и господа, нека да го разберем сами:

Пример 10

Определете реалните и имагинерните части на функцията. Проверете изпълнението на условията на Коши-Риман.

Нарочно избрах по-трудни примери, защото всеки изглежда може да се справи с нещо, като белени фъстъци. В същото време ще тренирате вниманието си! Крекер за ядки в края на урока.

Е, в заключение ще разгледам още един интересен пример, когато сложен аргумент е в знаменателя. Случвало се е няколко пъти на практика, нека да разгледаме нещо просто. Ех, остарях...

Пример 11

Определете реалните и имагинерните части на функцията. Проверете изпълнението на условията на Коши-Риман.

Решение:Отново е необходимо да се разграничат реалните и имагинерните части на функцията.
Ако , тогава

Възниква въпросът какво да правим, когато в знаменателя е Z?

Всичко е просто - стандартният ще помогне метод за умножаване на числителя и знаменателя по спрегнатия израз, вече е използвано в примерите от урока Комплексни числа за манекени. Да си припомним училищната формула. Вече имаме в знаменателя, което означава, че спрегнатият израз ще бъде . Следователно трябва да умножите числителя и знаменателя по:

Препис

1 Условия на Коши-Риман.) Проверете изпълнението на условията на Коши-Риман за функцията w zi e. За функция, която има производна в точка z, се казва, че е диференцируема в тази точка. Условия на Коши - Риман (D'Alembert - Euler, Euler - D'Alembert): w f z u, iv, тогава във всяка точка на диференцируемост на функцията f z Ако z i равенствата са изпълнени, u v u v Записваме тази функция в алгебрична форма, задавайки z i : zi ii i i ние e e e e cos isin e cos isin e cos ie sin Нека изберем реалните u и въображаемите v части на функцията w: u, e cos v, e sin Изчисляваме частните производни: u cos e e cos v e sin e cos u e cos e sin v e sin e sin - условията на Коши-Риман са изпълнени. Литература :) Gusak A.A. „Теория на функциите на комплексна променлива и операционно смятане“, 00, стр. 59 (пример 9), стр. 0 (пример); Написано от Д.Т. "Лекции по висша математика", 006, стр. 530, стр. (Условия на Ойлер-Д'Аламберт, аналитичност на функцията). Проверете изпълнението на условията на Коши-Риман за функцията w z 4iz. Нека запишем тази функция в алгебрична форма, задавайки z i: w i 4i i i 4 i i

2 Нека изберем реалните u и въображаемите v части на функцията w: u, 4 v, 4 Изчисляваме частните производни: u 4 v 4 u 4 4 v условията на Коши-Риман са изпълнени. 3) Проверете изпълнението на условията на Коши-Риман за функцията sin iz. Нека изразим тригонометричната функция sin z чрез експоненциала: iz iz e e sin z i и вземем предвид, че z i: ii ii ii ii i i e e e e e e e e sin iz i i i e i i e e e e e cos isin e cos isin e sin icose sin icos e sin icose sin icos e sin ie cose sin ie cos sin cos e e i e e Реални и имагинерни части на числото u iv: u, sin e e, cos v e e

3 Изчисляваме частните производни: u sin sin e e e e v cos e e sin e e sin e e и u sin cos e e e e cos cos e e e e v Както виждаме, условията на Коши-Риман u v u v sin iz са изпълнени. за функция 4) Използвайки условията на Коши-Риман, проверете дали функцията w f z е аналитична: Функция wsin z3 z. w f z се нарича аналитичен в точка z, ако е диференцируем както в самата точка z, така и в някои от нейните околности. Функция w f z, диференцируема във всяка точка от някаква област D, се нарича аналитична функция в тази област. Условия на Коши - Риман (D'Alembert - Euler, Euler - D'Alembert): Ако z i w f z u, iv, тогава във всяка точка на диференцируемост на функцията f z равенствата u v u v са изпълнени. Нека напишем тази функция в алгебрична форма, задавайки z i: i 3 i w sin ii ii e 3i3 i i i e 3i3 i i i e e e 3i3 i e cos isin e cosisin 3i3 i e cos ie sin e cos i e sin 3 i3 i 3

4 cos e e i e e sin 3i3 i cos i e e e e sin 3i3 e e e sin i e e cos 3i3 e e sin 3i e e cos 3 ch sin 3 sh i cos 3 Формули, използвани в трансформациите: iz iz e e sin z i, zc e e sh, Re e ch, R Изберете реални и имагинерни части w z u, i v, u, chsin 3 v, shcos3: Изчислете частичните производни: u ch sin 3 ch cos3 v sh cos3 ch cos3 u ch sin 3 sh sin v sh cos 3 sh sin И така, системата на Коши-Риман условия u v u v , изпълнени; следователно функцията sin w f z z3 z е аналитична. 4

5 5) Докажете аналитичността на функцията и намерете производната: z z e w e Запишете тази функция в алгебрична форма, задавайки z i: i i e e w e cos isin e cosisin e cos isin e cos isin e cos ie sin e cos ie sin cos e e i e e sin e e e e cos i sin ch cos ish sin Нека изберем реалните и въображаемите части w z u, i v, u, chcos v, shsin Изчисляваме частните производни: u ch cos sh cos v sh sin sh cos u ch cos ch sin v sh sin ch sin: Условия на Коши-Риман u v u v, изпълнени; следователно функцията w f z e z e z е аналитична. За всяка аналитична функция f z u, i v, частични производни на функциите u u и v v, : производна f u v v u u u v v f z i i i i Изчисляваме производната на производните на функциите на функциите u и v, : z се изразява чрез f z, използвайки израза за производна на функцията w z z z e e u v w z i sh cos ich sin z по отношение на частично 5

6 или директно: z z e e z z z z w e e z e e z i i i i e e e e e e cos isin e cosisin e cos isin e cos isin cos sin e e e e e e e e cos i sin sh cos ich i 6) представляват iz w, където z i, във формата w u, i v ,. Проверете дали ще бъде аналитично, ако е така, тогава намерете производната в точката z0 6. Нека изрично идентифицираме реалните u и въображаемите части в това число, ep ep ep ep e cos i sin e cos i e sin v: i w iz i i i i e e - комплексно число се получава в алгебричен запис. Re w u, e cos Im w v, e sin За всяка аналитична функция f z u, i v, частните производни на функциите u u и v v, : производната f u v v u u u v v f z i i i i z се изразява чрез Нека изчислим частните производни u, e cos, sin v e u e cos sin e u cos e cos e v e sin sin e v sin e cos e Тъй като условията на Коши-Риман са изпълнени (u v, u v) за всички точки на равнината O, изследваната функция е аналитична в цялата равнина и нейната производна 6

7 u v w z i e i e sin cos 6 6 w zesin iecos e 3 ie 3 3 В точка z0 i0: Литература:) Gusak A.A. "Теория на функциите на комплексна променлива и операционно смятане", 00, стр. 59 (пример 9), стр. 0 (пример). Изчислете стойността на функцията. 7) Изчислете стойността на функцията на комплексната променлива w cos z в точка z0 i. e За всяко z C: cos z iz e iz Тогава ii ii i i i i e e e e e e e wicosi e cos isin e cos isin cos e e isin e e e e e e cos i sin ch cos i sh sin Отговор: i cos ch cos ish sin Литература:) Морозова В.Д. "Теория на функциите на комплексна променлива", 009, том 0, изд. MSTU, стр. 06;) Lunts G.L., Elsgolts L.E. "Функции на комплексна променлива", 00, страница) Изчислете стойността на функцията на комплексна променлива w th z в точка z 0 ln 3 в алгебрична форма. z z e e За всяко z C: th z z z e e Така че i i ln 3 i ln 3 i e 4 e w z 0 i e e th ln 3 i ln 3 i i i e 4 e 4 e 4 3 e 4 3 i 4, запишете отговора 7

8 i i 9cos isin cos isin 9e 4 e i i 9e 4 e 4 9cos isin cos isin i i 9 i i 9 i i 9 i i 9 i9 i 8 i0 45i 9 i9 i 0 i 8 5 4i 4 5i5 4i 0 5i6i0 40 9i 40 9 i 54i54i резултат изчисления в алгебрична форма. 9) Изчислете стойността на функцията на комплексната променлива Ln z в точка z 0. Посочете главната стойност на функцията. Логаритмична функция Ln ln arg z z i z k kz Главната стойност на логаритъма на числото z е стойността, съответстваща на основната стойност на аргумента на числото z; тези. получаваме основната стойност на логаритъма при k 0: ln z ln z i arg z Модул и аргумент на числото z0 0 i: z 0 arg z 0 Следователно Ln ln i k 0k i kz са стойностите на функцията на a комплексна променлива в точката z 0, записана в алгебрична форма. (логаритмичната функция Ln z е многозначна) Основната стойност на логаритъма на числото z ln 0 i 8

9 0) Изчислете стойността на функцията на комплексната променлива i z в точка z i 0. За всяко w z C: w z z Ln w e. i iln i iln i iarg i ki i e e, kz Модул и аргумент на числото w i: i arg iarctg 4 ln i ln i ki i k i k i i ln i iarg i ki ln i i e 4 e 4 e 4 ln k i k 4 ln ln e e e 4 cos isin, kz - стойности на функцията на комплексна променлива z в точка z0 i, записана в тригонометрична форма (многозначна функция).) Изчислете стойността на функцията на комплексна променлива arcctg z в точка z0 i, напишете отговора в алгебрична форма. i z i Arcctg z Ln z i Ln z ln z iarg z k, kz (при k 0 получаваме главната стойност на логаритъма ln z ln z i arg z) z0 i ii i i3i i3i3 4i i z i ii 3i 3i3i z0 i Ln Ln iln iarctg k z i ln iarctg k ln 5iarctg k, kz 5 и z0 i ln ln 5 i arctg z i 0 i arcctg z0 ln 5 iarcg t arctg i ln 5 0,3 i 0,40 4 (основна стойност на Arcctg i) 9

10) Изчислете стойността на функцията на комплексната променлива arccos z в точка z0 i, запишете отговора в алгебрична форма. Arccos z iln z z Ln z ln z i arg z k, kz Когато k 0 получаваме главната стойност на логаритъма ln z ln z i arg z и главната стойност на аркосинуса arccos z arg z z iln z z Корен квадратен от комплексно число дава две стойности; За основна стойност на функцията избираме тази, чийто аргумент попада в диапазона 0 ;. В този случай: arccos ln ln iln i i Коренът на числото i i i i i i i i приема две стойности. Нека ги намерим: cos arctg i sin arctg i arctg k arctg k i 5 cos isin 4 arctg arctg 5cos isin, k 0 i 4 arctg arctg 5 cos i sin, k cos Използвайки формулите cos cosarctg 5, получаваме: cos и sin, и като се има предвид, че arctg 5 5 cos 0 arctg 5 5 sin 0 и след това i, k 0 i, k i i, k i, k 0 0 0

11 и 5 5 i, k 0 i i 5 5 i, k От двете стойности избираме втората, т.к. неговият аргумент попада в диапазона 0 ;. И така, i i 5 i arccos z arg z z iln z z arctg 5 5 iln i 5 5 arctg 5 5 i ln 5 arctg 5 i l n 5 5 5, 7 i 0, 59 5 (основната стойност на Arccos i) Литература :) Morozova V.D. . "Теория на функциите на комплексна променлива", 009, том 0, изд. MSTU, стр. 06;) Lunts G.L., Elsgolts L.E. "Функции на комплексна променлива", 00, 40.

Комплексното число е израз на формата x y (алгебрична форма на комплексно число), където x, y R; x Re - реална част от комплексно число; y Im е имагинерната част на комплексно число; - въображаем

Тема 11 Основни сведения от теорията на комплексните числа. Комплексното число е подредена двойка реални числа, записана във формата, където i е „въображаемата единица“, за която i = -1; - същинска част

Комплексни числа. Полиноми. Комплексни числа. 1. Основни дефиниции и формули за решаване на задачи Комплексното число в алгебрична форма е израз на формата = x + y, където x и y са реални

1 Основни понятия за функции на комплексна променлива Основните понятия, свързани с функция на комплексна променлива, се намират по същия начин, както в реалната област. Нека два комплекта сложни

Санкт Петербургски държавен университет Катедра по математически анализ МЕТОДОЛОГИЧЕСКИ ИНСТРУКЦИИ за провеждане на практически занятия по теория на функциите на комплексна променлива част 1 Начални глави

Указания за теста по математика Тема 1. Функции на комплексна променлива Нека дефинираме функцията на комплексна променлива. Определение. Казват, че на множеството D от комплексни точки

Вариант Задача Изчислете стойността на функцията, дайте отговора в алгебрична форма: a sh ; b l Решение a Нека използваме формулата за връзката между тригонометричния синус и хиперболичния синус: ; sh -s Get

Вариант Проблем Изчислете стойността на функцията (дайте отговора в алгебрична форма: a th(; b L(sh(/ Решение a Нека изразим тангенса чрез синус и косинус: th(Приложете ch(/ формули за синус разлика и косинус)

Министерство на образованието и науката на Руската федерация РУСКИЯТ ДЪРЖАВЕН УНИВЕРСИТЕТ ПО НЕФТ И ГАЗ НА И. М. ГУБКИН В Мелников, Н. О. Фастовец ТЕОРИЯ НА ФУНКЦИИТЕ НА КОМПЛЕКСНАТА ПРОМЕНЛИВА

Тема: Комплексни числа и функции. Дефиниция на комплексно число, алгебрична форма на комплексно число. Реални и имагинерни части на комплексно число. Операции събиране и умножение на комплексни числа.

Комплексен анализ Функции на комплексна променлива Никита Александрович Евсеев Факултет по физика, Новосибирски държавен университет Китайско-руски институт, Университет Хейлундзянг

Теми: Наименование на раздела, теми Общ брой аудиторни часове Лекции, часове Практически занятия, часове 1 2 3 4 Тема 1. Аналитична геометрия и линейна алгебра 68 34 34 Тема 2. Въведение в математическия анализ

В. Д. Михайлов Функции на комплексна променлива в примери и задачи 04 УДК 57.5 ББК.6 М69 Михайлов В. Д. Функции на комплексна променлива в примери и задачи: Учебник. Санкт Петербург, 04.30 p. Урок

Страница 1 от 14 2-ри урок. Експоненциална форма на комплексно число Матем. анализ, прил. математика, 4-ти семестър A1 Намерете модулите и аргументите на следните комплексни числа и запишете тези числа във формата z = ρe iϕ,

МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НА РУСКАТА Федерална държавна бюджетна образователна институция за висше професионално образование "Тулски държавен университет" Институт за високоточни системи на името на V.P.

МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НА RF АНГАРСКА ДЪРЖАВНА ТЕХНИЧЕСКА АКАДЕМИЯ Мусева Т.Н. Свердлова О.Л. Туркина Н.М. ЕЛЕМЕНТИ НА ТЕОРИЯТА ЗА ФУНКЦИЯТА НА КОМПЛЕКСНА ПРОМЕНЛИВА Учебник Ангарск СЪДЪРЖАНИЕ

ЕЛЕМЕНТИ НА ТЕОРИЯТА НА ФУНКЦИИТЕ НА ОПЕРАЦИОННО СЧИТАНЕ С КОМПЛЕКСНА ПРОМЕНЛИВА В резултат на изучаването на тази тема студентът трябва да научи: намира тригонометричните и експоненциалните форми на комплексно число според

ЗАДАЧИ ЗА САМОПОДГОТОВКА Комплексни числа и действия с тях Дадени са комплексни числа и Намерете:)))) 5): а) б) Запишете това комплексно число:) в тригонометрична форма) в степенна форма

ВАРИАНТ ЗАДАЧАТА Е ДА ИЗЧИСЛИМ СТОЙНОСТТА НА ФУНКЦИЯТА (ОТГОВОРЪТ Е ДАДЕН В АЛГЕБРИЧНА ФОРМА: a Arch; b РЕШЕНИЕ A ЩЕ ИЗЧИСЛИМ ARH ПО ФОРМУЛАТА Arch(L(В ТОЗИ ПРИМЕР ZI, СЛЕДОВА, Arch L(± L( ± ДОПЪЛНИТЕЛНА УПОТРЕБА

Вариант 9 Задача Изчислете стойността на функцията (дайте отговора в алгебрична форма: a cos(; b l(Решение a Използване на тригонометричната формула cos(-cos cos(s s(Използваме формулите за връзка между тригонометрични

ФЕДЕРАЛНА АГЕНЦИЯ ПО ОБРАЗОВАНИЕТО ДЪРЖАВНА ОБРАЗОВАТЕЛНА ИНСТИТУЦИЯ ЗА ВИСШЕ ПРОФЕСИОНАЛНО ОБРАЗОВАНИЕ “САМАРСКИ ДЪРЖАВЕН ТЕХНИЧЕСКИ УНИВЕРСИТЕТ” Катедра по приложна математика

Лекция.7. Разширяване на понятието число. Комплексни числа, операции с тях Анотация: В лекцията се изтъква необходимостта от обобщаване на понятието число от естествено към комплексно. алгебричен,

ВАРИАНТ ЗАДАЧА ИЗЧИСЛЕТЕ СТОЙНОСТТА НА ФУНКЦИЯ ДАЙТЕ ОТГОВОРА В АЛГЕБРИЧНА ФОРМА: a Arch b РЕШЕНИЕ A ЩЕ ИЗЧИСЛИМ ARH ИЗПОЛЗВАЩИ ФОРМУЛАТА Arch L В ТОЗИ ПРИМЕР ZI, СЛЕДОВАТЕЛНО Arch L± L± ПО-нататъшно използване

Лекция..3. Неопределен интеграл Резюме: Неопределеният интеграл се дефинира като набор от първоизводни функции на интегранта. Разглеждат се свойствата на неопределения интеграл и

“знак за действие” a+(-b)=a-b 1) Защо са въведени отрицателните числа? “знак за количество”) Защо върху тях действията се извършват по такива и такива правила, а не по други? Защо е отрицателно при умножение и деление?

Практически урок Аналитични функции Условия на Коши-Риман Производна и диференциал на функция на комплексна променлива Условия на Коши-Риман 3 Геометричен смисъл на модула и аргумент на производната 4 Конформен

Лекция 2 2.1 Поредици от комплексни числа Комплексно число a се нарича граница на поредица от комплексни числа (z n ), ако за всяко число ε > 0 съществува число n 0 n 0 (ε), такова че

Вариант Задача Изчислете стойността на функцията (дайте отговора в алгебрична форма: a cos(; b l(Решение a Използване на тригонометричната формула cos(cos cos(-s s(Използваме формулите за връзка между тригонометрични

Федерална агенция за образование Държавна образователна институция за висше професионално образование "Уралски държавен педагогически университет" Факултет по математика

Министерство на образованието и науката на Руската федерация Федерална държавна бюджетна образователна институция за висше професионално образование "Комсомолск на Амур Държавен технически

МОСКОВСКИЯТ ДЪРЖАВЕН ТЕХНИЧЕСКИ УНИВЕРСИТЕТ ЗА ГРАЖДАНСКА АВИАЦИЯ O.G. Иларионова, И.В. Платонова ВИСША МАТЕМАТИКА Учебно-методическо ръководство за изпълнение на практически задачи за студенти II

Концепцията за комплексна променлива Граница и непрекъснатост на комплексна променлива Нека са дадени два набора от комплексни числа D и Δ и всяко число z D е свързано с число ω Δ, което се означава

Комплексен анализ Примери за функции на комплексна променлива Никита Александрович Евсеев Факултет по физика, Новосибирски държавен университет Китайско-руски институт, Университет Хейлундзянг

ЛЕКЦИЯ N34. Числови редове със сложни членове. Степенен ред в комплексната област. Аналитични функции. Обратни функции..числови редове със сложни членове.....степенни редове в комплексната област....

МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НА ФЕДЕРАЛНАТА ДЪРЖАВНА БЮДЖЕТНА ОБРАЗОВАТЕЛНА ИНСТИТУЦИЯ ЗА ВИСШЕ ПРОФЕСИОНАЛНО ОБРАЗОВАНИЕ Департамент „САМАРСКИ ДЪРЖАВЕН ТЕХНИЧЕСКИ УНИВЕРСИТЕТ“

Въведение 1 Запишете числото в алгебрична форма Find, Re, Im, arg, Arg = 5 + i 3 + i Решение Умножете и разделете числото на числото, спрегнато към знаменателя: 5 + i 3 + i = 5 + i) 3 i) 3 + i) 3 i) = 15

1 Комплексни функции 1.1 Комплексни числа Спомнете си, че комплексните числа могат да бъдат дефинирани като набор от подредени двойки реални числа C = ((x, y) : x, y R), z = x + iy, където i е имагинерната единица ( аз

Основни понятия 1 КОМПЛЕКСНИ ЧИСЛА Комплексното число е израз на формата i, където и са реални числа, i е имагинерна единица, която отговаря на условието i 1 Числото се нарича реална част от комплекс

Лекция 3. Неопределен интеграл. Антипроизводна и неопределен интеграл В диференциалното смятане проблемът е решен: дадена функция f(), намерете нейната производна (или диференциал). Интегрално смятане

ГЛАВА ТЕОРИЯ НА ФУНКЦИИТЕ НА КОМПЛЕКСНА ПРОМЕНЛИВА Концепцията за функция на комплексна променлива Непрекъснатост на fcp Дефиницията на fcp е в много отношения подобна на дефиницията на fcp Те казват, че върху определено множество от комплекс

Функции Диференциране на функции 1 Правила за диференциране Тъй като производната на функция се определя както в реалната област, т.е. под формата на граница, тогава, използвайки тази дефиниция и свойствата на границите,

Вариант Задача Изчислете стойността на функцията (дайте отговора в алгебрична форма: a Arctg; b (Решение a Като цяло Arctg arctg + kπ Нека намерим други стойности в комплекса + равнина Ще изчислим Arctg с помощта на формулата

Функции на няколко променливи Функции на няколко променливи Екстремум на функция на няколко променливи. Намиране на максималните и минималните стойности на функция в затворена област Условен екстремум Комплекс

БАНКА ЗАДАЧИ за приемни тестове за магистърска програма (основна част) Задачи от билети, 4 5 Раздели, 4, 5, 6, 7, 8, 9, 6, 7, 8, 4, 5, 9 Брой точки 5 b b 5 b Раздел Съдържание Производна, частно

Лекция 5 Производни на основни елементарни функции Анотация: Разгледани са физически и геометрични интерпретации на производната на функция на една променлива.

Самостоятелна работа Задача Определете вида на кривата, зададена параметрично и изобразете кривата t t t t 5 7 t t б) e e, 0 t π в) t t t 5 Отговори затворен лъч y, 0, y, преминат два пъти, лъчът е изобразен

С. А. Зотова, В. Б. Светличная ПРАКТИЧЕСКО РЪКОВОДСТВО ПО ТЕОРИЯ НА ФУНКЦИИТЕ НА КОМПЛЕКСНИТЕ ПРОМЕНЛИВИ МАТЕМАТИКА УДК 5 Рецензенти - дф-мн, проф. Горяйнов В. В. до ф-мн, доц. Кулков В. Г. Зотова С. А., Светличная В. Б. Практ.

7 ПОКАЗНИ И ЛОГАРИТМИЧНИ УРАВНЕНИЯ И НЕРАВЕНСТВА 7. ОСНОВНИ ПОНЯТИЯ И ФОРМУЛИ. Равенствата log a b и a b са еквивалентни за a > 0, a, b > 0. log. Основна логаритмична идентичност: a a b b, a > 0,

Производни на основни елементарни функции Производната на функция може да бъде намерена по следната схема: даваме на аргумента x увеличение за функцията y намираме съответното увеличение y y правим връзка намираме

ФУНКЦИИ НА КОМПЛЕКСНА ПРОМЕНЛИВА ИЗДАТЕЛСТВО TSTU Министерство на образованието и науката на Руската федерация Държавна образователна институция за висше професионално образование "Тамбовски държавен технически университет" ФУНКЦИИ НА КОМПЛЕКСНА ПРОМЕНЛИВА Методологическа

Въпроси за изпита Въпроси за проверка на усвоеността „ЗНАМ” Основни понятия от теорията на редовете Критерий на Коши за сходимост на числови редове Необходим признак за сходимост на числови редове Достатъчни знаци

Федерална агенция за образование Държавна образователна институция за висше професионално образование Държавен технически университет Ухта КОМПЛЕКСНИ ЧИСЛА Насоки

Комплексен анализ Геометрия на комплексни числа Никита Александрович Евсеев Физически факултет, Новосибирски държавен университет 2015 Комплексен анализ 1 / 31 Числова линия R Комплекс

ВАРИАНТНА ЗАДАЧА ЗА ИЗЧИСЛЯВАНЕ НА СТОЙНОСТТА НА ФУНКЦИЯТА (ОТГОВОРЪТ Е ДАДЕН В АЛГЕБРИЧНА ФОРМА: s(; b a РЕШЕНИЕ A ПО ТРИГОНОМЕТРИЧНАТА ФОРМУЛА SIN(ISIN OSIOS SINI ИЗПОЛЗВАМЕ ФОРМУЛИТЕ ЗА ВРЪЗКА МЕЖДУ ТРИГОНОМЕТРИЧНАТА И ХИПЕРБОЛИЧНАТА

Светличная В. Б., Агишева Д. К., Матвеева Т. А., Зотова С. А. Специални глави на математиката. Теория на функциите на комплексна променлива Волгоград 0 Министерство на образованието и науката на Руската федерация Volzhsky Polytechnic

ТИПОВО ИЗЧИСЛЯВАНЕ „Теория на функциите на комплексна променлива” Практически задачи Зад. Дадено е числото s. Намерете c arg c и запишете числото c в тригонометрична и експоненциална форма:))))) 8 6) 7) 8) 9)

МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО НА РУСКАТА ФЕДЕРАЦИЯ ТЕОРИЯ НА ФУНКЦИИТЕ НА КОМПЛЕКСНА ПРОМЕНЛИВА Методическо ръководство Съставител: MDUlymzhiev LIInkheyeva IBYumov SZhyumova Преглед на методическото ръководство по теория на функциите

Комплексни числа, функции и операции върху тях y модул R реална част реално число, yim имагинерна част реално число iy алгебрична форма на запис на комплексни числа Основна стойност на аргумента

Тема: Производна. Кратка теоретична информация. Таблица на производните. (c) 0 (arcsin) () (arccos) (sin) cos (cos) sin (arctg) (tg) cos (arcctg) (ctg) sin v vln u vln u v v (u) (e) e (

Математически анализ Раздел: Теория на функциите на комплексна променлива Тема: Неалгебрични операции в C. Основни елементарни функции в C. Б.б. последователности от комплексни числа Лектор O.V. Januszczyk

Предмет. функция. Методи за възлагане. Неявна функция. Обратна функция. Класификация на функциите. Елементи на теорията на множествата. Основни понятия Едно от основните понятия на съвременната математика е понятието за множество.

Контролна работа В интервала между сесиите студентите трябва да проведат самостоятелна подготовка Работа с теоретичен материал от лекции по темата „Функции на много променливи“ (Представен материал

МИРЕЯ. Типично пресмятане за математически анализ. Тестови задачи по темата Комплексни числа, ТФКП. Задача 1. Решете уравнения, изобразете множеството решения на комплексната равнина A) 4 i + 81i 0 B)

ОПЕРАЦИОННО ИЗЧИСЛЕНИЕ Преобразуване на Лаплас и формула за инверсия Нека в интервала на Дирихле, а именно: Интеграл на Фурие (l l) a) е ограничен в този интервал; функцията удовлетворява условията б) частично непрекъсната

Функции на комплексна променлива Аналитични функции Както преди, освен ако не е посочено друго, имаме работа с еднозначна функция w = f(z). Определение 1. Функцията f(z) се нарича аналитична

МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НА ДЪРЖАВНАТА ТЕХНИЧЕСКА АКАДЕМИЯ RF АНГАРА Иванова С.В., Евсевлеева Л.Г., Бикова Л.М., Добринина Н.Н. ФУНКЦИИ НА КОМПЛЕКСНА ПРОМЕНЛИВА И ОПЕРАЦИОННО СЧИСЛЯВАНЕ

Нека функцията У = f(З) е дадено на някакво множество и З 0 , принадлежи на д, граничната точка на това множество. Нека добавим З 0 = х 0 + аз· г 0 увеличение Δ З = Δ х+ аз· Δ гда посоча З = З 0 + Δ Зпринадлежал на мнозина д. След това функцията У = u+ аз· v = f(З) = u(х, г)+ аз· v(х, г). Получаваме увеличението Δ У = Δ u+ аз· Δ v = f(З 0 + Δ З) - f(З 0 ) = Δ f(З 0 ) ,
.

Ако има ограничена граница
, тогава се нарича производна на функциятаf(З) в точкаЗ 0 от многод, и се обозначава
,
,
, У" .

Формално, производната функция на комплексна променлива се дефинира точно по същия начин като производната на реална променлива, но тяхното съдържание е различно.

В дефиницията на производната на функция f(х) реална променлива в точка х 0 , х→ x 0 по права линия. В случай на функция на комплексна променлива f(З), Зможе да се стреми към З 0 по всяка равнина, водеща до точка З 0 .

Следователно изискването за съществуване на производна на функция на комплексна променлива е много строго. Това обяснява, че дори прости функции на сложна променлива нямат производна.

Пример.

Помислете за функцията У = = х- аз· г. Нека покажем, че тази функция няма производна в нито една точка. Да вземем всяка точка З 0 = х 0 + аз· г 0 , нека да му дадем увеличение Δ З = Δ х+ аз· Δ г, тогава функцията ще получи увеличение. Средства

,
,

Първо ще разгледаме Δ З = Δ х + аз· Δ гтака че Δ х → 0 и Δ г = 0 , т.е. точка З 0 + Δ З → З 0 по хоризонтална права линия. В този случай получаваме това

Сега ще разгледаме увеличението ∆ Зтака че ∆ х = 0 и ∆ г → 0 , т.е. Кога З 0 + ∆ З→ З 0 по вертикална права линия и ще бъде очевидно
.

Получените граници са различни, така че съотношението няма ограничение при ∆ З → 0 , тоест функцията
няма производна в нито една точка З 0 .

Нека разберем значението на производната по отношение на множество. Позволявам де реалната ос и У = f(З) = х, тогава това е обикновена реална функция на реална променлива f(х) = хи неговата производна ще бъде равна 1 (
).

Нека сега д- това е целият самолет (Z). Нека покажем, че функцията f(З) = хв този случай няма производна в нито една точка. Наистина, в този случай
.От това става ясно, че ако
А
, Че
. Ако
, А
, Че
.Оттук и отношението няма ограничение при
, така че функцията f(З) = хняма производна в нито една точка
.

Обърнете внимание, че ако се разглежда функция с комплексни стойности на реална променлива, тогава от дефиницията на производната веднага следва, че
, следователно (това е производната по отношение на реалната ос).

Формула за нарастващи функции.

Нека функцията У = f(З) има в точката З 0 производна
. Нека покажем, че представянето (1) е валидно, където количеството
, Кога
.

Наистина, по дефиниция на производната имаме
, следователно стойността
, Кога
. Следователно има представяне (1) (умножете двете страни по
и го преместете
от лявата страна).

Лекция № 8 Диференцируемост и диференциал на функция на комплексна променлива

функция У = f(З) Наречен диференцируеми в точкатаЗ 0 , ако в тази точка има представяне (2), където А е фиксирано комплексно число, а количеството
клони към нула, когато
.

Ако функцията У = f(З) диференцируеми в точката З 0 , тогава главната линейна спрямо
част от него А·
нарастване
в точката З 0 Наречен диференциална функция f(З) в точката и е обозначен
.

Теоремата е валидна.

Теорема.

За да може функциятаУ = f(З) беше диференцируем в точкатаЗ 0 , е необходимо и достатъчно той да има крайна производна в тази точка
и винаги се оказва, че в представянето (2)
.

Доказателство.

Необходимост.Нека функцията е диференцируема в точката З 0 . Нека покажем, че има крайна производна в тази точка и че тази производна е равна на числото А. Поради диференциация f(З) в точката З 0 представяне (2) се осъществява, което означава
(3). Преминаване до лимита тук при
разбираме това
, Средства
.

Адекватност.Нека функцията f(З) има в точката З 0 крайна производна
. Нека покажем, че представянето (2) е валидно. Поради съществуването на производната
има репрезентация (1), но това е и репрезентация (2), в която А =
. Установена е достатъчност.

Както знаем, диференциалът, взет като диференциал на независимата променлива З нарастването му
, т.е
, можем да пишем
и следователно
(това е съотношение на диференциали, а не един символ).

Нека функция = u(x,y)+iv(x,y) се определя в близост до точката z = х+iy. Ако променливата zнарастване  z= х+аз г, след това функцията
ще получи увеличение


= (z+ z)–
=u(х+ х, г+ г)+

+ iv(х+ х, г+ г) - u(x,y) - iv(x,y) = [u(х+ х, г+ г) –

– u(x,y)] + аз[v(х+ х, г+ г) - v(x,y)] =

= u(x,y) + аз v(x,y).

Определение. Ако има ограничение

=

,

тогава тази граница се нарича производна на функцията
в точката zи се обозначава с f(z) или
. Така, по дефиниция,

=

=

. (1.37)

Ако функцията
има производна в точката z, тогава те казват, че функцията
диференцируеми в точката z. Очевидно, за да бъде функцията диференцируема
необходимо е функциите u(x,y) И v(x,y) бяха диференцируеми. Това обаче не е достатъчно за съществуването на деривата f(z). Например за функцията w== х–iyфункции u(x,y)=х

И v(x,y)=–гдиференцируеми във всички точки M( x,y), но границата на съотношението
при  х0,  г0 не съществува, защото ако  г= 0,  х 0, тогава  w/ z= 1,

ако  х = 0,  г 0, тогава  w/z = -1.

Няма едно ограничение. Това означава, че функцията

w= няма производна в нито една точка z. За съществуването на производна на функция на комплексна променлива са необходими допълнителни условия. Кои точно? Отговорът на този въпрос се дава от следната теорема.

Теорема.Нека функциите u(x,y) И v(x,y) са диференцируеми в точката M( x,y). След това за функцията

= u(x,y) + iv(x,y)

имаше производна в точката z = х+iy, е необходимо и достатъчно равенствата да са в сила

Равенствата (1.38) се наричат ​​условия на Коши-Риман.

Доказателство. 1) Необходимост. Нека функцията
има производна в точка z, тоест има граница

=

=
.(1.39)

Границата от дясната страна на равенството (1.39) не зависи от това кой път поема точката  z =  х+аз гсе стреми

до 0. По-специално, ако y = 0, x  0 (фиг. 1.10), тогава

Ако x = 0, y  0 (фиг. 1.11), тогава

(1.41)

Фиг.1.10 Фиг. 1.11

Левите страни в равенства (1.40) и (1.41) са равни. Това означава, че десните страни също са равни

Следва, че

Така от предположението за съществуването на производното f(z) следва равенството (1.38), т.е. условията на Коши-Риман са необходими за съществуването на производната f(z).

1) Достатъчност. Нека сега приемем, че равенствата (1.38) са изпълнени:

и докажете, че в този случай функцията
има производна в точката z= х+iy, тоест границата (1.39)

=

съществува.

Тъй като функциите u(x,y) И v(x,y) са диференцируеми в точката M( x,y), тогава общото увеличение на тези функции в точката M( x,y) могат да бъдат представени във формата

,

където  1 0,  2 0,  1 0,  2 0 при  х0, г0.

Тъй като по силата на (1.38),

следователно

=
,

 1 =  1 +аз 1 0,  2 =  2 +аз 2 0 при z =  х+азг0.

По този начин,

От  z 2 =  х 2 + г 2 , след това  х/ z1,  г/z1. Ето защо

при  z  0.

От това следва, че дясната страна на равенството (1.42) има граница при  z 0, следователно лявата страна също има граница при  z 0 и това ограничение не зависи от това кой път  zклони към 0. Така е доказано, че ако в точката M(x,y) условията (1.38) са изпълнени, тогава функцията
има производна в точката z = х+iy, и

.

Теоремата е напълно доказана.

В процеса на доказване на теоремата бяха получени две формули (1.40) и (1.42) за производната на функция на комплексна променлива

,

.

Използвайки формули (1.38), можем да получим още две формули

, (1.43)

. (1.44)

Ако функцията f(z) има производна във всички точки на областта D, тогава казваме, че функцията
е диференцируем в област D. За това е необходимо и достатъчно условията на Коши-Риман да бъдат изпълнени във всички точки на област D.

Пример.Проверете условията на Коши-Риман за

функции д z .

защото д z = д x+iy = д х(тъй като г + азгрях г),

Че u(х, г) = Re д z = д х cos г, v(х, г) = Im д z = д хгрях г,

,
,

,
,

следователно,

Условия на Коши-Риман за функция д zизпълнени във всички точки z. Така че функцията д zе диференцируем в цялата равнина на комплексна променлива и

Диференцируемостта се доказва по абсолютно същия начин

функции z н , cos z, грях z,гл z,ш z, Ln z, и валидността на формулите

(з н) = n z n-1, (cos z) = -грех z, (грех z) = cos z,

(гл z) = sh z, (ш z) = гл z, (Ln z) = 1/z.

За функции на комплексна променлива всички правила за диференциране на функции на реална променлива остават в сила. Доказателството на тези правила следва от дефиницията на производната по същия начин, както при функции на реална променлива.