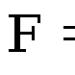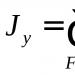Главните, три взаимно перпендикулярни оси, прекарани през к.-л. точка на тялото и имащи свойството, че ако се приемат за координатни оси, тогава центробежните инерционни моменти на тялото спрямо тези оси ще бъдат равни на нула. Ако телевизията тяло, фиксирано в една точка, се привежда във въртене около ос, която в дадена точка се проявява. основен О. и., тогава тялото, при липса на външни сили, ще продължи да се върти около тази ос, сякаш около неподвижна. Концепцията за главния О. и. играе важна роля в динамиката на телевизията. тела.
Физически енциклопедичен речник. - М.: Съветска енциклопедия..1983 .
ИНЕРЦИОННА ОС
Основните са три взаимно перпендикулярни оси, прекарани през к.н. точка на тялото, съвпадаща с осите на елипсоида на инерцията на тялото в тази точка. Главен О. и. имат свойството, че ако се приемат като координатни оси, тогава центробежните инерционни моменти на тялото спрямо тези оси ще бъдат равни на нула. Ако една от координатните оси напр. ос ое за целта ОТНОСНОглавни O. и., центробежни моменти на инерция, чиито индекси включват името на оста, т.е. аз xyИ аз xz, са равни на нула. Ако твърдо тяло, фиксирано в една точка, се върти около ос, която в дадена точка е главната О. и., Тогава тялото при липса на външен. силите ще продължат да се въртят около тази ос, сякаш около неподвижна.
Физическа енциклопедия. В 5 тома. - М.: Съветска енциклопедия.Главен редактор А. М. Прохоров.1988 .
Формулите (31.5), (32.5) и (34.5) ни позволяват да установим как се променят стойностите на инерционните моменти на секцията, когато осите се завъртат на произволен ъгъл a. За някои стойности на ъгъла a, стойностите на аксиалните моменти на инерция достигат максимум и минимум. Екстремните (максимални и минимални) стойности на аксиалните инерционни моменти на сечението се наричат основни инерционни моменти. Осите, около които аксиалните инерционни моменти имат екстремни стойности, се наричат главни оси на инерция.
От формула (33.5) следва, че ако аксиалният инерционен момент спрямо определена ос е максимален (т.е. тази ос е основната), тогава аксиалният инерционен момент спрямо оста, перпендикулярна на нея, е минимален (т.е. тази ос е и основната), така че сумата от аксиалните моменти на инерция около две взаимно перпендикулярни оси не зависи от ъгъла a.
По този начин главните инерционни оси са взаимно перпендикулярни.
За да намерим основните инерционни моменти и положението на главните инерционни оси, определяме първата производна по отношение на ъгъла a от инерционния момент [виж. формула (31.5) и фиг. 19.5]:
Приравняваме този резултат към нула:
където е ъгълът, на който трябва да се завъртят координатните оси y, така че да съвпадат с главните оси.
Сравнявайки изразите (35.5) и (34.5), установяваме това
![]()
Следователно, по отношение на главните оси на инерция, центробежният момент на инерция е нула. Следователно главните инерционни оси могат да се нарекат оси, около които центробежният инерционен момент е равен на нула.
Както вече е известно, центробежният инерционен момент на сечението спрямо осите, едната или двете от които съвпадат с осите на симетрия, е равен на нула.
Следователно взаимно перпендикулярните оси, едната или двете от които съвпадат с осите на симетрия на сечението, винаги са главни оси на инерция. Това правило позволява в много случаи директно (без изчисление) да се установи позицията на главните оси.
Нека решим уравнение (35.5) по отношение на ъгъла
Във всеки конкретен случай уравнение (36.5) се удовлетворява от редица стойности, като се избира всяка една от тях. Ако е положителен, тогава за да се определи позицията на една от главните инерционни оси от него, оста трябва да се завърти на ъгъл обратно на часовниковата стрелка, а ако е отрицателен, тогава с въртене по посока на часовниковата стрелка; другата главна инерционна ос е перпендикулярна на първата. Една от главните инерционни оси е максималната ос (спрямо нея аксиалният инерционен момент на сечението е максимален), а другата е минималната ос (спрямо нея аксиалният инерционен момент на сечението е минимален ).

Максималната ос винаги сключва по-малък ъгъл с този на осите (y или ), спрямо които аксиалният инерционен момент има по-голяма стойност. Това обстоятелство улеснява установяването коя от главните инерционни оси е максималната ос и коя е минималната ос. Така например, ако главните инерционни оси и и v са разположени, както е показано на фиг. 20.5, тогава оста е максималната ос (тъй като образува по-малък ъгъл с оста у, отколкото с оста), а оста v е минималната ос.
Когато решавате конкретна числена задача за определяне на основните инерционни моменти, можете да замените избраната стойност на ъгъла и стойността във формула (31.5) или (32.5).
Нека решим тази задача в обща форма. Използвайки формули от тригонометрията, използвайки израз (36.5), намираме

Замествайки тези изрази във формула (31.5), след прости трансформации получаваме
Главните инерционни оси могат да бъдат начертани през всяка точка, взета в равнината на сечението. Въпреки това, само главните оси, минаващи през центъра на тежестта на сечението, т.е. основните централни инерции, са от практическо значение за изчисляването на структурните елементи. Инерционните моменти спрямо тези оси (основните централни инерционни моменти) ще бъдат допълнително означени като
Нека разгледаме няколко специални случая.
1. Ако след това формула (34.5) дава стойността на центробежния момент на инерция спрямо всяка двойка взаимно перпендикулярни оси, равна на нула, и следователно всички оси, получени чрез въртене на координатната система, са главните оси на инерция (също като осите). В такъв случай
2. За фигури с повече от две оси на симетрия аксиалните инерционни моменти спрямо всички централни оси са равни. Наистина, нека насочим една от осите () по една от осите на симетрия, а другата - перпендикулярна на нея. За тези оси Ако една фигура има повече от две оси на симетрия, тогава една от тях сключва остър ъгъл с оста. Нека означим такава ос и перпендикулярната на нея ос
Центробежен момент на инерция, тъй като оста е оста на симетрия. По формула (34.5).
Да видим как се променят инерционните моменти при завъртане на координатните оси. Да приемем, че са дадени инерционните моменти на определено сечение спрямо осите x, y(не непременно централно). Трябва да се определи Дж u , Дж v , Дж uv -- инерционни моменти спрямо осите и, v,завъртян спрямо първата система на ъгъл (фиг. 3).
Проектиране на затворен четириъгълник OAVSOпо оста ИИ v.Тъй като проекцията на начупената линия е равна на проекцията на задната линия, намираме:
u = y sin +x cos, v = y cos -- x sin
В изрази (3), замествайки u и v вместо x 1 и y 1, съответно, ние изключваме u и v
Нека разгледаме първите две уравнения. Добавяйки ги член по член, получаваме, че сумата от аксиалните моменти на инерция около две взаимно перпендикулярни оси не зависи от ъгъла и остава постоянна, когато осите се въртят. При което
където е разстоянието от началото на координатите до елементарната област (фиг. 3). По този начин,
Дж х + Дж г = Дж стр
Където Дж стр-- полярен момент на инерция
чиято стойност естествено не зависи от въртенето на осите ху.
С промяна на ъгъла на въртене на осите, всяко от количествата Дж uИ Дж v се променя, но сборът им остава непроменен. Следователно има такъв , при което един от инерционните моменти достига максималната си стойност, докато другият инерционен момент приема минимална стойност.
Разграничаване на израза Дж u(5) чрез и приравнявайки производната на нула, намираме
При тази стойност на ъгъла единият от аксиалните моменти ще бъде най-големият, а другият - най-малкият. В същото време центробежният инерционен момент Дж uvпри посочения ъгъл става нула, което лесно се установява от третата формула (5).
Оси, за които центробежният момент на инерция е нула и аксиалните моменти приемат екстремни стойности, се наричат главни оси.Ако са и централни, тогава се наричат главни централни оси.Наричат се аксиални моменти на инерция спрямо главните оси основни инерционни моменти.За да определим това, пренаписваме първите две формули (5) във формуляра

Горният знак съответства на максималния инерционен момент, а долният знак съответства на минималния. След като разрезът е начертан в мащаб и положението на главните оси е показано на чертежа, не е трудно да се установи коя от двете оси отговаря на максималния и коя на минималния инерционен момент.
Ако едно сечение има ос на симетрия, тогава тази ос винаги ще бъде основната. Центробежният инерционен момент на частта от сечението, разположена от едната страна на оста, ще бъде равен на момента на частта, разположена от другата страна, но противоположна по знак. следователно Дж xy = 0 и оси хИ приса основните.
Аксиални инерционни моменти на сечениетоспрямо осите хИ при(виж Фиг. 32, а)се наричат определени интеграли на формата
При определяне на аксиалните моменти на инерция в някои случаи е необходимо да се срещне с друга нова геометрична характеристика на сечението - центробежният момент на инерция.
Центробежен момент на инерциясечения спрямо две взаимно перпендикулярни оси x y(виж Фиг. 32, а)
Полярен момент на инерцияраздели спрямо произхода ОТНОСНО(виж Фиг. 32, а)се нарича определен интеграл от формата
Където Р- разстояние от началото до елементарното място dA.
Аксиалните и полярните моменти на инерция винаги са положителни, а центробежният момент, в зависимост от избора на оси, може да бъде положителен, отрицателен или равен на нула. Единиците за обозначаване на инерционните моменти са cm 4, mm 4.
Съществува следната връзка между полярните и аксиалните моменти на инерция:

Съгласно формула (41) сумата от аксиалните инерционни моменти около две взаимно перпендикулярни оси е равна на полярния инерционен момент около пресечната точка на тези оси (начало).
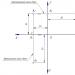
Инерционни моменти на сечения спрямо успоредни оси, едната от които е централна (x s,yc)>се определят от изразите: 
Където и Ив-координати на центъра на тежестта C на сечението (фиг. 34).
Формули (42), които имат голямо практическо приложение, гласят следното: инерционният момент на сечение спрямо всяка ос е равен на инерционния момент около ос, успоредна на нея и минаваща през центъра на тежестта на сечението, плюс произведението на площта на напречното сечение и квадрата на разстоянието между осите.
Забележка: координати a и cтрябва да бъдат заменени в горните формули (42), като се вземат предвид техните знаци.

Ориз. 34.
От формули (42) следва, че от всички инерционни моменти около успоредни оси най-малкият момент ще бъде около оста, минаваща през центъра на тежестта на сечението, т.е. централният инерционен момент.
Формулите за определяне на якостта и твърдостта на конструкцията включват моменти на инерция, които се изчисляват спрямо осите, които са не само централни, но и главни. За да се определи кои оси, минаващи през центъра на тежестта, са основните, трябва да можете да определите инерционните моменти спрямо осите, завъртяни една спрямо друга под определен ъгъл.
Връзките между инерционните моменти при въртене на координатните оси (фиг. 35) имат следната форма:

Където А- ъгъл на завъртане на оста ИИ vспрямо осите кънасъответно. Разглежда се ъгъл a положителен, ако въртенето на осите Ии ти се случва обратно на часовниковата стрелка.

Ориз. 35.
Сумата от аксиалните моменти на инерция спрямо всички взаимно перпендикулярни оси не се променя, когато се въртят:
Когато осите се въртят около началото на координатите, центробежният инерционен момент се променя непрекъснато, следователно при определено положение на осите става равно на нула.
Две взаимно перпендикулярни оси, около които центробежният инерционен момент на сечението е равен на нула, се наричат главни инерционни оси.
Посоката на главните инерционни оси може да се определи, както следва:

Две ъглови стойности, получени от формула (43) Асе различават една от друга на 90° и дават позицията на главните оси. Както виждаме, по-малкият от тези ъгли по абсолютна стойност не надвишава л/4.По-нататък ще използваме само по-малкия ъгъл. Главната ос, начертана под този ъгъл, ще бъде обозначена с буквата И.На фиг. 36 показва някои примери за обозначаване на главните оси в съответствие с това правило. Началните оси са обозначени с букви хей да

Ориз. 36.
При проблеми с огъване е важно да се знаят аксиалните моменти на инерция на сеченията спрямо онези главни оси, които минават през центъра на тежестта на сечението.
Главните оси, минаващи през центъра на тежестта на сечението, се наричат главни централни оси.По-нататък, като правило, за краткост ще наричаме тези оси просто главни оси, като се пропуска думата „централен“.
Оста на симетрия на плоска секция е главната централна ос на инерция на тази секция, втората ос е перпендикулярна на нея. С други думи, оста на симетрия и всяка друга, перпендикулярна на нея, образуват система от главни оси.
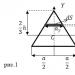
Ако плосък участък има поне две оси на симетрия, които не са перпендикулярни една на друга, тогава всички оси, минаващи през центъра на тежестта на такъв участък, са неговите главни централни оси на инерция. И така, на фиг. Фигура 37 показва някои видове сечения (кръг, пръстен, квадрат, правилен шестоъгълник и т.н.), които имат следното свойство: всяка ос, минаваща през техния център на тежест, е главна.

Ориз. 37.
Трябва да се отбележи, че нецентралните главни оси не представляват интерес за нас.
В теорията на огъването най-голямо значение имат инерционните моменти относно главните централни оси.
Основните централни моменти на инерцияили основни инерционни моментисе наричат инерционни моменти спрямо главните централни оси. Освен това, по отношение на една от главните оси, инерционният момент максимум, относително различни - минимален:

Аксиалните инерционни моменти на сеченията, показани на фиг. 37, изчислени спрямо главните централни оси, са равни една на друга: Джи,Тогава: J u = J x cos 2 a +J y sin a = Jx.
Инерционните моменти на сложно сечение са равни на сумата от инерционните моменти на неговите части. Следователно, за да определим моментите на инерция на сложен участък, можем да напишем:
gd eJ xi , J y „ J xiyi са инерционните моменти на отделните части на сечението.
NB: ако секцията има дупка, тогава е удобно да се счита за секция с отрицателна площ.
За извършване на якостни изчисления в бъдеще ще въведем нова геометрична характеристика на якостта на греда, подложена на право огъване. Тази геометрична характеристика се нарича аксиален момент на съпротивление или момент на съпротивление при огъване.
Съотношението на инерционния момент на сечение спрямо оста към разстоянието от тази ос до най-отдалечената точка на сечението се нарича аксиален момент на съпротивление:
Моментът на съпротивление има размери mm 3, cm 3.
Моментите на инерция и моментите на съпротивление на най-често срещаните прости секции се определят по формулите, дадени в табл. 3.
За валцовани стоманени греди (I-образни греди, канали, ъглови греди и др.) Моментите на инерция и моментите на съпротивление са дадени в таблици с асортименти от валцована стомана, където в допълнение към размерите, площите на напречното сечение, позициите на центровете на гравитацията и други характеристики са дадени.
В заключение, нека представим концепцията радиус на въртенесечения спрямо координатните оси хИ при - i xИ аз гсъответно, които се определят по следните формули.
оси,за който центробежният инерционен момент е равен на нула се нарича главни оси(понякога се нарича главни инерционни оси).През всяка точка, взета в равнината на сечението, в общия случай може да се начертае двойка главни оси (в някои специални случаи може да има безкраен брой от тях). За да проверим валидността на това твърдение, нека разгледаме как се променя центробежният инерционен момент, когато осите се завъртят на 90" (фиг. b.7). За произволна площ dA, взета в първия квадрант на xOy осна система и двете координати, поради което произведението им е положително. В новата координатна система x,Oy, завъртяна спрямо първоначалната на 90", произведението на координатите на въпросния обект е отрицателно. Абсолютна стойносттози продукт не се променя, т.е. xy = - x1y,. очевидно , същото важи и за всеки друг елементарен сайт. Това означава, че знакът на сбора dAxy, който е центробежният инерционен момент на сечението, се променя на противоположния, когато осите се завъртят на 90", т.е. J = = - J.
По време на въртенето на осите центробежният инерционен момент се променя непрекъснато,следователно при определено положение на осите тя става равна на нула. Тези оси са основните.
Въпреки че установихме, че главните оси могат да бъдат начертани през всяка точка на сечението, практически интерес представляват само тези от тях, които минават през центъра на тежестта на сечението - главни централни оси.По-нататък, като правило, за краткост ще ги наричаме просто главни оси,пропускане на думата "централен".
В общия случай на сечения с произволна форма, за да се определи позицията на главните оси, е необходимо да се проведе специално изследване. Тук ще се ограничим до разглеждане на специални случаи на сечения, които имат поне една ос на симетрия (фиг. 6.8).
Ние ще ви преведем. центърът на тежестта на сечението е оста Ox, перпендикулярна на оста на симетрия Oy, и определя центробежния инерционен момент J. Нека използваме свойството на определен интеграл, известен от курса на математиката (интегралът на сумата е равно на сумата от интеграли) и представя J s под формата на два члена:
тъй като за всяка елементарна област, разположена вдясно от оста на симетрия, има съответстваща вляво, за която произведението на координатите се различава само по знак.
По този начин центробежният момент на инерция спрямо осите Ox и Oy се оказа равен на нула, т.е. главни оси.Така че, за да намерите главните оси на симетрично сечение, достатъчно е да намерите позицията на неговия център на тежестта. Една от основните централни оси е оста на симетрия, втората ос е перпендикулярна на нея. Разбира се, горното доказателство остава валидно, ако оста, перпендикулярна на оста на симетрия, не минава през центъра на тежестта на сечението, т.е. Оста на симетрия и всяка друга, перпендикулярна на нея, образуват система от главни оси.
Нецентралните главни оси, както вече беше посочено, не представляват интерес.
Наричат се аксиални моменти на инерция около главните централни оси главен централен(или накратко основните) моменти на инерция.Инерционният момент е максимален спрямо една от главните оси и минимален спрямо другата. Например, за секцията, показана на фиг. 6.8, максималният инерционен момент J
(спрямо оста Ox). Разбира се, когато говорим за крайната точка на главните инерционни моменти, имаме предвид само тяхното сравнение с други инерционни моменти, изчислени спрямо осите, минаващи през тях същата точка на сечение.По този начин фактът, че единият от главните моменти на инерция е максимален, а другият е минимален, може да се счита за обяснение на факта, че те (и съответните оси) се наричат главни. Равенството на нула на центробежния инерционен момент спрямо главните оси е удобен знак за намирането му. Някои видове сечения, например кръг, квадрат, правилен шестоъгълник и др. (фиг. 6.9), имат безброй главни централни оси. За тези секции всяка централна ос е основната.
Без да предоставяме доказателство, посочваме, че ако двата основни централни инерционни момента на сечение са равни, тогава за това сечение всяка централна ос е главна и всички главни централни инерционни моменти са еднакви.