Прожекционен апарат
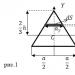
Проекционният апарат (фиг. 1) включва три проекционни равнини:
π 1 –хоризонтална проекционна равнина;
π 2 –фронтална равнина на проекции;
№ 3– профилна проекционна равнина .
Проекционните равнини са взаимно перпендикулярни ( π 1^ π 2^ № 3), а техните пресечни линии образуват осите:
Пресичане на равнини π 1И π 2образуват ос 0X (π 1∩ π 2 = 0X);
Пресичане на равнини π 1И № 3образуват ос 0Г (π 1∩ № 3 = 0Г);
Пресичане на равнини π 2И № 3образуват ос 0Z (π 2∩ № 3 = 0Z).
Пресечната точка на осите (OX∩OY∩OZ=0) се счита за начална точка (точка 0).
Тъй като равнините и осите са взаимно перпендикулярни, такъв апарат е подобен на декартовата координатна система.
Проекционните равнини разделят цялото пространство на осем октанта (на фиг. 1 те са обозначени с римски цифри). Проекционните равнини се считат за непрозрачни и зрителят винаги е вътре аз-ти октант.
Ортогонална проекция с проекционни центрове S 1, S 2И S 3съответно за хоризонтални, фронтални и профилни проекционни равнини.
А.
От прожекционни центрове S 1, S 2И S 3излизат прожектиращи лъчи l 1, l 2И l 3 А
- A 1 А;
- А 2– фронтална проекция на точка А;
- A 3– профилна проекция на точка А.
Една точка в пространството се характеризира със своите координати А(x,y,z). Точки A x, A yИ A zсъответно по осите 0X, 0ГИ 0Zпокажи координати x, yИ zточки А. На фиг. 1 дава всички необходими означения и показва връзките между точката Апространството, неговите проекции и координати.
Точкова диаграма
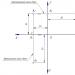
За да получите графика на точка А(фиг. 2), в проекционния апарат (фиг. 1) равнината π 1 A 1 0X π 2. След това самолетът № 3с точкова проекция A 3, завъртете обратно на часовниковата стрелка около оста 0Z, докато се изравни с равнината π 2. Посока на въртене на равнината π 2И № 3показано на фиг. 1 стрели. При това направо A 1 A xИ A 2 A x 0Xперпендикулярен A 1 A 2, и правите линии A 2 A xИ A 3 A xще бъдат разположени на обща ос 0Zперпендикулярен A 2 A 3. По-нататък ще наричаме тези редове съответно вертикален И хоризонтална комуникационни линии.
Трябва да се отбележи, че при преминаване от проекционния апарат към диаграмата проектираният обект изчезва, но цялата информация за неговата форма, геометрични размери и местоположението му в пространството се запазва.
А(x A, y A, z Ax A, y AИ zAв следната последователност (фиг. 2). Тази последователност се нарича метод за конструиране на точкова диаграма.
1. Осите са начертани ортогонално OX, OYИ OZ.
2. По оста ОХ xAточки Аи вземете позицията на точката A x.
3. През точката A xперпендикулярно на оста ОХ
A xпо оста ойнанася се числената стойност на координатата у аточки А A 1на диаграмата.
A xпо оста OZнанася се числената стойност на координатата zAточки А А 2на диаграмата.

6. През точката А 2успоредна на оста ОХначертана е хоризонтална комуникационна линия. Пресечната точка на тази права и оста OZще даде позицията на точката A z.
7. По хоризонтална съобщителна линия от точка A zпо оста ойнанася се числената стойност на координатата у аточки Аи се определя позицията на профилната проекция на точката A 3на диаграмата.
Характеристики на точките
Всички точки в пространството са разделени на точки с частно и общо положение.
Точки с особено положение. Точките, принадлежащи на проекционния апарат, се наричат точки с определено положение. Те включват точки, принадлежащи на проекционни равнини, оси, начални точки и проекционни центрове. Характерните особености на определени позиционни точки са:
Метаматематически - една, две или всички числени координатни стойности са равни на нула и (или) безкрайност;
На диаграма две или всички проекции на точка са разположени върху осите и (или) разположени в безкрайност.
Точки на общо положение. Точките с общо положение включват точки, които не принадлежат към проекционния апарат. Например точка Ана фиг. 1 и 2.
В общия случай числените стойности на координатите на точка характеризират нейното разстояние от проекционната равнина: координата хот самолета № 3; координирам гот самолета π 2; координирам zот самолета π 1. Трябва да се отбележи, че знаците за числените стойности на координатите показват посоката, в която точката се отдалечава от проекционните равнини. В зависимост от комбинацията от знаци за числените стойности на координатите на дадена точка зависи в кой октан е тя.
Метод с две изображения
В практиката, освен метода на пълната проекция, се използва методът на две изображения. Различава се по това, че този метод елиминира третата проекция на обекта. За да се получи проекционният апарат на метода с две изображения, профилната проекционна равнина с неговия проекционен център се изключва от пълния проекционен апарат (фиг. 3). Освен това по оста 0Xе зададена референтна точка (точка 0 ) и от него перпендикулярно на оста 0Xв проекционни равнини π 1И π 2начертайте оси 0ГИ 0Zсъответно.

В това устройство цялото пространство е разделено на четири квадранта. На фиг. 3 те са обозначени с римски цифри.
Проекционните равнини се считат за непрозрачни и зрителят винаги е вътре аз-ти квадрант.
Нека разгледаме работата на устройството, използвайки примера за проектиране на точка А.
От прожекционни центрове S 1И S 2излизат прожектиращи лъчи l 1И l 2. Тези лъчи преминават през точката Аи пресичащи се с проекционните равнини образуват неговите проекции:
- A 1– хоризонтална проекция на точка А;
- А 2– фронтална проекция на точка А.
За да получите графика на точка А(фиг. 4), в проекционния апарат (фиг. 3) равнината π 1с получената проекция на точката A 1завъртете по посока на часовниковата стрелка около ос 0X, докато се изравни с равнината π 2. Посока на въртене на равнината π 1показано на фиг. 3 стрели. В този случай на диаграмата на точка, получена по метода на две изображения, остава само едно вертикаленкомуникационна линия A 1 A 2.

На практика начертаване на точка А(x A, y A, z A) се извършва според числените стойности на неговите координати x A, y AИ zAв следната последователност (фиг. 4).
1. Начертана е оста ОХи се задава референтна точка (точка 0 ).
2. По оста ОХнанася се числената стойност на координатата xAточки Аи вземете позицията на точката A x.
3. През точката A xперпендикулярно на оста ОХначертана е вертикална комуникационна линия.
4. По вертикална съобщителна линия от точка A xпо оста ойнанася се числената стойност на координатата у аточки Аи се определя положението на хоризонталната проекция на точката A 1 ойне е начертано, но се приема, че положителните му стойности са разположени под оста ОХ, а отрицателните са по-високи.
5. По вертикална съобщителна линия от точка A xпо оста OZнанася се числената стойност на координатата zAточки Аи се определя положението на фронталната проекция на точката А 2на диаграмата. Трябва да се отбележи, че в диаграмата ос OZне е начертано, но се приема, че положителните му стойности са разположени над оста ОХ, а отрицателните са по-ниски.
Конкурентни точки
Точките на една и съща изпъкнала греда се наричат конкурентни точки. По посока на изпъкналия лъч те имат обща за тях проекция, т.е. проекциите им са идентични. Характерна особеност на конкуриращите се точки на диаграмата е идентичното съвпадение на техните едноименни проекции. Конкуренцията е във видимостта на тези проекции спрямо наблюдателя. С други думи, в пространството за наблюдател една от точките е видима, другата не. И съответно на чертежа: една от проекциите на конкуриращите се точки е видима, а проекцията на другата точка е невидима.
На модела на пространствена проекция (фиг. 5) от две конкуриращи се точки АИ INвидима точка Аспоред две взаимно допълващи се характеристики. Съдейки по веригата S 1 → A → Bточка Апо-близо до наблюдателя от точката IN. И съответно по-далеч от равнината на проекцията π 1(тези. zA > zA).

Ориз. 5 Фиг.6
Ако се вижда самата точка А, то неговата проекция също се вижда A 1. По отношение на съвпадащата с него проекция Б 1. За по-голяма яснота и, ако е необходимо, на диаграмата, невидимите проекции на точки обикновено се поставят в скоби.
Нека премахнем точките от модела АИ IN. Техните съвпадащи проекции върху равнината ще останат π 1и отделни проекции – на π 2. Нека условно оставим фронталната проекция на наблюдателя (⇩), разположена в центъра на проекцията S 1. След това по веригата от изображения ⇩ → А 2 → Б 2това ще може да се прецени zA > з би че самата точка се вижда Аи неговата проекция A 1.
Нека по подобен начин разгледаме конкурентните точки СЪСИ дна външен вид спрямо равнината π 2. Тъй като общият прожектиращ лъч на тези точки l 2успоредна на оста 0Г, след това знак за видимост на конкурентни точки СЪСИ допределени от неравенството y C > y D. Следователно тази точка дзатворен с точка СЪСи съответно проекцията на точката D 2ще бъдат обхванати от проекцията на точката C 2на повърхността π 2.
Нека разгледаме как се определя видимостта на конкуриращи се точки в сложен чертеж (фиг. 6).
Съдейки по съвпадащите прогнози A 1≡В 1самите точки АИ INса върху една издадена греда, успоредна на оста 0Z. Това означава, че координатите могат да се сравняват zAИ з бтези точки. За целта използваме равнината на предната проекция с отделни изображения на точките. В такъв случай zA > з б. От това следва, че проекцията е видима A 1.
Точки ° СИ дв разглеждания комплексен чертеж (фиг. 6) също са на същата изпъкнала греда, но само успоредно на оста 0Г. Следователно, от сравнение y C > y Dзаключаваме, че проекцията C 2 е видима.
Общо правило. Видимостта за съвпадащи проекции на конкуриращи се точки се определя чрез сравняване на координатите на тези точки в посоката на общ проекционен лъч. Вижда се проекцията на точката, чиято координата е по-голяма. В този случай координатите се сравняват върху равнината на проекцията с отделни изображения на точките.
Намерете острия ъгъл между диагоналите на успоредник, построен с помощта на вектори
5) Определете координатите на вектор c, насочен по ъглополовящата на ъгъла между векторите a и b, ако вектор c = 3 корена от 42. a=(2;-3;6), b=(-1;2; -2)
Нека намерим единичния вектор e_a, съпосочен с a:
по подобен начин e_b = b/|b|,
тогава желаният вектор ще бъде насочен по същия начин като векторната сума e_a+e_b, т.к (e_a+e_b) е диагоналът на ромб, който е ъглополовяща на неговия ъгъл.
Нека означим (e_a+e_b)=d,
Нека намерим единичен вектор, който е насочен по ъглополовящата: e_c = d/|d|
Ако |c| = 3*sqrt(42), тогава c = |c|*e_c. Това е всичко.
Намерете линейната зависимост между тези четири некомпланарни вектора: p=a+b; q=b-c; r=a-b+c; s=b+(1/2)*c
От първите три равенства опитайте да изразите „a,b,c“ чрез „p,q,r“ (започнете с добавяне на второто и третото уравнения). След това заменете „b“ и „c“ в последното уравнение с изразите, които сте намерили по отношение на „p,q,r“.
13) Намерете уравнението на равнината, минаваща през точки A(2, -1, 4) и B(3, 2, -1), перпендикулярни на равнината x + y + 2z – 3 = 0.Търсеното уравнение на равнината има формата: Ax + By + Cz + D = 0, нормалният вектор към тази равнина (A, B, C). Векторът (1, 3, -5) принадлежи на равнината. Дадената ни равнина, перпендикулярна на желаната, има нормален вектор (1, 1, 2). защото точки A и B принадлежат на двете равнини и равнините са взаимно перпендикулярни, тогава нормалният вектор е (11, -7, -2). защото точка А принадлежи на желаната равнина, тогава нейните координати трябва да удовлетворяват уравнението на тази равнина, т.е. 11×2 + 7×1 - 2×4 + D = 0; D = -21. Като цяло получаваме уравнението на равнината: 11x - 7y – 2z – 21 = 0.
14) Уравнението на равнина, минаваща през права, успоредна на вектор.
Нека желаната равнина минава през правата линия (x-x1)/a1 = (y-y1)/b1 = (z-z1)/c1, успоредна на правата линия (x-x2)/a2 = (y-y2) /b2 = (z -z2)/c2.
Тогава нормалният вектор на равнината е векторният продукт на насочващите вектори на тези прави:
Нека координатите на векторното произведение са (A;B;C). Желаната равнина минава през точката (x1;y1;z1). Нормалният вектор и точката, през която равнината минава, еднозначно определят уравнението на желаната равнина:
A·(x-x1) + B·(y-y1) + C·(z-z1) = 0
17) Намерете уравнението на правата, минаваща през точката A(5, -1) перпендикулярно на правата 3x - 7y + 14 = 0.
18) Напишете уравнение за права линия, минаваща през точка M, перпендикулярна на дадената равнина M(4,3,1) x+3y+5z-42=0
(x - x0) / n = (y - y0) / m = (z - z0) / p
M(x0,y0,z0) - вашата точка M(4,3,1)
(n, m, p) - насочващият вектор на правата, известен също като нормален вектор за дадена повърхност (1, 3, 5) (коефициенти за променливите x, y, z в уравнението на равнината)
Намерете проекцията на точка върху равнина
Точка M(1,-3,2), равнина 2x+5y-3z-19=0
ПРОЕКТИРАНЕ НА ТОЧКА ВЪРХУ ДВЕ ПРОЕКЦИОННИ РАВНИНИ
Образуването на прав сегмент AA 1 може да бъде представено като резултат от движението на точка А във всяка равнина H (фиг. 84, а), а образуването на равнина като движение на прав сегмент AB (фиг. 84, б).
Точката е основният геометричен елемент на линия и повърхност, следователно изучаването на правоъгълната проекция на обект започва с изграждането на правоъгълни проекции на точка.
В пространството на двустенния ъгъл, образуван от две перпендикулярни равнини - фронталната (вертикална) равнина на проекциите V и хоризонталната равнина на проекциите H, поставяме точка А (фиг. 85, а).
Линията на пресичане на проекционните равнини е права линия, която се нарича проекционна ос и се обозначава с буквата x.
V-равнината е изобразена тук като правоъгълник, а H-равнината като успоредник. Наклонената страна на този успоредник обикновено се чертае под ъгъл от 45° спрямо хоризонталната му страна. Дължината на наклонената страна се приема равна на 0,5 от нейната действителна дължина.
От точка A перпендикулярите се спускат върху равнините V и H. Точките a" и a на пресечната точка на перпендикулярите с проекционните равнини V и H са правоъгълни проекции на точка A. Фигурата Aaa x a" в пространството е правоъгълник. Страничната ос на този правоъгълник във визуалното изображение е намалена 2 пъти.

Нека подравним равнините H с равнината V, като завъртим V около линията на пресичане на равнините x. Резултатът е цялостен чертеж на точка А (фиг. 85, b)
За да се опрости сложният чертеж, границите на проекционните равнини V и H не са посочени (фиг. 85, c).
Перпендикулярите, прекарани от точка А към проекционните равнини, се наричат проекционни линии, а основите на тези проекционни линии - точките а и а" - се наричат проекции на точка А: а" е фронталната проекция на точка А, а е хоризонталната проекция от точка А.
Линия a" a се нарича вертикална линия на проекционна връзка.
Местоположението на проекцията на точка в сложен чертеж зависи от позицията на тази точка в пространството.

Ако точка А лежи върху хоризонталната равнина на проекциите H (фиг. 86, а), тогава нейната хоризонтална проекция a съвпада с дадената точка, а фронталната проекция a" е разположена на оста. Когато точка B е разположена на фронталната равнина на проекции V, нейната фронтална проекция съвпада с тази точка, а хоризонталната проекция лежи на оста x. Хоризонталната и фронталната проекции на дадена точка C, лежаща на оста x, съвпадат с тази точка. Сложен чертеж на точки A, B и C е показано на фиг. 86, b.
ПРОЕКТИРАНЕ НА ТОЧКА ВЪРХУ ТРИ ПРОЕКЦИОННИ РАВНИНИ
В случаите, когато е невъзможно да си представим формата на даден обект от две проекции, той се проектира върху три проекционни равнини. В този случай се въвежда профилна проекционна равнина W, перпендикулярна на равнините V и H. Визуално представяне на системата от три проекционни равнини е дадено на фиг. 87, а.
Ръбовете на тристенния ъгъл (пресечната точка на проекционните равнини) се наричат проекционни оси и се означават с x, y и z. Пресечната точка на проекционните оси се нарича начало на проекционните оси и се обозначава с буквата O. Нека пуснем перпендикуляр от точка A към проекционната равнина W и, маркирайки основата на перпендикуляра с буквата "a", ние вземете профилна проекция на точка А.
За да се получи сложен чертеж на точка А, равнините H и W се комбинират с равнина V, завъртайки ги около осите Ox и Oz. Изчерпателен чертеж на точка А е показан на фиг. 87, б и в.

Сегментите на проектиращите прави от точка А към проекционните равнини се наричат координати на точка А и се обозначават: x A, y A и z A.
Например, координатата z A на точка A, равна на сегмента a"a x (фиг. 88, a и b), е разстоянието от точка A до хоризонталната проекционна равнина H. Координатата y на точка A, равна на сегментът aa x, е разстоянието от точка А до фронталната равнина на проекциите V. Координата x A, равна на сегмента aa y - разстоянието от точка А до профилната равнина на проекциите W.
По този начин разстоянието между проекцията на точка и проекционната ос определя координатите на точката и е ключът към разчитането на нейния комплексен чертеж. От две проекции на точка могат да се определят и трите координати на точката.
Ако са дадени координатите на точка A (например x A = 20 mm, y A = 22 mm и z A = 25 mm), тогава могат да се построят три проекции на тази точка.
За да направите това, от началото на координатите O в посоката на оста Oz се отлага координатата z A и надолу се отлага координатата y A. От краищата на отложените сегменти - точки a z и a y (фиг. 88, а) - начертайте прави линии, успоредни на оста Ox, и ги поставете на сегменти, равни на координатата x A. Получените точки a" и a са фронталните и хоризонталните проекции на точка A.
Използвайки две проекции a" и a на точка A, можете да конструирате нейната профилна проекция по три начина:
1) от началото на координатите O, начертайте спомагателна дъга с радиус Oa y, равен на координатата (фиг. 87, b и c), от получената точка a y1 начертайте права линия, успоредна на оста Oz, и положете извън сегмент, равен на z A;
2) от точка a y начертайте спомагателна права линия под ъгъл 45 ° спрямо оста Oy (фиг. 88, а), получете точка a y1 и т.н.;
3) от началото O начертайте спомагателна права линия под ъгъл 45 ° спрямо оста Oy (фиг. 88, b), получете точка a y1 и т.н.

Позицията на точка в пространството може да бъде определена чрез нейните две ортогонални проекции, например хоризонтална и фронтална, фронтална и профилна. Комбинацията от произволни две ортогонални проекции ви позволява да намерите стойността на всички координати на точка, да конструирате трета проекция и да определите октанта, в който се намира. Нека разгледаме няколко типични задачи от курса по дескриптивна геометрия.
За даден комплексен чертеж на точки A и B е необходимо:
Нека първо определим координатите на точка А, които могат да бъдат записани във формата A (x, y, z). Хоризонтална проекция на точка A - точка A", с координати x, y. Нека начертаем перпендикуляри от точка A" към осите x, y и да намерим съответно A x, A y. Координатата x за точка A е равна на дължината на сегмента A x O със знак плюс, тъй като A x лежи в областта на положителните стойности на оста x. Като вземем предвид мащаба на чертежа, намираме x = 10. Координатата y е равна на дължината на сегмента A y O със знак минус, тъй като т. A y лежи в областта на отрицателните стойности на y ос. Като се има предвид мащабът на чертежа, y = –30. Фронталната проекция на точка А - точка А"" има координати x и z. Нека спуснем перпендикуляра от A"" към оста z и да намерим A z. Z координатата на точка A е равна на дължината на сегмента A z O със знак минус, тъй като A z лежи в областта на отрицателните стойности на оста z. Като се вземе предвид мащабът на чертежа z = –10. Така координатите на точка А са (10, –30, –10).
Координатите на точка B могат да бъдат записани като B (x, y, z). Помислете за хоризонталната проекция на точка B - точка B". Тъй като тя лежи на оста x, тогава B x = B" и координатата B y = 0. Абсцисата x на точка B е равна на дължината на сегмента B x O със знак плюс. Като се вземе предвид мащабът на чертежа x = 30. Фронталната проекция на точка B е t.B˝ има координати x, z. Нека начертаем перпендикуляр от B"" към оста z, като по този начин намерим B z. Приложението z на точка B е равно на дължината на сегмента B z O със знак минус, тъй като B z лежи в областта на отрицателните стойности на оста z. Като вземем предвид мащаба на чертежа, определяме стойността z = –20. Така че координатите на B са (30, 0, -20). Всички необходими конструкции са представени на фигурата по-долу.

Построяване на проекции на точки
Точките A и B в равнината P 3 имат следните координати: A""" (y, z); B""" (y, z). В този случай A"" и A""" лежат на един и същ перпендикуляр на оста z, тъй като имат обща z координата. По същия начин B"" и B""" лежат на общ перпендикуляр на оста z. За да намерим профилната проекция на точка А, нанасяме по оста у стойността на съответната координата, намерена по-рано. На фигурата това се прави с помощта на кръгова дъга с радиус A y O. След това начертайте перпендикуляр от A y, докато се пресече с перпендикуляра, възстановен от точка A"" към оста z. Пресечната точка на тези два перпендикуляра определя позицията на A""".
Точка B""" лежи на оста z, тъй като ординатата y на тази точка е нула. За да намерите профилната проекция на точка B в тази задача, трябва само да начертаете перпендикуляр от B"" към оста z. пресечната точка на този перпендикуляр с оста z е B """.

Определяне на положението на точките в пространството
Визуално си представяйки пространственото оформление, съставено от проекционни равнини P 1, P 2 и P 3, местоположението на октантите, както и реда на трансформиране на оформлението в диаграми, можете директно да определите, че точка А се намира в III октант , а точка B лежи в равнината P 2.
Друг вариант за решаване на този проблем е методът на изключенията. Например координатите на точка А са (10, -30, -10). Положителната абциса x ни позволява да преценим, че точката се намира в първите четири октанта. Отрицателна y-ордината показва, че точката е във втория или третия октант. И накрая, отрицателният апликат z показва, че точка А се намира в третия октант. Следната таблица ясно илюстрира горното разсъждение.
| Октанти | Координатни знаци | ||
| х | г | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Координати на точка B (30, 0, -20). Тъй като ординатата на точка B е нула, тази точка се намира в проекционната равнина P 2. Положителната абсциса и отрицателният апликат на t.B показват, че той се намира на границата на третия и четвъртия октант.
Изграждане на визуално изображение на точки в системата от равнини P 1, P 2, P 3

С помощта на фронтална изометрична проекция изградихме пространствено оформление на III октант. Това е правоъгълен тристен, чиито лица са равнините P 1, P 2, P 3, а ъгълът (-y0x) е 45 º. В тази система сегментите по осите x, y, z ще бъдат начертани в естествен размер без изкривяване.
Нека започнем да конструираме визуално изображение на точка A (10, -30, -10) с нейната хоризонтална проекция A. След като начертаем съответните координати по абсцисната и ординатната ос, намираме точките A x и A y. Пресечната точка на перпендикулярите реконструиран съответно от A x и A y към осите x и y, определя позицията на точка A". Отлагайки от A" успоредно на оста z към неговите отрицателни стойности сегмента AA", чиято дължина е 10, намираме позицията на точка A.
Визуалното изображение на точка B (30, 0, -20) се изгражда по подобен начин - в равнината P2 по осите x и z трябва да нанесете съответните координати. Пресечната точка на перпендикулярите, реконструирани от B x и B z, ще определи позицията на точка B.
В тази статия ще намерим отговори на въпроси как да създадем проекция на точка върху равнина и как да определим координатите на тази проекция. В теоретичната част ще разчитаме на понятието проекция. Ще дефинираме термините и ще предоставим информация с илюстрации. Нека затвърдим придобитите знания чрез решаване на примери.
Проекция, видове проекция
За удобство при разглеждане на пространствени фигури се използват чертежи, изобразяващи тези фигури.
Определение 1
Проекция на фигура върху равнина– рисуване на пространствена фигура.
Очевидно има редица правила, използвани за конструиране на проекция.
Определение 2
Проекция– процесът на конструиране на чертеж на пространствена фигура върху равнина с помощта на правила за конструиране.
Проекционна равнина- това е равнината, в която се изгражда изображението.
Използването на определени правила определя вида на проекцията: централенили паралелен.
Специален случай на паралелна проекция е перпендикулярната проекция или ортогоналната: в геометрията се използва главно. Поради тази причина самото прилагателно „перпендикулярно“ често се пропуска в речта: в геометрията те просто казват „проекция на фигура“ и под това имат предвид конструиране на проекция, използвайки метода на перпендикулярна проекция. В специални случаи, разбира се, може да се договори и нещо друго.
Нека отбележим факта, че проекцията на фигура върху равнина е по същество проекция на всички точки на тази фигура. Следователно, за да можете да изучавате пространствена фигура в чертеж, е необходимо да придобиете основното умение за проектиране на точка върху равнина. За какво ще говорим по-долу.
Нека припомним, че най-често в геометрията, когато се говори за проекция върху равнина, те имат предвид използването на перпендикулярна проекция.
Нека направим конструкции, които ще ни дадат възможност да получим дефиниция на проекцията на точка върху равнина.
Да кажем, че е дадено триизмерно пространство и в него има равнина α и точка M 1, която не принадлежи на равнината α. Начертайте права през дадената точка M Аперпендикулярна на дадена равнина α. Означаваме пресечната точка на права линия a и равнина α като H 1; по конструкцията тя ще служи като основа на перпендикуляр, пуснат от точка M 1 към равнина α.
Ако е дадена точка M 2, принадлежаща на дадена равнина α, то M 2 ще служи като проекция на себе си върху равнината α.

Определение 3
- това е или самата точка (ако принадлежи на дадена равнина), или основата на перпендикуляр, пуснат от дадена точка към дадена равнина.
Намиране на координатите на проекцията на точка върху равнина, примери
Нека в тримерното пространство са дадени: правоъгълна координатна система O x y z, равнина α, точка M 1 (x 1, y 1, z 1). Необходимо е да се намерят координатите на проекцията на точка M 1 върху дадена равнина.
Решението следва очевидно от дадената по-горе дефиниция на проекцията на точка върху равнина.
Нека означим проекцията на точката M 1 върху равнината α като H 1 . Съгласно дефиницията H 1 е пресечната точка на дадена равнина α и права a, прекарана през точката M 1 (перпендикулярна на равнината). Тези. Координатите на проекцията на точка M1, от която се нуждаем, са координатите на пресечната точка на права линия a и равнина α.
По този начин, за да намерите координатите на проекцията на точка върху равнина, е необходимо:
Получаване на уравнението на равнината α (ако не е посочено). Тук ще ви помогне статия за видовете уравнения на равнината;
Определете уравнението на права a, минаваща през точка M 1 и перпендикулярна на равнината α (проучете темата за уравнението на права, минаваща през дадена точка, перпендикулярна на дадена равнина);
Намерете координатите на пресечната точка на правата a и равнината α (статия - намиране на координатите на пресечната точка на равнината и правата). Получените данни ще бъдат координатите, от които се нуждаем за проекцията на точка M 1 върху равнината α.
Нека да разгледаме теорията с практически примери.
Пример 1
Определете координатите на проекцията на точка M 1 (- 2, 4, 4) върху равнината 2 x – 3 y + z - 2 = 0.
Решение
Както виждаме, уравнението на равнината ни е дадено, т.е. няма нужда да се компилира.
Нека запишем каноничните уравнения на права a, минаваща през точката M 1 и перпендикулярна на дадената равнина. За тези цели определяме координатите на насочващия вектор на правата линия a. Тъй като права a е перпендикулярна на дадена равнина, векторът на посоката на права a е нормалният вектор на равнината 2 x - 3 y + z - 2 = 0. По този начин, a → = (2, - 3, 1) – насочващ вектор на права a.
Сега нека съставим каноничните уравнения на права в пространството, минаваща през точката M 1 (- 2, 4, 4) и имаща насочващ вектор a → = (2 , - 3 , 1) :
x + 2 2 = y - 4 - 3 = z - 4 1
За да намерите необходимите координати, следващата стъпка е да определите координатите на пресечната точка на правата x + 2 2 = y - 4 - 3 = z - 4 1 и равнината 2 x - 3 y + z - 2 = 0 . За тези цели преминаваме от каноничните уравнения към уравненията на две пресичащи се равнини:
x + 2 2 = y - 4 - 3 = z - 4 1 ⇔ - 3 · (x + 2) = 2 · (y - 4) 1 · (x + 2) = 2 · (z - 4) 1 · ( y - 4) = - 3 (z + 4) ⇔ 3 x + 2 y - 2 = 0 x - 2 z + 10 = 0
Нека създадем система от уравнения:
3 x + 2 y - 2 = 0 x - 2 z + 10 = 0 2 x - 3 y + z - 2 = 0 ⇔ 3 x + 2 y = 2 x - 2 z = - 10 2 x - 3 y + z = 2
И нека го решим с помощта на метода на Cramer:
∆ = 3 2 0 1 0 - 2 2 - 3 1 = - 28 ∆ x = 2 2 0 - 10 0 - 2 2 - 3 1 = 0 ⇒ x = ∆ x ∆ = 0 - 28 = 0 ∆ y = 3 2 0 1 - 10 - 2 2 2 1 = - 28 ⇒ y = ∆ y ∆ = - 28 - 28 = 1 ∆ z = 3 2 2 1 0 - 10 2 - 3 2 = - 140 ⇒ z = ∆ z ∆ = - 140 - 28 = 5
По този начин необходимите координати на дадена точка M 1 на дадена равнина α ще бъдат: (0, 1, 5).
Отговор: (0 , 1 , 5) .
Пример 2
В правоъгълна координатна система O x y z на триизмерното пространство са дадени точки A (0, 0, 2); B (2, - 1, 0); C (4, 1, 1) и M 1 (-1, -2, 5). Необходимо е да се намерят координатите на проекцията M 1 върху равнината A B C
Решение
Първо, записваме уравнението на равнина, минаваща през три дадени точки:
x - 0 y - 0 z - 0 2 - 0 - 1 - 0 0 - 2 4 - 0 1 - 0 1 - 2 = 0 ⇔ x y z - 2 2 - 1 - 2 4 1 - 1 = 0 ⇔ ⇔ 3 x - 6 y + 6 z - 12 = 0 ⇔ x - 2 y + 2 z - 4 = 0
Нека запишем параметричните уравнения на правата a, която ще минава през точката M 1 перпендикулярно на равнината A B C. Равнината x – 2 y + 2 z – 4 = 0 има нормален вектор с координати (1, - 2, 2), т.е. вектор a → = (1, - 2, 2) – насочващ вектор на права линия a.
Сега, като имаме координатите на точката на линията M 1 и координатите на вектора на посоката на тази линия, записваме параметричните уравнения на линията в пространството:
След това определяме координатите на пресечната точка на равнината x – 2 y + 2 z – 4 = 0 и правата линия
x = - 1 + λ y = - 2 - 2 λ z = 5 + 2 λ
За да направите това, заместваме в уравнението на равнината:
x = - 1 + λ, y = - 2 - 2 λ, z = 5 + 2 λ
Сега, използвайки параметричните уравнения x = - 1 + λ y = - 2 - 2 · λ z = 5 + 2 · λ, намираме стойностите на променливите x, y и z за λ = - 1: x = - 1 + (- 1) y = - 2 - 2 · (- 1) z = 5 + 2 · (- 1) ⇔ x = - 2 y = 0 z = 3
Така проекцията на точка M 1 върху равнината A B C ще има координати (- 2, 0, 3).
Отговор: (- 2 , 0 , 3) .
Нека се спрем отделно на въпроса за намирането на координатите на проекцията на точка върху координатни равнини и равнини, които са успоредни на координатните равнини.
Нека са дадени точки M 1 (x 1, y 1, z 1) и координатни равнини O x y, O x z и O y z. Координатите на проекцията на тази точка върху тези равнини ще бъдат съответно: (x 1, y 1, 0), (x 1, 0, z 1) и (0, y 1, z 1). Нека разгледаме и равнини, успоредни на дадените координатни равнини:
C z + D = 0 ⇔ z = - D C , B y + D = 0 ⇔ y = - D B
И проекциите на дадена точка M 1 върху тези равнини ще бъдат точки с координати x 1, y 1, - D C, x 1, - D B, z 1 и - D A, y 1, z 1.
Нека демонстрираме как е получен този резултат.
Като пример, нека дефинираме проекцията на точка M 1 (x 1, y 1, z 1) върху равнината A x + D = 0. Останалите случаи са подобни.
Дадената равнина е успоредна на координатната равнина O y z и i → = (1, 0, 0) е нейният нормален вектор. Същият вектор служи като насочващ вектор на правата, перпендикулярна на равнината O y z. Тогава параметричните уравнения на права линия, начертана през точката M 1 и перпендикулярна на дадена равнина, ще имат формата:
x = x 1 + λ y = y 1 z = z 1
Нека намерим координатите на пресечната точка на тази права и дадената равнина. Нека първо заместим равенствата в уравнението A x + D = 0: x = x 1 + λ , y = y 1 , z = z 1 и да получим: A · (x 1 + λ) + D = 0 ⇒ λ = - D A - x 1
След това изчисляваме необходимите координати, като използваме параметричните уравнения на правата линия с λ = - D A - x 1:
x = x 1 + - D A - x 1 y = y 1 z = z 1 ⇔ x = - D A y = y 1 z = z 1
Тоест проекцията на точка M 1 (x 1, y 1, z 1) върху равнината ще бъде точка с координати - D A, y 1, z 1.
Пример 2
Необходимо е да се определят координатите на проекцията на точка M 1 (- 6, 0, 1 2) върху координатната равнина O x y и върху равнината 2 y - 3 = 0.
Решение
Координатната равнина O x y ще съответства на непълното общо уравнение на равнината z = 0. Проекцията на точка M 1 върху равнината z = 0 ще има координати (- 6, 0, 0).
Уравнението на равнината 2 y - 3 = 0 може да бъде записано като y = 3 2 2. Сега просто запишете координатите на проекцията на точка M 1 (- 6, 0, 1 2) върху равнината y = 3 2 2:
6 , 3 2 2 , 1 2
Отговор:(- 6 , 0 , 0) и - 6 , 3 2 2 , 1 2
Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter