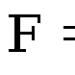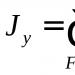Частичните производни се използват в задачи, включващи функции на няколко променливи. Правилата за намиране са абсолютно същите като за функциите на една променлива, с единствената разлика, че една от променливите трябва да се счита за константа (постоянно число) в момента на диференциране.
Формула
Частичните производни за функция на две променливи $ z(x,y) $ се записват в следната форма $ z"_x, z"_y $ и се намират с помощта на формулите:
Частични производни от първи ред
$$ z"_x = \frac(\partial z)(\partial x) $$
$$ z"_y = \frac(\partial z)(\partial y) $$
Частични производни от втори ред
$$ z""_(xx) = \frac(\partial^2 z)(\partial x \partial x) $$
$$ z""_(yy) = \frac(\partial^2 z)(\partial y \partial y) $$
Смесен дериват
$$ z""_(xy) = \frac(\partial^2 z)(\partial x \partial y) $$
$$ z""_(yx) = \frac(\partial^2 z)(\partial y \partial x) $$
Частична производна на сложна функция
а) Нека $ z (t) = f(x(t), y(t)) $, тогава производната на сложна функция се определя от формулата:
$$ \frac(dz)(dt) = \frac(\partial z)(\partial x) \cdot \frac(dx)(dt) + \frac(\partial z)(\partial y) \cdot \frac (dy)(dt)$$
б) Нека $ z (u,v) = z(x(u,v),y(u,v)) $, тогава частните производни на функцията се намират по формулата:
$$ \frac(\partial z)(\partial u) = \frac(\partial z)(\partial x) \cdot \frac(\partial x)(\partial u) + \frac(\partial z)( \partial y) \cdot \frac(\partial y)(\partial u) $$
$$ \frac(\partial z)(\partial v) = \frac(\partial z)(\partial x) \cdot \frac(\partial x)(\partial v) + \frac(\partial z)( \partial y) \cdot \frac(\partial y)(\partial v) $$
Частични производни на неявна функция
а) Нека $ F(x,y(x)) = 0 $, тогава $$ \frac(dy)(dx) = -\frac(f"_x)(f"_y) $$
b) Нека $ F(x,y,z)=0 $, тогава $$ z"_x = - \frac(F"_x)(F"_z); z"_y = - \frac(F"_y)( F"_z) $$
Примери за решения
| Пример 1 |
| Намерете частични производни от първи ред $ z (x,y) = x^2 - y^2 + 4xy + 10 $ |
| Решение |
|
За да намерим частната производна по отношение на $ x $, ще считаме $ y $ за постоянна стойност (число): $$ z"_x = (x^2-y^2+4xy+10)"_x = 2x - 0 + 4y + 0 = 2x+4y $$ За да намерим частната производна на функция по отношение на $y$, дефинираме $y$ чрез константа: $$ z"_y = (x^2-y^2+4xy+10)"_y = -2y+4x $$ Ако не можете да разрешите проблема си, изпратете го до нас. Ние ще предоставим подробно решение. Ще можете да видите напредъка на изчислението и да получите информация. Това ще ви помогне да получите оценката си от вашия учител навреме! |
| Отговор |
| $$ z"_x = 2x+4y; z"_y = -2y+4x $$ |
| Пример 2 |
| Намерете частните производни на функцията от втори ред $ z = e^(xy) $ |
| Решение |
|
Първо трябва да намерите производните от първи ред и след това като ги знаете, можете да намерите производните от втори ред. Нека $y$ е константа: $$ z"_x = (e^(xy))"_x = e^(xy) \cdot (xy)"_x = ye^(xy) $$ Нека сега зададем $ x $ да бъде постоянна стойност: $$ z"_y = (e^(xy))"_y = e^(xy) \cdot (xy)"_y = xe^(xy) $$ Познавайки първите производни, по подобен начин намираме втората. Задайте $y$ на константа: $$ z""_(xx) = (z"_x)"_x = (ye^(xy))"_x = (y)"_x e^(xy) + y(e^(xy))"_x = 0 + ye^(xy)\cdot (xy)"_x = y^2e^(xy) $$ Задаваме $ x $ на константа: $$ z""_(yy) = (z"_y)"_y = (xe^(xy))"_y = (x)"_y e^(xy) + x(e^(xy))"_y = 0 + x^2e^(xy) = x^2e^(xy) $$ Сега всичко, което остава, е да намерим смесената производна. Можете да разграничите $ z"_x $ по $ y $ и можете да разграничите $ z"_y $ по $ x $, тъй като според теоремата $ z""_(xy) = z""_(yx) $ $$ z""_(xy) = (z"_x)"_y = (ye^(xy))"_y = (y)"_y e^(xy) + y (e^(xy))"_y = ye^(xy)\cdot (xy)"_y = yxe^(xy) $$ |
| Отговор |
| $$ z"_x = ye^(xy); z"_y = xe^(xy); z""_(xy) = yxe^(xy) $$ |
| Пример 4 |
| Нека $ 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ дефинира неявната функция $ F(x,y,z) = 0 $. Намерете частични производни от първи ред. |
| Решение |
|
Записваме функцията във формата: $ F(x,y,z) = 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ и намираме производните: $$ z"_x (y,z - const) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_x = 3 x^2 z - 4 $$ $$ z"_y (x,y - const) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_y = 3z^2 $$ |
| Отговор |
| $$ z"_x = 3x^2 z - 4; z"_y = 3z^2; $$ |
Помислете за функция на две променливи:
Тъй като променливите $x$ и $y$ са независими, за такава функция можем да въведем концепцията за частична производна:
Частната производна на функцията $f$ в точка $M=\left(((x)_(0));((y)_(0)) \right)$ по отношение на променливата $x$ е лимитът
\[(((f)")_(x))=\underset(\Delta x\to 0)(\mathop(\lim ))\,\frac(f\left(((x)_(0) )+\Делта x;((y)_(0)) \right))(\Делта x)\]
По подобен начин можете да дефинирате частичната производна по отношение на променливата $y$:
\[(((f)")_(y))=\underset(\Delta y\to 0)(\mathop(\lim ))\,\frac(f\left(((x)_(0) );((y)_(0))+\Delta y \right))(\Delta y)\]
С други думи, за да намерите частичната производна на функция от няколко променливи, трябва да фиксирате всички други променливи с изключение на желаната и след това да намерите обикновената производна по отношение на тази желана променлива.
Това води до основната техника за изчисляване на такива производни: просто приемете, че всички променливи с изключение на тази са константа и след това диференцирайте функцията, както бихте диференцирали „обикновена“ – с една променлива. Например:
$\begin(align)& ((\left(((x)^(2))+10xy \right))_(x))^(\prime )=((\left(((x)^(2 )) \right))^(\prime ))_(x)+10y\cdot ((\left(x \right))^(\prime ))_(x)=2x+10y, \\& (( \left(((x)^(2))+10xy \right))_(y))^(\prime )=((\left(((x)^(2)) \right))^(\ просто ))_(y)+10x\cdot ((\left(y \right))^(\prime ))_(y)=0+10x=10x. \\\край (подравняване)$
Очевидно частните производни по отношение на различни променливи дават различни отговори - това е нормално. Много по-важно е да разберем защо, да речем, в първия случай ние спокойно премахнахме $10y$ под знака за производна, а във втория случай напълно занулихме първия член. Всичко това се дължи на факта, че всички букви, с изключение на променливата, чрез която се извършва диференциацията, се считат за константи: те могат да бъдат извадени, „изгорени“ и т.н.
Какво е "частична производна"?
Днес ще говорим за функции на няколко променливи и частни производни от тях. Първо, какво е функция на няколко променливи? Досега сме свикнали да разглеждаме функция като $y\left(x \right)$ или $t\left(x \right)$, или всяка променлива и една единствена функция от нея. Сега ще имаме една функция, но няколко променливи. Тъй като $y$ и $x$ се променят, стойността на функцията ще се променя. Например, ако $x$ се удвои, стойността на функцията ще се промени, а ако $x$ се промени, но $y$ не се промени, стойността на функцията ще се промени по същия начин.
Разбира се, функция на няколко променливи, точно както функция на една променлива, може да бъде диференцирана. Въпреки това, тъй като има няколко променливи, е възможно да се направи разграничение според различните променливи. В този случай възникват специфични правила, които не съществуват при диференцирането на една променлива.
На първо място, когато изчисляваме производната на функция от която и да е променлива, от нас се изисква да посочим за коя променлива изчисляваме производната - това се нарича частична производна. Например, имаме функция на две променливи и можем да я изчислим както в $x$, така и в $y$ - две частни производни за всяка от променливите.
Второ, щом фиксираме една от променливите и започнем да изчисляваме частната производна по отношение на нея, всички останали, включени в тази функция, се считат за константи. Например, в $z\left(xy \right)$, ако разгледаме частичната производна по отношение на $x$, тогава където и да срещнем $y$, ние го считаме за константа и я третираме като такава. По-специално, когато изчисляваме производната на продукт, можем да извадим $y$ извън скоби (имаме константа), а когато изчисляваме производната на сума, ако някъде получим производна на израз, съдържащ $y$ и не съдържа $x$, тогава производната на този израз ще бъде равна на „нула“ като производна на константа.
На пръв поглед може да изглежда, че говоря за нещо сложно и много ученици в началото са объркани. Въпреки това, в частичните производни няма нищо свръхестествено и сега ще видим това на примера на конкретни задачи.
Задачи с радикали и полиноми
Задача No1
За да не губим време, нека започнем от самото начало със сериозни примери.
Като начало, нека ви напомня тази формула:
Това е стандартната стойност на таблицата, която знаем от стандартния курс.
В този случай производната $z$ се изчислява, както следва:
\[(((z)")_(x))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(x)=\frac( 1)(2\sqrt(\frac(y)(x)))((\left(\frac(y)(x) \right))^(\prime ))_(x)\]
Нека го направим отново, тъй като коренът не е $x$, а някакъв друг израз, в този случай $\frac(y)(x)$, тогава първо ще използваме стандартната стойност на таблицата и след това, тъй като коренът е не $x $, а друг израз, трябва да умножим нашата производна по друга от този израз по отношение на същата променлива. Нека първо изчислим следното:
\[((\left(\frac(y)(x) \right))^(\prime ))_(x)=\frac(((((y)"))_(x))\cdot x-y \cdot ((((x)"))_(x)))(((x)^(2)))=\frac(0\cdot x-y\cdot 1)(((x)^(2)) )=-\frac(y)(((x)^(2)))\]
Връщаме се към нашия израз и пишем:
\[(((z)")_(x))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(x)=\frac( 1)(2\sqrt(\frac(y)(x)))((\left(\frac(y)(x) \right))^(\prime ))_(x)=\frac(1) (2\sqrt(\frac(y)(x)))\cdot \left(-\frac(y)(((x)^(2))) \right)\]
По принцип това е всичко. Въпреки това е погрешно да го оставим в тази форма: такава конструкция е неудобна за използване за по-нататъшни изчисления, така че нека я трансформираме малко:
\[\frac(1)(2\sqrt(\frac(y)(x)))\cdot \left(-\frac(y)(((x)^(2))) \right)=\frac (1)(2)\cdot \sqrt(\frac(x)(y))\cdot \frac(y)(((x)^(2)))=\]
\[=-\frac(1)(2)\cdot \sqrt(\frac(x)(y))\cdot \sqrt(\frac(((y)^(2)))(((x)^ (4))=-\frac(1)(2)\sqrt(\frac(x\cdot ((y)^(2)))(y\cdot ((x)^(4)))) =-\frac(1)(2)\sqrt(\frac(y)(((x)^(3))))\]
Отговорът е намерен. Сега нека се заемем с $y$:
\[(((z)")_(y))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot ((\left(\frac(y)(x) \right))^(\prime ))_(y)\]
Нека го запишем отделно:
\[((\left(\frac(y)(x) \right))^(\prime ))_(y)=\frac(((((y)"))_(y))\cdot x-y \cdot ((((x)"))_(y)))(((x)^(2)))=\frac(1\cdot x-y\cdot 0)(((x)^(2)) )=\frac(1)(x)\]
Сега записваме:
\[(((z)")_(y))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot ((\left(\frac(y)(x) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot \frac(1)(x)=\]
\[=\frac(1)(2)\cdot \sqrt(\frac(x)(y))\cdot \sqrt(\frac(1)(((x)^(2))))=\frac (1)(2)\sqrt(\frac(x)(y\cdot ((x)^(2))))=\frac(1)(2\sqrt(xy))\]
Свършен.
Проблем No2
Този пример е едновременно по-прост и по-сложен от предишния. По-сложно е, защото има повече действия, но е по-просто, защото няма корен и освен това функцията е симетрична спрямо $x$ и $y$, т.е. ако разменим $x$ и $y$, формулата няма да се промени. Тази забележка допълнително ще опрости нашето изчисление на частната производна, т.е. достатъчно е да преброите един от тях, а във втория просто да размените $x$ и $y$.
Да се залавяме за работа:
\[(((z)")_(x))=((\left(\frac(xy)(((x)^(2))+((y)^(2))+1) \right ))^(\prime ))_(x)=\frac(((\left(xy \right))^(\prime ))_(x)\left(((x)^(2))+( (y)^(2))+1 \right)-xy((\left(((x)^(2))+((y)^(2))+1 \right))^(\prime ) )_(x))(((\left(((x)^(2))+((y)^(2))+1 \right))^(2)))\]
Нека преброим:
\[((\left(xy \right))^(\prime ))_(x)=y\cdot ((\left(x \right))^(\prime ))=y\cdot 1=y\ ]
Много студенти обаче не разбират това обозначение, така че нека го напишем така:
\[((\left(xy \right))^(\prime ))_(x)=((\left(x \right))^(\prime ))_(x)\cdot y+x\cdot ((\left(y \right))^(\prime ))_(x)=1\cdot y+x\cdot 0=y\]
Така още веднъж се убеждаваме в универсалността на алгоритъма за частични производни: както и да ги изчисляваме, ако всички правила се прилагат правилно, отговорът ще бъде същият.
Сега нека разгледаме още една частична производна от нашата голяма формула:
\[((\left(((x)^(2))+((y)^(2))+1 \right))^(\prime ))_(x)=((\left((( x)^(2)) \right))^(\prime ))_(x)+((\left(((y)^(2)) \right))^(\prime ))_(x) +(((1)")_(x))=2x+0+0\]
Нека заместим получените изрази в нашата формула и ще получим:
\[\frac(((\left(xy \right))^(\prime ))_(x)\left(((x)^(2))+((y)^(2))+1 \ дясно)-xy((\left(((x)^(2))+((y)^(2))+1 \right))^(\prime ))_(x))(((\left (((x)^(2))+((y)^(2))+1 \right))^(2)))=\]
\[=\frac(y\cdot \left(((x)^(2))+((y)^(2))+1 \right)-xy\cdot 2x)(((\left((( x)^(2))+((y)^(2))+1 \right))^(2)))=\]
\[=\frac(y\left(((x)^(2))+((y)^(2))+1-2((x)^(2)) \right))(((\ ляво(((x)^(2))+((y)^(2))+1 \дясно))^(2)))=\frac(y\ляво(((y)^(2)) -((x)^(2))+1 \right))(((\left(((x)^(2))+((y)^(2))+1 \right))^(2 )))\]
Въз основа на преброени $x$. И за да изчислим $y$ от същия израз, нека не изпълняваме същата последователност от действия, а да се възползваме от симетрията на нашия оригинален израз - ние просто заместваме всички $y$ в нашия оригинален израз с $x$ и обратно:
\[(((z)")_(y))=\frac(x\left(((x)^(2))-((y)^(2))+1 \right))((( \left(((x)^(2))+((y)^(2))+1 \right))^(2)))\]
Поради симетрията изчислихме този израз много по-бързо.
Нюанси на решението
За частичните производни работят всички стандартни формули, които използваме за обикновените, а именно производната на частното. В същото време обаче възникват специфични особености: ако разглеждаме частната производна на $x$, тогава когато я получим от $x$, ние я разглеждаме като константа и следователно нейната производна ще бъде равна на „нула“ .
Както в случая с обикновените производни, коефициентът (една и съща производна) може да се изчисли по няколко различни начина. Например, същата конструкция, която току-що изчислихме, може да бъде пренаписана както следва:
\[((\left(\frac(y)(x) \right))^(\prime ))_(x)=y\cdot ((\left(\frac(1)(x) \right)) ^(\prime ))_(x)=-y\frac(1)(((x)^(2)))\]
\[((\left(xy \right))^(\prime ))_(x)=y\cdot (((x)")_(x))=y\cdot 1=y\]
В същото време, от друга страна, можете да използвате формулата от производната сума. Както знаем, тя е равна на сбора от производните. Например, нека напишем следното:
\[((\left(((x)^(2))+((y)^(2))+1 \right))^(\prime ))_(x)=2x+0+0=2x \]
Сега, знаейки всичко това, нека се опитаме да работим с по-сериозни изрази, тъй като реалните частни производни не се ограничават само до полиноми и корени: има и тригонометрия, и логаритми, и експоненциална функция. Сега нека направим това.
Задачи с тригонометрични функции и логаритми
Задача No1
Нека напишем следните стандартни формули:
\[((\left(\sqrt(x) \right))^(\prime ))_(x)=\frac(1)(2\sqrt(x))\]
\[((\left(\cos x \right))^(\prime ))_(x)=-\sin x\]
Въоръжени с тези знания, нека се опитаме да решим:
\[(((z)")_(x))=((\left(\sqrt(x)\cdot \cos \frac(x)(y) \right))^(\prime ))_(x )=((\left(\sqrt(x) \right))^(\prime ))_(x)\cdot \cos \frac(x)(y)+\sqrt(x)\cdot ((\left (\cos \frac(x)(y) \right))^(\prime ))_(x)=\]
Нека напишем една променлива отделно:
\[((\left(\cos \frac(x)(y) \right))^(\prime ))_(x)=-\sin \frac(x)(y)\cdot ((\left( \frac(x)(y)\right))^(\prime ))_(x)=-\frac(1)(y)\cdot \sin \frac(x)(y)\]
Да се върнем към нашия дизайн:
\[=\frac(1)(2\sqrt(x))\cdot \cos \frac(x)(y)+\sqrt(x)\cdot \left(-\frac(1)(y)\cdot \sin \frac(x)(y) \right)=\frac(1)(2\sqrt(x))\cdot \cos \frac(x)(y)-\frac(\sqrt(x))( y)\cdot \sin \frac(x)(y)\]
Това е всичко, намерихме го за $x$, сега нека направим изчисленията за $y$:
\[(((z)")_(y))=((\left(\sqrt(x)\cdot \cos \frac(x)(y) \right))^(\prime ))_(y )=((\left(\sqrt(x) \right))^(\prime ))_(y)\cdot \cos \frac(x)(y)+\sqrt(x)\cdot ((\left (\cos \frac(x)(y) \right))^(\prime ))_(y)=\]
Отново, нека изчислим един израз:
\[((\left(\cos \frac(x)(y) \right))^(\prime ))_(y)=-\sin \frac(x)(y)\cdot ((\left( \frac(x)(y) \right))^(\prime ))_(y)=-\sin \frac(x)(y)\cdot x\cdot \left(-\frac(1)(( (y)^(2))) \right)\]
Връщаме се към първоначалния израз и продължаваме решението:
\[=0\cdot \cos \frac(x)(y)+\sqrt(x)\cdot \frac(x)(((y)^(2)))\sin \frac(x)(y) =\frac(x\sqrt(x))(((y)^(2)))\cdot \sin \frac(x)(y)\]
Свършен.
Проблем No2
Нека запишем формулата, от която се нуждаем:
\[((\left(\ln x \right))^(\prime ))_(x)=\frac(1)(x)\]
Сега нека броим с $x$:
\[(((z)")_(x))=((\left(\ln \left(x+\ln y \right) \right))^(\prime ))_(x)=\frac( 1)(x+\ln y).((\left(x+\ln y \right))^(\prime ))_(x)=\]
\[=\frac(1)(x+\ln y)\cdot \left(1+0 \right)=\frac(1)(x+\ln y)\]
Намерено за $x$. Ние броим по $y$:
\[(((z)")_(y))=((\left(\ln \left(x+\ln y \right) \right))^(\prime ))_(y)=\frac( 1)(x+\ln y).((\left(x+\ln y \right))^(\prime ))_(y)=\]
\[=\frac(1)(x+\ln y)\left(0+\frac(1)(y) \right)=\frac(1)(y\left(x+\ln y \right))\ ]
Проблемът е решен.
Нюанси на решението
Така че, независимо от каква функция вземаме частичната производна, правилата остават същите, независимо дали работим с тригонометрия, с корени или с логаритми.
Класическите правила за работа със стандартни производни остават непроменени, а именно производната на сбор и разлика, частно и комплексна функция.
Последната формула най-често се среща при решаване на задачи с частни производни. Срещаме ги почти навсякъде. Никога не е имало нито една задача, в която да не сме я срещали. Но без значение каква формула използваме, все пак имаме добавено още едно изискване, а именно особеността на работата с частични производни. След като коригираме една променлива, всички останали са константи. По-специално, ако разгледаме частичната производна на израза $\cos \frac(x)(y)$ по отношение на $y$, тогава $y$ е променливата и $x$ остава постоянна навсякъде. Същото работи и обратното. Тя може да бъде извадена от знака за производна, а производната на самата константа ще бъде равна на „нула“.
Всичко това води до факта, че частичните производни на един и същи израз, но по отношение на различни променливи, могат да изглеждат напълно различно. Например, нека разгледаме следните изрази:
\[((\left(x+\ln y \right))^(\prime ))_(x)=1+0=1\]
\[((\left(x+\ln y \right))^(\prime ))_(y)=0+\frac(1)(y)=\frac(1)(y)\]
Задачи с експоненциални функции и логаритми
Задача No1
Като начало нека напишем следната формула:
\[((\left(((e)^(x)) \right))^(\prime ))_(x)=((e)^(x))\]
Знаейки този факт, както и производната на сложна функция, нека се опитаме да изчислим. Сега ще го реша по два различни начина. Първият и най-очевиден е производното на продукта:
\[(((z)")_(x))=((\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right) )^(\prime ))_(x)=((\left(((e)^(x)) \right))^(\prime ))_(x)\cdot ((e)^(\frac (x)(y)))+((e)^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ) )_(x)=\]
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot ((\left(\frac(x)(y) \right))^(\prime ))_(x)=\]
Нека решим отделно следния израз:
\[((\left(\frac(x)(y) \right))^(\prime ))_(x)=\frac(((((x)"))_(x))\cdot y-x .((((y)"))_(x)))(((y)^(2)))=\frac(1\cdot y-x\cdot 0)(((y)^(2))) =\frac(y)(((y)^(2)))=\frac(1)(y)\]
Връщаме се към нашия оригинален дизайн и продължаваме с решението:
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot \frac(1)(y)=((e)^(x))\cdot ((e)^(\frac(x)(y)))\left(1 +\frac(1)(y)\right)\]
Всичко, $x$ се изчислява.
Обаче, както обещах, сега ще се опитаме да изчислим същата частна производна по различен начин. За да направите това, имайте предвид следното:
\[((e)^(x))\cdot ((e)^(\frac(x)(y)))=((e)^(x+\frac(x)(y)))\]
Нека го напишем така:
\[((\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right))^(\prime ))_(x)=( (\left(((e)^(x+\frac(x)(y))) \right))^(\prime ))_(x)=((e)^(x+\frac(x)(y) )))\cdot ((\left(x+\frac(x)(y) \right))^(\prime ))_(x)=((e)^(x+\frac(x)(y)) )\cdot \left(1+\frac(1)(y) \right)\]
В резултат на това получихме абсолютно същия отговор, но количеството изчисления се оказа по-малко. За да направите това, беше достатъчно да се отбележи, че при изпълнение на продукта могат да се добавят индикатори.
Сега нека броим по $y$:
\[(((z)")_(y))=((\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right) )^(\prime ))_(y)=((\left(((e)^(x)) \right))^(\prime ))_(y)\cdot ((e)^(\frac (x)(y)))+((e)^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ) )_(y)=\]
\[=0\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac(x)(y))) \cdot ((\left(\frac(x)(y) \right))^(\prime ))_(y)=\]
Нека решим един израз отделно:
\[((\left(\frac(x)(y) \right))^(\prime ))_(y)=\frac(((((x)"))_(y))\cdot y-x \cdot ((((y)"))_(y)))(((y)^(2)))=\frac(0-x\cdot 1)(((y)^(2))) =-\frac(1)(((y)^(2)))=-\frac(x)(((y)^(2)))\]
Нека продължим да решаваме нашата първоначална конструкция:
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))\cdot \left(-\frac(x)(((y)^(2) )) \right)=-\frac(x)(((y)^(2)))\cdot ((e)^(x))\cdot ((e)^(\frac(x)(y) ))\]
Разбира се, същата тази производна може да се изчисли по втория начин и отговорът ще бъде същият.
Проблем No2
Нека броим по $x$:
\[(((z)")_(x))=((\left(x \right))_(x))\cdot \ln \left(((x)^(2))+y \right )+x\cdot ((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\]
Нека изчислим един израз отделно:
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\frac(1)(((x )^(2))+y)\cdot ((\left(((x)^(2))+y \right))^(\prime ))_(x)=\frac(2x)((( x)^(2))+y)\]
Нека продължим с решаването на оригиналната конструкция: $$
Това е отговорът.
Остава да намерим по аналогия с $y$:
\[(((z)")_(y))=((\left(x \right))^(\prime ))_(y).\ln \left(((x)^(2)) +y \right)+x\cdot ((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(y)=\]
Както винаги, изчисляваме един израз отделно:
\[((\left(((x)^(2))+y \right))^(\prime ))_(y)=((\left(((x)^(2)) \right) )^(\prime ))_(y)+(((y)")_(y))=0+1=1\]
Продължаваме да решаваме основния дизайн:
Всичко е изчислено. Както можете да видите, в зависимост от това коя променлива се взема за диференциране, отговорите са напълно различни.
Нюанси на решението
Ето един поразителен пример за това как производната на една и съща функция може да се изчисли по два различни начина. Вижте тук:
\[(((z)")_(x))=\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right)=( (\left(((e)^(x)) \right))^(\prime ))_(x)\cdot ((e)^(\frac(x)(y)))+((e) ^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ))_(x)=\]
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot \frac(1)(y)=((e)^(x))\cdot ((e)^(^(\frac(x)(y))))\ ляво(1+\frac(1)(y) \дясно)\]
\[(((z)")_(x))=((\left(((e)^(x)).((e)^(\frac(x)(y))) \right)) ^(\prime ))_(x)=((\left(((e)^(x+\frac(x)(y))) \right))^(\prime ))_(x)=(( e)^(x+\frac(x)(y))).((\left(x+\frac(x)(y) \right))^(\prime ))_(x)=\]
\[=((e)^(x))\cdot ((e)^(^(\frac(x)(y))))\left(1+\frac(1)(y) \right)\ ]
При избора на различни пътища количеството изчисления може да е различно, но отговорът, ако всичко е направено правилно, ще бъде същият. Това се отнася както за класическите, така и за частичните производни. В същото време напомням още веднъж: в зависимост от това коя променлива се взема производната, т.е. диференциация, отговорът може да се окаже съвсем различен. Виж:
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\frac(1)(((x )^(2))+y)\cdot ((\left(((x)^(2))+y \right))^(\prime ))_(x)=\frac(1)((( x)^(2))+y)\cdot 2x\]
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(y)=\frac(1)(((x )^(2))+y)\cdot ((\left(((x)^(2))+y \right))^(\prime ))_(y)=\frac(1)((( x)^(2))+y)\cdot 1\]
В заключение, за да консолидираме целия този материал, нека се опитаме да изчислим още два примера.
Задачи с тригонометрични функции и функции с три променливи
Задача No1
Нека запишем следните формули:
\[((\left(((a)^(x)) \right))^(\prime ))=((a)^(x))\cdot \ln a\]
\[((\left(((e)^(x)) \right))^(\prime ))=((e)^(x))\]
Нека сега решим нашия израз:
\[(((z)")_(x))=((\left(((3)^(x\sin y)) \right))^(\prime ))_(x)=((3 )^(x.\sin y))\cdot \ln 3\cdot ((\left(x\cdot \sin y \right))^(\prime ))_(x)=\]
Нека изчислим отделно следната конструкция:
\[((\left(x\cdot \sin y \right))^(\prime ))_(x)=(((x)")_(x))\cdot \sin y+x((\ ляво(\sin y \right))^(\prime ))_(x)=1\cdot \sin y+x\cdot 0=\sin y\]
Продължаваме да решаваме оригиналния израз:
\[=((3)^(x\sin y))\cdot \ln 3\cdot \sin y\]
Това е крайният отговор на частната променлива на $x$. Сега нека броим по $y$:
\[(((z)")_(y))=((\left(((3)^(x\sin y)) \right))^(\prime ))_(y)=((3 )^(x\sin y))\cdot \ln 3\cdot ((\left(x\sin y \right))^(\prime ))_(y)=\]
Нека решим един израз отделно:
\[((\left(x\cdot \sin y \right))^(\prime ))_(y)=(((x)")_(y))\cdot \sin y+x((\ ляво(\sin y \right))^(\prime ))_(y)=0\cdot \sin y+x\cdot \cos y=x\cdot \cos y\]
Нека решим нашата конструкция до края:
\[=((3)^(x\cdot \sin y))\cdot \ln 3\cdot x\cos y\]
Проблем No2
На пръв поглед този пример може да изглежда доста сложен, защото има три променливи. Всъщност това е една от най-лесните задачи в днешния видео урок.
Намерете по $x$:
\[(((t)")_(x))=((\left(x((e)^(y))+y((e)^(z)) \right))^(\prime ) )_(x)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(x)+((\left(y\cdot ((e) ^(z)) \right))^(\prime ))_(x)=\]
\[=((\left(x \right))^(\prime ))_(x)\cdot ((e)^(y))+x\cdot ((\left(((e)^(y) )) \right))^(\prime ))_(x)=1\cdot ((e)^(y))+x\cdot o=((e)^(y))\]
Сега нека се заемем с $y$:
\[(((t)")_(y))=((\left(x\cdot ((e)^(y))+y\cdot ((e)^(z)) \right))^ (\prime ))_(y)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(y)+((\left(y\cdot ((e)^(z)) \right))^(\prime ))_(y)=\]
\[=x\cdot ((\left(((e)^(y)) \right))^(\prime ))_(y)+((e)^(z))\cdot ((\left (y \right))^(\prime ))_(y)=x\cdot ((e)^(y))+((e)^(z))\]
Намерихме отговора.
Сега всичко, което остава, е да намерим по $z$:
\[(((t)")_(z))=((\left(x\cdot ((e)^(y))+((y)^(z)) \right))^(\prime ))_(z)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(z)+((\left(y\cdot ((e) )^(z)) \right))^(\prime ))_(z)=0+y\cdot ((\left(((e)^(z)) \right))^(\prime )) _(z)=y\cdot ((e)^(z))\]
Изчислихме третата производна, което завършва решението на втората задача.
Нюанси на решението
Както можете да видите, в тези два примера няма нищо сложно. Единственото, в което сме убедени е, че производната на сложна функция се използва често и в зависимост от това коя частна производна изчисляваме, получаваме различни отговори.
В последната задача бяхме помолени да разберем функция на три променливи едновременно. В това няма нищо лошо, но накрая се убедихме, че всички те са значително различни един от друг.
Ключови точки
Последните изводи от днешния видео урок са следните:
- Частните производни се изчисляват по същия начин като обикновените, но за да изчислим частната производна по отношение на една променлива, ние приемаме всички други променливи, включени в тази функция, като константи.
- Когато работим с частни производни, използваме същите стандартни формули, както с обикновените производни: сума, разлика, производна на произведението и частното и, разбира се, производна на сложна функция.
Разбира се, самото гледане на този видео урок не е достатъчно, за да разберете напълно тази тема, така че в момента на моя уебсайт има набор от задачи за това видео, специално посветено на днешната тема - влезте, изтеглете, решете тези задачи и проверете отговора . И след това няма да имате проблеми с частни производни нито на изпити, нито на самостоятелна работа. Разбира се, това не е последният урок по висша математика, така че посетете нашия уебсайт, добавете VKontakte, абонирайте се за YouTube, харесайте и останете с нас!
Нека е дадена функция на две променливи. Нека да дадем увеличение на аргумента и да оставим аргумента непроменен. Тогава функцията ще получи увеличение, което се нарича частично увеличение по променлива и се обозначава:
По същия начин, фиксирайки аргумента и давайки увеличение на аргумента, получаваме частично увеличение на функцията по променлива:
Количеството се нарича общо нарастване на функцията в точка.
Определение 4. Частната производна на функция на две променливи по отношение на една от тези променливи е границата на съотношението на съответното частично увеличение на функцията към увеличението на дадена променлива, когато последната клони към нула (ако тази граница съществува). Частичната производна се означава по следния начин: или, или.
Така по дефиниция имаме:
Частичните производни на функциите се изчисляват по същите правила и формули като функция на една променлива, като се има предвид, че при диференциране по променлива тя се счита за константа, а при диференциране по променлива се счита за константа .
Пример 3. Намерете частични производни на функции:
Решение. а) За да намерим, ние го считаме за постоянна стойност и го диференцираме като функция на една променлива:
По същия начин, приемайки постоянна стойност, намираме:
Определение 5. Общият диференциал на функция е сумата от произведенията на частните производни на тази функция и увеличенията на съответните независими променливи, т.е.
Като се има предвид, че диференциалите на независимите променливи съвпадат с техните нараствания, т.е. , формулата за общия диференциал може да бъде записана като
Пример 4. Намерете пълния диференциал на функцията.
Решение. Тъй като използвайки общата диференциална формула, която намираме
Частични производни от по-висок порядък
Частичните производни се наричат частни производни от първи ред или първи частни производни.
Определение 6. Частните производни от втори ред на функция са частните производни на частните производни от първи ред.
Има четири частични производни от втори ред. Те се обозначават, както следва:
Частичните производни от 3-ти, 4-ти и по-високи разряди се определят по подобен начин. Например за функция имаме:
Частните производни от втори или по-висок ред, взети по отношение на различни променливи, се наричат смесени частни производни. За функция това са производни. Забележете, че в случая, когато смесените производни са непрекъснати, тогава равенството е в сила.
Пример 5. Намерете частни производни от втори ред на функция
Решение. Частичните производни от първи ред за тази функция се намират в пример 3:
Диференцирайки по отношение на променливите x и y, получаваме
Частни производни на функция на две променливи.
Концепция и примери за решения
В този урок ще продължим запознаването си с функцията на две променливи и ще разгледаме може би най-често срещаната тематична задача - намирането частни производни от първи и втори ред, както и общия диференциал на функцията. Задочните студенти по правило се сблъскват с частни производни през 1-ва година през 2-ри семестър. Освен това, по мои наблюдения, задачата за намиране на частни производни почти винаги се появява на изпита.
За да изучавате ефективно материала по-долу, вие необходимода можете повече или по-малко уверено да намирате „обикновени“ производни на функции на една променлива. Можете да научите как да боравите правилно с производни в уроци Как да намерим производната?И Производна на сложна функция. Ще ни трябва и таблица с производни на елементарни функции и правила за диференциране, най-удобно е, ако е под ръка в печатна форма. Можете да получите справочни материали на страницата Математически формули и таблици.
Нека бързо повторим концепцията за функция на две променливи, ще се опитам да се огранича до минимума. Функция на две променливи обикновено се записва като , като променливите се извикват независими променливиили аргументи.
Пример: – функция на две променливи.
Понякога се използва нотацията. Има и задачи, в които се използва буквата вместо буква.
От геометрична гледна точка функция на две променливи най-често представлява повърхност в тримерното пространство (равнина, цилиндър, сфера, параболоид, хиперболоид и др.). Но всъщност това е по-скоро аналитична геометрия и на дневен ред е математическият анализ, който моят университетски учител никога не ми позволи да отпиша и е моята „силна страна“.
Нека да преминем към въпроса за намиране на частични производни от първи и втори ред. Имам някои добри новини за тези, които са изпили няколко чаши кафе и се настройват към невероятно труден материал: частните производни са почти същите като "обикновените" производни на функция на една променлива.
За частните производни са валидни всички правила за диференциране и таблицата с производни на елементарни функции. Има само няколко малки разлики, с които ще се запознаем точно сега:
...да, между другото, за тази тема, която създадох малка pdf книга, което ще ви позволи да „вкарате зъбите си“ само за няколко часа. Но като използвате сайта, със сигурност ще получите същия резултат - само може би малко по-бавно:
Пример 1
Намерете частичните производни от първи и втори ред на функцията
Първо, нека намерим частните производни от първи ред. Двама са.
Наименования:
или – частична производна по отношение на „x“
или – частична производна по отношение на „y“
Да започнем с. Когато намерим частната производна по отношение на "x", променливата се счита за константа (постоянно число).
Коментари за извършените действия:
(1) Първото нещо, което правим, когато намираме частната производна, е да заключим всичкофункция в скоби под прайм с долен индекс.
Внимание, важно!НИЕ НЕ ГУБИМ индекси по време на процеса на решаване. В този случай, ако нарисувате „щрих“ някъде без , тогава учителят, като минимум, може да го постави до заданието (незабавно отхапете част от точката за невнимание).
(2) Използваме правилата за диференциране 
, . За прост пример като този и двете правила могат лесно да се приложат в една стъпка. Обърнете внимание на първия термин: тъй като се счита за константа и всяка константа може да бъде извадена от знака за производна, след това го изваждаме от скоби. Тоест в тази ситуация не е по-добър от обикновен номер. Сега нека да разгледаме третия термин: тук, напротив, няма какво да извадим. Тъй като е константа, тя също е константа и в този смисъл не е по-добра от последния термин - „седем“.
(3) Използваме таблични производни и .
(4) Нека опростим или, както обичам да казвам, „ощипваме“ отговора.
Сега . Когато намерим частната производна по отношение на "y", тогава променливатасчита се за константа (постоянно число).
(1) Използваме същите правила за диференциация 
, . В първия член изваждаме константата от знака на производната, във втория член не можем да изваждаме нищо, тъй като тя вече е константа.
(2) Използваме таблицата с производни на елементарни функции. Нека мислено променим всички „X“ в таблицата на „I“. Тоест тази таблица е еднакво валидна за (и наистина за почти всяка буква). По-конкретно формулите, които използваме, изглеждат така: и .
Какво е значението на частичните производни?
По същество частните производни от 1-ви ред наподобяват "обикновена" производна:
- Това функции, които характеризират темп на промянафункции по посока на осите и съответно. Така например функцията 
характеризира стръмността на „издиганията“ и „наклоните“ повърхностипо посока на абсцисната ос, а функцията ни казва за “релефа” на същата повърхност по посока на ординатната ос.
! Забележка : тук имаме предвид посоки, които паралеленкоординатни оси.
За по-добро разбиране, нека разгледаме конкретна точка на равнината и да изчислим стойността на функцията („височина“) в нея:
– а сега си представете, че сте тук (НА ПОВЪРХНОСТТА).
Нека изчислим частната производна по отношение на "x" в дадена точка:
Отрицателният знак на производната „X“ ни говори за намаляващифункционира в точка по посока на абсцисната ос. С други думи, ако направим малък, малък (безкрайно малко)стъпка към върха на оста (успоредно на тази ос), тогава ще се спуснем по наклона на повърхността.
Сега откриваме естеството на „терена“ по посока на ординатната ос:
Производната по отношение на "y" е положителна, следователно в точка по посока на оста функцията се увеличава. Казано по-просто, тук ни чака изкачване.
В допълнение, частната производна в точка характеризира темп на промянафункционира в съответната посока. Колкото по-голяма е получената стойност по модул– колкото по-стръмна е повърхността, и обратно, колкото по-близо е до нулата, толкова по-равна е повърхността. Така че в нашия пример „наклонът“ по посока на абсцисната ос е по-стръмен от „планината“ по посока на ординатната ос.
Но това бяха два частни пътя. Съвсем ясно е, че от точката, в която се намираме, (и като цяло от всяка точка на дадена повърхност)можем да тръгнем в друга посока. По този начин има интерес към създаването на обща "навигационна карта", която да ни информира за "ландшафта" на повърхността ако е възможновъв всяка точка област на дефиниране на тази функцияпо всички налични пътища. Ще говоря за това и други интересни неща в един от следващите уроци, но засега нека се върнем към техническата страна на въпроса.
Нека систематизираме елементарните приложени правила:
1) Когато диференцираме по отношение на , променливата се счита за константа.
2) Когато се извършва диференциация според, тогава се счита за константа.
3) Правилата и таблицата на производните на елементарни функции са валидни и приложими за всяка променлива (или всяка друга), по която се извършва диференцирането.
Стъпка втора. Намираме частни производни от втори ред. Има четири от тях.
Наименования:
или – втора производна по отношение на „x“
или – втора производна по отношение на „y“
или - смесенпроизводно на „x от igr“
или - смесенпроизводно на "Y"
Няма проблеми с втората производна. С прости думи, втората производна е производната на първата производна.
За удобство ще пренапиша вече намерените частични производни от първи ред: 
Първо, нека намерим смесени производни:
Както можете да видите, всичко е просто: вземаме частичната производна и я диференцираме отново, но в този случай - този път според "Y".
По същия начин:
В практически примери можете да се съсредоточите върху следното равенство:
По този начин чрез смесени производни от втори ред е много удобно да проверим дали сме намерили правилно частичните производни от първи ред.
Намерете втората производна по отношение на „x“.
Без изобретения, да вземем 
и го разграничете отново с „x“:
По същия начин:
Трябва да се отбележи, че когато намирате, трябва да покажете повишено внимание, тъй като няма чудотворни равенства, които да ги проверят.
Вторите производни също намират широки практически приложения, по-специално те се използват в проблема с намирането екстремуми на функция на две променливи. Но всичко има своето време:
Пример 2
Изчислете частичните производни от първи ред на функцията в точката. Намерете производни от втори ред.
Това е пример, който можете да решите сами (отговорите в края на урока). Ако ви е трудно да разграничите корените, върнете се към урока Как да намерим производната?Като цяло, доста скоро ще се научите да намирате такива производни „в движение“.
Нека станем по-добри в по-сложните примери:
Пример 3
Провери това . Запишете общия диференциал от първи ред.
Решение: Намерете частичните производни от първи ред: 
Обърнете внимание на долния индекс: , до „Х” не е забранено да пише в скоби, че е константа. Тази бележка може да бъде много полезна за начинаещи, за да улесни навигацията в решението.
Допълнителни коментари:
(1) Взимаме всички константи извън знака на производната. В този случай и , и следователно техният продукт се счита за постоянно число.
(2) Не забравяйте как правилно да разграничавате корените.
(1) Изваждаме всички константи от знака на производната; в този случай константата е .
(2) Под простото число остава продуктът на две функции, следователно трябва да използваме правилото за диференциране на продукта 
.
(3) Не забравяйте, че това е сложна функция (макар и най-простата от сложните). Използваме съответното правило: 
.
Сега намираме смесени производни от втори ред:
Това означава, че всички изчисления са извършени правилно.
Нека запишем общия диференциал. В контекста на разглежданата задача няма смисъл да казваме какъв е общият диференциал на функция на две променливи. Важно е, че тази разлика много често трябва да бъде записана в практически задачи.
Общ диференциал от първи редфункцията на две променливи има формата: 
В такъв случай:
Тоест, просто трябва глупаво да замените вече намерените частични производни от първи ред във формулата. В тази и подобни ситуации е най-добре да напишете диференциални знаци в числители:
И според многократните искания на читатели, пълен диференциал от втори ред.
Изглежда така:
Нека ВНИМАТЕЛНО намерим "еднобуквените" производни от 2-ри ред: 
и запишете „чудовището“, като внимателно „прикрепите“ квадратите, продукта и не забравяйте да удвоите смесената производна: 
Добре е, ако нещо изглежда трудно; винаги можете да се върнете към производните по-късно, след като сте усвоили техниката на диференциране:
Пример 4
Намерете частични производни от първи ред на функция 
. Провери това . Запишете общия диференциал от първи ред.
Нека да разгледаме серия от примери със сложни функции:
Пример 5
Намерете частичните производни от първи ред на функцията.
Решение: 
Пример 6
Намерете частични производни от първи ред на функция 
.
Запишете общия диференциал.
Това е пример, който можете да решите сами (отговорете в края на урока). Няма да ви дам пълно решение, защото е доста просто.
Доста често всички горепосочени правила се прилагат в комбинация.
Пример 7
Намерете частични производни от първи ред на функция 
.
(1) Използваме правилото за диференциране на сумата
(2) Първият член в този случай се счита за константа, тъй като в израза няма нищо, което да зависи от “x” - само “y”. Знаеш ли, винаги е хубаво, когато една дроб може да се превърне в нула). За втория член прилагаме правилото за диференциране на продукта. Между другото, в този смисъл нищо нямаше да се промени, ако вместо това беше дадена функция - важното е, че тук продукт на две функции, ВСЕКИ от които зависи от "Х"и следователно трябва да използвате правилото за диференциране на продукта. За трети член прилагаме правилото за диференциране на сложна функция.
(1) Първият член както в числителя, така и в знаменателя съдържа „Y“, следователно трябва да използвате правилото за диференциране на коефициентите: 
. Вторият член зависи САМО от "x", което означава, че се счита за константа и се превръща в нула. За трети член използваме правилото за диференциране на сложна функция.
За тези читатели, които смело стигнаха почти до края на урока, ще ви разкажа един стар виц на Мехматов за облекчение:
Един ден зла производна се появи в пространството на функциите и започна да разграничава всички. Всички функции са разпръснати във всички посоки, никой не иска да се трансформира! И само една функция не бяга. Производното се приближава до нея и я пита:
- Защо не избягаш от мен?
- Ха Но не ме интересува, защото съм „e на степен X“ и няма да ми направите нищо!
На което злата производна с коварна усмивка отговаря:
- Тук грешите, ще ви различавам по "Y", така че трябва да сте нула.
Който е разбрал шегата, е усвоил производните, поне до ниво „С“).
Пример 8
Намерете частични производни от първи ред на функция 
.
Това е пример, който можете да решите сами. Пълното решение и пример на задачата са в края на урока.
Е, това е почти всичко. И накрая, не мога да не зарадвам любителите на математиката с още един пример. Дори не става дума за аматьори, всеки има различно ниво на математическа подготовка - има хора (и то не толкова редки), които обичат да се състезават с по-трудни задачи. Въпреки че последният пример в този урок не е толкова сложен, колкото е тромав от изчислителна гледна точка.
Нека да обобщим как намирането на частични производни се различава от намирането на „обикновени“ производни на функция на една променлива:
1) Когато намерим частната производна, Че променлива се счита за константа.
2) Когато намерим частната производна, Че променлива се счита за константа.
3) Правилата и таблицата с производни на елементарни функции са валидни и приложими за всяка променлива ( , или някои други), чрез които се извършва диференциация.
Стъпка втора. Намираме частни производни от втори ред. Има четири от тях.
Обозначения:
Или – втората производна по „х“
Или – втората производна по отношение на “Y”
Или - смесенпроизводно "от x igrek"
Или - смесенпроизводно "от igrek x"
Няма нищо сложно в концепцията за втората производна. С прости думи, втората производна е производната на първата производна.
За по-голяма яснота ще пренапиша вече намерените частични производни от първи ред:
Първо, нека намерим смесени производни:
Както можете да видите, всичко е просто: вземаме частичната производна и я диференцираме отново, но в този случай - този път според "Y".
По същия начин:
За практически примери, когато всички частични производни са непрекъснати, е валидно следното равенство:
По този начин чрез смесени производни от втори ред е много удобно да проверим дали сме намерили правилно частичните производни от първи ред.
Намерете втората производна по отношение на „x“.
Без изобретения, да вземем и го разграничете отново с „x“:
По същия начин:
Трябва да се отбележи, че когато намирате, трябва да покажете повишено внимание, тъй като няма прекрасни равенства за проверка.
Пример 2
Намерете частичните производни от първи и втори ред на функцията
Това е пример, който можете да решите сами (отговорете в края на урока).
С известен опит частни производни от примери № 1 и 2 ще решавате устно от вас.
Нека да преминем към по-сложни примери.
Пример 3
Провери това . Запишете общия диференциал от първи ред.
Решение: Намерете частичните производни от първи ред:
Обърнете внимание на долния индекс: , до „Х” не е забранено да пише в скоби, че е константа. Тази бележка може да бъде много полезна за начинаещи, за да улесни навигацията в решението.
Допълнителни коментари:
(1) Взимаме всички константи извън знака на производната. В този случай и , и следователно техният продукт се счита за постоянно число.
(2) Не забравяйте как правилно да разграничавате корените.
(1) Изваждаме всички константи от знака на производната; в този случай константата е .
(2) Под простото число остава продуктът на две функции, следователно трябва да използваме правилото за диференциране на продукта 
.
(3) Не забравяйте, че това е сложна функция (макар и най-простата от сложните). Използваме съответното правило: 
.
Сега намираме смесени производни от втори ред:
Това означава, че всички изчисления са извършени правилно.
Нека запишем общия диференциал. В контекста на разглежданата задача няма смисъл да казваме какъв е общият диференциал на функция на две променливи. Важно е, че тази разлика много често трябва да бъде записана в практически задачи.
Общият диференциал от първи ред на функция от две променливи има формата:
В такъв случай:
Тоест, просто трябва да замените вече намерените частични производни от първи ред във формулата. В тази и подобни ситуации е най-добре да напишете диференциални знаци в числители:
Пример 4
Намерете частични производни от първи ред на функция 
. Провери това . Запишете общия диференциал от първи ред.
Това е пример, който можете да решите сами. Пълното решение и пример на задачата са в края на урока.
Нека разгледаме поредица от примери, които включват сложни функции.
Пример 5
Намерете частичните производни от първи ред на функцията.
(1) Прилагаме правилото за диференциране на сложни функции . От класа Производна на сложна функциятрябва да запомните много важен момент: когато превръщаме синус (външна функция) в косинус с помощта на таблицата, тогава имаме вграждане (вътрешна функция) не се променя.
(2) Тук използваме свойството на корените: , изваждаме константата от знака на производната и представяме корена във формата, необходима за диференциране.
По същия начин: 
Нека запишем пълния диференциал от първи ред:
Пример 6
Намерете частични производни от първи ред на функция 
.
Запишете общия диференциал.
Това е пример, който можете да решите сами (отговорете в края на урока). Няма да ви дам пълно решение, защото е доста просто.
Доста често всички горепосочени правила се прилагат в комбинация.
Пример 7
Намерете частични производни от първи ред на функция 
.
(1) Използваме правилото за диференциране на сбора.
(2) Първият член в този случай се счита за константа, тъй като в израза няма нищо, което да зависи от “x” - само “y”.
(Знаеш ли, винаги е хубаво, когато една дроб може да се превърне в нула).
За втория член прилагаме правилото за диференциране на продукта. Между другото, нищо нямаше да се промени в алгоритъма, ако вместо това беше дадена функция - важно е, че тук имаме произведение на две функции, ВСЯКА от които зависи от "x", така че трябва да използвате правилото за диференциране на продукта. За трети член прилагаме правилото за диференциране на сложна функция.
