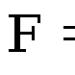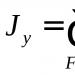ОПРЕДЕЛЕНИЕ
Аксиален (или екваториален) момент на инерциясечение спрямо оста се нарича количество, което се определя като:
Израз (1) означава, че за изчисляване на аксиалния инерционен момент, сумата от продуктите на безкрайно малки площи (), умножени по квадратите на разстоянията от тях до оста на въртене, се взема върху цялата площ S:
Сумата от аксиалните инерционни моменти на сечението спрямо взаимно перпендикулярни оси (например спрямо осите X и Y в декартовата координатна система) дава полярния момент на инерция () спрямо пресечната точка на тези оси:
ОПРЕДЕЛЕНИЕ
Полярен моментинерция се нарича моментът на инерционния участък по отношение на някаква точка.
Аксиалните моменти на инерция винаги са по-големи от нула, тъй като в техните дефиниции (1) под интегралния знак има стойността на площта на елементарната област (), винаги положителна, и квадратът на разстоянието от тази област до оста.
Ако имаме работа със сечение със сложна форма, тогава често в изчисленията използваме факта, че аксиалният инерционен момент на сложен участък спрямо оста е равен на сумата от аксиалните инерционни моменти на частите на този участък спрямо същата ос. Трябва обаче да се помни, че е невъзможно да се сумират моментите на инерция, които се намират спрямо различни оси и точки.
Аксиалният инерционен момент спрямо оста, минаваща през центъра на тежестта на сечението, има най-малката стойност от всички моменти спрямо успоредните на него оси. Инерционният момент спрямо всяка ос (), при условие че е успоредна на оста, минаваща през центъра на тежестта, е равен на:
където е инерционният момент на сечението спрямо оста, минаваща през центъра на тежестта на сечението; - площ на напречното сечение; - разстояние между осите.
Примери за решаване на проблеми
ПРИМЕР 1
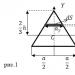
| Упражнение | Какъв е аксиалният инерционен момент на равнобедрен триъгълник по отношение на оста Z, минаваща през центъра на тежестта () на триъгълника, успоредна на основата му? Височината на триъгълника е . |
| Решение | Нека изберем правоъгълна елементарна област върху триъгълно сечение (виж фиг. 1). Намира се на разстояние от оста на въртене, дължината на едната страна е , другата страна е . От фиг. 1 следва, че:
Площта на избрания правоъгълник, като се вземе предвид (1.1), е равна на: За да намерим аксиалния инерционен момент, използваме неговата дефиниция във формата: |
| Отговор |
ПРИМЕР 2
| Упражнение | Намерете аксиалните моменти на инерция спрямо перпендикулярните оси X и Y (фиг. 2) на сечение под формата на кръг, чийто диаметър е равен на d. |
| Решение | За да разрешите проблема, е по-удобно да започнете с намирането на полярния момент спрямо центъра на сечението (). Нека разделим цялото сечение на безкрайно тънки пръстени с дебелина , чийто радиус ще бъде означен с . Тогава намираме елементарната площ като: |
Аксиалният инерционен момент е равен на сумата от произведенията на елементарните площи и квадрата на разстоянието до съответната ос.
(8)
Знакът винаги е "+".
Не може да бъде равно на 0.
Имот:Приема минимална стойност, когато пресечната точка на координатните оси съвпада с центъра на тежестта на сечението.
Аксиалният момент на инерция на сечение се използва при изчисляване на якост, твърдост и стабилност.
1.3. Полярен инерционен момент на сечението Jρ
(9)
Връзка между полярните и аксиалните моменти на инерция:
(10)
(11)
Полярният инерционен момент на сечението е равен на сумата от аксиалните моменти.
Имот:
Когато осите се въртят в произволна посока, единият от аксиалните моменти на инерция се увеличава, а другият намалява (и обратно). Сумата от аксиалните инерционни моменти остава постоянна.
1.4. Центробежен инерционен момент на сечението Jxy
Центробежният инерционен момент на сечението е равен на сумата от произведенията на елементарните площи и разстоянията до двете оси
(12)
Мерна единица [cm 4 ], [mm 4 ].
Знак "+" или "-".
, ако координатните оси са оси на симетрия (пример - I-лъч, правоъгълник, кръг), или една от координатните оси съвпада с оста на симетрия (пример - канал).
Така за симетрични фигури центробежният инерционен момент е 0.
Координатни оси u И v , преминаващи през центъра на тежестта на сечението, около което центробежният момент е равен на нула, се наричат основните централни инерционни оси на сечението.Наричат се главни, защото центробежният момент спрямо тях е нула, а централни, защото преминават през центъра на тежестта на сечението.
За сечения, които не са симетрични спрямо осите х
или г
, например, на ъгъла, 
няма да е равно на нула. За тези участъци се определя положението на осите u
И v
чрез изчисляване на ъгъла на завъртане на осите х
И г
(13)
Центробежен момент около осите u
И v
-
Формула за определяне на аксиалните инерционни моменти относно главните централни оси u И v :
(14)
Където 
- аксиални инерционни моменти спрямо централните оси,
- центробежен момент на инерция спрямо централните оси.
1.5. Инерционен момент спрямо ос, успоредна на централната (теорема на Щайнер)
Теорема на Щайнер:
Инерционният момент около ос, успоредна на централната, е равен на централния аксиален момент на инерция плюс произведението на площта на цялата фигура и квадрата на разстоянието между осите.
(15)
Доказателство на теоремата на Щайнер.
Според фиг. 5 разстояние при към елементарния сайт dF
Заместване на стойността привъв формулата, получаваме:
Срок 
, тъй като точка C е центърът на тежестта на сечението (вижте свойството на статичните моменти на секционната площ спрямо централните оси).
За правоъгълник с височинач и ширинаb :
Аксиален инерционен момент:
Момент на огъване:
моментът на съпротивление на огъване е равен на съотношението на инерционния момент към разстоянието на най-отдалеченото влакно от неутралната линия:
защото 
, Че 
За кръг:
Полярен инерционен момент: 
Аксиален инерционен момент: 
Момент на усукване: 
защото 
, Че 
Момент на огъване: 
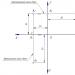
Пример 2. Определете инерционния момент на правоъгълно напречно сечение около централната ос СЪС х .
Решение. Нека разделим площта на правоъгълника на елементарни правоъгълници с размери b (ширина) и dy (височина). Тогава площта на такъв правоъгълник (защрихована на фиг. 6) е равна на dF=bdy. Нека изчислим стойността на аксиалния инерционен момент Дж х
По аналогия пишем
- аксиален инерционен момент на сечението спрямо централния
Центробежен момент на инерция
, тъй като осите СЪС
х
и С г
са оси на симетрия.
Пример 3. Определете полярния инерционен момент на кръгло напречно сечение.
Решение. Нека разделим кръга на безкрайно тънки пръстени с дебелина
радиус 
, площта на такъв пръстен 
. Заместване на стойността 
Интегрирайки в израза за полярния инерционен момент, получаваме
Отчитане на равенството на аксиалните моменти на кръгло сечение 
И
, получаваме
Аксиалните инерционни моменти на пръстена са равни
с– отношението на диаметъра на изреза към външния диаметър на вала.
Лекция No2 „Главни оси иглавни точкиинерция
Нека разгледаме как се променят инерционните моменти при завъртане на координатните оси. Да приемем, че са дадени инерционните моменти на определено сечение спрямо нулевите оси х, 0при(не непременно централно) -
,
- аксиални инерционни моменти на сечението. Трябва да се определи 
,
- аксиални моменти около осите u,v, завъртяна спрямо първата система на ъгъл 
(фиг. 8)
Тъй като проекцията на начупената линия OABC е равна на проекцията на задната линия, намираме:
(15)
Нека изключим u и v от изразите за инерционните моменти:
(18)
Нека разгледаме първите две уравнения. Добавяйки ги термин по термин, получаваме
По този начин сумата от аксиалните моменти на инерция около две взаимно перпендикулярни оси не зависи от ъгъла 
и остава постоянна, когато осите се въртят. Нека същевременно да отбележим, че
Където 
- разстояние от началото на координатите до елементарната площадка (виж фиг. 5). По този начин
Където 
- вече познатият полярен момент на инерция:
Нека определим аксиалния инерционен момент на кръга спрямо диаметъра.
Тъй като поради симетрията 
но, както знаете, 
Следователно, за кръг
С промяна на ъгъла на въртене на осите 
моментни стойности
И 
промяна, но сумата остава същата. Следователно има такъв смисъл 
, при което един от инерционните моменти достига максимална стойност, а другият момент приема минимална стойност. Разграничаване на израза 
по ъгъл 
и приравнявайки производната на нула, намираме
(19)
При тази стойност на ъгъла 
единият от аксиалните моменти ще бъде най-големият, а другият ще бъде най-малкият. В същото време центробежният инерционен момент
изчезва, което може лесно да се провери чрез приравняване на формулата за центробежния инерционен момент на нула
.
Оси, за които центробежният момент на инерция е нула и аксиалните моменти приемат екстремни стойности, се наричат основенбрадви.Ако те също са централни (началната точка съвпада с центъра на тежестта на сечението), тогава те се наричат главни централни оси (u;
v).
Наричат се аксиални моменти на инерция спрямо главните оси основни моменти на инерция -
И
И тяхната стойност се определя по следната формула:
(20)
Знакът плюс съответства на максималния инерционен момент, знакът минус на минималния.
Има и друга геометрична характеристика - радиус на въртене секции. Тази стойност често се използва в теоретични заключения и практически изчисления.
Радиусът на въртене на сечението спрямо дадена ос, например 0
х
,
се нарича количеството
,
определени от равенството
(21)
Е – площ на напречното сечение,
- аксиален инерционен момент на сечението,
От дефиницията следва, че радиусът на въртене е равен на разстоянието от оста 0 хдо точката, в която площта на напречното сечение F трябва да бъде концентрирана (условно), така че инерционният момент на тази една точка да е равен на инерционния момент на цялото сечение. Познавайки инерционния момент на сечението и неговата площ, можете да намерите радиуса на въртене спрямо оста 0 х:
(22)
Радиусите на въртене, съответстващи на главните оси, се наричат главни радиуси на инерцияи се определят по формулите
(23)
Лекция 3. Усукване на пръти с кръгло напречно сечение.
Ако m = 1, n = 1, тогава получаваме характеристиката
което се нарича центробежен момент на инерция.
Центробежен момент на инерцияспрямо координатните оси – сумата от произведенията на елементарни площи dAна разстоянията им до тези оси, взети по цялата площ на напречното сечение А.
Ако поне една от осите гили zе оста на симетрия на сечението, центробежният инерционен момент на такова сечение спрямо тези оси е равен на нула (тъй като в този случай всяка положителна стойност z·y·dAможем да поставим в съответствие абсолютно същото, но отрицателно, от другата страна на оста на симетрия на сечението, виж фигурата).
Нека разгледаме допълнителни геометрични характеристики, които могат да бъдат получени от основните изброени и също често се използват при изчисления на якост и твърдост.
Полярен момент на инерция
Полярен момент на инерция Jpназовете характеристиката
От друга страна,
Полярен момент на инерция(спрямо дадена точка) – сумата от произведенията на елементарни площи dAчрез квадратите на техните разстояния 
до тази точка, взети върху цялата площ на напречното сечение А.
Размерът на инерционните моменти е m 4 в SI.
Момент на съпротива
Момент на съпротиваспрямо някаква ос – стойност, равна на инерционния момент спрямо същата ос, разделен на разстоянието ( ymaxили z макс) до най-отдалечената от тази ос точка
Размерът на моментите на съпротивление е m 3 в SI.
Радиус на инерция
Радиус на инерциясечение спрямо определена ос се нарича стойност, определена от връзката:
Радиусите на въртене се изразяват в SI единици m.
коментар:напречните сечения на елементите на съвременните конструкции често представляват определен състав от материали с различна устойчивост на еластична деформация, характеризиращ се, както е известно от курса по физика, от модула на Юнг д. В най-общия случай на нехомогенно сечение модулът на Юнг е непрекъсната функция от координатите на точките на сечението, т.е. E = E(z, y). Следователно твърдостта на участък, който е нехомогенен по еластични свойства, се характеризира с характеристики, които са по-сложни от геометричните характеристики на хомогенно сечение, а именно еластично-геометрични от формата
2.2. Изчисляване на геометрични характеристики на прости фигури
Правоъгълно сечение
Нека определим аксиалния инерционен момент на правоъгълника спрямо оста z. Нека разделим площта на правоъгълника на елементарни области с размери b(ширина) и dy(височина). Тогава площта на такъв елементарен правоъгълник (защрихована) е равна на dA = b dy. Заместване на стойността dAв първата формула, получаваме
По аналогия записваме аксиалния момент спрямо оста при:
Аксиални моменти на съпротивление на правоъгълник:
; 
По подобен начин можете да получите геометрични характеристики за други прости фигури.
Кръгло сечение
Удобно е първо да се намери полярен инерционен момент J p .
Тогава, като се има предвид това за кръг J z = J y, А J p = J z + J y, ще намерим Джей Зи =Джи = Jp / 2.
Нека разделим кръга на безкрайно малки пръстени с дебелина dρи радиус ρ ; площ на такъв пръстен dA = 2 ∙ π ∙ ρ ∙ dρ. Заместване на израза за dAв израз за Jpи интегрирайки, получаваме
2.3. Изчисляване на инерционните моменти спрямо успоредни оси
zИ г:
Необходимо е да се определят инерционните моменти на тази секция спрямо „новите“ оси z 1И y 1, успоредни на централните и отдалечени от тях на разстояние аИ bсъответно:
Координати на всяка точка в „новата“ координатна система z 1 0 1 y 1може да се изрази чрез координати в „старите” оси zИ гТака:
Тъй като брадвите zИ г– централен, след това статичен момент S z = 0.
И накрая, можем да запишем формулите за „преход“ за паралелно прехвърляне на оси:
Имайте предвид, че координатите аИ bтрябва да бъдат заменени, като се вземе предвид техният знак (в координатната система z 1 0 1 y 1).
2.4. Изчисляване на инерционните моменти при въртене на координатни оси
Нека са известни инерционните моменти на произволно сечение спрямо централните оси z, y:
; 
;
Да завъртим осите z, гпод ъгъл α обратно на часовниковата стрелка, като ъгълът на въртене на осите в тази посока се счита за положителен.
Необходимо е да се определят инерционните моменти спрямо „новите“ (завъртани) оси z 1И y 1:
Координати на елементарната площадка dAв „новата” координатна система z 1 0y 1може да се изрази чрез координати в „старите“ оси по следния начин:
Заменяме тези стойности във формулите за инерционните моменти в „новите“ оси и интегрираме термин по термин:
След като направихме подобни трансформации с останалите изрази, най-накрая ще запишем формулите за „преход“ при завъртане на координатните оси:
Обърнете внимание, че ако добавим първите две уравнения, получаваме
т.е. полярният инерционен момент е количеството инвариант(с други думи, непроменен при въртене на координатните оси).
2.5. Главни оси и главни инерционни моменти
Досега се разглеждаха геометричните характеристики на сечения в произволна координатна система, но най-голям практически интерес представлява координатната система, в която сечението се описва с най-малък брой геометрични характеристики. Тази „специална“ координатна система се определя от позицията на главните оси на сечението. Нека представим понятията: главни осиИ основни инерционни моменти.
Главни оси– две взаимно перпендикулярни оси, спрямо които центробежният инерционен момент е нула, докато аксиалните инерционни моменти приемат екстремни стойности (максимум и минимум).
Главните оси, минаващи през центъра на тежестта на сечението, се наричат главни централни оси.
Инерционните моменти около главните оси се наричат основни инерционни моменти.
Главните централни оси обикновено се обозначават с букви uИ v; основни инерционни моменти - J uИ Jv(a-приори J uv = 0).
Нека изведем изрази, които ни позволяват да намерим положението на главните оси и големината на главните инерционни моменти. Знаейки това J uv= 0, използваме уравнение (2.3):
Ъгъл α 0 определя позицията на главните оси спрямо всяка централна ос zИ г. Ъгъл α 0 отложени между оста zи ос uи се счита за положителен в посока обратна на часовниковата стрелка.
Имайте предвид, че ако едно сечение има ос на симетрия, тогава, в съответствие със свойството на центробежния инерционен момент (вижте раздел 2.1, параграф 4), такава ос винаги ще бъде главната ос на сечението.
Без ъгъл α в изрази (2.1) и (2.2), използвайки (2.4), получаваме формули за определяне на основните аксиални моменти на инерция:
Нека запишем правилото: максималната ос винаги сключва по-малък ъгъл с този на осите (z или y), спрямо които инерционният момент има по-голяма стойност.
2.6. Рационални форми на напречните сечения
Нормалните напрежения в произволна точка от напречното сечение на гредата по време на директно огъване се определят по формулата:
, (2.5)
Където М– огъващ момент в разглежданото напречно сечение; при– разстоянието от разглежданата точка до главната централна ос, перпендикулярна на равнината на действие на огъващия момент; J x– основният централен инерционен момент на сечението.
Най-големите нормални напрежения на опън и натиск в дадено напречно сечение възникват в точките, които са най-отдалечени от неутралната ос. Те се определят по формулите:
; 
,
Където на 1И на 2– разстояния от главната централна ос хдо най-отдалечените опънати и компресирани влакна.
За греди, изработени от пластмасови материали, когато [σ p ] = [σ c ] ([σ p ], [σ c ] са допустимите напрежения за материала на гредата съответно при опън и натиск), сеченията, симетрични спрямо централната ос, са използвани. В този случай условието за якост има формата:
≤
[σ], (2.6)
Където W x = J x / y макс– момент на съпротивление на площта на напречното сечение на гредата спрямо главната централна ос; ymax = з/2(ч– височина на секцията); M макс– най-големият огъващ момент по абсолютна стойност; [σ] – допустимото напрежение на огъване на материала.
Освен условието за якост, гредата трябва да отговаря и на условието за икономичност. Най-икономични са тези форми на напречно сечение, за които най-големият съпротивителен момент се получава с най-малко количество материал (или с най-малка площ на напречното сечение). За да бъде формата на сечението рационална, е необходимо, ако е възможно, сечението да се разпредели далеч от главната централна ос.
Например стандартната I-греда е приблизително седем пъти по-здрава и тридесет пъти по-твърда от квадратна греда със същото напречно сечение, изработена от същия материал.
Трябва да се има предвид, че когато позицията на сечението се промени по отношение на действащото натоварване, якостта на гредата се променя значително, въпреки че площта на напречното сечение остава непроменена. Следователно сечението трябва да бъде разположено така, че силовата линия да съвпада с тази на главните оси, спрямо които инерционният момент е минимален. Трябва да се стремите да гарантирате, че огъването на гредата се извършва в равнината на най-голямата му твърдост.
Често чуваме изразите: „инертен е“, „движи се по инерция“, „инерционен момент“. В преносен смисъл думата „инерция“ може да се тълкува като липса на инициатива и действие. Интересуваме се от прякото значение.
Какво е инерция
Според определението инерциявъв физиката това е способността на телата да поддържат състояние на покой или движение при отсъствие на външни сили.
Ако всичко е ясно със самата концепция за инерция на интуитивно ниво, тогава момент на инерция– отделен въпрос. Съгласете се, трудно е да си представите какво е това. В тази статия ще научите как да решавате основни задачи по темата "Момент на инерция".
Определяне на инерционния момент
От училищния курс се знае, че маса - мярка за инерцията на тялото. Ако бутаме две колички с различна маса, тогава по-тежката ще бъде по-трудна за спиране. Тоест, колкото по-голяма е масата, толкова по-голямо е външното влияние, необходимо за промяна на движението на тялото. Разгледаното се отнася за постъпателното движение, когато количката от примера се движи по права линия.
По аналогия с масовото и транслационното движение, инерционният момент е мярка за инерцията на тялото по време на въртеливо движение около ос.
Момент на инерция– скаларна физична величина, мярка за инерцията на тялото при въртене около ос. Означава се с буквата Дж и в системата SI измерено в килограми по квадратен метър.
Как да изчислим инерционния момент? Във физиката има обща формула, по която се изчислява инерционният момент на всяко тяло. Ако едно тяло е натрошено на безкрайно малки парчета с маса дм , тогава инерционният момент ще бъде равен на сумата от произведенията на тези елементарни маси на квадрата на разстоянието до оста на въртене.
Това е общата формула за инерционния момент във физиката. За материална точка от маса м , въртящи се около ос на разстояние r от него тази формула приема формата:
Теорема на Щайнер
От какво зависи инерционният момент? От масата, положението на оста на въртене, формата и размера на тялото.
Теоремата на Хюйгенс-Щайнер е много важна теорема, която често се използва при решаване на проблеми.
Между другото! За нашите читатели вече има 10% отстъпка от всякакъв вид работа
Теоремата на Хюйгенс-Щайнер гласи:
Инерционният момент на тялото спрямо произволна ос е равен на сумата от инерционния момент на тялото спрямо ос, минаваща през центъра на масата, успоредна на произволна ос, и произведението на масата на тялото с квадрата от разстоянието между осите.
За тези, които не искат постоянно да интегрират, когато решават задачи за намиране на инерционния момент, представяме чертеж, показващ инерционните моменти на някои еднородни тела, които често се срещат в задачи:
Пример за решаване на задача за намиране на инерционния момент
Нека разгледаме два примера. Първата задача е да се намери инерционният момент. Втората задача е да се използва теоремата на Хюйгенс-Щайнер.
Задача 1. Намерете инерционния момент на хомогенен диск с маса m и радиус R. Оста на въртене минава през центъра на диска.
Решение:
Нека разделим диска на безкрайно тънки пръстени, чийто радиус варира от 0 преди Ри помислете за един такъв пръстен. Нека неговият радиус е r, а масата – дм. Тогава инерционният момент на пръстена е:
Масата на пръстена може да бъде представена като:
Тук дз– височина на пръстена. Нека заместим масата във формулата за инерционния момент и интегрираме:
Резултатът беше формула за инерционния момент на абсолютно тънък диск или цилиндър.
Задача 2. Нека отново има диск с маса m и радиус R. Сега трябва да намерим инерционния момент на диска спрямо оста, минаваща през средата на един от неговите радиуси.
Решение:
От предишната задача е известен инерционният момент на диска спрямо оста, минаваща през центъра на масата. Нека приложим теоремата на Щайнер и да намерим:
Между другото, в нашия блог можете да намерите други полезни материали по физика и решаване на проблеми.
Надяваме се, че ще намерите нещо полезно за себе си в статията. Ако възникнат трудности в процеса на изчисляване на тензора на инерцията, не забравяйте за студентската служба. Нашите специалисти ще ви посъветват по всеки въпрос и ще помогнат за решаването на проблема за няколко минути.
