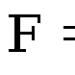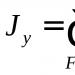Изкривяване на кривата
Нека γ( T) - правилна крива в д-мерно евклидово пространство, параметризирано по дължина. Тогава
Наречен кривина на криватаγ в точка стр = γ( T), тук означава втората производна по отношение на T. вектор
Наречен вектор на кривинаγ в точка стр = γ( T 0) .
За крива, дефинирана параметрично в общия случай (параметърът не е непременно дължината), кривината се дава по формулата
,където и съответно означават първата и втората производни на радиус вектора γ в търсената точка.
За да съвпадне кривата γ с определен сегмент от права или с цялата права, е необходимо и достатъчно кривината (или векторът на кривината) да е идентично равна на нула.
Реципрочната стойност на кривината на кривата се нарича радиус на кривина; той съвпада с радиуса на оскулиращата окръжност в дадена точка от кривата. Центърът на този кръг се нарича център на кривина.
Повърхностна кривина
Нека Φ е правилна повърхност в тримерното евклидово пространство. Позволявам стр- точка Φ, T стр- допирателна равнина към Φ в точката стр , н- нормална единица към Φ в точката стр, a - π дсамолет, преминаващ през ни някакъв единичен вектор д V T стр. γ крива д, което се получава като пресечната точка на равнината π дс повърхност Φ се нарича нормална секцияповърхност Φ в точка стрв посоката д. величина
където означава скаларното произведение, и к - вектор на кривина γ дв точката стр, Наречен нормална кривинаповърхност Φ по посока д. С точност до знак нормалната кривина е равна на кривината на кривата γ д .
В допирателната равнина T стрима две перпендикулярни посоки д 1 и д 2 така, че нормалната кривина в произволна посока може да бъде представена с помощта на т.нар Формули на Ойлер:
κ д= κ 1 cos 2 α + κ 2 sin 2 αкъдето α е ъгълът между д 1 и д 2, а стойностите κ 1 и κ 2 са нормални кривини в посоките д 1 и д 2, те се наричат основни кривинии упътвания д 1 и д 2 - основни направленияповърхност в точка стр. Основните кривини са екстремни стойности на нормалните кривини. Удобно е да се изобрази графично структурата на нормалните кривини в дадена точка на повърхността с помощта на индикатриса на Дюпен.
величина
з= κ 1 + κ 2, (понякога)Наречен средна кривинаповърхности. величина
К= κ 1 κ 2Наречен Гаусова кривинаповърхности.
Кривината на Гаус е обект на вътрешната геометрия на повърхностите; по-специално, тя не се променя по време на изометрично огъване.
Вижте също
Литература
- Погорелов А.И.Диференциална геометрия (6-то издание). М.: Наука, 1974.
- Рашевски П.К.Курс по диференциална геометрия (3-то издание). M.-L.: GITTL, 1950.
Фондация Уикимедия. 2010 г.
налягането непосредствено под изпъкнала повърхност на течност е по-голямо от налягането под плоска повърхност на течност, а налягането под вдлъбната повърхност на течност е по-малко от налягането под плоска повърхност.
Изчисляване на налягане под сферична повърхност на течност
Това е тънък слой вода, който има две ограничителни повърхности: вътрешна и външна. Радиусите на кривината на тези повърхности могат да се считат за еднакви, тъй като дебелината на филма е хиляди пъти по-малка от радиуса на балона. Водата постепенно се оттича от този слой, слоят изтънява и накрая се счупва. Така че мехурчетата не плуват във водата много дълго: от части от секундата до десетки секунди. Трябва да се отбележи, че когато водният филм изтънява, размерът на мехурчето остава практически непроменен.
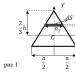
Нека изчислим излишното налягане в такъв балон. За простота разглеждаме еднослойна полусфера с радиус r, разположена на хоризонтална повърхност; ние също ще приемем, че няма въздух навън. Филмът се задържа върху защрихованата повърхност чрез намокряне (фиг. 2.3). В този случай по протежение на границата на контакт с повърхността върху нея действа сила на повърхностно напрежение, равна на
където е коефициентът на повърхностно напрежение на течността,
Дължината на интерфейса филм-повърхност е равна на .
Тоест имаме:
![]() .
.
Тази сила, действаща върху филма и чрез него върху въздуха, е насочена перпендикулярно на повърхността (виж Фигура 2.3). Така че налягането на въздуха на повърхността и следователно вътре в мехура може да се изчисли, както следва:
Където F е силата на повърхностното напрежение, равна на,
S - повърхност: .
Замествайки стойността на силата F и площта S във формулата за изчисляване на налягането, получаваме:
 и накрая.
и накрая.
В нашия пример с въздушно мехурче на повърхността на водата филмът е двоен и следователно свръхналягането е равно на .
Фигура 2.4 показва примери за еднослойни сферични повърхности, които могат да се образуват върху повърхността на течност. Над течността има газ под налягане.
Капилярността (от латински capillaris - коса), капилярен ефект е физическо явление, състоящо се в способността на течностите да променят нивото в тръби, тесни канали с произволна форма, порести тела. Покачване на течността възниква в случаите, когато каналите са намокрени от течности, например вода в стъклени тръби, пясък, почва и т.н. Намаляване на течността възниква в тръби и канали, които не са намокрени от течност, например живак в стъклена тръба.
Животът на животните и растенията, химическите технологии и ежедневните явления (например повдигане на керосин по фитила на керосинова лампа, избърсване на ръцете с кърпа) се основават на капилярността. Капилярността на почвата се определя от скоростта, с която водата се издига в почвата и зависи от размера на пространствата между почвените частици.
Формула на Лаплас
Нека разгледаме тънък течен филм, чиято дебелина може да бъде пренебрегната. В стремежа си да минимизира своята свободна енергия, филмът създава разлика в налягането от различни страни. Това обяснява съществуването на сапунени мехурчета: филмът се компресира, докато налягането вътре в мехурчето надвиши атмосферното налягане с размера на допълнителното налягане на филма. Допълнителното налягане в точка на повърхността зависи от средната кривина в тази точка и се дава от формулата на Лаплас:
![]()
Тук R 1,2 са радиусите на основните кривини в точката. Те имат един и същ знак, ако съответните центрове на кривина лежат от една и съща страна на допирателната равнина в точка, и различен знак, ако са от различни страни. Например за сфера центровете на кривината във всяка точка на повърхността съвпадат с центъра на сферата, следователно
За случая на повърхността на кръгъл цилиндър с радиус R имаме
Клас 5а, 18 YVTO 1-ви ДОКАЗАТЕЛСТВА ПО ART ETENI.
ОПИСАНИЕ на устройството за определяне на кривината на кладенци.
1930 (удостоверение за кандидатстване No 68898).
Вече са известни инструменти за определяне на кривината на кладенци с помощта на магнитна стрелка за определяне на азимута на ъгъла на отклонение, както е известно и използването в такива инструменти на сферична повърхност с приложена към нея географска мрежа.Това устройство се състои от полусферично махало, окачено на карданен кръг с изпъкнал Географската решетка има следните характеристики: за закрепване на полукълбото в позицията, приета, когато кладенецът е огънат, се използват скоби, които работят от движението надолу на клапани с наклонени прорези. отпечатък на хартията върху лентата, използва се кубче, разположено на ос във вилицата, притиснато заедно с движещите се ролки с лента и с копирна хартия, поставена върху повърхността на захванатата полусфера. В същото време спускането на клапани, натискане на куба, завъртане на лентовите ролки и разпръскване на водещите крила се постига чрез използване на болт, завъртян от зъбни колела от ролка, завъртяна от верижна трансмисия от повърхността на земята.
На чертежа Фиг. 1 изобразява вертикален разрез на устройството по линия C - I на фиг. 2; фиг. 2 - хоризонтално сечение по линия А - В на фиг. 1; фиг. 3 - изглед отгоре на устройството.
Масивно махало-полусфера 1 (фиг. 2) с изпъкнали краища на ос 2, навлизаща. двата срещуположни отвора 4 на пръстена 3 (фиг. 1), който също има отвори, разположени към първата двойка отвори под ъгъл 90, в които влизат аксиални тръби 5, закрепени в единия край към щранговете b. В тръбите 5, с вмъкнати крака 8 на две вдлъбнати скоби 9, има надлъжни процепи 7. В другия край на краката 8 има проходен пръст 10, който с изпъкналите си краища се движи по процепа 7 в тръбите 5 , С помощта на два клапана 11, свързани последователно
Използвайки U-образна щанга 22 с наклонени прорези 11, скобите 9 се движат в една посока към топката 1, след това обратно.
Под полусферата 1 (фиг. 1) има трета скоба 14 с вдлъбната повърхност. част, обърната към същото полукълбо 1. Скобата 14 с крака си 16 се движи свободно в тръбата 17, завинтена към диска 18 с разположен! на него има 15 лоста, закачени на ограничители 15. Лостове 15. когато единият край е натиснат от клапана 11, другият край действа върху третата скоба 14, която се издърпва от полусферата 1 от пружини 19. В центъра на полусферата 1 е монтирана игла 12 върху нейната пресечена (горна част) хоризонтална) страна, чийто остър край служи за опора. магнетизирана куха полусфера 13, която служи като компас, чиято външна изпъкнала повърхност е решетка с изпъкнали линии и числа, концентрични спрямо ръбовете на компаса, показващи градуси и меридиани. Цифрите са разположени по цялата повърхност на компаса. На пръта 22, в прорезите на осите 23, ролките 24 и 24 се въртят с хартиена лента 25, навита върху тях; една ролка, приемащата ролка 24, е снабдена с набраздена ролка отстрани. В средата, ленти 22, отдолу има куб 28, разположен на вилицата 27, въртяща се на ос 29, а на същата ос има набраздена ролка, разположена близо до куба от едната страна и зъби 31 от друг, закрепен към куба 28, покрит с четири свободни отстрани с гума за еластично прилягане към компаса. Копирната хартия е залепена върху гумата и хартиена лента 25 преминава върху нея от едната ролка 24 към другата, приемащата ролка 124, прилепваща плътно към долната страна на куба 28. Набраздените ролки на куба 28 и приемащата ролка 24, за едновременното им въртене, имат общ безконечен спирален пружинен шнур 30, преметнат върху тези ролки. На лента 20, прикрепена към лявата стойка b, има 26 лапи с пружини. Отгоре на пръта 22 има съединител 32, прикрепен към него, който чрез завъртане на болта 33 или премества куба от компаса, след това го притиска върху компаса и чрез преместване на клапаните 11, той или освобождава полусфера 1 и компас 13 от скобите, или те също захващат полусферата и компаса, правейки ги неподвижни. Болт 33, прекаран през уплътнението 34 на диска 35 (херметично затварящ целия описан механизъм), в единия край има зъбно колело 39, завъртано от винтова ос 40 в лагери в общи стелажи на набраздена ролка 38 с гнезда за отделни звена на веригата разположени по жлеба (като колело от часове с вдигане на гири). Ролката 38 се задвижва във въртеливо движение
s двете страни, чрез издърпване на верига през нея, удължена в двата края с въжета с дължина, равна на дълбочината на кладенеца. За да поставите тялото на устройството в положение, успоредно на кладенеца. в средата на външния диск 37 има ос 46 на зъбното колело 42, задвижвана във въртене от оста на винта 43 на набраздената ролка 44, същото действие като на набраздената ролка 38 и по същия начин чрез издърпване на определена дължина от верига, също удължена в двата края с шнурове. На оста 46 (фиг. 3) е твърдо монтиран кръст 45, чиито четири края са шарнирно свързани с свързващия прът 47 и в същото време шарнирно свързани с крилата 42, които имат формата на жлеб, вдлъбнатата страна е в съседство с външната цилиндрична страна на тялото на устройството. Само крилата са шарнирно свързани с тялото на устройството и имат
Целта на изпъкналата му страна, отдалечавайки се от тялото, е да приляга плътно към стените на кладенеца, за да даде
1 положение на тялото на устройството успоредно на кладенеца. Ролките 49 (фиг. 1) са монтирани на ролки по тялото на устройството, за да се елиминира триенето на устройството по стените на кладенеца.
Работата на устройството е както следва. Устройството се спуска в кладенеца на въже и съответният край на кабела на външния механизъм се издърпва, което кара ролката 42 да се върти, докато крилата 48 се отклоняват настрани, опирайки се в стените на кладенеца . Това действие поставя устройството в стационарно положение, успоредно на кладенеца.
След изчакване на времето, необходимо на компаса да се успокои, а) другият, опънат през набраздената ролка 38, се изтегля на определена дължина от съответния му край, б) рамката (шина 22) и клапаните се понижени. В същото време скобите 9 и 14 привеждат полукълбото 1 и компаса 13 в неподвижно състояние, кубът 28, захванал лапите 26 със зъбно колело 31, прави една четвърт от своя оборот и в същото време, с долната си страна плътно притиска хартиената лента 25 към компаса 13, от вътрешната страна на която, до копирната хартия, ще се отпечата онази част от компаса с мрежата и цифрите, която се е отклонила от вертикалата, и следователно азимутът ще бъде маркиран. След това този шнур се издърпва за другия си край, raaa 22 се повдига, компас 13 и полусфера 1 се освобождават от скобите, след което първият кабел също се издърпва от другия край и по този начин устройството се освобождава от контакт със стените на добре.
Снимката е направена. Това действие може да се повтори веднага или, ако желаете, спускане или повдигане на устройството до желаната дълбочина. По този начин, в едно изпълнение на устройството е възможно да се направи цяла поредица от определяния, чийто брой ще зависи само от дължината на хартиената лента 25. Предмет на изобретението.
Устройство за определяне на кривината на кладенци, което се състои от полукълбо, окачено върху карта от нов кръг на махало с вертикална игла, която служи като опора за магнетизирано полукълбо с нанесена изпъкнала географска решетка, характеризиращо се с това, че за закрепване на полукълбото в позицията, приета, когато кладенецът е крив, се използват скоби 9 - 9 и 14. действайки от движението надолу на клапаните А с наклонени процепи 11 и за получаване на решетъчен отпечатък върху лентата, се използва куб 28, разположен на оста 29 във вилицата 27, притиснат заедно с лентата, движеща се между ролките 24 и 24 и с копирна хартия, поставена върху повърхността на захванатата полусфера 13, която За да спуснете клапаните 9 - 9 и 14, натиснете куба 28, завъртете лентовите ролки, а също и за разширяване на водещите крила 48, използвайте болт 33. въртя се чрез зъбни колела от ролка 38, върти се от верижна трансмисия от повърхността на земята. (фиг. 2)
Подобни патенти:
Радиусът на кривина на изпъкнала повърхност може да се изчисли по следната формула:
където: T1 - радиус на кривина на изпъкналата повърхност, mm;
T2 - радиус на кривина на оптичната зона на вдлъбната повърхност, mm;
D - върхово пречупване на лещата, в диоптри; n е коефициентът на пречупване на материала на лещата; t е дебелината в центъра на лещата по нейната ос, mm.
Залепващият восък се нанася върху предварително загрят сферичен дорник с радиус, съответстващ на радиуса на оптичната зона на полуфабриката и полуготовият продукт се залепва от страната на обработената вдлъбната повърхност. Центрирането се извършва на специално центриращо устройство с точност 0,02-0,04 mm.
След охлаждане дорникът, заедно с центрирания върху него полуготов продукт, се монтира върху конуса за кацане на сферичен струг за обработка на изпъкнала повърхност.
Изчисленият радиус се определя от индикатора, разположен на въртящия се шублер. С помощта на друг индикатор, инсталиран на шпиндела на машината, се определя дебелината на слоя материал, отстранен по време на обработката. Струговането на изпъкнала повърхност се извършва в няколко прохода (подобно на обработката на вдлъбната повърхност), докато се постигне определената дебелина в центъра на лещата.
Полирането на изпъкнала повърхност се извършва със специална полираща подложка, навлажнена с полираща суспензия на полираща машина (едно- или многошпинделна). Времето за полиране е от 2 до 5 минути (в зависимост от материала).
Чистотата на оптичната повърхност на лещата се контролира с помощта на бинокулярен микроскоп или лупа непосредствено след производството на лещата, преди да се извади от дорника с централен отвор. Оптичната мощност се измерва с помощта на диоптричен уред. Ако по време на контролния процес се окаже, че резултатите от обработката не са задоволителни, тогава процесът се коригира.
След приключване на полирането и контрола на оптиката, лещата се изважда от рамката и се почиства от лепилна вакса.
При производството на външната повърхност на лещи с отрицателно пречупване, първо сферичната повърхност с изчисления радиус на кривина на оптичната зона се обработва до дадена дебелина в центъра, а след това лещовидната зона се обработва с дадена дебелина на ръба, докато се свърже с оптичната зона. Радиусът на кривината на зоната на лещата се изчислява и зависи от конструктивните характеристики на лещата. При изчисляване трябва да се има предвид, че дебелината на лещата по ръба не трябва да надвишава 0,2 mm, а диаметърът на оптичната зона на външната повърхност трябва да бъде най-малко 7,5 mm.
Когато правите външната повърхност на лещи с положително пречупване, първо шлайфайте сферичната повърхност с изчислен радиус до дебелина в центъра, която надвишава необходимата с 0,03 mm. Размерът на радиуса зависи от дебелината на лещата в центъра и по ръба. След това лещовидната зона се обработва, като се започне от ръба на детайла до изчисления диаметър на оптичната зона на външната повърхност, която се избира с 0,4-0,5 mm по-голяма от диаметъра на вътрешната повърхност. Индикаторът задава изчисления радиус на оптичната зона. Чрез завъртане на опората за монтиране на ножа и съответното подаване на детайла, върхът на ножа се подравнява с периферната част на оптичната зона и оптичната зона на изпъкналата повърхност се обработва.
Полирането се извършва на полираща машина с помощта на специална полираща подложка, навлажнена със суспензия.
Производството на GPZhKL се извършва по същата схема, но за почистване и полиране на тези материали се използват по-малко интензивни режими на обработка и специални състави.
Когато се обработват сферични лещи, първо вдлъбнатата сферична повърхност на лещата се обработва по описания по-горе метод и след това, за да се получи торична повърхност в периферията, се обработва с торичен инструмент (обикновено шлайф и полираща машина) с дадени радиуси на кривина на повърхностите в две взаимно перпендикулярни равнини fis. 76). Броят на подготвените торични инструменти зависи от необходимия брой торични повърхности в зоната на сплескване (плъзгане).
За шлайфане на мелницата използвайте специален струг, предназначен за производство на торични инструменти. В този случай трябва да се спазват следните правила:
1. Въз основа на разликата между радиусите в главните меридиани се определя страничното изместване на шпиндела спрямо въртящата се опора. Движението се следи с помощта на циферблат. Например, за торичен инструмент с радиуси 8,0/8,5 mm, тази стойност, наречена торична разлика, ще бъде равна на 0,5 mm.
2. Чрез въртене на въртящия се шублер заготовката на инструмента се обработва на дълбочина
Ориз. 76. Схема на торична полираща подложка.
добре, не повече от 0,05 mm за всяко преминаване, докато се получи определеният радиус, измерен с индикатора на въртящия се шублер.
След това произведеният инструмент се монтира в специално устройство (“торична вилка”) на полиращата машина.
Субстратът с обработения детайл е здраво фиксиран към водача на торичната вилка. След това водачът се монтира в жлебовете на вилицата, така че вдлъбнатата повърхност на детайла да лежи върху работната повърхност на торичния инструмент. ПИН
Горният шпиндел на полиращата машина е фиксиран с торична вилка. Чрез вертикално преместване на люлеещата се глава на довършителната машина е необходимо да се постигне такова положение на детайла, че той да се движи само в централната част на торичния инструмент. Шлифоването се извършва с шлифовъчен прах М7 и М3 до получаване на зададения размер на оптичната зона. Времето за смилане зависи от съотношението на радиусите на лещите и торичната разлика на инструмента. Полученият размер на оптичната зона се наблюдава с помощта на увеличение на измервателното увеличение от 10x.
Въведение
Класификация на точки върху правилна повърхност
Изпъкнали тела и повърхнини
1 Основни понятия
2 Изкривяване
4 Негъвкавост на сферата
Седлови повърхности
3 Проблем с платото
Заключение
Библиография
Въведение
Тази работа е посветена на изучаването на външната геометрия на повърхности с постоянен тип точки. Включва въпроси, свързани с изпъкнали и седловидни повърхности.
Проблемът на това изследване е актуален в съвременния свят. Това се доказва от честото изучаване на повдигнатите въпроси, много произведения са посветени на тяхното изследване. По принцип материалът, представен в учебната литература, е от общ характер.
Диференциална геометрия през 19 век. разработен в тясна връзка с механиката и анализа, особено с теорията на частичните диференциални уравнения. Тъй като през този период в анализа се работи много по въпросите на формалната интеграция, тогава за диференциалната геометрия беше естествено да се занимава с проблемите на формалната аналитична посока. Основният обект на теорията на повърхностите бяха правилните повърхности, разглеждани „в малките“.
През 20 век, дори в началото, въпросите от формално естество вече не могат да се считат за релевантни за механиката и анализа. Междувременно в теорията на повърхностите преобладаващата част от изследванията все още продължават традициите на 19 век. Така се образува пропаст между класическата теория на повърхностите, от една страна, и анализа и механиката, от друга. По-съвременните проблеми и качествените методи за анализ и механика се оказаха чужди на класическата теория на повърхностите. И в рамките на класическата теория на повърхностите се появи нов клон, предмет на който останаха правилните повърхности, но изучавани „като цяло“; този клон също се сля със съвременния анализ. Но тук е много важно да се отбележи следното: докато тези отдели на геометрията „като цяло“, където се изучават свойствата на твърдите повърхности, отдавна имат доста изчерпателна система от общи методи (поне за изпъкнали повърхности), изследванията на повърхностните деформации и връзките между тях вътрешни и външни свойства („като цяло”) бяха фрагментарни. Всичко това се обяснява с факта, че геометрите, които са работили в областта на геометрията „като цяло“, са подхождали към проблемите на тази област все още със средствата на класическия анализ, който в повечето случаи се оказва малко полезен тук. За успешното развитие на смислена теория на повърхностите се оказа спешно необходимо да се изгради система от общи директни методи за изследване на вътрешните свойства на повърхността. Това е направено от А. Д. Александров (с участието на неговите ученици И. М. Либерман и С. П. Оловянишников). Изпъкналите повърхности естествено осигуряват особено благоприятно поле за конкретни и геометрично ясни резултати. Но не става въпрос само за индивидуалните резултати. За развитието на всеки отдел по математика е важно общото ниво на неговите проблеми и методи, важно е това ниво да съответства на прогреса на науката. За развитието на повърхностната теория е важно тя да не бъде изолирана, самостоятелна дисциплина. Изследванията на A.D. Александров, A.V. Pogorelov, A.L. Вернер и други математици са от голямо значение за теорията на повърхностите, тъй като те отварят нови области на проблемите и съответните методи в нея, в крак с преките методи на съвременния анализ.
Актуалността на тази работа се дължи, от една страна, на големия интерес към тази тема в съвременната наука, а от друга страна, на нейното недостатъчно развитие. Разглеждането на въпроси, свързани с тази тема, има както теоретично, така и практическо значение.
Целта на изследването е да се проучат теоретичните аспекти на темата „Външна геометрия на повърхности с постоянен тип точки“ от гледна точка на най-новите местни и чуждестранни изследвания по подобни въпроси.
1. Класификация на точки върху правилна повърхност
Повърхност S, определена от векторното уравнение , ще се обадим -редовно, ако в областта за настройка на параметри D функцията има непрекъснати производни от ред k (k 2) и във всички точки от областта D неравенството .
Втората квадратична форма на повърхността S е скаларното произведение на вектори и n:
. (1)
Лесно е да се забележи, че във всяка точка от повърхността S, формата (1) е квадратна форма по отношение на диференциалите и .
За коефициентите на втората квадратна форма се приема следната нотация:
което ни позволява да го запишем в следния вид: .
Нека S е правилна повърхност и е неговият радиус вектор.
Нека изберем някаква точка от повърхността S и помислете за самолета , която докосва повърхността S в тази точка.
Случайно точково отклонение повърхност S от равнината дефинирайте по формулата
, (2)
Където е единичният нормален вектор към повърхността в точка .
Това отклонение, взето в абсолютна стойност, е равно на разстоянието от точката да рендосвам . Отклонението е положително, ако точката и края на вектора легнете от едната страна на самолета и отрицателни, ако тези точки лежат на противоположните страни на равнината (Фигура 1).
Нека се обърнем към формула (2). Разлика позволява следното представяне:
къде .
Нека умножим двете страни на равенството (3) скаларно по вектора. След това, поставяне
разбираме това
. (4)
Имайте предвид, че коефициентите И във формула (4) се изчисляват в точка .
Така че трябва да отхвърлим следното представяне:
, (5)
къде през означава втората квадратна форма на повърхността, изчислена в точката , и при .
Използваме получената формула (5), за да изследваме структурата на повърхността S в близост до точката .
Нека изчислим дискриминанта на втората квадратна форма
в точката . Възможни са следните случаи.
) е знаково определен.
Нека го поправим в точка някаква посока на повърхността; за сигурност.
След това всяка друга посока на повърхността в точката може да се посочи с помощта на ъгъл , която образува с избраната посока (фиг. 2).
Нека го поставим. Тогава
(6)
Лесно е да се покаже това
къде е константата
и по силата на условието е положителен.
Така че неравенството
се извършва независимо от избора на ъгъл.
Тъй като редът на клонене към нула при втори срок от дясната страна на формула (5) е по-висока от две, тогава от последната оценка може да се направи следното заключение.
отклонение запазва знака, съвпадащ със знака на втората квадратна форма , за всички достатъчно малки стойности независимо от избора на посока на повърхността.
Това означава, че всички точки от повърхността S, които са достатъчно близо до точката разположен от едната страна на допирателната равнина повърхност S в тази точка. Такава точка на повърхността се нарича елипсовидна (фиг. 3)
) - втора квадратна форма на повърхността в точка е знакоредуващ се.
Нека покажем, че в този случай в точката Можете да посочите две колинеарни посоки върху повърхност, които имат следните свойства:
а) за стойностите на диференциалите, определящи тези посоки, втората квадратна форма на повърхността, изчислена в точката , отива на нула;
б) всички други посоки на повърхността в точка са разделени на два класа - за диференциали, които определят посоките на един от класовете, втората квадратна форма положителни и отрицателни за другите.
Нека някаква насока положителен клас се дава от ъгъла . В съответствие с формула (6) имаме
Където .
Както се вижда от формула (5), знакът на отклонението за всички достатъчно малки стойности във въпросната посока съвпада със знака на втората квадратна форма . Следователно, ако точката повърхност S е достатъчно близо до точката , то това отклонение е положително.
Разсъждавайки по подобен начин, можем да посочим точки на повърхността близо до точката , за които отклонението отрицателна (фиг. 4).
Горното разсъждение показва, че близо до точката , повърхността S е разположена от противоположните страни на допирателната равнина . В този случай проекциите на повърхностни точки, чиито отклонения са положителни, върху допирателната равнина попълнете комплекта, отбелязан на горната фигура (фиг. 5).
В разглеждания случай точката се нарича хиперболична точка на повърхността S.
) , но поне един от коефициентите е различен от нула.
Нека за сигурност . Тогава втората квадратна форма на повърхността S в точката може да се запише в следната форма:
Така в зависимост от знака форма или неотрицателна ( ) или неположителен ( ). Освен това на повърхността S в точката можете да посочите посоката , така че диференциалите, които го определят И обърнете втората квадратна форма до нула. За всички други посоки на повърхността в точка форма има същия знак (съвпадащ със знака) (фиг. 6).
В този случай точката се нарича параболична точка на повърхността S.
Такава точка се нарича точка на сплескване на повърхността. Разположението на точките на повърхността близо до точката на сплескване спрямо допирателната равнина на повърхността в тази точка може да бъде изключително разнообразно (фиг. 7).
В зависимост от вида на точките се разграничават следните видове повърхност:
· ако всички точки на повърхността са елиптични, тогава повърхността е изпъкнала;
· ако всички точки на повърхността са хиперболични, тогава повърхността е седло.
2. Изпъкнали тела и повърхнини
1 Основни понятия
Множество M в тримерното евклидово пространство се нарича изпъкнало, ако заедно с произволни две от своите точки X и Y съдържа отсечка от права линия, която ги свързва (фиг. 8). Затворено плоско изпъкнало множество с вътрешни точки се нарича изпъкнала област.
Свързаната част от границата на изпъкнала област се нарича изпъкнала крива. Границата на крайна изпъкнала област се нарича затворена изпъкнала крива. Затворената изпъкнала крива е хомеоморфна на окръжност. Права g, минаваща през точка X от границата на изпъкнала област G, се нарича опорна линия, ако цялата област е разположена в една от полуравнините, определени от тази линия. Поне една опорна линия минава през всяка гранична точка на изпъкналата област.
Ако изпъкнала крива е границата на изпъкнала област G или част от нейната граница, тогава референтната линия във всяка точка на кривата към областта G се нарича още еталонна права крива.
Точките на изпъкнала крива са разделени на гладки и ъглови. А именно точка X на изпъкнала крива се нарича гладка, ако една опорна линия минава през тази точка. В противен случай точка X се нарича ъглова точка. В ъглова точка опорните прави запълват определен вертикален ъгъл с върха в тази точка, като страните на този ъгъл също са опорни прави (фиг. 10).
Всяка изпъкнала крива е поправима, т.е. има определена дължина. Ако затворена крива обхваща изпъкнала крива , след това дължината не надвишава дължината.
Изпъкнало тяло е затворено изпъкнало множество в пространството, което има вътрешни точки. За да бъде затворено изпъкнало множество изпъкнало тяло е необходимо и достатъчно да няма равнина, съдържаща това множество. Пресечната част (обща част) на всяка колекция от изпъкнали тела, ако съдържа вътрешни точки, също е изпъкнало тяло.
Областта (свързаното отворено множество) на границата на изпъкнало тяло се нарича изпъкнала повърхност. Свързаната компонента на границата на изпъкнало тяло се нарича пълна изпъкнала повърхност. Ако изключим двата тривиални случая, когато изпъкнало тяло е цялото пространство или област между две успоредни равнини, тогава пълната изпъкнала повърхност може да се дефинира просто като границата на изпъкнало тяло. Границата на крайно изпъкнало тяло е хомеоморфна на сфера и се нарича затворена изпъкнала повърхност. Всяка пълна изпъкнала повърхност е хомеоморфна на равнина, сфера или цилиндър. В последния случай самата повърхност е цилиндър.
Точно както в случая на изпъкнали плоски области, концепцията за референтна равнина се въвежда за изпъкнали тела. А именно самолет , минаваща през граничната точка X на тялото K, се нарича референтна точка в тази точка X, ако всички точки на тялото са разположени от една и съща страна на равнината , т.е. в едно от полупространствата, които определя. През всяка гранична точка на изпъкнало тяло минава поне една базова равнина. Единичен вектор, перпендикулярен на базовата равнина и насочен в полупространство, което не съдържа точки на тялото, се нарича външна нормала към тази базова равнина.
Изпъкнало тяло V, съставено от полуправи, излизащи от точката S, се нарича изпъкнал конус; това изключва случая, когато тялото V съвпада с цялото пространство. Концепцията за изпъкнал конус, дефинирана по този начин, съдържа като частен случай двустенен ъгъл и полупространство. Повърхността на изпъкнал конус обикновено се нарича още изпъкнал конус. В тези два специални случая говорим за израждане на конус като повърхност в двустенен ъгъл или равнина.
Всяка точка S от границата на изпъкнало тяло K е естествено свързана с определен конус V(S), образуван от полуправи, излизащи от точката S и пресичащи тялото K в поне една точка, различна от S (фиг. 11). ).
Този конус се нарича допирателен конус в точка S, а повърхността му се нарича допирателен конус на изпъкналата повърхнина, ограничаваща тялото.
В зависимост от вида на допирателния конус точките на изпъкналата повърхност се делят на конични, оребрени и гладки. Това е точката X на изпъкнала повърхност, която се нарича конична, ако допирателният конус V(X) в тази точка не се изражда. Ако допирателният конус V(X) се изражда в двустенен ъгъл или равнина, тогава X се нарича оребрена или съответно гладка точка. Негладките точки върху изпъкнала повърхност са в известен смисъл изключение. А именно, множеството от ръбови точки има мярка нула, а множеството от конични точки е най-много изброимо.
Най-простото нетривиално изпъкнало тяло е изпъкнал полиедър - пресечната точка на краен брой полупространства. Повърхнината на изпъкнал многостен е съставена от изпъкнали плоски многоъгълници и се нарича още изпъкнал многостен. Многоъгълниците, които образуват повърхността на многостена, се наричат лица на многостена, техните страни се наричат ръбове на многостена, а върховете им се наричат върхове на многостена.
В теорията на изпъкналите тела концепцията за изпъкнала обвивка играе важна роля. Изпъкналата обвивка на множество M е пресечната точка на всички полупространства, съдържащи M. Следователно, това е изпъкнало множество и, освен това, най-малкото сред всички изпъкнали множества, съдържащи M. Всеки изпъкнал полиедър е изпъкналата обвивка на своите върхове (крайни и в безкрайност), и следователно се определя еднозначно от тях.
За последователност от изпъкнали повърхности се дефинира понятието конвергенция. Казва се, че последователност от изпъкнали повърхности се събира към изпъкнала повърхност F, ако всяко отворено множество G едновременно пресича или не пресича повърхността F и всички повърхности при . Всяка изпъкнала повърхност може да бъде представена като граница на изпъкнали полиедри или правилни изпъкнали повърхности.
Безкрайните колекции от изпъкнали повърхности имат важно свойство на компактност, което се състои във факта, че от всяка последователност от пълни изпъкнали повърхности, които не отиват до безкрайност, винаги може да се изолира конвергентна подпоследователност с граница под формата на изпъкнала повърхност, евентуално дегенериращ (в двойно покрита плоска област, права, полулиния или сегмент).
Нека отбележим много общото свойство на конвергенция на опорните равнини на конвергентна последователност от изпъкнали повърхности. Позволявам - последователност от изпъкнали повърхности, събиращи се към изпъкнала повърхност F, - точка на повърхността И - референтна равнина в тази точка. Тогава, ако последователността от точки се събира в точка X на повърхността F и последователността от референтни равнини се събира в равнина , тогава тази равнина е опорната равнина за повърхността F в точка X. От тук по-специално следва, че ако последователността от точки на изпъкнала повърхност F се събира в точка X на тази повърхност и опорните равнини по точки се събират в равнина , тогава тази равнина ще бъде референтната равнина в точка X.
2 Изкривяване
Нека G е всяка област на повърхността F. Ще начертаем във всички точки на областта G всички допирателни (опорни) равнини към повърхността F и ще начертаем радиуси от центъра на някаква единична сфера S, насочени успоредно на външните нормали към тези поддържащи самолети. Наборът от точки върху сферата S, образувана от краищата на радиусите, начертани по този начин, се нарича сферичен образ на областта G. Площта на това сферично изображение на областта G ще се нарича външна кривина на тази област (фиг. 12).
При сферично изображение на изпъкнала повърхност посоката на преминаване на сферичния образ на площта върху повърхността съвпада с посоката на преминаване на самата тази област. Следователно кривината на изпъкнала повърхност винаги е положително число.
Оказва се, че външната кривина е напълно адитивна функция върху изпъкнала повърхност, дефинирана за всички Borel набори.
Доказателството на тази теорема се основава на следните две твърдения:
Сферичен образ на затворено множество върху изпъкнала повърхност е затворено множество.
Множеството от онези точки от сферичния образ на изпъкнала повърхнина, всяка от които има най-малко две обратни изображения на повърхнината, има площ, равна на нула.
За външни кривини на изпъкнали повърхности са валидни следните теореми за конвергенция:
Ако последователност от изпъкнали повърхности конвергира към изпъкнала повърхност F и последователност от затворени множества , лежащи върху повърхности , се сближава към затворено множество M върху F, тогава , Където означава външната кривина на съответното множество.
Нека последователността от изпъкнали повърхности конвергира към изпъкнала повърхност F, и G са отворени множества върху повърхности и F, и И - затваряния на тези набори. Тогава, ако комплектите се сближават с , и комплекти се събират към F-G, а външните кривини на множествата конвергират към външната кривина , след това външните изкривявания конвергират към външната кривина G.
Ако X е конична точка на повърхността F, то нейното сферично изображение само образува цяла област върху сферата S (фиг. 13). Ако L е неправолинеен ръб на повърхнината, тогава сферичният му образ също покрива цялата област на сферата S (фиг. 14).
Вътрешната кривина се определя като функция на набора върху повърхността, т.е. На всяко множество M от определен клас множества се задава номер - кривина на множеството M. В съответствие с терминологията, приета в диференциалната геометрия, трябва да говорим за пълната (или интегрална) вътрешна кривина, но за краткост ще пропуснем и двете прилагателни, което няма да доведе до недоразумения , тъй като с една дума „кривина” ние не Нека го наречем по друг начин.
Триъгълникът е фигура, която е хомеоморфна на окръжност и ограничена от три най-къси дъги. Самите най-къси дъги се наричат страни, а точките, в които се събират по двойки, се наричат върхове на триъгълника.
Вътрешна кривина се определя първо за основните множества - точки, отворени най-къси дъги и отворени триъгълници - както следва.
Ако M е точка и е пълният ъгъл около него на повърхността, тогава вътрешната кривина M е равна на .
Ако M е отворен най-кратък път, т.е. най-кратък с изключени краища, тогава .
Ако M е отворен триъгълник, т.е. триъгълник с изключени страни и върхове, тогава , Където - ъгли на триъгълник.
За такива комплекти.
Доказано е, че така определената вътрешна кривина на елементарни множества не зависи от начина на представяне на множеството като сума от основни. Доказателството се основава на следната теорема.
Теорема: Нека P е вътрешната част на геодезичен многоъгълник с ъгли и характеристика на Ойлер . Тогава кривината P е равна на .
Очевидно вътрешната кривина на елементарни множества върху изпъкнала повърхност е адитивна функция.
Досега вътрешната кривина на изпъкнала повърхност беше дефинирана само за елементарни множества. Нека го дефинираме за затворени множества като точната ниска стойност на вътрешните кривини на елементарни множества, съдържащи дадено затворено множество. И накрая, за всяко Борелово множество ние дефинираме вътрешната кривина като върховната сума на вътрешните кривини на затворените множества, съдържащи се в него.
Спомнете си, че множествата на Борел са тези, които са получени от затворени и отворени множества, като се използва не повече от изброим набор от операции за обединение и пресичане. Очевидно обединението на изброимо множество от Борелови множества ще бъде Борелово множество.
Фактът, че определението за присъща кривина за затворени и борелови множества като цяло не противоречи на въведената по-рано дефиниция за присъща кривина за елементарни множества, се гарантира от следната фундаментална теорема.
Теорема: Вътрешната кривина на всяко Борелово множество върху изпъкнала повърхност е равна на външната му кривина, т.е. площ на сферичното изображение.
3 Специфична кривина на изпъкнала повърхност
Всяка област G на изпъкнала повърхност има определена площ S(G) и кривина . Поведение се нарича специфична кривина на област G. Ако за всички области G е ограничена до определена константа, тогава такава повърхност се нарича повърхност с ограничена кривина.
Свойството на повърхността да има ограничена специфична кривина се запазва при преминаване към границата. Ето защо е валидна следната теорема.
Теорема: Ако последователност от изпъкнали повърхности с равномерно ограничени специфични кривини се събира към повърхността F, тогава тази повърхност е повърхност с ограничена кривина.
Доказателството се основава на теоремите за сближаване на области и кривини на сходяща серия от изпъкнали повърхности.
Специфична кривина на изпъкнала повърхност в точка X, т.е. лимит , когато областта G се свие до точка X, се нарича Гаусова кривина на повърхността в тази точка. Лесно е да се докаже, че ако Гаусовата кривина съществува във всяка точка от повърхността, тогава тя е непрекъсната.
Повърхностите с ограничена кривина имат редица свойства на правилните изпъкнали повърхности. По-специално, от всяка точка на изпъкнала повърхност с ограничена кривина във всяка посока е възможно да се начертае най-краткият път на разстояние, което зависи само от специфичната кривина на повърхността.
Наличие на най-кратък път от дадена точка във всяка посока по дължина ви позволява да въведете полярни координати в близост до тази точка . Ако в допълнение повърхността има определена Гаусова кривина във всяка точка, тогава метриката на повърхността в параметризираната околност може да бъде определена от линейния елемент , където коефициентът G е непрекъсната функция, два пъти диференцируема по отношение на r. Връзката между този коефициент и гаусовата кривина на повърхността се установява по добре известната формула.
Ако гаусовата кривина на повърхността е постоянна и по-голяма от нула, тогава, както е лесно да се види, коефициентът G, удовлетворяващ уравнението , трябва да изглежда като .
Следователно, такава повърхност е локално изометрична на сфера с радиус .
Ако в триъгълник върху изпъкнала повърхност специфична кривина , то неговите ъгли не са по-малки (не са по-големи) от съответните ъгли на триъгълника със същите страни на сфера с радиус .
Ако в триъгълник върху изпъкнала повърхност специфична кривина , тогава площта S на този триъгълник не е по-малка (не повече) от площта на триъгълника със същите страни на сферата на радиуса . Освен това има оценки:
ако е в триъгълник специфична кривина и
ако е в триъгълник специфична кривина.
Позволявам И - две най-къси линии, излизащи от точка O върху изпъкнала повърхност. Позволявам И - променливи точки на И , , , И - ъгъл в триъгълник със страни , обратната страна , на сферата радиус . Казват, че метриката повърхността удовлетворява условието за K-изпъкналост или е K-изпъкнала, ако за всяка най-къса дъга И ъгъл е ненарастваща функция във всеки интервал , , в който има най-кратък . Казват, че метриката удовлетворява условието за K-вдлъбната форма или е K-вдлъбната, ако е ненамаляваща функция на в същия интервал (фиг. 15). Важи следната теорема.
Теорема: Ако върху изпъкнала повърхност специфичната кривина , тогава условието за K-изпъкналост (K-вдлъбнатост) е изпълнено на тази повърхност.
Точките върху изпъкнала повърхност могат да бъдат три вида: конични, където допирателният конус не се изражда и следователно общият ъгъл е по-малък , оребрени - с допирателен конус, израждащ се в двустенен ъгъл, и плоски, при които допирателният конус се изражда в равнина. Очевидно не може да има конични точки върху повърхност с ограничена кривина, тъй като в такива точки специфичната кривина е равна на безкрайност. Оребрените точки могат да бъдат и върху повърхност с ограничена кривина. В сила е обаче следната теорема.
Теорема: Ако на изпъкнала повърхност специфичната кривина на всеки достатъчно малък регион, съдържащ точка А, не надвишава някакво постоянно число, тогава точка А е или гладка, или прав ръб на повърхността минава през нея.
Следователно, като следствие, се оказва, че затворена изпъкнала повърхност с ограничена кривина е гладка. Безкрайна пълна изпъкнала повърхност с ограничена кривина, която не е цилиндър в нито една крайна част, е гладка.
Ако сегмент от права линия минава през точка А на изпъкнала повърхност, тогава върху повърхността има произволно малки области, съдържащи точка А и имащи произволно малка специфична кривина.
Следователно, ако специфичната кривина на изпъкнала повърхност е в положителни граници за всички области на повърхността, тогава такава повърхност е гладка.
4 Негъвкавост на сферата
Достатъчно малко парче повърхност винаги може да бъде подложено на промяна във формата, която запазва дължината му. Това не важи за повърхността като цяло. Още през 1838 г. Миндинг излага като предположение твърдението, че повърхността на една сфера като цяло има твърдост. Но едва през 1899 г. Либман обосновава това твърдение. Тъй като според теоремата на Гаус при изометрични преобразувания мярката на кривината остава непроменена, теоремата на Либман може да се формулира по следния начин: сферата е единствената затворена повърхност, която има постоянна кривина.
Ако не въвеждате ограничителни изисквания за коректност, то това твърдение очевидно е невярно. Всъщност, ако отрежем сегмент от него от сферата и заменим този сегмент с неговия огледален образ спрямо равнината на сечението, тогава ще получим „намачкана“ сфера, която, въпреки че има постоянна мярка на кривина, има ръб. Отсега нататък ще приемаме, че имаме работа с аналитични повърхности, които са правилни навсякъде.
Ако вземем нейните линии на кривина като параметрични линии на повърхнина, тогава от формулите за главните кривини
поставяйки ги на първо място и тогава получаваме:
. (1)
За реципрочни ще имаме:
. (2)
Използване на формули на Кодаци на формата
и формули (2) получаваме , (3)
. (4)
Когато доказваме теоремата на Либман, можем да приемем, че . Всъщност случаят е изключено, тъй като тези повърхности имат праволинейни генератори и следователно са очевидно незатворени повърхности. По същия начин не може да съществува затворена повърхност, чиято кривина е отрицателна навсякъде: . Наистина, в най-високата точка на такава повърхност мярката на кривината трябва да е положителна: . Така остава да се разгледа само случаят , и в този случай трансформацията по подобие винаги може да се направи или, което е същото, .
Ако на нашата повърхност връзката е валидна навсякъде , тогава всички точки от повърхността са заоблени точки и следователно имаме сфера. Ако вземем повърхност, различна от сфера и получена чрез огъване на последната, тогава на такава повърхност със сигурност трябва да съществуват точки, за които . Можем да считаме и двете от тези величини за непрекъснати функции; поради затвореността на повърхността и двете величини И достигат максимум на повърхността. Един от тези максимуми във всеки случай е по-голям от 1. Нека например стойността достига до точката максимум, който е по-голям от 1. Тогава за някаква околност на точката ние имаме: , и величина в точката достига минимум. защото не е закръглена точка, тогава в нейната близост има правилна мрежа от линии на кривина.
Поради връзката можем да напишем уравнения вместо формули (3)-(4):
. (5)
Интегрирайки ги, получаваме:
. (6)
Тъй като елементите на дъгата от линии на кривина И изразени с формули , , тогава имаме , и формули (6) поради отношенията дай: в близост до точката.
Тъй като в точката величина достига максимум, а стойността - минимум, тогава в този момент трябва да са налице следните условия:
След това формули (3) и (4) ще ни дадат: . (7)
Заместване във формулата на Гаус
получаваме за целта:
Дясната страна на тази формула, поради отношенията (7), е отрицателна, докато лявата страна, според нашето предположение, е положителна и равна на 1. Така че предположението, че нашата повърхност не е сфера, води до противоречие. Доказателството е пълно.
Полученият резултат може да се формулира и по следния начин: вътре в част от повърхност с постоянна положителна кривина, за точка, която не е закръглена точка, нито един от основните радиуси на кривина не може да има нито максимална, нито минимална стойност.
Ако произволно малък отвор се изреже в повърхността на сферата, тогава повърхността може да бъде извита.
5 Сфера като единствената овална повърхност с постоянна средна кривина
Теорема, подобна на предишната, също е в сила, ако изискваме вместо мярката за кривина на повърхността, средната кривина да бъде постоянна:
Тази теорема е доказана и от Либман. Затворена изпъкнала повърхнина, която ще приемем, че е навсякъде правилна и аналитична и освен това има положителна мярка на кривина навсякъде, ще наричаме овална повърхнина. Тогава теоремата може да се формулира по следния начин: сферата е единствената овална повърхност, която има постоянна средна кривина.
Тази теорема може да се редуцира до предишната с помощта на техниката, посочена от Боне. За целта е необходимо първо да се установи следното твърдение: сред повърхности, успоредни на някаква повърхност с постоянна положителна кривина, има такава, чиято средна кривина е постоянна и обратно.
Позволявам има повърхност, за която , остави има средна кривина . Наистина, за линии на повърхностна кривина
Линии на повърхностна кривина , защото
Доказателството на прякото твърдение е пълно.
Нека докажем обратното твърдение, т.е. сред повърхности, успоредни на някаква повърхност с постоянна средна кривина, съществува повърхност, чиято гаусова кривина е постоянна.
Имаме овална повърхност, чиято средна кривина удовлетворява уравнението , А е единичният вектор на неговата нормала. След това повърхността, успоредна на него има гаусова кривина . Това следва от следното разсъждение. За линии на повърхностна кривина имаме според формулите на Родригес:
Линии на повърхностна кривина съответстват на линиите на повърхностната кривина , защото . Съответните главни радиуси на кривина са свързани със съотношението . Следователно по силата на връзката имаме:
Доказателството е пълно.
Теоремата за твърдостта на сфера може да бъде разширена в намален обем до произволни овални повърхности. Ние също дължим това разпространение на Либман. Теоремата гласи следното: ако промяната, на която претърпява една овална повърхност, трябва да бъде непрекъсната и изометрична, тогава тази повърхност може да се движи само като твърдо тяло.
3. Седлови повърхности
1 Основни понятия и свойства
Седловините в известен смисъл са противоположни по свойства на изпъкналите повърхности. Подобно на изпъкналите повърхности, те могат да бъдат определени чисто геометрично и в нормалния случай имат проста аналитична характеристика - неположителността на гаусовата кривина.
Нека F е повърхността, определена от потапянето двумерен колектор V . Казва се, че равнината P отрязва гърбицата от F, ако сред компонентите на прообраза на множеството F\P в има компонент G с компактно затваряне. Част повърхност F, съответстваща на този компонент на G, се нарича гърбица. Очевидно гърбица ще бъде повърхност, която има граница , лежаща в равнината P. Примери за гърбици са показани на фиг. 16.
Повърхност F в се нарича седло, ако не позволява гърбиците да бъдат отсечени от която и да е равнина. Примери за седлообразни повърхности са еднослоен хиперболоид, хиперболичен параболоид, всяка линейчата повърхност, катеноид и др.
От определението следва, че сред седловите повърхности в без затворени повърхности.
Дефиницията на седловидни повърхности не е свързана, както в случая с изпъкнали повърхности, с никакви изисквания за редовност. Това дава възможност да се изследват неправилни повърхности на седлото.
Теорема: За да има повърхност от клас F V е седло, е необходимо и достатъчно във всяка точка X от повърхността F нейната гаусова кривина K(X) да е неположителна.
Доказателство.
Необходимост. Нека F е седлова повърхност. Нека приемем, че в момента Гаусова кривина . След това малко квартал точки на F лежи от едната страна на допирателната равнина T към F в точката , и редът на седлото е равно на 0. Всяка равнина , успореден на T, достатъчно близо до T и лежащ с от едната страна на Т, отрязва върха от F, което е невъзможно (фиг. 17).
Следователно навсякъде е на F.
Адекватност. Позволявам навсякъде по F. Да приемем, че равнината P отсича от F гърбицата Φ с границата . Комплект от F компактен в . Следователно можем да вземем елиптичен параболоид P, от който P отрязва такава гърбица , че F се намира между и P, и - празен комплект (фиг. 18). Нека разгледаме семейство параболоиди, получени от P чрез афинна компресия към равнината P. В това семейство има параболоид , което има допирна точка с Ф , но F се намира между P и върха , отсечена от Ф с равнина Р. В точката повърхности F и докосване и всички нормални изкривявания на F и в този момент имат същия знак. Следователно в точката Гаусова кривина . Получихме противоречие с условията на теоремата. Теоремата е доказана.
Следствие: На всяка гърбица на правилна повърхност има точка, в която Гаусовата кривина е положителна.
Нека сега да преминем към конструирането примери за пълни повърхности с отрицателна гаусова кривина, чиято характеристика на Ойлер може да приеме всякаква стойност . Освен това сред конструираните примери има повърхности от всякакъв вид. Методът за конструиране на такива повърхности е посочен от J. Hadamard през 1898 г.
Отбележете първо, че ако F е хиперболичен параболоид, тогава , и ако F е еднолистов хиперболоид, тогава . Сега ще построим повърхност F, за която .
Нека вземем два еднолистови хиперболоида на революцията И дадени от уравненията
Хиперболоиди И се пресичат в равнината Q: чрез хипербола. Нека повърхността получен от И както следва: от , ; от частта, лежаща в двустенния ъгъл, се отрязва , ; останалите части са залепени по клона хиперболи , лежаща в горната полуравнина на равнината Q (фиг. 19). заедно повърхност има седловиден ръб, а под равнината P: на другия клон на хиперболата - самопресичане.
Изгладете ръба на повърхността . R самолет: кръстове над сегмента по кривата , дадено от уравнението
(3)
Над сегмента нека зададем функцията
(4)
така че равенствата да са изпълнени
(5)
Коефициенти се определят от равенства (5). На интервала нека зададем функцията
(6)
От равенства (3)-(6) следва, че И . Лесно е да се изчисли това . В групата U: на равнината P дефинираме функцията
. (7)
Неговата графика ще бъде повърхността отрицателна кривина, т.к
. (8)
Над лентата : повърхност съвпада с хиперболоида , и над лентата : - с хиперболоид . Следователно, замяна на част от повърхността над лентата U , лежаща над равнината P, повърхност , получаваме повърхността , във всяка точка на което Гаусовата кривина е отрицателна. Повърхността F има характеристика на Ойлер.
Очевидно е, че чрез увеличаване на броя на първоначалните хиперболоиди и изглаждане на различен брой получени ръбове е възможно да се получи повърхност F на всяка характеристика на Ойлер и всякакъв вид с произволен брой точки в безкрайност (Фиг. 20) Регулярността на изглаждането може да се увеличи до клас поради последваща апроксимация чрез средни функции.
За изглаждане на плоските ръбове на седалковите повърхности, E.R. Rosendorn разработи редица общи методи. През 1961 г. той конструира пример, който опровергава хипотезата, считана за много правдоподобна дотогава, че всяка пълна повърхност на седлото в ще бъде неограничен. Конструирането на такъв пример изисква серия от трудоемки изчисления. Без да ги възпроизвеждаме тук, представяме доста подробна диаграма на конструкцията на примера на ER Rosendorn.
Нека вземем числова последователност със следните свойства:
(9)
Да вградим система от концентрични сфери с радиуси и център във фиксирана точка O. Граница за сфера S има радиус R. Нека построим in графика G, състояща се от сегменти с права линия и имаща следните свойства:
) графът G е хомеоморфен на графа Г - универсалното покритие на букет от две окръжности;
) ранг възли графики G лежат върху сферата (предполагаме, че);
) всякакви четири точки - краищата на четири сегмента, излизащи от един възел графика , - ще бъдат върховете на тетраедъра, вътре в който се намира възелът ; тетраедърът, съдържащ точката, е правилен;
) дължина на всяка връзка с ранг колона G, т.е. връзка, свързваща рангов възел с ранг на възел, повече ;
) графът G няма самосечения.
Графика G може да бъде построена. Обърнете внимание, че условие 4) показва, че ъглите между връзките от ранг и радиуси на сфери , привлечени към края си, склонни да , Кога . От съотношения (9) следва, че дължината на начупената линия , свързващ точката с О, стреми се , когато точка А отива в сфера S, т.е. графиката G е пълна по отношение на своята вътрешна метрика. Графика G е като "скелет", около който ще бъде изградена необходимата пълна повърхност на седлото. Тази повърхност се състои от подобни части. Нека опишем структурата на такава част. Вземете правилен тетраедър T с върхове в точките . Нека запишем четири конуса в T с върхове в точки , чиито водачи ще бъдат окръжности, вписани в лицето, противоположно на върха . Да вземем конус и през ребрата Нека начертаем равнини, разделящи наполовина съответните двустенни ъгли на тетраедъра T. Тези равнини ще отрежат от някаква част с връх в точка , ограничена от три дъги от елипси с краища в центровете на лицата (фиг. 21). Частите се определят по подобен начин , , конуси , , . Нека изградим повърхност.
Повърхност има четири конични точки и шест плоски седловидни ребра, разположени по краищата на повърхностите . Ако от премахване на точки и изглаждаме плоските седлови ръбове, тогава можем да получим гладка седлова повърхност P, която има четири гранични точки (фиг. 22).
Сега на всеки линк на графика G фиксираме някаква точка . Четири точки , лежащ във връзки , имащи общ връх , ще бъдат върховете на тетраедъра . Позволявам е афинна трансформация, която приема T в , А . Нека изградим "повърхност"
. (10)
(Няколко няма да бъде повърхност, тъй като точките нямам на съседство хомеоморфно на окръжността.) В околността на всяка точка оправете "повърхността" , заменяйки част от тази „повърхност“ със седловидна пръстеновидна повърхност, която се докосва . След като направихме всички такива замествания, получаваме желаната пълна гладка повърхност на седлото F, разположена вътре в сферата S (фиг. 23).
Горните конструкции могат да бъдат леко модифицирани и получени в пълна повърхност на седлото , лежаща вътре в S, чиято гаусова кривина изчезва само върху изброимо множество от изолирани точки, съответстващи на центровете на лицата на тетраедрите.
През 1915 г. S.N. Bernstein изследва структурата на пълни седловидни повърхности, дадени от уравнението над цялата равнина.
Теорема 1: Нека повърхността F е дадена от уравнението
, (11)
Където и определени на цялата равнина . Ако гаусовата кривина K на повърхността P е неположителна и има точки, в които K<0, то
. (12)
При доказването на тази теорема всъщност се използва само формата на седлото на повърхността F. Това позволи на Г. М. Аделсън-Велски да докаже следното обобщение на теоремата на С. Н. Бърнщайн.
Теорема 2: Нека повърхността на седлото F е навътре дадено от уравнението , където е непрекъсната функция определени на цялата равнина . Тогава ако , тогава F е цилиндрична повърхност.
В допълнение, S.N. Bernstein получава следното обобщение на теорема 1.
Теорема 3: Ако повърхността F удовлетворява условията на Теорема 1, тогава е възможно да се уточни такава това неравенство
не е възможно за всички , каквото и да е даденото число.
Като приложение на теорема 1, представяме теоремата на Бърнщайн за минимални повърхности в . Спомнете си, че минимална повърхност е повърхност, на която средната кривина е .
Теорема 4: Ако минималната повърхност определени по цялата равнина уравнение , тогава F е равнина.
2 Неограничени седалкови тръби
Тъй като в няма затворени седлови повърхности, тогава въпросът за неограничеността на пълните седлови повърхности се свежда до получаване на достатъчни условия за неограничеността на седловините в . Че има ограничени седлови тръби , показва примерът на Е. Р. Розендорн.
Нека да преминем към специален клас седлови тръби - седлови рога. А именно, по-долу ще докажем теоремата, че в неограничен е всеки правилен седловиден рог Т. Установяването на този резултат попада в два случая, различни по метода на доказване. Първо, разглеждаме такъв рог Т, на който е точната долна граница на дължините на коланите и след това клаксона, за който . Ако , тогава рогът T се нарича остър, а ако , тогава неостър.
Теорема 5 (Yu.D. Burago): Ако T е седловиден рог от класа V И , тогава рогът T е неограничен в .
Теорема 6 (A.L. Werner): Правилно остро седло (клас ) рог Т в не е ограничено.
За да докажем тази теорема, ще са необходими следните леми.
Лема 1: Особена точка A върху ограничен остър седловиден рог T не може да бъде отсечена.
Лема 2: Нека F е пълна повърхност или тръба , дадено -потапяне f: F . Ако неориентираната сферична карта :F по отношение на някое непразно отворено множество G има множественост не повече , след това множеството от всички гранични точки за всички възможни разминаващи се последователности никъде не е плътен в G и F е неограничен в .
Доказателство на теорема 6. Да приемем, че T е ограничено в . Тогава, съгласно лема 1, сингулярната точка A на рога T не е отсечена и T A ще бъде седловидна повърхност с ръб L и една особена точка - точка A.
Можем да приемем, че ръбът на рога T ще бъде крива L, състояща се от краен брой плоски изпъкнали дъги , . Такава крива L може да бъде конструирана от изпъкнали дъги на нормални участъци от рога T, които не вървят в асимптотични посоки. За всяка равнина P в задайте П L има най-много компонент, тъй като всяко множество P има най-много два компонента.
Нека покажем, че картографирането има крайна кратност.
Тъй като точка А не е отрязана, тогава границата всеки компонент G от комплекта или има дъга върху окръжност Г= , и следователно общия брой компоненти в И за всякакви И не повече . По-специално, до точката O в комплектите И пасва не повече от компонент, т.е. точка A може да се разглежда на T като седлова точка, в която редът на седлото не е по-висок от .
Фиксиране на някаква посока . Нека T лежи между равнините И , . Нека означим с брой компоненти на комплекта . очевидно, , А . Ще увеличим от преди и следете за промени . Значение се увеличава с 1 поради появата на нов компонент всеки път локално поддържащи L по отношение на някакъв компонент , и в близост до компонента кривата L е отгоре , т.е. в минималната точка на проекцията на кривата L върху . Означаваме броя на тези точки на L с . очевидно, .
Намаляване на стойността става пред всички , когато самолетът докосва T, по едно за всяка точка на контакт и при , Кога минава през точка А. В последния случай намалява с , Където - брой компоненти на комплекта , на чиято граница лежи точка О.
Ако през означаваме броя на точките на T, включително точките на L, в които допирателните равнини към T са ортогонални на , получаваме, че
следователно
Следва, че има на кратността не е по-висока . По лема 2 рогът на T трябва да е неограничен. Имаме противоречие. Теоремата е доказана.
Теореми 5 и 6 предполагат общ резултат за седловината.
Теорема 7: Правилен седловиден рог е неограничен в .
Тази теорема ни позволява да проучим подробно външната структура на рога на седлото. Това проучване е проведено от A.L. Werner.
Лема 3: Минимизираща последователност от колани на обикновен седлов рог се разминава в , т.е. не съдържа никакви ограничения подпоследователности.
Лема 4: Нека T е правилен седловиден рог в , - минимизиране на последователността на коланите на T и A - всяка фиксирана точка в . Ако точката , след това всяка последователност от сегменти се събира към някакъв лъч при .
Лема 5: Правилният седлов рог е външно завършен , т.е. всяка последователност от точки, разминаващи се на клаксона, се разминава при .
Лема 6: Пуснете рога на Т вътре отговаря на условията, формулирани по-горе. Ако изпъкнала крива - граница , тогава T лежи вътре в цилиндъра C с водач и генератори, успоредни на лъча.
Теорема 8: Нека T е правилен седловиден рог в . Тогава за всяка точка А и всяка последователност от точки , разминаващи се в Т, сегменти се събират към определен лъч - посоката на рога Т. Рогът Т лежи вътре в затворен цилиндър, чиито образуващи са успоредни на лъча.
Теорема 9: Нека T е правилен седловиден рог в . Тогава, ако въртенето на клаксона , след това комплекта ще бъде кръг голям кръг върху единичната сфера , чиято равнина е перпендикулярна на направлението на рога Т. Ако , тогава или , или ще бъде дъга на , не по-малко от полукръг.
Забележка: Пример за пълна повърхност F с отрицателна кривина, имаща рог, за който , дадени в цилиндрични координати уравнение показва че може да бъде полукръг (фиг. 24). Повърхността F има едновалентен сферичен образ. Нека отбележим също, че ако , тогава плоските пояси на T имат самопресичания.
3.3 Проблем с платото
Проблемът на платото се формулира по следния начин: дадена е затворена крива. Необходимо е да се начертае повърхност с минимална площ през тази извита повърхност. На желаните повърхности трябва да има връзка . Уравнението представлява диференциалното уравнение на екстремумите на нашия вариационен проблем. Повърхности с еднакво нулева средна кривина, тъй като те са решения на проблема с минималното плато, се наричат минимални повърхности. Изследванията, свързани с минималните повърхности, са извършени от Лагранж, Монж, Риман, Вайерщрас, Шварц, Белтрами, Ли и Рибокорт. Ако предварително се ограничим само до аналитични повърхности, тогава определянето на минимални повърхности може лесно да се сведе до намиране на изотропни криви. Нека въведем върху някаква извита повърхност две семейства изотропни криви, за които , като параметрични линии. Ще има , а за средната кривина получаваме:
Ако , тогава трябва да има връзка . Диференциращи съотношения , от И , ще получим И . Имайки предвид равенството , Където - единичен нормален вектор, имаме: линейно независими. Следва, че изчезва идентично. имаме, следователно, . По силата на равенството получаваме .
Намереният резултат може да се изрази по следния начин: минималните повърхности са повърхности на срязване, чиито водачи са изотропни криви. По този начин интегрирането на диференциалното уравнение се свежда до дефиницията на изотропни криви.
4 Завършени седлови повърхности със сферични изображения едно към едно
Ако правилна ориентируема повърхност F in има локално топологична сферична карта , тогава Гаусовата кривина на K върху F не променя знака. Въз основа на това A.L. Werner предложи следната класификация на сферично едновалентни седлови повърхности.
Приемаме, че повърхността F е пълна. Тогава, ако К , тогава F е изпъкнала повърхност и следователно едно към едно. Ако К , тогава F може да има всяка характеристика на Ойлер.
Нека разгледаме пълните редовни (клас ) седловидни повърхности със сферично картографиране едно към едно. Класът на такива повърхнини означаваме с E. Повърхнините от този клас се наричат сферично едновалентни седлови повърхнини.
Заедно с пълните изпъкнали повърхности сферично едновалентните седловидни повърхности образуват клас пълни повърхности със сферично картографиране едно към едно.
Лема 1: Върху сферично едновалентна седлова повърхнина няма две несвързани прости затворени геодезични.
Ще приемем, че повърхността определен в чрез потапяне f: . Тъй като F и W са хомеоморфни на региона , тогава F и W са от род нула. Следователно можем да приемем, че W ще бъде сфера , от които са премахнати краен брой точки - точки в безкрайност на многообразието W. Освен това , защото . Точки ще наричаме също безкрайните точки на повърхнината F. Всяка безкрайна точка F съответства на тръба , имайки неговата безкрайно далечна точка. Тръба може да бъде рог или чаша. Следователно, за всяка точка в безкрайността ще кажем, че съответства на рог или купа на F. Считаме тръбите на F еквивалентни, ако имат еднакви точки в безкрайността, и нееквивалентни в противен случай.
Граница сферично изображение повърхност F има същия брой компоненти , , колко точки в безкрайност има на повърхността F. Приемаме, че компонентът съответства на точка , т.е. е набор за слушалка с точка в безкрайността , и се обадете сферично изображение на безкрайна точка.
Да приемем, че точката съвпада с клаксона . Тогава много ще бъде или голям кръг на , Кога има ненулева ротация , или дъга от голям кръг, не по-малък от полукръг, когато .
Тъй като комплектите двойки нямат общи точки, тогава от горното и свойството на сферичния образ на геодезическа следва
Лема 2: На повърхността може да има най-много една точка в безкрайност, съответстваща на клаксона с ненулево въртене. Ако има такава точка, тогава останалите точки в безкрайност на повърхността F съответстват на купи и няма проста затворена геодезическа на F.
Нека разгледаме допустимите случаи за F въз основа на възможния брой нееквивалентни рога или купи на F.
). Повърхнината F е хомеоморфна , има уникална точка в безкрайността , и тази точка съответства на купата. Пример за това е хиперболичен параболоид (фиг. 25).
2) . Повърхнина F е хомеоморфна на цилиндър и има две точки в безкрайност И . Поне един от тях отговаря на купа. Следователно са възможни следните случаи:
а) Всяка точка в безкрайност И съответства на купа, пример: еднолистов хиперболоид (фиг. 26);
б) Една точка в безкрайност, да речем точка , съответства на рог с ненулева ротация и на точка - купа. Пример: повърхност F: . В такъв случай - голям кръг на , и следователно лежи в едно полукълбо, ограничено от .
в) Точка съответства на клаксона на нулево въртене и на точката - купа. Пример: повърхност, определена от уравнение . Повърхнина от разглеждания тип винаги има самопресичания.
) . Трябва да има купа на повърхност F. Но няма две еквивалентни купи на F. По лема 2 F също не може да има рог с ненулево въртене, тъй като F има геодезичен цикъл, хомотопен на поясите на купата на повърхността F. Следователно, в разглеждания случай, една точка в безкрайността на повърхността F съответства на купата, а другите две съответстват на роговете с ненулево въртене.
) . Ако F имаше поне една купа, тогава щеше да има два несвързани геодезични цикъла върху F: единият от тях би бил хомотопен на поясите на тази купа, а другият би разделил една двойка точки в безкрайност на F от другата. Това е невъзможно по лема 1. Следователно няма чаши на F и по лема 2 всички рогове могат да имат само нулева ротация. Фактът, че такива повърхности не съществуват, е доказан от П. Ш. Речевски и С. З. Шефел.
По този начин повърхността може да принадлежи само към един от петте изброени подкласове: 1), 2a), b), c) и 3), и все още не са намерени примери за повърхности от подклас 3).
Сред повърхностите на тези подкласове най-простите и геометрично ясни свойства са тези, които имат рог на ненулево въртене, т.е. повърхности от подклас 2b). Нека разгледаме такава повърхност.
Теорема: Нека F е сферично едновалентна седлообразна повърхност с рог с ненулева ротация. Ако - Декартови координати в и ос има посоката на повърхностния рог F, тогава в тези координати F може да се даде от уравнението , и домейнът за указване на функцията - проекция на F върху равнина P: - ще има площ , където M е ограничено затворено изпъкнало множество върху P, съответстващо на безкрайно отдалечената точка на рога на повърхността F.
Доказателство. Ще приемем, че F е дадено чрез потапяне , и , точка съответства на рога, а точката - повърхност на купа F. Сферично изображение точка в безкрайността рогата ще бъдат екватора на сферата . Ние вярваме, че F е ориентирано така, че неговият сферичен образ лежи в горната полусфера на сферата .
Нека равнината Q е успоредна на оста z и (Q) е пълният обратен образ на множеството F Q в W. Равнината Q не може да бъде допирателна към F. Следователно компонентите на множеството (Q) нямат точки на разклонение. Сред тези компоненти няма затворени криви, тъй като изображението на такъв компонент върху F би имало вертикална допирателна линия, а след това F би имало вертикална (т.е. успоредна на оста z) допирателна равнина, което е невъзможно. Следователно компонентите (Q) може да има само прости дъги с краища в точки И . Изображенията на тези компоненти върху F ще бъдат прости незатворени криви, пълни по отношение на F. Те нямат вертикални допирателни и следователно всяка такава крива е уникално проектирана върху P.
Позволявам - компонент (Q). От свойствата на седловината (теорема 8, параграф 2.2) следва, че не може да има и двата края , така че са възможни два случая.
а) Двата края лежат в една точка . След това чрез проекция ще има права линия върху P, тъй като s е безкрайна по дължина и в двете посоки, а допирателните към s образуват ъгли с P, които не са по-големи от определено .
б) дъга идва от точка към основния въпрос . В този случай s отива към рога в една посока и следователно проекцията му върху P от тази страна е ограничена, а в обратната посока проекцията на s върху P отново е неограничена, т.е. в този случай проекцията на s върху P ще бъде лъч.
Сега ще пресечем F с равнини Р( ): z= . Сред такива равнини може би само една ще бъде допирателна към F. Следователно има такава за какво в изобилие , Където , компонентите нямат точки на разклонение и един от компонентите ще бъде цикъл, съдържащ точка вътре (Теорема 8, параграф 2.2). На F цикъл ще има колан , отрязвайки рога на T от F . Тъй като F не позволява отрязване на върховете, тогава влиза само един компонент може да е цикъл. Тъй като хорн Т отива в посоката на оста z, след това навътре няма други компоненти на комплекта . Нека затворена изпъкнала крива и C - изпъкнал цилиндър с G водач и образуващи, успоредни на оста z. Хорн Т се намира вътре в C . Нека означим с част от повърхността F, разположена извън C.
От горните свойства на проекцията на кривата върху P е лесно да се проследи, че проекцията на частта на П ще има набор P\ .
Нека сега разгледаме набора . Позволявам е негов обратен образ в W. Set компактен в W. Следователно неговите компоненти могат да бъдат само цикли. Образите на тези цикли върху F не могат да имат вертикални допирателни и следователно всички криви от имат смисъл вътре , т.е. техните изображения ще бъдат колани на F. Ако има повече от един компонент, тогава ще има пръстенна област U върху F, чиято граница ще се състои от две затворени криви, лежащи върху C . Очевидно U лежи вътре в C , тъй като U не позволява отрязване на върховете. Позволявам - проекция на U върху P . Нека вземем точка X, лежаща на границата на множеството , но не и на G и начертайте права линия през X успоредна на оста z. Направо ще бъде допирателна към F и следователно има вертикална допирателна равнина на U, така че p
Всяка образуваща на цилиндър С кръстове , а оттам и F, при същия брой точки. Това число (означаваме го с ) е равен на броя на оборотите около цилиндъра. Това ще бъде същото за всеки цилиндър C, вътре в който се намира C , и следователно еднакви за всички, когато .
Плавни цикли И са хомотопни в W, и лежи вътре . Позволявам - затворен регион в W между И , а D е неговият образ върху F. Множеството D може да бъде разделено на краен брой такива части , всеки от които е уникално проектиран върху P . Нека се свържем вътре извивки И еднопараметрично семейство гладки криви , Където , , , и при извивки се сближават с заедно с допирателните. През нека обозначим образите на кривите върху F.
Позволявам И - прогнози И на П . Дъгова крива , лежи вътре , няма самопресичания. Следователно, с последователно преминаване на кривите въртене на полетата на допирателната крива всеки има едно и също нещо и е равно на въртенето на допирателното поле на кривата , т.е. равно на . И след това за плоска крива въртенето на външното нормално поле също е равно на . Но нормално да са проекции върху P нормали към F в съответните точки на кривата . Тъй като сферичното изображение на кривата ще има Йорданова крива , за достатъчно големи възможно най-близо до екватора , след това завъртането на нормалното поле към е равно на +1, т.е. . И това означава, че F е проектирано едно към едно върху P.
Проекция на F върху P или, което е същото, на P ще има такава площ , това е затворено множество ще бъдат просто свързани и ограничени. Множеството M ще бъде изпъкнало. В противен случай би било възможно да се отреже от F чрез вертикалната равнина Q част от U, ограничена от плоска крива L, чийто обратен образ в W има двата края в точката , което е невъзможно, както беше доказано по-горе. Така че M е изпъкнал. Теоремата е доказана.
Заключение
В тази статия разгледах теоретичните аспекти, свързани с повърхности с постоянен тип точки, по-специално въпроси, свързани с изпъкнали и седловидни повърхности. Запознах се с класификацията на точките върху правилна повърхнина, с някои свойства на външната геометрия на изпъкнали и седловидни повърхнини и разгледах връзката на повърхнини с постоянен тип точки с теорията на сферичните изображения и теорията на кривината.
Работният материал може да се използва от студенти при получаване на висше професионално образование, както и от преподаватели за провеждане на учебни занятия.
Библиография
Александров А.Д. Вътрешна геометрия на изпъкнали повърхнини. - М.: ОГИЗ, 1948.
Bakelman I.Ya., Werner A., L., Kantor B.E. Въведение в диференциалната геометрия "общо". - М.: Наука, 1973.
Blaschke V. Диференциална геометрия. - М.: ОНТИ, 1935.
Вернер А.Л. Относно външната геометрия на най-простите пълни повърхности с неположителна кривина. - М., 1968.
Дубровин А.А. За редовността на изпъкнала повърхност с правилна метрика в пространства с постоянна кривина. - Укр., 1965.
Дубровин Б.А., Новиков С.П., Фоменко А.Т. Съвременна геометрия. - М.: Наука, 1979.
Ефимов Н.В. Появата на сингулярности върху повърхности с отрицателна кривина. - М., 1964.
Kohn-Fossen S.E. Гъвкавост на повърхността "като цяло". - М .: UMN, 1936.
Мишченко А.С., Фоменко А.Т. Кратък курс по диференциална геометрия и топология. - М.: ФИЗМАЛИТ, 2004.
Норден А.П. Теория на повърхнините. - М.: Гостехиздат, 1956.
Погорелов А.В. Външна геометрия на изпъкнали повърхнини. - М.: Наука
Погорелов А.В. Огъване на изпъкнали повърхности. - М.: Гостехиздат
Позняк Е.Г., Шикин Е.В. Диференциална геометрия: Първо запознаване. Изд. 2-ро, коригирано. и допълнителни - М .: Редакция URSS, 2003.
Рашевски П.К. Курс по диференциална геометрия. - М.: Гостехиздат, 1956. седло за кривина на повърхностната сфера
Розендорн Е.Р. Върху пълни повърхнини с отрицателна кривина в евклидови пространства. - М., 1962.
Http://slovari.yandex.ru/dict/bse/article/00015/74000.htm
Обучение
Нуждаете се от помощ при изучаване на тема?
Нашите специалисти ще съветват или предоставят услуги за обучение по теми, които ви интересуват.
Изпратете вашата кандидатурапосочване на темата точно сега, за да разберете за възможността за получаване на консултация.