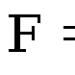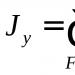Изведени са понятията за центробежни инерционни моменти. Центробежен момент на инерция. Теорема на Хюйгенс - Щайнер

Значи е едно и също навсякъде

J a = ρ ∫ (V) r 2 d V . (\displaystyle J_(a)=\rho \int \limits _((V))r^(2)dV.)

Теорема на Хюйгенс - Щайнер

Инерционният момент на твърдо тяло спрямо всяка ос зависи от масата, формата и размера на тялото, както и от положението на тялото спрямо тази ос. Според теоремата на Хюйгенс-Щайнер инерционният момент на тялото Джспрямо произволна ос е равна на сумата от инерционния момент на това тяло J cспрямо ос, минаваща през центъра на масата на тялото, успоредна на разглежданата ос, и произведението на масата на тялото мна квадрат разстояние дмежду осите:

J = J c + m d 2 , (\displaystyle J=J_(c)+md^(2),)

Където м- общо телесно тегло.

Например инерционният момент на прът спрямо ос, минаваща през края му, е равен на:

J = J c + m d 2 = 1 12 m l 2 + m (l 2) 2 = 1 3 m l 2. (\displaystyle J=J_(c)+md^(2)=(\frac (1)(12))ml^(2)+m\left((\frac (l)(2))\right)^ (2)=(\frac (1)(3))ml^(2).)

Осови моменти на инерция на някои тела

Моменти на инерцияхомогенни тела с най-проста форма спрямо определени оси на въртене

Тяло	Описание	Позиция на оста а	Момент на инерция Я а
	Маса на материалната точка м	На разстояние rот точка, неподвижен
	Кух тънкостенен цилиндър или радиус пръстен rи маси м	Ос на цилиндъра	m r 2 (\displaystyle mr^(2))
	Плътен цилиндър или радиус диск rи маси м	Ос на цилиндъра	1 2 m r 2 (\displaystyle (\frac (1)(2))mr^(2))
	Кух дебелостенен масов цилиндър мс външен радиус r 2 и вътрешен радиус r 1	Ос на цилиндъра	m r 2 2 + r 1 2 2 (\displaystyle m(\frac (r_(2)^(2)+r_(1)^(2))(2)))
	Плътна дължина на цилиндъра л, радиус rи маси м		1 4 m ⋅ r 2 + 1 12 m ⋅ l 2 (\displaystyle (1 \over 4)m\cdot r^(2)+(1 \over 12)m\cdot l^(2))
	Кух тънкостенен цилиндър (пръстен) дълж л, радиус rи маси м	Оста е перпендикулярна на цилиндъра и минава през неговия център на масата	1 2 m ⋅ r 2 + 1 12 m ⋅ l 2 (\displaystyle (1 \over 2)m\cdot r^(2)+(1 \over 12)m\cdot l^(2))
	Прът с права тънка дължина ли маси м	Оста е перпендикулярна на пръта и минава през неговия център на масата	1 12 m l 2 (\displaystyle (\frac (1)(12))ml^(2))
	Прът с права тънка дължина ли маси м	Оста е перпендикулярна на пръта и минава през края му	1 3 m l 2 (\displaystyle (\frac (1)(3))ml^(2))
	Тънкостенна радиус сфера rи маси м	Оста минава през центъра на сферата	2 3 m r 2 (\displaystyle (\frac (2)(3))mr^(2))
	Радиус топка rи маси м	Оста минава през центъра на топката	2 5 m r 2 (\displaystyle (\frac (2)(5))mr^(2))
	Радиус конус rи маси м	Конична ос	3 10 m r 2 (\displaystyle (\frac (3)(10))mr^(2))
	Равнобедрен триъгълник с надморска височина ч, основа аи маса м	Оста е перпендикулярна на равнината на триъгълника и минава през върха	1 24 m (a 2 + 12 h 2) (\displaystyle (\frac (1)(24))m(a^(2)+12h^(2)))
	Правилен триъгълник със страна аи маса м	Оста е перпендикулярна на равнината на триъгълника и минава през центъра на масата	1 12 m a 2 (\displaystyle (\frac (1)(12))ma^(2))
	Квадрат със страна аи маса м	Оста е перпендикулярна на равнината на квадрата и минава през центъра на масата	1 6 m a 2 (\displaystyle (\frac (1)(6))ma^(2))
	Правоъгълник със страни аИ bи маса м	Оста е перпендикулярна на равнината на правоъгълника и минава през центъра на масата	1 12 m (a 2 + b 2) (\displaystyle (\frac (1)(12))m(a^(2)+b^(2)))
	Правилен n-ъгълник с радиус rи маса м	Оста е перпендикулярна на равнината и минава през центъра на масата	m r 2 6 [ 1 + 2 cos ⁡ (π / n) 2 ] (\displaystyle (\frac (mr^(2))(6))\left)
	Тор (кух) с радиус на водещата окръжност Р, радиус на генериращата окръжност rи маса м	Оста е перпендикулярна на равнината на водещата окръжност на торуса и минава през центъра на масата	I = m (3 4 r 2 + R 2) (\displaystyle I=m\left((\frac (3)(4))\,r^(2)+R^(2)\right))

Извеждане на формули

Тънкостенен цилиндър (пръстен, обръч)

Извеждане на формулата

Инерционният момент на тялото е равен на сумата от инерционните моменти на съставните му части. Нека разделим тънкостенен цилиндър на елементи с маса дми моменти на инерция dJ i. Тогава

J = ∑ d J i = ∑ R i 2 d m . (1) . (\displaystyle J=\sum dJ_(i)=\sum R_(i)^(2)dm.\qquad (1).)

Тъй като всички елементи на тънкостенен цилиндър са на едно и също разстояние от оста на въртене, формула (1) се трансформира във формата

J = ∑ R 2 d m = R 2 ∑ d m = m R 2 . (\displaystyle J=\sum R^(2)dm=R^(2)\sum dm=mR^(2).)

Дебелостенен цилиндър (пръстен, обръч)

Извеждане на формулата

Нека има хомогенен пръстен с външен радиус Р, вътрешен радиус Р 1, дебел чи плътност ρ. Нека го начупим на тънки пръстени с дебелина д-р. Маса и инерционен момент на пръстен с тънък радиус rще бъде

d m = ρ d V = ρ ⋅ 2 π r h d r ; d J = r 2 d m = 2 π ρ h r 3 d r . (\displaystyle dm=\rho dV=\rho \cdot 2\pi rhdr;\qquad dJ=r^(2)dm=2\pi \rho hr^(3)dr.)

Нека намерим инерционния момент на дебелия пръстен като интеграл

J = ∫ R 1 R d J = 2 π ρ h ∫ R 1 R r 3 d r = (\displaystyle J=\int _(R_(1))^(R)dJ=2\pi \rho h\int _ (R_(1))^(R)r^(3)dr=) = 2 π ρ h r 4 4 | R 1 R = 1 2 π ρ h (R 4 − R 1 4) = 1 2 π ρ h (R 2 − R 1 2) (R 2 + R 1 2) . (\displaystyle =2\pi \rho h\left.(\frac (r^(4))(4))\right|_(R_(1))^(R)=(\frac (1)(2 ))\pi \rho h\left(R^(4)-R_(1)^(4)\right)=(\frac (1)(2))\pi \rho h\left(R^(2) )-R_(1)^(2)\вдясно)\вляво(R^(2)+R_(1)^(2)\вдясно).)

Тъй като обемът и масата на пръстена са равни

V = π (R 2 − R 1 2) h ; m = ρ V = π ρ (R 2 − R 1 2) h , (\displaystyle V=\pi \left(R^(2)-R_(1)^(2)\right)h;\qquad m= \rho V=\pi \rho \left(R^(2)-R_(1)^(2)\right)h,)

получаваме крайната формула за инерционния момент на пръстена

J = 1 2 m (R 2 + R 1 2) . (\displaystyle J=(\frac (1)(2))m\left(R^(2)+R_(1)^(2)\right).)

Хомогенен диск (твърд цилиндър)

Извеждане на формулата

Разглеждайки цилиндър (диск) като пръстен с нулев вътрешен радиус ( Р 1 = 0), получаваме формулата за инерционния момент на цилиндъра (диска):

J = 1 2 m R 2 . (\displaystyle J=(\frac (1)(2))mR^(2).)

Плътен конус

Извеждане на формулата

Начупваме конуса на тънки дискове с дебелина dh, перпендикулярна на оста на конуса. Радиусът на такъв диск е равен на

r = R h H , (\displaystyle r=(\frac (Rh)(H)),)

Където Р– радиус на основата на конуса, з– височина на конуса, ч– разстояние от върха на конуса до диска. Масата и инерционният момент на такъв диск ще бъдат

d J = 1 2 r 2 d m = 1 2 π ρ r 4 d h = 1 2 π ρ (R h H) 4 d h ; (\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \left((\frac (Rh)(H))\right)^(4)dh;)

Интегрирайки, получаваме

J = ∫ 0 H d J = 1 2 π ρ (R H) 4 ∫ 0 H h 4 d h = 1 2 π ρ (R H) 4 h 5 5 | 0 H == 1 10 π ρ R 4 H = (ρ ⋅ 1 3 π R 2 H) 3 10 R 2 = 3 10 m R 2 . (\displaystyle (\begin(aligned)J=\int _(0)^(H)dJ=(\frac (1)(2))\pi \rho \left((\frac (R)(H)) \right)^(4)\int _(0)^(H)h^(4)dh=(\frac (1)(2))\pi \rho \left((\frac (R)(H) )\right)^(4)\left.(\frac (h^(5))(5))\right|_(0)^(H)==(\frac (1)(10))\pi \rho R^(4)H=\left(\rho \cdot (\frac (1)(3))\pi R^(2)H\right)(\frac (3)(10))R^( 2)=(\frac (3)(10))mR^(2).\end(подравнено)))

Твърда хомогенна топка

Извеждане на формулата

Нека счупим топката на тънки дискове с дебелина dh, перпендикулярна на оста на въртене. Радиусът на такъв диск, разположен на височина чот центъра на сферата, намираме го с помощта на формулата

r = R 2 − h 2 . (\displaystyle r=(\sqrt (R^(2)-h^(2))).)

Масата и инерционният момент на такъв диск ще бъдат

d m = ρ d V = ρ ⋅ π r 2 d h ; (\displaystyle dm=\rho dV=\rho \cdot \pi r^(2)dh;) d J = 1 2 r 2 d m = 1 2 π ρ r 4 d h = 1 2 π ρ (R 2 − h 2) 2 d h = 1 2 π ρ (R 4 − 2 R 2 h 2 + h 4) d h . (\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \left(R^(2)-h^(2)\right)^(2)dh=(\frac (1)(2))\pi \rho \left(R^( 4)-2R^(2)h^(2)+h^(4)\right)dh.)

Намираме инерционния момент на топката чрез интегриране:

J = ∫ − R R d J = 2 ∫ 0 R d J = π ρ ∫ 0 R (R 4 − 2 R 2 h 2 + h 4) d h = = π ρ (R 4 h − 2 3 R 2 h 3 + 1 5 часа 5) | 0 R = π ρ (R 5 − 2 3 R 5 + 1 5 R 5) = 8 15 π ρ R 5 = = (4 3 π R 3 ρ) ⋅ 2 5 R 2 = 2 5 m R 2 . (\displaystyle (\begin(aligned)J&=\int _(-R)^(R)dJ=2\int _(0)^(R)dJ=\pi \rho \int _(0)^(R )\left(R^(4)-2R^(2)h^(2)+h^(4)\right)dh=\\&=\pi \rho \left.\left(R^(4) h-(\frac (2)(3))R^(2)h^(3)+(\frac (1)(5))h^(5)\right)\right|_(0)^( R)=\pi \rho \left(R^(5)-(\frac (2)(3))R^(5)+(\frac (1)(5))R^(5)\right) =(\frac (8)(15))\pi \rho R^(5)=\\&=\left((\frac (4)(3))\pi R^(3)\rho \right) \cdot (\frac (2)(5))R^(2)=(\frac (2)(5))mR^(2).\end(aligned)))

Тънкостенна сфера

Извеждане на формулата

За да изведем това, използваме формулата за инерционния момент на хомогенна топка с радиус Р :

J 0 = 2 5 M R 2 = 8 15 π ρ R 5 . (\displaystyle J_(0)=(\frac (2)(5))MR^(2)=(\frac (8)(15))\pi \rho R^(5).)

Нека изчислим колко ще се промени инерционният момент на топката, ако при постоянна плътност ρ нейният радиус се увеличи с безкрайно малко количество дР .

J = d J 0 d R d R = d d R (8 15 π ρ R 5) d R = = 8 3 π ρ R 4 d R = (ρ ⋅ 4 π R 2 d R) 2 3 R 2 = 2 3 m R2. (\displaystyle (\begin(aligned)J&=(\frac (dJ_(0))(dR))dR=(\frac (d)(dR))\left((\frac (8)(15))\ pi \rho R^(5)\right)dR=\\&=(\frac (8)(3))\pi \rho R^(4)dR=\left(\rho \cdot 4\pi R^ (2)dR\right)(\frac (2)(3))R^(2)=(\frac (2)(3))mR^(2).\end(aligned)))

Тънък прът (оста минава през центъра)

Извеждане на формулата

Нека счупим пръта на малки фрагменти с дължина д-р. Масата и инерционният момент на такъв фрагмент са равни на

d m = m d r l ; d J = r 2 d m = m r 2 d r l . (\displaystyle dm=(\frac (mdr)(l));\qquad dJ=r^(2)dm=(\frac (mr^(2)dr)(l)).)

Интегрирайки, получаваме

J = ∫ − l / 2 l / 2 d J = 2 ∫ 0 l / 2 d J = 2 m l ∫ 0 l / 2 r 2 d r = 2 m l r 3 3 | 0 l / 2 = 2 m l l 3 24 = 1 12 m l 2 . (\displaystyle J=\int _(-l/2)^(l/2)dJ=2\int _(0)^(l/2)dJ=(\frac (2m)(l))\int _ (0)^(l/2)r^(2)dr=(\frac (2m)(l))\left.(\frac (r^(3))(3))\right|_(0) ^(l/2)=(\frac (2m)(l))(\frac (l^(3))(24))=(\frac (1)(12))ml^(2.)

Тънък прът (оста минава през края)

Извеждане на формулата

Когато оста на въртене се движи от средата на пръта към края му, центърът на тежестта на пръта се премества спрямо оста на разстояние l ⁄ 2. Според теоремата на Щайнер новият инерционен момент ще бъде равен на

J = J 0 + m r 2 = J 0 + m (l 2) 2 = 1 12 m l 2 + 1 4 m l 2 = 1 3 m l 2 . (\displaystyle J=J_(0)+mr^(2)=J_(0)+m\left((\frac (l)(2))\right)^(2)=(\frac (1)( 12))ml^(2)+(\frac (1)(4))ml^(2)=(\frac (1)(3))ml^(2.)

Безразмерни инерционни моменти на планети и спътници

Техните безразмерни инерционни моменти са от голямо значение за изследване на вътрешната структура на планетите и техните спътници. Безразмерен инерционен момент на тяло с радиус rи маси ме равно на отношението на нейния инерционен момент спрямо оста на въртене към инерционния момент на материална точка със същата маса спрямо фиксирана ос на въртене, разположена на разстояние r(равна на г-н 2). Тази стойност отразява разпределението на масата по дълбочина. Един от методите за измерването му в близост до планети и спътници е да се определи доплеровото изместване на радиосигнала, предаван от AMS, летящ близо до дадена планета или сателит. За тънкостенна сфера безразмерният инерционен момент е 2/3 (~0,67), за хомогенна топка е 0,4 и като цяло колкото по-малък е, толкова по-голяма маса на тялото е концентрирана в центъра му. Например, Луната има безразмерен инерционен момент, близък до 0,4 (равен на 0,391), така че се приема, че е относително хомогенна, нейната плътност се променя малко с дълбочината. Безразмерният инерционен момент на Земята е по-малък от този на хомогенна топка (равен на 0,335), което е аргумент в полза на съществуването на плътно ядро.

Центробежен момент на инерция

Центробежните инерционни моменти на тялото спрямо осите на правоъгълна декартова координатна система са следните величини:

J x y = ∫ (m) x y d m = ∫ (V) x y ρ d V , (\displaystyle J_(xy)=\int \limits _((m))xydm=\int \limits _((V))xy\ rho dV,) J x z = ∫ (m) x z d m = ∫ (V) x z ρ d V , (\displaystyle J_(xz)=\int \limits _((m))xzdm=\int \limits _((V))xz\ rho dV,) J y z = ∫ (m) y z d m = ∫ (V) y z ρ d V , (\displaystyle J_(yz)=\int \limits _((m))yzdm=\int \limits _((V))yz\ rho dV,)

Където х , гИ z- координати на малък елемент от тялото с обем dV, плътност ρ и маса дм .

Оста OX се нарича главната инерционна ос на тялото, ако центробежните инерционни моменти J xyИ J xzса едновременно равни на нула. През всяка точка на тялото могат да бъдат начертани три основни инерционни оси. Тези оси са взаимно перпендикулярни една на друга. Инерционни моменти на тялотоспрямо трите главни инерционни оси, начертани в произволна точка Отела се наричат основни инерционни моментина това тяло.

Главните инерционни оси, минаващи през центъра на масата на тялото, се наричат главни централни инерционни оси на тялото, а инерционните моменти около тези оси са неговите основни централни моменти на инерция. Оста на симетрия на хомогенно тяло винаги е една от основните му централни инерционни оси.

Геометрични моменти на инерция

Геометричен момент на инерция на обема

J V a = ∫ (V) r 2 d V , (\displaystyle J_(Va)=\int \limits _((V))r^(2)dV,)

където, както преди r- разстояние от елемента dVкъм оста а .

Геометричен инерционен момент на площспрямо оста - геометрична характеристика на тялото, изразена по формулата:

J S a = ∫ (S) r 2 d S , (\displaystyle J_(Sa)=\int \limits _((S))r^(2)dS,)

където интегрирането се извършва по повърхността С, А dS- елемент от тази повърхност.

Измерение JSa- дължина на четвърта степен ( d i m J S a = L 4 (\displaystyle \mathrm (dim) J_(Sa)=\mathrm (L^(4)) )), съответно мерната единица SI е 4. В строителните изчисления, литературата и асортиментите от валцувани метали често се посочва в cm 4.

Съпротивителният момент на сечението се изразява чрез геометричния инерционен момент на площта:

W = J S a r m a x. (\displaystyle W=(\frac (J_(Sa))(r_(макс))).)

Тук r макс- максимално разстояние от повърхността до оста.

Геометрични моменти на инерция на площта на някои фигури
Височина на правоъгълник h (\displaystyle h)и ширина b (\displaystyle b):	J y = b h 3 12 (\displaystyle J_(y)=(\frac (bh^(3))(12))) J z = h b 3 12 (\displaystyle J_(z)=(\frac (hb^(3))(12)))
Правоъгълно кутийно сечение с височина и ширина по външни контури H (\displaystyle H)И B (\displaystyle B), и за вътрешни h (\displaystyle h)И b (\displaystyle b)съответно	J z = B H 3 12 − b h 3 12 = 1 12 (B H 3 − b h 3) (\displaystyle J_(z)=(\frac (BH^(3))(12))-(\frac (bh^( 3))(12))=(\frac (1)(12))(BH^(3)-bh^(3))) J y = H B 3 12 − h b 3 12 = 1 12 (H B 3 − h b 3) (\displaystyle J_(y)=(\frac (HB^(3))(12))-(\frac (hb^( 3))(12))=(\frac (1)(12))(HB^(3)-hb^(3)))
Диаметър на кръга d (\displaystyle d)	J y = J z = π d 4 64 (\displaystyle J_(y)=J_(z)=(\frac (\pi d^(4))(64)))

Инерционният момент спрямо самолета

Инерционният момент на твърдо тяло спрямо определена равнина е скаларна величина, равна на сумата от произведенията на масата на всяка точка от тялото на квадрата на разстоянието от тази точка до въпросната равнина.

Ако през произволна точка O (\displaystyle O)начертайте координатни оси x, y, z (\displaystyle x,y,z), тогава инерционните моменти спрямо координатните равнини x O y (\displaystyle xOy), y O z (\displaystyle yOz)И z O x (\displaystyle zOx)ще се изрази с формулите:

J x O y = ∑ i = 1 n m i z i 2 , (\displaystyle J_(xOy)=\sum _(i=1)^(n)m_(i)z_(i)^(2)\ ,) J y O z = ∑ i = 1 n m i x i 2 , (\displaystyle J_(yOz)=\sum _(i=1)^(n)m_(i)x_(i)^(2)\ ,) J z O x = ∑ i = 1 n m i y i 2 . (\displaystyle J_(zOx)=\сума _(i=1)^(n)m_(i)y_(i)^(2)\ .)

При твърдо тяло сумирането се заменя с интегриране.

Централен инерционен момент

Централен инерционен момент (инерционен момент относно точка О, инерционен момент около полюса, полярен инерционен момент) J O (\displaystyle J_(O))е количеството, определено от израза:

J a = ∫ (m) r 2 d m = ∫ (V) ρ r 2 d V , (\displaystyle J_(a)=\int \limits _((m))r^(2)dm=\int \limits _((V))\rho r^(2)dV,)

Централният инерционен момент може да се изрази чрез главните аксиални инерционни моменти, както и чрез инерционните моменти относно равнините:

J O = 1 2 (J x + J y + J z) , (\displaystyle J_(O)=(\frac (1)(2))\left(J_(x)+J_(y)+J_(z) \точно)) J O = J x O y + J y O z + J x O z. (\displaystyle J_(O)=J_(xOy)+J_(yOz)+J_(xOz).)

Тензор на инерцията и елипсоид на инерцията

Инерционният момент на тяло спрямо произволна ос, минаваща през центъра на масата и имаща посока, определена от единичния вектор s → = ‖ s x , s y , s z ‖ T , | s → | = 1 (\displaystyle (\vec (s))=\left\Vert s_(x),s_(y),s_(z)\right\Vert ^(T),\left\vert (\vec (s) )\right\vert =1), могат да бъдат представени под формата на квадратна (билинейна) форма:

I s = s → T ⋅ J ^ ⋅ s → , (\displaystyle I_(s)=(\vec (s))^(T)\cdot (\hat (J))\cdot (\vec (s)) ,\qquad) (1)

където е тензорът на инерцията. Матрицата на тензора на инерцията е симетрична и има размери 3 × 3 (\displaystyle 3\пъти 3)и се състои от компоненти на центробежни моменти:

J ^ = ‖ J x x − J x y − J x z − J y x J y y − J y z − J z x − J z y J z z ‖ , (\displaystyle (\hat (J))=\left\Vert (\begin(array )(ccc)J_(xx)&-J_(xy)&-J_(xz)\\-J_(yx)&J_(yy)&-J_(yz)\\-J_(zx)&-J_(zy) &J_(zz)\end(array))\right\Vert ,) J x y = J y x, J x z = J z x, J z y = J y z, (\displaystyle J_(xy)=J_(yx),\quad J_(xz)=J_(zx),\quad J_(zy)= J_(yz),\quad )J x x = ∫ (m) (y 2 + z 2) d m, J y y = ∫ (m) (x 2 + z 2) d m, J z z = ∫ (m) (x 2 + y 2) d m. (\displaystyle J_(xx)=\int \limits _((m))(y^(2)+z^(2))dm,\quad J_(yy)=\int \limits _((m)) (x^(2)+z^(2))dm,\quad J_(zz)=\int \limits _((m))(x^(2)+y^(2))dm.)

Чрез избора на подходяща координатна система матрицата на тензора на инерцията може да се редуцира до диагонална форма. За да направите това, трябва да решите проблема със собствените стойности за тензорната матрица J ^ (\displaystyle (\hat (J))):

J ^ d = Q ^ T ⋅ J ^ ⋅ Q ^ , (\displaystyle (\hat (J))_(d)=(\hat (Q))^(T)\cdot (\hat (J))\ cdot (\hat (Q)),) J ^ d = ‖ J X 0 0 0 J Y 0 0 0 J Z ‖ , (\displaystyle (\hat (J))_(d)=\left\Vert (\begin(array)(ccc)J_(X)&0&0\ \0&J_(Y)&0\\0&0&J_(Z)\end(масив))\right\Vert ,)

Където Q ^ (\displaystyle (\hat (Q)))- ортогонална матрица на преход към собствената база на инерционния тензор. В правилната основа координатните оси са насочени по главните оси на тензора на инерцията и съвпадат с главните полуоси на елипсоида на тензора на инерцията. Количества J X , J Y , J Z (\displaystyle J_(X),J_(Y),J_(Z))- основни инерционни моменти. Изразът (1) в собствената си координатна система има формата:

I s = J X ⋅ s x 2 + J Y ⋅ s y 2 + J Z ⋅ s z 2 , (\displaystyle I_(s)=J_(X)\cdot s_(x)^(2)+J_(Y)\cdot s_(y )^(2)+J_(Z)\cdot s_(z)^(2),)

от което получаваме уравнението на елипсоида в собствените му координати. Разделяйки двете страни на уравнението на I s (\displaystyle I_(s))

(s x I s) 2 ⋅ J X + (s y I s) 2 ⋅ J Y + (s z I s) 2 ⋅ J Z = 1 (\displaystyle \left((s_(x) \over (\sqrt (I_(s)) ))\right)^(2)\cdot J_(X)+\left((s_(y) \over (\sqrt (I_(s))))\right)^(2)\cdot J_(Y) +\left((s_(z) \over (\sqrt (I_(s))))\right)^(2)\cdot J_(Z)=1)

и извършване на замени:

ξ = s x I s, η = s y I s, ζ = s z I s, (\displaystyle \xi =(s_(x) \over (\sqrt (I_(s)))),\eta =(s_(y ) \over (\sqrt (I_(s)))),\zeta =(s_(z) \over (\sqrt (I_(s)))),)

получаваме каноничната форма на уравнението на елипсоида в координати ξ η ζ (\displaystyle \xi \eta \zeta ):

ξ 2 ⋅ J X + η 2 ⋅ J Y + ζ 2 ⋅ J Z = 1. (\displaystyle \xi ^(2)\cdot J_(X)+\eta ^(2)\cdot J_(Y)+\zeta ^( 2)\cdot J_(Z)=1.)

Разстоянието от центъра на елипсоида до определена точка е свързано със стойността на инерционния момент на тялото по права линия, минаваща през центъра на елипсоида и тази точка:

r 2 = ξ 2 + η 2 + ζ 2 = (s x I s) 2 + (s y I s) 2 + (s z I s) 2 = 1 I s. (\displaystyle r^(2)=\xi ^(2)+\eta ^(2)+\zeta ^(2)=\left((s_(x) \over (\sqrt (I_(s))) )\right)^(2)+\left((s_(y) \over (\sqrt (I_(s)))\right)^(2)+\left((s_(z) \over (\ sqrt (I_(s))))\right)^(2)=(1 \over I_(s)).)

Аксиалният инерционен момент е равен на сумата от произведенията на елементарните площи и квадрата на разстоянието до съответната ос.

(8)

Знакът винаги е "+".

Не може да бъде равно на 0.

Имот:Приема минимална стойност, когато пресечната точка на координатните оси съвпада с центъра на тежестта на сечението.

Аксиалният момент на инерция на сечение се използва при изчисляване на якост, твърдост и стабилност.

1.3. Полярен инерционен момент на сечението Jρ

(9)

Връзка между полярните и аксиалните моменти на инерция:

(10)

(11)

Полярният инерционен момент на сечението е равен на сумата от аксиалните моменти.

Имот:

Когато осите се въртят в произволна посока, единият от аксиалните моменти на инерция се увеличава, а другият намалява (и обратно). Сумата от аксиалните инерционни моменти остава постоянна.

1.4. Центробежен инерционен момент на сечението Jxy

Центробежният инерционен момент на сечението е равен на сумата от произведенията на елементарните площи и разстоянията до двете оси

(12)

Мерна единица [cm 4 ], [mm 4 ].

Знак "+" или "-".

, ако координатните оси са оси на симетрия (пример - I-лъч, правоъгълник, кръг), или една от координатните оси съвпада с оста на симетрия (пример - канал).

Така за симетрични фигури центробежният инерционен момент е 0.

Координатни оси u И v , преминаващи през центъра на тежестта на сечението, около което центробежният момент е равен на нула, се наричат основните централни инерционни оси на сечението.Наричат ​​се главни, защото центробежният момент спрямо тях е нула, а централни, защото преминават през центъра на тежестта на сечението.

За сечения, които не са симетрични спрямо осите х или г , например, на ъгъла, няма да е равно на нула. За тези участъци се определя положението на осите u И v чрез изчисляване на ъгъла на завъртане на осите х И г

(13)

Центробежен момент около осите u И v -

Формула за определяне на аксиалните инерционни моменти относно главните централни оси u И v :

(14)

Където
- аксиални инерционни моменти спрямо централните оси,

- центробежен момент на инерция спрямо централните оси.

1.5. Инерционен момент спрямо ос, успоредна на централната (теорема на Щайнер)

Теорема на Щайнер:

Инерционният момент около ос, успоредна на централната, е равен на централния аксиален момент на инерция плюс произведението на площта на цялата фигура и квадрата на разстоянието между осите.

(15)

Доказателство на теоремата на Щайнер.

Според фиг. 5 разстояние при към елементарния сайт dF

Заместване на стойността привъв формулата, получаваме:

Срок
, тъй като точка C е центърът на тежестта на сечението (вижте свойството на статичните моменти на секционната площ спрямо централните оси).

За правоъгълник с височинач и ширинаb :

Аксиален инерционен момент:

Момент на огъване:

моментът на съпротивление на огъване е равен на съотношението на инерционния момент към разстоянието на най-отдалеченото влакно от неутралната линия:

защото
, Че

За кръг:

Полярен инерционен момент:

Аксиален инерционен момент:

Момент на усукване:

защото
, Че

Момент на огъване:

Пример 2. Определете инерционния момент на правоъгълно напречно сечение около централната ос СЪС х .

Решение. Нека разделим площта на правоъгълника на елементарни правоъгълници с размери b (ширина) и dy (височина). Тогава площта на такъв правоъгълник (защрихована на фиг. 6) е равна на dF=bdy. Нека изчислим стойността на аксиалния инерционен момент Дж х

По аналогия пишем

- аксиален инерционен момент на сечението спрямо централния

Центробежен момент на инерция

, тъй като осите СЪС х и С г са оси на симетрия.

Пример 3. Определете полярния инерционен момент на кръгло напречно сечение.

Решение. Нека разделим кръга на безкрайно тънки пръстени с дебелина
радиус , площта на такъв пръстен
. Заместване на стойността
Интегрирайки в израза за полярния инерционен момент, получаваме

Отчитане на равенството на аксиалните моменти на кръгло сечение
И

, получаваме

Аксиалните инерционни моменти на пръстена са равни

с– отношението на диаметъра на изреза към външния диаметър на вала.

Лекция No2 „Главни оси иглавни точкиинерция

Нека разгледаме как се променят инерционните моменти при завъртане на координатните оси. Да приемем, че са дадени инерционните моменти на определено сечение спрямо нулевите оси х, 0при(не непременно централно) - ,- аксиални инерционни моменти на сечението. Трябва да се определи ,- аксиални моменти около осите u,v, завъртяна спрямо първата система на ъгъл
(фиг. 8)

Тъй като проекцията на начупената линия OABC е равна на проекцията на задната линия, намираме:

(15)

Нека изключим u и v от изразите за инерционните моменти:

(18)

Нека разгледаме първите две уравнения. Добавяйки ги термин по термин, получаваме

По този начин сумата от аксиалните моменти на инерция около две взаимно перпендикулярни оси не зависи от ъгъла
и остава постоянна, когато осите се въртят. Нека същевременно да отбележим, че

Където - разстояние от началото на координатите до елементарната площадка (виж фиг. 5). По този начин

Където - вече познатият полярен момент на инерция:

Нека определим аксиалния инерционен момент на кръга спрямо диаметъра.

Тъй като поради симетрията
но, както знаете,

Следователно, за кръг

С промяна на ъгъла на въртене на осите
моментни стойности И промяна, но сумата остава същата. Следователно има такъв смисъл
, при което един от инерционните моменти достига максимална стойност, а другият момент приема минимална стойност. Разграничаване на израза по ъгъл
и приравнявайки производната на нула, намираме

(19)

При тази стойност на ъгъла
единият от аксиалните моменти ще бъде най-големият, а другият ще бъде най-малкият. В същото време центробежният инерционен момент
изчезва, което може лесно да се провери чрез приравняване на формулата за центробежния инерционен момент на нула
.

Оси, за които центробежният момент на инерция е нула и аксиалните моменти приемат екстремни стойности, се наричат основенбрадви.Ако те също са централни (началната точка съвпада с центъра на тежестта на сечението), тогава те се наричат главни централни оси (u; v). Наричат ​​се аксиални моменти на инерция спрямо главните оси основни моменти на инерция -И

И тяхната стойност се определя по следната формула:

(20)

Знакът плюс съответства на максималния инерционен момент, знакът минус на минималния.

Има и друга геометрична характеристика - радиус на въртене секции. Тази стойност често се използва в теоретични заключения и практически изчисления.

Радиусът на въртене на сечението спрямо дадена ос, например 0 х , се нарича количеството , определени от равенството

(21)

Е – площ на напречното сечение,

- аксиален инерционен момент на сечението,

От дефиницията следва, че радиусът на въртене е равен на разстоянието от оста 0 хдо точката, в която площта на напречното сечение F трябва да бъде концентрирана (условно), така че инерционният момент на тази една точка да е равен на инерционния момент на цялото сечение. Познавайки инерционния момент на сечението и неговата площ, можете да намерите радиуса на въртене спрямо оста 0 х:

(22)

Радиусите на въртене, съответстващи на главните оси, се наричат главни радиуси на инерцияи се определят по формулите

(23)

Лекция 3. Усукване на пръти с кръгло напречно сечение.

Центробежният инерционен момент около две координатни оси се нарича сумата от произведенията на масата на всяка точка от тялото и координатите по съответните оси.

Ако тялото има ос на симетрия, тогава центробежният инерционен момент на тялото е нула, а осите y и x са основните.

17. Теорема на Хюйгенс-Щайнер за изчисляване на моменти около успоредни оси.

Инерционният момент на твърдо тяло спрямо ос, която не минава през центъра на масата, е равен на сумата от инерционните моменти спрямо централната ос, минаваща през центъра на масата и успоредна на дадената, и произведението на телесната маса на квадрата на разстоянието между осите.

JC е известният инерционен момент около ос, минаваща през центъра на масата на тялото,

J е желаният инерционен момент спрямо успоредната ос,

m - телесно тегло,

d е разстоянието между посочените оси.

18. Изчисляване на инерционните моменти на еднородни тела: тънка плоча, тънък прът, пръстен, цилиндър, конус.

Тънък прът: Тънък цилиндър:

Тънка плоча: Конус:

Тънък пръстен: Топка:

Изчисляване на инерционните моменти относно произволни оси.

Позволява ви да намерите инерционния момент спрямо всяка ос, минаваща през координатните оси и компонентите на въглищата

С тези оси, чрез стойностите на аксиалните и центробежните моменти на инерция на тези оси.

Елипсоид на инерцията. Централни инерционни оси. Екстремни свойства на инерционните моменти.

Центърът на елипсоида е в началото.

Трите оси на симетрия на елипсоида се наричат ​​главни инерционни оси, а инерционните моменти около главните оси се наричат ​​главни инерционни моменти.

Ако вземем главните инерционни оси като координатни оси, тогава центробежните инерционни моменти около тези оси ще бъдат равни на нула.

ЕЛИСПОИД НА ИНЕРЦИЯ - повърхност, характеризираща разпределението на инерционните моменти на тялото спрямо лъч от оси, минаващи през фиксирана точка O. E. и. като geom. местоположението на краищата на отсечките OK = 1/, положени по Ol от точка O, където Ol е произволна ос, минаваща през точка O; I е инерционният момент на тялото спрямо тази ос (фиг.). Център Е. и. съвпада с точка O и нейното уравнение в произволно начертани координатни оси Oxyz има формата

където Ix, Iy, Iz са аксиални, а Ixу, Iyz, Lzx са центробежните инерционни моменти на тялото спрямо посочените координатни оси. На свой ред, познавайки Е. и. за точка O можете да намерите инерционния момент около всяка ос Ol, минаваща през тази точка от равенството Il = 1/R2, измервайки разстоянието R = OK в съответните единици.

Ако m = 1, n = 1, тогава получаваме характеристиката

което се нарича центробежен момент на инерция.

Центробежен момент на инерцияспрямо координатните оси – сумата от произведенията на елементарни площи dAна разстоянията им до тези оси, взети по цялата площ на напречното сечение А.

Ако поне една от осите гили zе оста на симетрия на сечението, центробежният инерционен момент на такова сечение спрямо тези оси е равен на нула (тъй като в този случай всяка положителна стойност z·y·dAможем да поставим в съответствие абсолютно същото, но отрицателно, от другата страна на оста на симетрия на сечението, виж фигурата).

Нека разгледаме допълнителни геометрични характеристики, които могат да бъдат получени от основните изброени и също често се използват при изчисления на якост и твърдост.

Полярен момент на инерция

Полярен момент на инерция Jpназовете характеристиката

От друга страна,

Полярен момент на инерция(спрямо дадена точка) – сумата от произведенията на елементарни площи dAчрез квадратите на техните разстояния до тази точка, взети върху цялата площ на напречното сечение А.

Размерът на инерционните моменти е m 4 в SI.

Момент на съпротива

Момент на съпротиваспрямо някаква ос – стойност, равна на инерционния момент спрямо същата ос, разделен на разстоянието ( ymaxили z макс) до най-отдалечената от тази ос точка

Размерът на моментите на съпротивление е m 3 в SI.

Радиус на инерция

Радиус на инерциясечение спрямо определена ос се нарича стойност, определена от връзката:

Радиусите на въртене се изразяват в SI единици m.

коментар:напречните сечения на елементите на съвременните конструкции често представляват определен състав от материали с различна устойчивост на еластична деформация, характеризиращ се, както е известно от курса по физика, от модула на Юнг д. В най-общия случай на нехомогенно сечение модулът на Юнг е непрекъсната функция от координатите на точките на сечението, т.е. E = E(z, y). Следователно твърдостта на участък, който е нехомогенен по еластични свойства, се характеризира с характеристики, които са по-сложни от геометричните характеристики на хомогенно сечение, а именно еластично-геометрични от формата

2.2. Изчисляване на геометрични характеристики на прости фигури

Правоъгълно сечение

Нека определим аксиалния инерционен момент на правоъгълника спрямо оста z. Нека разделим площта на правоъгълника на елементарни области с размери b(ширина) и dy(височина). Тогава площта на такъв елементарен правоъгълник (защрихована) е равна на dA = b dy. Заместване на стойността dAв първата формула, получаваме

По аналогия записваме аксиалния момент спрямо оста при:

Аксиални моменти на съпротивление на правоъгълник:

;

По подобен начин можете да получите геометрични характеристики за други прости фигури.

Кръгло сечение

Удобно е първо да се намери полярен инерционен момент J p .

Тогава, като се има предвид това за кръг J z = J y, А J p = J z + J y, ще намерим Джей Зи =Джи = Jp / 2.

Нека разделим кръга на безкрайно малки пръстени с дебелина dρи радиус ρ ; площ на такъв пръстен dA = 2 ∙ π ∙ ρ ∙ dρ. Заместване на израза за dAв израз за Jpи интегрирайки, получаваме

2.3. Изчисляване на инерционните моменти спрямо успоредни оси

zИ г:

Необходимо е да се определят инерционните моменти на тази секция спрямо „новите“ оси z 1И y 1, успоредни на централните и отдалечени от тях на разстояние аИ bсъответно:

Координати на всяка точка в „новата“ координатна система z 1 0 1 y 1може да се изрази чрез координати в „старите” оси zИ гТака:

Тъй като брадвите zИ г– централен, след това статичен момент S z = 0.

И накрая, можем да запишем формулите за „преход“ за паралелно прехвърляне на оси:

Имайте предвид, че координатите аИ bтрябва да бъдат заменени, като се вземе предвид техният знак (в координатната система z 1 0 1 y 1).

2.4. Изчисляване на инерционните моменти при въртене на координатни оси

Нека са известни инерционните моменти на произволно сечение спрямо централните оси z, y:

; ;

Да завъртим осите z, гпод ъгъл α обратно на часовниковата стрелка, като ъгълът на въртене на осите в тази посока се счита за положителен.

Необходимо е да се определят инерционните моменти спрямо „новите“ (завъртани) оси z 1И y 1:

Координати на елементарната площадка dAв „новата” координатна система z 1 0y 1може да се изрази чрез координати в „старите“ оси по следния начин:

Заменяме тези стойности във формулите за инерционните моменти в „новите“ оси и интегрираме термин по термин:

След като направихме подобни трансформации с останалите изрази, най-накрая ще запишем формулите за „преход“ при завъртане на координатните оси:

Обърнете внимание, че ако добавим първите две уравнения, получаваме

т.е. полярният инерционен момент е количеството инвариант(с други думи, непроменен при въртене на координатните оси).

2.5. Главни оси и главни инерционни моменти

Досега се разглеждаха геометричните характеристики на сечения в произволна координатна система, но най-голям практически интерес представлява координатната система, в която сечението се описва с най-малък брой геометрични характеристики. Тази „специална“ координатна система се определя от позицията на главните оси на сечението. Нека представим понятията: главни осиИ основни инерционни моменти.

Главни оси– две взаимно перпендикулярни оси, спрямо които центробежният инерционен момент е нула, докато аксиалните инерционни моменти приемат екстремни стойности (максимум и минимум).

Главните оси, минаващи през центъра на тежестта на сечението, се наричат главни централни оси.

Инерционните моменти около главните оси се наричат основни инерционни моменти.

Главните централни оси обикновено се обозначават с букви uИ v; основни инерционни моменти - J uИ Jv(a-приори J uv = 0).

Нека изведем изрази, които ни позволяват да намерим положението на главните оси и големината на главните инерционни моменти. Знаейки това J uv= 0, използваме уравнение (2.3):

Ъгъл α 0 определя позицията на главните оси спрямо всяка централна ос zИ г. Ъгъл α 0 отложени между оста zи ос uи се счита за положителен в посока обратна на часовниковата стрелка.

Имайте предвид, че ако едно сечение има ос на симетрия, тогава, в съответствие със свойството на центробежния инерционен момент (вижте раздел 2.1, параграф 4), такава ос винаги ще бъде главната ос на сечението.

Без ъгъл α в изрази (2.1) и (2.2), използвайки (2.4), получаваме формули за определяне на основните аксиални моменти на инерция:

Нека запишем правилото: максималната ос винаги сключва по-малък ъгъл с този на осите (z или y), спрямо които инерционният момент има по-голяма стойност.

2.6. Рационални форми на напречните сечения

Нормалните напрежения в произволна точка от напречното сечение на гредата по време на директно огъване се определят по формулата:

, (2.5)

Където М– огъващ момент в разглежданото напречно сечение; при– разстоянието от разглежданата точка до главната централна ос, перпендикулярна на равнината на действие на огъващия момент; J x– основният централен инерционен момент на сечението.

Най-големите нормални напрежения на опън и натиск в дадено напречно сечение възникват в точките, които са най-отдалечени от неутралната ос. Те се определят по формулите:

; ,

Където на 1И на 2– разстояния от главната централна ос хдо най-отдалечените опънати и компресирани влакна.

За греди, изработени от пластмасови материали, когато [σ p ] = [σ c ] ([σ p ], [σ c ] са допустимите напрежения за материала на гредата съответно при опън и натиск), сеченията, симетрични спрямо централната ос, са използвани. В този случай условието за якост има формата:

≤ [σ], (2.6)

Където W x = J x / y макс– момент на съпротивление на площта на напречното сечение на гредата спрямо главната централна ос; ymax = з/2(ч– височина на секцията); M макс– най-големият огъващ момент по абсолютна стойност; [σ] – допустимото напрежение на огъване на материала.

Освен условието за якост, гредата трябва да отговаря и на условието за икономичност. Най-икономични са тези форми на напречно сечение, за които най-големият съпротивителен момент се получава с най-малко количество материал (или с най-малка площ на напречното сечение). За да бъде формата на сечението рационална, е необходимо, ако е възможно, сечението да се разпредели далеч от главната централна ос.

Например стандартната I-греда е приблизително седем пъти по-здрава и тридесет пъти по-твърда от квадратна греда със същото напречно сечение, изработена от същия материал.

Трябва да се има предвид, че когато позицията на сечението се промени по отношение на действащото натоварване, якостта на гредата се променя значително, въпреки че площта на напречното сечение остава непроменена. Следователно сечението трябва да бъде разположено така, че силовата линия да съвпада с тази на главните оси, спрямо които инерционният момент е минимален. Трябва да се стремите да гарантирате, че огъването на гредата се извършва в равнината на най-голямата му твърдост.