(pi / 3) na nekoliko načina.
Metoda 1.
Metodu najčešće koriste školarci, ali i studenti, a jedna je od najjednostavnijih.
Funkcija i njezin argument nalaze se u zajedničkim argumentima i, na njihovom sjecištu, vrijednost ove funkcije dobiva se iz zadanog argumenta.
Pomoću tablice nalazimo vrijednost sinusa od pi / 3 - to je korijen od 3 podijeljen s 2.
Zapišimo matematički:
![]()
Metoda 2.
Drugi način je (ili krug). 
Ovdje se vrijednosti sinusa nalaze na y-osi (oy-os). Pokušajmo izračunati vrijednost sinusa od pi / 3.
Argument sinusa je pi / 3 - pronađimo ovu vrijednost na kružnici. Zatim spuštamo okomicu na os koja sadrži vrijednosti sinusa - os Oy. Na kraju okomice dobivamo vrijednost korijena od 3 / 2. Dakle, sinus od pi / 3 jednak je korijenu od 3 / 2.
Metoda 3.
Drugi način za izračunavanje vrijednosti sinusa je korištenje.
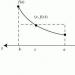
Na primjer, na sinusnom grafu (sinusoidu), nalazimo vrijednost pi / 3 na osi Ox, a zatim povlačimo ravnu liniju okomitu na ovu os dok se ne siječe s grafom. Dobivamo točku koju projiciramo na os Oy i dobivamo vrijednost korijena od 3/2.
Postoji nekoliko opcija za izračunavanje vrijednosti izraza cos (3 / 2 Pi).
Prva opcija. Korištenje
Ova je opcija najlakša i najjednostavnija i sastoji se u činjenici da morate pronaći odgovarajuće vrijednosti u tablici.
Postoje mnoge varijacije tablice, od kojih neke predstavljaju argumente samo u radijanima, druge u stupnjevima, a neke sadrže vrijednosti za radijane i stupnjeve.
Ponekad je još uvijek korisno pretvoriti vrijednost kuta u stupnjeve kako bi se lakše uočila vrijednost kosinusa. Ali nije zabranjeno koristiti tablicu sa stupnjevima i radijanima)).
Iz tablice određujemo vrijednost kosinusa od 3 Pi / 2 - to je 0.
Matematički zapis:
![]()
Druga opcija. .
Prikladna opcija ako tablica trigonometrijskih funkcija nije dostupna. Ovdje se vrijednost trigonometrijske funkcije može odrediti pomoću trigonometrijskog kruga. 
Na trigonometrijskoj kružnici (ili kružnici) na osi x nalaze se vrijednosti kosinusne funkcije.
Prema zadatku, argument funkcije je 3 Pi / 2. Na kružnici je ova vrijednost na y-osi na samom dnu. Da biste izračunali vrijednost zadane funkcije, trebate spustiti okomicu na os Ox, nakon čega dobivamo vrijednost 0. Dakle, kosinus od 3 Pi / 2 je 0.
Treća opcija. Korištenje .
Ako nema tablice, a teško je kretati se po trigonometrijskom krugu, onda je korisno koristiti kosinusni graf, koji se također može koristiti za određivanje vrijednosti. 
Tablica vrijednosti trigonometrijskih funkcija sastavljeno za kutove od 0, 30, 45, 60, 90, 180, 270 i 360 stupnjeva i njihovi odgovarajući kutovi u radijani. Iz trigonometrijske funkcije tablica pokazuje sinus, kosinus, tangenta, kotangens, sekansa i kosekant. Radi praktičnosti rješavanja školskih primjera vrijednosti trigonometrijske funkcije u tablici su zapisani kao razlomak uz očuvanje predznaka vađenja kvadratnog korijena brojeva, što vrlo često pomaže u smanjenju složenih matematičkih izraza. Za tangens i kotangens neki kutovi se ne mogu odrediti. Za vrijednosti tangens i kotangens takvi kutovi u tablici vrijednosti trigonometrijskih funkcija je crtica. Općenito je prihvaćeno da tangens i kotangens takvi kutovi jednaki su beskonačnosti. Na zasebnoj stranici nalaze se formule za redukciju trigonometrijskih funkcija.
Tablica vrijednosti za trigonometrijsku funkciju sinus prikazuje vrijednosti za sljedeće kutove: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 u mjeri stupnja , što odgovara sin 0 pi, sin pi / 6 , sin pi / 4, sin pi / 3, sin pi / 2, sin pi, sin 3 pi / 2, sin 2 pi u radijanskoj mjeri kutova. Školska tablica sinusa.
Za trigonometrijsku kosinusnu funkciju, tablica prikazuje vrijednosti za sljedeće kutove: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 u stupnjskoj mjeri, što odgovara cos 0 pi, cos pi do 6, cos pi za 4, cos pi za 3, cos pi za 2, cos pi, cos 3 pi za 2, cos 2 pi u radijanskoj mjeri kutova. Školska tablica kosinusa.
Trigonometrijska tablica za tangentu trigonometrijske funkcije daje vrijednosti za sljedeće kutove: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 u stupnjskoj mjeri, što odgovara tg 0 pi, tg pi / 6, tg pi / 4, tg pi/3, tg pi, tg 2 pi u radijanskoj mjeri kutova. Sljedeće vrijednosti trigonometrijskih funkcija tangente nisu definirane tg 90, tg 270, tg pi/2, tg 3 pi/2 i smatraju se jednakima beskonačnosti.
Za kotangens trigonometrijske funkcije u trigonometrijskoj tablici dani su sljedeći kutovi: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 u stupnjevima, što odgovara ctg pi / 6, ctg pi / 4, ctg pi / 3 , tg pi / 2, tg 3 pi/2 u radijanskoj mjeri kutova. Sljedeće vrijednosti trigonometrijskih kotangensnih funkcija nisu definirane ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi i smatraju se jednakima beskonačnosti.
Vrijednosti trigonometrijskih funkcija sekansa i kosekansa dane su za iste kutove u stupnjevima i radijanima kao sinus, kosinus, tangent, kotangens.

Tablica vrijednosti trigonometrijskih funkcija nestandardnih kutova prikazuje vrijednosti sinusa, kosinusa, tangenta i kotangensa za kutove u stupnjevima 15, 18, 22,5, 36, 54, 67,5 72 stupnja i u radijanima pi/12 , pi/10, pi/8, pi/5, 3pi/8, 2pi/5 radijana. Vrijednosti trigonometrijskih funkcija izražene su u razlomcima i kvadratnim korijenima kako bi se pojednostavilo smanjenje razlomaka u školskim primjerima.

Još tri čudovišta trigonometrije. Prvi je tangent od 1,5 stupnjeva i pol, ili pi podijeljen sa 120. Drugi je kosinus od pi podijeljen s 240, pi/240. Najduži je kosinus od pi podijeljen sa 17, pi/17.

Trigonometrijski krug vrijednosti funkcija sinusa i kosinusa vizualno predstavlja znakove sinusa i kosinusa ovisno o veličini kuta. Posebno za plavuše, vrijednosti kosinusa podcrtane su zelenom crticom kako bi bile manje zbunjene. Pretvorba stupnjeva u radijane također je vrlo jasno prikazana, kada se radijani izražavaju kroz pi.

Ova trigonometrijska tablica prikazuje vrijednosti sinusa, kosinusa, tangenta i kotangensa za kutove od 0 nula do 90 devedeset stupnjeva u intervalima od jednog stupnja. Za prvih četrdeset i pet stupnjeva nazivi trigonometrijskih funkcija moraju se pogledati na vrhu tablice. Prvi stupac sadrži stupnjeve, vrijednosti sinusa, kosinusa, tangenta i kotangensa upisane su u sljedeća četiri stupca.
Za kutove od četrdeset pet stupnjeva do devedeset stupnjeva, nazivi trigonometrijskih funkcija ispisani su na dnu tablice. Posljednji stupac sadrži stupnjeve, vrijednosti kosinusa, sinusa, kotangensa i tangenta upisane su u prethodna četiri stupca. Treba biti oprezan jer se nazivi trigonometrijskih funkcija u donjem dijelu trigonometrijske tablice razlikuju od naziva u gornjem dijelu tablice. Sinusi i kosinusi se izmjenjuju, baš kao tangenta i kotangens. To je zbog simetrije vrijednosti trigonometrijskih funkcija.

Znakovi trigonometrijskih funkcija prikazani su na gornjoj slici. Sinus ima pozitivne vrijednosti od 0 do 180 stupnjeva ili od 0 do pi. Negativne vrijednosti sinusa su od 180 do 360 stupnjeva ili od pi do 2 pi. Vrijednosti kosinusa su pozitivne od 0 do 90 i 270 do 360 stupnjeva, odnosno 0 do 1/2 pi i 3/2 do 2 pi. Tangent i kotangens imaju pozitivne vrijednosti od 0 do 90 stupnjeva i od 180 do 270 stupnjeva, što odgovara vrijednostima od 0 do 1/2 pi i od pi do 3/2 pi. Negativne vrijednosti tangenta i kotangensa su 90 do 180 stupnjeva i 270 do 360 stupnjeva, odnosno 1/2 pi do pi i 3/2 pi do 2 pi. Prilikom određivanja predznaka trigonometrijskih funkcija za kutove veće od 360 stupnjeva ili 2 pi, treba koristiti svojstva periodičnosti tih funkcija.
Trigonometrijske funkcije sinus, tangent i kotangens su neparne funkcije. Vrijednosti ovih funkcija za negativne kutove bit će negativne. Kosinus je parna trigonometrijska funkcija - vrijednost kosinusa za negativni kut bit će pozitivna. Prilikom množenja i dijeljenja trigonometrijskih funkcija morate slijediti pravila znakova.
Korijen od 2/2 je koliko pi?- To se događa na različite načine (vidi sliku). Morate znati koja je trigonometrijska funkcija jednaka korijenu dva podijeljenom s dva.
Ako vam se svidio post i želite znati više, u procesu sam rada na drugim materijalima.
cos pi podijeljeno sa 2
Početna > Imenik > Matematičke formule.
Matematičke formule.
Pretvorite radijane u stupnjeve.
A d = A r * 180 / pi
Pretvorite stupnjeve u radijane.
A r = A d * pi / 180
Gdje je A d kut u stupnjevima, A r je kut u radijanima.
Opseg.
L = 2 * pi * R
Duljina luka kružnice.
L=A*R
Površina trokuta.
p=(a+b+c)/2 - poluperimetar.
Područje kruga.
S = pi * R 2
Područje sektora.
S \u003d L d * R / 2 \u003d (A * R 2) / 2
Površina kugle.
S = 4 * pi * R 2
S = 2 * Pi * R * H
Gdje je S površina bočne površine cilindra, R je polumjer baze cilindra, H je visina cilindra.
S = pi * R * L
S = pi * R * L + pi * R 2
Volumen lopte.
V = 4 / 3 * pi * R 3
Volumen cilindra.
V = pi * R 2 * H
Volumen konusa.
Objavljeno: 15.01.13
Ažurirano: 15.11.14
Ukupno pregleda: 10754
danas: 1
Početna > Imenik > Matematičke formule.
Egor
Dobra večer! Vrlo ste pitali interes Pitajte nadamo se da vam možemo pomoći.
Kako riješiti C1. Lekcija 2
Ti i ja moramo riješiti sljedeći problem: pronaći cos pi podijeljen s 2.
Najčešće je za rješavanje takvih problema potrebno odrediti kosinusne ili sinusne pokazatelje. Za kutove od 0 do 360 stupnjeva, gotovo bilo koja vrijednost cos ili sin može se lako pronaći u odgovarajućim pločama koje postoje i koje su uobičajene, kao što su ove:
![]()
Ali nemamo sinus (grijeh), nego kosinus. Prvo shvatimo što je kosinus. Cos (kosinus) je jedan od trigonometrijska funkcija. Kako bi se izračunao kosinus akutnog pravokutni trokut Morat ćete znati omjer uključenog kraka kuta i hipotenuze. Kosinus od pi podijeljen s 2 može se lako izračunati pomoću trigonometrijske formule, koja pripada standardnim trigonometrijskim formulama. Ali ako govorimo o vrijednosti kosinusa pi podijeljenom s 2, tada ćemo za to koristiti tablicu koju smo već spomenuli više puta:
![]()
Sretno u budućim ovakvim nastojanjima!
Odgovor: ![]()
Početna > Imenik > Matematičke formule.
Matematičke formule.
Pretvorite radijane u stupnjeve.
A d = A r * 180 / pi
Pretvorite stupnjeve u radijane.
A r = A d * pi / 180
Gdje je A d kut u stupnjevima, A r je kut u radijanima.
Opseg.
L = 2 * pi * R
Gdje je L opseg, R je polumjer kružnice.
Duljina luka kružnice.
L=A*R
Gdje je L duljina luka kružnice, R je polumjer kružnice, A je središnji kut izražen u radijanima
Za kružnicu A = 2*pi (360 stupnjeva), dobivamo L = 2*pi*R.
Površina trokuta.
S = (p * (p-a) * (p-b) * (p-c)) 1/2
Gdje je S površina trokuta, a, b, c su duljine stranica,
p=(a+b+c)/2 - poluperimetar.
Područje kruga.
S = pi * R 2
Gdje je S površina kruga, R je polumjer kružnice.
Područje sektora.
S \u003d L d * R / 2 \u003d (A * R 2) / 2
Gdje je S površina sektora, R je polumjer kružnice, L d je duljina luka.
Površina kugle.
S = 4 * pi * R 2
Gdje je S površina lopte, R je polumjer lopte.
Područje bočne površine cilindra.
S = 2 * Pi * R * H
Gdje je S površina bočne površine cilindra, R je polumjer baze cilindra, H je visina cilindra.
Ukupna površina cilindra.
S = 2 * pi * R * H + 2 * pi * R 2
Gdje je S površina bočne površine cilindra, R je polumjer baze cilindra, H je visina cilindra.
Područje bočne površine stošca.
S = pi * R * L
Gdje je S površina bočne površine stošca, R je polumjer baze stošca, L je duljina generatrike stošca.
Ukupna površina stošca.
S = pi * R * L + pi * R 2
Gdje je S površina pune površine stošca, R je polumjer baze stošca, L je duljina generatrike stošca.
Volumen lopte.
V = 4 / 3 * pi * R 3
Gdje je V volumen lopte, R je polumjer lopte.
Volumen cilindra.
V = pi * R 2 * H
Gdje je V volumen cilindra, R je polumjer baze cilindra, H je visina cilindra.
Volumen konusa.
V = pi * R * L = pi * R * H/cos (A/2) = pi * R * R/sin (A/2)
Gdje je V volumen stošca, R je polumjer baze stošca, L je duljina generatrike stošca, A je kut na vrhu stošca.
Objavljeno: 15.01.13
Ažurirano: 15.11.14
Ukupno pregleda: 10742
danas: 1
Početna > Imenik > Matematičke formule.
Egor
Žicu na terminalima akumulatora Krona možete pričvrstiti cijevi odsječenom od poklopca medicinske igle.
Jednostavno rečeno, riječ je o povrću kuhanom u vodi po posebnom receptu. Razmotrit ću dvije početne komponente (salatu od povrća i vodu) i gotov rezultat - boršč. Geometrijski, ovo se može predstaviti kao pravokutnik u kojem jedna strana označava salatu, a druga voda. Zbroj ove dvije strane označavat će boršč. Dijagonala i površina takvog pravokutnika "boršč" su čisto matematički koncepti i nikada se ne koriste u receptima za boršč.
Kako se salata i voda u matematičkom smislu pretvaraju u boršč? Kako se zbroj dvaju segmenata može pretvoriti u trigonometriju? Da bismo to razumjeli, potrebne su nam funkcije linearnog kuta.
U udžbenicima matematike nećete pronaći ništa o funkcijama linearnog kuta. Ali bez njih ne može biti matematike. Zakoni matematike, kao i zakoni prirode, djeluju bez obzira na to znamo da postoje ili ne.
Linearne kutne funkcije su zakoni zbrajanja. Pogledajte kako se algebra pretvara u geometriju, a geometrija u trigonometriju.
Je li moguće bez linearnih kutnih funkcija? Možete, jer matematičari se i dalje snalaze bez njih. Trik matematičara je u tome što nam uvijek govore samo o onim problemima koje sami mogu riješiti, a nikad nam ne govore o onim problemima koje ne mogu riješiti. Vidjeti. Ako znamo rezultat zbrajanja i jednog člana, koristimo oduzimanje da bismo pronašli drugi član. Sve. Druge probleme ne poznajemo i nismo u stanju riješiti. Što učiniti ako znamo samo rezultat zbrajanja, a ne znamo oba pojma? U ovom slučaju, rezultat zbrajanja se mora rastaviti na dva člana korištenjem linearnih kutnih funkcija. Nadalje, sami biramo što može biti jedan član, a linearne kutne funkcije pokazuju kakav bi trebao biti drugi član da bi rezultat zbrajanja bio upravo ono što nam treba. Takvih parova pojmova može postojati beskonačan broj. U svakodnevnom životu se jako dobro snalazimo bez razlaganja zbroja, dovoljno nam je oduzimanje. Ali u znanstvenim proučavanjima zakona prirode, proširenje zbroja u izraze može biti vrlo korisno.
Još jedan zakon zbrajanja o kojem matematičari ne vole govoriti (još jedan njihov trik) zahtijeva da izrazi imaju istu mjernu jedinicu. Za zelenu salatu, vodu i boršč, to mogu biti jedinice težine, volumena, cijene ili jedinice mjere.
Slika prikazuje dvije razine razlike za matematiku. Prva razina su razlike u polju brojeva, koje su naznačene a, b, c. To rade matematičari. Druga razina su razlike u području mjernih jedinica koje su prikazane u uglastim zagradama i označene slovom U. To rade fizičari. Možemo razumjeti treću razinu - razlike u opsegu opisanih objekata. Različiti objekti mogu imati isti broj istih mjernih jedinica. Koliko je to važno, vidimo na primjeru boršč trigonometrije. Ako istoj oznaci mjernih jedinica za različite objekte dodamo indekse, možemo reći koje točno matematička vrijednost opisuje određeni objekt i kako se mijenja tijekom vremena ili u odnosu na naše radnje. pismo W Vodu ću označiti slovom S Salatu ću označiti slovom B- borsch. Evo kako bi izgledale funkcije linearnog kuta za boršč.
Ako uzmemo dio vode i dio salate, zajedno će se pretvoriti u jednu porciju boršča. Ovdje predlažem da se malo odmorite od boršča i prisjetite se svog dalekog djetinjstva. Sjećate li se kako su nas učili spajati zečiće i patke? Trebalo je pronaći koliko će životinja ispasti. Što smo onda učili da radimo? Učili su nas odvajati jedinice od brojeva i zbrajati brojeve. Da, bilo koji broj se može dodati bilo kojem drugom broju. Ovo je izravan put do autizma suvremene matematike - ne razumijemo što, nije jasno zašto, a jako slabo razumijemo kako se to odnosi na stvarnost, jer od tri razine razlike matematičari operiraju samo na jednoj. Bit će ispravnije naučiti kako prijeći s jedne mjerne jedinice na drugu.
I zečići, i patke, i male životinje mogu se nabrojati u komadima. Jedna zajednička mjerna jedinica za različite objekte omogućuje nam da ih zbrojimo. Ovo je dječja verzija problema. Pogledajmo sličan problem za odrasle. Što dobijete kada dodate zečiće i novac? Ovdje postoje dva moguća rješenja.
Prva opcija. Određujemo tržišnu vrijednost zečića i dodajemo je raspoloživoj gotovini. Dobili smo ukupnu vrijednost našeg bogatstva u novcu.
Druga opcija. Broj zečića možete dodati broju novčanica koje imamo. Dobit ćemo iznos pokretne imovine u komadima.
Kao što vidite, isti zakon zbrajanja omogućuje vam da dobijete različite rezultate. Sve ovisi o tome što točno želimo znati.
Ali vratimo se našem boršu. Sada možemo vidjeti što će se dogoditi za različite vrijednosti kuta funkcija linearnog kuta.
Injekcija nula. Imamo salatu, ali nemamo vodu. Ne možemo kuhati boršč. Količina boršča je također nula. To uopće ne znači da je nula boršča jednaka nuli vode. Nula borsch može biti i na nula salata (pravi kut).
Za mene osobno, ovo je glavni matematički dokaz činjenice da . Nula ne mijenja broj kada se doda. To je zato što je samo zbrajanje nemoguće ako postoji samo jedan član, a drugi član nedostaje. Možete se odnositi prema ovome kako želite, ali zapamtite - sve matematičke operacije s nulom izmislili su sami matematičari, pa odbacite svoju logiku i glupo trpajte definicije koje su izmislili matematičari: "dijeljenje s nulom je nemoguće", "bilo koji broj pomnožen s nulom jednako nuli" , "iza nulte točke" i ostale gluposti. Dovoljno je jednom zapamtiti da nula nije broj i nikada se nećete postaviti pitanje je li nula prirodan broj ili nije, jer takvo pitanje općenito gubi svaki smisao: kako se može smatrati brojem ono što nije broj . To je kao da pitate kojoj boji pripisati nevidljivu boju. Dodavanje nule broju je kao slikanje bojom koja ne postoji. Mahali su suhim kistom i govorili svima da smo "naslikali". Ali malo sam odstupio.
Kut je veći od nule, ali manji od četrdeset pet stupnjeva. Imamo puno zelene salate, ali malo vode. Kao rezultat, dobivamo debeli boršč.
Kut je četrdeset pet stupnjeva. Imamo jednake količine vode i zelene salate. Ovo je savršeni boršč (neka mi kuharice oproste, to je samo matematika).
Kut je veći od četrdeset pet stupnjeva, ali manji od devedeset stupnjeva. Imamo puno vode i malo zelene salate. Uzmite tekući boršč.
Pravi kut. Imamo vodu. Od zelene salate ostaju samo sjećanja, dok nastavljamo mjeriti kut od linije koja je nekada označavala salatu. Ne možemo kuhati boršč. Količina boršča je nula. U tom slučaju, držite se i pijte vodu dok je dostupna)))
Ovdje. Nešto kao ovo. Ovdje mogu ispričati druge priče koje će ovdje biti više nego prikladne.
Dva prijatelja imala su svoje udjele u zajedničkom poslu. Nakon ubistva jednog od njih, sve je otišlo na drugoga.
Pojava matematike na našem planetu.
Sve ove priče ispričane su jezikom matematike pomoću linearnih kutnih funkcija. Neki drugi put ću ti pokazati pravo mjesto ove funkcije u strukturi matematike. U međuvremenu, vratimo se na trigonometriju boršča i razmotrimo projekcije.
Subota, 26.10.2019
Pogledao sam zanimljiv video o Grandijev red Jedan minus jedan plus jedan minus jedan - Numberphile. Matematičari lažu. U svom obrazloženju nisu proveli test jednakosti.
Ovo rezonira s mojim razmišljanjem o .
Pogledajmo pobliže znakove da nas matematičari varaju. Na samom početku razmišljanja matematičari kažu da zbroj niza OVISI o tome je li broj elemenata u njemu paran ili ne. Ovo je OBJEKTIVNO UTVRĐENA ČINJENICA. Što se dalje događa?
Zatim matematičari oduzimaju niz od jedinice. čemu to vodi? To dovodi do promjene broja elemenata u nizu – paran broj se mijenja u neparan, a neparan u paran broj. Uostalom, slijedu smo dodali jedan element jednak jednom. Unatoč svoj vanjskoj sličnosti, slijed prije transformacije nije jednak nizu nakon transformacije. Čak i ako govorimo o beskonačnom nizu, moramo zapamtiti da beskonačan niz s neparnim brojem elemenata nije jednak beskonačnom nizu s parnim brojem elemenata.
Stavljajući znak jednakosti između dva niza različita po broju elemenata, matematičari tvrde da zbroj niza NE OVISI o broju elemenata u nizu, što je u suprotnosti s OBJEKTIVNO UTVRĐENOM ČINJENICOM. Daljnje razmišljanje o zbroju beskonačnog niza je pogrešno, jer se temelji na lažnoj jednakosti.
Ako vidite da matematičari tijekom dokazivanja stavljaju zagrade, preuređuju elemente matematičkog izraza, dodaju ili uklanjaju nešto, budite jako oprezni, najvjerojatnije vas pokušavaju prevariti. Poput čaranja karata, matematičari vam skreću pažnju raznim manipulacijama izraza kako bi vam na kraju dali lažni rezultat. Ako ne možete ponoviti kartaški trik, a da ne znate tajnu varanja, onda je u matematici sve puno jednostavnije: čak ni ne sumnjate u varanje, ali ponavljanje svih manipulacija s matematičkim izrazom omogućuje vam da uvjerite druge u ispravnost rezultata, baš kao kad su vas uvjerili.
Pitanje iz publike: A beskonačnost (kao broj elemenata u nizu S), je li paran ili neparan? Kako možete promijeniti paritet nečega što nema paritet?
Beskonačnost za matematičare je poput nebeskog kraljevstva za svećenike - tamo nitko nikada nije bio, ali svi točno znaju kako tamo sve funkcionira))) Slažem se, nakon smrti bit ćete potpuno ravnodušni jeste li živjeli paran ili neparan broj dana , ali ... Dodavanjem samo jednog dana na početak vašeg života, dobit ćemo sasvim drugu osobu: njegovo prezime, ime i patronimij su potpuno isti, samo je datum rođenja potpuno drugačiji - rođen je jedan dan prije tebe.
A sada na stvar))) Pretpostavimo da konačni niz koji ima paritet izgubi ovaj paritet kada ide u beskonačnost. Tada svaki konačni segment beskonačnog niza također mora izgubiti parnost. Mi to ne promatramo. Činjenica da ne možemo sa sigurnošću reći je li broj elemenata u beskonačnom nizu paran ili neparan uopće ne znači da je parnost nestala. Paritet, ako postoji, ne može netragom nestati u beskonačnost, kao u rukavu oštrije karte. Postoji vrlo dobra analogija za ovaj slučaj.
Jeste li ikada pitali kukavicu koja sjedi u satu u kojem smjeru se okreće kazaljka na satu? Za nju se strelica okreće u smjeru suprotnom od onoga što nazivamo "kazaljkom na satu". Možda zvuči paradoksalno, ali smjer rotacije ovisi isključivo o tome s koje strane promatramo rotaciju. I tako, imamo jedan kotač koji se okreće. Ne možemo reći u kojem smjeru se rotacija događa, jer je možemo promatrati i s jedne i s druge strane ravnine rotacije. Možemo samo posvjedočiti da postoji rotacija. Potpuna analogija s paritetom beskonačnog niza S.
Sada dodajmo drugi rotirajući kotač čija je ravnina rotacije paralelna s ravninom rotacije prvog rotirajućeg kotača. Još uvijek ne možemo točno odrediti u kojem smjeru se ti kotači vrte, ali možemo sa apsolutnom sigurnošću reći vrte li se oba kotača u istom smjeru ili u suprotnim smjerovima. Usporedba dva beskonačna niza S i 1-S, pokazao sam uz pomoć matematike da ti nizovi imaju različit paritet i stavljanje znaka jednakosti između njih je pogreška. Osobno vjerujem u matematiku, ne vjerujem matematičarima))) Usput, za puno razumijevanje geometrije transformacija beskonačnih nizova, potrebno je uvesti pojam "istovremenost". Ovo će se morati nacrtati.
Srijeda, 7. kolovoza 2019
Završavajući razgovor o , Moramo razmotriti beskonačan skup. Dao u tome da koncept "beskonačnosti" djeluje na matematičare, kao boa constrictor na zeca. Drhtavi užas beskonačnosti lišava matematičare zdravog razuma. Evo primjera:
Izvorni izvor se nalazi. Alfa označava pravi broj. Znak jednakosti u gornjim izrazima označava da ako dodate broj ili beskonačnost beskonačnosti, ništa se neće promijeniti, rezultat će biti ista beskonačnost. Ako uzmemo za primjer beskonačan skup prirodni brojevi, razmatrani primjeri mogu se prikazati u sljedećem obliku:
Kako bi vizualno dokazali svoj slučaj, matematičari su smislili mnogo različitih metoda. Osobno na sve te metode gledam kao na plesove šamana s tamburama. U biti, svi se svode na to da ili neke sobe nisu zauzete i da se u njih smjeste novi gosti, ili da se dio posjetitelja izbacuje u hodnik da se napravi mjesta za goste (vrlo ljudski). Svoje viđenje takvih odluka iznio sam u obliku fantastične priče o Plavuši. Na čemu se temelji moje razmišljanje? Premještanje beskonačnog broja posjetitelja traje beskonačno vrijeme. Nakon što napustimo prvu gostinjsku sobu, jedan od posjetitelja će uvijek hodati hodnikom od svoje sobe do sljedeće do kraja vremena. Naravno, faktor vremena može se glupo zanemariti, ali to će već biti iz kategorije "zakon nije pisan za budale". Sve ovisi o tome što radimo: prilagođavamo stvarnost matematičkim teorijama ili obrnuto.
Što je "beskonačan hotel"? Infinity gostionica je gostionica koja uvijek ima bilo koji broj slobodnih mjesta, koliko god soba bilo zauzeto. Ako su sve sobe u beskrajnom hodniku "za posjetitelje" zauzete, postoji još jedan beskrajni hodnik sa sobama za "goste". Takvih će hodnika biti beskonačan broj. Istovremeno, "beskonačni hotel" ima beskonačan broj katova u beskonačnom broju zgrada na beskonačnom broju planeta u beskonačnom broju svemira stvorenih od beskonačnog broja bogova. Matematičari, s druge strane, nisu u stanju odmaknuti se od banalnih svakodnevnih problema: Bog-Allah-Buddha je uvijek samo jedan, hotel je jedan, hodnik je samo jedan. Tako matematičari pokušavaju žonglirati serijskim brojevima hotelskih soba, uvjeravajući nas da je moguće "ugurati nepogurnute".
Pokazat ću vam logiku svog razmišljanja na primjeru beskonačnog skupa prirodnih brojeva. Prvo morate odgovoriti na vrlo jednostavno pitanje: koliko skupova prirodnih brojeva postoji - jedan ili više? Ne postoji točan odgovor na ovo pitanje, budući da smo sami izmislili brojeve, u prirodi nema brojeva. Da, priroda zna savršeno računati, ali za to koristi druge matematičke alate koji nam nisu poznati. Kako priroda misli, reći ću vam drugi put. Budući da smo izmislili brojeve, sami ćemo odlučiti koliko skupova prirodnih brojeva postoji. Razmotrite obje opcije, kako i priliči pravom znanstveniku.
Prva opcija. "Neka nam se da" jedan skup prirodnih brojeva, koji mirno leži na polici. Uzimamo ovaj set s police. To je to, na polici nema drugih prirodnih brojeva i nema ih kamo uzeti. Ne možemo ga dodati ovom skupu, jer ga već imamo. Što ako stvarno želiš? Nema problema. Možemo uzeti jedinicu iz seta koji smo već uzeli i vratiti na policu. Nakon toga možemo uzeti jedinicu s police i dodati je onome što nam je ostalo. Kao rezultat, opet dobivamo beskonačan skup prirodnih brojeva. Sve naše manipulacije možete napisati ovako:
Zapisao sam operacije u algebarskom zapisu i u zapisu teorije skupova, detaljno navodeći elemente skupa. Indeks označava da imamo jedan i jedini skup prirodnih brojeva. Ispada da će skup prirodnih brojeva ostati nepromijenjen samo ako se od njega oduzme jedan i doda isti.
Opcija dva. Na polici imamo mnogo različitih beskonačnih skupova prirodnih brojeva. Naglašavam – DRUGAČIJE, unatoč tome što se praktički ne razlikuju. Uzimamo jedan od ovih setova. Zatim uzmemo jedan iz drugog skupa prirodnih brojeva i dodamo ga skupu koji smo već uzeli. Možemo čak dodati dva skupa prirodnih brojeva. Evo što dobivamo:
Podskripti "jedan" i "dva" označavaju da su ti elementi pripadali različitim skupovima. Da, ako beskonačnom skupu dodate jedan, rezultat će također biti beskonačan skup, ali neće biti isti kao izvorni skup. Ako se jedan beskonačan skup doda drugom beskonačnom skupu, rezultat je novi beskonačan skup koji se sastoji od elemenata prva dva skupa.
Skup prirodnih brojeva koristi se za brojanje na isti način kao i ravnalo za mjerenja. Sada zamislite da ste ravnalu dodali jedan centimetar. Ovo će već biti druga linija, ne jednaka originalu.
Možete prihvatiti ili ne prihvatiti moje obrazloženje - to je vaša stvar. Ali ako ikada naiđete na matematičke probleme, razmislite jeste li na putu lažnog rasuđivanja, kojim su kročile generacije matematičara. Uostalom, satovi matematike, prije svega, u nama formiraju stabilan stereotip mišljenja, a tek onda nam dodaju mentalne sposobnosti (ili obrnuto, uskraćuju nam slobodno mišljenje).
pozg.ru
Nedjelja, 4. kolovoza 2019
Pisao sam postscript za članak o i vidio ovaj prekrasan tekst na Wikipediji:
Čitamo: „...bogat teorijska pozadina Babilonska matematika nije imala holistički karakter i bila je svedena na skup različitih tehnika, lišenih zajednički sustav i baza dokaza.
Vau! Koliko smo pametni i koliko dobro vidimo nedostatke drugih. Je li nam slabo gledati modernu matematiku u istom kontekstu? Malo parafrazirajući gornji tekst, osobno sam dobio sljedeće:
Bogata teorijska osnova moderne matematike nema holistički karakter i svedena je na skup različitih dijelova, lišenih zajedničkog sustava i baze dokaza.
Neću ići daleko da potvrdim svoje riječi - ima jezik i simbole koji se razlikuju od jezika i simboli mnoge druge grane matematike. Isti nazivi u različitim granama matematike mogu imati različita značenja. Želim posvetiti cijeli ciklus publikacija najočitijim greškama moderne matematike. Vidimo se uskoro.
Subota, 3. kolovoza 2019
Kako podijeliti skup na podskupove? Da biste to učinili, morate unijeti novu mjernu jedinicu koja je prisutna u nekim elementima odabranog skupa. Razmotrimo primjer.
Neka nas bude mnogo ALI koji se sastoji od četiri osobe. Ovaj skup je formiran na temelju "ljudi" Označimo elemente ovog skupa kroz slovo a, indeks s brojem će označavati redni broj svake osobe u ovom skupu. Uvedimo novu mjernu jedinicu "seksualna karakteristika" i označimo je slovom b. Budući da su spolne karakteristike svojstvene svim ljudima, svaki element skupa umnožavamo ALI o spolu b. Primijetite da je naš skup "ljudi" sada postao skup "ljudi sa rodom". Nakon toga možemo podijeliti spolne karakteristike na muške bm i ženski bw spolne karakteristike. Sada možemo primijeniti matematički filtar: odabiremo jednu od ovih spolnih karakteristika, nije važno koja je muška ili ženska. Ako je prisutan u osobi, onda ga množimo s jedan, ako nema takvog znaka, množimo ga s nulom. A onda primjenjujemo uobičajenu školsku matematiku. Vidi što se dogodilo.
Nakon množenja, redukcije i preuređivanja, dobili smo dva podskupa: muški podskup bm i podskup žena bw. Otprilike na isti način razmišljaju matematičari kada primjenjuju teoriju skupova u praksi. No, ne puštaju nas u detalje, već nam daju gotov rezultat - "puno ljudi se sastoji od podskupine muškaraca i podskupa žena". Naravno, možda imate pitanje, koliko je pravilno primijenjena matematika u gornjim transformacijama? Usuđujem se uvjeravati vas da su zapravo transformacije ispravno izvedene, dovoljno je poznavati matematičko opravdanje aritmetike, Booleove algebre i drugih dijelova matematike. Što je? Neki drugi put ću vam pričati o tome.
Što se tiče superskupova, moguće je kombinirati dva skupa u jedan nadskup odabirom mjerne jedinice koja je prisutna u elementima ova dva skupa.
Kao što možete vidjeti, mjerne jedinice i uobičajena matematika čine teoriju skupova prošlošću. Znak da s teorijom skupova nije sve u redu je to što su matematičari smislili svoj vlastiti jezik i notaciju za teoriju skupova. Matematičari su radili ono što su nekada radili šamani. Samo šamani znaju "ispravno" primijeniti svoje "znanje". To "znanje" oni nas uče.
U zaključku, želim vam pokazati kako matematičari manipuliraju
Recimo, Ahilej trči deset puta brže od kornjače i tisuću koraka je iza nje. Tijekom vremena tijekom kojeg Ahilej pretrči ovu udaljenost, kornjača puzi stotinu koraka u istom smjeru. Kad Ahilej pretrči stotinu koraka, kornjača će puzati još deset koraka, i tako dalje. Proces će se nastaviti u nedogled, Ahilej nikada neće sustići kornjaču.
Ovo razmišljanje postalo je logičan šok za sve sljedeće generacije. Aristotel, Diogen, Kant, Hegel, Gilbert... Svi su oni, na ovaj ili onaj način, smatrali Zenonove aporije. Šok je bio toliko jak da je " ... rasprave se nastavljaju u današnje vrijeme, znanstvena zajednica još nije uspjela doći do zajedničkog mišljenja o biti paradoksa ... matematička analiza, teorija skupova, novi fizički i filozofski pristupi uključeni su u proučavanje problematike ; nijedan od njih nije postao općeprihvaćeno rješenje problema..."[Wikipedia," Zeno's Aporias "]. Svi razumiju da su prevareni, ali nitko ne razumije u čemu je obmana.
S gledišta matematike, Zenon je u svojim aporijama jasno pokazao prijelaz s vrijednosti na. Ovaj prijelaz podrazumijeva primjenu umjesto konstanti. Koliko sam shvatio, matematički aparat za primjenu varijabilnih mjernih jedinica ili još nije razvijen, ili nije primijenjen na Zenonove aporije. Primjena naše uobičajene logike vodi nas u zamku. Mi, po inerciji mišljenja, primjenjujemo stalne jedinice vremena na recipročno. S fizičke točke gledišta, to izgleda kao usporavanje vremena sve dok se potpuno ne zaustavi u trenutku kada Ahilej sustigne kornjaču. Ako vrijeme stane, Ahilej više ne može prestići kornjaču.
Ako okrenemo logiku na koju smo navikli, sve dolazi na svoje mjesto. Ahil trči s konstantna brzina. Svaki sljedeći segment njegovog puta je deset puta kraći od prethodnog. Sukladno tome, vrijeme utrošeno na prevladavanje je deset puta manje od prethodnog. Ako u ovoj situaciji primijenimo koncept „beskonačnosti“, tada bi bilo ispravno reći „Ahilej će beskrajno brzo prestići kornjaču“.
Kako izbjeći ovu logičnu zamku? Ostanite u stalnim jedinicama vremena i ne prelazite na recipročne vrijednosti. Na Zenonovom jeziku to izgleda ovako:
Za vrijeme koje je Ahileju potrebno da pretrči tisuću koraka, kornjača puzi stotinu koraka u istom smjeru. Tijekom sljedećeg vremenskog intervala, jednakog prvom, Ahilej će pretrčati još tisuću koraka, a kornjača će puzati stotinu koraka. Sada je Ahilej osamsto koraka ispred kornjače.
Ovaj pristup primjereno opisuje stvarnost bez ikakvih logičkih paradoksa. Ali ovo nije potpuno rješenje problema. Einsteinova izjava o nepremostivosti brzine svjetlosti vrlo je slična Zenonovoj aporiji "Ahilej i kornjača". Taj problem tek trebamo proučiti, preispitati i riješiti. A rješenje se mora tražiti ne u beskonačno velikim brojevima, već u mjernim jedinicama.
Još jedna zanimljiva Zenonova aporija govori o letećoj strijeli:
Leteća strijela je nepomična, budući da u svakom trenutku miruje, a budući da miruje u svakom trenutku, uvijek miruje.
U ovoj se aporiji logički paradoks prevladava vrlo jednostavno – dovoljno je razjasniti da u svakom trenutku vremena leteća strijela miruje na različitim točkama prostora, što je, zapravo, kretanje. Ovdje treba napomenuti još jednu stvar. Iz jedne fotografije automobila na cesti nemoguće je utvrditi ni činjenicu njegovog kretanja, ni udaljenost do njega. Za utvrđivanje činjenice kretanja automobila potrebne su dvije fotografije snimljene s iste točke u različitim vremenskim trenucima, ali se njima ne može odrediti udaljenost. Da biste odredili udaljenost do automobila, potrebne su vam dvije fotografije snimljene iz različitih točaka u svemiru u isto vrijeme, ali ne možete utvrditi činjenicu kretanja iz njih (naravno, još su vam potrebni dodatni podaci za izračune, pomoći će vam trigonometrija). Ono što želim posebno istaknuti je da su dvije točke u vremenu i dvije točke u prostoru dvije različite stvari koje se ne smiju brkati jer pružaju različite mogućnosti za istraživanje.
Pokazat ću proces na primjeru. Odabiremo "crvenu čvrstu boju u bubuljici" - ovo je naša "cjelina". U isto vrijeme vidimo da su te stvari s lukom, a postoje i bez luka. Nakon toga odaberemo dio "cjeline" i formiramo set "s mašnom". Ovako se šamani hrane vezujući svoju teoriju skupova za stvarnost.
Sada napravimo mali trik. Uzmimo "čvrsto u bubuljicu s mašnom" i ujedinimo ove "cjeline" po boji, odabirom crvenih elemenata. Dobili smo puno "crvenih". Sada škakljivo pitanje: jesu li primljeni setovi "s mašnom" i "crvenim" isti set ili dva različita seta? Samo šamani znaju odgovor. Točnije, oni sami ništa ne znaju, ali kako kažu, neka bude.
Ovaj jednostavan primjer pokazuje da je teorija skupova potpuno beskorisna kada je u pitanju stvarnost. u čemu je tajna? Formirali smo set "crvenih čvrstih prištića s mašnicom". Formiranje se odvijalo prema četiri različite mjerne jedinice: boja (crvena), čvrstoća (puna), hrapavost (u kvržici), ukrasi (s mašnom). Samo skup mjernih jedinica omogućuje primjereno opisivanje stvarnih objekata jezikom matematike. Evo kako to izgleda.
Slovo "a" s različitim indeksima označava različite mjerne jedinice. U zagradama su istaknute mjerne jedinice prema kojima se u preliminarnoj fazi dodjeljuje "cjelina". Iz zagrada se vadi mjerna jedinica prema kojoj se skup formira. Posljednji redak prikazuje konačni rezultat - element skupa. Kao što vidite, ako koristimo jedinice za formiranje skupa, tada rezultat ne ovisi o redoslijedu naših radnji. A ovo je matematika, a ne plesovi šamana s tamburicama. Šamani mogu "intuitivno" doći do istog rezultata, argumentirajući ga "očiglednošću", jer mjerne jedinice nisu uključene u njihov "znanstveni" arsenal.
Uz pomoć mjernih jedinica vrlo je lako razbiti jedan ili kombinirati nekoliko setova u jedan superset. Pogledajmo pobliže algebru ovog procesa.
Jednostavno rečeno, riječ je o povrću kuhanom u vodi po posebnom receptu. Razmotrit ću dvije početne komponente (salatu od povrća i vodu) i gotov rezultat - boršč. Geometrijski, ovo se može predstaviti kao pravokutnik u kojem jedna strana označava salatu, a druga voda. Zbroj ove dvije strane označavat će boršč. Dijagonala i površina takvog pravokutnika "boršč" su čisto matematički koncepti i nikada se ne koriste u receptima za boršč.
Kako se salata i voda u matematičkom smislu pretvaraju u boršč? Kako se zbroj dvaju segmenata može pretvoriti u trigonometriju? Da bismo to razumjeli, potrebne su nam funkcije linearnog kuta.
U udžbenicima matematike nećete pronaći ništa o funkcijama linearnog kuta. Ali bez njih ne može biti matematike. Zakoni matematike, kao i zakoni prirode, djeluju bez obzira na to znamo da postoje ili ne.
Linearne kutne funkcije su zakoni zbrajanja. Pogledajte kako se algebra pretvara u geometriju, a geometrija u trigonometriju.
Je li moguće bez linearnih kutnih funkcija? Možete, jer matematičari se i dalje snalaze bez njih. Trik matematičara je u tome što nam uvijek govore samo o onim problemima koje sami mogu riješiti, a nikad nam ne govore o onim problemima koje ne mogu riješiti. Vidjeti. Ako znamo rezultat zbrajanja i jednog člana, koristimo oduzimanje da bismo pronašli drugi član. Sve. Druge probleme ne poznajemo i nismo u stanju riješiti. Što učiniti ako znamo samo rezultat zbrajanja, a ne znamo oba pojma? U ovom slučaju, rezultat zbrajanja se mora rastaviti na dva člana korištenjem linearnih kutnih funkcija. Nadalje, sami biramo što može biti jedan član, a linearne kutne funkcije pokazuju kakav bi trebao biti drugi član da bi rezultat zbrajanja bio upravo ono što nam treba. Takvih parova pojmova može postojati beskonačan broj. U svakodnevnom životu se jako dobro snalazimo bez razlaganja zbroja, dovoljno nam je oduzimanje. Ali u znanstvenim proučavanjima zakona prirode, proširenje zbroja u izraze može biti vrlo korisno.
Još jedan zakon zbrajanja o kojem matematičari ne vole govoriti (još jedan njihov trik) zahtijeva da izrazi imaju istu mjernu jedinicu. Za zelenu salatu, vodu i boršč, to mogu biti jedinice težine, volumena, cijene ili jedinice mjere.
Slika prikazuje dvije razine razlike za matematiku. Prva razina su razlike u polju brojeva, koje su naznačene a, b, c. To rade matematičari. Druga razina su razlike u području mjernih jedinica koje su prikazane u uglastim zagradama i označene slovom U. To rade fizičari. Možemo razumjeti treću razinu - razlike u opsegu opisanih objekata. Različiti objekti mogu imati isti broj istih mjernih jedinica. Koliko je to važno, vidimo na primjeru boršč trigonometrije. Ako istom zapisu dodamo indekse za mjerne jedinice različitih objekata, možemo točno reći koja matematička veličina opisuje određeni objekt i kako se mijenja tijekom vremena ili u vezi s našim djelovanjem. pismo W Vodu ću označiti slovom S Salatu ću označiti slovom B- borsch. Evo kako bi izgledale funkcije linearnog kuta za boršč.
Ako uzmemo dio vode i dio salate, zajedno će se pretvoriti u jednu porciju boršča. Ovdje predlažem da se malo odmorite od boršča i prisjetite se svog dalekog djetinjstva. Sjećate li se kako su nas učili spajati zečiće i patke? Trebalo je pronaći koliko će životinja ispasti. Što smo onda učili da radimo? Učili su nas odvajati jedinice od brojeva i zbrajati brojeve. Da, bilo koji broj se može dodati bilo kojem drugom broju. Ovo je izravan put do autizma suvremene matematike - ne razumijemo što, nije jasno zašto, a jako slabo razumijemo kako se to odnosi na stvarnost, jer od tri razine razlike matematičari operiraju samo na jednoj. Bit će ispravnije naučiti kako prijeći s jedne mjerne jedinice na drugu.
I zečići, i patke, i male životinje mogu se nabrojati u komadima. Jedna zajednička mjerna jedinica za različite objekte omogućuje nam da ih zbrojimo. Ovo je dječja verzija problema. Pogledajmo sličan problem za odrasle. Što dobijete kada dodate zečiće i novac? Ovdje postoje dva moguća rješenja.
Prva opcija. Određujemo tržišnu vrijednost zečića i dodajemo je raspoloživoj gotovini. Dobili smo ukupnu vrijednost našeg bogatstva u novcu.
Druga opcija. Broj zečića možete dodati broju novčanica koje imamo. Dobit ćemo iznos pokretne imovine u komadima.
Kao što vidite, isti zakon zbrajanja omogućuje vam da dobijete različite rezultate. Sve ovisi o tome što točno želimo znati.
Ali vratimo se našem boršu. Sada možemo vidjeti što će se dogoditi za različite vrijednosti kuta funkcija linearnog kuta.
Kut je nula. Imamo salatu, ali nemamo vodu. Ne možemo kuhati boršč. Količina boršča je također nula. To uopće ne znači da je nula boršča jednaka nuli vode. Nula borsch može biti i na nula salata (pravi kut).
Za mene osobno, ovo je glavni matematički dokaz činjenice da . Nula ne mijenja broj kada se doda. To je zato što je samo zbrajanje nemoguće ako postoji samo jedan član, a drugi član nedostaje. Možete se odnositi prema ovome kako želite, ali zapamtite - sve matematičke operacije s nulom izmislili su sami matematičari, pa odbacite svoju logiku i glupo trpajte definicije koje su izmislili matematičari: "dijeljenje s nulom je nemoguće", "bilo koji broj pomnožen s nulom jednako nuli" , "iza nulte točke" i ostale gluposti. Dovoljno je jednom zapamtiti da nula nije broj i nikada se nećete postaviti pitanje je li nula prirodan broj ili nije, jer takvo pitanje općenito gubi svaki smisao: kako se može smatrati brojem ono što nije broj . To je kao da pitate kojoj boji pripisati nevidljivu boju. Dodavanje nule broju je kao slikanje bojom koja ne postoji. Mahali su suhim kistom i govorili svima da smo "naslikali". Ali malo sam odstupio.
Kut je veći od nule, ali manji od četrdeset pet stupnjeva. Imamo puno zelene salate, ali malo vode. Kao rezultat, dobivamo debeli boršč.
Kut je četrdeset pet stupnjeva. Imamo jednake količine vode i zelene salate. Ovo je savršeni boršč (neka mi kuharice oproste, to je samo matematika).
Kut je veći od četrdeset pet stupnjeva, ali manji od devedeset stupnjeva. Imamo puno vode i malo zelene salate. Uzmite tekući boršč.
Pravi kut. Imamo vodu. Od zelene salate ostaju samo sjećanja, dok nastavljamo mjeriti kut od linije koja je nekada označavala salatu. Ne možemo kuhati boršč. Količina boršča je nula. U tom slučaju, držite se i pijte vodu dok je dostupna)))
Ovdje. Nešto kao ovo. Ovdje mogu ispričati druge priče koje će ovdje biti više nego prikladne.
Dva prijatelja imala su svoje udjele u zajedničkom poslu. Nakon ubistva jednog od njih, sve je otišlo na drugoga.
Pojava matematike na našem planetu.
Sve ove priče ispričane su jezikom matematike pomoću linearnih kutnih funkcija. Neki drugi put pokazat ću vam pravo mjesto ovih funkcija u strukturi matematike. U međuvremenu, vratimo se na trigonometriju boršča i razmotrimo projekcije.
Subota, 26.10.2019
Pogledao sam zanimljiv video o Grandijev red Jedan minus jedan plus jedan minus jedan - Numberphile. Matematičari lažu. U svom obrazloženju nisu proveli test jednakosti.
Ovo rezonira s mojim razmišljanjem o .
Pogledajmo pobliže znakove da nas matematičari varaju. Na samom početku razmišljanja matematičari kažu da zbroj niza OVISI o tome je li broj elemenata u njemu paran ili ne. Ovo je OBJEKTIVNO UTVRĐENA ČINJENICA. Što se dalje događa?
Zatim matematičari oduzimaju niz od jedinice. čemu to vodi? To dovodi do promjene broja elemenata u nizu – paran broj se mijenja u neparan, a neparan u paran broj. Uostalom, slijedu smo dodali jedan element jednak jednom. Unatoč svoj vanjskoj sličnosti, slijed prije transformacije nije jednak nizu nakon transformacije. Čak i ako govorimo o beskonačnom nizu, moramo zapamtiti da beskonačan niz s neparnim brojem elemenata nije jednak beskonačnom nizu s parnim brojem elemenata.
Stavljajući znak jednakosti između dva niza različita po broju elemenata, matematičari tvrde da zbroj niza NE OVISI o broju elemenata u nizu, što je u suprotnosti s OBJEKTIVNO UTVRĐENOM ČINJENICOM. Daljnje razmišljanje o zbroju beskonačnog niza je pogrešno, jer se temelji na lažnoj jednakosti.
Ako vidite da matematičari tijekom dokazivanja stavljaju zagrade, preuređuju elemente matematičkog izraza, dodaju ili uklanjaju nešto, budite jako oprezni, najvjerojatnije vas pokušavaju prevariti. Poput čaranja karata, matematičari vam skreću pažnju raznim manipulacijama izraza kako bi vam na kraju dali lažni rezultat. Ako ne možete ponoviti kartaški trik, a da ne znate tajnu varanja, onda je u matematici sve puno jednostavnije: čak ni ne sumnjate u varanje, ali ponavljanje svih manipulacija s matematičkim izrazom omogućuje vam da uvjerite druge u ispravnost rezultata, baš kao kad su vas uvjerili.
Pitanje iz publike: A beskonačnost (kao broj elemenata u nizu S), je li paran ili neparan? Kako možete promijeniti paritet nečega što nema paritet?
Beskonačnost za matematičare je poput nebeskog kraljevstva za svećenike - tamo nitko nikada nije bio, ali svi točno znaju kako tamo sve funkcionira))) Slažem se, nakon smrti bit ćete potpuno ravnodušni jeste li živjeli paran ili neparan broj dana , ali ... Dodavanjem samo jednog dana na početak vašeg života, dobit ćemo sasvim drugu osobu: njegovo prezime, ime i patronimij su potpuno isti, samo je datum rođenja potpuno drugačiji - rođen je jedan dan prije tebe.
A sada na stvar))) Pretpostavimo da konačni niz koji ima paritet izgubi ovaj paritet kada ide u beskonačnost. Tada svaki konačni segment beskonačnog niza također mora izgubiti parnost. Mi to ne promatramo. Činjenica da ne možemo sa sigurnošću reći je li broj elemenata u beskonačnom nizu paran ili neparan uopće ne znači da je parnost nestala. Paritet, ako postoji, ne može netragom nestati u beskonačnost, kao u rukavu oštrije karte. Postoji vrlo dobra analogija za ovaj slučaj.
Jeste li ikada pitali kukavicu koja sjedi u satu u kojem smjeru se okreće kazaljka na satu? Za nju se strelica okreće u smjeru suprotnom od onoga što nazivamo "kazaljkom na satu". Možda zvuči paradoksalno, ali smjer rotacije ovisi isključivo o tome s koje strane promatramo rotaciju. I tako, imamo jedan kotač koji se okreće. Ne možemo reći u kojem smjeru se rotacija događa, jer je možemo promatrati i s jedne i s druge strane ravnine rotacije. Možemo samo posvjedočiti da postoji rotacija. Potpuna analogija s paritetom beskonačnog niza S.
Sada dodajmo drugi rotirajući kotač čija je ravnina rotacije paralelna s ravninom rotacije prvog rotirajućeg kotača. Još uvijek ne možemo točno odrediti u kojem smjeru se ti kotači vrte, ali možemo sa apsolutnom sigurnošću reći vrte li se oba kotača u istom smjeru ili u suprotnim smjerovima. Usporedba dva beskonačna niza S i 1-S, pokazao sam uz pomoć matematike da ti nizovi imaju različit paritet i stavljanje znaka jednakosti između njih je pogreška. Osobno vjerujem u matematiku, ne vjerujem matematičarima))) Usput, da bismo u potpunosti razumjeli geometriju transformacija beskonačnih nizova, potrebno je uvesti koncept "istovremenost". Ovo će se morati nacrtati.
Srijeda, 7. kolovoza 2019
Završavajući razgovor o , Moramo razmotriti beskonačan skup. Dao u tome da koncept "beskonačnosti" djeluje na matematičare, kao boa constrictor na zeca. Drhtavi užas beskonačnosti lišava matematičare zdravog razuma. Evo primjera:
Izvorni izvor se nalazi. Alfa označava pravi broj. Znak jednakosti u gornjim izrazima označava da ako dodate broj ili beskonačnost beskonačnosti, ništa se neće promijeniti, rezultat će biti ista beskonačnost. Ako za primjer uzmemo beskonačan skup prirodnih brojeva, onda se razmatrani primjeri mogu predstaviti na sljedeći način:
Kako bi vizualno dokazali svoj slučaj, matematičari su smislili mnogo različitih metoda. Osobno na sve te metode gledam kao na plesove šamana s tamburama. U biti, svi se svode na to da ili neke sobe nisu zauzete i da se u njih smjeste novi gosti, ili da se dio posjetitelja izbacuje u hodnik da se napravi mjesta za goste (vrlo ljudski). Svoje viđenje takvih odluka iznio sam u obliku fantastične priče o Plavuši. Na čemu se temelji moje razmišljanje? Premještanje beskonačnog broja posjetitelja traje beskonačno vrijeme. Nakon što napustimo prvu gostinjsku sobu, jedan od posjetitelja će uvijek hodati hodnikom od svoje sobe do sljedeće do kraja vremena. Naravno, faktor vremena može se glupo zanemariti, ali to će već biti iz kategorije "zakon nije pisan za budale". Sve ovisi o tome što radimo: prilagođavamo stvarnost matematičkim teorijama ili obrnuto.
Što je "beskonačan hotel"? Infinity gostionica je gostionica koja uvijek ima bilo koji broj slobodnih mjesta, koliko god soba bilo zauzeto. Ako su sve sobe u beskrajnom hodniku "za posjetitelje" zauzete, postoji još jedan beskrajni hodnik sa sobama za "goste". Takvih će hodnika biti beskonačan broj. Istovremeno, "beskonačni hotel" ima beskonačan broj katova u beskonačnom broju zgrada na beskonačnom broju planeta u beskonačnom broju svemira stvorenih od beskonačnog broja bogova. Matematičari, s druge strane, nisu u stanju odmaknuti se od banalnih svakodnevnih problema: Bog-Allah-Buddha je uvijek samo jedan, hotel je jedan, hodnik je samo jedan. Tako matematičari pokušavaju žonglirati serijskim brojevima hotelskih soba, uvjeravajući nas da je moguće "ugurati nepogurnute".
Pokazat ću vam logiku svog razmišljanja na primjeru beskonačnog skupa prirodnih brojeva. Prvo morate odgovoriti na vrlo jednostavno pitanje: koliko skupova prirodnih brojeva postoji - jedan ili više? Ne postoji točan odgovor na ovo pitanje, budući da smo sami izmislili brojeve, u prirodi nema brojeva. Da, priroda zna savršeno računati, ali za to koristi druge matematičke alate koji nam nisu poznati. Kako priroda misli, reći ću vam drugi put. Budući da smo izmislili brojeve, sami ćemo odlučiti koliko skupova prirodnih brojeva postoji. Razmotrite obje opcije, kako i priliči pravom znanstveniku.
Prva opcija. "Neka nam se da" jedan skup prirodnih brojeva, koji mirno leži na polici. Uzimamo ovaj set s police. To je to, na polici nema drugih prirodnih brojeva i nema ih kamo uzeti. Ne možemo ga dodati ovom skupu, jer ga već imamo. Što ako stvarno želiš? Nema problema. Možemo uzeti jedinicu iz seta koji smo već uzeli i vratiti na policu. Nakon toga možemo uzeti jedinicu s police i dodati je onome što nam je ostalo. Kao rezultat, opet dobivamo beskonačan skup prirodnih brojeva. Sve naše manipulacije možete napisati ovako:
Zapisao sam operacije u algebarskom zapisu i u zapisu teorije skupova, detaljno navodeći elemente skupa. Indeks označava da imamo jedan i jedini skup prirodnih brojeva. Ispada da će skup prirodnih brojeva ostati nepromijenjen samo ako se od njega oduzme jedan i doda isti.
Opcija dva. Na polici imamo mnogo različitih beskonačnih skupova prirodnih brojeva. Naglašavam – DRUGAČIJE, unatoč tome što se praktički ne razlikuju. Uzimamo jedan od ovih setova. Zatim uzmemo jedan iz drugog skupa prirodnih brojeva i dodamo ga skupu koji smo već uzeli. Možemo čak dodati dva skupa prirodnih brojeva. Evo što dobivamo:
Podskripti "jedan" i "dva" označavaju da su ti elementi pripadali različitim skupovima. Da, ako beskonačnom skupu dodate jedan, rezultat će također biti beskonačan skup, ali neće biti isti kao izvorni skup. Ako se jedan beskonačan skup doda drugom beskonačnom skupu, rezultat je novi beskonačan skup koji se sastoji od elemenata prva dva skupa.
Skup prirodnih brojeva koristi se za brojanje na isti način kao i ravnalo za mjerenja. Sada zamislite da ste ravnalu dodali jedan centimetar. Ovo će već biti druga linija, ne jednaka originalu.
Možete prihvatiti ili ne prihvatiti moje obrazloženje - to je vaša stvar. Ali ako ikada naiđete na matematičke probleme, razmislite jeste li na putu lažnog rasuđivanja, kojim su kročile generacije matematičara. Uostalom, satovi matematike, prije svega, u nama formiraju stabilan stereotip mišljenja, a tek onda nam dodaju mentalne sposobnosti (ili obrnuto, uskraćuju nam slobodno mišljenje).
pozg.ru
Nedjelja, 4. kolovoza 2019
Pisao sam postscript za članak o i vidio ovaj prekrasan tekst na Wikipediji:
Čitamo: "...bogata teorijska osnova matematike Babilona nije imala holistički karakter i bila je svedena na skup različitih tehnika, lišenih zajedničkog sustava i baze dokaza."
Vau! Koliko smo pametni i koliko dobro vidimo nedostatke drugih. Je li nam slabo gledati modernu matematiku u istom kontekstu? Malo parafrazirajući gornji tekst, osobno sam dobio sljedeće:
Bogata teorijska osnova moderne matematike nema holistički karakter i svedena je na skup različitih dijelova, lišenih zajedničkog sustava i baze dokaza.
Neću ići daleko da potvrdim svoje riječi – ima jezik i konvencije koji se razlikuju od jezika i konvencija mnogih drugih grana matematike. Isti nazivi u različitim granama matematike mogu imati različita značenja. Želim posvetiti cijeli ciklus publikacija najočitijim greškama moderne matematike. Vidimo se uskoro.
Subota, 3. kolovoza 2019
Kako podijeliti skup na podskupove? Da biste to učinili, morate unijeti novu mjernu jedinicu koja je prisutna u nekim elementima odabranog skupa. Razmotrimo primjer.
Neka nas bude mnogo ALI koji se sastoji od četiri osobe. Ovaj skup je formiran na temelju "ljudi" Označimo elemente ovog skupa kroz slovo a, indeks s brojem će označavati redni broj svake osobe u ovom skupu. Uvedimo novu mjernu jedinicu "seksualna karakteristika" i označimo je slovom b. Budući da su spolne karakteristike svojstvene svim ljudima, svaki element skupa umnožavamo ALI o spolu b. Primijetite da je naš skup "ljudi" sada postao skup "ljudi sa rodom". Nakon toga možemo podijeliti spolne karakteristike na muške bm i ženski bw spolne karakteristike. Sada možemo primijeniti matematički filtar: odabiremo jednu od ovih spolnih karakteristika, nije važno koja je muška ili ženska. Ako je prisutan u osobi, onda ga množimo s jedan, ako nema takvog znaka, množimo ga s nulom. A onda primjenjujemo uobičajenu školsku matematiku. Vidi što se dogodilo.
Nakon množenja, redukcije i preuređivanja, dobili smo dva podskupa: muški podskup bm i podskup žena bw. Otprilike na isti način razmišljaju matematičari kada primjenjuju teoriju skupova u praksi. No, ne puštaju nas u detalje, već nam daju gotov rezultat - "puno ljudi se sastoji od podskupine muškaraca i podskupa žena". Naravno, možda imate pitanje, koliko je pravilno primijenjena matematika u gornjim transformacijama? Usuđujem se uvjeravati vas da su zapravo transformacije ispravno izvedene, dovoljno je poznavati matematičko opravdanje aritmetike, Booleove algebre i drugih dijelova matematike. Što je? Neki drugi put ću vam pričati o tome.
Što se tiče superskupova, moguće je kombinirati dva skupa u jedan nadskup odabirom mjerne jedinice koja je prisutna u elementima ova dva skupa.
Kao što možete vidjeti, mjerne jedinice i uobičajena matematika čine teoriju skupova prošlošću. Znak da s teorijom skupova nije sve u redu je to što su matematičari smislili svoj vlastiti jezik i notaciju za teoriju skupova. Matematičari su radili ono što su nekada radili šamani. Samo šamani znaju "ispravno" primijeniti svoje "znanje". To "znanje" oni nas uče.
U zaključku, želim vam pokazati kako matematičari manipuliraju
Recimo, Ahilej trči deset puta brže od kornjače i tisuću koraka je iza nje. Tijekom vremena tijekom kojeg Ahilej pretrči ovu udaljenost, kornjača puzi stotinu koraka u istom smjeru. Kad Ahilej pretrči stotinu koraka, kornjača će puzati još deset koraka, i tako dalje. Proces će se nastaviti u nedogled, Ahilej nikada neće sustići kornjaču.
Ovo razmišljanje postalo je logičan šok za sve sljedeće generacije. Aristotel, Diogen, Kant, Hegel, Gilbert... Svi su oni, na ovaj ili onaj način, smatrali Zenonove aporije. Šok je bio toliko jak da je " ... rasprave se nastavljaju u današnje vrijeme, znanstvena zajednica još nije uspjela doći do zajedničkog mišljenja o biti paradoksa ... matematička analiza, teorija skupova, novi fizički i filozofski pristupi uključeni su u proučavanje problematike ; nijedan od njih nije postao općeprihvaćeno rješenje problema..."[Wikipedia," Zeno's Aporias "]. Svi razumiju da su prevareni, ali nitko ne razumije u čemu je obmana.
S gledišta matematike, Zenon je u svojim aporijama jasno pokazao prijelaz s vrijednosti na. Ovaj prijelaz podrazumijeva primjenu umjesto konstanti. Koliko sam shvatio, matematički aparat za primjenu varijabilnih mjernih jedinica ili još nije razvijen, ili nije primijenjen na Zenonove aporije. Primjena naše uobičajene logike vodi nas u zamku. Mi, po inerciji mišljenja, primjenjujemo stalne jedinice vremena na recipročno. S fizičke točke gledišta, to izgleda kao usporavanje vremena sve dok se potpuno ne zaustavi u trenutku kada Ahilej sustigne kornjaču. Ako vrijeme stane, Ahilej više ne može prestići kornjaču.
Ako okrenemo logiku na koju smo navikli, sve dolazi na svoje mjesto. Ahilej trči stalnom brzinom. Svaki sljedeći segment njegovog puta je deset puta kraći od prethodnog. Sukladno tome, vrijeme utrošeno na prevladavanje je deset puta manje od prethodnog. Ako u ovoj situaciji primijenimo koncept „beskonačnosti“, tada bi bilo ispravno reći „Ahilej će beskrajno brzo prestići kornjaču“.
Kako izbjeći ovu logičnu zamku? Ostanite u stalnim jedinicama vremena i ne prelazite na recipročne vrijednosti. Na Zenonovom jeziku to izgleda ovako:
Za vrijeme koje je Ahileju potrebno da pretrči tisuću koraka, kornjača puzi stotinu koraka u istom smjeru. Tijekom sljedećeg vremenskog intervala, jednakog prvom, Ahilej će pretrčati još tisuću koraka, a kornjača će puzati stotinu koraka. Sada je Ahilej osamsto koraka ispred kornjače.
Ovaj pristup primjereno opisuje stvarnost bez ikakvih logičkih paradoksa. Ali ovo nije potpuno rješenje problema. Einsteinova izjava o nepremostivosti brzine svjetlosti vrlo je slična Zenonovoj aporiji "Ahilej i kornjača". Taj problem tek trebamo proučiti, preispitati i riješiti. A rješenje se mora tražiti ne u beskonačno velikim brojevima, već u mjernim jedinicama.
Još jedna zanimljiva Zenonova aporija govori o letećoj strijeli:
Leteća strijela je nepomična, budući da u svakom trenutku miruje, a budući da miruje u svakom trenutku, uvijek miruje.
U ovoj se aporiji logički paradoks prevladava vrlo jednostavno – dovoljno je razjasniti da u svakom trenutku vremena leteća strijela miruje na različitim točkama prostora, što je, zapravo, kretanje. Ovdje treba napomenuti još jednu stvar. Iz jedne fotografije automobila na cesti nemoguće je utvrditi ni činjenicu njegovog kretanja, ni udaljenost do njega. Za utvrđivanje činjenice kretanja automobila potrebne su dvije fotografije snimljene s iste točke u različitim vremenskim trenucima, ali se njima ne može odrediti udaljenost. Da biste odredili udaljenost do automobila, potrebne su vam dvije fotografije snimljene iz različitih točaka u svemiru u isto vrijeme, ali ne možete utvrditi činjenicu kretanja iz njih (naravno, još su vam potrebni dodatni podaci za izračune, pomoći će vam trigonometrija). Ono što želim posebno istaknuti je da su dvije točke u vremenu i dvije točke u prostoru dvije različite stvari koje se ne smiju brkati jer pružaju različite mogućnosti za istraživanje.
Pokazat ću proces na primjeru. Odabiremo "crvenu čvrstu boju u bubuljici" - ovo je naša "cjelina". U isto vrijeme vidimo da su te stvari s lukom, a postoje i bez luka. Nakon toga odaberemo dio "cjeline" i formiramo set "s mašnom". Ovako se šamani hrane vezujući svoju teoriju skupova za stvarnost.
Sada napravimo mali trik. Uzmimo "čvrsto u bubuljicu s mašnom" i ujedinimo ove "cjeline" po boji, odabirom crvenih elemenata. Dobili smo puno "crvenih". Sada škakljivo pitanje: jesu li primljeni setovi "s mašnom" i "crvenim" isti set ili dva različita seta? Samo šamani znaju odgovor. Točnije, oni sami ništa ne znaju, ali kako kažu, neka bude.
Ovaj jednostavan primjer pokazuje da je teorija skupova potpuno beskorisna kada je u pitanju stvarnost. u čemu je tajna? Formirali smo set "crvenih čvrstih prištića s mašnicom". Formiranje se odvijalo prema četiri različite mjerne jedinice: boja (crvena), čvrstoća (puna), hrapavost (u kvržici), ukrasi (s mašnom). Samo skup mjernih jedinica omogućuje primjereno opisivanje stvarnih objekata jezikom matematike. Evo kako to izgleda.
Slovo "a" s različitim indeksima označava različite mjerne jedinice. U zagradama su istaknute mjerne jedinice prema kojima se u preliminarnoj fazi dodjeljuje "cjelina". Iz zagrada se vadi mjerna jedinica prema kojoj se skup formira. Posljednji redak prikazuje konačni rezultat - element skupa. Kao što vidite, ako koristimo jedinice za formiranje skupa, tada rezultat ne ovisi o redoslijedu naših radnji. A ovo je matematika, a ne plesovi šamana s tamburicama. Šamani mogu "intuitivno" doći do istog rezultata, argumentirajući ga "očiglednošću", jer mjerne jedinice nisu uključene u njihov "znanstveni" arsenal.
Uz pomoć mjernih jedinica vrlo je lako razbiti jedan ili kombinirati nekoliko setova u jedan superset. Pogledajmo pobliže algebru ovog procesa.