Метод Крамера заснований на використанні визначників у вирішенні систем лінійних рівнянь. Це значно прискорює процес розв'язання.
Метод Крамера може бути використаний у вирішенні системи стільки лінійних рівнянь, скільки в кожному рівнянні невідомих. Якщо визначник системи не дорівнює нулю, то метод Крамера може бути використаний у рішенні, якщо ж дорівнює нулю, то не може. Крім того, метод Крамера може бути використаний у вирішенні систем лінійних рівнянь, що мають єдине рішення.
Визначення. Визначник, складений із коефіцієнтів при невідомих, називається визначником системи та позначається (дельта).
Визначники
виходять шляхом заміни коефіцієнтів за відповідних невідомих вільними членами:
;
.
Теорема Крамера. Якщо визначник системи відмінний від нуля, то система лінійних рівнянь має одне єдине рішення, причому невідоме дорівнює відношенню визначників. У знаменнику – визначник системи, а чисельнику – визначник, отриманий з визначника системи шляхом заміни коефіцієнтів у своїй невідомому вільними членами. Ця теорема має місце системи лінійних рівнянь будь-якого порядку.
приклад 1.Розв'язати систему лінійних рівнянь:
Згідно теоремі Крамерамаємо:
Отже, рішення системи (2):
онлайн-калькулятором, вирішальним методом Крамера.
Три випадки під час вирішення систем лінійних рівнянь
Як випливає з теореми Крамера, При вирішенні системи лінійних рівнянь можуть зустрітися три випадки:
Перший випадок: система лінійних рівнянь має єдине рішення
(Система спільна та визначена)
Другий випадок: система лінійних рівнянь має безліч рішень
(Система спільна та невизначена)
** 
,
тобто. коефіцієнти при невідомих та вільні члени пропорційні.
Третій випадок: система лінійних рівнянь рішень не має
(Система несумісна)
Отже, система mлінійних рівнянь з nзмінними називається несумісний, якщо вона не має жодного рішення, і спільноїякщо вона має хоча б одне рішення. Спільна система рівнянь, що має лише одне рішення, називається певної, а більше одного – невизначеною.
Приклади розв'язання систем лінійних рівнянь методом Крамера
Нехай дана система
.
На підставі теореми Крамера
………….
,
де 
-
визначник системи. Інші визначники отримаємо, замінюючи стовпець з коефіцієнтами відповідної змінної (невідомого) вільними членами:
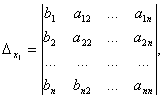
приклад 2.
.
Отже, система є певною. Для знаходження її рішення обчислюємо визначники
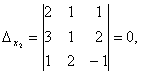
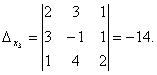
За формулами Крамера знаходимо:
Отже, (1; 0; -1) – єдине рішення системи.
Для перевірки рішень систем рівнянь 3Х3 і 4Х4 можна скористатися онлайн-калькулятором, вирішальним методом Крамера.
Якщо в системі лінійних рівнянь в одному або кількох рівняннях відсутні будь-які змінні, то у визначнику відповідні елементи дорівнюють нулю! Такий такий приклад.
приклад 3.Розв'язати систему лінійних рівнянь методом Крамера:
.
Рішення. Знаходимо визначник системи:
Уважно подивіться на систему рівнянь і на визначник системи і повторіть відповідь на питання, в яких випадках один або кілька елементів визначника дорівнюють нулю. Отже, визначник не дорівнює нулю, отже система є певною. Для знаходження її рішення обчислюємо визначники за невідомих
За формулами Крамера знаходимо:
Отже, рішення системи – (2; -1; 1).
Для перевірки рішень систем рівнянь 3Х3 і 4Х4 можна скористатися онлайн-калькулятором, вирішальним методом Крамера.
На початок сторінки
Продовжуємо вирішувати системи методом Крамера разом
Як мовилося раніше, якщо визначник системи дорівнює нулю, а визначники при невідомих не дорівнюють нулю, система несовместна, тобто рішень немає. Проілюструємо наступний приклад.
Приклад 6.Розв'язати систему лінійних рівнянь методом Крамера:
Рішення. Знаходимо визначник системи:
Визначник системи дорівнює нулю, отже, система лінійних рівнянь або несумісна і певна, або несумісна, тобто немає рішень. Для уточнення обчислюємо визначники при невідомих
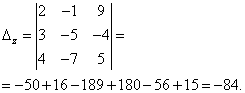
Визначники при невідомих не дорівнюють нулю, отже, система несумісна, тобто немає рішень.
Для перевірки рішень систем рівнянь 3Х3 і 4Х4 можна скористатися онлайн-калькулятором, вирішальним методом Крамера.
У задачах системи лінійних рівнянь зустрічаються і такі, де крім літер, що позначають змінні, є ще й інші літери. Ці букви позначають деяке число, найчастіше дійсне. На практиці до таких рівнянь та систем рівнянь наводять завдання на пошук загальних властивостейбудь-яких явищ та предметів. Тобто винайшли ви який-небудь новий матеріалабо пристрій, а для опису його властивостей, загальних незалежно від величини або кількості екземпляра, потрібно вирішити систему лінійних рівнянь, де замість деяких коефіцієнтів при змінних - літери. За прикладами далеко не треба ходити.
Наступний приклад - на аналогічне завдання, тільки збільшується кількість рівнянь, змінних, і букв, що позначають деяке дійсне число.
Приклад 8.Розв'язати систему лінійних рівнянь методом Крамера:
Рішення. Знаходимо визначник системи:
Знаходимо визначники при невідомих
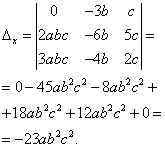
У § 3.3 були показані обмеження, що виникають при стеженні за сигналами частоти, що змінюється за допомогою системи другого порядку. Розглянемо тепер можливість пом'якшення деяких із цих обмежень шляхом введення в систему другого інтегратора. Виявляється, що процес захоплення для системи третього порядку менш стійкий, ніж для системи другого порядку, але за допомогою другого інтегратора можна розширити діапазон стеження за системою, яка в початковий момент була вже захоплена. Передатна функція фільтра тепер має вигляд
і з (3.1) випливає:
Після підстановки цей вираз наводиться до вигляду
Нормуючи та вводячи позначення отримаємо
Звичайний метод фазової площини не застосовується до диференціальних рівнянь третього порядку внаслідок того, що в цьому випадку є три початкові умови, що відповідають трьом змінним: фазі, частоті та швидкості зміни частоти (у механічних системах - зміщення, швидкості та прискорення). У принципі траєкторії, що визначаються рівнянням третього порядку, можна було б уявити у тривимірному просторі. Будь-яка спроба спроектувати ці траєкторії для J безлічі початкових умов на площину призвела б до такої заплутаної діаграми, що з неї було б неможливо зробити будь-які загальні висновки.
З іншого боку, якщо обмежитися однією сукупністю початкових умов, можна отримати проекцію траєкторії на площину . Особливе значення представляє наступна сукупність початкових умов: Іншими словами, система в початковий момент захоплена, так що помилки по частоті та фазі дорівнюють нулю, коли опорна частота починає лінійно змінюватися.
Легко змінити структуру аналогового обчислювального пристрою, щоб врахувати запровадження другого інтегратора.
Мал. 3.19. Проекції траєкторій у фазовому просторі для петлі третього порядку
(Див. скан)
На рис. 3.19 зображено низку траєкторій, спроектованих на площину. У всіх розглянутих випадках так що. У гіпотетичному тривимірному «фазовому просторі» траєкторії починаються в точці та закінчуються на осі
На рис. 3.19, а показано поведінку системи другого порядку за таких самих початкових умов. Остаточне, або що встановилося, значення фази так само, як було показано в § 3.3. Введення другого інтегратора призводить до зменшення встановленої помилки по фазі до нуля тим швидше, чим більше. 3.19 ж). Нарешті, система стає нестійкою.
Поліпшення, що отримується шляхом збільшення порядку системи, ілюструється на рис. 3.20. Тут як і раніше, але . У § 3.3 було показано, що за такої чи більшої швидкості лінійної зміни частоти система не могла здійснювати стеження. Мал. 3.20, а підтверджує цю обставину. З іншого боку, навіть при найменшому ступені впливу другого інтегратора виходить нульова помилка, що встановилася по фазі. Найбільше миттєве значення фазового неузгодженості зменшується зі збільшенням коефіцієнта але за система знову робиться нестійкою.
Аналогічні особливості помітні на рис. 3.21-3.23, за винятком тієї обставини, що при зростанні відносини для підтримки системи в стані захоплення потрібні всі зростаючі значення коефіцієнта Зрештою при наближенні відношення до 2 або необхідно, щоб було близько 1/2. Але із рис. 3.19, ж - 3.23, видно, що при цьому значенні система нестійка. Діапазон значень коефіцієнта у яких система залишається може захоплення залежно від відношення представлений на рис. 3.24-3.26 при значення відповідно. Заштрихована область допустимих значень коефіцієнта Видно, що при лінійній зміні частоти введення системи третього порядку дозволило розширити діапазон, при якому виходить стеження, приблизно
Мал. 3.20. Проекції траєкторій у фазовому просторі для петлі третього порядку
(Див. скан)
Мал. 3.21. Проекції траєкторій у фазовому просторі для петлі третього порядку
(Див. скан)
Мал. 3.22. Проекції траєкторій у фазовому просторі для петлі третього порядку
(Див. скан)
Мал. 3.23. Проекції траєкторій у фазовому просторі для петлі третього порядку
(Див. скан)
Мал. 3.24. Область стану захоплення системи третього порядку
Мал. 3.25. Область стану захоплення системи третього порядку
Мал. 3.26. Область стану захоплення системи третього порядку
вдвічі більше в порівнянні з системою другого порядку при і навіть ще більше при менших значеннях
Можна теоретично пояснити коливальний характер зміни коефіцієнта b при його значення близько або більше 1/2. Продиференціювавши рівняння (3.41), отримаємо
Для більш глибокого розуміння того, що відбувається в цій статті, можна ознайомитися з .Розглянемо однорідну систему диференціальних рівнянь третього порядку
Тут x(t), y(t), z(t) - шукані функції на проміжку (a, b), a ij (i, j = 1, 2, 3) - речові числа.
Запишемо вихідну систему у матричному вигляді
,
де 
Рішення вихідної системи будемо шукати у вигляді
,
де 
, C 1 , C 2 , C 3 - довільні постійні.
Щоб знайти фундаментальну систему рішень, потрібно вирішити так зване характеристичне рівняння 
Це рівняння є рівнянням алгебри третього порядку, отже воно має 3 кореня. При цьому можливі такі випадки:
1. Коріння (власні значення) дійсне і різне.
2. Серед коренів (власних значень) є комплексно-сполучені, нехай
- дійсний корінь
=
3. Коріння (власні значення) дійсне. Один із коренів кратний.
Щоб розібратися, як діяти в кожному з цих випадків, нам знадобляться:
Теорема 1.
Нехай попарно різні власні значення матриця А, а відповідні їм власні вектори. Тоді
утворюють фундаментальну систему рішень вихідної системи.
Зауваження
.
Нехай - дійсне власне значення матриця А (дійсний корінь характеристичного рівняння) - відповідний йому власний вектор.
= - комплексні власні значення матриці А; - відповідний - власний вектор. Тоді
(Re - дійсна частина, Im - уявна)
утворюють фундаментальну систему рішень вихідної системи. (Тобто і = розглядаються разом)
Теорема 3.
Нехай - корінь характеристичного рівняння кратності 2. Тоді вихідна система має 2 лінійно незалежні рішення виду 
,
де , - Постійні вектор. Якщо ж кратності 3, то існує 3 лінійно незалежних рішення виду
.
Вектори знаходяться підставою рішень (*) і (**) у вихідну систему.
Щоб краще зрозуміти метод знаходження рішень виду (*) та (**), дивися розібрані типові приклади нижче.
Тепер розглянемо докладніше кожен із вищеописаних випадків.
1. Алгоритм вирішення однорідних систем диференціальних рівнянь третього порядку у разі різних дійсних коренів характеристичного рівняння.
Дана система
1) Складаємо характеристичне рівняння
- дійсні та різні власні значення 9корені цього рівняння).
2) Будуємо, де 
3) Будуємо, де
- Власний вектор матриці А, відповідний , тобто. - будь-яке рішення системи 
4) Будуємо, де
- Власний вектор матриці А, відповідний , тобто. - будь-яке рішення системи 
5)
становлять фундаментальну систему рішень. Далі записуємо загальне рішення вихідної системи у вигляді
,
тут C 1 , C 2 , C 3 - довільні постійні,
,
або в координатному вигляді 
Розглянемо кілька прикладів:
приклад 1.
2) Знаходимо 
3) Знаходимо 
4) Вектор-функції 
або в координатному записі 
приклад 2.
1)Складаємо та вирішуємо характеристичне рівняння: 
2) Знаходимо 
3) Знаходимо 
4) Знаходимо 
5) Вектор-функції 
утворюють фундаментальну систему. Загальне рішення має вигляд 
або в координатному записі 
2. Алгоритм розв'язання однорідних систем диференціальних рівнянь третього порядку у разі комплексно-сполучених коренів характеристичного рівняння.
- дійсний корінь,
2) Будуємо, де
 |
3) Будуємо
| - Власний вектор матриці А, відповідний , тобто. задовольняє системі |  |
Тут Re - дійсна частина
Im - уявна частина
4) становлять фундаментальну систему рішень. Далі записуємо загальне рішення вихідної системи:
, де
З 1 , 2 ,З 3 довільні постійні.
приклад 1.
1) Складаємо та вирішуємо характеристичне рівняння 
2) Будуємо
3) Будуємо
, де
Перше рівняння скоротимо на 2. Потім другого рівняння додамо перше, помножене на 2i, а від третього рівняння віднімемо перове, помножене на 2. 
Далі 
Отже, 
4) – фундаментальна система рішень. Запишемо загальне рішення вихідної системи: 
приклад 2.
1) Складаємо та вирішуємо харктеристичне рівняння 
2) Будуємо
(тобто і розглядаємо разом), де
Друге рівняння помножимо на (1-i) і скоротимо на 2. 
Отже, 
3)
Загальне рішення вихідної системи
або 
2. Алгоритм розв'язання однорідних систем диференціальних рівнянь третього порядку у разі кратного коріння характеристичного рівняння.
Складаємо та вирішуємо характеристичне рівняння
Можливі два випадки: 
Розглянемо випадок а) 1) , де
| - Власний вектор матриці А, що відповідає , тобто задовольняє системі | |
2) Пошлемося на Теорему 3, з якої випливає, що існують два лінійно незалежні рішення виду 
,
де , - Постійні вектори. Їх візьмемо за.
3) – фундаментальна система рішень. Далі записуємо загальне рішення вихідної системи:
Розглянемо випадок б):
1) Пошлемося на Теорему 3, з якої випливає, що існує три лінійно незалежні рішення виду
,
де , , - Постійні вектори. Їх візьмемо за.
2) – фундаментальна система рішень. Далі записуємо загальне рішення вихідної системи.
Щоб краще зрозуміти, як знаходити рішення виду (*), розглянемо кілька типових прикладів.
приклад 1.
Складаємо та вирішуємо характеристичне рівняння: 
Маємо випадок а)
1) Будуємо 
, де
З другого рівняння віднімаємо перше:
? третій рядок подібний до другого, його викреслюємо. З першого рівняння віднімемо друге: 
2) = 1 (кратність 2)
Цьому кореню по Т.3 має відповідати два лінійно незалежні рішення виду.
Спробуємо визначити всі лінійно незважальні рішення, які мають , тобто. рішення виду
.
Такий вектор буде рішенням і тоді, коли - власний вектор, відповідний =1, тобто.
, або 
, другий і третій рядки подібні до першого, викидаємо їх. 
Система звелася до одного рівняння. Отже, є два вільні невідомі, наприклад, і . Дамо їм спочатку значення 1, 0; потім значення 0, 1. Отримаємо такі рішення: 
.
Отже, 
.
3) – фундаментальна система рішень. Залишилось записати загальне рішення вихідної системи: 
. .. Таким чином існує тільки одне рішення виду Підставимо X 3 в цю систему: Викреслимо третій рядок (вона подібна до другого). Система спільна (має рішення) за будь-якого с. Нехай =1. 
або 
Габріель Крамер – математик, творець однойменного методу розв'язання систем лінійних рівнянь
Габріель Крамер – відомий математик, який народився 31 липня 1704 року. Ще в дитинстві Габріель вражав своїми інтелектуальними здібностями, особливо математики. Коли Крамеру було 20 років, він улаштувався в Женевський університет штатним викладачем.
Під час подорожі Європою Габріель познайомився з математиком Йоганном Бернуллі, який і став його наставником. Тільки завдяки Йоганну, Крамер написав багато статей з геометрії, історії математики та філософії. А у вільний від роботи час вивчав математику дедалі більше.
Нарешті настав той день, коли Крамер знайшов спосіб, за допомогою якого можна було б легко вирішувати не лише легкі, а й складні системи лінійних рівнянь.
У 1740 році у Крамера було опубліковано кілька робіт, де доступно викладено рішення квадратних матрицьта описаний алгоритм, як знаходити зворотну матрицю . Далі математик описував знаходження лінійних рівнянь різної складності, де можна застосувати його формули. Тому тему і назвали: «Рішення систем лінійних рівнянь методом Крамера».
Вчений помер у віці 48 років (1752 року). Він мав ще багато планів, але, на жаль, він так і не встиг їх здійснити.
Нехай дана система лінійних рівнянь такого виду:
де , , - невідомі змінні, - це числові коефіцієнти, - вільні члени.
Рішенням СЛАУ (систем лінійних рівнянь алгебри) називаються такі невідомі значення при яких всі рівняння даної системи перетворюються на тотожності.
Якщо записати систему в матричному вигляді, тоді виходить , де
У цій головній матриці знаходяться елементи, коефіцієнти яких при невідомих змінних,
Це матриця-стовпець вільних членів, але є ще матриця-стовпець невідомих змінних:
Після того, як знайдуться невідомі змінні, матриця і буде рішенням системи рівнянь, а наша рівність перетворюється на тотожність. . Якщо помножити, тоді. Виходить: .
Якщо матриця – невироджена, тобто, її визначник не дорівнює нулю, тоді СЛАУ має лише одне єдине рішення, яке знаходиться за допомогою методу Крамера.
Як правило, для вирішення систем лінійних рівнянь методом Крамера, потрібно звертати увагу на дві властивості, на яких і заснований цей метод:
1. Визначник квадратної матриці дорівнює сумі творів елементів будь-якого з рядків (стовпця) на їх додатки алгебри:
Тут - 1, 2, ..., n; - 1, 2, 3, ..., n.
2. Сума творів елементів даної матриці будь-якого рядка або будь-якого стовпця на додатки алгебри певних елементів другого рядка (стовпця) дорівнює нулю:
де - 1, 2, ..., n; - 1, 2, 3, ..., n. .
Отже, тепер можна знайти перше невідоме. Для цього необхідно помножити обидві частини першого рівняння системи на частини з другого рівняння на обидві частини третього рівняння на і т. д. Тобто, кожне рівняння однієї системи потрібно множити на певні додатки алгебри першого стовпця матриці :
Тепер додамо всі ліві частини рівняння, згрупуємо доданки, враховуючи невідомі змінні і прирівняємо цю суму до суми правих частин системи рівняння:
Можна звернутися до вищеописаних властивостей визначників і тоді отримаємо:
І попередня рівність вже виглядає так:
Звідки і виходить.
Аналогічно знаходимо. Для цього треба помножити обидві частини рівнянь на додатки алгебри, які знаходяться в другому стовпці матриці .
Тепер потрібно скласти всі рівняння системи та згрупувати доданки при невідомих змінних. Для цього пригадаємо властивості визначника:
Звідки виходить.
Аналогічно перебувають решта невідомих змінних.
Якщо позначити:
тоді виходять формули, завдяки яким перебувають невідомі змінні методом Крамера:
Зауваження.
Тривіальне рішення може бути тільки в тому випадку, якщо система рівнянь є однорідною . Якщо всі вільні члени нульові, тоді і визначники дорівнюють нулю, тому що в них міститься стовпець з нульовими елементами. Звичайно ж, тоді формули , , дадуть
Метод Крамера – теореми
Перш ніж розв'язувати рівняння, необхідно знати:
- теорему анулювання;
- теорему заміщення.
Теорема заміщення
Теорема
Сума творів додатків алгебри будь-якого стовпця (рядки) на довільні числа дорівнює новому визначнику, в якому цими числами замінені відповідні елементи початкового визначника, що відповідають даним алгебраїчним доповненням.
Наприклад,
де - Додатки алгебри елементів першого стовпця початкового визначника:
Теорема анулювання
Теорема
Сума творів елементів одного рядка (стовпця) на додатки алгебри відповідних елементів іншого рядка (стовпця) дорівнює нулю.
Наприклад:
Алгоритм розв'язання рівнянь методом Крамера
Метод Крамера – простий спосіб вирішення лінійних систем алгебраїчних рівнянь. Такий варіант застосовується виключно до СЛАУ, у яких збігається кількість рівнянь із кількістю невідомих, а визначник відмінний від нуля.
Отже, коли вивчили всі етапи, можна переходити до алгоритму розв'язання рівнянь методом Крамера. Запишемо його послідовно:
Крок 1. Обчислюємо головний визначник матриці
і необхідно переконатися, що визначник відмінний від нуля (не дорівнює нулю).
Крок 2. Знаходимо визначники
Це і є визначники матриць, які виходили із матриці при заміні стовпців на вільні члени.
Крок 3. Обчислюємо невідомі змінні
Тепер згадуємо формули Крамера, за якими обчислюємо коріння (невідомі змінні):
Крок 4. Виконуємо перевірку
Виконуємо перевірку рішення за допомогою підстановки у вихідну СЛАУ. Абсолютно всі рівняння в системі повинні бути перетворені на тотожність. Також можна вирахувати добуток матриць. Якщо у результаті вийшла матриця, яка дорівнює , тоді система вирішена правильно. Якщо ж не дорівнює , Швидше за все в одному з рівнянь є помилка.
Давайте для початку розглянемо систему двох лінійних рівнянь, тому що вона простіша і допоможе зрозуміти, як правильно використовувати правило Крамера. Якщо ви зрозумієте прості та короткі рівняння, тоді зможете вирішити складніші системи трьох рівнянь із трьома невідомими.
Крім іншого, є системи рівнянь із двома змінними, які вирішуються виключно завдяки правилу Крамеру.
Отже, дана система двох лінійних рівнянь:
Для початку обчислюємо головний визначник (визначник системи):
Значить, якщо , тоді система або багато рішень, або система не має рішень. У цьому випадку користуватися правилом Крамера немає сенсу, оскільки рішення не вийде і потрібно згадувати метод Гаусса, за допомогою якого цей приклад вирішується швидко і легко.
У випадку, якщо , тоді система має всього одне рішення, але для цього необхідно обчислити ще два визначники і знайти коріння системи.
Часто практично визначники можуть позначатися як , а й латинської літерою , що теж правильно.
Коріння рівняння знайти просто, оскільки головне знати формули:
Так як ми змогли вирішити систему двох лінійних рівнянь, тепер без проблем вирішимо систему трьох лінійних рівнянь, а для цього розглянемо систему:
Тут алгебраїчні доповнення елементів – перший стовпець. Під час рішення не забувайте про додаткові елементи. Отже, у системі лінійних рівнянь потрібно знайти три невідомі – при відомих інших елементах.
Створимо визначник системи з коефіцієнтів при невідомих:
Помножимо почленно кожне рівняння відповідно на , , – додатки алгебри елементів першого стовпця (коефіцієнтів при ) і додамо всі три рівняння. Отримуємо:
Відповідно до теореми про розкладання, коефіцієнт дорівнює . Коефіцієнти при і дорівнюватимуть нулю по теоремі анулювання. Права частина рівності за теоремою заміщення дає новий визначник, який називається допоміжним та позначається
Після цього можна записати рівність:
Для знаходження і перемножимо кожне з рівнянь початкової системи у першому випадку відповідно на , у другому – і додамо. Згодом перетворень отримуємо:
Якщо , тоді в результаті одержуємо формули Крамера:
Порядок розв'язання однорідної системи рівнянь
Окремий випадок – це однорідні системи:
Серед рішень однорідної системи може бути, як нульові рішення , і рішення відмінні від нуля.
Теорема
Якщо визначник однорідної системи (3) відмінний від нуля, тоді така система може мати лише одне рішення.
Дійсно, допоміжні визначники, як такі, у яких є нульовий стовпець і тому, за формулами Крамера
Теорема
Якщо однорідна система має відмінне від нуля рішення, тоді її визначник дорівнює нулю
Справді, нехай одна з невідомих, наприклад, відмінна від нуля. Відповідно до однорідності Рівність (2) запишеться: . Звідки випливає, що
Приклади рішення методом Крамера
Розглянемо на прикладі рішення методом Крамера і ви побачите, що складного нічого немає, але будьте дуже уважно, тому що часті помилки у знаках призводять до невірної відповіді.
Приклад 1
Завдання
Рішення
Перше, що треба зробити – обчислити визначник матриці:
Як бачимо, тому по теоремі Крамера система має єдине рішення (система спільна). Далі слід обчислювати допоміжні визначники. Для цього замінюємо перший стовпець із визначника на стовпець вільних коефіцієнтів. Виходить:
Аналогічно знаходимо інші визначники:
І перевіряємо:
Відповідь
Приклад 2
Завдання
Розв'язати систему рівнянь методом Крамера:
Рішення
Знаходимо визначники:
Відповідь
= = = = = =
Перевірка
Рівняння має єдине рішення.
Відповідь
Приклад 3
Завдання
Вирішити систему методом Крамера
Рішення
Як ви розумієте, спочатку знаходимо головний визначник:
Як бачимо, головний визначник не дорівнює нулю і тому система має єдине рішення. Тепер можна обчислити решту визначників:
За допомогою формул Крамера знаходимо коріння рівняння:
Щоб переконатися у правильності рішення, необхідно перевірити:
Як бачимо, підставивши в рівняння розв'язане коріння, у нас відповідь вийшла та сама, що і на початку завдання, що говорить про правильне вирішення рівнянь.
Відповідь
Система рівнянь має єдине рішення: , , .
Є приклади, коли рівняння рішень немає. Це може бути в тому випадку, коли визначник системи дорівнює нулю, а визначники за невідомих нерівні нулю. У такому разі кажуть, що система несумісна, тобто немає рішень. Подивимося на прикладі, як таке може бути.
Приклад 4
Завдання
Розв'язати систему лінійних рівнянь методом Крамера:
Рішення
Як і попередніх прикладах знаходимо головний визначник системи:
У цій системі визначник дорівнює нулю, відповідно система несумісна і визначена або ж несумісна і не має рішень. Щоб уточнити, треба знайти визначники за невідомих так, як ми робили раніше:
Ми знайшли визначники при невідомих і побачили, що всі вони не дорівнюють нулю. Тому система несумісна і немає рішень.
Відповідь
Система немає рішень.
Часто в завданнях на системи лінійних рівнянь зустрічаються такі рівняння, де є не однакові літери, тобто, окрім літер, які позначають змінні, є ще й інші літери, і вони означають деяке дійсне число. На практиці до таких рівнянь та систем рівнянь наводять завдання на пошук загальних властивостей будь-яких явищ та предметів. Тобто винайшли ви якийсь новий матеріал або пристрій, а для опису його властивостей, загальних незалежно від величини або кількості екземпляра, потрібно вирішити систему лінійних рівнянь, де замість деяких коефіцієнтів при змінних – літери. Давайте розглянемо такий приклад.
Використовуючи формули Крамера, знаходимо:
Відповідь
І нарешті, ми перейшли до найскладнішої системи рівнянь із чотирма невідомими. Принцип рішення такий самий, як і в попередніх прикладах, але у зв'язку з великою системою можна заплутатися. Тому розглянемо таке рівняння з прикладу.
У початковому визначники з елементів другого рядка ми забирали елементи четвертого рядка, а з елементів третього рядка відбиралися елементи четвертого рядка, які множилися на 2. Також вилучали з елементів четвертого рядка елементи першого рядка, помноженого на два. Перетворення початкових визначників за трьох перших невідомих зроблено за такою ж схемою. Тепер можна знаходити визначники при невідомих:
Для перетворення визначника при четвертому невідомому з елементів першого рядка ми вичитали елементи четвертого рядка.
Тепер за формулами Крамера потрібно знайти:
Відповідь
Отже, ми знайшли коріння системи лінійного рівняння:
Підведемо підсумки
За допомогою методу Крамера можна вирішувати системи лінійних рівнянь алгебри в тому випадку, якщо визначник не дорівнює нулю. Такий метод дозволяє знаходити визначники матриць такого порядку, як завдяки формулам Крамера, коли потрібно знайти невідомі змінні. Якщо всі вільні члени нульові, тоді їх визначники дорівнюють нулю, тому що в них міститься стовпець з нульовими елементами. І звичайно ж, якщо визначники дорівнюють нулю, краще вирішувати систему методом Гауса Метод Крамера в Excel від 2007 (XLSX)
Метод Крамера – теорема, приклади рішеньоновлено: 22 листопада, 2019 автором: Статті.Ру
Матриці. Події над матрицями. Властивості операцій над матрицями. Види матриць.
Матриці (і відповідно математичний розділ – матрична алгебра)мають важливе значення у прикладній математиці, оскільки дозволяють записати у досить простій формі значну частину математичних моделей об'єктів та процесів. Термін "матриця" з'явився 1850 року. Вперше згадувалися матриці ще в стародавньому Китаї, Пізніше у арабських математиків.
Матрицею A=A mnпорядку m*n називається прямокутна таблиця чисел, що містить m - рядків та n - стовпців.
Елементи матриці a ij ,у яких i=j називаються діагональними і утворюють головну діагональ.
Для квадратної матриці (m=n) головну діагональ утворюють елементи a 11 , a 22 ,..., a nn .
Рівність матриць.
A=Bякщо порядки матриць Aі Bоднакові та a ij = b ij (i=1,2,...,m; j=1,2,...,n)
Події над матрицями.
1. Додавання матриць - поелементна операція
Віднімання матриць - поелементна операція
3. Добуток матриці на число - поелементна операція
4. Множення A*Bматриць за правилом рядок на стовпець(число стовпців матриці А має дорівнювати числу рядків матриці B)
A mk * B kn = C mnпричому кожен елемент з ijматриці C mn дорівнює сумітворів елементів i-го рядка матриці А на відповідні елементи j-го стовпця матриці B.
Покажемо операцію множення матриць на прикладі:
6. Транспонування матриці А. Транспоновану матрицю позначають A T або A
Рядки та стовпці помінялися місцями
приклад
Властивості операцій над матрицями
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
Види матриць
1. Прямокутні: mі n- довільні позитивні цілі числа
2. Квадратні: m=n
3. Матриця рядок: m=1. Наприклад, (1 3 5 7) - у багатьох практичних завданнях така матриця називається вектором
4. Матриця стовпець: n=1. Наприклад
5. Діагональна матриця: m=nі a ij = 0, якщо i≠j. Наприклад
6. Поодинока матриця: m=nі
7. Нульова матриця: a ij =0, i=1,2,...,m
j=1,2,...,n
8. Трикутна матриця: всі елементи нижче головної діагоналі дорівнюють 0.
9. Квадратна матриця: m=nі a ij = a ji(тобто на симетричних щодо головної діагоналі місцях стоять рівні елементи), а отже A"=A
Наприклад,
Зворотна матриця- така матриця A −1при множенні на яку вихідна матриця Aдає в результаті поодиноку матрицю E:
Квадратна матриця оборотна тоді і лише тоді, коли вона невироджена, тобто її визначник не дорівнює нулю. Для неквадратних матриць та вироджених матриць зворотних матриць не існує. Однак можна узагальнити це поняття і ввести псевдозворотні матриці, схожі на зворотні за багатьма властивостями.
Приклади розв'язання систем лінійних рівнянь алгебри матричним методом.
Розглянемо матричний метод на прикладах. У деяких прикладах ми не детально описуватимемо процес обчислення визначників матриць.
приклад.
За допомогою зворотної матрицізнайдіть розв'язок системи лінійних рівнянь
.
Рішення.
У матричній формі вихідна система запишеться як, де 
. Обчислимо визначник основної матриці та переконаємося, що він відмінний від нуля. Інакше ми зможемо вирішити систему матричним методом. Маємо 
, отже, для матриці Аможе бути знайдена зворотна матриця. Таким чином, якщо ми знайдемо зворотну матрицю, то рішення СЛАУ визначимо як . Отже, завдання звелося до побудови зворотної матриці. Знайдемо її.
Зворотну матрицю можна знайти за такою формулою:
де - визначник матриці А, - транспонована матриця алгебраїчних доповнень відповідних елементів матриці .
Поняття зворотної матриці існує лише для квадратних матриць, матриць "два на два", "три на три" і т.д.
Полярні координати. У полярній системі координат положення точки М
М
ПРЯМОКУТНІ КООРДИНАТИ В ПРОСТОРІ
ПРЯМА
1. Загальне рівнянняпрямий.Будь-яке рівняння першого ступеня щодо х і у, тобто рівняння виду:
(1) Ах + Ву + С = 0 зв. громад рівнянням прямої (+ ≠0),A,B,C-ПОСТОЯННІ КОЕФІЦІЄНТИ.
КРИВІ ДРУГОГО ПОРЯДКУ
1. Коло.Окружність-це безліч точок площини, рівновіддалений -
рівновіддалених від цієї точки (центру). Якщо г - радіус кола, а точка С (а; Ь) - її центр, то рівняння кола має вигляд:
Гіперболу. Гіперболою називається безліч точок площини, абсолютна
величина різниці відстаней яких до двох даних точок, званих фо-
кусами, є постійна величина (її позначають через 2а), причому ця постійна менше відстані між фокусами. Якщо помістити фокуси гіперболи в точках F1 (с; 0) і F2 (- с; 0), то вийде канонічне рівняння гіперболи 
АНАЛІТИЧНА ГЕОМЕТРІЯ У ПРОСТОРІ
ПЛОЩИНА І ПРЯМА
площині,названий нормальним вектором.
Поверхня другого порядку
Поверхня другого порядку- геометричне місце точок тривимірного простору, прямокутні координати яких задовольняють рівняння виду
в якому принаймні один з коефіцієнтів , , , , відмінний від нуля.
Типи поверхонь другого порядку
Циліндричні поверхні
Поверхня називається циліндричною поверхнею з твірноюякщо для будь-якої точки цієї поверхні пряма, що проходить через цю точку паралельно утворює , цілком належить поверхні .
Теорема (про рівняння циліндричної поверхні).
Якщо в деякій декартовій системі прямокутної координат поверхня має рівняння , то - циліндрична поверхня з твірною, паралельної осі .
Крива, що задається рівнянням у площині, називається спрямовуючоюциліндричної поверхні.
Якщо напрямна циліндричної поверхні задається кривою другого порядку, то така поверхня називається циліндричною поверхнею другого порядку .
| Еліптичний циліндр: | Параболічний циліндр: | Гіперболічний циліндр: |
 |  |
|
 |  |  |
| Пара прямих, що збіглися: | Пара площин, що збіглися: | Пара площин, що перетинаються: |
 |  |
Конічні поверхні
Конічна поверхня.
Основна стаття:Конічна поверхня
Поверхня називається конічною поверхнеюз вершиною в точціякщо для будь-якої точки цієї поверхні пряма, що проходить через і , цілком належить цій поверхні.
Функція називається однорідного порядку, якщо виконується таке:
Теорема (про рівняння конічної поверхні).
Якщо в деякій декартовій системі прямокутної координат поверхня задана рівнянням 
де - однорідна функція, то - конічна поверхня з вершиною на початку координат.
Якщо поверхня задана функцією , що є однорідним багаточленом алгебри другого порядку, то називається конічною поверхнею другого порядку .
· Канонічне рівняння конуса другого порядку має вигляд:
Поверхні обертання]
Поверхня називається поверхнею обертання навколо осі, якщо для будь-якої точки 
цієї поверхні коло, що проходить через цю точку в площині з центром і радіусом 
, повністю належить цій поверхні.
Теорема (про рівняння поверхні обертання).
Якщо в деякій декартовій прямокутній системі координат поверхня задана рівнянням, то поверхня обертання навколо осі.
| Еліпсоід: | Однопорожнинний гіперболоїд: | Двопорожнинний гіперболоїд: | Еліптичний параболоїд: |
 |  |  |  |
 |  |  |  |
Якщо перераховані вище поверхні є поверхнями обертання.
Еліптичний параболоїд
Рівняння еліптичного параболоїда має вигляд
Якщо , то еліптичний параболоїд є поверхнею обертання, утворену обертанням параболи, параметр якої 
навколо вертикальної осі, що проходить через вершину і фокус цієї параболи.
Перетин еліптичного параболоїда з площиною є еліпсом.
Перетин еліптичного параболоїда з площиною або параболою.
Гіперболічний параболоїд]
Гіперболічний параболоїд.
Рівняння гіперболічного параболоїда має вигляд
Перетин гіперболічного параболоїда з площиною є гіперболою.
Перетин гіперболічного параболоїда з площиною або параболою.
Через геометричну схожість гіперболічний параболоїд часто називають «сідлом».
Центральні поверхні
Якщо центр поверхні другого порядку існує і єдиний, його координати можна знайти, вирішивши систему рівнянь:
Таким чином, знак, який при цьому приписується мінору відповідного елемента визначника, визначається наступною таблицею:
У наведеній вище рівністі, що виражає визначник третього порядку,
у правій частині стоїть сума творів елементів 1-го рядка визначника з їхньої алгебраїчні доповнення.
Теорема 1. Визначник третього порядку дорівнює сумі творів
елементів будь-якого його рядка або стовпця на їх додатки алгебри.
Ця теорема дозволяє обчислювати значення визначника, розкриваючи його за
елементам будь-якого його рядка чи стовпця.
Теорема 2. Сума творів елементів будь-якого рядка (стовпця)
визначника на додатки алгебри елементів іншого рядка (стовпця) дорівнює нулю.
Властивості визначників.
1°. Визначник не зміниться, якщо рядки визначника замінити стовп-
ними, а стовпці-відповідними рядками.
2 °. Загальний множник елементів якогось рядка (або стовпця) може
бути винесений за знак визначника.
3 °. Якщо елементи одного рядка (стовпця) визначника відповідно
рівні елементам іншого рядка (стовпця), то визначник дорівнює нулю.
4 °. При перестановці двох рядків (стовпців) визначник змінює знак на
протилежний.
5 °. Визначник не зміниться, якщо до елементів одного рядка (стовпця)
додати відповідні елементи іншого рядка (стовпця), помножені на те саме число (теорема про лінійну комбінацію паралельних рядів визначника).
Розв'язання системи трьох лінійних рівнянь із трьома невідомими.
знаходиться за формулами Крамера
У цьому передбачається, що D ≠0 (якщо D = 0, вихідна система або невизначена, або несовместная).
Якщо система однорідна, тобто має вигляд 
і її визначник відмінний від нуля, вона має єдине рішення х= 0,
Якщо ж визначник однорідної системи дорівнює нулю, система зводиться
або до двох незалежних рівнянь (третє є їх наслідком), або до
одному рівнянню (інші два є його наслідками). Перший випадок
має місце тоді, коли серед мінорів визначника однорідної системи є
хоча б один відмінний від нуля, другий-тоді, коли всі мінори цього опреде лителя дорівнюють нулю. В обох випадках однорідна система має безліч рішень.
Обчислити визначник третього порядку
