Представлені основні тригонометричні формули та основні підстановки. Викладено методи інтегрування тригонометричних функцій- інтегрування раціональних функцій, добуток статечних функцій від sin x і cos x, добуток багаточлена, експоненти та синуса чи косинуса, інтегрування зворотних тригонометричних функцій. Торкнулися нестандартних методів.
ЗмістСтандартні методи інтегрування тригонометричних функцій
Загальний підхід
Спочатку, якщо це необхідно, підінтегральний вираз потрібно перетворити, щоб тригонометричні функції залежали від одного аргументу, який збігався б із змінною інтегрування.
Наприклад, якщо підінтегральний вираз залежить від sin(x+a)і cos(x+b), то слід виконати перетворення:
cos(x+b) = cos(x+a - (a-b)) = cos (x+a) cos (b-a) + sin ( x+a ) sin (b-a).
Після цього зробити заміну z = x + a. У результаті тригонометричні функції залежатимуть тільки від змінної інтегрування z .
Коли тригонометричні функції залежать від одного аргументу, що збігається зі змінною інтегрування (припустимо це z), тобто підінтегральний вираз складається тільки з функцій типу sin z,
cos z,
tg z,
ctg z, то потрібно зробити підстановку
.
Така підстановка призводить до інтегрування раціональних чи ірраціональних функцій (якщо є коріння) і дозволяє обчислити інтеграл, якщо він інтегрується до елементарних функцій.
Однак часто можна знайти інші методи, які дозволяють обчислити інтеграл більш коротким способом, ґрунтуючись на специфіці підінтегрального виразу. Нижче наведено виклад основних таких методів.
Методи інтегрування раціональних функцій від sin x та cos x
Раціональні функції від sin xі cos x- це функції, утворені з sin x,
cos xі будь-яких постійних за допомогою операцій складання, віднімання, множення, поділу та зведення в цілий ступінь. Вони позначаються так: R (sin x, cos x). Сюди також можуть входити тангенси та котангенси, оскільки вони утворені розподілом синуса на косинус і навпаки.
Інтеграли від раціональних функцій мають вигляд:
.
Методи інтегрування раціональних тригонометричних функцій такі.
1) Підстановка завжди призводить до інтегралу від раціонального дробу. Однак, у деяких випадках, існують підстановки (вони представлені нижче), які призводять до більш коротких обчислень.
2) Якщо R (sin x, cos x) cos x → - cos x sin x.
3) Якщо R (sin x, cos x)множиться на -1 під час заміни sin x → sin x, то виконується підстановка t = cos x.
4) Якщо R (sin x, cos x)не змінюється як за одночасної заміни cos x → - cos x, і sin x → sin x, то застосовується підстановка t = tg xабо t = ctg x.
Приклади:
,
,
.
Добуток статечних функцій від cos x і sin x
Інтеграли виду
є інтегралами від раціональних тригонометричних функцій. Тому до них можна застосувати методи, викладені у попередньому розділі. Нижче розглянуто методи, що базуються на специфіці таких інтегралів.
Якщо m і n – раціональні числа, то однією з підстановок t = sin xабо t = cos xінтеграл зводиться до інтегралу від диференціального бінома.
Якщо m та n - цілі числа, то інтегрування виконується за допомогою формул приведення:
;
;
;
.
Приклад:
.
Інтеграли від твору багаточлена та синуса чи косинуса
Інтеграли виду:
,
,
де P(x) - многочлен від x, інтегруються частинами. При цьому виходять такі формули:
;
.
Приклади:
,
.
Інтеграли від твору багаточлена, експоненти та синуса чи косинуса
Інтеграли виду:
,
,
де P(x) - багаточлен від x інтегруються за допомогою формули Ейлера
e iax = cos ax + isin ax(Де i 2 = - 1
).
Для цього методом, викладеним у попередньому пункті, обчислюють інтеграл
.
Виділивши з результату дійсну та уявну частину, отримують вихідні інтеграли.
Приклад:
.
Нестандартні методи інтегрування тригонометричних функцій
Нижче наведено низку нестандартних методів, які дозволяють виконати чи спростити інтегрування тригонометричних функцій.
Залежність від (a sin x + b cos x)
Якщо підінтегральний вираз залежить лише від a sin x + b cos x, то корисно застосувати формулу:
,
де.
Наприклад
Розкладання дробу з синусів і косинусів на простіші дроби
Розглянемо інтеграл
.
Найбільш простий спосіб інтегрування полягає в розкладанні дробу на простіші, застосовуючи перетворення:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)
Інтегрування дробів першого ступеня
При обчисленні інтегралу
,
зручно виділити цілу частину дробу та похідну знаменника
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)′ .
Постійні A і B виходять із порівняння лівої та правої частин.
Використана література:
Н.М. Гюнтер, Р.О. Кузьмін, Збірник завдань з вищої математики, "Лань", 2003.
Будуть і завдання для самостійного рішення, до яких можна переглянути відповіді.
Підінтегральний вираз можна перетворити з твору тригонометричних функцій на суму
Розглянемо інтеграли, в яких підінтегральна функція є твір синусів і косінусів першого ступеня від іксу, помноженого на різні множники, тобто інтеграли виду
Скориставшись відомими тригонометричними формулами
(2)
(3)
(4)
можна перетворити кожен із творів в інтегралах виду (31) в алгебраїчну сумута проінтегрувати за формулами
![]() (5)
(5)
![]() (6)
(6)
приклад 1.Знайти
![]()
Рішення. За формулою (2) при



приклад 2.Знайти інтеграл від тригонометричної функції
![]()
Рішення. За формулою (3) при ![]()

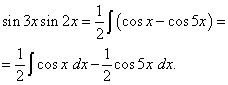
![]()
приклад 3.Знайти інтеграл від тригонометричної функції
![]()
Рішення. За формулою (4) при ![]() отримуємо наступне перетворення підінтегрального виразу:
отримуємо наступне перетворення підінтегрального виразу:

Застосовуючи формулу (6), отримаємо
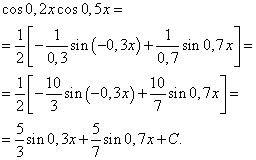
Інтеграл твору ступенів синуса та косинуса одного і того ж аргументу
Розглянемо тепер інтеграли від функцій, які є твір ступенів синуса і косинуса однієї й тієї ж аргументу, тобто.
![]() (7)
(7)
У окремих випадках один із показників ( mабо n) може дорівнювати нулю.
При інтегруванні таких функцій використовують те, що парний ступінь косинуса можна виразити через синус, а диференціал синуса дорівнює cos x dx(або парний ступінь синуса можна виразити через косинус, а диференціал косинуса дорівнює - sin x dx ) .
Слід розрізняти два випадки: 1) хоча б один із показників mі nнепарний; 2) обидва показники парні.
Нехай має місце перший випадок, а саме показник n = 2k+ 1 – непарний. Тоді, враховуючи, що
![]()
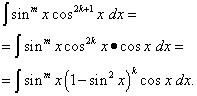
Подинтегральное вираз представлено у вигляді, що його частина – функція лише синуса, іншу – диференціал синуса. Тепер за допомогою заміни змінної t= sin xрішення зводиться до інтегрування багаточлена щодо t. Якщо ж лише ступінь mнепарна, то чинять аналогічно, виділяючи множник sin x, висловлюючи решту підінтегральної функції через cos xі вважаючи t= cos x. Цей прийом можна використовувати і при інтегруванні приватного ступенів синуса та косинуса , коли хоча б один із показників - непарний . Вся справа в тому, що приватне ступенів синуса та косинуса - це окремий випадок їх твору : коли тригонометрична функція знаходиться в знаменнику підінтегрального виразу, її ступінь - негативний. Але бувають і випадки приватного тригонометричних функцій, коли їх ступеня – лише парні. Про них – наступний абзац.
Якщо ж обидва показники mі n– парні, то, використовуючи тригонометричні формули

знижують показники ступеня синуса та косинуса, після чого вийде інтеграл того самого типу, що й вище. Тому інтегрування слід продовжувати за тією самою схемою. Якщо ж один із парних показників - негативний, тобто розглядається приватне парних ступенів синуса та косинуса, то дана схема не годиться . Тоді використовується заміна змінної залежно від цього, як можна перетворити подынтегральное вираз. Такий випадок буде розглянуто у наступному параграфі.
приклад 4.Знайти інтеграл від тригонометричної функції
![]()
Рішення. Показник ступеня косинуса – непарний. Тому уявімо
t= sin x(тоді dt= cos x dx ). Тоді отримаємо

Повертаючись до старої змінної, остаточно знайдемо
![]()
Приклад 5.Знайти інтеграл від тригонометричної функції
![]() .
.
Рішення. Показник ступеня косинуса, як і попередньому прикладі – непарний, але більше. Уявимо
![]()
і зробимо заміну змінної t= sin x(тоді dt= cos x dx ). Тоді отримаємо
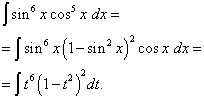
Розкриємо дужки
![]() і отримаємо
і отримаємо

Повертаючись до старої змінної, отримуємо рішення

Приклад 6.Знайти інтеграл від тригонометричної функції
![]()
Рішення. Показники ступеня синуса та косинуса – парні. Тому перетворимо підінтегральну функцію так:
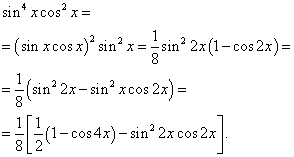
Тоді отримаємо
У другому інтегралі зробимо заміну змінної, вважаючи t= sin2 x. Тоді (1/2)dt= cos2 x dx . Отже,


Остаточно отримуємо
![]()
Використання методу заміни зміною
Метод заміни змінноїпри інтегруванні тригонометричних функцій можна застосовувати у випадках, коли в підінтегральному вираженні присутній тільки синус або тільки косинус, добуток синуса і косинуса, в якому або синус або косинус - в першому ступені, тангенс або котангенс, а також приватне парних ступенів синуса і косинуса одного і того ж аргументу. При цьому можна проводити перестановки не тільки в sin x = tі sin x = t, Але і tg x = tта ctg x = t .
Приклад 8.Знайти інтеграл від тригонометричної функції
![]() .
.
Рішення. Зробимо заміну змінної: , Тоді . Підинтегральний вираз, що вийшов, легко інтегрується за таблицею інтегралів:
![]() .
.
![]()
Приклад 9.Знайти інтеграл від тригонометричної функції
Рішення. Перетворюємо тангенс у відношенні синуса та косинуса:
Зробимо заміну змінної: , Тоді . Підинтегральний вираз, що вийшов, являє собою табличний інтегралзі знаком мінус:
![]() .
.
Повертаючись до початкової змінної, остаточно отримуємо:
![]() .
.
приклад 10.Знайти інтеграл від тригонометричної функції
Рішення. Зробимо заміну змінної: , Тоді .
Перетворимо підінтегральний вираз, щоб застосувати тригонометричну тотожність ![]() :
:
Здійснюємо заміну змінної, не забуваючи перед інтегралом поставити знак мінус (дивіться вище, чому одно dt). Далі розкладаємо підінтегральний вираз на множники та інтегруємо за таблицею:
Повертаючись до початкової змінної, остаточно отримуємо:
![]() .
.
Знайти інтеграл від тригонометричної функції самостійно, а потім переглянути рішення
Універсальна тригонометрична підстановка
Універсальну тригонометричну підстановку можна застосовувати у випадках, коли підінтегральний вираз не підпадає під випадки, розібрані у попередніх параграфах. В основному, коли синус або косинус (або те й інше) знаходяться в знаменнику дробу. Доведено, що синус та косинус можна замінити іншим виразом, що містить тангенс половини вихідного кута наступним чином:
Але зауважимо, що універсальна тригонометрична підстановка часто спричиняє досить складні. алгебраїчні перетворенняТому її краще застосовувати, коли ніякий інший метод не працює. Розберемо приклади, коли разом із універсальною тригонометричною підстановкою використовуються підведення під знак диференціалу та метод невизначених коефіцієнтів.
приклад 12.Знайти інтеграл від тригонометричної функції
![]() .
.
Рішення. Рішення. Скористаємося універсальною тригонометричною підстановкою. Тоді  .
.
Дроби в чисельнику та знаменнику множимо на , а двійку виносимо і ставимо перед знаком інтеграла. Тоді
Докладно розглянуті приклади рішень інтегралів частинами, подинтегральное вираз яких є твором многочлена на експоненту (е ступеня х) чи синус (sin x) чи косинус (cos x).
ЗмістДив. також: Метод інтегрування частинами
Таблиця невизначених інтегралів
Методи обчислення невизначених інтегралів
Основні елементарні функції та їх властивості
Формула інтегрування частинами
При вирішенні прикладів цього розділу використовується формула інтегрування частинами:
;
.
Приклади інтегралів, що містять добуток багаточлена і sin x, cos x або e x
Ось приклади таких інтегралів:
, , .
Для інтегрування подібних інтегралів, многочлен позначають через u , а частину, що залишилася - через v dx . Далі застосовують формулу інтегрування частинами.
Нижче дається докладне рішенняцих прикладів.
Приклади вирішення інтегралів
Приклад з експонентою, е в ступені х
Визначити інтеграл:
.
Введемо експоненту під знак диференціалу:
e - x dx = - e - x d(-x) = - d(e - x).
Інтегруємо частинами.
тут
.
Інтеграл, що залишився, також інтегруємо частинами.
.
.
.
Остаточно маємо:
.
Приклад визначення інтеграла із синусом
Обчислити інтеграл:
.
Введемо синус під знак диференціалу:
Інтегруємо частинами.
тут u = x 2 , v = cos(2 x+3), du = (
x 2 )′
dx
Інтеграл, що залишився, також інтегруємо частинами. І тому вводимо косинус під знак диференціала.
тут u = x, v = sin(2 x+3), du = dx
Остаточно маємо:
Приклад твору багаточлена та косинуса
Обчислити інтеграл:
.
Введемо косинус під знак диференціалу:
Інтегруємо частинами.
тут u = x 2 + 3 x + 5, v = sin 2 x, du = (
x 2 + 3 x + 5 )′
dx
Інтеграли від тригонометричних функцій.
Приклади рішень
На даному уроці ми розглянемо інтеграли від тригонометричних функцій, тобто начинкою інтегралів у нас будуть синуси, косінуси, тангенси та котангенси у різних комбінаціях. Всі приклади будуть розібрані докладно, доступно та зрозуміло навіть для чайника.
Для успішного вивчення інтегралів від тригонометричних функцій Ви повинні добре орієнтуватися у найпростіших інтегралах, а також мати деякі прийоми інтегрування. Ознайомитись із цими матеріалами можна на лекціях Невизначений інтеграл. Приклади рішеньта .
А зараз нам знадобляться: Таблиця інтегралів, Таблиця похіднихі Довідник тригонометричних формул. Усе методичні посібникиможна знайти на сторінці Математичні формули та таблиці. Рекомендую все надрукувати. Особливо загострюю увагу на тригонометричних формулах, вони мають бути перед очима- Без цього ефективність роботи помітно знизиться.
Але спочатку про те, яких інтегралів у цій статті ні. Тут не знайдеться інтегралів виду, ![]() - косинус, синус, помножений на якийсь багаточлен (рідше що-небудь з тангенсом або котангенсом). Такі інтеграли інтегруються частинами, і для вивчення методу відвідайте урок Інтегрування частинами. Приклади рішень. Також тут не знайдеться інтегралів з «арками» – арктангенсом, арксинусом та ін., вони теж найчастіше інтегруються частинами.
- косинус, синус, помножений на якийсь багаточлен (рідше що-небудь з тангенсом або котангенсом). Такі інтеграли інтегруються частинами, і для вивчення методу відвідайте урок Інтегрування частинами. Приклади рішень. Також тут не знайдеться інтегралів з «арками» – арктангенсом, арксинусом та ін., вони теж найчастіше інтегруються частинами.
При знаходженні інтегралів від тригонометричних функцій використовують ряд методів:
(4) Використовуємо табличну формулу ![]() , єдина відмінність, замість «ікса» у нас складний вираз.
, єдина відмінність, замість «ікса» у нас складний вираз.
Приклад 2
Приклад 3
Знайти невизначений інтеграл.
Класика жанру для тих, хто тоне на заліку. Як Ви, мабуть, помітили, у таблиці інтегралів немає інтеграла від тангенсу та котангенсу, але, проте, такі інтеграли знайти можна.
(1) Використовуємо тригонометричну формулу
(2) Підводимо функцію під знак диференціала.
(3) Використовуємо табличний інтеграл ![]() .
.
Приклад 4
Знайти невизначений інтеграл.
Це приклад для самостійного рішення, повне рішення та відповідь – наприкінці уроку.
Приклад 5
Знайти невизначений інтеграл.
Ступені у нас потихеньку підвищуватимуться =).
Спочатку рішення:

(1) Використовуємо формулу
(2) Використовуємо основне тригонометричне тотожність ![]() , з якого випливає, що
, з якого випливає, що ![]() .
.
(3) Почленно ділимо чисельник на знаменник.
(4) Використовуємо властивість лінійності невизначеного інтегралу.
(5) Інтегруємо за допомогою таблиці.
Приклад 6
Знайти невизначений інтеграл.
Це приклад для самостійного рішення, повне рішення та відповідь – наприкінці уроку.
Також існують інтеграли від тангенсів і котангенсів, які перебувають у більш високих ступенях. Інтеграл від тангенсу у кубі розглянуто на уроці Як обчислити площу плоскої фігури?Інтеграли від тангенсу (котангенсу) у четвертому та п'ятому ступенях можна роздобути на сторінці Складні інтеграли.
Зниження ступеня підінтегральної функції
Даний прийом працює, коли підінтегральні функції нафаршировані синусами та косинусами в парнихступенях. Для зниження ступеня використовують тригонометричні формули ![]() ,
, ![]() і , причому остання формула частіше використовується в зворотному напрямку:
і , причому остання формула частіше використовується в зворотному напрямку: ![]() .
.
Приклад 7
Знайти невизначений інтеграл.
Рішення:
У принципі нічого нового тут немає, за винятком того, що ми застосували формулу ![]() (зменшивши ступінь підінтегральної функції). Зауважте, що я скоротив рішення. У міру накопичення досвіду інтеграл можна знаходити усно, це економить час і цілком припустимо при чистовому оформленні завдань. В даному випадку доцільно не розписувати і правило
(зменшивши ступінь підінтегральної функції). Зауважте, що я скоротив рішення. У міру накопичення досвіду інтеграл можна знаходити усно, це економить час і цілком припустимо при чистовому оформленні завдань. В даному випадку доцільно не розписувати і правило ![]() спочатку усно беремо інтеграл від 1, потім - від .
спочатку усно беремо інтеграл від 1, потім - від .
Приклад 8
Знайти невизначений інтеграл.
Це приклад для самостійного рішення, повне рішення та відповідь – наприкінці уроку.
Таке обіцяне підвищення ступеня:
Приклад 9
Знайти невизначений інтеграл.
Спочатку рішення, потім коментарі:

(1) Готуємо підінтегральну функцію для застосування формули ![]() .
.
(2) Власне застосовуємо формулу.
(3) Зводимо знаменник квадрат і виносимо константу за знак інтеграла. Можна було зробити трохи інакше, але, як на мене, так зручніше.
(4) Використовуємо формулу
(5) У третьому доданку знову знижуємо ступінь, але вже за допомогою формули ![]() .
.
(6) Наводимо подібні доданки (тут я почленно розділив ![]() і виконав додавання).
і виконав додавання).
(7) Власне беремо інтеграл, правило лінійності ![]() та метод підведення функції під знак диференціала виконуємо усно.
та метод підведення функції під знак диференціала виконуємо усно.
(8) Зачісуємо відповідь.
! У невизначеному інтегралінерідко відповідь можна записати кількома способами
У прикладі остаточну відповідь можна було записати інакше – розкрити дужки і навіть це зробити ще до інтегрування виразу, тобто цілком допустима наступна кінцівка прикладу:

Цілком можливо, що такий варіант навіть зручніший, просто я пояснив так, як сам звик вирішувати). Ось ще один характерний прикладдля самостійного вирішення:
Приклад 10
Знайти невизначений інтеграл. ![]()
Це приклад вирішується двома способами, і у Вас можуть вийти дві абсолютно різні відповіді(точніше кажучи, вони виглядатимуть абсолютно по-різному, а з математичної точки зору є еквівалентними). Швидше за все, Ви не побачите найбільш раціональний спосіб і помучитеся із розкриттям дужок, використанням інших тригонометричних формул. Найбільш ефективне рішення наведено наприкінці уроку.
Підсумовуючи параграф, зробимо висновок: будь-який інтеграл виду ![]() , де і - парнічисла, вирішується шляхом зниження ступеня підінтегральної функції.
, де і - парнічисла, вирішується шляхом зниження ступеня підінтегральної функції.
На практиці мені зустрічалися інтеграли з 8 і 10 ступенями, вирішувати їх жахливий гемор доводилося, знижуючи ступінь кілька разів, у результаті виходили довгі-довгі відповіді.
Метод заміни змінної
Як уже згадувалося у статті Метод заміни змінної у невизначеному інтегралі, Основною передумовою для використання методу заміни є той факт, що в підінтегральному вираженні є деяка функція та її похідна :
(функції, не обов'язково перебувають у творі)
Приклад 11
Знайти невизначений інтеграл.
Дивимося в таблицю похідних і помічаємо формули ![]() , тобто, у нашому підінтегральному вираженні є функція та її похідна. Однак ми бачимо, що при диференціюванні косинус і синус взаємно перетворюються один на одного, і виникає питання: як виконати заміну змінної і що ж означати за синус чи косинус?! Питання можна вирішити методом наукового тику: якщо ми неправильно виконаємо заміну, то нічого хорошого не вийде.
, тобто, у нашому підінтегральному вираженні є функція та її похідна. Однак ми бачимо, що при диференціюванні косинус і синус взаємно перетворюються один на одного, і виникає питання: як виконати заміну змінної і що ж означати за синус чи косинус?! Питання можна вирішити методом наукового тику: якщо ми неправильно виконаємо заміну, то нічого хорошого не вийде.
Загальний орієнтир: у схожих випадках потрібно позначити функцію, яка знаходиться в знаменнику.
![]()
Перериваємо рішення та проводимо заміну

У знаменнику у нас все добре, все залежить тільки від , тепер залишилося з'ясувати, на що перетвориться.
Для цього знаходимо диференціал:
Або, якщо коротше:
З отриманої рівності за правилом пропорції висловлюємо потрібне нам вираз:
Отже: 
Тепер все підінтегральне вираження у нас залежить тільки від і можна продовжувати рішення

Готово. Нагадую, що мета заміни – спростити підінтегральне вираження, у разі все звелося до інтегрування статечної функції по таблиці.
Я не випадково так докладно розписав цей приклад, це зроблено з метою повторення та закріплення матеріалів уроку Метод заміни змінної у невизначеному інтегралі.
А зараз два приклади для самостійного вирішення:
Приклад 12
Знайти невизначений інтеграл.
Приклад 13
Знайти невизначений інтеграл.
Повні рішення та відповіді наприкінці уроку.
Приклад 14
Знайти невизначений інтеграл.
![]()
Тут знову в підінтегральному вираженні знаходяться синус з косинус (функція з похідною), але вже у творі, і виникає дилема - що ж позначати за, синус або косинус?
Можна спробувати провести заміну методом наукового тику, і якщо нічого не вийде, то позначити за іншу функцію, але є:
Загальний орієнтир: потрібно позначити ту функцію, яка, образно кажучи, знаходиться в «незручному положенні».
Ми бачимо, що в даному прикладі студент косинус «мучиться» від ступеня, а синус – так сидить, сам по собі.
Тому проведемо заміну: 
Якщо у кого залишилися труднощі з алгоритмом заміни змінної та знаходженням диференціалу, слід повернутися до уроку Метод заміни змінної у невизначеному інтегралі.
Приклад 15
Знайти невизначений інтеграл.
Аналізуємо підінтегральну функцію, що необхідно позначити за ?
Згадуємо наші орієнтири:
1) Функція, швидше за все, знаходиться у знаменнику;
2) Функція перебуває у «незручному положенні».
До речі, ці орієнтири справедливі як для тригонометричних функцій.
Під обидва критерії (особливо під другий) підходить синус, тому напрошується заміна. В принципі, заміну можна вже проводити, але спочатку непогано було б розібратися, а що робити з ? По-перше, «відщипуємо» один косинус:
![]()
Ми резервуємо під наш «майбутній» диференціал
А виражаємо через синус за допомогою основного тригонометричного тотожності: ![]()
Ось тепер заміна:

Загальне правило: Якщо в підінтегральній функції одна з тригонометричних функцій (синус або косинус) знаходиться в непарноюступеня, то потрібно від непарного ступеня «відкусити» одну функцію, а потім – позначити іншу функцію.Йдеться лише про інтеграли, де є косинуси та синуси.
У розглянутому прикладі непарною мірою у нас знаходився косинус, тому ми відщипнули від ступеня один косинус, а за позначили синус.
Приклад 16
Знайти невизначений інтеграл.
![]()
Ступені йдуть на зліт =).
Це приклад самостійного рішення. Повне рішення та відповідь наприкінці уроку.
Універсальна тригонометрична підстановка
Універсальна тригонометрична підстановка – це найчастіший випадок методу заміни змінної. Її можна спробувати застосувати, коли не знаєш, що робити. Але насправді є деякі орієнтири для її застосування. Типовими інтегралами, де потрібно застосувати універсальну тригонометричну підстановку, є такі інтеграли: ![]() , , ,
, , , ![]() і т.д.
і т.д.
Приклад 17
Знайти невизначений інтеграл.
![]()
Універсальна тригонометрична підстановка у разі реалізується в такий спосіб. Проведемо заміну: . Я використовую не букву, а букву, це не є якимось правилом, просто знову ж таки я так звик вирішувати.
Тут зручніше знаходити диференціал, для цього з рівності, я висловлюю:
Навішую на обидві частини арктангенс: ![]()
Арктангенс та тангенс взаємно знищуються:
Таким чином: ![]()
На практиці можна не розписувати так докладно, а просто скористатися готовим результатом:
!
Вираз справедливий лише в тому випадку, якщо під синусами та косинусами у нас просто «ікси», для інтегралу ![]() (про яке ми ще поговоримо) все буде трохи інакше!
(про яке ми ще поговоримо) все буде трохи інакше!
При заміні синуси та косинуси у нас перетворюються на такі дроби:
, , ці рівності засновані на відомих тригонометричних формулах:  ,
, 
Отже, чистове оформлення може бути таким:
![]()
Проведемо універсальну тригонометричну підстановку: ![]()
![]()
Для інтегрування раціональних функцій виду R(sin x, cos x) застосовують підстановку, яка називається універсальною тригонометричною підстановкою. Тоді. Універсальна тригонометрична підстановка часто призводить до великих обчислень. Тому, наскільки можна, користуються такими підстановками. ![]()
Інтегрування функцій, що раціонально залежать від тригонометричних функцій
1. Інтеграли виду ∫ sin n xdx , ∫ cos n xdx , n>0a) Якщо n непарне, то один ступінь sinx (або cosx) слід внести під знак диференціала, а від решти парного ступеняслід перейти до протилежної функції.
б) Якщо n парне, то користуємося формулами зниження ступеня
2. Інтеграли виду ∫ tg n xdx , ∫ ctg n xdx , де n – ціле.
Необхідно використовувати формули
3. Інтеграли виду ∫ sin n x·cos m x dx
а) Нехай m і n різної парності. Застосовуємо підстановку t = sin x, якщо n - непарне або t = cos x, якщо m - непарне.
б) Якщо m і n парні, то користуємося формулами зниження ступеня
2sin 2 x=1-cos2x, 2cos 2 x=1+cos2x.
4. Інтеграли виду
Якщо числа m і n однакової парності, використовуємо підстановку t=tg x . Часто буває зручним застосувати прийом тригонометричної одиниці.
5. ∫ sin(nx)·cos(mx)dx , ∫ cos(mx)·cos(nx)dx , ∫ sin(mx)·sin(nx)dx
Скористаємося формулами перетворення твору тригонометричних функцій на їх суму:
- sin α·cos β = ½(sin(α+β)+sin(α-β))
- cos α·cos β = ½(cos(α+β)+cos(α-β))
- sin α·sin β = ½(cos(α-β)-cos(α+β))
Приклади
1. Обчислити інтеграл ∫ cos 4 x sin 3 xdx .
Робимо заміну cos(x)=t. Тоді ∫ cos 4 x·sin 3 xdx = ![]()
![]()
2. Обчислити інтеграл.
Роблячи заміну sin x = t, отримуємо
![]()
3. Знайти інтеграл.
Робимо заміну tg (x) = t. Підставляючи, отримуємо
![]()
Інтегрування виразів виду R(sinx, cosx)
Приклад №1. Обчислити інтеграли: 
Рішення.
а) Інтегрування виразів виду R(sinx, cosx) , де R - раціональна функція від sin x і cos x перетворюються в інтеграли від раціональних функцій за допомогою універсальної тригонометричної підстановки tg(x/2) = t.
Тоді маємо
Універсальна тригонометрична підстановка дає можливість перейти від інтеграла виду R(sinx, cosx) dx до інтегралу від дробової раціональної функції, але часто така заміна веде до громіздких виразів. За певних умов ефективними виявляються простіші підстановки:
- Якщо виконується рівність R(-sin x, cos x) = -R(sin x, cos x) dx, то застосовується підстановка cos x = t.
- Якщо виконується рівність R(sin x, -cos x) = -R(sin x, cos x) dx, то підстановка sin x = t.
- Якщо виконується рівність R(-sin x, -cos x) = R(sin x, cos x) dx, то підстановка tgx = t або ctg x = t.

застосуємо універсальну тригонометричну підстановку tg(x/2) = t.
Тоді Відповідь:










