По универсален начиндефиниране на закона за разпределение, подходящ както за дискретни, така и за непрекъснати случайни променливи, е функцията на разпределение.
Функция на разпределение на случайна величина X наречена функция Е(х), определяйки за всяка стойност хвероятността, че случайна променлива Xще вземе стойност по-малка от х, т.е
Е(х) = П(X < х).
Основни свойства на функцията на разпределение Е(х) :
1. Тъй като по дефиниция Е(х) е равна на вероятността на събитието, всички възможни стойности на функцията на разпределение принадлежат към сегмента:
0 £ Е(х) £ 1.
2. Ако тогава е така Е(х) е ненамаляваща функция на своя аргумент.
3. Вероятността една случайна променлива да приеме стойност, принадлежаща на полуинтервала [ а, b), е равно на увеличението на функцията на разпределение на този интервал:
П(а £ X < b) = Е(b) - Е(а).
4. Ако всички възможни стойности на случайна променлива принадлежат на интервала [ а, b], Това
Е(х) = 0, при х £ а; Е(х) = 1, с х > b.
Функцията на разпределение на дискретни случайни променливи може да се определи по формулата
Ако е известна серията на разпределение на дискретна случайна променлива, е лесно да се изчисли и конструира нейната функция на разпределение. Нека демонстрираме как се прави това, използвайки пример 23.
Пример 25.Изчислете и конструирайте функцията на разпределение за дискретна случайна променлива, чийто закон за разпределение има формата:
| x i | 0,1 | 1,2 | 2,3 | 4,5 |
| p i | 0,1 | 0,2 | 0,6 | 0,1 |
Решение. Нека определим стойностите на функцията Е(х) = П(X < х) за всички възможни стойности х:
при хО (- ¥; 0,1] няма нито една стойност на случайната променлива X, по-малко от тези стойности х, тоест няма нито един член в сумата (15):
Е(х) = 0;
при хО (0.1; 1.2] само една възможна стойност ( X= 0,1) по-малко от разглежданите стойности х. Тоест, когато хО (0,1; 1,2] Е(х) = П(X = 0,1) = 0,1;
при хО (1.2; 2.3] две стойности ( X= 0,1 и X= 1,2) по-малко от тези стойности х, следователно, Е(х) = П(X = 0,1) + П(X = 1,2) = 0,1 + 0,2 = 0,3;
при хО (2.3; 4.5] три стойности ( X = 0,1, X= 1,2 и X= 2,3) по-малко от тези стойности х, следователно, Е(х) = П(X = 0,1) + П(X = 1,2) + П(X = 2,3) = 0,1 + 0,2 + 0,6 = 0,9 ;
при хО (4,5, ¥) всички възможни стойности на случайната променлива Xще бъде по-малко от тези стойности х, И Е(х) = П(X = 0,1) + П(X = 1,2) + П(X = 2,3) +
+ П(X = 4,5) = 0,1 + 0,2 + 0,6 + 0,1 = 1.
Така,
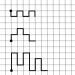
Графика на функция Е(х) е показано на фигура 8.
Като цяло разпределителната функция Е(х) дискретна случайна променлива Xе прекъсната стъпкова функция, непрекъсната отляво, чиито скокове се случват в точки, съответстващи на възможните стойности X 1 , X 2 , ... случайна променлива Xи са равни на вероятностите стр 1 , стр 2 , ... тези стойности.
Функция на разпределение на непрекъснати случайни променливи.Сега можем да дадем по-точна дефиниция на непрекъснати случайни променливи: случайна променлива Xнаречен непрекъснато, ако неговата функция на разпределение Е(х) за всички стойности хе непрекъсната и освен това има производна навсякъде, с изключение може би на отделни точки.
От непрекъснатостта на функцията Е(х) следва, че вероятността за всяка отделна стойност на непрекъсната случайна променлива е нула.
Тъй като вероятността за всяка отделна стойност на непрекъсната случайна променлива е 0, свойство 3 на функцията на разпределение за непрекъсната случайна променлива ще бъде от формата
П(а £ X < b) = П(а £ X £ b) = П(а < X £ b) = П(а < X < b) = Е(b) - Е(а).
Пример 26.Вероятностите за попадение в целта за всеки от двамата стрелци са съответно равни на: 0,7; 0,6. Случайна променлива X- броя на пропуските, при условие че всеки стрелец е стрелял по един изстрел. Създайте поредица от разпределения на случайна променлива X, изграждане на стълбовидна диаграма и функция на разпределение.
Решение. Възможни стойности на тази случайна променлива X: 0, 1, 2. Условието на проблема може да се разглежда като поредица от п= 2 независими опита. В този случай, за да се изчислят вероятностите за възможни стойности на случайна променлива Xможете да използвате теоремите за събиране на вероятностите за несъвместими събития и умножаване на вероятностите за независими събития:
Нека обозначим събитията:
Ааз = ( аз-тият стрелец уцели целта) аз = 1, 2.
Според условието, вероятността от събитие А 1 П(А 1) = 0,7, вероятност за събитие А 2 - П(А 2) = 0,6. Тогава вероятностите за противоположни събития: , .
Нека определим всички елементарни събития от даден случаен експеримент и съответните вероятности:
| Елементарни събития | събития | Вероятности |
| Общо |
(Нека проверим това).
Серия на разпределение на дадена случайна променлива Xизглежда като
| x i | Общо | |||
| p i | 0,42 | 0,46 | 0,12 |
Стълбовата графика, съответстваща на тази серия на разпределение, е показана на фигура 9.
Нека изчислим функцията на разпределение на тази случайна променлива:
при х Î (- ¥, 0] ;
при хО (0, 1] ;
при хО (1, 2] ;
при хО (2, +¥);
И така, функцията на разпределение на разглежданата случайна променлива има формата:
Графика на функция Е(х) е показано на фигура 10.
Функция на плътността на вероятността на непрекъсната случайна променлива.
Плътност на разпределение на вероятноститенепрекъсната случайна променлива Xв точката хпроизводната на неговата функция на разпределение в тази точка се нарича:
f(х) = Е¢( х).
Според значението на стойностите на функцията f(х) са пропорционални на вероятността изследваната случайна променлива да приеме стойност някъде в непосредствена близост до точката х.
Функция на разпределение на плътността f(х), както и функцията на разпределение Е(х), е една от формите за определяне на закона за разпределение, но е приложима само за непрекъснати случайни променливи. Функция на плътността на вероятността f(х) наричан още диференциална функция на разпределение, докато разпределителната функция Е(х) се наричат съответно кумулативна функция на разпределение.
Диаграма на разпределение на плътността f(х) се нарича крива на разпределение.
Нека разгледаме свойствата, които има функцията на плътността на разпределението на непрекъсната случайна променлива.
Имот 1.Плътността на вероятностното разпределение е неотрицателна функция:
f(х) ³ 0
(геометрично:кривата на разпределение не лежи под оста x).
Имот 2.Вероятността случайна променлива да попадне в областта от a до b се определя по формулата
(геометрично:тази вероятност е равна на площта на криволинейния трапец, ограничен от кривата f(х), ос ои прав х= а и х= б).
Имот 3.
(геометрично: площта на фигурата, ограничена от кривата на разпределение и оста x, е равна на едно).
По-специално, ако всички възможни стойности на случайна променлива принадлежат на интервала [ а, b], Това
Имот 4.Разпределителна функция Е(х) може да се намери от известната функция на плътността на разпределението, както следва:
Пример 27.Непрекъсната случайна променлива се определя от функция на разпределение
Определете диференциалната функция на плътността на разпределението.
Решение. Нека дефинираме диференциалната функция на плътността на разпределението
Пример 28.Дали всяка от следните функции е плътността на разпределение на някаква случайна променлива?
Въпроси за самоконтрол
1. Какво се нарича случайна променлива?
2. Какви величини се наричат дискретни? непрекъснато?
3. Как се нарича законът за разпределение на случайна величина?
4. По какви начини може да се определи законът за разпределение на дискретна случайна променлива? непрекъснато?
5. Какво характеризира функцията на разпределение F(x)случайна променлива?
6. Как да се определи вероятността случайна променлива да попадне в определен интервал с помощта на функцията на разпределение?
7. Какво характеризира функцията на плътността на разпределението на случайна променлива? Посочете нейното вероятностно значение.
8. За какви количества е дефинирана функцията за плътност на разпределението?
9. Може ли функцията за плътност на разпределението да приема отрицателни стойности?
10. Как функциите са свързани една с друга F(x)И f(х)?
11. Какви случайни променливи се наричат непрекъснати?
12. Каква е площта на фигурата, ограничена от кривата на разпределение и оста x?
13. Как да се определи вероятността непрекъсната случайна променлива да попадне в определен интервал с помощта на функцията за плътност на разпределението?
Плътност на разпространение вероятности Xизвикайте функцията f(x)– първата производна на функцията на разпределението F(x):
Концепцията за плътност на разпределение на вероятността на случайна променлива XЗа дискретна стойностнеприложимо.
Плътност на разпределение на вероятностите f(x)- викат те диференциална функцияразпределения:

Имот 1.Плътността на разпределение е неотрицателна величина:
Имот 2.Неправилният интеграл на плътността на разпределението в диапазона от до е равен на единица:
Пример 1.25.Дадена е функцията на разпределение на непрекъсната случайна променлива X:

f(x).
Решение:Плътността на разпределение е равна на първата производна на функцията на разпределение:

1. Дадена е функцията на разпределение на непрекъсната случайна променлива X:

Намерете плътността на разпределение.
2. Дадена е функцията на разпределение на непрекъсната случайна променлива X:

Намерете плътността на разпределение f(x).
1.3. Числени характеристикинепрекъснат произволен
количества
Очакваненепрекъсната случайна променлива X, чиито възможни стойности принадлежат на цялата ос о, се определя от равенството:

Приема се, че интегралът се сближава абсолютно.
а,б), това:

f(x)– плътност на разпределение на случайна величина.
дисперсия непрекъсната случайна променлива X, чиито възможни стойности принадлежат на цялата ос, се определя от равенството:

Специален случай. Ако стойностите на случайна променлива принадлежат на интервала ( а,б), това:

Вероятността, че Xще приема стойности, принадлежащи на интервала ( а,б), се определя от равенството:
 .
.
Пример 1.26.Непрекъсната случайна променлива X

Намерете математическото очакване, дисперсията и вероятността за попадение на случайна променлива Xв интервала (0;0,7).
Решение:Случайната променлива е разпределена в интервала (0,1). Нека определим плътността на разпределение на непрекъсната случайна променлива X:

а) Математическо очакване  :
:

б) Дисперсия 

![]()
V) 

Задачи за самостоятелна работа:
1. Случайна променлива Xдадено от функцията на разпределение:

M(x);
б) дисперсия D(x);
Xв интервала (2,3).
2. Случайна променлива X

Намерете: а) математическо очакване M(x);
б) дисперсия D(x);
в) определяне на вероятността за попадение на произволна променлива Xв интервала (1;1.5).
3. Случайна променлива Xдадено от кумулативната функция на разпределение:

Намерете: а) математическо очакване M(x);
б) дисперсия D(x);
в) определяне на вероятността за попадение на произволна променлива Xв интервала
1.4. Закони за разпределение на непрекъсната случайна величина
1.4.1. Равномерно разпределение
Непрекъсната случайна променлива Xима равномерно разпределениена сегмента [ а,б], ако на този сегмент плътността на разпределение на вероятностите на случайната променлива е постоянна, а извън него е равна на нула, т.е.







ориз. 4.
; ![]() ;
; ![]() .
.
![]()
Пример 1.27.Автобус по определен маршрут се движи равномерно на интервали от 5 минути. Намерете вероятността една равномерно разпределена случайна променлива X– времето за изчакване на автобуса ще бъде по-малко от 3 минути.
Решение:Случайна променлива X– равномерно разпределени в интервала .
Плътност на вероятността: ![]() .
.
За да не надвишава времето за изчакване 3 минути, пътникът трябва да се яви на спирката в рамките на 2 до 5 минути след тръгването на предишния автобус, т.е. случайна променлива Xтрябва да попада в интервала (2;5). това. необходима вероятност:

Задачи за самостоятелна работа:
1. а) намерете математическото очакване на случайна променлива Xразпределени равномерно в интервала (2;8);
б) намерете дисперсията и стандартното отклонение на случайната променлива X,разпределени равномерно в интервала (2;8).
2. Минутната стрелка на електрически часовник се премества рязко в края на всяка минута. Намерете вероятността в даден момент часовникът да показва време, което се различава от истинското с не повече от 20 секунди.
1.4.2. Експоненциално разпределение
Непрекъсната случайна променлива Xсе разпределя по експоненциалния закон, ако неговата плътност на вероятността има формата:

където е параметърът на експоненциалното разпределение.

Така 




ориз. 5.
Числени характеристики:
Пример 1.28.Случайна променлива X– време на работа на електрическа крушка – има експоненциално разпределение. Определете вероятността времето на работа на електрическата крушка да бъде най-малко 600 часа, ако средното време на работа е 400 часа.
Решение:Според условията на задачата математическото очакване на случайна променлива Xсе равнява на 400 часа, следователно:
; ![]()
Необходимата вероятност, където
Накрая:
Задачи за самостоятелна работа:
1. Напишете функцията на плътност и разпределение на експоненциалния закон, ако параметърът .
2. Случайна променлива X

Намерете математическото очакване и дисперсията на количество X.
3. Случайна променлива Xдадено от функцията на разпределение на вероятностите:

Намерете математическото очакване и стандартното отклонение на случайна променлива.
1.4.3. Нормално разпределение
нормалносе нарича вероятностно разпределение на непрекъсната случайна променлива X, чиято плътност има формата:

Къде А– математическо очакване, – стандартно отклонение X.
Вероятността, че Xще приеме стойност, принадлежаща на интервала:
![]() , Къде
, Къде
 – Функция на Лаплас.
– Функция на Лаплас.
Разпределение, за което ; , т.е. с плътност на вероятността  наречен стандартен.
наречен стандартен.

ориз. 6.
Вероятност абсолютната стойност да бъде отхвърлена по-малко от положително число:
![]() .
.
По-специално, когато а= 0 равенството е вярно:
![]()
Пример 1.29.Случайна променлива Xнормално разпределени. Стандартно отклонение. Намерете вероятността, че отклонението на случайна променлива от нейното математическо очакване е с абсолютна стойностще бъде по-малко от 0,3.
Решение: .
Задачи за самостоятелна работа:
1. Напишете плътността на вероятността на нормалното разпределение на случайната променлива X, знаейки това M(x)= 3, D(x)= 16.

2. Очакване и стандартно отклонение на нормално разпределена случайна променлива Xсъответно равни на 20 и 5. Намерете вероятността в резултат на теста Xще приеме стойността, съдържаща се в интервала (15;20).
3. Случайните грешки при измерване се подчиняват на нормалния закон със стандартно отклонение от mm и математическо очакване а= 0. Намерете вероятността от 3 независими измервания грешката на поне едно да не надвишава 4 mm по абсолютна стойност.
4. Определено вещество се претегля без систематични грешки. Случайните грешки при претеглянето се подчиняват на нормалния закон със стандартно отклонение r. Намерете вероятността претеглянето да бъде извършено с грешка, която не надвишава 10 g по абсолютна стойност.
Резултатът от всеки случаен експеримент може да бъде характеризиран качествено и количествено. Качественарезултат от случаен експеримент - случаен събитие. Всякакви количествена характеристика, който в резултат на случаен експеримент може да приеме една от определен набор от стойности, - случайна променлива.Случайна променлива е едно от централните понятия на теорията на вероятностите.
Нека е произволно вероятностно пространство. Случайна променливае реална числена функция x =x (w), w W такава, че за всяко реално х ![]() .
.
Събитие Прието е да се записва във формата x< х. По-нататък случайните променливи ще бъдат означавани с малки букви гръцки букви x, h, z, …
Случайна променлива е броят точки, получени при хвърляне на зарове, или височината на ученик, произволно избран от учебната група. В първия случай имаме работа с дискретнислучайна променлива (взема стойности от дискретен набор от числаМ= непрекъснато дискретни(1, 2, 3, 4, 5, 6) ; във втория случай - с=).
(взема стойности от непрекъснат набор от числа - от интервала на числовата линия аз.
Всяка случайна променлива се определя изцяло от нейната Е(х) = разпределителна функция(х) = ПАко x е случайна променлива, тогава функцията< х) се нарича F x(x ПАко x е случайна променлива, тогава функцията<разпределителна функцияслучайна променлива x. тук х.
х ) - вероятността случайната променлива x да приеме стойност, по-малка от Важно е да се разбере, че функцията на разпределение е „паспортът“ на случайна променлива: тя съдържа цялата информация за случайната променлива и следователноизследването на една случайна променлива се състои в нейното изучаване разпределителни функции,.
което често се нарича просто
разпространение х 1 <разпределителна функция 2 < … <Функцията на разпределение на всяка случайна променлива има следните свойства: < … с вероятностями стр 1 <Ако x е дискретна случайна променлива, приемаща стойностите 2 < … <x i < …, то таблица вида
| х 1 | х 2 | … | x i | … |
| стр 1 | стр 2 | … | p i | … |
стр p i.
наречен

Дискретна случайна променлива има функция на разпределение на стъпки. Например, за произволния брой точки, получени при едно хвърляне на зар, разпределението, функцията на разпределение и графиката на функцията на разпределение са:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |


Ако функцията на разпределение разпределителна функция(х) е непрекъсната, тогава се извиква случайната променлива x непрекъсната случайна променлива.
Ако функцията на разпределение на непрекъсната случайна променлива диференцируеми, тогава по-визуално представяне на случайната променлива се дава от плътност на вероятността на случайната променлива p x(х), което е свързано с разпределителната функция разпределителна функция(х) формули
 И
И ![]() .
.
От тук по-специално следва, че за всяка случайна променлива .
При решаването на практически проблеми често е необходимо да се намери стойността х, при което функцията на разпределение разпределителна функция(х) случайната променлива x приема дадена стойност стр, т.е. уравнението трябва да бъде решено разпределителна функция(х) = стр. хРешения на такова уравнение (съответстващи стойности ) в теорията на вероятностите се наричат
квантили. стрКвантил x p ( стр-квантил, квантил на ниво разпределителна функция(х) случайна променлива с функция на разпределение ), наречено решение xp разпределителна функция(х) = стр, струравнения стр(0, 1). За някои разпределителна функция(х) = струравнение
може да има няколко решения, за някои - нито едно. Това означава, че за съответната случайна променлива някои квантили не са еднозначно дефинирани, а някои квантили не съществуват.
Функция на вероятностното разпределение и нейните свойства.< х}.
Функцията на разпределение на вероятността F(x) на случайна променлива X в точка x е вероятността, че в резултат на експеримент случайната променлива ще приеме стойност, по-малка от x, т.е. F(x)=P(X
Нека разгледаме свойствата на функцията F(x).< -∞}. Событие (X < -∞) является невозможным событием: F(-∞)=P{X < - ∞}=p{V}=0.
1. F(-∞)=lim (x→-∞) F(x)=0. Наистина, по дефиниция F(-∞)=P(X< ∞}. Событие Х < ∞ является достоверным событием. Следовательно, F(∞)=P{X < ∞}=p{U}=1.
2. F(∞)=lim (x→∞) F(x)=1, тъй като по дефиниция F(∞)=P(X<Β}=F(Β)-F(Α).
3. Вероятността една случайна променлива да приеме стойност от интервала [Α Β] е равна на увеличението на функцията на разпределение на вероятностите върху този интервал. P(Α ≤X
4. F(x 2)≥ F(x 1), ако x 2, > x 1, т.е. Функцията на вероятностното разпределение е ненамаляваща функция.
5. Функцията на вероятностното разпределение остава непрекъсната. FΨ(x o -0)=limFΨ(x)=FΨ(x o) за x→ x o< x ≤ x 2 , то левее х находится всего одно возможное значение, а именно, значение х 1 .
Разликите между функциите на вероятностното разпределение на дискретни и непрекъснати случайни променливи могат да бъдат добре илюстрирани с графики. Нека, например, дискретна случайна променлива има n възможни стойности, вероятностите за които са равни на P(X=x k )=p k , k=1,2,..n. Ако x ≤ x 1, тогава F(X)=0, тъй като няма възможни стойности на случайната променлива отляво на x. Ако x 1< x ≤ x 3 слева от х находится уже два возможных значения, поэтому F(x)=P{X=x 1 }+P{X=x 2 }=p 1 +p 2 . Рассуждая аналогично,приходим к выводу, что если х k < x≤ x k+1 , то F(x)=1, так как функция будет равна сумме вероятностей всех возможных значений, которая по условию нормировки равна еденице. Таким образом, график функции распределения дискретной случайной величины является ступенчатым. Возможные значения непрерывной величины располагаются плотно на интервале задания этой величины, что обеспечивает плавное возрастания функции распределения F(x), т.е. ее непрерывность.
Нека разгледаме вероятността случайна променлива да попадне в интервала, Δx>0: P(x≤X< x+Δx}=F(x+ Δx)-F(x). Перейдем к пределу при Δx→0:
lim (Δx→0) P(x≤ X< x+Δx}=lim (Δx→0) F(x+Δx)-F(x). Предел равен вероятности того, что случайная величина примет значение, равное х. Если функция F(x) непрерывна в точке х, то lim (Δx→0) F(x+Δx)=F(x), т.е. P{X=x}=0.
Ако F(x) има прекъсване в точка x, тогава вероятността P(X=x) ще бъде равна на скока на функцията в тази точка. По този начин вероятността всяка възможна стойност да се появи за непрекъснато количество е нула. Изразът P(X=x)=0 трябва да се разбира като границата на вероятността случайна променлива да попадне в безкрайно малка околност на точка x при P(Α< X≤ Β},P{Α ≤ X< Β},P{Α< X< Β},P{Α ≤ X≤ Β} равны, если Х - непрерывная случайная величина.
За дискретни променливи тези вероятности не са еднакви в случай, че границите на интервала Α и (или) Β съвпадат с възможните стойности на случайната променлива. За дискретна случайна променлива е необходимо стриктно да се вземе предвид вида на неравенството във формулата P(Α ≤X<Β}=F(Β)-F(Α).
Случайна променлива е променлива, която може да приема определени стойности в зависимост от различни обстоятелства и случайната променлива се нарича непрекъсната , ако може да приема произволна стойност от всеки ограничен или неограничен интервал. За непрекъсната случайна променлива е невъзможно да се посочат всички възможни стойности, така че ние обозначаваме интервали от тези стойности, които са свързани с определени вероятности.
Примери за непрекъснати случайни променливи включват: диаметър на част, която се шлифова до даден размер, височина на човек, обхват на полета на снаряд и др.
Тъй като за непрекъснати случайни променливи функцията Е(х), за разлика от дискретни случайни променливи, няма скокове никъде, тогава вероятността за всяка отделна стойност на непрекъсната случайна променлива е нула.
Това означава, че за непрекъсната случайна променлива няма смисъл да се говори за разпределение на вероятностите между нейните стойности: всяка от тях има нулева вероятност. Въпреки това, в известен смисъл, сред стойностите на непрекъсната случайна променлива има „повече и по-малко вероятни“. Например, едва ли някой би се съмнявал, че стойността на случайна променлива - височината на случайно срещнат човек - 170 см - е по-вероятно от 220 см, въпреки че и двете стойности могат да се появят на практика.
Функция на разпределение на непрекъсната случайна променлива и плътност на вероятността
Като закон за разпределение, който има смисъл само за непрекъснати случайни променливи, се въвежда концепцията за плътност на разпределение или плътност на вероятността. Нека подходим към него, като сравним значението на функцията на разпределение за непрекъсната случайна променлива и за дискретна случайна променлива.
И така, функцията на разпределение на случайна променлива (както дискретна, така и непрекъсната) или интегрална функциясе нарича функция, която определя вероятността стойността на случайна променлива Xпо-малко или равно на граничната стойност X.
За дискретна случайна променлива в точките на нейните стойности х1 , х 2 , ..., хаз,...маси от вероятности са концентрирани стр1 , стр 2 , ..., страз,..., а сумата от всички маси е равна на 1. Нека прехвърлим тази интерпретация към случая на непрекъсната случайна променлива. Нека си представим, че маса, равна на 1, не е концентрирана в отделни точки, а непрекъснато се „размазва“ по абсцисната ос ос известна неравномерна плътност. Вероятност случайна променлива да попадне в произволна област Δ хще се тълкува като маса на секция, а средната плътност на тази секция като съотношение на маса към дължина. Току-що въведохме важна концепция в теорията на вероятностите: плътност на разпределение.
Плътност на вероятността f(х) на непрекъсната случайна променлива е производната на нейната функция на разпределение:
![]() .
.
Познавайки функцията на плътността, можете да намерите вероятността стойността на непрекъсната случайна променлива да принадлежи към затворения интервал [ а; b]:

вероятността непрекъсната случайна променлива Xще вземе всяка стойност от интервала [ а; b], е равен на определен интеграл от неговата плътност на вероятността, варираща от акъм b:
![]()
![]() .
.
В този случай общата формула на функцията Е(х) вероятностно разпределение на непрекъсната случайна променлива, което може да се използва, ако е известна функцията на плътността f(х) :
![]() .
.
Графиката на плътността на вероятността на непрекъсната случайна променлива се нарича нейната крива на разпределение (фигурата по-долу).

Площ на фигура (защрихована на фигурата), ограничена от крива, прави линии, начертани от точки аИ bперпендикулярна на оста x и оста о, показва графично вероятността стойността на непрекъсната случайна променлива Xе в рамките на акъм b.
Свойства на функцията за плътност на вероятността на непрекъсната случайна променлива
1. Вероятността случайна променлива да приеме произволна стойност от интервала (и областта на фигурата, която е ограничена от графиката на функцията f(х) и ос о) е равно на едно:
2. Функцията за плътност на вероятността не може да приема отрицателни стойности:
и извън съществуването на разпределението стойността му е нула
Плътност на разпространение f(х), както и функцията на разпределение Е(х), е една от формите на закона за разпределение, но за разлика от функцията на разпределение, тя не е универсална: плътността на разпределението съществува само за непрекъснати случайни променливи.
Нека споменем двата най-важни типа разпределение на непрекъсната случайна променлива на практика.
Ако функцията за плътност на разпределение f(х) непрекъсната случайна променлива в някакъв краен интервал [ а; b] приема постоянна стойност В, а извън интервала приема стойност, равна на нула, тогава това разпределението се нарича равномерно .
Ако графиката на функцията за плътност на разпределението е симетрична спрямо центъра, средните стойности се концентрират близо до центъра, а при отдалечаване от центъра се събират тези, които са по-различни от средната (графиката на функцията прилича на част от звънец), тогава това разпределението се нарича нормално .
Пример 1.Функцията на разпределение на вероятността на непрекъсната случайна променлива е известна:

Намиране на функция f(х) плътност на вероятността на непрекъсната случайна променлива. Постройте графики на двете функции. Намерете вероятността непрекъсната случайна променлива да приеме произволна стойност в интервала от 4 до 8: .
Решение. Получаваме функцията за плътност на вероятността, като намерим производната на функцията за разпределение на вероятностите:

Графика на функция Е(х) - парабола:

Графика на функция f(х) - прав:

Нека намерим вероятността непрекъсната случайна променлива да приеме произволна стойност в диапазона от 4 до 8:
Пример 2.Функцията на плътност на вероятността на непрекъсната случайна променлива се дава като:

Изчислете коефициента В. Намиране на функция Е(х) вероятностно разпределение на непрекъсната случайна променлива. Постройте графики на двете функции. Намерете вероятността непрекъсната случайна променлива да приеме произволна стойност в диапазона от 0 до 5: .
Решение. Коефициент Внамираме, използвайки свойство 1 на функцията за плътност на вероятността:

По този начин функцията на плътност на вероятността на непрекъсната случайна променлива е:

Чрез интегриране намираме функцията Е(х) вероятностни разпределения. Ако х < 0 , то Е(х) = 0 . Ако 0< х < 10 , то
![]() .
.
х> 10 тогава Е(х) = 1 .
Така пълният запис на функцията на разпределение на вероятностите е:

Графика на функция f(х) :

Графика на функция Е(х) :

Нека намерим вероятността непрекъсната случайна променлива да приеме произволна стойност в диапазона от 0 до 5:
Пример 3.Плътност на вероятността на непрекъсната случайна променлива Xсе дава от равенството , и . Намерете коефициент А, вероятността непрекъсната случайна променлива Xще приеме произволна стойност от интервала ]0, 5[, функцията на разпределение на непрекъсната случайна променлива X.
Решение. По условие стигаме до равенство

Следователно, , откъде . така че
![]() .
.
Сега намираме вероятността една непрекъсната случайна променлива Xще вземе всяка стойност от интервала]0, 5[:

Сега получаваме функцията на разпределение на тази случайна променлива:

Пример 4.Намерете плътността на вероятността на непрекъсната случайна променлива X, която приема само неотрицателни стойности, и нейната функция на разпределение ![]() .
.