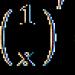- 1. Skupina Z cijeli brojevi s operacijom zbrajanja.
- 2. Grupa svih složenih korijena stupnja n iz jedne s operacijom množenja. Budući da je ciklički broj izomorfizam
grupa je ciklička i element je generirajući.
Vidimo da cikličke grupe mogu biti konačne ili beskonačne.
3. Neka je proizvoljna grupa i proizvoljan element. Skup je ciklička grupa s generatorskim elementom g. Zove se ciklička podgrupa generirana elementom g, a njen red je red elementa g. Prema Lagrangeovom teoremu, red elementa je djelitelj reda grupe. Prikaz
radeći prema formuli:
je očito homomorfizam i njegova se slika podudara s. Preslikavanje je surjektivno ako i samo ako grupa G- ciklički i g njegov sastavni element. U ovom slučaju ćemo nazvati standardni homomorfizam za cikličku grupu G s odabranom generatrisom g.
Primjenom teorema o homomorfizmu u ovom slučaju dobivamo važno svojstvo cikličkih grupa: svaka ciklička grupa je homomorfna slika grupe Z .
U bilo kojoj skupini G može se odrediti stupnjeva element s cjelobrojnim indikatorima:
Imanje drži
Ovo je očito ako . Razmotrimo slučaj kada . Zatim
Ostali slučajevi se tretiraju na sličan način.
Iz (6) slijedi da
Štoviše, po definiciji. Dakle, moći elementa čine podskupinu u skupini G. To se zove ciklička podgrupa generirana elementom, a označava se sa .
Moguća su dva bitno različita slučaja: ili su svi stupnjevi elementa različiti ili nisu. U prvom slučaju podgrupa je beskonačna. Razmotrimo drugi slučaj detaljnije.
Neka ,; Zatim. Najmanje od prirodni brojevi T, za koje se u ovom slučaju poziva u redu element i označava se sa .
Rečenica 1. Ako , To
Dokaz. 1) Podijelite m na P sa ostatkom:
Zatim, po definiciji reda
Zbog prethodnog
Posljedica. Ako mo podskupina sadrži n elemenata.
Dokaz. Stvarno,
a svi navedeni elementi su različiti.
U slučaju kada nema takvog prirodnog T, da se (tj. dogodi prvi od gore opisanih slučajeva), vjeruje se . Imajte na umu da; redovi svih ostalih elemenata grupe su veći od 1.
U grupi aditiva ne govorimo o moćima elementa , i o njemu višestruki, koji su označeni sa . U skladu s tim redoslijed elemenata aditivne skupine je G-- je najmanji prirodni broj T(ako takvi postoje) za koje
PRIMJER 1. Karakteristika polja je poredak bilo kojeg različitog od nule elementa u njegovoj aditivnoj skupini.
PRIMJER 2. Očito je da je u konačnoj grupi poredak bilo kojeg elementa konačan. Pokažimo kako se računaju redoslijedi elemenata grupe.Supstitucija se zove ciklus duljina i označava se s ako se ciklički preuređuje
a sve ostale brojeve ostavlja na mjestu. Očito je red duljine ciklusa jednak R. Ciklusi se nazivaju neovisan, ako među brojevima koje stvarno preuređuju nema zajedničkih; u ovom slučaju . Svaka se supstitucija može jedinstveno rastaviti na produkt neovisnih ciklusa. Na primjer,
što je jasno prikazano na slici, gdje je radnja zamjene prikazana strelicama. Ako se supstitucija rastavi na produkt neovisnih ciklusa duljine , Da
PRIMJER 3. Narudžba složeni broj c u grupi je konačan ako i samo ako je taj broj korijen neke potencije jedinice, koja se pak javlja ako i samo ako je a razmjerno c, tj. .
PRIMJER 4. Nađimo elemente konačnog reda u skupini gibanja ravnine. Neka bude. Za bilo koju točku
ciklički preuređena kretanjem , pa im težište O relativno nepomičan. Dakle, - ili rotacija za kut gledanja oko točke O, ili refleksija u odnosu na neku ravnu liniju koja prolazi kroz O.
PRIMJER 5. Nađimo poredak matrice
kao element grupe. Imamo
Tako. Naravno, ovaj primjer je posebno odabran: vjerojatnost da će poredak slučajno odabrane matrice biti konačan je nula.
Prijedlog 2. Ako , To
Dokaz. Neka
Tako. Imamo
Stoga, .
Definicija 1 . Skupina G nazvao ciklički, ako takav element postoji , Što . Svaki takav element se zove generirajući element skupine G.
PRIMJER 6. Aditivna skupina cijelih brojeva je ciklička jer je generirana elementom 1.
PRIMJER 7. Aditivna skupina odbitaka po modulu n je ciklički jer ga generira element .
PRIMJER 8. Multiplikativna skupina složenih korijena n-ti stupanj od 1 je ciklički. Doista, ovi korijeni su brojevi
Jasno je da . Stoga je grupu generirao element.
Lako je vidjeti da su u beskonačnoj cikličkoj grupi jedini generirajući elementi i. Dakle, u grupi Z jedini generirajući elementi su 1 i -- 1.
Broj elemenata konačne skupine G nazvao ju je u redu a označava se sa. Red konačne cikličke grupe jednak je redu njenog generirajućeg elementa. Stoga iz tvrdnje 2 slijedi
Rečenica 3 . Element cikličke grupe reda n je generirajući ako i samo ako
PRIMJER 9. Generirajući elementi grupe nazivaju se primitivni korijeni n th potencije od 1. Ovo su korijeni vrste , Gdje. Na primjer, primitivni korijeni 12. stupnja iz 1 are.
Cikličke grupe su najjednostavnije grupe koje se mogu zamisliti. (Konkretno, oni su Abelovi.) Sljedeći teorem daje njihov potpuni opis.
Teorem 1. Svaka beskonačna ciklička grupa je izomorfna grupi. Svaka konačna ciklička grupa reda n je izomorfna grupi.
Dokaz. Ako je beskonačna ciklička grupa, tada je prema formuli (4) preslikavanje izomorfizam.
Neka je konačna ciklička grupa reda P. Razmotrite mapiranje
tada je preslikavanje dobro definirano i bijektivno. Vlasništvo
slijedi iz iste formule (1). Dakle, to je izomorfizam.
Teorem je dokazan.
Za razumijevanje strukture skupine, poznavanje njezinih podskupina igra važnu ulogu. Sve podskupine cikličke skupine mogu se lako opisati.
Teorema 2. 1) Svaka podskupina cikličke grupe je ciklička.
2)U cikličkoj grupi reda n redoslijed bilo koje podskupine dijeli n i za bilo koji djelitelj q broja n postoji točno jedna podgrupa reda q.
Dokaz. 1) Neka je ciklička grupa i N-- njena podskupina, različita od (Podskupina identiteta je očito ciklička.) Imajte na umu da ako za bilo koju, tada i . Neka T-- najmanji od prirodnih brojeva za koje . Dokažimo to . Neka . Podijelimo se Do na T sa ostatkom:
odakle, na temelju definicije broja T slijedi da i, prema tome, .
2) Ako , tada se prethodno razmišljanje odnosi na (u ovom slučaju ), pokazuje da . pri čemu
I N je jedina podskupina reda q u grupi G. Natrag ako q-- bilo koji djelitelj brojeva P I , zatim podskup N, definiran jednakošću (9), podskupina je reda q. Teorem je dokazan.
Posljedica . U cikličkoj grupi primarnog reda svaka netrivijalna podgrupa koincidira s cijelom grupom.
PRIMJER 10. U skupini svaka podskupina ima oblik where.
PRIMJER 11. U grupi n-ti korijeni potencije 1 bilo koja podgrupa je grupa korijena q- stupanj od 1, gdje.
Konačne grupe
Grupa (polugrupa) naziva se ultimativno, ako se sastoji od konačnog broja elemenata. Broj elemenata konačne grupe naziva se njen u redu. Svaka podgrupa konačne grupe je konačna. I ako NÍ G– podskupina grupe G, zatim za bilo koji element AÎ G gomila Na={x: x=h◦a, za bilo koji hÎ H) Zove se lijevo coset Za G relativno N. Jasno je da broj elemenata u Na jednak redoslijedu N. (Definicija se može formulirati na sličan način a N– desni coset s obzirom na N).
Bitno je da za bilo koju podskupinu N skupine G bilo koja dva lijeva (desna) kozeta prema N ili se podudaraju ili se ne sijeku, stoga se svaka grupa može prikazati kao unija disjunktnih lijevih (desnih) kozeta pomoću N.
Doista, ako dvije klase N a I Hb, Gdje a, bÎ G, imaju zajednički element x, onda postoji tÎ H takav da x = t◦a. A onda je lijevi razred za x: N x={g: g=h◦x= h◦(t◦a) = (h◦t)◦a} Í H a, Ali a=t ‑1 ◦x I N a={g: g=h◦a= h◦(t ‑1 ◦x) = (h◦t ‑1)◦x} Í Hx. Odavde N x=N a. Slično se može pokazati da N x=N b. I stoga N a=N b. Ako razredi N a I Hb Nemati zajednički elementi, tada se ne sijeku.
Ovo dijeljenje grupe na lijeve (desne) kosetove naziva se razlaganje grupe na podskupinu H.
Teorem 2.6.1. Red konačne grupe dijeli se redom bilo koje od njezinih podgrupa.
Dokaz. Jer G je konačna grupa, onda je takva i svaka njena podgrupa N ima konačan red. Razmotrimo dekompoziciju grupe na podskupinu N. U svakom kosetu u ovoj dekompoziciji broj elemenata je isti i jednak redu N. Stoga, ako n– grupni poredak G, A k– redoslijed podskupina N, To n=m× k, Gdje m– broj košeta prema N u grupnoj dekompoziciji G.
Ako za bilo koji element aÎ G Þ N a=a N(lijevi i desni kozeti po podskupini N podudarati), zatim N nazvao normalni djelitelj skupine G.
Izjava: Ako G je komutativna grupa, onda svaka njena podgrupa N je normalni djelitelj G.
Zbog asocijativnosti djelovanja u skupini (polugrupi), možemo govoriti o „proizvodu“ tri elementa ( A◦b◦c) =(A◦b)◦c = A◦(b◦c). Slično tome, koncept složenog proizvoda n elementi: A 1 ◦A 2 ◦…◦i n = ◦ i n = = ◦.
Raditi n identični elementi grupe nazivaju se stupanj elementa i naznačen je a n=. Ova definicija ima smisla za svaki prirodni n. Za bilo koji element grupe aÎ G označiti A 0 =e– neutralni element grupe G. I negativne moći elementa a ‑ n definirano kao ( a ‑1)n ili ( a n) -1 , gdje je a-1 – inverzni element prema A. Obje definicije a ‑ n podudarati, jer a n◦(a ‑1)n = (A◦A◦ ¼◦ A)◦(a ‑1 ◦a‑1◦ ¼◦ a ‑1) = A◦A◦¼◦( A◦a ‑1)◦a-1 ◦¼◦ a ‑1 =e n =e. Tako, ( a ‑1)n = (a n) ‑1 .
U aditivnoj skupini analog stupnja elementa je a n htjeti n njegov višestruki, obično označen na, što ne treba shvatiti kao djelo n na A, jer nÎℕ i možda nÏ G. Da. na⇋, gdje n Oℕ i 0 A=e⇋0 i (- n)a = ‑(na) = n(‑a) za bilo koji prirodni n, Gdje (- a) – inverzno prema aÎ G.
Lako je to pokazati odabranim zapisom za bilo koje cijele brojeve m I n i za bilo koga aÎ G ispunjena su poznata svojstva: A) u multiplikativnom zapisu a n ◦a m = a n + m i ( a n)m = a nm; b) u aditivnom zapisu na+ma = (n+m)a I n(ma)=(nm)a.
Razmotrimo podskup grupe G, sastavljen od svih potencija proizvoljnog elementa gÎ G. Označimo to A g. Tako, A g ={g 0 , g 1 , g ‑1 , g 2 , g-2,¼). Očito, A g je podskupina grupe G, jer za bilo koje elemente x,naÎ A g slijedi da ( x◦na)Î A g, i za bilo koji element xÎ A g biti će x‑1 O A g, Osim, g 0 =eÎ A g.
Podskupina A g nazvao ciklička podskupina skupine G, generiran elementom g. Ova podgrupa je uvijek komutativna, čak i ako je sama G nije komutativno. Ako grupa G podudara s jednom od svojih cikličkih podskupina, tada se naziva ciklička grupa, generiran elementom g.
Ako sve moći elementa g su različiti, zatim grupa G nazvao beskrajan ciklička grupa i element g– element beskonačni red.
Ako među elementima cikličke grupe ima jednakih, npr. g k=g m na k>m, To g k‑m=e; i, označavanje k-m kroz n, dobivamo g n=e, nÎℕ.
Najmanji prirodni pokazatelj n takav da g n=e, nazvao redoslijed elementa g, i sam element g nazvao element konačnog reda.
Takav će se element uvijek naći u konačnoj skupini, ali može biti i u beskonačnoj skupini.
Grupe čiji svi elementi imaju konačan red nazivaju se periodički.
Budući da svaki element konačne grupe ima konačan red, sve su konačne grupe periodične. Štoviše, sve cikličke podskupine konačne grupe su periodične, jer su konačne, a svaki element konačnog reda n generira cikličku grupu istog reda n, koji se sastoji od elemenata ( g 0 , g 1 , g 2 ¼, g n-1 ). Doista, kada bi broj elemenata bio jednak nekim k<n, Zatim g k=e=g n, što je u suprotnosti s izborom n, kao najmanji stupanj takav da g n=e; na drugoj strani, k>n također nemoguće, jer u ovom slučaju postojali bi identični elementi.
Izjava: 1) svi stupnjevi g 0 , g 1 , g 2 ¼, g n-1 su različiti, jer kad bi bilo jednakih, npr. g i=g j (ja>j), To g i - j=e, Ali ( ja‑j)<n, i po definiciji n – najmanji stupanj je takav da g n=e.
2) Bilo koja druga diploma g, pozitivan ili negativan, jednak jednom od elemenata g 0 , g 1 , g 2 ¼, g n-1, jer bilo koji cijeli broj k može se predstaviti izrazom: k=nq+r, Gdje q,rÎℤ i 0£ r<n, r– ostatak i g k=g nq + r= g nq° gr= (g n)q° gr= e q° gr= gr.
1) Svaka grupa ima jedinstven element prvog reda ( e), generirajući cikličku podgrupu prvog reda koja se sastoji od jednog elementa e.
2) Razmotrimo skupinu supstitucija S 3, koji se sastoji od elemenata: , , , , , . Narudžba S 3 =6. Redoslijed elemenata A je jednako 2, jer . Redoslijed elemenata b također je jednako 2, jer . Redoslijed elemenata S je jednako 3, jer i . Redoslijed elemenata f također je jednako 3, jer i . I na kraju red d je jednako 2, jer . Dakle, cikličke podskupine S 3 generiran elementima e, a, b, d, c I f, odnosno jednako: ( e}, {e, a}, {e, b}, {e, d}, {e, c, f) i ( e, f, c), gdje se posljednja dva podudaraju. Primijetite također da poredak svake cikličke podskupine dijeli poredak grupe bez ostatka. Sljedeći teorem je istinit.
Teorem 2.7.1. (Lagrange) Red konačne grupe dijeli se redom bilo kojeg od njezinih elemenata (budući da se red elementa i red cikličke podgrupe koju on stvara podudaraju).
Također slijedi da bilo koji element konačne grupe, kada se podigne na potenciju reda grupe, daje jedinicu grupe. (Jer g m=g nk=e k=e, Gdje m– grupni red, n– poredak elemenata g, k– cijeli broj).
U skupini S postoje 3 podskupine N={e, c, f) je normalni djelitelj, ali podskupine 2. reda nisu normalni djelitelji. To se lako može provjeriti pronalaženjem lijevog i desnog kozeta po N za svaki element grupe. Na primjer, za element A lijevo coset Na={e ◦ a, S◦ A, f◦ a} = {A, b, d) i desna košeta a N={a ◦ e, A◦ c, A◦ f} = {A, d, b) podudarati se. Isto tako i za sve ostale elemente S 3 .
3) Skup svih cijelih brojeva sa zbrajanjem tvori beskonačnu cikličku grupu s generirajućim elementom 1 (ili –1), jer svaki cijeli broj je višekratnik 1.
4) Razmotrimo skup korijena n- moć jedinstva: E n=. Ovaj skup je grupa s obzirom na operaciju množenja korijena. Doista, proizvod bilo koja dva elementa e k I e m iz E n, Gdje k, m £ n-1 će također biti element E n, budući da je = = , gdje je r=(k+m) mod n I r £ n-1; množenje asocijativni, neutralni element e=e 0 =1 i za bilo koji element e k postoji obrnuto i . Ova grupa je ciklička, njen generirajući element je primitivni korijen. Lako je vidjeti da su sve ovlasti različite: , dalje za k³ n korijeni se počinju ponavljati. Na kompleksnoj ravnini korijeni se nalaze na kružnici jediničnog radijusa i dijele je na n jednakih lukova, kao što je prikazano na slici 11.
Posljednja dva primjera u biti iscrpljuju sve cikličke grupe. Budući da je sljedeći teorem istinit.
Teorem 2.7.2. Sve beskonačne cikličke grupe su međusobno izomorfne. Sve konačne cikličke grupe reda n su izomorfne jedna drugoj.
Dokaz. Neka ( G, ∘) je beskonačna ciklička grupa s generirajućim elementom g. Zatim postoji bijektivno preslikavanje f: ℤ ® G tako da za bilo koje cijele brojeve k I m njihove slike f(k) I f(m), jednaki respektivno g k I g m, su elementi G. I pri čemu f(k+m)=f(k)∘f(m), jer g k + m=g k∘ g m.
Neka sada ( G, ∘) je konačna ciklička grupa reda n s generirajućim elementom g. Zatim svaki element g kÎ G jedini način za podudaranje elementa je e kÎ E n(0£ k<n), prema pravilu f(g k)=e k. I u isto vrijeme za bilo koji g k I g mÎ G slijedi to f(g k∘ g m)=f(g k) ∘f(g m), jer f(g k∘ g m)=f(g k + m)=f(gr), Gdje r=(k+m) mod n, I f(gr)=e r=e k× e m. Jasno je da je takvo preslikavanje bijektivno preslikavanje.
Grupa O se naziva ciklička ako su svi njeni elementi potencije istog elementa. Taj element se naziva generator cikličke grupe O. Svaka ciklička grupa je očito Abelova.
Ciklička grupa je, na primjer, grupa cijelih brojeva zbrajanjem. Ovu ćemo grupu označiti simbolom 2. Njen generator je broj 1 (kao i broj - 1). Ciklička grupa je također grupa koja se sastoji od samo jednog elementa (jednog).
U proizvoljnoj grupi O, potencije bilo kojeg elementa g tvore cikličku podgrupu s generatorom g. Redoslijed ove podskupine očito se podudara s redoslijedom elementa g. Odavde, na temelju Lagrangeovog teorema (vidi stranicu 32), slijedi da poredak bilo kojeg elementa grupe dijeli poredak grupe (primijetite da su svi elementi konačne grupe elementi konačnog reda).
Dakle, za svaki element g konačne grupe reda vrijedi jednakost
Ovo jednostavno zapažanje često je od pomoći.
Doista, ako je grupa O ciklička i njezin generator, tada je redoslijed elementa jednak . Obrnuto, ako grupa O ima element reda, tada među moćima tog elementa postoje različite, pa stoga te moći iscrpljuju cijelu grupu O.
Vidimo, dakle, da ciklička grupa može imati više različitih generatora (naime, svaki element reda je generator).
Zadatak. Dokažite da je svaka grupa primarnog reda ciklička grupa.
Zadatak. Dokažite da ciklička grupa reda ima točno generatore, gdje je broj pozitivnih brojeva manji od i suprosti s .
Uz poredak, svakoj konačnoj grupi može se pripisati i broj - najmanji zajednički višekratnik redova svih njezinih elemenata.
Zadatak. Dokažite da za bilo koju konačnu grupu O broj dijeli red grupe.
Očito, za cikličku grupu broj se podudara s redoslijedom. Suprotno, općenito govoreći, nije točno. Ipak, vrijedi sljedeća izjava koja karakterizira cikličke grupe u klasi konačnih Abelovih grupa:
konačna Abelova grupa O kojoj je broj jednak njenom redu je ciklička grupa.
Doista, neka
Redovi svih mogućih nejediničnih elemenata konačne Abelove grupe O su reda , i neka je njihov najmanji zajednički višekratnik.
Proširimo broj u umnožak potencija različitih prostih brojeva:
![]()
Neka Budući da je broj, po definiciji, najmanji zajednički višekratnik brojeva (1), među tim brojevima postoji barem jedan broj koji je djeljiv točno sa, tj. ima oblik , gdje je b koprost s . Neka taj broj bude redoslijed elementa g. Tada element ima red (vidi Korolar 1) na stranici 29).
Dakle, za bilo koga u skupini O postoji barem jedan element reda.Odabravši po jedan takav element za svakoga, razmatramo njegov produkt. Prema tvrdnji dokazanoj na stranicama 29-30, poredak ovog proizvoda jednak je umnošku narudžbi, tj. jednak broju. Kako je zadnji broj po uvjetu jednak , time je dokazano da postoji element reda n u grupi O. Prema tome, ova grupa je ciklička grupa.
Neka je sada O proizvoljna ciklička grupa s generatorom i H neka njena podgrupa. Budući da je bilo koji element podskupine H element skupine O, može se prikazati u obliku , gdje je d neki pozitivan ili negativan cijeli broj (općenito govoreći, nije jednoznačno definiran). Promotrimo skup svih pozitivnih brojeva za koje element pripada podskupini H. Budući da je taj skup neprazan (zašto?), onda sadrži najmanji broj. Ispada da je svaki element h podskupine H snaga elementa. Doista, po definiciji, postoji broj d takav da (broj d može biti negativan). Podijeli (s ostatkom) broj d brojem
Kako je , dakle, zbog minimalnosti broja, ostatak mora biti jednak nuli. Tako, .
Time je dokazano da je element generator skupine H, tj. da je skupina H ciklička. Dakle, svaka podskupina cikličke grupe je ciklička grupa.
Zadatak. Dokažite da je broj jednak indeksu podgrupe H i, prema tome, dijeli red grupe O (ako je grupa O konačna).
Napomenimo također da za bilo koji djelitelj reda konačne cikličke grupe Q u grupi O postoji jedna i samo jedna podgrupa H reda (naime, podgrupa s generatorom
To implicira da ako je konačna ciklička grupa jednostavna, onda je njen redoslijed prost (ili jedinica).
Napokon primijetimo da je svaka kvocijent grupa (dakle, svaka homomorfna slika) cikličke grupe Q ciklička grupa.
Da bismo to dokazali, dovoljno je uočiti da je generator grupe koset koji sadrži generator grupe O.
Konkretno, svaka kvocijentna skupina skupine cijelih brojeva Z je ciklička skupina. Proučimo ove cikličke grupe detaljnije.
Kako je grupa Z Abelova, svaka njena podgrupa H je normalni djelitelj. S druge strane, prema onome što je gore dokazano, podskupina H je ciklička grupa. Kako su nam kvocijent grupe po trivijalnim podgrupama poznate, možemo podgrupu H smatrati netrivijalnom. Neka je broj generator podgrupe H. Taj broj možemo smatrati pozitivnim (zašto?) i stoga većim od jedan.
Podskupina N. očito se sastoji od svih cijelih brojeva djeljivih s . Dakle, dva broja pripadaju istom kosetu u podskupini H ako i samo ako je njihova razlika djeljiva s , tj. kada su usporedivi po modulu (vidi Tečaj, str. 277). Prema tome, kozeti u podskupini H nisu ništa više od klasa brojeva međusobno usporedivih po modulu.
Drugim riječima, kvocijent skupine Z prema podskupini H je skupina (zbrajanjem) klasa brojeva međusobno usporedivih po modulu. Ovu grupu ćemo označiti s Njen generator je klasa koja sadrži broj 1.
Ispada da je svaka ciklička grupa izomorfna ili grupi Z (ako je beskonačna) ili jednoj od grupa (ako je njen red konačan).
Doista, neka je generator grupe O. Definirajmo preslikavanje iz grupe 2 u grupu O, postavljajući
Definicija 1.22. Neka R- Glavni broj. Skupina G nazvao p-grupa, ako je poredak svakog elementa grupe jednak nekoj potenciji prostog broja R.
Definicija 1.23. Silovsky r-podskupina konačna grupa G p-podskupina dane skupine naziva se ono što nije sadržano u većoj p-podskupini dane skupine.
Teorem 1.25. Konačna Abelova grupa jednaka je izravnom umnošku svojih Sylowovih p-podgrupa.
Dokaz. Promotrimo konačnu Abelovu grupu G reda n i neka n = R"! str 2 2 p* 1 k - proširenje broja P u umnožak potencija različitih prostih brojeva. za 1, 2,..., Do označimo s I, Sylow r podskupinu i s I, podskupinu koju generiraju svi I; Za; * ja Lako je dokazati da je I, n I, = (e). Stoga ja = (N 1,H 2,...,N k) = N 1 xN 2 x...xN k. Pretpostavimo da postoji element g e G, tako da je g g Y. Korolarom 2 iz Lagrangeovog teorema |G| : |g|. Iz toga slijedi da
|g| = pf"pjf 2 Pk k > g D e Pi - a ja D za bilo koji i = 1, 2, Do. Prema korolariji teorema 1.23, postoje elementi g 1; g2, ..., gk e G, tako da je = x x... x (g k) i | g,-1 = pf 1 za i = 1, 2, ..., /s. Ako pretpostavimo da je g, g I, za neko g, tada dobivamo p-podgrupu (gi, ja,) F I, što je u suprotnosti s definicijom Sylowove p-podgrupe. Dakle, za bilo koji i = 1, 2,..., /npr e Ja sam odakle g e N. Stoga, H = G i teorem je dokazan.
Teorem 1.26. Konačna Abelova p-grupa jednaka je izravnom umnošku cikličkih podgrupa.
Dokaz. Neka je dana konačna Abelova p-grupa G. Odaberimo element u njemu A maksimalnog reda p", i neka je H maksimalna podgrupa takva da je (a) n H = (e). Tada je (a, R) = (a) x R. Označimo Gj = (a) x R.
Hajdemo to pretvarati G F G y Od svih elemenata koji ne pripadaju G x biramo element g minimalnog reda rR. Uz pretpostavku da je gPg Gb onda od |gp| = rR- 1, dolazimo do kontradikcije s izborom elementa g. Prema tome, gP e G x = (a) x I i postoje cijeli broj /c i element h e I, tako da je gP = a fc /i. Odavde a k= gp/i -1. Ako je gcd(/c, p) = 1, tada je gcd(/c, p°9 = 1 i postoje cijeli brojevi u, v takvi da je /c + p a v = 1. Zatim
Zbog maksimalnosti | a = p a imamo gP“ = e i e F aR“ _1 = = (gP"/i _u)P“ _1 =gP“h~ u P a ~ 1 =/i _u p““ 1 e I, što je u suprotnosti s uvjetom (a) p I = (e). Prema tome, /s: r.
Neka Do= r/s x. Zatim aP fc i = a k =gPh~ 1, gdje h = a~P k igP == (a _fc ig)P. Označimo gj=a _/c ig. Zatim gf -heH. Uz pretpostavku da je gj =ar fc "geG] =(a)xN, tada g e G x , što je u suprotnosti s izborom elementa g. Prema tome, g x g G x, a time i gj g I. Budući da je I maksimalna podgrupa s uvjetom (A) n I = (e), zatim (a) n (g x , I) ^ (e). Stoga postoje t, str e Z i element hj e I, takav da je e * a t= gf
Pod pretpostavkom da p:p,top=pp 1 kod nekih n,eZ i e g a m = gf/ij = gf ni /ii e I, što je u suprotnosti s uvjetom (a) n I = = (e). Prema tome, GCD(n,p) = 1 Hgf =a m /if 1 . Ako je |g x | =pY, tada je GCD(n, p’O = 1 i postoje u x , v x g Z, tako da je gsh x -t-pYv x = 1. Stoga je g, =gf u i + P Yv i = gf Ul gf Yvi = gf Ul =(a m /i 1 - 1) u i Opet smo došli do kontradikcije. Ostaje, dakle, prihvatiti to G - (a)x R. Sada u podskupini R na sličan način odabiremo izravnim faktorom cikličku podskupinu maksimuma u N poredak itd. dok ne dobijemo dekompoziciju grupe G u izravni proizvod cikličkih podskupina. Teorem je dokazan.
Teorem 1.27. Konačna Abelova grupa jednaka je izravnom umnošku cikličkih p-podgrupa.
Dokaz slijedi iz teorema 1.25 i 1.26.
Za kraj poglavlja o grupama, napominjemo da se grupa može smatrati skupom s jednom binarnom operacijom, koja je asocijativna, i za sve elemente A I Kommersant jednadžbe su jedinstveno rješive sjekira = b uua-b. Ovakav pogled na skupinu dovodi do dvije generalizacije. S jedne strane, može se usredotočiti na proučavanje značenja asocijativnosti operacije, a to vodi do koncepta polugrupe kao skupa s jednom asocijativnom operacijom (vidi rad). S druge strane, može se zanemariti zahtjev asocijativnosti, a to dovodi do koncepta kvazigrupe kao skupa s jednom binarnom operacijom, u odnosu na koju su gore navedene jednadžbe jednoznačno rješive. Kvazigrupa s identitetom naziva se petlja (vidi rad). Teorija polugrupa i teorija kvazigrupa pretvorile su se u dvije neovisno razvijajuće sadržajne teorije. Ne spominjemo ih u glavnom tekstu iz razloga “maksimalnog mogućeg minimuma” volumena.