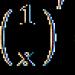Reći ćemo da prirodni broj i više nego prirodni broj b(i označiti a > b), ako postoji prirodan broj k takav da je a = b + k.

Teorem 1. Jedan nije veći od bilo kojeg prirodnog broja.

Doista, uvjet 1 > a povlači za sobom 1 = a + k, što je nemoguće: za k = 1 dobivamo 1 = a /, što je u suprotnosti s prvim aksiomom prirodni brojevi; za k ¹ 1 nalazimo njegovog prethodnika i opet dolazimo do iste kontradikcije.

Ovaj odnos "više" je antirefleksni(nije točno da je a > a) i tranzitivan(a > b /\ b > c => a > c), tj odnos strogog reda. Štoviše, ova relacija je relacija linearnog reda, odnosno za skup prirodnih brojeva vrijedi teorem o trihotomiji:

Teorem o trihotomiji: Za bilo koja dva prirodna broja istinita je jedna i samo jedna od sljedeće tri tvrdnje:

Dokaz: Prvo pokazujemo da dva od tri uvjeta nisu zadovoljena istovremeno. Pretpostavimo da su ispunjeni uvjeti 1 i 2. Tada

a = b + k, b = a + n => a = a + (n + k) => a > a,

što proturječi antirefleksivnosti stava “više”. Slično se utvrđuje nekompatibilnost uvjeta 2 i 3 i uvjeta 1 i 3.

Sada ćemo dokazati da jedan od tri uvjeta nužno vrijedi za bilo koje brojeve a i b. Koristimo matematičku indukciju na b. Za b = 1, ovisno o a: ili a = 1 = b, ili za a postoji prethodnik, tada

a = c / = c + 1 = 1 + c = b + c => a > b.

Dakle, za b = 1 teorem je točan. Pretpostavimo indukcijom da teorem vrijedi za neki x, naime da je x usporediv s brojem a, odnosno moguće su tri opcije: ili a > x, ili x > a, ili x = a. Zatim dokazujemo da je x/ također usporediv s a. U prvom slučaju a > x, odnosno a = x + k. Ovisno o tome je li dani k jednak 1 ili ne, dobivamo

a) a = x + 1 = x / (teorem je točan)

b) a = x + c / = x + c + 1 = x + 1 + c = x / + c => a > x / .

U drugom slučaju x > a, ali tada

x / = (a + m) +1 = a + (m + 1),

odnosno x / > a. Slično, za x = a vrijedi x / = x + 1 = a + 1, odnosno opet je x / > a. Teorem je u potpunosti dokazan.

Sada možete predstaviti koncepte<, £, ³.

a< b ó b >a;

a £ b ó a< b \/ a = b

a ³ b ó a > b \/ a = b.

Svojstva monotonosti:

Za operaciju dodavanja:

1) a > b => a + c > b + c;

2) a + c > b + c => a > b;

3) a > b /\ c > d=> a + c > b + d.

<, £, ³.

Za operaciju množenja:

4) a > b => a×c > b×c;

5) Zakon kontrakcije: ac = bc => a = b

6) ac > bc => a > b;

7) a > b /\ c > d=> ac > bd.

Ista svojstva javljaju se i za druge znakove<, £, ³.

Navedimo kao primjer dokaz svojstava 4 i 5. Kako je a > b, po definiciji a = b + k, tada je a×c = (b + k)×c = b×c + k×c, što znači da je a ×c > b×c, a svojstvo 4 je dokazano. Svojstvo 5 dokazujemo kontradikcijom. Neka je ac = bc, ali pretpostavimo da je a ≠ b, ali tada, prema teoremu o trihotomiji, ili a > b, ili b > a, ali to znači, prema svojstvu 4, da ili ac > bc, ili bc > ac, što je u suprotnosti s uvjetom (ac = bc).

Teorem o diskretnosti. Ne možete umetnuti prirodni broj između dva susjedna prirodna broja:

(" a, x O N) nije istina da je a< x < a /

Dokaz(metodom kontradikcije). Neka a< x < a / . Тогда х = а + k,

a / = x + n = a + k + n => a + 1 = a + k + n => 1 = k + n.

Posljednja jednakost je nemoguća, jer je u suprotnosti s teoremom da jedan nije veći od bilo kojeg prirodnog broja.

Arhimedov toranj. Za bilo koje prirodne brojeve a i b postoji prirodan broj n takav da je a< bn.

Dokaz izvodimo indukcijom na b. Za b = 1, n = a / . Pretpostavimo induktivno da za b = k postoji traženi n, odnosno a< kn. Но тогда тем более a < k / n = kn + k. Теорема доказана.

Najmanji element skupa M nazvat ćemo element s O M takav da za bilo koje elemente m O M vrijedi nejednakost: s ≤ m.

Teorem najmanjeg elementa. Svaki neprazan podskup skupa prirodnih brojeva ima najmanji element.

Dokaz: Ako je M podskup od N koji sadrži 1, tada će 1 biti željeni najmanji element. Ako 1 nije uključen u skup M, tada razmotrimo pomoćni skup A koji se sastoji od svih prirodnih brojeva manjih od svih prirodnih brojeva iz skupa M:

A = (a O N| (" m O M) a< m}.

Iz ove konstrukcije, naime, proizlazi da skupovi A i M nemaju zajednički elementi. Osim toga, A nije prazan, budući da je 1 Î A. U A također postoji element b, takav da je b / Ï A. Doista, da ne postoji takav element, tada bi aksiomom indukcije bilo moguće dokazati da je A = N, ali tada bi M bio prazan, što ne odgovara uvjetima teorema. Element b / = c bit će upravo najmanji element u skupu M. Doista, c £ m za bilo koji m OM (da to nije tako, tada bi nejednakost c > m vrijedila za barem jedan prirodni m, ali b O A , pa b< m < c = b / , что противоречит теореме о дискретности). Кроме того, с не может быть строго меньше всех элементов множества М, иначе с Î А, что противоречит его выбору. Таким образом, с равен хотя бы одному элементу из М, а значит с Î М, то есть действительно с – наименьший элемент множества М. Теорема доказана.

Imajte na umu da nema svaki podskup skupa prirodnih brojeva najveći element, ali ako je taj podskup konačan, tada također ima najveći element. Vrijedi i suprotno. Ako podskup skupa prirodnih brojeva ima najveći element, tada je taj podskup konačan. Moguće je dokazati još općenitiju tvrdnju: neprazan podskup skupa prirodnih brojeva ograničen je odozgo ako i samo ako je konačan (ima najveći element).

Zadaci za neovisna odluka

Broj 1.8. Dokažite da je relacija “više od” antirefleksivna i tranzitivna na skupu prirodnih brojeva.

Broj 1.9. Dokažite svojstva monotonosti 1, 2, 3, 6, 7 iz ovog odjeljka.

Broj 1.10. Dokažite nejednakosti za sve prirodne brojeve n

a) 5 n > 7n – 3;

b) 2n +2> 2n + 5;

Kao što znate, skup prirodnih brojeva može se poredati pomoću relacije "manje od". Ali pravila za konstruiranje aksiomatske teorije zahtijevaju da ovaj odnos bude ne samo definiran, već i napravljen na temelju koncepata koji su već definirani u ovoj teoriji. To se može učiniti definiranjem odnosa "manje od" zbrajanjem.

Definicija. Broj a manji je od broja b (a< b) тогда и только тогда, когда существует такое натуральное число с, что а + с = b.

Pod ovim uvjetima također se kaže da broj b više A i napiši b > a.

Teorem 12. Za bilo koje prirodne brojeve A I b vrijedi jedna i samo jedna od tri relacije: a = b, a > b, A < b.

Izostavljamo dokaz ovog teorema.. Iz ovog teoreme slijedi da ako

a¹ b, ili A< b, ili a > b, oni. relacija “manje” ima svojstvo povezanosti.

Teorem 13. Ako A< b I b< с. Da A< с.

Dokaz. Ovaj teorem izražava svojstvo tranzitivnosti relacije "manje od".

Jer A< b I b< с. onda po definiciji relacije “manje od” postoje prirodni brojevi Do Pa što b = a + k i c = b + I. Ali onda c = (a + k)+ / i na temelju svojstva asocijativnosti zbrajanja dobivamo: c = a + (k +/). Jer k + ja - prirodan broj, tada, prema definiciji "manje od", A< с.

Teorem 14. Ako A< b, nije istina da b< а. Dokaz. Ovaj teorem izražava svojstvo antisimetrija odnos "manje".

Dokažimo prvo da ni za jedan prirodni broj A ne ti-!>! ■ )njezin stav A< A. Pretpostavimo suprotno, tj. Što A< а javlja se. Tada, prema definiciji relacije “manje od”, postoji prirodan broj S,Što A+ S= A, a to je u suprotnosti s teoremom 6.

Dokažimo sada da ako A< b, onda to nije istina b < A. Pretpostavimo suprotno, tj. što ako A< b , To b< а izvedena. Ali iz ovih jednakosti, prema teoremu 12 imamo A< а, što je nemoguće.

Budući da je relacija “manje od” koju smo definirali antisimetrična i tranzitivna te ima svojstvo povezanosti, to je relacija linearnog reda, a skup prirodnih brojeva linearno uređeni skup.

Iz definicije "manje od" i njegovih svojstava možemo izvesti poznata svojstva skupa prirodnih brojeva.

Teorem 15. Od svih prirodnih brojeva jedan je najmanji broj, tj. ja< а для любого натурального числа a¹1.

Dokaz. Neka A - bilo koji prirodni broj. Tada su moguća dva slučaja: a = 1 i a¹ 1. Ako a = 1, onda postoji prirodan broj b, slijedi a: a = b " = b + ja = 1 + b, tj., prema definiciji odnosa "manje od", 1< A. Dakle, svaki prirodni broj je jednak 1 ili veći od 1. Ili, jedan je najmanji prirodni broj.

Relacija "manje od" povezana je sa zbrajanjem i množenjem brojeva svojstvima monotonosti.

Teorem 16.

a = b => a + c = b + c i a c = b c;

A< b =>a + c< b + с и ас < bс;

a > b => a + c > b + c i ac > bc.

Dokaz. 1) Valjanost ove tvrdnje proizlazi iz jedinstvenosti zbrajanja i množenja.

2) Ako A< b, onda postoji takav prirodan broj k,Što A + k = b.
Zatim b+ c = (a + k) + c = a + (k + c) = a + (c+ Do)= (a + c) + k. Jednakost b+ c = (a + c) + k znači da a + c< b + S.

Na isti način se dokazuje da A< b =>ak< bс.

3) Dokaz je sličan.

Teorem 17(obrnuto od teorema 16).

1) A+ c = b + c ili ac ~ bc-Þ a = b

2) a + c< Ь + с ili ak< prije KristaÞ A< Ь:

3) a + c > b+ sa ili ac > bcÞ a > b.

Dokaz. Dokažimo npr. da iz ak< bс trebao bi A< b Pretpostavimo suprotno, tj. da zaključak teoreme ne vrijedi. Onda to ne može biti to a = b. budući da bi tada jednakost bila zadovoljena ac = bs(teorem 16); ne može biti A> b, jer bi tada bilo ac > bs(Teorem!6). Prema tome, prema teoremu 12, A< b.

Iz teorema 16 i 17 možemo izvesti dobro poznata pravila za član po član zbrajanje i množenje nejednadžbi. Izostavljamo ih.

Teorem 18. Za bilo koje prirodne brojeve A I b; postoji prirodan broj n takav da p b> a.

Dokaz. Za bilo koga A postoji takav broj P, Što n > a. Da biste to učinili, dovoljno je uzeti n = a + 1. Množenje nejednakosti član po član P> A I b> 1, dobivamo pb > A.

Iz razmatranih svojstava relacije “manje od” slijede bitne značajke skupa prirodnih brojeva koje iznosimo bez dokaza.

1. Ni za jedan prirodan broj A ne postoji takav prirodni broj P,Što A< п < а + 1. Ovo svojstvo se zove vlasništvo
diskretnost skupovi prirodnih brojeva i brojevi A I a + 1 se zove susjedni.

2. Svaki neprazan podskup prirodnih brojeva sadrži
najmanji broj.

3. Ako M- neprazan podskup skupa prirodnih brojeva
i postoji takav broj b, da za sve brojeve x iz M nije izvršeno
jednakost x< b, tada u izobilju M Tamo je najveći broj.

Ilustrirajmo svojstva 2 i 3 primjerom. Neka M- skup dvoznamenkastih brojeva. Jer M je podskup prirodnih brojeva i za sve brojeve u tom skupu vrijedi nejednakost x< 100, то в множестве M je najveći broj 99. Najmanji broj sadržan u danom skupu M, - broj 10.

Dakle, odnos "manje od" omogućio je razmatranje (au nekim slučajevima i dokazivanje) značajnog broja svojstava skupa prirodnih brojeva. Konkretno, on je linearno uređen, diskretan i ima najmanji broj 1.

S relacijom “manje” (“veće od”) za prirodne brojeve osnovnoškolci se upoznaju na samom početku školovanja. A često se uz njegovu teoretsku interpretaciju implicitno koristi i definicija koju smo dali u okviru aksiomatske teorije. Na primjer, učenici mogu objasniti da je 9 > 7 jer je 9 7+2. Uobičajena je i implicitna upotreba svojstava monotonosti zbrajanja i množenja. Na primjer, djeca objašnjavaju da je “6 + 2< 6 + 3, так как 2 < 3».

Vježbe

1, Zašto se skup prirodnih brojeva ne može poredati pomoću relacije "odmah slijedi"?

Definirajte stav a > b i dokazati da je tranzitivan i antisimetričan.

3. Dokažite da ako a, b, c su prirodni brojevi, tada:

A) A< b Þ ас < bс;

b) A+ S< b + sÞ> A< Ь.

4. Koje teoreme o monotonosti zbrajanja i množenja mogu
koristiti mlađi školarci, izvršavajući zadatak "Usporedi bez izvođenja izračuna":

a) 27 + 8 ... 27 + 18;

b) 27-8 ... 27 -18.

5. Koja svojstva skupa prirodnih brojeva implicitno koriste osnovnoškolci pri izvođenju sljedećih zadataka:

A) Zapiši brojeve koji su veći od 65 i manji od 75.

B) Navedite prethodni i sljedeći broj u odnosu na broj 300 (800,609,999).

C) Navedi najmanji i najveći troznamenkasti broj.

Oduzimanje

U aksiomatskoj konstrukciji teorije prirodnih brojeva oduzimanje se obično definira kao inverzna operacija zbrajanja.

Definicija. Oduzimanje prirodnih brojeva a i b je operacija koja zadovoljava uvjet: a - b = c ako i samo ako je b + c = a.

Broj a - b naziva se razlika brojeva a i b, broj A– minuend, broj b- odbitni.

Teorem 19. Razlika prirodnih brojeva A- b postoji ako i samo ako b< а.

Dokaz. Neka razlika A- b postoji. Tada, prema definiciji razlike, postoji prirodan broj S,Što b + c = a,što znači da b< а.

Ako b< а, tada, prema definiciji relacije “manje od”, postoji prirodan broj c takav da b + c = a. Zatim, prema definiciji razlike, c = a - b, oni. razlika a - b postoji.

Teorem 20. Ako je razlika prirodnih brojeva A I b postoji, onda je jedinstven.

Dokaz. Pretpostavimo da postoje dvije različite vrijednosti razlike između brojeva A I b;: a – b= s₁ I a - b= s₂, i s₁ ¹ s₂ . Tada, prema definiciji razlike, imamo: a = b + c₁, I a = b + c₂ : . Iz toga slijedi da b+ c ₁ = b + c₂ : i na temelju teorema 17 zaključujemo, s₁ = s₂.. Došli smo do kontradikcije s pretpostavkom, što znači da je netočna, ali ovaj teorem je točan.

Na temelju definicije razlike prirodnih brojeva i uvjeta njezina postojanja mogu se opravdati poznata pravila oduzimanja broja od zbroja i zbroja od broja.

Teorem 21. Neka A. b I S- cijeli brojevi.

i ako a > c, tada je (a + b) - c = (a - c) + b.

b) Ako b > c. zatim (a + b) - c - a + (b - c).

c) Ako a > c i b > c. tada možete koristiti bilo koju od ovih formula.
Dokaz. U slučaju a) razlika brojeva A I c postoji jer a > s. Označimo to sa x: a - c = x. gdje a = c + x. Ako (A+ b) - c = y. tada, prema definiciji razlike, A+ b = S+ na. Umjesto toga zamijenimo u ovu jednakost A izraz c + x:(c + x) + b = c + y. Iskoristimo svojstvo asocijativnosti zbrajanja: c + (x + b) = c+ na. Transformirajmo ovu jednakost na temelju svojstva monotonosti zbrajanja i dobijemo:

x + b = u..Zamjenjujući x u ovoj jednakosti izrazom a - c, imat će (A - G) + b = y. Dakle, dokazali smo da ako a > c, tada je (a + b) - c = (a - c) + b

Slično se dokazuje iu slučaju b).

Dokazani teorem može se formulirati u obliku pravila koje je zgodno za pamćenje: da bi se od zbroja oduzeo broj, dovoljno je oduzeti taj broj od jednog člana zbroja i dodati drugi član dobivenom rezultatu.

Teorem 22. Neka a, b i c - cijeli brojevi. Ako a > b+ s, dakle A- (b + c) = (a - b) - c ili a - (b + c) = (a - c) - b.

Dokaz ove teorije sličan je dokazu teorema 21.

Teorem 22 može se formulirati kao pravilo: da bi se od broja oduzeo zbroj brojeva, dovoljno je od tog broja oduzeti svaki član jedan po jedan.

U osnovno obrazovanje matematička definicija oduzimanja kao obrnutog zbrajanja u opći pogled, u pravilu, nije zadan, ali se stalno koristi, počevši od izvođenja operacija na jednoznamenkastim brojevima. Učenici bi trebali jasno razumjeti da je oduzimanje povezano sa zbrajanjem i koristiti taj odnos u izračunima. Oduzimajući, na primjer, broj 16 od broja 40, učenici razmišljaju ovako: „Oduzimanje broja 16 od 40 znači pronaći takav broj da kada se pribroji broju 16 dobije rezultat 40; ovaj broj će biti 24, budući da je 24 + 16 = 40. Dakle. 40 - 16 = 24."

Pravila za oduzimanje broja od zbroja i zbroja od broja u osnovnom tečaju matematike su teorijska osnova razne metode izračuna. Na primjer, vrijednost izraza (40 + 16) - 10 može se pronaći ne samo izračunavanjem zbroja u zagradama i potom od njega oduzimanjem broja 10, već i na ovaj način;

a) (40 + 16) - 10 = (40 - 10) + 16 = 30 + 16 = 46:

b) (40 + 16) - 10 = 40 + (16- 10) = 40 + 6 = 46.

Vježbe

1. Je li točno da se svaki prirodni broj dobiva od neposredno sljedećeg oduzimanjem jedan?

2. Što je posebno u logičkoj strukturi teorema 19? Može li se to formulirati riječima "potrebno i dovoljno"?

3. Dokažite da je:

i ako b > c, Da (a + b) - c = a + (b - c);

b) ako a > b + c, To a - (b+ c) = (a - b) - c.

4. Može li se bez izračunavanja reći koji će izrazi imati iste vrijednosti:

a) (50 + 16)- 14; d) 50 + (16 -14 ),

b) (50 - 14) + 16; e) 50 - (16 - 14);
c) (50 - 14) - 16, f) (50 + 14) - 16.

a) 50 - (16 + 14); d) (50 - 14) + 16;

b) (50 - 16) + 14; e) (50 - 14) - 16;

c) (50 - 16) - 14; e) 50 - 16-14.

5. Koja su svojstva oduzimanja teorijska osnova za sljedeće računske tehnike koje se proučavaju u početnom tečaju matematike:

12 - 2-3 12 -5 = 7

b) 16-7 = 16-6 - P;

c) 48 - 30 = (40 + 8) - 30 = 40 + 8 =18;

d) 48 - 3 = (40 + 8) - 3 = 40 + 5 = 45.

6. Opišite moguće načine vrednovanja vrijednosti izraza oblika. a - b- S te ih ilustrirati konkretnim primjerima.

7. Dokaži da kada b< а a svaki prirodni c jednakost je istinita (a – b) c = ac - bc.

Bilješka. Dokaz se temelji na aksiomu 4.

8. Odredite vrijednost izraza bez izvođenja pisanih izračuna. Obrazložite svoje odgovore.

a) 7865 × 6 – 7865 × 5: b) 957 × 11 – 957; c) 12 × 36 – 7 × 36.

Podjela

U aksiomatskoj konstrukciji teorije prirodnih brojeva dijeljenje se obično definira kao operacija obratna od množenja.

Definicija. Dijeljenje prirodnih brojeva a i b je operacija koja zadovoljava uvjet: a: b = c ako i samo ako Do kada b× c = a.

Broj a:b nazvao privatna brojevima A I b, broj A djeljiv, broj b- djelitelj.

Kao što je poznato, dijeljenje na skupu prirodnih brojeva ne postoji uvijek i ne postoji tako zgodan znak postojanja kvocijenta kakav postoji za razliku. Postoji samo nužan uvjet za postojanje posebnog.

Teorem 23. Da bi postojao količnik dva prirodna broja A I b, potrebno je da b< а.

Dokaz. Neka kvocijent prirodnih brojeva A I b postoji, tj. postoji prirodan broj c takav da bc = a. Budući da za svaki prirodni broj 1 vrijedi nejednakost 1 £ S, zatim, množenjem oba njegova dijela prirodnim brojem b, dobivamo b£ prije Krista. Ali bc = a, stoga, b£ A.

Teorem 24. Ako je kvocijent prirodnih brojeva A I b postoji, onda je jedinstven.

Dokaz ovog teorema sličan je dokazu teorema o jedinstvenosti razlike prirodnih brojeva.

Na temelju definicije kvocijenta prirodnih brojeva i uvjeta za njegovo postojanje moguće je opravdati poznata pravila dijeljenja zbroja (razlike, umnoška) brojem.

Teorem 25. Ako brojevi A I b djeljiv brojem S, zatim njihov zbroj a + b podijeljeno s c, a kvocijent dobiven dijeljenjem zbroja A+ b po broju S, jednaka zbroju kvocijenata dobivenih dijeljenjem A na S I b na S, tj. (a + b):c = a:c + b:S.

Dokaz. Budući da broj A podjeljeno sa S, tada postoji prirodan broj x = A; to je a = cx. Slično tome, postoji takav prirodni broj y = b:S,Što

b= su. Ali onda a + b = cx+ cy = - c(x + y). To znači da a + b dijeli se s c, a kvocijent dobiven dijeljenjem zbroja A+ b brojem c, jednak x + y, oni. sjekira + b: c.

Dokazani teorem može se formulirati kao pravilo za dijeljenje zbroja s brojem: da bi se zbroj podijelio s brojem, dovoljno je svaki član podijeliti s tim brojem i zbrojiti dobivene rezultate.

Teorem 26. Ako prirodni brojevi A I b djeljiv brojem S I a > b, onda razlika a - b dijeli se s c, a kvocijent dobiven dijeljenjem razlike s brojem c jednak je razlici kvocijenata dobivenih dijeljenjem A na S I b na c, tj. (a - b):c = a:c - b:c.

Dokaz ovog teorema sličan je dokazu prethodnog teorema.

Ovaj se teorem može formulirati kao pravilo za dijeljenje razlike brojem: Za Da bi se razlika podijelila s brojem, dovoljno je umanjenik i umanjenik podijeliti s tim brojem i od prvog količnika oduzeti drugi.

Teorem 27. Ako je prirodan broj A djeljiv s prirodnim brojem c, tada za svaki prirodni broj b raditi ab podijeljen sa s. U ovom slučaju kvocijent dobiven dijeljenjem umnoška ab na broj s , jednak umnošku količnika dobivenog dijeljenjem A na S, i brojevima b: (a × b): c - (a: c) × b.

Dokaz. Jer A podjeljeno sa S, onda postoji prirodan broj x takav da a:c= x, gdje je a = cx. Množenje obje strane jednakosti sa b, dobivamo ab = (cx)b. Budući da je množenje asocijativno, dakle (cx) b = c(x b). Odavde (a b):c = x b= (a:c) b. Teorem se može formulirati kao pravilo za dijeljenje proizvoda s brojem: da bi se proizvod podijelio s brojem, dovoljno je podijeliti jedan od faktora s tim brojem i pomnožiti dobiveni rezultat s drugim faktorom.

U osnovnom matematičkom obrazovanju definicija dijeljenja kao operacije obratne množenju u pravilu se ne daje u općenitom obliku, ali se stalno koristi, počevši od prvih sati upoznavanja s dijeljenjem. Učenici bi trebali jasno razumjeti da je dijeljenje povezano s množenjem i koristiti taj odnos pri izračunima. Dijeleći npr. 48 sa 16, učenici razmišljaju ovako: „Podijeliti 48 sa 16 znači pronaći broj koji, pomnožen sa 16, daje 48; takav bi broj bio 3, budući da je 16×3 = 48. Prema tome, 48: 16 = 3.

Vježbe

1. Dokažite da je:

a) ako je kvocijent prirodnih brojeva a i b postoji, onda je jedinstven;

b) ako brojevi a i b dijele se na S I a > b, Da (a - b): c = a: c - b: c.
2. Može li se reći da su sve ove jednakosti istinite:
a) 48:(2×4) = 48:2:4; b) 56:(2×7) = 56:7:2;

c) 850:170 = 850:10:17.

Koje pravilo generalizira ove slučajeve? Formulirajte to i dokažite.

3. Koja su svojstva dijeljenja teorijska osnova
ispunjavanje sljedećih zadataka ponuđenih školarcima osnovne razrede:

Može li se bez dijeljenja reći koji će izrazi imati iste vrijednosti:

a) (40+ 8):2; c) 48:3; e) (20+ 28):2;

b) (30 + 16):3; g)(21+27):3; f) 48:2;

Jesu li jednakosti istinite:

a) 48:6:2 = 48:(6:2); b) 96:4:2 = 96:(4-2);

c) (40 - 28): 4 = 10-7?

4. Opišite moguće načine izračunavanja vrijednosti izraza
tip:

A) (A+ prije Krista; b) A:b: S; V) ( a × b): Sa .

Predložene metode ilustrirajte konkretnim primjerima.

5. Pronaći značenje izraza na racionalan način; njihov
opravdati svoje postupke:

a) (7 × 63):7; c) (15 × 18):(5× 6);

b) (3 × 4× 5): 15; d) (12 × 21): 14.

6. Opravdajte sljedeće načine dijeljenja dvoznamenkastim brojem:

a) 954:18 = (900 + 54): 18 = 900:18 + 54:18 =50 + 3 = 53;

b) 882:18 = (900 - 18): 18 = 900:18 - 18:18 = 50 - 1 =49;

c) 480:32 = 480: (8 × 4) = 480:8:4 = 60:4 = 15:

d) (560 × 32): 16 = 560 (32:16) = 560×2 = 1120.

7. Bez dijeljenja s kutom, pronađite najracionalnije
na kvocijentni način; Obrazložite odabranu metodu:

a) 495:15; c) 455:7; e) 275:55;

6) 425:85; d) 225:9; e) 455:65.

Predavanje 34. Svojstva skupa nenegativnih cijelih brojeva

1. Skup nenegativnih cijelih brojeva. Svojstva skupa nenegativnih cijelih brojeva.

2. Pojam segmenta prirodnog niza brojeva i brojni elementi konačnog skupa. Redni i kardinalni prirodni brojevi.

Vježbe

1.. Pomoću definicije množenja pronađite značenja izraza:
a) 3 3; 6) 3 4; c) 4 3.

2. Zapiši lijevo svojstvo distribucije množenja s obzirom na zbrajanje i dokaži ga. Koje su transformacije izraza moguće na temelju njega? Zašto je postalo potrebno razmotriti lijevu i desnu distributivnost množenja u odnosu na zbrajanje?

3. Dokažite asocijativnost množenja prirodnih brojeva. Koje su transformacije izraza moguće na temelju njega? Proučava li se ovo svojstvo osnovna škola?

4. Dokažite svojstvo komutativnosti množenja. Navedite primjere njegove uporabe u osnovnom tečaju matematike.

5. Koja se svojstva množenja mogu koristiti pri pronalaženju vrijednosti izraza:

a) 5 (10 + 4); 6) 125 15 6; c) (8 379) 125?

6. Poznato je da je 37 3 = 111. Koristeći ovu jednakost izračunajte:

a) 37 18; 6) 185 12.

Opravdajte sve izvršene transformacije.

7. Odredite vrijednost izraza bez izvođenja pisanih izračuna. Obrazložite svoj odgovor:

a) 8962 8 + 8962 2; b) 63402 3 + 63402 97; c) 849 +849 9.

8.. Koja će svojstva množenja učenici osnovne škole koristiti pri rješavanju sljedećih zadataka:

Može li se, bez računanja, reći koji će izrazi imati iste vrijednosti:

a) 3 7 + 3 5; 6) 7 (5 + 3): c) (7 + 5) 3?

Jesu li jednakosti istinite:

a) 18 5 2 = 18 (5 2); c) 5 6 + 5 7 = (6 + 7) 5;

b) (3 10) 17 = 3 10 17; d) 8 (7 + 9) = 8 7 + 9 8?
Je li moguće usporediti vrijednosti izraza bez izvođenja izračuna:

a) 70 32 + 9 32 ...79 30 + 79 2; 6) 87 70 + 87 8 ... 80 78 + 7 78?

Predavanje 33. Oduzimanje i dijeljenje cijelih nenegativnih brojeva

1. Red skupa prirodnih brojeva.

2. Definicija oduzimanja nenegativnih cijelih brojeva

3. Dijeljenje cijelih nenegativnih brojeva. Nemogućnost dijeljenja s nulom. Dijeljenje s ostatkom.

Kao što znate, skup prirodnih brojeva može se poredati pomoću relacije "manje od". Ali pravila za konstruiranje aksiomatske teorije zahtijevaju da ovaj odnos bude ne samo definiran, već i napravljen na temelju koncepata koji su već definirani u ovoj teoriji. To se može učiniti definiranjem odnosa "manje od" zbrajanjem.

Definicija. Broj a manji je od broja b (a< b) тогда и только тогда, когда существует такое натуральное число с, что а + с = b.

Pod ovim uvjetima također se kaže da broj b više A i napiši b > a.

Teorem 12. Za bilo koje prirodne brojeve A I b vrijedi jedna i samo jedna od tri relacije: a = b, a > b, A < b.

Izostavljamo dokaz ovog teorema.. Iz ovog teoreme slijedi da ako

a¹ b, ili A< b, ili a > b, oni. relacija “manje” ima svojstvo povezanosti.

Teorem 13. Ako A< b I b< с. Da A< с.

Dokaz. Ovaj teorem izražava svojstvo tranzitivnosti relacije "manje od".

Jer A< b I b< с. onda po definiciji relacije “manje od” postoje prirodni brojevi Do Pa što b = a + k i c = b + I. Ali onda c = (a + k)+ / i na temelju svojstva asocijativnosti zbrajanja dobivamo: c = a + (k +/). Jer k + ja - prirodan broj, tada, prema definiciji "manje od", A< с.

Teorem 14. Ako A< b, nije istina da b< а. Dokaz. Ovaj teorem izražava svojstvo antisimetrija odnos "manje".

Dokažimo prvo da ni za jedan prirodni broj A ne ti-!>! ■ )njezin stav A< A. Pretpostavimo suprotno, tj. Što A< а javlja se. Zatim, po definiciji relacije “manje od”, postoji takav prirodni broj S,Što A+ S= A, a to je u suprotnosti s teoremom 6.

Dokažimo sada da ako A< b, onda to nije istina b < A. Pretpostavimo suprotno, tj. što ako A< b , To b< а izvedena. Ali iz ovih jednakosti, prema teoremu 12 imamo A< а, što je nemoguće.

Budući da je relacija “manje od” koju smo definirali antisimetrična i tranzitivna te ima svojstvo povezanosti, to je relacija linearnog reda, a skup prirodnih brojeva linearno uređeni skup.

Iz definicije "manje od" i njegovih svojstava možemo izvesti poznata svojstva skupa prirodnih brojeva.

Teorem 15. Od svih prirodnih brojeva jedan je najmanji broj, tj. ja< а для любого натурального числа a¹1.

Dokaz. Neka A - bilo koji prirodni broj. Tada su moguća dva slučaja: a = 1 i a¹ 1. Ako a = 1, onda postoji prirodan broj b, slijedi a: a = b " = b + ja = 1 + b, tj., prema definiciji odnosa "manje od", 1< A. Dakle, svaki prirodni broj je jednak 1 ili veći od 1. Ili, jedan je najmanji prirodni broj.

Relacija "manje od" povezana je sa zbrajanjem i množenjem brojeva svojstvima monotonosti.

Naručeni setovi

Definicija 1. Gomila M nazvao naredio, ako se uspostavi neki odnos između njegovih elemenata a b(" a prethodio b"), koji ima sljedeća svojstva: 1) između bilo koja dva elementa a I b postoji jedan i samo jedan od tri odnosa: a = b, a b, b a; 2) za bilo koja tri elementa a, b I c iz a b, b c slijedi a c.

Prazan skup se smatra naručenim.

Komentar. Znak = uvijek shvaćamo u smislu istovjetnosti, podudarnosti elemenata. Snimiti a = b jednostavno znači da slovima a I b označava isti element skupa M. Dakle, iz svojstva 1) slijedi da između dva različita elementa vrijedi jedan i samo jedan od dva odnosa a b ili b a.

Ako a prethodio b, onda to kažu b slijedi a i napiši: b > a.

Stav a > b Ima, kao što se lako može provjeriti, svojstva slična 1) i 2). Može se uzeti kao glavni, pa kroz njega definirati relaciju a b.

Ako je u uređenom skupu M promijeniti uloge odnosa, tj. umjesto a b napisati a > b, i obrnuto, dobivamo novi naručeni skup M", za čiji redoslijed se kaže da je obrnut redu M. Na primjer, za gornji redoslijed u skupu prirodnih brojeva, redoslijed će biti obrnut:

Dva uređena skupa sastavljena od istih elemenata, ali poredanih različitim redoslijedom, smatraju se različitima. Stoga je pri definiranju uređenog skupa preko njegovih elemenata potrebno navesti njihov redoslijed. Pretpostavit ćemo da zapis slijeva na desno odgovara redoslijedu elemenata, a zadržat ćemo prethodni zapis s vitičastim zagradama. Isti skup se može naručiti na različite načine (ako sadrži najmanje dva elementa). Dakle, skup prirodnih brojeva može se poredati na uobičajeni način ili obrnutim redoslijedom; neparni brojevi se mogu staviti ispred parnih brojeva ili obrnuto, slažući oba u rastućem ili silaznom redoslijedu. Dobivamo naručene setove