както е известно, случайна величина се нарича променлива, която може да приеме определени стойности в зависимост от случая. Случайните променливи се означават с главни букви на латинската азбука (X, Y, Z), а техните стойности - със съответните малки букви (x, y, z). Случайните променливи се делят на прекъснати (дискретни) и непрекъснати.
Дискретна случайна променлива Наречен произволна стойност, който приема само краен или безкраен (изброим) набор от стойности с определени ненулеви вероятности.
Законът за разпределението на дискретна случайна величина е функция, която свързва стойностите на произволна променлива със съответните им вероятности. Законът за разпределението може да се уточни по един от следните начини.
1 . Законът за разпределението може да бъде даден от таблицата:
където λ>0, k = 0, 1, 2, … .
в)като се използва функция на разпределение F(x) , което определя за всяка стойност x вероятността случайната променлива X да приеме стойност, по-малка от x, т.е. F(x) = P(X< x).
Свойства на функцията F(x)
3 . Законът за разпределението може да бъде зададен графично – разпределителен многоъгълник (многоъгълник) (виж задача 3).
Имайте предвид, че за да разрешите някои проблеми, не е необходимо да знаете закона за разпределението. В някои случаи е достатъчно да знаете едно или повече числа, които отразяват най-важните характеристики на закона за разпределението. Това може да бъде число, което има значението на "средната стойност" на произволна променлива, или число, което показва средния размер на отклонението на произволна променлива от средната й стойност. Числата от този вид се наричат числови характеристики на произволна променлива.
Основен числени характеристикидискретна случайна променлива :
- Математическо очакване
(средна стойност) на дискретна случайна променлива M(X)=Σ x i p i.
За биномно разпределение M(X)=np, за разпределение на Поасон M(X)=λ - Дисперсия
дискретна случайна променлива D(X)=M2или D(X) = M(X 2) − 2. Разликата X–M(X) се нарича отклонение на произволна променлива от нейното математическо очакване.
За биномно разпределение D(X)=npq, за разпределение на Поасон D(X)=λ - Стандартно отклонение (стандартно отклонение) σ(X)=√D(X).
Примери за решаване на задачи по темата "Законът за разпределение на дискретна случайна променлива"
Задача 1.
Издадени са 1000 лотарийни билета: 5 от тях ще спечелят 500 рубли, 10 ще спечелят 100 рубли, 20 ще спечелят 50 рубли и 50 ще спечелят 10 рубли. Определете закона за разпределението на вероятностите на случайната променлива X - печалби на билет.
Решение. Според условието на задачата са възможни следните стойности на случайната променлива X: 0, 10, 50, 100 и 500.
Броят на билетите без печалба е 1000 - (5+10+20+50) = 915, тогава P(X=0) = 915/1000 = 0,915.
По същия начин намираме всички други вероятности: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01, P(X =500) = 5/1000=0,005. Представяме получения закон под формата на таблица:
Да намерим очаквана стойностстойности X: M(X) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2 +3 +4+5+6)/6 = 21/6 = 3,5
Задача 3.
Устройството се състои от три независимо работещи елемента. Вероятността за повреда на всеки елемент в един експеримент е 0,1. Начертайте закон за разпределение за броя на неуспешните елементи в един експеримент, изградете полигон за разпределение. Намерете функцията на разпределение F(x) и я начертайте. Намерете математическото очакване, дисперсията и стандартното отклонение на дискретна случайна променлива.
Решение. 1. Дискретната произволна променлива X=(брой неуспешни елементи в един експеримент) има следните възможни стойности: x 1 =0 (нито един от елементите на устройството не е неуспешен), x 2 =1 (един елемент е неуспешен), x 3 =2 ( два елемента не успяха) и x 4 = 3 (три елемента не успяха).
Отказите на елементите са независими един от друг, вероятностите за повреда на всеки елемент са равни една на друга, следователно е приложимо Формулата на Бернули
. Като се има предвид, че по условие, n=3, p=0,1, q=1-p=0,9, ние определяме вероятностите на стойностите:
P 3 (0) = C 3 0 p 0 q 3-0 \u003d q 3 = 0,9 3 = 0,729;
P 3 (1) \u003d C 3 1 p 1 q 3-1 = 3 * 0,1 * 0,9 2 = 0,243;
P 3 (2) \u003d C 3 2 p 2 q 3-2 = 3 * 0,1 2 * 0,9 = 0,027;
P 3 (3) = C 3 3 p 3 q 3-3 = p 3 = 0,1 3 = 0,001;
Проверете: ∑p i = 0,729+0,243+0,027+0,001=1.
Следователно желаният закон за биномиално разпределение X има формата:
Върху оста на абсцисата нанасяме възможните стойности x i, а на оста на ординатите - съответните вероятности p i . Нека построим точки M 1 (0; 0,729), M 2 (1; 0,243), M 3 (2; 0,027), M 4 (3; 0,001). Свързвайки тези точки с линейни сегменти, получаваме желания полигон за разпределение.
3. Намерете функцията на разпределение F(x) = P(X
За x ≤ 0 имаме F(x) = P(X<0) = 0;за 0< x ≤1 имеем F(x) = Р(Х<1) = Р(Х = 0) = 0,729;
за 1< x ≤ 2 F(x) = Р(Х<2) = Р(Х=0) + Р(Х=1) =0,729+ 0,243 = 0,972;
за 2< x ≤ 3 F(x) = Р(Х<3) = Р(Х = 0) + Р(Х = 1) + Р(Х = 2) = 0,972+0,027 = 0,999;
за x > 3 ще бъде F(x) = 1, тъй като събитието е сигурно.
 |
Графика на функцията F(x)
4.
За биномното разпределение X:
- математическо очакване М(X) = np = 3*0,1 = 0,3;
- дисперсия D(X) = npq = 3*0,1*0,9 = 0,27;
- стандартно отклонение σ(X) = √D(X) = √0,27 ≈ 0,52.
Дисперсиянепрекъсната случайна променлива X, чиито възможни стойности принадлежат на цялата ос Ox, се определя от равенството: ![]()
Възлагане на услугата. Онлайн калкулаторът е предназначен да решава проблеми, при които или плътност на разпределение f(x) или функция на разпределение F(x) (виж примера). Обикновено в такива задачи се изисква намиране математическо очакване, стандартно отклонение, графика на функциите f(x) и F(x).
Инструкция. Изберете типа на входните данни: плътност на разпределението f(x) или функция на разпределение F(x) .
Плътността на разпределение f(x) е дадена: 
Функцията на разпределение F(x) е дадена: 
Непрекъсната произволна променлива се дефинира от плътност на вероятността 
(Закон за разпределението на Релей – използва се в радиотехниката). Намерете M(x) , D(x) .
Извиква се произволната променлива X непрекъснато
, ако неговата функция на разпределение F(X)=P(X< x) непрерывна и имеет производную.
Функцията на разпределение на непрекъсната случайна променлива се използва за изчисляване на вероятностите случайна променлива да попадне в даден интервал:
P(α< X < β)=F(β) - F(α)
освен това за непрекъсната случайна променлива няма значение дали нейните граници са включени в този интервал или не:
P(α< X < β) = P(α ≤ X < β) = P(α ≤ X ≤ β)
Плътност на разпределение
непрекъсната случайна променлива се нарича функция
f(x)=F'(x) , производна на функцията на разпределение.
Свойства на плътност на разпределение
1. Плътността на разпределението на произволна променлива е неотрицателна (f(x) ≥ 0) за всички стойности на x.2. Условие на нормализиране:
Геометричното значение на условието за нормализиране: площта под кривата на плътността на разпределението е равна на единица.
3. Вероятността за удряне на произволна променлива X в интервала от α до β може да се изчисли по формулата
Геометрично, вероятността непрекъсната произволна променлива X да попадне в интервала (α, β) е равна на площта на криволинейния трапец под кривата на плътността на разпределението въз основа на този интервал.
4. Функцията на разпределение се изразява чрез плътност, както следва:
Стойността на плътността на разпределението в точката x не е равна на вероятността да вземем тази стойност; за непрекъсната случайна променлива можем да говорим само за вероятността да попаднем в даден интервал. Нека (фиг. 5.4). Намерете аналитичен израз за плътността на вероятността е(х) на цялата числова права.
Ориз. 5.4 Фиг. 5.5
5.16. Случайна стойност хразпределени по закона на "правоъгълния триъгълник" в интервала (0; 4) (фиг. 5.5). Намерете аналитичен израз за плътността на вероятността е(х) на цялата числова права.
Отговори
П (-1/2<х<1/2)=2/3.
П(2π /9<х< π /2)=1/2.
5.3. а) С=1/6, б) М(х)=3 , в) д(х)=26/81.
5.4. а) С=3/2, б) М(х)=3/5, в) д(х)=12/175.
б) М(х)= 3 , д(х)= 2/9, σ( х)= /3.
б) М(х)=2 , д(х)= 3 , σ( х)= 1,893.
5.7. а) c = ; б)
5.8. а) С=1/2; б)
5.9. а) 1/4; б) 0.
5.10. а) 3/5; б) 1.
5.11. а) С= 2; б) М(х)= 2; в 1- вътрешен 2 2 ≈ 0,5185.
5.12. а) М(х)= π /2 ; б) 1/2
………………………………………………………
An - произволна променлива X е приела стойността на An.
Очевидно сумата от събития A1 A2, . , An е определено събитие, тъй като случайната променлива задължително приема поне една от стойностите x1, x2, xn.
Следователно P (A1 È A2 È . È An) = 1.
Освен това събитията A1, A2, ., An са несъвместими, тъй като произволна променлива в един експеримент може да приеме само една от стойностите x1, x2, ., xn. Чрез теоремата за събиране за несъвместими събития получаваме
P(A1)+P(A2)+ .+P(An)=1,
т.е. p1+p2+ . +pn = 1, или, накратко,
Следователно сборът от всички числа, разположени във втория ред на таблица 1, който дава закона за разпределението на случайната променлива X, трябва да бъде равен на единица.
ПРИМЕР 1. Нека произволната променлива X е броят на точките, хвърлени при хвърляне на зар. Намерете закона за разпределение (под формата на таблица).
Случайната променлива X приема стойности
x1=1, x2=2, … , x6=6
с вероятности
p1= p2 = … = p6 =
Законът за разпределението е даден от таблицата:
таблица 2
ПРИМЕР 2.Биномиално разпределение. Помислете за случайна променлива X - броят на поява на събитие A в серия от независими експерименти, във всеки от които A се появява с вероятност p.
Случайната променлива X очевидно може да приеме една от следните стойности:
0, 1, 2, ., k, ., n.
Вероятността за събитие, състоящо се във факта, че случайната променлива X ще приеме стойност, равна на k, се определя от формулата на Бернули:
Рn(k)= където q=1- р.
Такова разпределение на произволна променлива се нарича биномно разпределение или разпределение на Бернули. Разпределението на Бернули е напълно определено от два параметъра: броя n на всички опити и вероятността p, с която събитието се случва във всеки отделен опит.
Условието за биномното разпределение приема формата:
![]()
За да се докаже валидността на това равенство, то е достатъчно в тъждеството
(q+px)n= ![]()
поставете x=1.
ПРИМЕР 3.Поасоново разпределение. Това е името на вероятностното разпределение на формата:
P(k)= ![]() .
.
Определя се от единичен (положителен) параметър a. Ако ξ е произволна променлива, която има разпределение на Поасон, тогава съответният параметър a - е средната стойност на тази произволна променлива:
a=Mξ=, където M е математическото очакване.
Случайната променлива е:
ПРИМЕР 4.експоненциално разпределение.
Ако времето е случайна променлива, нека го обозначим с τ, така че
където 0<λ=const, t ³ 0, причем, если t=0, то P(t)=0.
Средната стойност на случайната променлива t е:

Плътността на разпределение има формата:

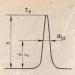
4) Нормално разпределение
Нека са независими, идентично разпределени случайни променливи и нека ![]() Ако членовете са достатъчно малки и числото n е достатъчно голямо, - ако за n à ∞ математическото очакване на случайната променлива Мξ и дисперсията Dξ, равна на Dξ=M(ξ–Мξ)2, са такива, че Мξ~ а, Dξ~σ2, тогава
Ако членовете са достатъчно малки и числото n е достатъчно голямо, - ако за n à ∞ математическото очакване на случайната променлива Мξ и дисперсията Dξ, равна на Dξ=M(ξ–Мξ)2, са такива, че Мξ~ а, Dξ~σ2, тогава
 - нормално или гаусово разпределение
- нормално или гаусово разпределение
![]() .
.
5) Геометрично разпределение. Нека ξ означава броя на опитите, предхождащи първия „успех“. Ако приемем, че всеки тест продължава единица време, тогава можем да разглеждаме ξ като времето за изчакване до първия „успех“. Разпределението изглежда така:
Р(k)=p(1-p)k, (k=0, 1, 2) p>0
6) Хипергеометрично разпределение.
Има N - обекти, сред които n - "специални обекти". Измежду всички обекти, k-обектите са избрани на случаен принцип. Намерете вероятността сред избраните обекти да е равна на r - "специални обекти". Разпределението изглежда така:
7) Разпределение на Паскал.
Нека x е общият брой на "провалите", предхождащи пристигането на r-ия "успех". Разпределението изглежда така:
Функцията за разпределение има формата:

Равновероятното разпределение предполага, че произволната променлива x може да приеме всяка стойност в интервала със същата вероятност. В този случай плътността на разпределението се изчислява като 
По-долу са представени графики на плътност на разпределение и функция на разпределение.

Преди да обясним понятието "бял шум", е необходимо да дадем редица дефиниции.
Случайна функция е функция на неслучаен аргумент t, който за всяка фиксирана стойност на аргумента е произволна променлива. Например, ако U е произволна променлива, тогава функцията X(t)=t2U е произволна.
Разделът на произволна функция е произволна променлива, съответстваща на фиксирана стойност на аргумента на произволната функция. По този начин една случайна функция може да се разглежда като набор от случайни променливи (X(t)), в зависимост от параметъра t.