В тази статия ще говорим за това как се прави уравнението на минаваща през него равнина дадена точкатриизмерно пространство, перпендикулярно на дадена права. Първо, ще анализираме принципа за намиране на уравнението на равнина, минаваща през дадена точка, перпендикулярна на дадена права линия, след което ще анализираме подробно решенията характерни примерии задачи.
Навигация в страницата.
Намиране на уравнението на равнина, минаваща през дадена точка от пространството, перпендикулярна на дадена права.
Нека си поставим следната задача.
Нека Oxyz е фиксиран в триизмерно пространство, дадена е точка, права a и се изисква да се напише уравнението на равнината, преминаваща през точката M 1, перпендикулярна на правата a.
Първо, нека си припомним един важен факт.
В уроците по геометрия гимназиядоказана е теорема: една равнина минава през дадена точка в триизмерно пространство, перпендикулярна на дадена права (доказателството на тази теорема можете да намерите в учебника по геометрия за 10-11 клас, посочен в списъка с литература на края на статията).
Сега ще покажем как се намира уравнението на тази единствена равнина, минаваща през дадена точка, перпендикулярна на дадена права.
В условието на задачата са ни дадени координатите x 1, y 1, z 1 на точката M 1, през която минава равнината. Тогава, ако намерим координатите на нормалния вектор на равнината, тогава можем да съставим необходимото уравнение на равнината, минаваща през дадена точка, перпендикулярна на дадената права линия.
Примери за съставяне на уравнението на равнина, минаваща през дадена точка, перпендикулярна на дадена права.
Разгледайте решенията на няколко примера, в които се намира уравнението на равнина, преминаваща през дадена точка от пространството, перпендикулярна на дадена права линия.
Пример.
Напишете уравнението на равнината, която минава през точката и е перпендикулярна на координатната права Oz.
Решение.
Векторът на посоката на координатната линия Oz очевидно е координатният вектор. Тогава нормалният вектор на равнината, чието уравнение трябва да съставим, има координати. Нека напишем уравнението на равнина, минаваща през точка и имаща нормален вектор с координати:
.
Нека покажем втория начин за решаване на този проблем.
Равнината, перпендикулярна на координатната линия Oz, определя непълно общо уравнение на равнината на формата . Нека намерим стойностите C и D, при които равнината минава през точката, като заменим координатите на тази точка в уравнението: . По този начин числата C и D са свързани с релацията. Като вземем C=1, получаваме D=-5. Заместваме намерените C=1 и D=-5 в уравнението и получаваме желаното уравнение на равнината, перпендикулярна на правата Oz и минаваща през точката . Изглежда като .
Отговор:
Пример.
Напишете уравнението за равнина, която минава през началото и е перпендикулярна на правата 
.
Решение.
Тъй като равнината, чието уравнение трябва да получим, е перпендикулярна на правата , то нормалният вектор на равнината може да се приеме за насочващ вектор на дадената права линия. Тогава 
. Остава да напишем уравнението на равнината, минаваща през точката и имаща нормален вектор : . Това е желаното уравнение на равнината, минаваща през началото, перпендикулярно на дадената права.
Отговор:
.
Пример.
Две точки и са дадени в правоъгълната координатна система Oxyz в триизмерно пространство. Равнината минава през точка А, перпендикулярна на правата АВ. Напишете уравнението на равнината на отсечки.
Решение.
Общо уравнение на равнина, минаваща през точка и имаща нормален равнинен вектор 
, ще бъде записано като .
Остава да преминем към необходимото уравнение на равнината на сегменти: 
.
Отговор:
.
В заключение отбелязваме, че има задачи, в които се изисква да се напише уравнението на равнина, минаваща през дадена точка и перпендикулярна на две дадени пресичащи се равнини. По същество решението на този проблем се свежда до съставяне на уравнението на равнина, минаваща през дадена точка, перпендикулярна на дадена права линия, тъй като две пресичащи се равнини определят права линия. В този случай основната трудност е процесът на намиране на координатите на нормалния вектор на равнината, чието уравнение трябва да се състави. 
Следователно векторът 
е нормален вектор на равнината, перпендикулярна на правата a . Нека напишем уравнението на равнината, минаваща през точката 
и имащ нормален вектор :
.
Това е желаното уравнение на равнина, минаваща през дадена точка, перпендикулярна на дадена права линия.
Отговор:
.
Библиография.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Е.Г., Юдина И.И. Геометрия. 7 - 9 клас: учебник за учебни заведения.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Е.Г. Геометрия. Учебник за 10-11 клас на гимназията.
- Погорелов А.В., Геометрия. Учебник за 7-11 клас на образователните институции.
- Бугров Я.С., Николски С.М. висша математика. Том първи: Елементи на линейната алгебра и аналитична геометрия.
- Илин В.А., Позняк Е.Г. Аналитична геометрия.
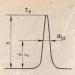
Да разгледаме равнина Q в пространството.Положението й се определя напълно чрез задаване на вектор N, перпендикулярен на тази равнина и някаква фиксирана точка, лежаща в равнината Q. Векторът N, перпендикулярен на равнината Q, се нарича нормален вектор на тази равнина. Ако обозначим с A, B и C проекциите на нормалния вектор N, тогава
Нека изведем уравнението на равнината Q, минаваща през дадена точка и имаща даден нормален вектор. За да направите това, разгледайте вектор, свързващ точка с произволна точка от равнината Q (фиг. 81).
За всяка позиция на точка M в равнината Q, векторът MXM е перпендикулярен на вектора на нормата N на равнината Q. Следователно, скаларното произведение Нека запишем скаларното произведение чрез проекции. Тъй като , и вектор , тогава
и следователно
Показахме, че координатите на всяка точка от Q равнината удовлетворяват уравнение (4). Лесно е да се види, че координатите на точки, които не лежат в равнината Q, не удовлетворяват това уравнение (в последния случай, ). Следователно, ние получихме необходимото уравнение на равнината Q. Уравнение (4) се нарича уравнение на равнината, преминаваща през дадена точка. Тя е от първа степен спрямо текущите координати
И така, ние показахме, че всяка равнина съответства на уравнение от първа степен по отношение на текущите координати.
Пример 1. Напишете уравнението на равнина, минаваща през точка, перпендикулярна на вектора.
Решение. Тук . Въз основа на формула (4) получаваме
или след опростяване,
Като дадем различни стойности на коефициентите A, B и C на уравнение (4), можем да получим уравнението на всяка равнина, минаваща през точката . Множеството от равнини, преминаващи през дадена точка, се нарича куп равнини. Уравнение (4), в което коефициентите A, B и C могат да приемат всякакви стойности, се нарича уравнение на сноп от равнини.
Пример 2. Напишете уравнение за равнина, минаваща през три точки, (фиг. 82).
Решение. Нека напишем уравнението за група равнини, преминаващи през точка
Тази статия дава представа как да се напише уравнение за равнина, минаваща през дадена точка в триизмерно пространство, перпендикулярно на дадена права. Нека анализираме горния алгоритъм, като използваме примера за решаване на типични проблеми.
Намиране на уравнението на равнина, минаваща през дадена точка от пространството, перпендикулярна на дадена права
Нека в него са дадени триизмерно пространство и правоъгълна координатна система O x y z. Дадени са също точката M 1 (x 1, y 1, z 1), правата a и равнината α, минаваща през точката M 1, перпендикулярна на правата a. Необходимо е да се запише уравнението на равнината α.
Преди да продължим с решаването на този проблем, нека си припомним теоремата за геометрията от програмата за 10 - 11 клас, която гласи:
Определение 1
Една равнина минава през дадена точка в триизмерното пространство и е перпендикулярна на дадена права.
Сега помислете как да намерите уравнението на тази единствена равнина, минаваща през началната точка и перпендикулярна на дадената права.
Възможно е да се напише общото уравнение на равнина, ако са известни координатите на точка, принадлежаща на тази равнина, както и координатите на нормалния вектор на равнината.
Съгласно условието на задачата ни са дадени координатите x 1, y 1, z 1 на точката M 1, през която минава равнината α. Ако определим координатите на нормалния вектор на равнината α, тогава ще можем да напишем желаното уравнение.
Нормалният вектор на равнината α, тъй като е различен от нула и лежи на правата a, перпендикулярна на равнината α, ще бъде всеки насочващ вектор на правата a. И така, задачата за намиране на координатите на нормалния вектор на равнината α се трансформира в задачата за определяне на координатите на насочващия вектор на правата линия a .
Определянето на координатите на насочващия вектор на правата линия a може да се извърши по различни методи: зависи от варианта на задаване на правата линия a в началните условия. Например, ако правата a в условието на задачата е дадена от канонични уравнения от вида
x - x 1 a x = y - y 1 a y = z - z 1 a z
или параметрични уравнения от вида:
x = x 1 + a x λ y = y 1 + a y λ z = z 1 + a z λ
тогава насочващият вектор на правата линия ще има координати a x, a y и a z. В случай, когато правата линия a е представена от две точки M 2 (x 2, y 2, z 2) и M 3 (x 3, y 3, z 3), тогава координатите на вектора на посоката ще бъдат определени като (x3 - x2, y3 - y2 , z3 – z2).
Определение 2
Алгоритъм за намиране на уравнението на равнина, минаваща през дадена точка, перпендикулярна на дадена права:
Определете координатите на насочващия вектор на правата линия a: a → = (a x, a y, a z) ;
Ние дефинираме координатите на нормалния вектор на равнината α като координатите на насочващия вектор на правата линия a:
n → = (A , B , C) , където A = a x , B = a y , C = a z;
Пишем уравнението на равнината, минаваща през точката M 1 (x 1, y 1, z 1) и имаща нормален вектор n→=(A, B, C) във формата A (x - x 1) + B (y - y 1) + C (z - z 1) = 0. Това ще бъде изискваното уравнение на равнина, която минава през дадена точка в пространството и е перпендикулярна на дадена права.
Полученото общо уравнение на равнината: A (x - x 1) + B (y - y 1) + C (z - z 1) \u003d 0 дава възможност да се получи уравнението на равнината на сегменти или нормалното уравнение на равнината.
Нека решим някои примери с помощта на алгоритъма, получен по-горе.
Пример 1
Дадена е точка M 1 (3, - 4, 5), през която минава равнината, като тази равнина е перпендикулярна на координатната права O z.
Решение
векторът на посоката на координатната линия O z ще бъде координатният вектор k ⇀ = (0 , 0 , 1) . Следователно нормалният вектор на равнината има координати (0 , 0 , 1) . Нека напишем уравнението на равнина, преминаваща през дадена точка M 1 (3, - 4, 5), чийто нормален вектор има координати (0, 0, 1):
A (x - x 1) + B (y - y 1) + C (z - z 1) = 0 ⇔ ⇔ 0 (x - 3) + 0 (y - (- 4)) + 1 (z - 5) = 0 ⇔ z - 5 = 0
Отговор: z - 5 = 0 .
Помислете за друг начин за решаване на този проблем:
Пример 2
Равнина, която е перпендикулярна на правата O z, ще бъде дадена от непълно общо уравнение на равнината от вида С z + D = 0 , C ≠ 0 . Нека дефинираме стойностите на C и D: тези, за които равнината минава през дадена точка. Заместваме координатите на тази точка в уравнението C z + D = 0 , получаваме: C · 5 + D = 0 . Тези. числа, C и D са свързани с - D C = 5 . Вземайки C \u003d 1, получаваме D = - 5.
Заменете тези стойности в уравнението C z + D = 0 и получете необходимото уравнение за равнина, перпендикулярна на правата O z и минаваща през точката M 1 (3, - 4, 5) .
Ще изглежда така: z - 5 = 0.
Отговор: z - 5 = 0 .
Пример 3
Напишете уравнение за равнина, минаваща през началото и перпендикулярна на правата x - 3 = y + 1 - 7 = z + 5 2
Решение
Въз основа на условията на задачата може да се твърди, че водещият вектор на дадена права линия може да се приеме като нормален вектор n → на дадена равнина. Така: n → = (- 3 , - 7 , 2) . Нека напишем уравнението на равнина, минаваща през точка O (0, 0, 0) и имаща нормален вектор n → \u003d (- 3, - 7, 2) :
3 (x - 0) - 7 (y - 0) + 2 (z - 0) = 0 ⇔ - 3 x - 7 y + 2 z = 0
Получихме необходимото уравнение за равнината, минаваща през началото, перпендикулярно на дадената права.
Отговор:- 3x - 7y + 2z = 0
Пример 4
Дадена е правоъгълна координатна система O x y z в триизмерно пространство, тя съдържа две точки A (2 , - 1 , - 2) и B (3 , - 2 , 4) . Равнината α минава през точка A, перпендикулярна на правата AB. Необходимо е да се състави уравнението на равнината α на отсечки.
Решение
Равнината α е перпендикулярна на правата A B, тогава векторът A B → ще бъде нормален вектор на равнината α. Координатите на този вектор се определят като разлика между съответните координати на точки B (3, - 2, 4) и A (2, - 1, - 2):
A B → = (3 - 2 , - 2 - (- 1) , 4 - (- 2)) ⇔ A B → = (1 , - 1 , 6)
Общото уравнение на равнината ще бъде записано в следния вид:
1 x - 2 - 1 y - (- 1 + 6 (z - (- 2)) = 0 ⇔ x - y + 6 z + 9 = 0
Сега съставяме желаното уравнение на равнината в сегментите:
x - y + 6 z + 9 = 0 ⇔ x - y + 6 z = - 9 ⇔ x - 9 + y 9 + z - 3 2 = 1
Отговор:x - 9 + y 9 + z - 3 2 = 1
Трябва също да се отбележи, че има проблеми, чието изискване е да се напише уравнение за равнина, минаваща през дадена точка и перпендикулярна на две дадени равнини. Най-общо решението на този проблем е да се напише уравнение за равнина, минаваща през дадена точка, перпендикулярна на дадена права, тъй като две пресичащи се равнини определят права линия.
Пример 5
Дадена е правоъгълна координатна система O x y z, в нея е точка M 1 (2, 0, - 5) . Дадени са и уравненията на две равнини 3 x + 2 y + 1 = 0 и x + 2 z - 1 = 0, които се пресичат по правата линия a . Необходимо е да се състави уравнение за равнина, минаваща през точката M 1 перпендикулярно на правата a.
Решение
Нека определим координатите на насочващия вектор на правата линия a . Той е перпендикулярен както на нормален вектор n 1 → (3 , 2 , 0) на равнината n → (1 , 0 , 2), така и на нормалния вектор 3 x + 2 y + 1 = 0 на равнината x + 2 z - 1 = 0 .
След това вземаме насочващия вектор α → права линия a векторен продуктвектори n 1 → и n 2 → :
a → = n 1 → × n 2 → = i → j → k → 3 2 0 1 0 2 = 4 i → - 6 j → - 2 k → ⇒ a → = (4 , - 6 , - 2 )
Така векторът n → = (4, - 6, - 2) ще бъде нормален вектор на равнината, перпендикулярна на правата a. Записваме желаното уравнение на равнината:
4 (x - 2) - 6 (y - 0) - 2 (z - (- 5)) = 0 ⇔ 4 x - 6 y - 2 z - 18 = 0 ⇔ ⇔ 2 x - 3 y - z - 9 = 0
Отговор: 2 x - 3 y - z - 9 = 0
Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter
За да получим общото уравнение на равнината, ние анализираме равнината, минаваща през дадена точка.
Нека в пространството има три координатни оси, които вече са ни известни - вол, ойи Оз. Дръжте листа хартия, така че да остане плосък. Равнината ще бъде самият лист и неговото продължение във всички посоки.
Позволявам Ппроизволна равнина в пространството. Всеки вектор, перпендикулярен на него, се нарича нормален вектор към този самолет. Естествено, говорим за ненулев вектор.
Ако някоя точка от равнината е известна Пи някакъв вектор на нормалата към него, то от тези две условия равнината в пространството е напълно определена(през дадена точка има само една равнина, перпендикулярна на даден вектор). Общото уравнение на равнината ще изглежда така:
И така, има условия, които задават уравнението на равнината. За да го получите сам равнинно уравнение, който има горната форма, поемаме в самолета Ппроизволен точка М с променливи координати х, г, z. Тази точка принадлежи на равнината само ако вектор перпендикулярно на вектора(Фиг. 1). За това според условието за перпендикулярност на векторите е необходимо и достатъчно скаларното произведение на тези вектори да е равно на нула, т.е.
Векторът е даден от условие. Координатите на вектора намираме по формулата 
:
.
Сега, използвайки формулата на точковото произведение на векторите 
, изразяваме скаларното произведение в координатна форма:
От точката M(x; y; z)е избран произволно на равнината, тогава последното уравнение се удовлетворява от координатите на всяка точка, лежаща на равнината П. За точка н, не лежащ на дадена равнина, , т.е. равенството (1) е нарушено.
Пример 1Напишете уравнение за равнина, минаваща през точка и перпендикулярна на вектор.
Решение. Използваме формула (1), погледнете я отново:
В тази формула числата А , Би ° Свекторни координати и числа х0 , г0 и z0 - координати на точката.
Изчисленията са много прости: заместваме тези числа във формулата и получаваме
Умножаваме всичко, което трябва да се умножи и събираме само числа (които са без букви). Резултат:
.
Необходимото уравнение на равнината в този пример се оказа изразено чрез общото уравнение от първа степен по отношение на променливи координати x, y, zпроизволна точка на равнината.
И така, уравнение на формата
Наречен общото уравнение на равнината .
Пример 2Изграждане в правоъгълна форма Декартова системакоординатна равнина, дадена от уравнението 
.
Решение. За да се построи равнина, е необходимо и достатъчно да се познават три от нейните точки, които не лежат на една права линия, например точките на пресичане на равнината с координатните оси.
Как да намеря тези точки? За намиране на пресечната точка с оста Оз, трябва да замените нули вместо x и y в уравнението, дадено в формулировката на проблема: х = г= 0 . Следователно получаваме z= 6 . Така дадена равнина пресича оста Озв точката А(0; 0; 6) .
По същия начин намираме пресечната точка на равнината с оста ой. В х = z= 0 получаваме г= −3 , тоест точка Б(0; −3; 0) .
И накрая, намираме точката на пресичане на нашата равнина с оста вол. В г = z= 0 получаваме х= 2 , тоест точка ° С(2; 0; 0) . Според трите точки, получени в нашето решение А(0; 0; 6) , Б(0; −3; 0) и ° С(2; 0; 0) изграждаме дадената равнина.
Помислете сега специални случаи общо уравнениесамолет. Това са случаи, когато определени коефициенти на уравнение (2) изчезват.
1. Кога D= 0 уравнение 
дефинира равнина, минаваща през началото, тъй като координатите на точка 0
(0; 0; 0) удовлетворяват това уравнение.
2. Кога A= 0 уравнение 
дефинира равнина, успоредна на оста вол, тъй като нормалният вектор на тази равнина е перпендикулярен на оста вол(проекцията му върху оста волравно на нула). По същия начин, когато B= 0 самолет 
успоредна ос ой, и когато C= 0 самолет 
успоредно на оста Оз.
3. Кога A=D= 0 уравнение дефинира равнина, минаваща през оста волзащото е успоредна на оста вол (A=D= 0). По същия начин равнината минава през оста ой, и равнината през оста Оз.
4. Кога A=B= 0 уравнение дефинира равнина, успоредна на координатната равнина xOyзащото е успоредна на осите вол (А= 0) и ой (Б= 0). По същия начин равнината е успоредна на равнината йОз, а самолетът - самолетът xOz.
5. Кога A=B=D= 0 уравнение (или z= 0) дефинира координатната равнина xOy, тъй като е успоредна на равнината xOy (A=B= 0) и минава през началото ( D= 0). По същия начин, уравнението y= 0 в пространството определя координатната равнина xOz, и уравнението x= 0 - координатна равнина йОз.
Пример 3Съставете уравнението на равнината Ппреминаващ през оста ойи точка.
Решение. Значи самолетът минава през оста ой. Така че в нейното уравнение г= 0 и това уравнение има вида . За определяне на коефициентите Аи ° Сизползваме факта, че точката принадлежи на равнината П .
Следователно сред неговите координати има такива, които могат да бъдат заместени в уравнението на равнината, което вече изведохме (). Нека отново да разгледаме координатите на точката:
М0 (2; −4; 3) .
Между тях х = 2 , z= 3 . Заменете ги в уравнението общ изгледи получаваме уравнението за нашия конкретен случай:
2А + 3° С = 0 .
Оставяме 2 Аот лявата страна на уравнението прехвърляме 3 ° Сот дясната страна и вземете
А = −1,5° С .
Заместване на намерената стойност Ав уравнението получаваме
или .
Това е уравнението, изисквано в примерното условие.
Решете сами задачата върху уравненията на равнината и след това погледнете решението
Пример 4Определете равнината (или равнините, ако са повече от една) по отношение на координатните оси или координатните равнини, ако равнината(ите) е дадена от уравнението .
Решения на типични проблеми, които са контролна работа- в наръчника "Задачи на равнина: успоредност, перпендикулярност, пресичане на три равнини в една точка" .
Уравнение на равнина, минаваща през три точки
Както вече споменахме, необходимо и достатъчно условие за построяване на равнина, освен една точка и нормален вектор, са и три точки, които не лежат на една права линия.
Нека има три различни точки , И , Не лежи на една и съща права линия. Тъй като тези три точки не лежат на една права линия, векторите и не са колинеарни и следователно всяка точка от равнината лежи в една и съща равнина с точките , и ако и само ако векторите , и 
компланарен, т.е. ако и само ако смесеното произведение на тези векториравно на нула.
Използвайки израза на смесено произведение в координати, получаваме равнинното уравнение
(3)
След разширяване на детерминанта това уравнение става уравнение от вида (2), т.е. общото уравнение на равнината.
Пример 5Напишете уравнение за равнина, минаваща през три дадени точки, които не лежат на права линия:
и да се определи конкретен случай на общото уравнение на правата, ако има такова.
Решение. Съгласно формула (3) имаме:
Нормално уравнение на равнината. Разстояние от точка до равнина
Нормалното уравнение на равнината е нейното уравнение, написано във формата
