КУРСОВА РАБОТА

по темата:

"Практическо приложение на свойствата на забележителни криви"

Въведение

Актуалност на темата е да демонстрира приложението на математическите знания в практическите човешки дейности. В хода на обучението аналитична геометрияне е предвидено разглеждане на свойствата на прекрасните криви, които се използват широко в живота.

Хипотеза : Използване този материалразширява кръгозора на учениците върху кривите и техните свойства и показва тяхното практическо приложение в човешкия живот.

Целта на тази работа : Съберете материал за използване по време на самоподготовкапрекрасни извивки.

Задачи : За да помогне на ученика. Използвайки минимално време, за да донесете максимална полза.

Практическо значение на работата: Вярвам, че работата ми ще бъде полезна на студентите по достъпен и нагледен начин за разбиране на материала. Покажете практическото приложение на свойствата на прекрасните криви, научете как да изграждате криви.

Избор на тема

В съвременно ниворазвитието на техническата мисъл има нужда от знания за забележителни криви. Те не са толкова редки в природата, имат практическо приложение в човешкия живот. Познанията за техните забележителни свойства се използват в различни механизми, използвани от човека в живота.

Избрах тази тема, защото смятам, че е интересна и смислена, развивайки познавателен интерес към аналитичната геометрия, отваряйки практическото приложение на геометрията в живота. Използването на този материал в лекциите по геометрия разширява кръгозора на студентите по изучаваните в програмата криви. в различни клонове на математиката и различни етапиизследване, срещаме се с криви, както от трети, така и от втори ред. Но никъде не се казва за забележителните свойства на тези криви и още повече за тяхното практическо приложение. Смятам, че е много важно учениците да познават прекрасните свойства на тези криви, които се използват широко в живота. Изучавайки и дори само опознавайки тези свойства, учениците виждат наистина практическото приложение на геометрията.

За целта се запознах с материала за прекрасните криви и техните свойства в различни учебници и енциклопедии по математика.

1. От историята на развитието на учението за линиите

Концепцията за линия възниква в човешкия ум в праисторически времена. Траекторията на хвърлен камък, очертанията на цветя и листа на растенията, криволичещата линия на речния бряг и други природни феномени отдавна привличат вниманието на хората. Наблюдавани многократно, те послужиха като основа за постепенното установяване на концепцията за линията. Но на нашите предци е отнел значителен период от време, за да сравнят формите на извити линии една с друга. Първите рисунки по стените на пещери, примитивни орнаменти върху домакински прибори показват, че хората са били в състояние не само да различават права линия от крива, но и да различават отделни извивки. Паметниците от древността свидетелстват, че на някакъв етап от своето развитие всички народи са имали понятията за права линия и своята обиколка. За конструирането на тези линии са използвани най-простите инструменти.

Но едва с появата на математическите теории теорията на линиите започва да се развива. Гръцки учени създават теорията за линиите от втори ред. Тези линии се разглеждат като сечение на конус от равнина, в резултат на което в древни времена са били наричани конични сечения. Коничните сечения са разгледани за първи път от Менехм, който е живял през 4-ти век пр.н.е. В търсене на решения на различни проблеми гръцките учени разглеждат и някои трансцендентални линии.

През средновековието важното постижение на гръцките учени е забравено. Математическата наука отново се обръща към изучаването на кривите едва през 7 век. За изследването на линиите от първостепенно значение беше методът на координатите, открит от Декарт и Ферма, който допринесе за появата на безкрайно малките смятане. Методът на координатите, съчетан с анализа на безкрайно малките, направи възможно да се премине към изследване на линиите по общ начин. Различни проблеми на механиката, астрономията, геодезията, оптиката, възникнали през 7-8 век, доведоха до откриването на много нови линии и изследването на техните геометрични механични свойства. Тези въпроси се занимават с голям ентусиазъм от най-големите математици на епохата - Декарт, Хюйгенс, Лайбниц, братя Бернули.

Следващата важна стъпка в изучаването на линиите е направена от Нютон, който започва развитието на теорията на кривите от трети ред. Впоследствие бяха поставени следните задачи: да се изследват криви от четвърти и по-високи порядки, да се създаде обща теория на алгебричните криви в равнината, да се премине към систематично изследване на алгебричните повърхности, като се започне от повърхността от втори ред. За решаването на последния проблем голям принос има известният математик от VIII Леонард Ойлер, академик на Санкт Петербургската академия на науките. Той описва първото ръководство по аналитична геометрия, което очертава теорията на линиите и повърхностите от втори ред.

. Забележителни линии от трети порядък

Всички прави линии и криви от втори ред (окръжности, елипси, параболи, хиперболи) са частни случаи на криви от трети ред.

В общия случай уравнението на крива линия от трети порядък може да бъде записано, както следва: x 3 + a 1 y 3 + 3a 2 x 2 y + 3a 3 xy 2 + 3a 4 x 2 + 3a 5 y 2 + 3a 6 xy + 3a 7 x + 3a 8 y + a 9 \u003d 0.

Приема се, че коефициентите не изчезват едновременно (в противен случай ще се получи уравнение от втора степен). Над 70 вида от тези линии. Тук разглеждаме само някои от тях, забележителни по своите свойства и приложения.

Декартов лист

. Характеристики на формата. Декартов лист се нарича крива от 3-ти ред, чието уравнение в правоъгълна система има вида

Понякога е удобно да се използват параметрични декартови уравнения, които могат да бъдат получени чрез задаване г= tx, добавяне на равенство (1) към това равенство и решаване на получената система по отношение на хи y,в резултат ще имаме:

откъдето следва, че декартовият лист е рационална крива.

Забележете също, че полярното декартово уравнение има формата

(3)

Координати хи ввъведете декартовото уравнение симетрично, откъдето следва, че кривата е симетрична спрямо ъглополовящата y=x.Обичайното проучване на специални точкиводи до заключението, че началото е възловата точка на декартовия лист. Уравнения на допирателни към алгебрична крива в нейната особена точка, съвпадаща с началото, могат да се получат, както е известно, чрез приравняване към нула на групата от най-ниска степен от уравнението на тази крива. В нашия случай имаме Z axy = 0,откъдето получаваме x = 0 и y = 0 - желаните уравнения на допирателните в възловата точка. Тези допирателни съвпадат с координатните оси и следователно в началото кривата се пресича под прав ъгъл. Лесно е да се види, че в първия координатен ъгъл кривата прави контур, който се пресича с правата линия y = хв точката

Точките на този контур, в които допирателните са успоредни на координатните оси, имат координати

И (виж фиг. 1)

За окончателното заключение за формата на кривата е необходимо също да се намери асимптотата.Замествайки y в уравнението на кривата с , ние приравняваме към нула в полученото уравнение коефициентите на два члена с по-високи степени Х.Вземи

и б = - а.Така декартовият лист има асимптота

y \u003d - x - a;следователно във 2-ри и 4-ти координатен ъгъл клоните на декартовия лист отиват в безкрайност.

Ориз. един

Често разглеждайте крива, завъртяна на 135 градуса. Нейните уравнения изглеждат така. В правоъгълна система: , където

Параметричен:

Извличане на уравненията на завъртяната крива:

Координатната система XOY се преобразува в координатна система UOV, която се получава чрез завъртане на осите OX и OY по часовниковата стрелка под ъгъл и преориентиране на оста OX в обратна посока:

Изразяването на старите координати XY по отношение на новите UVs изглежда така:

След заместване на изразите на старите координати с новото уравнение на декартовия лист, то се преобразува в следващ вид: .

Въвеждаме параметъра, последното уравнение ще бъде пренаписано, както следва:

Или .

Заменяме променливите u и v с обичайните x и y и получаваме уравнението на декартов лист в новата координатна система:

Замествайки предишното уравнение в уравнението, получаваме уравнението на декартов лист в полярната координатна система:

Решавайки този израз за ρ, получаваме:

.

2. Свойства.Според теоремата на Маклорен, ако в три точки от алгебрична крива от 3-ти ред, лежащи на една права линия, начертаем допирателни към тази крива, тогава точките на тяхното пресичане с кривата също ще лежат на права линия. Приложена към декартов лист, тази теорема е лесна за доказване. За целта извеждаме предварително условие за наличието на три точки от декартовия лист, съответстващи на стойностите T 1 , T 2 и T 3 параметър, на една права линия. Ако уравнението на права линия има вида г= kx+ б, тогава стойностите на параметрите, съответстващи на точките на пресичане на тази права линия с кривата, трябва да удовлетворяват системата

Тази система води до уравнението

чиито корени ще бъдат желаните стойности T 1 , T 2 и T 3 параметър, от който следва, че

Това равенство е условието за наличието на три точки М 1 (T 1) , М 2 (T 2 ), M 3 (t 3) Декартов лист върху една права линия.

При това условие ще покажем валидността на теоремата на Маклорен за декартов лист. Всъщност допирателната в точката М 1 (T 1 ) може да се разглежда като права линия, която пресича декартовия лист в две точки, съвпадащи една с друга, за което T 2 = T 1 , и в третата точка, за която съответната стойност на параметъра ще бъде обозначена с T 1 . Условието (4) приема формата T 1 2 T 1 = - 1. За допирателни в точки М 2и М 3 получаваме подобни отношения t 2 2 T 2 = -1 и t 3 2 T 3 = -1 . Умножавайки тези три равенства, имаме

(T 1 T 2 T 3 ) 2 T 1 T 2 T 3 = -1 . откъдето въз основа на (4) заключаваме, че и T 1 T 2 T 3 = -1, тези. точки н 1 (T 1 ), N 2 (T 2) и N 3 (T 3) лежат на една и съща права линия.

Определяйки площта, ограничена от цикъла на декартовия лист, получаваме:

. Метод на изграждане.Първо отбелязваме, че ако оста на симетрия на декартовия лист се вземе като абсцисната ос, тогава уравнението му ще приеме формата

(5)

Нека сега има окръжност с радиус r и център в точката

и директно x= -з. Вземете произволна точка Q от тази окръжност и начертайте права линия QAи директно QN, перпендикулярно на оста на абсцисата (фиг. 2). От пресечната точка Рправ QA с права линия x= - hначертайте права линия ROдокато се пресече в точка В 1 с права линия QN.Така че точката Вточка ще бъде присвоена на кръга Q1.Местоположението на точките Q 1 е декартов лист.

За да го докажете, обърнете внимание, че координатите на точката Вможе да се запише във формата

ъгълът, образуван от радиуса на окръжност, начертана до точка Q,с положителната посока на оста x. В съответствие с това, уравнението на права линия QAможе да се запише като

Приемайки в това уравнение x= -з, намерете ординатата

точки Р. От това следва, че уравнението на правата RQ 1 ще бъде записано във формуляра

(6)

В същото време, уравнението на права линия В 1 нима формата

(7)

Елиминиране от уравнения (6) и (7) на параметъра w, намираме уравнението на мястото на точките Q 1 във вида

Сравнявайки го с уравнение (5), заключаваме, че намереното място на точките е декартов лист.

Преобразуването на точките от окръжността в точки от декартовия лист, извършено с такава конструкция от него, се нарича Трансформация на Маклорен.

4. Историческа справка.За първи път в историята на математиката крива, по-късно наречена декартов лист, е дефинирана в писмо на Декарт до Ферма през 1638 г. като крива, за която сумата от обемите на кубовете, построени по абсцисата и ординатата на всяка точка е равна на обема на паралелепипеда, построен върху абсцисата, ординатата и някаква константа . Формата на кривата се установява за първи път от Робервал, който намира възловата точка на кривата, но в неговото представяне кривата се състои само от примка. Повтаряйки този цикъл в четири квадранта, той получава фигура, която му напомня за цвете с четири венчелистчета. Поетичното име на извивката "жасминово венчелистче" обаче не се вкорени. Пълният вид на кривата с наличието на асимптота е определен по-късно (1692) от Хюйгенс и И. Бернули. Името "декартов списък" е твърдо установено едва от началото на 18 век.

Цисоид на Диокъл

1. Характеристики на формата.Сред многото начини на образование цисоиди - крива, открита от древните в търсене на решение на известния проблем за удвояване на куба, първо ще се спрем на най-простото. Вземете кръг (наречен производство)с диаметър OA=2a и допирателна АБНа нея. Начертайте лъч OB през точка O и начертайте сегмент върху него OM=Слънце.Така конструираната точка M принадлежи на цисоида. завъртане на лъча 0Vпод определен ъгъл и след като направим посочената конструкция, ще намерим втората точка на цисоида и т.н. (фиг. 3).

Ако точката O се вземе като полюс, тогава откъдето получаваме полярното уравнение на цисоида

Използвайки формулите за прехода от полярни към декартови координати, намираме цисоидно уравнение в правоъгълна система:

(2)

Параметричните уравнения на цисоида могат да бъдат получени чрез задаване на x=ty, след което въз основа на уравнение (2) стигаме до системата

Ориз. 3

Уравнение (2) показва, че цисоидът е алгебрична крива от трети ред, а от уравнения (3) следва, че е рационална крива.

Цисоидът е симетричен спрямо оста на абсцисата, има безкрайни разклонения; допирателна към генериращата окръжност, т.е. прав х = 2а служи като асимптота за него; произходът е куспид от 1-ви вид.

2. Свойства.Кинематично цисоидът може да се получи като траектория на средната точка Мкрак слънцетриъгълник азбука,движейки се в равнината на чертежа, така че горната му част ATплъзга се по оста y, а другият крак ACвинаги минава през фиксирана точка Епо оста x. (фиг. 4)

Всъщност, обозначавайки средата на сегмента OEпрез д, забелязваме, че оттогава BC=EO,ê ВСИЧКИ=ê VEO,където /_ VEO = /_ SVE,и следователно ê NBE - равнобедрен, и тъй като Ед=EO/2=BC/2=BM,след това сегментът DMуспоредно на сегмента БЪДА. Нека, по-нататък, точката Да сеима пресечна точка с продължението на отсечката DMправа линия, минаваща през точка ATуспоредно на оста х. Нека опишем окръжност с център в началото и радиус, равен на OD , и начертайте допирателна към него във втората точка на пресичане с правата EO.Очевидно ще премине през точката ДА СЕ.Обозначаване на пресечната точка на линията DMKс кръг през Ф, Имайте предвид, че триъгълниците DOFи MVKса равни помежду си. От тяхното равенство следва, че Д.Ф.= МК, което означава и DM= FK. Последното равенство показва, че местоположението на точките Мще бъде цисоид.

Други начини за образуване на цисоид се основават на връзката му с парабола. Нека първо покажем това цисоидът е подерата на параболата по отношение на нейния връх.

Уравнението на тази парабола. Допирателно уравнение в произволна точка М(х, з ) Тази парабола може да се запише като уравнението на перпендикуляра, изпуснат от началото на тази допирателна, ще бъде координатите на точката нпресечната му точка с допирателната се определя от формулите

(4)

Елиминирайки параметъра h от тези равенства, получаваме уравнението

изразяващи цисоида.

Забележете освен това, че координатите на точка, симетрична на началото по отношение на допирателната към параболата на 2 = 2 пикселасе получават, ако десните части на формули (4) се удвоят и следователно се определят от формулите

Елиминирайки параметъра h от тези равенства, отново получаваме цисоида с уравнението. От това следва, че цисоидата е мястото на точките, които са симетрични на върха на параболата по отношение на нейните допирателни.

Трябва да се отбележи, че местоположението на точките, симетрични на началото по отношение на допирателната към параболата, може да се разглежда като траектория на върха на друга парабола, същата като дадена, която се търкаля по дадената парабола. По този начин възниква нов начин за кинематично формиране на цисоид като траектория на върха на парабола, която се търкаля без плъзгане по друга подобна парабола.

Строфоидна

Строфоидна (от гръцки stróphos - усукана лента и éidos - изглед)

Нека има неподвижна права AB и точка C извън нея на разстояние CO = а; права линия се върти около C, пресичаща AB в променлива точка N. Ако от точката N начертаем сегменти NM \u003d NM "\u003d NO от двете страни на правата линия AB, тогава мястото на точки M и M" за всички позиции на въртящата се греда CN е строфоида. Уравнение в правоъгълни координати: ; в полярни координати: r = - a cos 2j/cosj. Строфоидът е изследван за първи път от Е. Торичели (1645), името е въведено в средата на 19 век. Ориз. 6

Верзиера Агнези

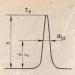
Верзиера (версиера) Агнези ( понякога извивката на Агнези) е равна крива, местоположението на точки M, за които е валидно отношението, където OA е диаметърът на окръжността, BC е полухордата на тази окръжност, перпендикулярна на OA. Версиерата на Агнези е кръстена на италианската математика Мария Гаетана Агнези, която изучава тази крива.

Уравнения

O = (0,0), A = (0, a)

В правоъгълна координатна система:

Координатите на точка M, лежаща върху версера, са x = BM, y = OB. OA = a и по дефиниция изграждаме пропорция

Оттук

От друга страна, BC може да се намери от уравнението на кръга:

Знаем, че y = OB, така че изразяваме:

Приравнете двата израза за BC:

Квадратиране, превеждане и поставяне в скоби:

Изразяваме y (y=0 не е подходящо по дефиниция):

, където е ъгълът между OA и OC.

Имоти:

1. Verzier - крива от трети ред.

Диаметърът OA е единствената ос на симетрия на кривата.

Кривата има един максимум - A (0; a) и две точки на огъване -

В близост до връх A, версията се приближава до кръг с диаметър OA. В точка А се получава допиране и кривата съвпада с окръжността. Това се показва от стойността на радиуса на кривината в точка A: .

Площ под графиката S = πa2. Изчислява се чрез интегриране на уравнението върху всички .

Обемът на тялото на въртене на версира около неговата асимптота (ос OX) .

Анé Зи Мария Гаетана(Агнези Мария Гаетана), род. 16.05.1718, Милано - умр. 01/09/1799, пак там. Италиански математик, професор в университета в Болоня (от 1750 г.). Работата на Агнези „Основи на анализа за използване на италианската младеж“ („Instituzioni analitiche ad uso della gioventú italiana“, v. 1-2, Mil., 1748) съдържа представяне на аналитичната геометрия, по-специално крива от трети порядък наречена "къдрица на Агнези" се разглежда там (или версия), чието уравнение е y=a 3 / (x 2 + a 2).

За да се построи тази права, е необходимо да се начертае окръжност с радиус a, центрирана в точката (0, a). След това от началото се изтеглят прави линии и се маркират две точки. Точка А (x1, y1) е пресечната точка на правата и окръжността, точка B (x2,2a) е пресечната точка на правата и горната хоризонтална допирателна към окръжността. След това се конструира точка на крива (x2, y1).

Английският математик Джон Колсън се зае да преведе Принципите на анализа от италиански. За него обаче, европеец от 18-ти век, не е било лесно да приеме, че авторът на книгата е жена и че за нея, за автора, една извивка може да бъде свързана с прическа. В резултат на това в англоезичната литература кривата беше наречена вещицата на Агнези. - нещо от областта на полетите до плешивата планина ...

3. Забележителни линии от четвърти и по-високи порядки

Линия (крива) от четвърти ред позвънете на дефинираната линия алгебрично уравнениечетвърта степен спрямо декартови правоъгълни координати. По подобен начин се дефинират линии (криви) от пети, шести и други порядки.

Наборът от линии (криви) от четвърти ред вече не съдържа десетки, а хиляди линии от определен тип. Наборите от линии от пети и шести ред са още по-разнообразни. Тук разглеждаме определени видове линии от четвърти и по-висок порядък, които имат интересни свойства и практически приложения.

Лемнискате Бернули

Нека се обърнем към кривата, описана от точка M на равнината, така че произведението p на разстоянията на тази точка до две конкретни точки F 1 и F 2 от същата равнина да остане непроменено. Такава крива се нарича лемниската (лемниската на гръцки означава "лента"). Ако дължината на отсечката F 1 F 2 е c, тогава разстоянията от средата O на отсечката F 1 F 2 до F1 и F2 са равни на c / 2 и произведението на тези разстояния е - c 2 /4. Нека първо изискваме стойността на p на неизменното произведение да е точно равна на 2/4; тогава

точка O ще лежи върху лемниската, а самата лемниската ще изглежда като „лежаща осмица“ (фиг. 8). Ако продължим отсечката F 1 F 2 в двете посоки до пресечната точка с лемниската, тогава получаваме две точки A 1 и A 2. Изразяваме разстоянието между A 1 A 2 \u003d x чрез известно разстояние c:

Фокусите на лемниската са F1 (− c; 0) и F2 (c; 0). Вземете произволна точка M (x; y). Произведението на разстоянията от фокусите до точката M е

И по дефиниция е равно на c2:

Квадратираме двете страни на уравнението:

Разширете скобите от лявата страна:

Отваряме скобите и свиваме новия квадрат на сумата:

Изваждаме общия фактор и прехвърляме:

В този случай a е радиусът на окръжността, описваща лемниската. След като извършихме прости трансформации, можем да получим изрично уравнение:

Правим квадрат и отваряме скобите:

Довеждаме до ума

то квадратно уравнениепо отношение на y". Решавайки го, получаваме

Като вземем корена и отхвърлим опцията с отрицателен втори член, получаваме:

където положителният вариант определя горната половина на лемниската, отрицателният вариант определя долната.

Ако стойността на константното произведение p не е равна на 2/4, тогава лемниската ще промени формата си. А когато p е по-малко от c 2 /4, лемниската се състои от два овала, всеки от които съдържа съответно точки F 1 и F 2 (фиг. 9).

Че. като зададем различни условия за p и c 2 /4, ще получим лемнискати от различни видове (фиг. 10).

Ориз. десет

Нека сега вземем произволен брой точки от равнината. F 1 , F 2 ,..., F n Нека получим крива, чиято форма ще зависи от това как точките F 1 , F 2 ,…, F n са разположени една спрямо друга и каква е стойността на константното произведение. Тази крива се нарича лемниската с n фокуса.

По-горе разгледахме лемнискати с две огнища. Като вземем различен брой фокуси, подредим ги по различни начини и припишем тази или онази стойност на произведението на разстоянията, могат да се получат лемнискати с най-странни очертания. Нека изведем точката на молива от определена точка A, без да я сваляме от хартията, така че накрая да се върне в началната точка A. Тогава тя ще опише определена крива; изискваме само тази крива да не се пресича никъде

себе си. Очевидно по този начин могат да се получат извивки, имащи например очертанията на човешка глава или птица (фиг. 11). Оказва се, че имайки такава произволна крива, човек може да избере числото n и разположението на фокусите по такъв начин

F 1 , F 2 ,..., F n

и задайте такава стойност за постоянно произведение на разстоянията

МF 1 МF 2 … МF n = p

че съответната лемниската на око няма да се различава от тази крива. С други думи, възможните отклонения на точка M, която описва лемниската, от начертаната крива - няма да надвишават ширината на щриха на молива (моливът може да бъде заточен предварително, както желаете, така че щрихът да е много тесен). Този забележителен факт, който говори за изключителното разнообразие и богатство на формите на лемнискати с много огнища, се доказва доста строго, но много трудно, с помощта на висшата математика.

Охлювът на Паскал

Местоположението на точки M и M", разположени върху линиите на молива (чийто център O лежи върху окръжност с радиус R) на разстояние a от двете страни на точката P на пресичане на правите с окръжността; по този начин PM = PM" = а. уравнение в правоъгълни координати: ( x 2 + y 2 - 2Rx)2 - а 2(x 2 + y 2) = 0, в полярни координати: r = 2 Р cos j + а. В а = 2Рцикълът се свива до точка, в който случай ушната мида на Паскал се превръща в кардиоид. Името е кръстено на френския учен Б. Паскал (1588-1651), който пръв го изследва.

Циклоидни криви

Представете си, че определена крива се търкаля, без да се плъзга по друга крива; всяка точка, неизменно свързана с първата крива, ще опише нова крива. Така че можете да си представите елипса, търкаляща се по друга елипса и да изследвате линията, по която ще се движи нейният център, или да определите траекторията на фокуса на парабола, търкаляща се по права линия, и т.н.

Сред образуваните по този начин криви се разграничават криви, които са траектории на точка, неизменно свързана с окръжност, която се търкаля, без да се плъзга по друга окръжност. Получените линии се наричат циклоидна.

При формиране на циклоидни криви точката на начертаване се отделя от центъра на генериращата (движеща се) окръжност на определено разстояние. В конкретен случай е на обиколката на генериращия кръг. При това условие получените криви се подразделят на епициклоиди и хипоциклоиди в зависимост от това дали генериращият кръг е разположен от външната или от вътрешната страна на фиксирания кръг.

Алгебричните криви включват такива добре познати криви като кардиоида, астроида, нека разгледаме тези криви.

Кардиоиден

1. Уравнението. Кардиоида може да се дефинира като траектория на точка, лежаща върху обиколката на окръжност с радиус r, която се търкаля по обиколката на неподвижна окръжност със същия радиус. Така тя ще бъде епициклоида с модул m равен на 1.

Това обстоятелство ни позволява незабавно да запишем параметричните уравнения на кардиоида, като заменим модула m с единица в горните параметрични уравнения на епициклоидата. Ще има:

(1)

За да се получи полярното уравнение на кардиоида, е удобно да се вземе точка А за полюс (фиг. 13) и да се насочи полярната ос по абсцисата. Тъй като четириъгълникът AOO 1 M ще бъде равнобедрен трапец, тогава полярният ъгъл j на точка M ще бъде равно на ъгълазавъртане на генериращия кръг, т.е. параметър t. Имайки предвид това обстоятелство, нека заменим y във второто уравнение на системата (1) чрез r sin t. Намалявайки така полученото равенство с sin t, получаваме полярното уравнение на кардиоида

Според това уравнение

можем да заключим, че кардиоидът е един от охлювите на Паскал. Следователно може да се определи като конхоида на кръг.

От това уравнение следва, че кардиоидът е алгебрична крива от 4-ти порядък.

2. Свойства. На първо място, тъй като кардиоидата е епициклоида с m=1, всички свойства на епициклоидите, разгледани в предишния параграф, могат да бъдат прехвърлени на нея.

Ето характеристиките и спецификациите.

Допирателната в произволна точка на кардиоида минава през точката на окръжността на генериращата окръжност, диаметрално противоположна на точката на контакт на окръжностите, а нормалата минава през точката на техния контакт.

Ъгълът m, който е допирателната към кардиоида с радиус вектора на допирателната точка, наполовинаъгълът, образуван от този радиус вектор с полярната ос. Наистина ли

От това отношение пряко следва, че ъгълът, направен от допирателната към кардиоида с оста на абсцисата, е (както външен ъгълтриъгълник AMN Фиг. четиринадесет). Като имаме формула, можем да докажем, че допирателните към кардиоида, изтеглени в краищата на хордата, преминаваща през полюса, са взаимно перпендикулярни.

Наистина, тъй като

Ориз. четиринадесет

Отбелязваме също, че мястото на пресечните точки на тези допирателни е кръг. Действително, уравнението на първата допирателна, базирано на уравнения (1) на кардиоида, ще има вида

И втората допирателна Елиминирайки параметъра от тези уравнения, получаваме уравнението на посочения кръг.

Радиусът на кривината в произволна точка на кардиоида се определя от формулата

Може също да се покаже, че радиусът на кривината е 2/3 от полярната норма N в дадена точка.

Наистина, откъдето на базата на (4) получаваме Тази връзка може да се използва за конструиране на центъра на кривината на кардиоида.

Еволюта на кардиоида, според общото свойство на еволюта на епициклоида, също ще бъде кардиоид, подобен на дадения, с коефициент на подобие, равен на 1/3, и завъртян спрямо дадения на ъгъл от 180°.

Дължината на кардиоидната дъга от точка A до произволна точка M се определя по формулата

Ако дължината на дъгата се брои от точка A 1, диаметрално противоположна на точка A, тогава формулата за определяне на дължината на дъгата може да се запише като

(6)

Естественото уравнение на кардиоида се получава, ако параметърът се изключи от равенства (4) и (6). Ще изглежда така

(7)

Площта, ограничена от кардиоида, се определя по формулата

и, както се вижда, е равна на площта на шестте колела на генериращия кръг.

Дължината на целия кардиоид се определя по формулата

и, както се вижда, е равна на осем диаметъра на генериращия кръг. Обемът на тялото, получен от въртенето на кардиоида около оста му, е равен на

Повърхността на тялото, получена от въртенето на кардиоида около оста му, е равна на

Видяхме, че кардиоидът е органично свързан с кръга. Това е конхоида от кръг и епициклоида. Той има различно отношение с окръжността - кардиоидът е под-ера на окръжност по отношение на точка, принадлежаща на тази окръжност.

Наистина, нека OM е перпендикулярът, спуснат към допирателната към окръжността с радиус, равен на 2r, начертан в точката N.

Тъй като OM = OB + BM, или r = 2r cos j + 2r, тогава мястото на точки M ще бъде кардиоид с уравнението r \u003d 2r (1 + cos j)

В заключение отбелязваме, че кардиоидът също принадлежи към семейството на синусоидалните спирали и неговите отделни свойства повтарят общите свойства на тези криви. От тези свойства следва по-специално, че инверсията на кардиоида по отношение на куспида дава парабола.

Astroid

1. Свойства.Астроидът е специален случай на хипоциклоиди, а именно хипоциклоид с модул m равен на 1/4. Следователно това е траекторията на точка, лежаща върху окръжността на окръжност с радиус r, която се търкаля по вътрешността на друг фиксиран кръг, чийто радиус R е четири пъти по-голям.

Параметричните уравнения на астроида могат да бъдат получени чрез поставяне на хипоциклоиди в уравненията, m=1/4. Ето уравненията:

където t, както преди, е ъгълът на завъртане на генериращия кръг (фиг. 16)

Елиминирайки параметъра t от уравнения (1), получаваме:

Уравнение (2) предполага, че астроидът е алгебрична крива от шести порядък.

Параметричните уравнения (1) на астроида могат да се сведат до вида

(3)

Елиминирайки параметъра t от тези уравнения, получаваме често използваната форма на уравнението на астроида

(4)

Като приемем в изведените по-рано общи отношения за циклоидни криви модула

m = -1/4, получаваме съответните отношения за астроида:

) радиусът на кривината в произволна точка на астроида се определя по формулата

(5)

) дължината на дъгата на астроида от точка A до произволна точка M(t) се определя по формулата

дължината на единия клон е равна на и дължината на цялата крива е 6R;

), за да получим естественото уравнение на астроида, първо отбелязваме, че ако началната точка за дължината на дъгата не е точката A, за която t = 0, а точката, за която t = p, тогава дължината на дъгата се определя по формулата

изключвайки параметъра t от уравнения (5) и (6), получаваме естественото уравнение на астроида

) еволюцията на астроида е също астроид, подобен на дадения, с коефициент на подобие равен на 2, завъртян спрямо дадения на ъгъл p/4 (фиг. 16)

) площта, ограничена от целия астроид, е равна на обема на тялото, получен от въртенето на астроида, равна на 32/105p R 3

повърхността на тялото, образувана от въртенето на астроида, е равна на

Нека сега се обърнем към разглеждането на някои специфични свойства на астроида.

Астроидът е обвивката на сегмент с постоянна дължина, завършва. които се плъзгат по две взаимно перпендикулярни прави линии.

Приемаме тези прави като координатни оси и, като означаваме ъгъла на наклон на плъзгащия се сегмент ND=R през a (фиг. 4), ще имаме уравнението на правата ND във вида

Диференцирайки това уравнение по отношение на параметъра a, получаваме:

На практика движението на сегмента ND може да се извърши с помощта на така наречените карданни кръгове. Едната от тези окръжности с радиус R е неподвижна, а другата с радиус r, два пъти по-малка, се търкаля по вътрешната страна на неподвижната окръжност. Всякакви две диаметрално противоположни точки N и D на търкалящата се окръжност ще се движат по два взаимно перпендикулярни диаметъра Ox и Oy на неподвижната окръжност. Ясно е, че обвивката на диаметъра на търкалящия се кръг ще бъде астроида.

Ориз. 17

Ориз. осемнадесет

Разгледаният метод за образуване на астроид също може да се тълкува по следния начин. Правоъгълник ODCN, чиито две страни лежат на две взаимно перпендикулярни прави, се деформира така, че диагоналът му да запази дължина, равна на R, обвивката на диагонала ще бъде астроида. Тъй като в този случай перпендикулярът, спуснат от върха C към диагонала DN, служи като нормал към обвивката, астроида е мястото на основите на перпендикулярите, изпуснати от върха C на правоъгълника до неговия диагонал.

За , тези уравнения изразяват директния астроид, разгледан по-рано.

. Някои трансцендентални линии

трансцендентен се наричат ​​прави, чиито уравнения в правоъгълни декартови координати не са алгебрични. Най-простите примери за трансцендентални линии са графиките на функциите, y=, y= и други тригонометрични функции. Нека разгледаме някои други трансцендентални линии.

Спирала на Архимед

Представете си безкрайно дълга секундна стрелка, по която, започвайки от центъра на циферблата, малък бръмбар неуморно тича с постоянна скорост v cm/s. След минута буболечката ще бъде на разстояние 60v см от центъра, за две - 120v и т.н. Като цяло, след t секунди след началото на бягането, разстоянието на бъг от центъра ще бъде равно на vt см. През това време стрелката ще се завърти под ъгъл, съдържащ 6 t ° (в края на краищата за една секунда той успява да се завърти под ъгъл от 360 °: 60 \u003d 6 °). Следователно, позицията на бъг в равнината на циферблата след произволен брой t секунди след началото на движението е както следва. Необходимо е ъгълът a, съдържащ 6t°, да се отложи от първоначалното положение на стрелката по посока на нейното въртене и да се измери разстоянието r = vt cm от центъра по новата позиция на стрелката. Тук ще изпреварим грешката (фиг. 21).

Ориз. 21.

Очевидно съотношението между ъгъла на завъртане a на стрелката (в градуси) и изминатото разстояние r (в сантиметри) ще бъде:

С други думи, r е право пропорционално на a, а коефициентът на пропорционалност е k = v/6.

Нека прикрепим към нашия бегач малко, но неизчерпаемо бурканче с черна боя и да предположим, че боята, изтичаща през малка дупчица, оставя следа върху хартията от буболечката, отнесена със стрелката. Тогава кривата, изследвана за първи път от Архимед (287 - 212 г. пр. н. е.), постепенно ще се появи на хартия. В негова чест се нарича спиралата на Архимед. Трябва само да се каже, че Архимед не говори нито за втора стрелка (тогава нямаше и часовници с пружина: те са изобретени едва през 17-ти век), нито за бъг. Включихме ги тук за яснота.

Ориз. 22 Фиг. 23.

Спиралата на Архимед се състои от безкрайно много завои. Започва от центъра на циферблата и все повече и повече се отдалечава от него с увеличаване на броя на оборотите. На фиг. 22 показва първия завой и част от втория.

Сигурно сте чували, че с помощта на пергел и линейка е невъзможно да се раздели произволно взет ъгъл на три равни части (в специални случаи, когато ъгълът съдържа например 180°, 135° или 90°, това проблемът се решава лесно). Но ако използвате спретнато начертана архимедова спирала, тогава всеки ъгъл може да бъде разделен на произволно число равни части.

Да разделим, например, ъгъла AOB на три равни части (фиг. 23.). Ако приемем, че стрелката е обърната точно до този ъгъл, тогава бъгът ще бъде в точка N от страната на ъгъла. Но когато ъгълът на въртене беше три пъти по-малък, тогава бъгът беше три пъти по-близо до центъра O. За да намерим тази позиция, първо разделяме сегмента ON на три равни части. Това може да се направи с пергел и линийка. Получаваме отсечката ON 1, чиято дължина е три пъти по-малка от ON. За да върнете грешката в спиралата, трябва да направите прорез на тази крива с радиус ON 1 (отново компас!). Получаваме точката M. Ъгълът AOM и ще бъде три пъти по-малък от ъгъла AON.

Циклоида

Ще прикрепим линийка към долния ръб на черната дъска и ще навием обръч или кръг (картон или дървен) по него, като го притиснем към линийката и към дъската. Ако прикрепите парче тебешир към обръч или кръг (в точката на контакт с линийката), тогава тебеширът ще начертае крива (фиг. 24), наречена циклоида (което на гръцки означава „кръг“). Едно завъртане на обръча отговаря на една "арка" на циклоидата MM"M""N", ако обръчът се търкаля по-нататък, тогава ще се получават все повече и повече арки от същата циклоида.

Ориз. 24.

За да изградим върху хартия приблизително една арка от циклоида, описана чрез търкаляне на обръч с диаметър, равен например на три сантиметра, отделяме на прав сегмент, равен на 3x3,14 = 9,42 cm.

Получаваме сегмент, чиято дължина е равна на дължината на ръба на обръча, т.е. кръг с диаметър три сантиметра. Нека по-нататък разделим този сегмент на определен брой равни части, например на 6, и за всяка точка на деление ще изобразим нашия обръч в неговото положение, когато той лежи точно върху тази точка (фиг. 24), като ги номерираме позиции с числа:

О, 1, 2, 3, 4, 5, 6.

За да се премести от една позиция в друга, обръчът трябва да се завърти с една шеста от целия оборот (тъй като разстоянието между съседните точки на разделяне е равно на една шеста от окръжността). Следователно, ако в позиция 0 тебеширът ще бъде в точка M 0, то в позиция 1 тя ще лежи в точка M 1 - една шеста от окръжността от точката на контакт, в позиция 2 - в точка M 2 - две шести от точката на допир, и t .d. За да получите точки M 1, M 2, M 3 и т.н., трябва само да направите прорези на съответния кръг, започвайки от точката на контакт, с радиус, равен на

Ориз. 25.

5 см., а в позиция 1 е необходим един сериф, в позиция 2 - два серифа направени един след друг, в позиция 3 - три засечки и т.н. Сега, за да нарисувате циклоида, остава да свържете точките

M 0, M 1, M 2, M 3, M 4, M 5, M 6

гладка крива (на око).

Крива на най-краткото спускане

Сред многото забележителни свойства на циклоида отбелязваме едно, поради което той заслужаваше силно звучащо сложно име: „брахистохрон“. Това име е съставено от две гръцки думи, означаващи „най-кратко“ и „време“.

Помислете за този въпрос: каква форма трябва да се даде на добре полиран метален улей, свързващ две дадени точкиА и Б (фиг. 26.), така че полирано метално топче да се търкаля по този улей от точка А до точка Б за възможно най-кратко време? На пръв поглед изглежда, че трябва да спрем на прав улей, тъй като само по него топката ще премине най-краткия път от A до B. Не говорим обаче за най-краткия път, а за най-краткото време; времето зависи не само от дължината на пътя, но и от скоростта, с която върви топката. Ако улеят е огънат надолу, тогава неговата част, започваща от точка А, ще падне по-стръмно, отколкото в случай на прав улей, и топката, падаща по него, ще придобие скорост, по-голяма, отколкото в участък със същата дължина от прав улей. Но ако го направите начална частмного стръмна и относително дълга, тогава частта, съседна на точка B, ще бъде много нежна и също относително дълга; първата част от топката ще премине бързо, втората много бавно и топката може да закъснее да пристигне в точка B. Така че, очевидно, улукът трябва да получи вдлъбната форма, но огъването не трябва да бъде твърде значително

Ориз. 26

Ориз. 27.

Италианският физик и астроном Галилей (1564-1642) смята, че коритото на най-краткото време трябва да бъде извито по дъга на окръжност. Но швейцарските математици, братята Бернули, преди около триста години доказаха чрез точни изчисления, че това не е така и че улеят трябва да бъде огънат по дъгата на циклоидата (обърнат надолу, фиг. 27.). Оттогава циклоидата си спечели прозвището брахистохрона, а доказателствата на Бернули послужиха за начало на нов клон на математиката – вариационното смятане. Последният се занимава с намирането на типа криви, за които една или друга интересуваща ни величина достига най-малката (а в някои въпроси и най-голямата) стойност.

логаритмична спирала

Тази крива може да бъде кръстена на Декарт, тъй като за първи път се споменава в едно от неговите писма (1638 г.). Въпреки това, подробно проучване на неговите свойства е извършено едва половин век по-късно от Якоб Бернули. Тези свойства направиха силно впечатление на съвременните математици. Върху каменната плоча, издигната на гроба на този известен математик, са изобразени завои на логаритмична спирала.

Архимедовата спирала се описва от точка, движеща се по протежение на гредата („безкрайна стрелка“), така че разстоянието от началото на лъча се увеличава пропорционално на ъгъла на неговото завъртане: r = ka. Логаритмична спирала ще се получи, ако се изисква не самото разстояние, а неговият логаритъм да се увеличава право пропорционално на ъгъла на въртене. Обикновено уравнението на логаритмична спирала се записва като се използва числото e, различно от Peer, като основа на системата от логаритми (раздел 25). Такъв логаритъм на числото r се нарича естествен логаритъм и се означава с In r. И така, уравнението на логаритмична спирала се записва като ln r = ka

Разбира се, ъгълът на въртене a все още може да бъде измерен в градуси. Но математиците предпочитат да го измерват в радиани, т.е. вземете като мярка за ъгъла съотношението на дължината на дъгата на окръжност между страните на централния ъгъл към радиуса на тази окръжност. Тогава завъртането на стрелката под прав ъгъл ще бъде измерено с числото l 1,57, завъртането със стойността на разширения ъгъл - с числото на l 3,14, а пълният завой, измерен в градуси с числото 360, в радиани ще се измерва с числото 2 l 6,28.

Ориз. 28.

От многото свойства на логаритмичната спирала отбелязваме едно нещо: всеки лъч, излизащ от началото, пресича всеки завой на спиралата под същия ъгъл. Стойността на този ъгъл зависи само от числото k в спиралното уравнение. В този случай под ъгъл между лъча и спиралата се разбира ъгълът между този лъч и допирателната към спиралата, начертана в пресечната точка (фиг. 28).

Заключение

В хода на разглеждане на кривите от трети и четвърти порядък

запознахме се с някои наистина прекрасни извивки, които обитават прекрасен святаналитична геометрия, които се срещат в живота ни много по-често, отколкото изглежда. Разгледахме тяхното практическо приложение в човешкия живот, значението на техните забележителни свойства в различни механизми, използвани от човек в живота. В тази статия събрахме материал с акцент върху практическото изграждане на криви.

И така, целта беше постигната и посочените, съответно, задачи към целта бяха решени.

литература

ред трансцендентна спирала

1. Маркушевич A.I. Забележителни извивки. - М.: Краснопролетарская, 1951. -23 с.; 1978 г., - 48 стр. с илюстрации.

История на математиката от древни времена до началото на XIXвек / Изд. А.П. Юшкевич. - М.: Наука, 1970, т. 1. - 352 с.; 1970, т. 2. - 300 с.; 1972, т. 3 - 496 с.

Никифоровски В.А., Фрайман Л.С. Раждането на нова математика. - М.: Наука, 1976. - 198 с.

Савелов А.А. Плоски криви. - М.: Физматгиз, 1960 - 294 с.

Илин В.А., Позняк Е.Г. Аналитична геометрия. - М.: Наука, 1971. - 232 с.

Тишкевич Р.И., Феденко А.С. Линейна алгебра и аналитична геометрия. - 2-ро изд. - Минск: Виш. Шк., 1976.544 с.

Кривата или линията е геометрично понятие, което се дефинира различно в различните секции.

КРИВА (линия), следа, оставена от движеща се точка или тяло. Обикновено кривата се представя само като плавно извита линия, като парабола или кръг. Но математическата концепция за крива обхваща както права линия, така и фигури, съставени от линейни сегменти, например триъгълник или квадрат.

Кривите могат да бъдат разделени на плоски и пространствени. Равнинска крива, като парабола или права линия, се образува в пресечната точка на две равнини или равнина и тяло и следователно лежи изцяло в една равнина. Пространствена крива, например спирала, оформена като спирална пружина, не може да се получи като пресичане на която и да е повърхност или тяло с равнина и тя не лежи в една равнина. Кривите също могат да бъдат разделени на затворени и отворени. Затворена крива, като квадрат или кръг, няма краища, т.е. движещата се точка, генерираща такава крива, периодично повтаря своя път.

Кривата е локус или набор от точки, които удовлетворяват някакво математическо условие или уравнение.

Например окръжността е мястото на точки в равнина, които са на еднакво разстояние от дадена точка. Кривите, определени от алгебрични уравнения, се наричат ​​алгебрични криви.

Например, уравнението на права линия y = mx + b, където m е наклон, и b е сегментът, отрязан по оста y, е алгебричен.

Криви, чиито уравнения съдържат трансцендентални функции, като логаритми или тригонометрични функции, се наричат ​​трансцендентални криви.

Например, y = log x и y = tg x са уравнения на трансцендентални криви.

Формата на алгебричната крива може да се определи от степента на нейното уравнение, която съвпада с най-високата степен на членовете на уравнението.

Ако уравнението от първа степен, например Ax + By + C = 0, тогава кривата има формата на права линия.

Ако уравнение от втора степен, напр.

Ax 2 + By + C = 0 или Ax 2 + By 2 + C = 0, тогава кривата е квадратична, т.е. представлява едно от коничните сечения; такива криви включват параболи, хиперболи, елипси и окръжности.

Изброяваме общите форми на уравненията на коничните сечения:

x 2 + y 2 \u003d r 2 - кръг,

x 2 / a 2 + y 2 / b 2 \u003d 1 - елипса,

y \u003d брадва 2 - парабола,

x 2 / a 2 - y 2 / b 2 \u003d 1 - хипербола.

Криви, съответстващи на уравненията на трето, четвърто, пето, шесто и т.н. градуси се наричат ​​криви на трета, четвърта, пета, шеста и т.н. поръчка. Като цяло, колкото по-висока е степента на уравнението, толкова повече завои ще има отворената крива.

Много сложни криви са получили специални имена.

Циклоида е равна крива, описана от неподвижна точка на окръжност, търкаляща се по права линия, наречена образуваща на циклоидата; циклоида се състои от поредица от повтарящи се дъги.

Епициклоида е равна крива, описана от неподвижна точка върху окръжност, търкаляща се по друга фиксирана окръжност извън нея.

Хипоциклоида е равна крива, описана от фиксирана точка на кръг, търкаляща се отвътре по фиксирана окръжност.

Спиралата е плоска крива, която се развива един след друг. фиксирана точка(или го увийте).

Математиците изучават свойствата на кривите от древни времена и имената на много необичайни криви са свързани с имената на тези, които първи са ги изучавали. Такива са например спиралата на Архимед, ключалката на Агнези, цисоидата на Диокъл, кохоида на Никомед и лемниската на Бернули.

В рамките на елементарната геометрия понятието за крива не получава ясно формулировка и понякога се определя като „дължина без ширина“ или като „граница на фигура“. По същество в елементарната геометрия изучаването на кривите се свежда до разглеждане на примери (, , , и т.н.). Липсвайки общи методи, елементарната геометрия проникна доста дълбоко в изследването на свойствата на специфични криви (, някоии също), като се използват специални техники за всеки отделен случай.

Най-често кривата се дефинира като непрекъснато картографиране от сегмент към:

В този случай кривите могат да бъдат различни, дори и да сасъвпада. Такива криви се наричатпараметризирани кривиили ако[ а , б ] = , начини.

Понякога кривата се дефинира до , тоест до минималната еквивалентност, така че параметричните криви

са еквивалентни, ако съществува непрекъснат (понякога ненамаляващ) зот сегмента [ а 1 ,б 1 ] в сегмента [ а 2 ,б 2 ], така че

Тези, определени от тази връзка, се наричат ​​или просто криви.

Аналитични определения

В курсовете по аналитична геометрия се доказва, че сред линиите, записани в декартови правоъгълни (или дори общо афинни) координати общо уравнениевтора специалност

Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0

(където поне един от коефициентите A, B, C е различен от нула) има само следните осем вида линии:

а) елипса;

б) хипербола;

в) парабола (неизродени криви от втори ред);

г) двойка пресичащи се прави;

д) двойка успоредни прави;

е) двойка съвпадащи прави (един ред);

ж) една точка (изродени прави от втори ред);

з) "линия", която не съдържа никакви точки.

Обратно, всеки ред от всеки от тези осем типа се записва в декартови правоъгълни координати чрез някакво уравнение от втори ред. (В курсовете по аналитична геометрия обикновено се говори за девет (не осем) вида конични сечения, тъй като те разграничават „въображаема елипса“ и „двойка въображаеми успоредни прави“ – геометрично тези „прави“ са едни и същи, тъй като и двете не съдържат една точка, но аналитично се записват от различни уравнения.) Следователно (дегенерирани и недегенерирани) конични сеченияможе да се дефинира и като линии от втори ред.

ATкрива в равнина се дефинира като набор от точки, чиито координати удовлетворяват уравнениетоФ ( х , г ) = 0 . В същото време за функциятаФ се налагат ограничения, които гарантират, че това уравнение има безкраен брой несъвпадащи решения и

този набор от решения не запълва "парчето от самолета".

Алгебрични криви

Важен клас криви са тези, за които функциятаФ ( х , г ) имаот две променливи. В този случай кривата, определена от уравнениетоФ ( х , г ) = 0 , е наречен.

Алгебричните криви, дадени от уравнението от 1-ва степен, са .

Уравнение от 2-ра степен, което има безкраен брой решения, определя, тоест изродено и неизродено.

Примери за криви, дадени от уравнения от 3-та степен: , .

Примери за криви от 4-та степен: и .

Пример за крива от 6-та степен: .

Пример за крива, дефинирана от уравнението равномерна степен: (многофокус).

Алгебрични криви, дефинирани от уравнения по-високи степени, се разглеждат в. В същото време тяхната теория придобива по-голяма хармония, ако разглеждането се проведе на . В този случай алгебричната крива се определя от уравнение от вида

Ф ( z 1 , z 2 , z 3 ) = 0 ,

където Фе полином от три променливи, които са точки.

Типове криви

Равната крива е крива, чиито точки лежат в една и съща равнина.

(проста линия или йорданска дъга, също и контур) е набор от точки в равнина или пространство, които са в едно към едно и взаимно непрекъснато съответствие с отсечките.

Път - сегмент в .

аналитични криви, които не са алгебрични. По-точно, криви, които могат да бъдат дефинирани чрез линията на ниво на аналитична функция (или, в многомерния случай, система от функции).

синусоида,

циклоид,

Спирала на Архимед

трактор,

верижна линия,

Хиперболична спирала и др.

1. Начини за дефиниране на кривите:

аналитичен - кривата се дава с математическо уравнение;

графичен - кривата се задава визуално върху носителя на графична информация;

табличен - кривата се дава от координатите на поредица от точки.

параметричен (най-общият начин за определяне на уравнението на крива):

където - плавни функции на параметритеT, и

(х") 2 + (г") 2 + (z") 2 > 0 (условие на редовност).

Често е удобно да се използва инвариантната и компактна нотация на уравнението на кривата с:

където от лявата страна има точки от кривата, а дясната страна определя нейната зависимост от някакъв параметър T. Разширявайки тази нотация в координати, получаваме формула (1).

1. Циклоида.

Историята на изучаването на циклоидата е свързана с имената на такива велики учени, философи, математици и физици като Аристотел, Птолемей, Галилей, Хюйгенс, Торичели и др.

Циклоида(отκυκλοειδής - кръг) - който може да се определи като траектория на точка, лежаща на границата на кръг, търкалящ се без плъзгане по права линия. Този кръг се нарича генериращ кръг.

Един от най-старите начини за формиране на криви е кинематичният метод, при който кривата се получава като траектория на точка. Кривата, която се получава като траектория на точка, фиксирана върху окръжност, търкаляща се без плъзгане по права линия, по окръжност или друга крива, се нарича циклоидална, което се превежда от Гръцкиозначава кръгъл, напомнящ кръг.

Нека първо разгледаме случая, когато кръгът се търкаля по права линия. Крива, описана от точка, фиксирана върху кръг, търкалящ се без плъзгане по права линия, се нарича циклоида.

Нека кръг с радиус R се търкаля по права линия a. C е точка, фиксирана върху окръжност, в началния момент на времето е в позиция A (фиг. 1). Нека поставим на права отсечка AB, равна на обиколката на окръжността, т.е. AB \u003d 2 π R. Разделяме този сегмент на 8 равни части по точки A1, A2, ..., A8 \u003d B.

Ясно е, че когато окръжността, търкаляща се по права линия а, прави един оборот, т.е. се завърта на 360, след което ще заеме позиция (8), а точка C ще се премести от позиция A в позиция B.

Ако кръгът направи половин пълен оборот, т.е. се завърта на 180, след което ще заеме позиция (4), а точка C ще се премести в най-високата позиция C4.

Ако кръгът се завърти на ъгъл от 45, тогава кръгът ще се премести в позиция (1), а точка C ще се премести в позиция C1.

Фигура 1 показва и други точки на циклоидата, съответстващи на останалите ъгли на въртене на окръжността, които са кратни на 45.

Свързвайки построените точки с плавна крива, получаваме участък от циклоидата, съответстващ на един пълен оборот на окръжността. При следващите обороти ще се получат същите участъци, т.е. циклоидата ще се състои от периодично повтаряща се секция, наречена циклоидна дъга.

Нека обърнем внимание на положението на допирателната към циклоидата (фиг. 2). Ако колоездачът се движи по мокър път, капчиците, откъснати от колелото, ще летят тангенциално към циклоида и при липса на щитове могат да пръснат гърба на велосипедиста.

Първият човек, който изучава циклоидата, е Галилео Галилей (1564-1642). Той също измисли името му.

Свойства на циклоида:

Циклоида има редица забележителни свойства. Нека споменем някои от тях.

Свойство 1. (Ледената планина.) През 1696 г. И. Бернули поставя проблема за намирането на най-стръмната крива на спускане или, с други думи, проблема каква трябва да бъде формата на леден хълм, търкаляйки се по него, за да направи пътя от начална точка А до крайна точка В за най-кратко време (фиг. 3, а). Желаната крива се наричаше "брахистохрона", т.е. крива на най-краткото време.

Ясно е, че най-краткият път от точка A до точка B е отсечката AB. Въпреки това, с такива праволинейно движениескоростта нараства бавно и времето, прекарано в спускането, се оказва голямо (фиг. 3, б).

Скоростта се набира толкова по-бързо, колкото по-стръмно е спускането. При стръмно спускане обаче пътят по кривата се удължава и по този начин времето на преминаването й се увеличава.

Сред математиците, които решават тази задача, са: Г. Лайбниц, И. Нютон, Г. Лопитал и Дж. Бернули. Те доказаха, че желаната крива е обърната циклоида (фиг. 3, а). Методите, разработени от тези учени при решаването на проблема за брахистохрона, положиха основата на ново направление в математиката - вариационното смятане.

Свойство 2. (Часовници с махало.) Часовник с обикновено махало не може да работи точно, тъй като периодът на трептене на махалото зависи от неговата амплитуда: колкото по-голяма е амплитудата, толкова по-дълъг е периодът. Холандският учен Кристиан Хюйгенс (1629 - 1695) се чуди коя крива трябва да следва топката на струната на махалото, така че периодът на нейното трептене да не зависи от амплитудата. Забележете, че в обикновеното махало кривата, по която се движи топката, е кръг (фиг. 4).

Желаната крива се оказа обърната циклоида. Ако например се направи корито под формата на обърната циклоида и по него се прокара топка, тогава периодът на движение на топката под действието на гравитацията няма да зависи от първоначалното й положение и амплитуда (фиг. 5) . За това свойство циклоидата се нарича още "тавтохрон" - крива на равни времена.

Хюйгенс изработва две дървени дъски с циклоидни ръбове, ограничаващи движението на нишката наляво и надясно (фиг. 6). В този случай самата топка ще се движи по обърната циклоида и по този начин периодът на нейните трептения няма да зависи от амплитудата.

От това свойство на циклоида по-специално следва, че независимо от кое място на ледената пързалка под формата на обърната циклоида да започнем спускането, ще прекараме едно и също време чак до крайната точка.

Циклоидно уравнение

1. Удобно е да се напише циклоидното уравнение по отношение на α - ъгълът на въртене на окръжността, изразен в радиани, имайте предвид, че α също е равно на пътя, изминат от генериращата окръжност по права линия.

x=ra– rгрях α

y=r - r cos α

2. Да вземем хоризонталната координатна ос като права линия, по която се търкаля генериращата окръжност с радиус r.

Циклоидата се описва с параметричните уравнения

х = rt – rгрях T,

г = r – r cos T.

Уравнение в:

Циклоидата може да се получи като решение на диференциалното уравнение:

От историята на циклоида

Първият от учените обърна внимание на циклоидав, но сериозно проучване на тази крива започва едва в.

Първият, който започва да изучава циклоидата, е Галилео Галилей (1564-1642), известният италиански астроном, физик и педагог. Той също така измисли името „циклоида“, което означава: „напомнящ кръг“. Самият Галилей не е написал нищо за циклоида, но неговите произведения в тази посока се споменават от учениците и последователите на Галилей: Вивиани, Торичели и др. Торичели, известен физик, изобретателят на барометъра, посвети много време на математиката. През Ренесанса не е имало тесни специалисти учени. Талантлив човек се занимаваше с философия, физика и математика и навсякъде получаваше интересни резултати и прави големи открития. Малко по-късно от италианците французите се заеха с циклоида, наричайки го "рол" или "трохоид". През 1634 г. Робервал - изобретателят на добре познатата система от тежести на системата от тежести - изчислява площта, ограничена от арката на циклоидата и нейната основа. Съдържателно изследване на циклоидата е извършено от съвременник на Галилей. Сред , тоест криви, чието уравнение не може да бъде записано под формата на х , г, циклоидата е първата от изследваните.

Написа за циклоида:

Рулетката е толкова често срещана линия, че след правата линия и кръга няма повече обща линия; тя се рисува толкова често пред очите на всички, че човек трябва да се учуди, че древните не са го обмислили... защото това не е нищо друго освен пътят, описан във въздуха от пирона на колелото.

Новата крива бързо придоби популярност и беше подложена на задълбочен анализ, който включваше, , Нютон,, братя Бернули и други светила на науката от XVII-XVIII век. На циклоида, методите на възникващите през онези години. Фактът, че аналитичното изследване на циклоидата се оказва толкова успешно, колкото и анализът на алгебричните криви, прави голямо впечатление и се превръща във важен аргумент в полза на „изравняването на правата“ на алгебричните и трансценденталните криви. Епициклоид

Някои видове циклоиди

Епициклоид - траекторията на точка А, лежаща върху окръжност с диаметър D, която се търкаля без плъзгане по водеща окръжност с радиус R (външно докосване).

Изграждането на епициклоида се извършва в следната последователност:

От центъра 0 се начертава спомагателна дъга с радиус, равен на 000=R+r;

От точки 01, 02, ... 012, както от центрове, се чертаят окръжности с радиус r, докато се пресичат със спомагателни дъги в точки A1, A2, ... A12, които принадлежат на епициклоидата.

Хипоциклоид

Хипоциклоида - траекторията на точка А, лежаща върху окръжност с диаметър D, която се търкаля без плъзгане по водеща окръжност с радиус R (вътрешно докосване).

Конструкцията на хипоциклоида се извършва в следната последователност:

Генериращата окръжност с радиус r и водещата окръжност с радиус R са начертани така, че да се допират в точка A;

Генериращият кръг се разделя на 12 равни части, получават се точки 1, 2, ... 12;

От центъра 0 се начертава спомагателна дъга с радиус, равен на 000=R-r;

Централният ъгъл a се определя от формулата a = 360r / R.

Разделете дъгата на направляващата окръжност, ограничена от ъгъла а, на 12 равни части, вземете точки 11, 21, ... 121;

От центъра 0 през точки 11, 21, ... 121 прави линии се изтеглят до пресечната точка със спомагателната дъга в точки 01, 02, ... 012;

От центъра 0 се изтеглят спомагателни дъги през точките на разделяне 1, 2, ... 12 на генериращата окръжност;

От точки 01, 02, ... 012, както и от центрове, се чертаят окръжности с радиус r, докато се пресичат със спомагателни дъги в точки A1, A2, ... A12, които принадлежат на хипоциклоидата.

1. Кардиоиден.

Кардиоиден ( καρδία - сърце, Кардиоидът е специален случай. Терминът "кардиоид" е въведен от Кастийон през 1741 г.

Ако вземем окръжност и точка върху нея като полюс, тогава получаваме кардиоид само ако отделим отсечки, равни на диаметъра на окръжността. За други стойности на начертаните сегменти, конхоидите ще бъдат удължени или скъсени кардиоиди. Тези удължени и скъсени кардиоиди се наричат ​​иначе охлюви на Паскал.

Кардиоидът има различни приложения в инженерството. Под формата на кардиоид те правят ексцентрици, гърбици за автомобили. Понякога се използва при рисуване на зъбни колела. Освен това се използва в оптичните технологии.

Свойства на кардиоида

кардиоиден -В M на движещ се кръг ще опише затворена траектория. Тази плоска крива се нарича кардиоид.

2) Кардиоида може да се получи и по друг начин. Маркирайте точка в кръга Ои начертайте лъч от него. Ако от точка НОпресечната точка на този лъч с кръг, отложете сегмента сутринта,по дължината, равна на диаметъра на кръга, и завъртете лъча около точката О, след това точката Мще се движи по кардиоида.

3) Кардиоида може да бъде представена и като крива, допирателна към всички окръжности с център на дадена окръжност и минаваща през нейната неподвижна точка. Когато се изградят няколко кръга, кардиоидът се оказва изграден сякаш сам по себе си.

4) Има още един толкова елегантен, колкото и неочакван начин да видите кардиоида. На фигурата можете да видите точков източник на светлина върху кръг. След като светлинните лъчи се отразят за първи път от окръжността, те се допират до кардиоида. Представете си сега, че кръгът е ръбовете на чашата, в един момент той отразява ярка крушка. В чашата се налива черно кафе, което ви позволява да видите ярките отразени лъчи. В резултат на това кардиоидът се подчертава от лъчите на светлината.

1. Astroid.

Astroid (от гръцки astron - звезда и eidos - изглед), плоска крива, описана от точка върху окръжност, която докосва вътрешността на фиксиран кръг с четири пъти по-голям радиус и се търкаля по него, без да се плъзга. Принадлежи към хипоциклоидите. Астроид - алгебрична крива от 6-ти ред.

Astroid.

Дължината на целия астроид е равна на шест радиуса на фиксираната окръжност, а площта, ограничена от него, е три осми от фиксираната окръжност.

Сегмент от допирателна към астроида, затворен между два взаимно перпендикулярни радиуса на фиксирана окръжност, начертан на върха на астроида, равно на радиусафиксиран кръг, без значение как е избрана точката.

astroid свойства

Има четирикуспид .

Дължина на дъгата от точка 0 до обвивка

семейства от сегменти с постоянна дължина, чиито краища са разположени на две взаимно перпендикулярни линии.

Астроидът е от 6-ти порядък.

Астроидни уравнения

Уравнението в декартови правоъгълни координати е:| х | 2 / 3 + | y | 2/3 = R2/3параметрично уравнение:x = Rcos 3 t y = Rsin 3 t

Как да изградим astroid

Начертаваме две взаимно перпендикулярни прави линии и начертаваме серия от сегменти с дължинаР чиито крайни точки лежат на тези прави. Фигурата показва 12 такива сегмента (включително отсечките на самите взаимно перпендикулярни линии). Колкото повече сегменти начертаем, толкова по-точна ще бъде кривата. Нека сега да построим обвивката на всички тези сегменти. Този плик ще бъде astroid.

1. Заключение

В статията са дадени примери за задачи с различни видове криви, дефинирани от различни уравнения или удовлетворяващи някакво математическо условие. По-специално, циклоидни криви, начини за определянето им, различни методи на конструиране, свойства на тези криви.

Свойствата на циклоидните криви се използват много често в механиката в зъбните колела, което значително увеличава здравината на частите в механизмите.

- (от гръцката астронова звезда и изглед ейдос) плоска крива, описана от точка от окръжност, която докосва фиксиран кръг с четири пъти по-голям радиус отвътре и се търкаля по него, без да се плъзга. Принадлежи към хипоциклоидите. Astroid алгебрични ... ... Голям енциклопедичен речник

Съществува., Брой синоними: 1 крива (56) ASIS Synonym Dictionary. В.Н. Тришин. 2013 ... Синонимен речник

- (от гръцкия изглед ástron star и éidos), плоска крива, описана от точка върху окръжност, която докосва вътрешността на фиксиран кръг с четири пъти по-голям радиус и се търкаля по него, без да се плъзга. Принадлежи към хипоциклоидите. Astroid ... ... енциклопедичен речник

- (астро... гр. ейдос изглед) мат. плоска крива, описана от точка на окръжност, търкаляща се без плъзгане по вътрешната страна на друга, фиксирана окръжност с радиус четири пъти по-голям от този на първия; прилича на четирилъча звезда. Нов речник … Речник на чужди думи на руския език

Плоска алгебра. кривата ti ro на порядъка, до ръба се описва от точката на окръжността с радиус r, търкаляща се по вътрешната страна на окръжността с радиус R=4r; хипоциклоид с модул r=4. Уравнение в декартови декартови координати: Параметрично. уравнения... Математическа енциклопедия

Защо нашият свят е красив? Защото формите и цветовете на живата природа до голяма степен следват общите закони на хармонията, които се разкриват чрез строг математически анализ. Изучавайки природата, откриваме в нея все повече естетически особености, които по правило не се разкриват веднага, а след подробен математически анализ.

Човек различава предметите около себе си по форма. Интересът към формата на обект може да бъде продиктуван от жизнена необходимост или може да бъде причинен от красотата на формата. Формата, която се основава на комбинация от симетрия и златно сечение, допринася за най-доброто визуално възприятие и появата на усещане за красота и хармония.

Цялото винаги се състои от части, части с различни размери са в определено отношение една към друга и към цялото. Принципът на златното сечение е най-висшата проява на структурното и функционално съвършенство на цялото и неговите части в изкуството, науката, техниката и природата.

При използване на законите на геометрията на природата в нова ситуация, за изучаване на курсове по предмети, свързани с геометрични конструкции, преосмисляме наученото геометрични закони, развиват геометрична интуиция.

В процеса на изпълнение на творчески задачи с различно съдържание се запознахме с възможните области на приложение геометрични знания(художници, архитекти, дизайнери и др.).

Графичните средства за изобразяване на информация се използват във всички сфери на обществото. Те имат завършен образ, характеризират се със символика, компактност и относителна лекота на четене. Именно тези качества на графичните изображения определят тяхното разширено използване. В близко бъдеще повече от половината от представената информация ще има графична форма на представяне. Развитие теоретични основиописателната геометрия, инженерната графика и други сродни науки разшириха начините за получаване на графични изображения. Наред с ръчните методи за формиране на графични изображения, съставяне на проектна документация, все по-често се използват компютърни методи. Използването на нови информационни технологии осигурява създаване, редактиране, съхранение, репликация на графични изображения с помощта на различни софтуерни инструменти.

I. Уводна информация за алгебричните криви

1. Астроид

Астроид (от гръцки >-звезда) е крива, описана от точка върху движеща се окръжност, която докосва фиксиран кръг с четири пъти по-голям радиус отвътре и се търкаля по него, без да се плъзга. Площта, ограничена от астроида, е /8 от площта на фиксирания кръг, а общата дължина на астроида е равна на радиуса на този кръг, шест пъти.

Астроидното уравнение в декартови правоъгълни координати е:

x + y = R.

Конструирането на astroid графика беше извършено в >, както следва:

:: Построена функционална графика за y > 0 (радиус R = 5);

:: Изградихме функционална графика.

2. Кардиоид

Кардиоида (от гръцки >-сърце и eidos-изглед) е плоска крива, описана от неподвижна точка на окръжност, която отвън докосва неподвижна окръжност със същия радиус и се търкаля по нея, без да се плъзга. Кривата получава името си от приликата си със сърце.

Кардиоидното изобразяване също е направено в >.

3. Нефроид

Нефроид (от гръцки hephros-бъбрек, eidos-глед) - крива, която описва фиксирана точка на кръг, търкалящ се навън по два пъти по-голям кръг. За първи път свойствата на нефроида са изследвани през 17 век от саксонския благородник Е. В. Чирнгауз. Нефроидът се състои от две кардиоиди.

4. Охлювът на Паскал.

Охлювът на Паскал е плоска алгебрична крива. Наречен на Етиен Паскал (баща на Блез Паскал), който пръв го изследва. Уравнение в полярни координати. За l = 2a се получава кардиоид.

II. Приложение математическо моделиране.

1. Историята на създаването на нишкови графики

Графиката на нишките (или isothread) е графично изображение, изработени по специален начин с конци върху картон или друга здрава основа. Графиките на нишките понякога се наричат ​​​​изография или картонена бродерия.

В Русия се използва терминът > (филаментна графика или конец), в англоговорящите страни се използва фразата - бродерия върху хартия, в немскоговорящите страни - терминът.

Графиката на конеца, като вид изкуства и занаяти, се появява за първи път в Англия през 17 век. Английските тъкачи измислиха специален начин за тъкане на конци. Забиваха пирони в дъски и дърпаха конци върху тях в определена последователност. В резултат на това се получават ажурни дантелени изделия, които са използвани за украса на дома. (Възникна версия, че тези произведения са някакъв вид скици за модели върху плат). Съвременните консумативи ви позволяват да получите много ефективни продукти.

Наред с оригиналната техника на графиката на нишките има и друга посока на дизайна на конци - бродерия върху картон (конец), използвайки същите техники (метод за запълване на ъгъл и кръг).

Интересът към графиките с нишки се появи и след това изчезна. Един от върховете на популярност е в края на деветнадесети век. Бяха публикувани книги за ръкоделие, които описваха необичаен начин на бродиране на хартия, прост и лесен, достъпен за деца. В работата са използвани перфорирани карти ( готови шаблони) и Техника за запълване на ъгли, шевове >, > (за шиене на криви). Използвайки минимум средства, всеки човек (и най-важното деца) би могъл да направи луксозни сувенири за празниците.

Сега това изкуство се практикува в много страни по света.

У нас има малко информация за isothread, предимно от уводен характер: отделни публикации в списания > През 1995 г. книга на професор от Минск G. A. Branitsky > и книга на Nagibina M. I. > с малка глава за isothread.

След като анализирахме наличната информация, успяхме да установим, че са публикувани много книги за този вид ръкоделие под формата на инструкции стъпка по стъпка и албуми с идеи, в които навсякъде се използва само репродуктивният метод на работа.

Предимството на isothread е, че работи бързо и можете да измислите много интересни модели. Този вид творчество развива въображението, окото, фината моторика на пръстите, художествените способности и естетическия вкус. Използвайки техниката на графиката на нишките, можете да направите не само декоративни пана, но и поздравителни картички, корици за сувенири, отметки за книги.

И изонишките (графика на нишки или дизайн на нишки) могат да имат няколко посоки:

1) репродуктивен метод: работа по шаблон, инструкции стъпка по стъпка, разпространение на готови модели и комплекти за бродиране

2) частично търсене (проект): обучение за изчисляване върху картон (т.е. създаване на свои собствени шедьоври), търсене на свои собствени техники и комбинации, "играене" с фона, нишки - с материала за изпълнение

3) комбиниран - когато всичко започва с "азбуката", работим с готови схеми, но променяме вида на материала (цвят) и стигаме до "шедьовъра".

2. Основни техники на нишковата графика

Графиката на конеца е известна и под други имена: изонишка (т.е. изображение с нишка), графична бродерия. За да овладеете техниката, достатъчно е да знаете как се запълват ъгъл, кръг и дъга.

Прием 1. Попълване на ъгъла.

От грешната страна на картона начертайте ъгъл, разделете всяка страна на равен брой части. Пробиваме точките с щифт или тънко шило, вкарваме конеца в иглата и запълваме по схемата.

Прием 2. Попълване на кръга.

Начертайте кръг с компас. Разделете го на 12 равни части и попълнете по схемата.

Прием 3. Запълване на дъгата.

Нека начертаем дъга, да я разделим на равни части и да направим пробиви в точките на разделяне. Нанизваме иглата и я напълваме според шаблона

III. Изследователска работа.

Конструкции в програмата>.

Задача 1. Разделяне на отсечка на n равни части.

Решение 1. Разделянето на 2, 4, 8, 16 и т.н. части беше извършено в > чрез конструиране на средните точки на отсечката.

Решение 2. Извършихме също разделянето на отсечка на произволен брой части в > с помощта на теоремата на Талес.

Задача 2. Разделяне на кръга на 6, 12, 24 части.

Решение 1. Търсихме различни начини да разделим кръга на части. В програмата > начертахме кръг, произволно поставихме точки, измерихме получените ъгли и след това > преместихме точките по окръжността, докато се получи желаната стойност. Беше монотонна и безинтересна работа. Грешката на първото деление на 12 части беше + 0,15 см в дължината на акордите. Започнахме да анализираме ситуацията и да търсим най-добрите начини за решаване на задачите. В резултат на това намерихме няколко решения за разделяне на кръга на 6, 12, 24 части.

Решение 2. В окръжността бяха отбелязани 6 точки, измерени са всички ъгли, точките бяха подравнени така, че всеки ъгъл да е равен на 60 [o]. След това с помощта на програмата бяха начертани ъглополовящите на всеки ъгъл. Резултатът беше разделяне на 12 части. И за разделяне на 24 части, ъглите на получените ъгли отново бяха начертани. Грешката на такава конструкция се оказа + 0,01 градуса.

Решение 3. С помощта на програмата изградихме 3 кръга с един и същи радиус (приложение за копиране), комбинирахме ги, както е показано на фигурата. Маркирайте пресечните точки на окръжностите. Получените ъгли бяха измерени, те се оказаха равни на 60 [o]. След това изградихме ъглите на ъглите за разделяне на 12 и 24 части. Грешката на такова решение е нула.

Задача 3. Разделяне на кръга на 9, 18, 36 части.

След като намерихме оптималния начин за решаване на предишния проблем, ние по подобен начин започнахме да търсим начини да разделим кръга на 9, 18 и 36 части. Разделянето на 18 и 36 части може да се извърши само след построяване на 9 точки чрез прилагане на конструкцията на ъглополовящи.

Решение. 360 [o]: 9 = 40 [o]. Разделихме полукръгът на 4 дъги от приблизително 40 [o] и дъга от 20 [o]. С помощта на програмата извършихме всички необходими измервания на ъглите чрез преместване на точките. След това избрахме конструираните точки и с помощта на командата > отразихме точките на 180 градуса спрямо центъра на окръжността върху втория полукръг. Грешката на такава конструкция беше + 0,04 градуса.

Задача 4. Построяване на алгебрични криви

Astroid

Решение 1. Астроидът се изгражда върху координатната равнина по следния алгоритъм:

:: Трябва да свържете точките на оста y с точките на абсцисата, така че сборът от деленията да даде 10 (например: 1 и 9, 2 и 8, 3 и 7 и т.н.).

:: Свързваме точките в същата последователност в останалите четвърти на координатната равнина.

Решение 2. Начертайте кръг, изградете перпендикулярни диаметри, разделете всеки радиус на четен брой части. Свързахме точките със сегменти според предишния алгоритъм.

Решение 3. След като усвоихме оптималния метод за разделяне на кръга на 6 части, завършихме изграждането на 6-звезден астроид.

Решение 4. Построяването на 8-звезден астроид е извършено с построяване на ъглополовящи правоъгълни.

Кардиоиден

Решение. За да се конструира кардиоид, основата ще бъде кръг. Кардиоидът е построен по следния план:

:: нарисува кръг и го раздели на 36 части (по 10 градуса всяка);

:: номерирани външните точки от 1 до 36 обратно на часовниковата стрелка;

:: вътрешните точки са номерирани по схема 1;

:: свързани точки със същите вътрешни и външни номера;

:: плик и ще бъде кардиоид.

Схема 1 Схема 2

IV. Нашата креативност.

След като усвоихме основните техники на дизайн и моделиране в >, ние се опитахме да се реализираме в ролята на дизайнери и художници. Разработихме и приложим на практика следните работи:

Заключение, изводи

>, - отбеляза Аристотел преди 2500 години. Нашият съвременник Сухомлински вярваше, че >. А математиката е прекрасен предмет за изненада.

След като проучихме задълбочено наличния материал, се запознахме с нов метод за конструиране на криви - математическа бродерия, използвайки познати строителни техники. геометрични фигури(изграждане на ъгъл, разделяне на сегмент на равни части, свързване на точки в определена последователност, разделяне на окръжност на равни части в програмата>). Открихме удивителна прилика между математическата бродерия и отдавна познатия вид изкуства и занаяти - изоконец.

Има много снимки с бродерия с изо-нишка в интернет, в специална литература, но диаграми не са приложени към тях. Стигнахме до извода, че математическата бродерия е творчески процес. Познавайки основите на математическото моделиране, които са очертани в нашата работа, прилагайки творческо мислене, логика, търпение, можете да направите индивидуално > приложно изкуство.

Математическата бродерия заинтересува не само нас, но и много ученици от училището (както момичета, така и момчета). Вярваме, че модерно Информационни технологиище съчетае математика и изкуство.

Линия (крива) от четвърти ред наричаме права, определена от алгебрично уравнение от четвърта степен по отношение на декартовите правоъгълни координати. По подобен начин се дефинират линии (криви) от пети, шести и други порядки.

Наборът от линии (криви) от четвърти ред вече не съдържа десетки, а хиляди линии от определен тип. Наборите от линии от пети и шести ред са още по-разнообразни. Тук разглеждаме определени видове линии от четвърти и по-висок порядък, които имат интересни свойства и практически приложения.

Лемнискате Бернули

Нека се обърнем към кривата, описана от точка M на равнината, така че произведението p на разстоянията на тази точка до две конкретни точки F 1 и F 2 от същата равнина да остане непроменено. Такава крива се нарича лемниската (лемниската на гръцки означава "лента"). Ако дължината на отсечката F 1 F 2 е c, тогава разстоянията от средата O на отсечката F 1 F 2 до F1 и F2 са равни на c / 2 и произведението на тези разстояния е - c 2 /4. Нека първо изискваме стойността на p на неизменното произведение да е точно равна на 2/4; тогава

ред трансцендентна спирала

Ориз. 8

точка O ще лежи върху лемниската, а самата лемниската ще изглежда като „лежаща осмица“ (фиг. 8). Ако продължим отсечката F 1 F 2 в двете посоки до пресечната точка с лемниската, тогава получаваме две точки A 1 и A 2. Изразяваме разстоянието между A 1 A 2 \u003d x чрез известно разстояние c:

Лемнискатните огнища са F1 (? c; 0) и F2 (c; 0). Вземете произволна точка M (x; y). Произведението на разстоянията от фокусите до точката M е

И по дефиниция е равно на c2:

Квадратираме двете страни на уравнението:

Разширете скобите от лявата страна:

Отваряме скобите и свиваме новия квадрат на сумата:

Изваждаме общия фактор и прехвърляме:

В този случай a е радиусът на окръжността, описваща лемниската. След като извършихме прости трансформации, можем да получим изрично уравнение:

Правим квадрат и отваряме скобите:

Довеждаме до ума

Това е квадратно уравнение за y". Решавайки го, получаваме

Като вземем корена и отхвърлим опцията с отрицателен втори член, получаваме:

където положителният вариант определя горната половина на лемниската, отрицателният вариант определя долната.

Ако стойността на константното произведение p не е равна на 2/4, тогава лемниската ще промени формата си. А когато p е по-малко от c 2 /4, лемниската се състои от два овала, всеки от които съдържа съответно точки F 1 и F 2 (фиг. 9).

Ориз. 9

Че. като зададем различни условия за p и c 2 /4, ще получим лемнискати от различни видове (фиг. 10).

Ориз. 10

Нека сега вземем произволен брой точки от равнината. F 1 , F 2 ,..., F n Нека получим крива, чиято форма ще зависи от това как точките F 1 , F 2 ,…, F n са разположени една спрямо друга и каква е стойността на константното произведение. Тази крива се нарича лемниската с n фокуса.

По-горе разгледахме лемнискати с две огнища. Като вземем различен брой фокуси, подредим ги по различни начини и припишем тази или онази стойност на произведението на разстоянията, могат да се получат лемнискати с най-странни очертания. Нека изведем точката на молива от определена точка A, без да я сваляме от хартията, така че накрая да се върне в началната точка A. Тогава тя ще опише определена крива; изискваме само тази крива да не се пресича никъде

Ориз. 11

себе си. Очевидно по този начин могат да се получат извивки, имащи например очертанията на човешка глава или птица (фиг. 11). Оказва се, че имайки такава произволна крива, човек може да избере числото n и разположението на фокусите по такъв начин

F 1 , F 2 ,..., F n

и задайте такава стойност за постоянно произведение на разстоянията

МF 1 МF 2 … МF n = p

че съответната лемниската на око няма да се различава от тази крива. С други думи, възможните отклонения на точка M, която описва лемниската, от начертаната крива - няма да надвишават ширината на щриха на молива (моливът може да бъде заточен предварително, както желаете, така че щрихът да е много тесен). Този забележителен факт, който говори за изключителното разнообразие и богатство на формите на лемнискати с много огнища, се доказва доста строго, но много трудно, с помощта на висшата математика.

Охлювът на Паскал

Местоположението на точки M и M", разположени върху линиите на молива (чийто център O лежи върху окръжност с радиус R) на разстояние a от двете страни на точката P на пресичане на правите с окръжността; по този начин PM = PM" = a. уравнение в правоъгълни координати: (x2 + y2 - 2Rx)2 - a2(x2 + y2) = 0, в полярни координати: r = 2R cos j + a. Когато a = 2R, цикълът се свива до точка, в който случай кохлеата на Паскал се превръща в кардиоид. Името е кръстено на френския учен Б. Паскал (1588-1651), който пръв го изследва.

Циклоидни криви

Представете си, че определена крива се търкаля, без да се плъзга по друга крива; всяка точка, неизменно свързана с първата крива, ще опише нова крива. Така че можете да си представите елипса, търкаляща се по друга елипса и да изследвате линията, по която ще се движи нейният център, или да определите траекторията на фокуса на парабола, търкаляща се по права линия, и т.н.

Сред образуваните по този начин криви се разграничават криви, които са траектории на точка, неизменно свързана с окръжност, която се търкаля, без да се плъзга по друга окръжност. Получените линии се наричат циклоидна.

При формиране на циклоидни криви точката на начертаване се отделя от центъра на генериращата (движеща се) окръжност на определено разстояние. В конкретен случай е на обиколката на генериращия кръг. При това условие получените криви се подразделят на епициклоиди и хипоциклоиди в зависимост от това дали генериращият кръг е разположен от външната или от вътрешната страна на фиксирания кръг.

Алгебричните криви включват такива добре познати криви като кардиоида, астроида, нека разгледаме тези криви.

Кардиоиден

1. Уравнението. Кардиоида може да се дефинира като траектория на точка, лежаща върху обиколката на окръжност с радиус r, която се търкаля по обиколката на неподвижна окръжност със същия радиус. Така тя ще бъде епициклоида с модул m равен на 1.

Това обстоятелство ни позволява незабавно да запишем параметричните уравнения на кардиоида, като заменим модула m с единица в горните параметрични уравнения на епициклоидата. Ще има:

За да се получи полярното уравнение на кардиоида, е удобно да се вземе точка А за полюс (фиг. 13) и да се насочи полярната ос по абсцисата. Тъй като четириъгълникът AOO 1 M ще бъде равнобедрен трапец, тогава полярният ъгъл на точка M ще бъде равен на ъгъла на въртене на генериращата окръжност, т.е. параметър t. Имайки предвид това обстоятелство, нека заменим y във второто уравнение на системата (1) чрез sin t. Намалявайки така полученото равенство с sin t, получаваме полярното уравнение на кардиоида

Ориз. 13

Според това уравнение

можем да заключим, че кардиоидът е един от охлювите на Паскал. Следователно може да се определи като конхоида на кръг.

Превеждайки уравнение (2) в правоъгълна координатна система, получаваме:

От това уравнение следва, че кардиоидът е алгебрична крива от 4-ти порядък.

2. Свойства. На първо място, тъй като кардиоидата е епициклоида с m=1, всички свойства на епициклоидите, разгледани в предишния параграф, могат да бъдат прехвърлени на нея.

Ето характеристиките и спецификациите.

1. Допирателната в произволна точка на кардиоида минава през точката на окръжността на генериращата окръжност, диаметрално противоположна на точката на допир на окръжностите, а нормалата минава през точката на техния контакт.

2. Ъгълът, образуван от допирателната към кардиоида с радиус вектора на точката на контакт, е равен на половината от ъгъла, образуван от този радиус вектор с полярната ос. Наистина ли

От това съотношение директно следва, че ъгълът, съставен от допирателната към кардиоидата с оста на абсцисата, е равен (като външния ъгъл на триъгълника AMN фиг. 14). Като имаме формула, можем да докажем, че допирателните към кардиоида, изтеглени в краищата на хордата, преминаваща през полюса, са взаимно перпендикулярни.

Наистина, тъй като

Ориз. 14

Отбелязваме също, че мястото на пресечните точки на тези допирателни е кръг. Действително, уравнението на първата допирателна, базирано на уравнения (1) на кардиоида, ще има вида

и втората допирателна. Елиминирайки параметъра от тези уравнения, получаваме уравнението на посочения кръг.

3. Радиусът на кривината в произволна точка на кардиоида се определя по формулата

Може също да се покаже, че радиусът на кривината е 2/3 от полярната норма N в дадена точка.

Наистина, откъдето на базата на (4) получаваме Тази връзка може да се използва за конструиране на центъра на кривината на кардиоида.

4. Еволюта на кардиоида, според общото свойство на еволюта на епициклоида, също ще бъде кардиоид, подобен на дадения, с коефициент на подобие, равен на 1/3, и завъртян спрямо дадения с ъгъл от 180°.

5. Дължината на кардиоидната дъга от точка А до произволна точка М се определя по формулата

Ако дължината на дъгата се брои от точка A 1, диаметрално противоположна на точка A, тогава формулата за определяне на дължината на дъгата може да се запише като

6. Естественото уравнение на кардиоида се получава, ако параметърът се изключи от равенства (4) и (6). Ще изглежда така

7. Площта, ограничена от кардиоида, се определя по формулата

и, както се вижда, е равна на площта на шестте колела на генериращия кръг.

Дължината на целия кардиоид се определя по формулата

и, както се вижда, е равна на осем диаметъра на генериращия кръг. Обемът на тялото, получен от въртенето на кардиоида около оста му, е равен на

Повърхността на тялото, получена от въртенето на кардиоида около оста му, е равна на

Видяхме, че кардиоидът е органично свързан с кръга. Това е конхоида от кръг и епициклоида. Той има различно отношение с окръжността - кардиоидът е под-ера на окръжност по отношение на точка, принадлежаща на тази окръжност.

Ориз. 15

Наистина, нека OM е перпендикулярът, спуснат към допирателната към окръжността с радиус, равен на 2r, начертан в точката N.

Тъй като OM = OB + BM, или = 2r cos + 2r, тогава мястото на точки M ще бъде кардиоид с уравнението = 2r (1 + cos)

В заключение отбелязваме, че кардиоидът също принадлежи към семейството на синусоидалните спирали и неговите индивидуални свойства се повтарят общи свойстватези криви. От тези свойства следва по-специално, че инверсията на кардиоида по отношение на куспида дава парабола.

Astroid

1. Свойства.Астроидът е специален случай на хипоциклоиди, а именно хипоциклоид с модул m равен на 1/4. Следователно това е траекторията на точка, лежаща върху окръжността на окръжност с радиус r, която се търкаля по вътрешността на друг фиксиран кръг, чийто радиус R е четири пъти по-голям.

Параметричните уравнения на астроида могат да бъдат получени чрез поставяне на хипоциклоиди в уравненията, m=1/4. Ето уравненията:

Ориз. 16

където t, както преди, е ъгълът на завъртане на генериращия кръг (фиг. 16)

Елиминирайки параметъра t от уравнения (1), получаваме:

Уравнение (2) предполага, че астроидът е алгебрична крива от шести порядък.

Параметричните уравнения (1) на астроида могат да се сведат до вида

Елиминирайки параметъра t от тези уравнения, получаваме често използваната форма на уравнението на астроида

Като приемем в изведените по-рано общи отношения за циклоидни криви модула

m = -1/4, получаваме съответните отношения за астроида:

1) радиусът на кривината в произволна точка на астроида се определя по формулата

2) дължината на дъгата на астроида от точка A до произволна точка M(t) се определя по формулата

дължината на единия клон е равна на и дължината на цялата крива е 6R;

3) за да получим естественото уравнение на астроида, първо отбелязваме, че ако началната точка за дължината на дъгата не е точката A, за която t = 0, а точката, за която t =, тогава дължината на дъгата се определя по формулата

изключвайки параметъра t от уравнения (5) и (6), получаваме естественото уравнение на астроида

4) еволюцията на астроида е също астроид, подобен на дадения, с коефициент на подобие равен на 2, завъртян спрямо дадения на ъгъл /4 (фиг. 16)

5) площта, ограничена от целия астроид, е равна на обема на тялото, получен от въртенето на астроида, равна на 32/105 R 3

повърхността на тялото, образувана от въртенето на астроида, е равна на

Нека сега се обърнем към разглеждането на някои специфични свойства на астроида.

Астроидът е обвивката на сегмент с постоянна дължина, завършва. които се плъзгат по две взаимно перпендикулярни прави линии.

Приемаме тези прави като координатни оси и, като означаваме ъгъла на наклон на плъзгащия се сегмент ND=R през (фиг. 4), ще имаме уравнението на правата ND във вида

Диференцирайки това уравнение по отношение на параметъра, получаваме:

Елиминирайки параметъра от последното уравнение и уравнение (7), ще имаме уравнението на обвивката във вида т.е. astroid.

На практика движението на сегмента ND може да се извърши с помощта на така наречените карданни кръгове. Едната от тези окръжности с радиус R е неподвижна, а другата с радиус r, два пъти по-малка, се търкаля по вътрешната страна на неподвижната окръжност. Всякакви две диаметрално противоположни точки N и D на търкалящата се окръжност ще се движат по два взаимно перпендикулярни диаметъра Ox и Oy на неподвижната окръжност. Ясно е, че обвивката на диаметъра на търкалящия се кръг ще бъде астроида.

Ориз. 17	Ориз. 18

Разгледаният метод за образуване на астроид също може да се тълкува по следния начин. Правоъгълник ODCN, чиито две страни лежат на две взаимно перпендикулярни прави, се деформира така, че диагоналът му да запази дължина, равна на R, обвивката на диагонала ще бъде астроида. Тъй като в този случай перпендикулярът, спуснат от върха C към диагонала DN, служи като нормал към обвивката, астроида е мястото на основите на перпендикулярите, изпуснати от върха C на правоъгълника до неговия диагонал.

За , тези уравнения изразяват директния астроид, разгледан по-рано.