Modeli opisani sustavima dviju autonomnih diferencijalnih jednadžbi.
Fazna ravnina. Fazni portret. Isoclin metoda. Glavne izokline. Stabilnost stacionarnog stanja. Linearni sustavi. Vrste singularnih točaka: čvor, sedlo, fokus, centar. Primjer: kemijske reakcije prva narudžba.
Najzanimljiviji rezultati o kvalitativnom modeliranju svojstava bioloških sustava dobiveni su pomoću modela dviju diferencijalnih jednadžbi, koji omogućuju kvalitativno istraživanje metodom fazna ravnina. Razmotrimo sustav dviju autonomnih običnih diferencijalnih jednadžbi opći pogled
(4.1)
P(x,y), Q(x,y)- kontinuirane funkcije definirane u nekoj domeni G Euklidska ravnina ( x,y ‑ Kartezijeve koordinate) i imajući u ovom području kontinuirane izvodnice reda ne nižeg od prvog.
Regija G može biti neograničeno ili ograničeno. Ako varijable x, y imaju određeno biološko značenje (koncentracije tvari, broj vrsta) najčešće područje G predstavlja pozitivni kvadrant desne poluravnine:
0 £ x< ¥ ,0 £ g< ¥ .
Koncentracije tvari ili broj vrsta također se mogu ograničiti odozgo volumenom posude ili područjem staništa. Tada raspon varijabli ima oblik:
0 £ x< x 0 , 0 £ g< y 0 .
Varijable x, y promjena u vremenu u skladu sa sustavom jednadžbi (4.1), tako da svakom stanju sustava odgovara par varijabilnih vrijednosti ( x, y).
|
|
Obrnuto, svaki par varijabli ( x, y) odgovara određenom stanju sustava.
Razmotrimo ravninu s koordinatnim osima na kojima su ucrtane vrijednosti varijabli x,y. Svaki bod M ova ravnina odgovara određenom stanju sustava. Ta se ravnina naziva fazna ravnina i predstavlja ukupnost svih stanja sustava. Točku M(x,y) nazivamo reprezentirajućom ili prikaznom točkom.
Neka u početnom trenutku vremena t=t 0 koordinate reprezentativne točke M 0 (x(t 0), g(t 0)). U svakom sljedećem trenutku u vremenu t reprezentirajuća točka će se pomaknuti u skladu s promjenama u vrijednostima varijabli x(t), g(t). Skupljanje bodova M(x(t), y(t)) na faznoj ravnini čiji položaj odgovara stanjima sustava u procesu promjene varijabli tijekom vremena x(t), y(t) prema jednadžbama (4.1), naziva se fazna putanja.
Skup faznih trajektorija za različite početne vrijednosti varijabli daje lako vidljiv "portret" sustava. Izgradnja fazni portret omogućuje izvođenje zaključaka o prirodi promjena u varijablama x, y bez poznavanja analitičkih rješenja izvornog sustava jednadžbi(4.1).
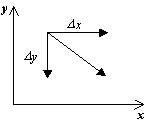
Za prikaz faznog portreta potrebno je u svakoj točki fazne ravnine konstruirati vektorsko polje pravaca trajektorija sustava. Postavljanje inkrementaD t>0,dobivamo odgovarajuće inkremente D x I D g iz izraza:
D x=P(x,y)D t,
D y=Q(x,y)D t.
Smjer vektora dy/dx u točki ( x, y) ovisi o predznaku funkcija P(x, y), Q(x, y) i može se dati tablicom:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Rješenje ove jednadžbe y = y(x,c), ili implicitno F(x,y)=c, Gdje S– konstanta integracije, daje obitelj integralnih krivulja jednadžbe (4.2) - fazne putanje sustav (4.1) na ravnini x, y.
Izoklina metoda
Za konstruiranje faznog portreta koriste se metoda izoklina – Na faznoj ravnini nacrtane su linije koje sijeku integralne krivulje pod određenim kutom. Jednadžba izokline može se lako dobiti iz (4.2). Stavimo
Gdje A– određena konstantna vrijednost. Značenje A predstavlja tangens kuta nagiba tangente na faznu putanju i može uzeti vrijednosti od –¥ na + ¥ . Umjesto toga zamijeniti dy/dx u (4.2) količina A dobivamo jednadžbu izokline:
.(4.3)
Jednadžba (4.3) definira u svakoj točki ravnine jedinstvenu tangentu na odgovarajuću integralnu krivulju, s izuzetkom točke u kojoj P(x,y)= 0, Q (x,y) = 0 , u kojem smjer tangente postaje neizvjestan, budući da vrijednost derivacije postaje neizvjesna:
.
Ova točka je sjecište svih izoklina - posebna točka. U njemu vremenske derivacije varijabli istovremeno nestaju x I g.
Dakle, u singularnoj točki, stope promjene varijabli su nula. Stoga, singularna točka diferencijalne jednadžbe faznih trajektorija (4.2) odgovara stacionarno stanje sustava(4.1), a njegove koordinate su stacionarne vrijednosti varijabli x, y.
Posebno su zanimljivi glavne izokline:
dy/dx=0, P(x,y)=0 – izoklina horizontalnih tangenti i
dy/dx=¥ ,Q(x,y)=0 – izoklina vertikalnih tangenti.
Konstruiranjem glavnih izoklina i pronalaženjem njihove sjecišne točke (x,y), čije koordinate zadovoljavaju uvjete:
time ćemo pronaći točku presjeka svih izoklina fazne ravnine, u kojoj je smjer tangenti na fazne putanje nesiguran. ovo - singularna točka, što odgovara stacionarno stanje sustava(Slika 4.2).
Sustav (4.1) ima onoliko stacionarnih stanja koliko ima sjecišta glavnih izoklina na faznoj ravnini.
Svaka fazna trajektorija odgovara skupu gibanja dinamičkog sustava, koji prolaze kroz ista stanja i razlikuju se jedan od drugog samo u početku odbrojavanja vremena.
 |
|
Ako su uvjeti Cauchyjevog teorema zadovoljeni, tada kroz svaku točku u prostoru x, y, t postoji samo jedna integralna krivulja. Isto vrijedi, zbog autonomije, za fazne putanje: jedna fazna putanja prolazi kroz svaku točku fazne ravnine.
Stabilnost stabilnog stanja
Neka je sustav u stanju ravnoteže.
Tada se reprezentativna točka nalazi u jednoj od singularnih točaka sustava, u kojoj je, po definiciji:
.
Je li singularna točka stabilna ili ne, određuje se time da li točka koja je predstavlja napušta s malim odstupanjem od stacionarnog stanja. U odnosu na sustav dviju jednadžbi, definicija stabilnosti u jezikue, dkako slijedi.
Stanje ravnoteže je stabilno ako za bilo koji zadani raspon odstupanja od stanja ravnoteže (e )možete odrediti područje d (e ), koji okružuje stanje ravnoteže i ima svojstvo da nema putanje koja počinje unutar regije d , nikada neće doći do granice e . (Sl. 4.4)
 |
|
Za veliku klasu sustava - grubi sustavi – čije se ponašanje ne mijenja s malom promjenom oblika jednadžbi, informacije o vrsti ponašanja u blizini stacionarnog stanja mogu se dobiti ispitivanjem ne izvornog, već pojednostavljenog linearizirano sustav.
Linearni sustavi.
Razmotrimo sustav od dva linearne jednadžbe:
.(4.4)
Ovdje a, b, c, d- konstante, x, y- Kartezijeve koordinate na faznoj ravnini.
Tražit ćemo opće rješenje u obliku:
.(4.5)
Zamijenimo te izraze u (4.4) i smanjimo za e l t:
(4.6)
Algebarski sustav jednadžbi (4.6) s nepoznanicama A, B ima rješenje različito od nule samo ako je njegova determinanta, sastavljena od koeficijenata za nepoznanice, jednaka nuli:
.
Proširujući ovu determinantu, dobivamo karakterističnu jednadžbu sustava:
.(4.7)
Rješavanje ove jednadžbe daje vrijednosti eksponental 1,2 , za koje su moguće vrijednosti različite od nule A I B rješenja jednadžbe (4.6). Ova značenja su
.(4.8)
Ako je radikalni izraz negativan, ondal 1,2 kompleksno konjugirani brojevi. Pretpostavimo da oba korijena jednadžbe (4.7) imaju realne dijelove različite od nule i da nema višestrukih korijena. Tada se opće rješenje sustava (4.4) može prikazati kao linearna kombinacija eksponencijala s eksponentimal 1 , l 2 :
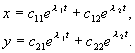(4.9)
Za analizu prirode mogućih putanja sustava na faznoj ravnini koristimo linearna homogena transformacija koordinata, koji će dovesti sustav do kanonski oblik:
,(4.10)
što omogućuje prikladniji prikaz na faznoj ravnini u usporedbi s izvornim sustavom (4.4). Uvedimo nove koordinateξ , η prema formulama:
(4.1)
Iz kolegija linearne algebre poznato je da u slučaju nejednakosti na nulu realni dijelovil 1 , l 2 izvorni sustav (4.4) uvijek se može transformirati pomoću transformacija (4.11) u kanonski oblik (4.10) i može se proučavati njegovo ponašanje na faznoj ravniniξ , η . Razmotrimo različite slučajeve koji se ovdje mogu pojaviti.
Korijeni λ 1 , λ 2 – valjana i istog predznaka
U ovom slučaju koeficijenti transformacije su realni, krećemo se iz realne ravninex,yna realnu ravninu ξ, η. Dijeljenjem druge jednadžbe (4.10) s prvom dobivamo:
.(4.12)
Integrirajući ovu jednadžbu, nalazimo:
Gdje .(4.13)
Dogovorimo se da pod λ razumijemo 2 korijen karakteristične jednadžbe s velikim modulom, što ne narušava općenitost našeg zaključivanja. Tada, budući da su u razmatranom slučaju korijeni λ 1 , λ 2 – valjana i istog znaka,a>1 , a radi se o integralnim krivuljama paraboličkog tipa.
Sve integralne krivulje (osim osi η , što odgovara ) dodiruju u ishodištu osi ξ, koja je ujedno i integralna krivulja jednadžbe (4.11). Ishodište koordinata je posebna točka.
Odredimo sada smjer kretanja prikazne točke po faznim putanjama. Ako je λ 1, λ 2 negativni, tada, kao što se može vidjeti iz jednadžbi (4.10), |ξ|, |η| smanjiti tijekom vremena. Predstavljajuća točka se približava ishodištu koordinata, ali ga nikada ne doseže. U suprotnom, to bi proturječilo Cauchyjevom teoremu, koji kaže da samo jedna fazna putanja prolazi kroz svaku točku fazne ravnine.
Takva posebna točka kroz koju prolaze integralne krivulje, baš poput obitelji parabola 
prolazi kroz ishodište i naziva se čvor (sl. 4.5)
Ravnotežno stanje tipa čvora na λ 1, λ 2 < 0 je Ljapunovljeva stabilna, budući da se reprezentativna točka pomiče duž svih integralnih krivulja prema ishodištu koordinata. Ovaj stabilan čvor. Ako je λ 1, λ 2 > 0, dakle |ξ|, |η| povećavaju tijekom vremena i reprezentna točka se udaljava od ishodišta koordinata. U ovom slučaju, posebna točka– nestabilan čvor .
Na faznoj ravnini x, y opća kvalitativna priroda ponašanja integralnih krivulja bit će sačuvana, ali tangente na integralne krivulje neće se podudarati s koordinatnim osima. Kut nagiba ovih tangenti odredit će se omjerom koeficijenata α , β , γ , δ u jednadžbama (4.11).
Korijeni λ 1 , λ 2 – valjane su i različitih predznaka.
Pretvori iz koordinate x,y na koordinate ξ, η opet pravi. Jednadžbe za kanonske varijable opet imaju oblik (4.10), ali sada predznaci λ 1, λ 2 su različiti. Jednadžba faznih trajektorija ima oblik:
Gdje ,(4.14)
Integrirajući (4.14), nalazimo
(4.15)
Ovaj jednadžba definira familiju krivulja hiperboličkog tipa, gdje su obje koordinatne osi– asimptote (at a=1 imali bismo obitelj jednakostraničnih hiperbola). Koordinatne osi su u ovom slučaju također integralne krivulje– to će biti jedine integralne krivulje koje prolaze kroz ishodište. Svakikoji se sastoji od tri fazne putanje: od dva kretanja u stanje ravnoteže (ili iz stanja ravnoteže) i iz stanja ravnoteže. Sve ostale integralne krivulje– su hiperbole koje ne prolaze kroz ishodište (sl. 4.6) Ova posebna točka zove se "sedlo ». Ravne linije u blizini planinskog sedla ponašaju se slično faznim putanjama u blizini sedla.
Razmotrimo prirodu gibanja reprezentativne točke duž faznih putanja u blizini stanja ravnoteže. Neka npr.λ 1 >0 , λ 2<0 . Zatim reprezentirajuća točka postavljena na os ξ , odmaknut će se od ishodišta i postaviti na os η – će se neograničeno približavati ishodištu koordinata, a da ga ne dostigne u konačnom vremenu. Gdje god je reprezentativna točka u početnom trenutku (s izuzetkom singularne točke i točaka na asimptoti η =0), na kraju će se udaljiti od ravnoteže, čak i ako se u početku kreće duž jedne od integralnih krivulja prema singularnoj točki.
Očito je da singularna točka kao što je sedlo uvijek je nestabilna . Samo pod posebno odabranim početnim uvjetima na asimptotiη =0 sustav će se približiti stanju ravnoteže. Međutim, to nije u suprotnosti s tvrdnjom o nestabilnosti sustava. Ako računamo, da su sva početna stanja sustava na faznoj ravnini jednako vjerojatna, tada je vjerojatnost takvog početnog stanja koje odgovara kretanju u smjeru Do singularna točka jednaka nuli. Stoga će svako stvarno kretanje izbaciti sustav iz stanja ravnoteže.Vratimo se koordinatamax,y,dobit ćemo istu kvalitativnu sliku prirode kretanja trajektorija oko ishodišta koordinata.
Granica između razmatranih slučajeva čvora i sedla je slučaj Kada jedan od karakterističnih pokazatelja npr λ 1 , nestaje, što se događa kada determinanta sustava- izraz ad-bc=0(vidi formulu 4.8 ). U tom su slučaju koeficijenti desnih strana jednadžbi (4.4) međusobno proporcionalni:
a sustav kao stanja ravnoteže ima sve točke pravca:
Preostale integralne krivulje su familija paralelnih ravnih linija s kutnim koeficijentom , duž kojeg se reprezentativne točke ili približavaju stanju ravnoteže ili se udaljavaju od njega, ovisno o predznaku drugog korijena karakteristične jednadžbe λ 2 = a+d.(Sl.4.7 ) U ovom slučaju koordinate stanja ravnoteže ovise o početnoj vrijednosti varijabli.
Korijeni λ 1 , λ 2 – komplekskonjugirati
U ovom slučaju, stvarnox I g hoćemo imaju kompleksne konjugate ξ , η (4.10) . Međutim, uvođenjem druge međutransformacije, moguće je iu ovom slučaju svesti razmatranje na pravu linearnu homogenu transformaciju. Stavimo:
(4.16)
Gdje a,b, I u,v – stvarne vrijednosti. Može se pokazati da transformacija izx,y Do u,v je, pod našim pretpostavkama, realan, linearan, homogen s determinantom različitom od nule. Na temelju jednadžbi(4.10, 4.16) imamo:
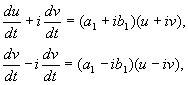
gdje
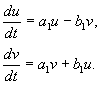(4.17)
Dijeljenje druge jednadžbe s prvom, dobivamo:
koje je lakše integrirati, idemo li u polarni koordinatni sustav (r, φ ) . Nakon zamjene dobivamo odakle:
.(4.18)
Dakle, na faznoj ravniniu, vimamo posla s obitelji logaritamskih spirala od kojih svaka imaasimptotska točka u ishodištu.Singularna točka, koja je asimptotska točka svih integralnih krivulja koje imaju oblik spirale, ugniježđeni u svakojprijatelju, zove se usredotočenost ( sl.4.8 ) .
Razmotrimo prirodu kretanja prikazne točke duž faznih putanja. Množenjem prve jednadžbe (4.17) su, a drugi na v i zbrajanjem dobivamo:
Gdje
Neka a 1 < 0 (a 1 = Ponovnoλ ) . Predstavljajuća točka tada se kontinuirano približava ishodištu koordinata bez da ga dosegne u konačnom vremenu. To znači da su fazne putanje uvijajuće spirale i odgovaraju prigušenim oscilacijama varijable. ovo - stalni fokus .
U slučaju stabilnog fokusa, kao i u slučaju stabilnog čvora, nije zadovoljen samo Ljapunovljev uvjet, već i stroži zahtjev. Naime, za bilo kakva početna odstupanja, sustav će se s vremenom vratiti što bliže željenom položaju ravnoteže. Takva stabilnost, u kojoj početna odstupanja ne samo da ne rastu, već opadaju, težeći nuli, naziva se apsolutna stabilnost .
Ako u formuli (4.18) a 1 >0 , tada se reprezentirajuća točka udaljava od ishodišta, a mi imamo posla s nestabilan fokus . Prilikom kretanja iz avionau,vna faznu ravninux, gspirale će također ostati spirale, ali će biti deformirane.
Razmotrimo sada slučaj kadaa 1
=0
. Fazne putanje u ravniniu, vbit će krugova 
koji u avionux,yodgovaraju elipsi:
Dakle, kadaa 1=0 kroz posebnu točkux= 0, y= 0 ne prolazi nikakva integralna krivulja. Takva izolirana singularna točka, blizu koje su integralne krivulje zatvorene krivulje, posebno elipse ugrađene jedna u drugu i zatvaraju singularnu točku, naziva se središtem.
Dakle, moguće je šest vrsta ravnotežnih stanja, ovisno o prirodi korijena karakteristične jednadžbe (4.7). Prikaz faznih putanja u ravnini x, y za ovih šest slučajeva prikazano je na sl. 4.9.
Riža. 4.9.Vrste faznih portreta u blizini stacionarnog stanja za sustav linearnih jednadžbi (4.4).
Pet vrsta stanja ravnoteže su grube; njihov karakter se ne mijenja s dovoljno malim promjenama u desnim stranama jednadžbi (4.4). U ovom slučaju, promjene ne samo u desnim stranama, već iu njihovim izvodnicama prvog reda trebale bi biti male. Šesto stanje ravnoteže – centar – nije grubo. S malim promjenama u parametrima desne strane jednadžbi, postaje stabilan ili nestabilan fokus.
Bifurkacijski dijagram
Uvedimo sljedeću oznaku:
.
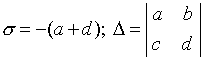(4.11)
Tada će karakteristična jednadžba biti zapisana kao:
.
(4.12)
Razmotrimo ravninu s pravokutnim Kartezijevim koordinatama s , D i označite na njemu područja koja odgovaraju jednoj ili drugoj vrsti stanja ravnoteže, što je određeno prirodom korijena karakteristične jednadžbe
.(4.13)
Uvjet za stabilnost stanja ravnoteže bit će prisutnost negativnog realnog dijela yl 1 i l 2 . Nužan i dovoljan uvjet za to je ispunjenje nejednakostis > 0, D > 0 . Na dijagramu (4.15) ovaj uvjet odgovara točkama koje se nalaze u prvoj četvrtini ravnine parametara. Jedinstvena točka bit će fokus akol 1 i l 2 kompleks. Ovo stanje odgovara onim točkama ravnine za koje , oni. točke između dvije grane paraboles 2 = 4 D. Osovinske točke s = 0, D>0, odgovaraju ravnotežnim stanjima tipa centra. Također,l 1 i l 2 - vrijede, ali su različitih predznaka, tj. singularna točka bit će sedlo ako D<0, itd. Kao rezultat toga, dobit ćemo dijagram particije ravnine parametara s, D, u područja koja odgovaraju različitim vrstama ravnotežnih stanja.
Riža. 4.10. Bifurkacijski dijagram
za sustav linearnih jednadžbi 4.4
Ako su koeficijenti linearnog sustava a, b, c, d ovise o određenom parametru, tada kada se ovaj parametar promijeni, vrijednosti će se također promijenitis , D . Prelaskom granica karakter faznog portreta se kvalitativno mijenja. Stoga se takve granice nazivaju bifurkacijskim granicama – na suprotnim stranama granice sustav ima dva topološki različita fazna portreta i sukladno tome dva različita tipa ponašanja.
Dijagram pokazuje kako se takve promjene mogu dogoditi. Ako izuzmemo posebne slučajeve - ishodište koordinata - onda je lako vidjeti da se sedlo može transformirati u čvor, stabilan ili nestabilan pri prelasku ordinatne osi. Stabilan čvor može ići ili u sedlo ili u stabilan fokus, itd. Imajte na umu da prijelazi stabilan čvor - stabilni fokus i nestabilan čvor - nestabilan fokus nisu bifurkacije, jer se topologija faznog prostora ne mijenja. Više ćemo govoriti o topologiji faznog prostora i bifurkacijskim prijelazima u predavanju 6.
Tijekom bifurkacijskih prijelaza mijenja se priroda stabilnosti singularne točke. Na primjer, stabilan fokus kroz središte može se pretvoriti u nestabilan fokus. Ova bifurkacija se zove Andronov-Hopfova bifurkacija po imenima znanstvenika koji su ga proučavali. Tijekom ove bifurkacije u nelinearnim sustavima rađa se granični ciklus i sustav postaje samooscilirajući (vidi predavanje 8).
Primjer. Sustav linearne kemijske reakcije
Supstanca x teče izvana konstantnom brzinom, pretvara se u tvar Y i brzinom proporcionalnom koncentraciji tvari Y, uklanja se iz sfere reakcije. Sve reakcije su prvog reda, s izuzetkom dotoka tvari izvana, koji je nultog reda. Shema reakcije izgleda ovako:
(4.14)
a opisuje se sustavom jednadžbi:
(4.15)
Stacionarne koncentracije dobivamo izjednačavanjem desnih strana s nulom:
.(4.16)
Razmotrimo fazni portret sustava. Podijelimo drugu jednadžbu sustava (4.16) s prvom. Dobivamo:
.(4.17)
Jednadžba (4.17) određuje ponašanje varijabli na faznoj ravnini. Konstruirajmo fazni portret ovog sustava. Najprije nacrtajmo glavne izokline na faznoj ravnini. Jednadžba izokline vertikalnih tangenti:
Jednadžba izokline horizontalnih tangenti:
Singularna točka (stacionarno stanje) nalazi se na sjecištu glavnih izoklina.
Sada odredimo pod kojim kutom se koordinatne osi sijeku s integralnim krivuljama.
Ako x= 0, zatim .
Dakle, tangenta tangente na integralne krivulje y=y(x), sijekući ordinatnu os x=0, negativan je u gornjoj poluravnini (zapamtite da varijable x, y imaju koncentracijske vrijednosti, pa nas stoga zanima samo gornji desni kvadrant fazne ravnine). U tom slučaju tangens tangentnog kuta raste s udaljenošću od ishodišta.
Razmotrite os y= 0. Na mjestu gdje ova os siječe integralne krivulje, one su opisane jednadžbom
Na tangens nagiba integralnih krivulja koje sijeku apscisnu os je pozitivan i raste od nule do beskonačnosti s porastom x.
U .
Zatim, daljnjim povećanjem, tangens kuta nagiba opada u apsolutnoj vrijednosti, ostaje negativan i teži -1 pri x ® ¥ . Poznavajući smjer tangenti na integralne krivulje na glavnim izoklinama i na koordinatnim osima, lako je konstruirati cjelokupnu sliku faznih putanja.
 |
|
Utvrdimo prirodu stabilnosti singularne točke metodom Ljapunova. Karakteristična determinanta sustava ima oblik:
.
Proširujući determinantu, dobivamo karakterističnu jednadžbu sustava: , tj. Oba korijena karakteristične jednadžbe su negativna. Prema tome, stacionarno stanje sustava je stabilan čvor. U ovom slučaju, koncentracija tvari x teži stacionarnom stanju uvijek monotono, koncentracija tvari Y može proći kroz min ili max. U takvom sustavu nemogući su oscilacijski modovi.
Osnovni pojmovi i definicije:
Nula analitičke funkcije f(z) je točka “a” za koju je f(a)=0.
Nula reda "n" funkcije f(z) je točka "a" ako je fn(a)¹0.
Singularna točka "a" naziva se izolirana singularna točka funkcije f(z) ako postoji okolina te točke u kojoj nema drugih singularnih točaka osim "a".
Postoje tri vrste izoliranih singularnih točaka: .
1 uklonjive singularne točke;
3 bitno singularne točke.
Tip singularne točke može se odrediti na temelju ponašanja zadane funkcije u pronađenoj singularnoj točki, kao i iz oblika Laurentovog niza dobivenog za funkciju u blizini pronađene singularne točke.
Određivanje vrste singularne točke ponašanjem funkcije u njoj.
1. Uklonjive singularne točke.
Izolirana singularna točka a funkcije f(z) naziva se uklonjivom ako postoji konačna granica.
2.Poljaci.
Izolirana singularna točka a funkcije f(z) naziva se polom ako 
.
3. Bitno singularne točke.
Izolirana singularna točka a funkcije f(z) naziva se bitno singularnom točkom ako ne postoji ni konačna ni beskonačna.
Sljedeći odnos postoji između nula i polova funkcije.
Da bi točka a bila pol reda n funkcije f(Z), potrebno je i dovoljno da ta točka bude nula reda n za funkciju .
Ako je n=1, pol se naziva prostim.
Definicija: Izolirana singularna točka nedvosmislene prirode naziva se:
a) uklonjivi ako nedostaje glavni dio raspadanja;
b) pol, ako glavni dio sadrži konačan broj članova;
c) bitno singularna točka ako glavni dio sadrži beskonačan broj članova.
a) Dakle, u blizini uklonjive singularne točke proširenje ima oblik:
ona izražava funkciju u svim točkama kružnice |z-a| U centru z=a jednakost nije istinita, jer funkcija pri z=a ima diskontinuitet, a desna strana je kontinuirana. Ako se promijeni vrijednost funkcije u središtu, uzimajući je jednaku vrijednosti desne strane, tada će praznina biti eliminirana - otuda i naziv - uklonjiv. b) U blizini pola reda m, proširenje Laurentovog niza ima oblik: c) U blizini jednostavnog stupa Odbici i formule za njihov izračun. Ostatak analitičke funkcije f(z) u izoliranoj singularnoj točki z 0 je kompleksan broj jednak vrijednosti integrala Ostatak funkcije f(z) u izoliranoj singularnoj točki z 0 označava se simbolom Res f(z 0) ili Res (f(z); z 0). Tako, Res f(z 0)= Ako stavimo n=-1 u formulu (22.15.1), dobivamo: C -1 = ili Res f(z 0)= C -1, oni. ostatak funkcije f(z) u odnosu na singularnu točku z 0 jednak je koeficijentu prvog člana s negativnim eksponentom u proširenju funkcije f(z) u Laurentov red. Obračun odbitaka. Pravilne ili uklonjive singularne točke. Očito, ako je z=z 0 pravilna ili uklonjiva singularna točka funkcije f(z), tada je Res f(z 0)=0 (Laurentovom proširenju u tim slučajevima nedostaje glavni dio, pa c-1=0) . Pol. Neka je točka z 0 jednostavni pol funkcije f(z). Tada Laurentov red za funkciju f(z) u okolici točke z 0 ima oblik: Odavde Stoga, prelazeći u ovoj jednakosti do granice na z --z 0, dobivamo Res f(z0)= U biti posebna točka. Ako je točka z 0 u biti singularna točka funkcije f(z), tada se za izračunavanje ostatka funkcije u toj točki obično izravno određuje koeficijent c-1 u proširenju funkcije u Laurentov red. Klasifikacija događaja. Zbroj, umnožak događaja, njihova svojstva, grafički prikaz. Događaji se dijele na: 1. Slučajno 2. Pouzdan 3. Nemoguće Pouzdan je događaj koji se nužno događa u danim uvjetima (noć slijedi jutro). Slučajni događaj je događaj koji se može i ne mora dogoditi (polaganje ispita). Nemogući događaj je događaj koji se neće dogoditi pod zadanim uvjetima (vađenje zelene olovke iz kutije sa samo crvenim). Definicija. Singularna točka funkcije naziva se izoliran,
ako je u nekoj okolini ove točke analitička funkcija (odnosno analitička u prstenu). Klasifikacija izoliranih singularnih točaka funkcije povezana je s ponašanjem te funkcije u blizini singularne točke. Definicija. Točka se zove uklonjivi
singularna točka funkcije ako postoji konačna granica te funkcije na . Primjer 5. Pokažite da funkcija ima uklonjivu singularnost u točki. Riješenje. Sjećajući se prve značajne granice, izračunavamo To znači da u točki data funkcija ima uklonjivu singularnost. Zadatak 4. Pokažite da je točka uklonjiva za . Definicija. Točka se zove pol
funkcija, ako ova funkcija neograničeno raste na , odnosno . Obratimo pozornost na povezanost pojmova nule i pola analitičke funkcije. Predstavimo funkciju u obliku . Ako je točka jednostavna nula funkcije, tada funkcija ima jednostavni pol Ako je točka nula reda za funkciju, onda je za funkciju to pol narudžba .
Primjer 6. Pokažite da funkcija ima pol trećeg reda u točki. Riješenje. Pod pretpostavkom da dobijemo . Kako težimo nuli, po bilo kojem zakonu imamo . Zatim , a s njim i sama funkcija raste neograničeno. Dakle, , odnosno singularna točka je pol. Za funkciju je ova točka očito trostruka nula. To znači da je za ovu funkciju točka pol trećeg reda. Zadatak 5. Pokažite da točka ima jednostavan pol. Definicija. Točka se zove značajno poseban
točka funkcije, ako u toj točki ne postoji niti konačna niti beskonačna granica funkcije (ponašanje funkcije nije definirano). Dopustiti biti bitno singularna točka funkcije . Tada za bilo koji kompleksni broj postoji niz točaka koje konvergiraju prema , duž kojih vrijednosti teže: ( Sohotskijev teorem).
Primjer 7. Pokažite da funkcija u točki ima bitnu značajku. Riješenje. Promotrimo ponašanje zadane funkcije u okolici točke. Kada duž pozitivnog dijela realne osi (tj.) imamo i ; ako je duž negativnog dijela realne osi (tj.), tada i . To znači da ne postoji ograničenje na . Po definiciji, u točki funkcija ima bitnu singularnost. Razmotrimo ponašanje funkcije na nuli sa stajališta Sokhotskog teorema. Neka je bilo koji kompleksni broj različit od nule i beskonačnosti. Iz jednakosti nalazimo . Uz pretpostavku , dobivamo niz točaka , . Očito,. U svakoj točki ovog niza funkcija je jednaka, dakle Zadatak 6. Pokažite da funkcija ima bitnu singularnost u točki. Točka u beskonačnosti uvijek se smatra posebnom za funkciju. Točka se naziva izolirana singularna točka funkcije ako ta funkcija nema druge singularne točke izvan određene kružnice sa središtem u ishodištu. Klasifikacija izoliranih singularnih točaka može se proširiti na slučaj. Primjer 8. Pokažite da funkcija ima dvostruki pol u beskonačnosti. Riješenje. Razmotrimo funkciju , gdje je analitička funkcija u susjedstvu točke , i . To znači da funkcija ima dvostruku nulu u beskonačnosti, ali tada je za funkciju točka dvostruki pol. Primjer 9. Pokažite da funkcija ima bitnu singularnost u beskonačnosti. Riješenje. Sličan problem razmatran je u Projektu 7. Razmotrimo ponašanje funkcije u blizini beskonačno udaljene točke. Kada uz pozitivni dio realne osi, a kada uz negativni dio realne osi. To znači da ne postoji ograničenje funkcije u točki i, na temelju definicije, ta je točka bitno posebna. Priroda singularnosti funkcije u točki može se prosuditi prema glavni dio
Laurentovo širenje u blizini ove točke. Teorem 1. Da bi poenta bila uklonjivi
singularne točke funkcije, potrebno je i dovoljno da odgovarajuće Laurentovo širenje nije sadržavao glavni dio.
Zadatak 6. Koristeći Taylorovu ekspanziju funkcije u susjedstvu točke , pokažite da ona ima uklonjivu singularnost na nuli. Teorem 2. Da bi poenta bila pol
funkcija je neophodna i dovoljna kako bi glavni dio
odgovarajuće Laurentovo proširenje sadržavala je konačan broj članova
: Broj najvećeg negativnog člana određuje redoslijed pola. U ovom slučaju funkcija se može prikazati kao gdje je funkcija analitička u točki, , redoslijed pola. Primjer 10. Pokažite da funkcija ima jednostavne polove u točkama. Riješenje. Razmotrimo poantu. Upotrijebimo Laurentovo širenje ove funkcije u okolini te točke, dobiveno u primjeru 2: Budući da je u glavnom dijelu ove ekspanzije najviši (i jedini) negativni stupanj jednak jedinici, tada je točka jednostavni pol ove funkcije. Ovaj rezultat se mogao dobiti i na drugi način. Predstavimo to u obliku i stavimo - to je funkcija koja je analitička u točki i . To znači da, na temelju (8), u točki ova funkcija ima jednostavan pol. Drugi način: razmotrite funkciju koja ima jednostavnu nulu u točki. To znači da u ovom trenutku ima jednostavan pol. Slično, ako funkciju napišemo u obliku , gdje je funkcija analitička u točki i , tada je odmah jasno da je točka jednostavni pol funkcije . Zadatak 7. Pokažite da funkcija ima pol 2. reda u točki i pol 4. reda u točki . Teorem 3. Da bi poenta bila značajno poseban
točka funkcije, potrebno je i dovoljno da glavni dio
Laurentovo širenje u blizini točke sadržavala beskonačan broj članova
. Primjer 11. Odredite prirodu singulariteta u točki funkcije Riješenje. U dobro poznatom proširenju kosinusa umjesto: To znači da Laurentovo širenje u okolini točke ima oblik Ovdje je točan dio jedan izraz. A glavni dio sadrži beskonačan broj pojmova, pa je poanta u biti posebna. Zadatak 8. Pokažite da u točki funkcija ima bitnu singularnost. Razmotrimo neku funkciju i napišimo njenu Laurentovu ekspanziju u točki: Napravimo zamjenu, i stvar ide na stvar. Sada u blizini točke u beskonačnosti imamo Ostalo je uvesti novu oznaku. Dobivamo gdje je glavni dio, a je točan dio Laurentovog širenja funkcije u okolini beskonačne točke. Dakle, u Laurentovom širenju funkcije u okolini točke, glavni dio je niz u pozitivnim potencijama, a točan dio je niz u negativnim potencijama. Uzimajući to u obzir, zamijenite Međutim, zadani kriteriji za određivanje prirode singulariteta ostaju važeći za točku u beskonačnosti. Primjer 12. Utvrdite prirodu singulariteta funkcije u točki. , tada se točka može pokazati neizoliranom. Primjer 15. Funkcija u beskonačnoj točki ima bitnu značajku. Pokažite da točka funkcije nije izolirana singularna točka. Riješenje. Funkcija ima beskonačan broj polova na nulama nazivnika, odnosno u točkama , . Od , Tada je točka u bilo kojem susjedstvu od kojih postoje polovi je granica za polove. Taylorov niz služi kao učinkovit alat za proučavanje funkcija koje su analitičke u krugu zol Za proučavanje funkcija koje su analitičke u domeni prstena, pokazalo se da je moguće konstruirati proširenja u pozitivnim i negativnim potencijama (z - zq) oblika koji generaliziraju Taylorova proširenja. Niz (1), shvaćen kao zbroj dvaju nizova, naziva se Laurentov niz. Jasno je da je područje konvergencije niza (1) zajednički dio područja konvergencije svakog niza (2). Pronađimo je. Područje konvergencije prvog niza je krug čiji je radijus određen Cauchy-Adamard formulom.Unutar kruga konvergencije niz (3) konvergira analitičkoj funkciji, au svakom krugu manjeg radijusa konvergira apsolutno i ravnomjerno. Drugi red je red potencije s obzirom na varijablu. Niz (5) konvergira unutar svoje kružnice konvergencije analitičkoj funkciji kompleksne varijable m-*oo, au bilo kojoj kružnici manjeg polumjera konvergira apsolutno i uniformno, što znači da je područje konvergencije niza (4) vanjska strana kruga - Ako tada postoji zajedničko područje konvergencije niza (3) i (4) - kružni prsten u kojem niz (1) konvergira u analitičku funkciju. Štoviše, u bilo kojem prstenu konvergira apsolutno i jednoliko. Primjer 1. Odredite područje konvergencije Rad Laurentovog niza Izolirane singularne točke i njihova klasifikacija M Područje konvergencije prvog niza je vanjski dio kruga, a područje konvergencije drugog niza je unutrašnjost kruga. Dakle, ovaj niz konvergira u kružnice. Teorem 15. Svaka funkcija f (z), jednoznačna i apolitična u kružnom prstenu, može se prikazati u tom prstenu kao zbroj konvergentnog niza, čiji su koeficijenti Cn jednoznačno određeni i izračunati prema formulama gdje je 7p kružnica polumjera m. Fiksirajmo proizvoljnu točku z unutar prstena R. Konstruirajmo kružnice sa središtima u točki r, čiji polumjeri zadovoljavaju nejednakosti i razmotrimo novi prsten. Koristeći Cauchyjev integralni teorem za višestruko povezanu domenu, imamo Svaki od integrala u zbroju (8) transformiramo posebno. Za sve točke £ duž kružnice 7d* zadovoljena je relacija de suma jednoliko konvergentnog niza 1 1. Stoga se razlomak ^ može prikazati u vi- / "/ Množenjem oba dijela kontinuiranom funkcijom (O i provođenjem počlanom integracijom po krugu, dobivamo da transformaciju drugog integrala provodimo nešto drugačije. Za sve točke £ na krugu ir> vrijedi odnos. Stoga se razlomak ^ može prikazati kao zbroj uniformno konvergentan niz. Množenjem obje strane kontinuiranom funkcijom) i integracijom po članovima duž kružnice 7/, dobivamo da Primijetite da su integrandi u formulama (10) i (12) analitičke funkcije u kružnom prstenu. Prema tome, prema Cauchyjevom teoremu, vrijednosti odgovarajućih integrala neće se promijeniti ako krugove 7/r i 7r/ zamijenimo bilo kojim krugom. To nam omogućuje kombiniranje formula (10) i (12). Zamjenom integrala na desnoj strani formule (8) s njihovim izrazima (9) odnosno (11) dobivamo traženo proširenje. Budući da je z proizvoljan točki prstena, slijedi da niz ( 14) svugdje u tom prstenu konvergira funkciji f(z), au svakom prstenu red konvergira toj funkciji apsolutno i uniformno. Dokažimo sada da je dekompozicija oblika (6) jedinstvena. Pretpostavimo da postoji još jedno proširenje.Tada ćemo posvuda unutar prstena R imati Na kružnici redovi (15) jednoliko konvergiraju. Pomnožimo obje strane jednakosti (gdje je m fiksni cijeli broj, i integrirajmo oba niza član po član. Kao rezultat, dobivamo na lijevoj strani, a na desnoj - Sch. Dakle, (4, = St. Budući da m je proizvoljan broj, posljednja jednakost dokazuje jedinstvenost proširenja. Niz (6), čiji se koeficijenti izračunavaju pomoću formula (7), naziva se Laurentov red funkcije f(z) u prstenu. skup članova ovog niza s nenegativnim potencijama naziva se regularni dio Laurentovog niza, a s negativnim - njegov glavni dio. Formule ( 7) za koeficijente Laurentovog niza rijetko se koriste u praksi, jer, kao pravilo, zahtijevaju glomazne izračune. Obično se, ako je moguće, koriste gotova Taylorova proširenja elementarnih funkcija. Na temelju jedinstvenosti proširenja, svaka pravna tehnika dovodi do istog rezultata. Primjer 2. Razmotrimo proširenja funkcija u Laurentov niz u različitim domenama, uz pretpostavku da f(r) ima dvije singularne točke: Posljedično, postoje tri prstenaste domene sa središtem u točki r = 0. U svakoj od njih funkcija f(r) je analitička: a ) kružni prsten izvana krug (slika 27). Nađimo Laurentova proširenja funkcije /(z) u svakom od ovih područja. Predstavimo /(z) kao zbroj elementarnih razlomaka a) Krug Relaciju (16) transformiramo na sljedeći način Koristeći se formulom za zbroj članova geometrijske progresije dobivamo Pronađena proširenja zamijenimo u formulu (17) : Ovo proširenje je Taylorov niz funkcije /(z). b) Prsten za funkciju -r ostaje konvergentan u tom prstenu, jer niz (19) za funkciju j^j za |z| > 1 se razilazi. Stoga transformiramo funkciju /(z) na sljedeći način: ponovnom primjenom formule (19) dobivamo da Ovaj niz konvergira za. Zamjenom proširenja (18) i (21) u relaciju (20) dobivamo c) Vanjski dio kružnice za funkciju -z za |z| > 2 divergira, a niz (21) za funk- Predstavimo funkciju /(z) u sljedećem obliku: /<*> Koristeći formule (18) i (19), dobivamo OR 1 Ovaj primjer pokazuje da za istu funkciju f(z) Laurentovo širenje, općenito govoreći, ima različit oblik za različite prstenove. Primjer 3. Pronađite ekspanziju 8. Laurentovog niza funkcije Laurentov niz Izolirane singularne točke i njihova klasifikacija u domeni prstena A Koristimo reprezentaciju funkcije f(z) u sljedećem obliku: i transformiramo drugi član koristeći formulom za zbroj članova geometrijske progresije dobivamo Zamjenom pronađenih izraza u formulu (22) imamo Primjer 4. Proširimo funkciju u Laurentov niz u području zq = 0. Za svaki kompleks imamo Neka je ovo proširenje vrijedi za bilo koju točku z F 0. U ovom slučaju prstenasto područje predstavlja cijelu kompleksnu ravninu s jednom odbačenom točkom z - 0. Ovo područje može se definirati sljedećom relacijom: Ova funkcija je analitička u području Iz formula ( 13) za koeficijente Laurentovog niza, korištenjem istog razmišljanja kao u prethodnom odlomku, mogu se dobiti Kouiwove nejednakosti. ako je funkcija f(z) ograničena na kružnicu, gdje je M konstanta), tada Izolirane singularne točke Točka zo se naziva izolirana singularna točka funkcije f(z) ako postoji prstenasto susjedstvo točke ( ovaj skup se ponekad naziva probušenom okolinom točke 2o), u kojoj je funkcija f(z) jedinstvena i analitička. U samoj točki zo funkcija je ili nedefinirana ili nije jednoznačna i analitička. Ovisno o ponašanju funkcije /(r) pri približavanju točki zo, razlikuju se tri tipa singularnih točaka. Izolirana singularna točka naziva se: 1) uklonjivom ako postoji konačna 2) pmusach ako 3) bitno singularnom točkom ako funkcija f(z) nema limit na Tip izolirane singularne točke usko je povezan s priroda Laurentovog proširenja funkcije probušenim središtem . Teorem 16. Izolirana singularna točka z0 funkcije f(z) je uklonjiva singularna točka ako i samo ako Laurentovo širenje funkcije f(z) u okolini točke zo ne sadrži glavni dio, tj. ima oblik Neka je zo uklonjiva singularna točka. Tada postoji konačna, stoga je funkcija f(z) ograničena u prokološkom susjedstvu točke z. Stavljamo Na temelju Cauchyjevih nejednakosti Budući da se p može odabrati da bude proizvoljno malen, tada su svi koeficijenti na negativnim potencijama (z - 20) jednaki su nuli: Obrnuto, neka Laurentov razvitak funkcije /(r) u okolini točke zq sadrži samo ispravan dio, odnosno ima oblik (23) i stoga je Taylor. Lako je vidjeti da za z -* z0 funkcija /(z) ima graničnu vrijednost: Teorem 17. Izolirana singularna točka zq funkcije f(z) je uklonjiva ako i samo ako je funkcija J(z) omeđeno u nekoj punktiranoj okolini točke zq, Zgmechai ne. Neka je r uklonjiva singularna točka funkcije /(r). Pretpostavimo da je funkcija /(r) analitička u nekoj kružnici sa središtem u točki r. To određuje naziv točke - uklonjiv. Teorem 18. Izolirana singularna točka zq funkcije f(z) je pol ako i samo ako glavni dio Laurentove ekspanzije funkcije f(z) u susjedstvu točke sadrži konačan (i pozitivan) broj nenula članova, tj. ima oblik 4 Neka je z0 pol. Od tada postoji punktirana okolina točke z0 u kojoj je funkcija f(z) analitička i različita od nule. Tada je u tom susjedstvu definirana analitička funkcija i Stoga je točka zq uklonjiva singularna točka (nula) funkcije ili gdje je h(z) analitička funkcija, h(z0) Φ 0. Tada je h(zo) Φ 0 je također analitička, tada je funkcija φ analitička u susjedstvu točke zq, i stoga, odakle dobivamo da Pretpostavimo sada da funkcija f(z) ima ekspanziju oblika (24) u probušenoj okolini točke točka zo. To znači da je u tom susjedstvu funkcija f(z) analitička zajedno s funkcijom. Za funkciju g(z) vrijedi ekspanzija iz koje se vidi da je zq uklonjiva singularna točka funkcije g(z) i postoji. Tada funkcija na 0 teži biti pol funkcije. Tu je još jedna jednostavna činjenica. Točka Zq je pol funkcije f(z) ako i samo ako se funkcija g(z) = yj može proširiti na analitičku funkciju u susjedstvu točke zq postavljanjem g(z0) = 0. Redoslijed pola funkcije f(z) naziva se nulti red funkcije jfa. Sljedeća tvrdnja slijedi iz teorema 16 i 18. Teorem 19. Izolirana singularna točka je bitno singularna ako i samo ako glavni dio Laurentove ekspanzije u probušenoj okolini te točke sadrži beskonačno mnogo članova različitih od nule. Primjer 5. Singularna točka funkcije je zo = 0. Imamo Laurentov niz Izolirane singularne točke i njihovu klasifikaciju. Prema tome, zo = O je uklonjiva singularna točka. Proširenje funkcije /(z) u Laurentov niz u blizini nultočke sadrži samo točan dio: Primjer7. /(z) = Singularna točka funkcije f(z) je zq = 0. Razmotrimo ponašanje ove funkcije na realnoj i imaginarnoj osi: na realnoj osi na x 0, na imaginarnoj osi. nije ni konačna ni beskonačna granica za f(z) pri z -* 0 ne postoji. To znači da je točka r = 0 bitno singularna točka funkcije f(z). Nađimo Laurentovo širenje funkcije f(z) u blizini nultočke. Za svaki kompleks C imamo Set. Tada Laurentovo širenje sadrži beskonačan broj članova s negativnim potencijama od z.
, uzeto u pozitivnom smjeru duž kružnice L sa središtem u točki z 0 koja leži u domeni analitičnosti funkcije f(z) (tj. u prstenu 0<|z-z0| . (22.15.1)
