Ministarstvo obrazovanja i znanosti Ruske Federacije

Državna obrazovna ustanova visokog obrazovanja

strukovno obrazovanje

„Tobolska državna socijalno-pedagoška akademija

ih. DI. Mendeljejev"

Odjel za matematiku, TIMOM

Neke diofantske jednadžbe

Tečajni rad

Studentica 3. godine FMF-a

Matajev Evgenij Viktorovič

Znanstveni savjetnik:

Kandidat fizičkih i matematičkih znanosti A.I. Valitskas

Ocjena: ____________

Tobolsk - 2011

Uvod……………………………………………………………………........2

§ 1. Linearne diofantske jednadžbe……………………………………..3

§ 2. Diofantova jednadžbax 2 – g 2 = a………………………………….....9

§ 3. Diofantova jednadžbax 2 + g 2 = a…………………………………... 12

§ 4. Jednadžba x 2 + x + 1 = 3y 2 …………………………………………….. 16

§ 5. Pitagorine trojke……………………………………………………….. 19

§6. Veliki teorem Farma…………………………………………………23

Zaključak………………………………………………………………….….....29

Bibliografija...........………………………………………………..30

UVOD

Diofantova jednadžba je jednadžba oblika P(x 1 , … , x n ) = 0 , gdje je lijeva strana polinom u varijablama x 1 , … , x n S cjelobrojni koeficijenti. Svaki naručeni set (u 1 ; … ; u n ) cijeli brojevi sa svojstvom P(u 1 , … , u n ) = 0 naziva se (parcijalno) rješenje Diofantove jednadžbe P(x 1 , … , x n ) = 0 . Riješiti Diofantovu jednadžbu znači pronaći sva njena rješenja, tj. opće rješenje ove jednadžbe.

Naš će cilj biti naučiti kako pronaći rješenja nekih diofantovih jednadžbi, ako su ta rješenja dostupna.

Da biste to učinili, morate odgovoriti na sljedeća pitanja:

A. Ima li Diofantova jednadžba uvijek rješenje, pronaći uvjete postojanja rješenja.

b. Postoji li algoritam koji omogućuje pronalaženje rješenja Diofantove jednadžbe.

Primjeri: 1. Diofantova jednadžba 5 x – 1 = 0 nema rješenja.

2. Diofantova jednadžba 5 x – 10 = 0 ima rješenje x = 2 , koji je jedini.

3. Jednadžba ul x – 8 x 2 = 0 nije Diofantov.

4. Često jednadžbe oblika P(x 1 , … , x n ) = Q(x 1 , … , x n ) , Gdje P(x 1 , … , x n ) , Q(x 1 , … , x n ) su polinomi s cjelobrojnim koeficijentima, koji se nazivaju i Diofantovi. Mogu se napisati u obliku P(x 1 , … , x n ) – Q(x 1 , … , x n ) = 0 , što je standardno za Diofantove jednadžbe.

5. x 2 – g 2 = a je Diofantova jednadžba drugog stupnja s dvije nepoznanice x i y za bilo koji cijeli broj a. Ima rješenja za a = 1 , ali nema rješenja za a = 2 .

§ 1. Linearne diofantske jednadžbe

Neka a 1 , … , a n , saZ . Vrsta jednadžbe a 1 x 1 + … + a n x n = c naziva se linearna Diofantova jednadžba s koeficijentima a 1 , … , a n , desna strana c i nepoznata x 1 , … , x n . Ako je desna strana c linearne Diofantove jednadžbe nula, tada se takva Diofantova jednadžba naziva homogenom.

Naš neposredni cilj je naučiti kako pronaći partikularna i opća rješenja linearnih Diofantovih jednadžbi u dvije nepoznanice. Očito, svaka homogena Diofantova jednadžba a 1 x 1 + … + a n x n = 0 uvijek ima određeno rješenje (0; … ; 0).

Očito je da linearna Diofantova jednadžba, čiji su svi koeficijenti jednaki nuli, ima rješenje samo u slučaju da joj je desna strana jednaka nuli. Općenito, imamo sljedeće

Teorem (o postojanju rješenja linearne Diofantove jednadžbe). Linearna diofantska jednadžba a 1 x 1 + … + a n x n = c, čiji koeficijenti nisu svi jednaki nuli, ima rješenje ako i samo ako GCD(a 1 , … , a n ) | c.

Dokaz. Nužnost uvjeta je očita: GCD(a 1 , … , a n ) | a ja (1 ja n) , Dakle GCD(a 1 , … , a n ) | (a 1 x 1 + … + a n x n ) , što znači da dijeli i

c = a 1 x 1 + … + a n x n .

Neka D= gcd(a 1 , … , a n ) , c =Dt I a 1 u 1 + … + a n u n = D – linearno širenje najvećeg zajedničkog djelitelja brojeva a 1 , … , a n. Množenje obje strane s t, dobivamo a 1 (u 1 t) + … + a n (u n t) = Dt = c, tj. cijeli broj

n-ka (x 1 t; … ; x n t) je rješenje izvorne jednadžbe s n nepoznato.

Teorem je dokazan.

Ovaj teorem daje konstruktivan algoritam za pronalaženje posebnih rješenja linearnih Diofantovih jednadžbi.

Primjeri: 1. Linearna diofantska jednadžba 12x+21y=5 nema rješenja jer gcd(12, 21) = 3 ne dijeli 5 .

2. Pronađite partikularno rješenje Diofantove jednadžbe 12x+21y = 6.

Očito sada gcd(12, 21) = 3 | 6, dakle rješenje postoji. Zapisujemo linearno širenje gcd(12, 21) = 3 = 122 + 21(–1). Stoga, par (2; –1) je posebno rješenje jednadžbe 12x+21y = 3, i par (4; –2) je posebno rješenje izvorne jednadžbe 12x+21y = 6.

3. Pronađite određeno rješenje linearne jednadžbe 12x + 21y - 2z = 5.

Jer (12, 21, –2) = ((12, 21), –2) = (3, –2) = 1 | 5 , onda rješenje postoji. Nakon dokaza teorema prvo nalazimo rješenje jednadžbe (12.21)x–2y=5, a zatim zamjenom linearnog širenja najvećeg zajedničkog djelitelja iz prethodnog zadatka dobivamo rješenje izvorne jednadžbe.

Za rješavanje jednadžbe 3x - 2y = 5 zapiši linearno širenje gcd(3, -2) = 1 = 31 - 21 očito. Dakle, par brojeva (1; 1) je rješenje jednadžbe 3 x – 2 g = 1 , i par (5; 5) je partikularno rješenje Diofantove jednadžbe 3x - 2y = 5.

Tako, (12, 21)5 – 25 = 5 . Zamjenjujući ovdje prethodno pronađeno linearno širenje (12, 21) = 3 = 122 + 21(–1) , dobivamo (122+21(–1))5 – 25 = 5 , ili 1210 + 21(–5) – 25 = 5 , tj. trojka cijelih brojeva (10; –5; 5) je partikularno rješenje izvorne Diofantove jednadžbe 12x + 21y - 2z = 5.

Teorem (o strukturi općeg rješenja linearne Diofantove jednadžbe). Za linearnu Diofantovu jednadžbu a 1 x 1 + … + a n x n = c sljedeće tvrdnje su istinite:

(1) ako = (u 1 ; … ; u n ), = (v 1 ; … ; v n ) su njegova posebna rješenja, zatim razlika (u 1 –v 1 ; … ; u n –v n ) je partikularno rješenje odgovarajuće homogene jednadžbe a 1 x 1 + … + a n x n = 0 ,

(2) skup partikularnih rješenja linearne Diofantove homogene jednadžbe a 1 x 1 + … + a n x n = 0 zatvoreno za zbrajanje, oduzimanje i množenje cijelim brojevima,

(3) ako M je opće rješenje zadane linearne Diofantove jednadžbe, i L je opće rješenje odgovarajuće homogene Diofantove jednadžbe, zatim za bilo koje posebno rješenje = (u 1 ; … ; u n ) izvorne jednadžbe, jednakost M = +L .

Dokaz. Oduzimanje jednakosti a 1 v 1 + … + a n v n = c od jednakosti a 1 u 1 + … + a n u n = c, dobivamo a 1 (u 1 –v 1 ) + … + a n (u n –v n ) = 0 , tj. skup

(u 1 –v 1 ; … ; u n –v n ) je partikularno rješenje linearne homogene Diofantove jednadžbe a 1 x 1 + … + a n x n = 0 . Dakle, dokazano je da

= (u 1 ; … ; u n ), = (v 1 ; … ; v n ) ML .

Ovo dokazuje tvrdnju (1).

Tvrdnja (2) se dokazuje na sličan način:

, L z Z L z L .

Da bismo dokazali (3), prvo zapazimo da M+L. Ovo proizlazi iz prethodnog: M+L .

Nasuprot tome, ako = (l 1 ; … ; l n ) L i = (u 1 ; … ; u n ) M, zatim M:

a 1 (u 1 +l 1 )+ …+a n (u n +l n ) = (a 1 u 1 + … + a n u n )+(a 1 l 1 + … + a n l n ) = c + 0 = c.

Tako, + LM, i na kraju M = +L .

Teorem je dokazan.

Dokazani teorem ima jasno geometrijsko značenje. Ako uzmemo u obzir linearnu jednadžbu a 1 x 1 + … + a n x n = c, Gdje x ja R, onda, kao što je poznato iz geometrije, određuje u prostoru R n hiperravnina dobivena iz ravnine L s homogenom jednadžbom a 1 x 1 + … +a n x n =0 prolazeći kroz ishodište koordinata pomakom za neki vektor R n. Površina pogleda + L naziva se i linearni razdjelnik s prostorom za vođenje L i vektor pomaka . Time je dokazano da je opće rješenje M diofantova jednadžba a 1 x 1 + … + a n x n = c sastoji se od svih točaka neke linearne mnogostrukosti koje imaju cjelobrojne koordinate. U ovom slučaju, koordinate vektora pomaka su također cijeli brojevi, a skup L rješenja homogene Diofantove jednadžbe a 1 x 1 + … + a n x n = 0 sastoji se od svih točaka u prostoru vodiča s cjelobrojnim koordinatama. Zbog toga se često kaže da skup rješenja proizvoljne Diofantove jednadžbe tvori linearni mnogoznačnik s vektorom pomaka i vodeći prostor L.

Primjer: za Diofantovu jednadžbu x - y \u003d 1 zajednička odluka M ima oblik (1+y; y), gdje je yZ, njegovo posebno rješenje = (1; 0) , i opće rješenje L homogena jednadžba x – y = 0 bit će zapisano u obrascu (y; y), Gdje naZ. Dakle, možemo nacrtati sljedeću sliku, u kojoj su rješenja izvorne Diofantove jednadžbe i odgovarajuće homogene Diofantove jednadžbe prikazane debelim točkama u linearnom mnogoznačniku M i prostora L odnosno.

2. Nađite opće rješenje Diofantove jednadžbe 12x + 21y - 2z = 5.

Privatno rješenje (10; –5; 5) ova jednadžba je pronađena ranije, nalazimo opće rješenje homogene jednadžbe 12x + 21y - 2z = 0, ekvivalentno Diofantovoj jednadžbi 12 x + 21 g = 2 z.

Da bi ova jednadžba bila rješiva ​​potrebno je i dovoljno da se ispuni uvjet gcd(12, 21) = 3 | 2z, oni. 3 | z ili z = 3t za neki cijeli broj t. Svodeći oba dijela na 3 , dobivamo 4x + 7y = 2t. Partikularno rješenje (2; –1) Diofantove jednadžbe 4x+7y= 1 pronađeno u prethodnom primjeru. Zato (4t ; -2t) je posebno rješenje jednadžbe 4x + 7y = 2t za bilo koji

t Z. Opće rješenje odgovarajuće homogene jednadžbe

(7 u ; –4 u) već pronađeno. Dakle, opće rješenje jednadžbe 4x + 7y = 2t izgleda kao: (4t + 7u; -2t - 4u) , te opće rješenje homogene jednadžbe 12x + 21y - 2z = 0 bit će napisano ovako:

(4t + 7u; -2t - 4u; 3t).

Lako je provjeriti da ovaj rezultat odgovara gore navedenom teoremu bez dokaza o rješenjima homogene Diofantove jednadžbe A 1 x 1 + … + a n x n = 0 : Ako P = , Da R I

(u; t) P je opće rješenje razmatrane homogene jednadžbe.

Dakle, opće rješenje Diofantove jednadžbe 12x + 21y - 2z = 5 izgleda ovako: (10 + 4t + 7u; –5 – 2t – 4u; 5+3t).

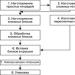
3. Na primjeru prethodne jednadžbe ilustriramo drugu metodu za rješavanje Diofantovih jednadžbi s mnogo nepoznanica, koja se sastoji u uzastopnom smanjivanju maksimalne vrijednosti modula njezinih koeficijenata.

12x + 21y - 2z = 5 12x + (102 + 1)y - 2z = 5

12x + y - 2 (z - 10y) = 5

Dakle, opće rješenje razmatrane jednadžbe može se napisati na sljedeći način: (x; 5 - 12x + 2u; 50 - 120x + 21u), Gdje x, u su proizvoljni cjelobrojni parametri.

§ 2. Diofantova jednadžbax 2 – g 2 = a

Primjeri: 1. Na a = 0 dobivamo beskonačan broj rješenja: x = g ili x = – g za bilo koga g Z.

2. Na a = 1 imamo x 2 – g 2 = 1 (x + g)(x – g) = 1 . Dakle, broj 1 se rastavlja na umnožak dvaju cjelobrojnih faktora x + g I x – g(važno, to x, g- cijeli!). Jer broj 1 samo dva proširenja u umnožak cjelobrojnih faktora 1 = 11 I 1 = (–1)(–1) , dobivamo dvije mogućnosti: .

3. Za a = 2 imamo x 2 – g 2 = 2 (x + g)(x – g) = 2. Postupajući slično prethodnom, razmatramo proširenja

2=12=21=(–1)(–2)=(–2)(–1), sastavljamo sustave:, koji za razliku od prethodnog primjera nemaju rješenja. Dakle, nema rješenja za razmatranu Diofantovu jednadžbu x 2 – g 2 = 2.

4. Prethodna razmatranja dovode do nekih zaključaka. Rješenja jednadžbi x 2 – g 2 = a su u raspadanju a = km u umnožak cijelih brojeva iz sustava . Ovaj sustav ima cijela rješenja ako i samo ako k + m I k – m su parni, tj. kada su brojevi k I m isti paritet (istodobno parni ili neparni). Dakle, Diofantova jednadžba x 2 – y 2 = a ima rješenje ako i samo ako se a može proširiti u umnožak dvaju cjelobrojnih faktora iste parnosti. Ostaje samo pronaći sve takve.

Teorem (o jednadžbix 2 – g 2 = a ). (1) Jednadžba x 2 – g 2 = 0 ima beskonačan broj rješenja .

(2) Svako rješenje jednadžbe dobiva se kao , Gdje a = km je rastavljanje broja a na umnožak dvaju cjelobrojnih faktora iste parnosti.

(3) Jednadžba x 2 – g 2 = a ima rješenje ako i samo ako a 2 (mod 4).

Dokaz.(1) već je dokazano.

(2) već je dokazano.

(3) () Neka prvo Diofantova jednadžba x 2 – g 2 = a ima rješenje. Dokažimo to a 2 (mod 4) . Ako a = km je proširenje u umnožak cijelih brojeva istog pariteta, zatim za par k I m imamo k = 2 l, m = 2 n I a = km = 4 ul 0 (mod 4) . U slučaju neparnih k, m njihov posao a također neparan, razlika a – 2 neparan i nedjeljiv sa 4 , tj. opet

a 2 (mod 4).

() Ako sada a 2 (mod 4) , tada možemo konstruirati rješenje jednadžbe x 2 – g 2 = a. Doista, ako je a neparan, onda a = 1 a je dekompozicija proizvoda neparnih cijelih brojeva, tako da je rješenje Diofantove jednadžbe. Ako je a paran, tada s obzirom na a 2 (mod 4) shvaćamo to 4 | a, a = 4 b = 2(2 b) je produkt dekompozicije parnih cijelih brojeva, tako da je rješenje Diofantove jednadžbe.

Teorem je dokazan.

Primjeri: 1. Diofantova jednadžba x 2 – g 2 = 2012 nema rješenja, jer 2010 = 4502 + 2 2 (mod 4).

2. Diofantova jednadžba x 2 – g 2 = 2011 ima rješenja, jer

2011 3 (mod 4). Imamo očita proširenja

2011 = 12011 = 20111 = (–1)(–2011) = (–2011)(–1),

za svaki od njih nalazimo rješenja (bilo koja kombinacija znakova). Drugih rješenja nema, jer broj 2011 jednostavno (?!).

§ 3. Diofantova jednadžbax 2 + g 2 = a

Primjeri: 1. 0 = 0 2 + 0 2 , 1 = 0 2 + 1 2 , k 2 = 0 2 + k 2 . Dakle, očito je da se svaki kvadrat može trivijalno prikazati kao zbroj dvaju kvadrata.

2. 2 = 1 2 + 1 2 , 5 = 1 2 + 2 2 , 8 = 2 2 + 2 2 , 10 = 1 2 + 3 2 , 13 = 2 2 + 3 2 , 17 = 1 2 + 4 2 , 18 = 3 2 + 3 2 , 20 = 2 2 + 4 2 , …

3. Nema rješenja za a = 3, 6 = 23, 7, 11, 12 = 2 2 3, 14 = 27, 15 = 35, 19, 21 = 37, 22 = 211, 23, 24 = 32 3 , …

Analiza gornjih rezultata može sugerirati da je nepostojanje rješenja na neki način povezano s prostim brojevima obrasca

4 n+3 prisutna u faktorizaciji brojeva koji se ne mogu prikazati kao zbrojevi dvaju kvadrata.

Teorem (o prikazivanju prirodnih brojeva zbrojevima dvaju kvadrata). Prirodni broj a može se prikazati kao zbroj dvaju kvadrata ako i samo ako, u njegovom kanonskom širenju, prosti brojevi oblika 4 n + 3 imaju parne eksponente.

Dokaz. Najprije dokažemo da ako se prirodni broj a može prikazati kao zbroj dvaju kvadrata, onda u njegovom kanonskom širenju svi prosti brojevi oblika 4 n + 3 moraju imati parne eksponente. Pretpostavimo, suprotno onome što je dokazano, da a= str 2 k +1 b = x 2 + g 2 , Gdje

R - prosti broj obrasca 4 n+3 I b str. Zamislite brojeve x I na kao

x =Dž, g = Dt, GdjeD= gcd(x, g) = str s w, str w; z, t, s N 0 . Tada dobivamo jednakost R 2 k +1 b = D 2 (z 2 + t 2 ) = str 2 s w 2 (z 2 + t 2 ) , tj. R 2( k – s )+1 b = w 2 (z 2 + t 2 ) . Na lijevoj strani jednakosti nalazi se p (neparna potencija nije jednaka nuli), što znači da je jedan od faktora na desnoj strani djeljiv s prostim brojem p. Jer str w, To p | (z 2 + t 2 ) , gdje su brojevi z, t međusobno jednostavni. Ovo je u suprotnosti sa sljedećom lemom (?!).

Lema (o djeljivosti zbroja dvaju kvadrata s prostim brojem oblika

4 n + 3 ). Ako je prost broj p = 4n+3 dijeli zbroj kvadrata dvaju prirodnih brojeva, zatim dijeli svaki od tih brojeva.

Dokaz. Iz suprotnog. Neka x 2 + g 2 0(mod str) , Ali x0(mod str) ili g 0 (mod str) . Jer x I g su simetrični, mogu se međusobno mijenjati, pa možemo pretpostaviti da x str.

Lema (o reverzibilnosti modulostr ). Za bilo koji cijeli broj x, nedjeljiv s prostim brojem str, postoji inverzni element modulo str – takav cijeli broj 1 u < str, Što xi 1 (mod str).

Dokaz. Broj x suprime sa str, tako da možemo napisati linearno širenje GCD(x, str) = 1 = xi + pv (u, v Z) . Jasno je da xi1(modp) , tj. u- inverzni element prema x modulo str. Ako u ne zadovoljava ograničenje 1 u < str, zatim dijeljenje u s uključenim ostatkom str, dobivamo ostatak r u (mod str) , za koji xr xi 1 (mod str) I 0 r < str.

Modulo reverzibilnost lema str dokazano.

Množenje usporedbe x 2 + g 2 0 (mod str) po kvadratu u 2 inverzni element to x modulo str, dobivamo 0 = 0u 2 x 2 u 2 +y 2 u 2 = (xu) 2 + (yu) 2 1+t 2 (mod p).

Dakle za t = yu usporedba obavljena t 2 –1 (mod str) , što dovodimo do kontradikcije. Jasno je da t str: inače t 0 (mod str) I 0 t 2 –1 (mod str) , što je nemoguće. Po Fermatovoj teoremi imamo t str –1 1 (mod str), koji zajedno sa t 2 –1 (mod str) I str = 4 n + 3 dovodi do kontradikcije:

1 t p–1 = t 4n+3–1 = t 2(2n+1) = (t 2 ) 2n+1 (–1) 2n+1 = –1 (modp).

Dobivena kontradikcija pokazuje da je pretpostavka o x 0 (mod str) nije bilo ispravno.

Lema o djeljivosti zbroja dvaju kvadrata s prostim brojem 4 n+3 dokazano.

Dakle, dokazano je da broj čija kanonska dekompozicija uključuje prost broj str = 4 n + 3 na neparnu potenciju, ne može se prikazati kao zbroj dvaju kvadrata.

Dokažimo sada da svaki broj u čijem kanonskom proširenju prosti brojevi str = 4 n + 3 sudjelovati samo u čak i moći, koji se može predstaviti kao zbroj dvaju kvadrata.

Ideja dokaza temelji se na sljedećem identitetu:

(A 2 +b 2 )(c 2 +d 2 ) = (ac – bd) 2 + (oglas + bc) 2 ,

koji se može dobiti iz poznatog svojstva modula kompleksni brojevi– modul proizvoda jednak je proizvodu moduli. Stvarno,

| z|| t| = | zt| | a + dvo|| c + di| = |(a + dvo)(c + di)|

|a+bi| 2 |c + di| 2 = |(ac – bd) + (ad + bc)i| 2

(A 2 +b 2 )(c 2 +d 2 ) = (ac – bd) 2 + (oglas + bc) 2 .

Iz ovog identiteta slijedi da ako se dva broja u, v mogu prikazati kao zbroj dvaju kvadrata: u = x 2 + g 2 , v = z 2 + t 2 , tada se njihov umnožak uv također može prikazati kao zbroj dvaju kvadrata: UV = (xz – yt) 2 + (xt + yz) 2 .

Bilo koje prirodni broj a > 1 može se napisati u obliku a= str 1 … R k m 2 , Gdje R ja su po paru različiti prosti brojevi, m N . Da bismo to učinili, dovoljno je pronaći kanonsku dekompoziciju , zapišite svaki stupanj obrasca r u obliku kvadrata (r) 2 za čak = 2, ili u obliku r = r(r) 2 za neparan = 2 + 1 , a zatim odvojeno grupirajte kvadrate i preostale proste brojeve. Na primjer,

29250 = 23 2 5 3 13 = 2513(35) 2 , m = 15.

Broj m 2 ima trivijalnu reprezentaciju kao zbroj dvaju kvadrata: m 2 = 0 2 + m 2 . Dokažemo li reprezentativnost kao zbroj dvaju kvadrata svih prostih brojeva R ja (1 ja k) , tada će se korištenjem identiteta dobiti i prikaz broja a. Po stanju, među brojevima R 1 , … , R k može samo upoznati 2 = 1 2 + 1 2 i prosti brojevi oblika 4 n + 1 . Dakle, ostaje dobiti prikaz u obliku zbroja dvaju kvadrata glavni broj p = 4m + 1. Ovu izjavu izdvajamo u zaseban teorem (vidi dolje)

Na primjer, za a = 29250 = 2513(15) 2 sukcesivno dobivamo:

2 = 1 2 + 1 2 , 5 = 1 2 + 2 2 , 13 = 2 2 + 3 2 ,

25 = (11 – 12) 2 + (12 + 11) 2 = 1 2 + 3 2 ,

2513 = (12 – 33) 2 + (13 + 32) 2 = 7 2 + 9 2 ,

29250 = 2513(15) 2 = (715) 2 + (915) 2 = 105 2 + 135 2 .

Teorem je dokazan.

§ 4. Jednadžbax + x + 1 = 3y

Pozabavimo se sada jednadžbom x+x+1=Zu. Već ima svoju povijest. R. Oblat je 1950. predložio da se uz rješavanje

x=y=1. nema drugih rješenja u prirodnim brojevima x, y gdje je x neparan broj. Iste je godine T. Nagel ukazao na rješenje x= 313, y = 181. Metoda slična gornjoj za jednadžbu x+x-2y=0, omogućit će nam da odredimo sva rješenja jednadžbe x+x+1=3y (1)

u prirodnim brojevima x, na. Hajdemo to pretvarati (x, y) je rješenje jednadžbe (1) u prirodnim brojevima, i x > 1. Lako se vidi da jednadžba (18) nema rješenja u prirodnim brojevima x, g, Gdje x = 2, 3, 4, 5, 6, 7, 8, 9; tako i treba biti x10.

Pokažimo to 12g<7 x+3, 7y>4x+ 2. 4y > 2x+1 . (2)

Kad bi bilo 12g> 7x+3, imali bi smo 144g> 49 x+42 x+9 . i budući da, s obzirom na (18), 144y= 48x+ 48 x + 48 , onda bi bilo x< 6 x +3 9, odakle

(x-z)< 48 i, prema tome, s obzirom na to x> 10, 7 < 148 , što je nemoguće. Time je prva od nejednakosti (2) dokazana.

Kad bi bilo 7g< 4 x+2 , imali bi smo 49g< 16 x+ 16 x+4 , a budući da je, s obzirom na (1), 16 x+ 16 x+ 16 = 48 god, onda bi bilo 49g< 48u- 12, što je nemoguće. Time je druga od nejednakosti (2) dokazana iz koje izravno proizlazi treća. Dakle, nejednakosti (2) su istinite.

Stavimo sada

w\u003d 7x - 12y + 3,h = -4 x+ 7u-2. (3)

Na temelju (2) nalazimo da w > 0 , h > 0 I X -w=3(4 g-2 x-1)>0 i stoga, w<х . Prema (3) imamo w 2 + w+1=3 h 2 odakle, s obzirom na (1), prihvaćamo g(x, y) = (7x - 12y + 3, -4x + 7y -2).

Dakle, možemo to reći, na temelju bilo kojeg rješenja (x, y) jednadžbe (1) u prirodnim brojevima, gdje x > 1, dobivamo novo rješenje (w, h) = g(x, y) jednadžbe (1) u prirodnim brojevima w, h Gdje w < х (a time i rješenje u manjim prirodnim brojevima). Stoga, djelujući kao gore, nalazimo da za svako rješenje jednadžbe (1) u prirodnim brojevima x, y, Gdje x > 1, postoji prirodan broj n takav da g(x, y) = (l, 1).

Prihvativši f(x, y) = (7x+12y + 3, 4x+ 7y + 2), (4) to lako možemo naći f(g(x, y)) = (x, y) i zbog toga (x, g) = f(1,1) S druge strane, lako je provjeriti da ako (x, y) je rješenje jednadžbe (1) u prirodnim brojevima, tada f(x, g) također postoji rješenje jednadžbe (1) u prirodnim brojevima (odnosno većim od x I na).

Prihvativši x=y=1(x, y) = f(1, 1) Za n=2,3,…..,

dobivamo niz { x, g} Za n= 1, 2,….., koji sadrži sva rješenja jednadžbe (1) u prirodnim brojevima i samo takva rješenja.

Evo imamo (X,g)= f(1,1)= f(x, y), dakle, zbog (4), dobivamo

x=7x+12y+3,g=4x+7y+2 (5) (n=1, 2, ...)

Formule koje vam omogućuju dosljedno određivanje svih rješenja (x, y) jednadžbe (1) u prirodnim brojevima. Na taj način lako dolazimo do rješenja (1,1),(22,13),(313,181),.(4366,2521),(60817,35113),..

Tih rješenja očito ima beskonačno mnogo. Od jednakosti

x=y=1 i (4) indukcijom lako nalazimo da brojevi x s neparnim indeksima su neparni, s parnim indeksima su parni, a brojevi g bit neparan za n = 1, 2, ... Da bismo dobili sva rješenja jednadžbe (1) u cijelim brojevima x, y, kao što je lako dokazati, slijedilo bi već dobivena rješenja (x, y) pridružiti (x, -y) I (-x-1,±y) Za n=1, 2, .. .

Dakle, ovdje imamo, na primjer, više takvih rješenja: (-2,1) (-23,13), (-314,181). A. Rotkevič je primijetio da od svih rješenja jednadžbe (1) u prirodnim brojevima x > 1 i y mogu dobiti sva rješenja jednadžbe (z+1)-z=y (6)

u prirodnim brojevima z, y. Doista, pretpostavimo da prirodni brojevi z, y zadovoljavaju jednadžbu (5). Stavljanje x=3z+l, dobivamo, kao što je lako provjeriti, prirodne brojeve x > 1 I na zadovoljavajući jednadžbu (1).

S druge strane, ako prirodni brojevi x > 1 I na zadovoljavaju jednadžbu (1), tada imamo, kao što je lako provjeriti, (x-1)= 3(y-x), odakle slijedi da je broj (prirodni) x-1 podjeljeno sa 3 , stoga x-1=3 z, gdje z je prirodan broj, a jednakost 3z=y-x=y3z-1 , što dokazuje da brojevi z I na zadovoljiti jednadžbu (6). Dakle, na temelju odluka (22,13),(313,181), (4366,2521) jednadžbe (1), dobivamo rješenja (7,13),(104,181),(1455,2521) jednadžbe (6). Ovdje također napominjemo da ako prirodni brojevi z, y zadovoljavaju jednadžbu (6), dokazuje se da na je zbroj dvaju uzastopnih kvadrata, na primjer 13=2+3,181=9+10, 2521=35+ 36 . Na sličan način, kao prije za jednadžbu (1), mogli bismo pronaći sva rješenja jednadžbe x+(x+1)= g u prirodnim brojevima x, y, uzimajući za x > 3 g (x. y) \u003d (3x -2y + 1, 3y - 4x - 2) i za x> 1 f(x, y) = (3x+ 2y+l, 4x + Zu + 2),što dovodi do formule ( x, y)f(3,5) te do zaključka da su sva rješenja jednadžbe (6) u prirodnim brojevima x, y sadržana u nizu { x, g} Za n= 1, 2,…., Gdje x=3, y=5, ix=3 x+2 g+1 . g = 4 x+3 g+2 (n=1, 2, ...). Na primjer, x \u003d 3 3 + 2 5 + 1 \u003d 20, y = 4 3 + Z 5 + 2 \u003d 29;x=119, y=169:x=69b, y=985;x=4059, y=5741.

Geometrijsko značenje razmatrane jednadžbe je u tome što daje sve Pitagorine trokute (pravokutne s prirodnim stranicama), čije su katete izražene uzastopnim prirodnim brojevima. Takvih je trokuta (*) beskonačno mnogo.

Jednadžba je x+(x+1)= g, dokazano je da nema rješenja u prirodnim brojevima x, y.

Linearno diofantske jednadžbe

Istraživački rad u algebri

Učenik 9. razreda MOU "Upshinskaya OOSh"

Antonov Jurij

„Ako želiš naučiti plivati, onda

hrabro uđite u vodu, a ako želite

naučite rješavati probleme, a zatim ih rješavajte.

D.Poya

Voditelj - Sofronova N.A. .

Zadatak

Za podove širine 3 metra postoje daske širine 11 cm i 13 cm. Koliko dasaka bilo koje veličine trebate?

Ako x - broj dasaka širine 11 cm, i na - broj dasaka širine 13 cm, tada moramo riješiti jednadžbu:

11 x + 13 y = 300

Značajke jednadžbe 11 x + 13 y \u003d 300: ▪ Koeficijenti 11, 13, 300 su cijeli brojevi. ▪ Broj nepoznanica premašuje broj jednadžbi. ▪ Rješenja ove jednadžbe x i y moraju biti cijeli brojevi pozitivni brojevi

Algebarske jednadžbe ili sustavi algebarskih jednadžbi s cijelim koeficijentima, u kojima je broj nepoznanica veći od broja jednadžbi i za koje je potrebno pronaći cjelobrojna rješenja, nazivaju se neodređenim ili diofantin, nazvan po grčkom matematičaru Diofant .

Primjeri diofantskih jednadžbi

1 . Pronađite sve parove cijelih brojeva

x , g , za što je istina jednakost

2 . Pokažite da jednadžba

ima beskonačan broj rješenja

cijeli brojevi

Cilj rada:

Shvatiti:

• Koji metode S postojati Za rješenja diofantskih jednadžbi?

Zadaci:

• Pronađite i i naučiti metode rješavanja linearni Diofantove jednadžbe u dvije varijable.

• Razmotriti mogućnosti teorije linearnih Diofantovih jednadžbi.

Pitagorine trojke

• Neodređene jednadžbe u cijelim brojevima rješavane su i prije Diofanta. Od velikog interesa bila je, primjerice, algebarska jednadžba x 2 + g 2 = z 2 , obvezujućih stranaka x , na , z pravokutni trokut. Cijeli brojevi x , g I z , koji su rješenja ove jednadžbe, nazivaju se "Pitagorine trojke" .

Fermatova jednadžba

• Diofantova djela također su izravno povezana s matematičkim istraživanjima francuskog matematičara Pierrea de Fermata. Vjeruje se da je upravo Fermatov rad započeo novi val u razvoju teorije brojeva. A jedan od njegovih problema je poznata Fermatova jednadžba

x n +y n =z n

Niti jedan veliki matematičar nije zaobišao teoriju Diofantovih jednadžbi.

Fermat, Euler, Lagrange, Gauss, Chebyshev ostavili su neizbrisiv trag u ovoj zanimljivoj teoriji.

1, (katalonski); ax 2 + bxy + su 2 + dx + ey + f \u003d 0, gdje su a, b, c, d, e, f cijeli brojevi, tj. opća nehomogena jednadžba drugog stupnja s dvije nepoznanice (P. Fermat, J Wallis, L. Euler, J. Lagrange i K. Gauss) "width="640"

Primjeri neodređenih jednadžbi riješili veliki matematičari 19. i 20. stoljeće: x 2 − ny 2 = 1 , Gdje n nije egzaktan kvadrat (Fermat, Pell); x z − g t = 1 , Gdje z , t 1, (katalonski); Oh 2 + b.xy + su 2 + dx + ej + f = 0 , Gdje A , b , S , d , e , f - cijeli brojevi, tj. opća nehomogena jednadžba drugog stupnja s dvije nepoznanice (P. Fermat, J. Vallis, L. Euler, J. Lagrange i K. Gauss)

Diofantove jednadžbe u 20. stoljeću

1900 Međunarodni matematički kongres.

Hilbertov 10. problem

Dana je Diofantova jednadžba s nekim brojem nepoznanica i racionalnim cijelim koeficijentima. Potrebno je osmisliti postupak koji bi u konačnom broju operacija mogao odrediti je li jednadžba rješiva ​​u cijelim racionalnim brojevima.

ruski matematičar Jurij Matijasevič dokazao :

Hilbertov 10. problem je nerješiv – traženi algoritam ne postoji.

Je li uvijek moguće pronaći sva cjelovita rješenja za određenu neodređenu jednadžbu ili dokazati nepostojanje takve?

• Problem rješavanja jednadžbi u cijelim brojevima u potpunosti je riješen samo za jednadžbe prvog stupnja s dvije ili tri nepoznanice.
• DE drugog stupnja s dvije nepoznanice već se teško rješava.
• DE drugog stupnja s više od dvije nepoznanice rješavaju se samo u nekim posebnim slučajevima, na primjer, jednadžba x 2 + g 2 = z 2 .
• DE stupnja višeg od drugog imaju u pravilu samo konačan broj rješenja (u cijelim brojevima).
• Za jednadžbe iznad drugog stupnja s dvije ili više nepoznanica čak je i problem postojanja cjelobrojnih rješenja prilično težak. Na primjer, nije poznato ima li jednadžba

x 3 + g 3 + z 3 = 30 barem jedno cjelobrojno rješenje.

• Za rješavanje pojedinačnih diferencijalnih jednadžbi, a ponekad i za specifične jednadžbe, potrebno je izmisliti nove metode. Očito, ne postoji algoritam koji bi omogućio pronalaženje rješenja proizvoljnog DE.

Linearne diofantske jednadžbe

Opći obrazac:

LDE s dvije varijable:

a x + prema = c

LDE s tri varijable:

a x + by + cz = d

LDE s dvije nepoznanice

LDE s dvije varijable:

a x + prema = c

rješenja:

x = x 0 - bt

na = na 0 + na

Homogeno:

a x + od = 0

rješenja:

x = - bt

na = na

Pronalaženje privatnog rješenja

Metode rješenja:

• Višestruka metoda.
• Primjena Euklidovog algoritma.
• Metoda ponavljanja.
• Metoda spuštanja.

• Metoda razmatranja ostataka od dijeljenja

Višestruka metoda

riješiti jednadžbu 11 x + 2 y = 69

Tražimo zbroj jednak 69: 55 + 14 = 69 Partikularno rješenje jednadžbe

x 0 = 5, y 0 = 7

Primjena Euklidovog algoritma

riješiti jednadžbu 4 x + 7 y = 16

• Nađimo gcd brojeva 4 i 7 koristeći Euklidov algoritam: gcd(4,7) = 1

• Izrazimo broj 1 kroz koeficijente A = 4 i b =7 korištenjem GCD teorema o linearnom širenju:

GCD ( A, b ) = au+bv .

• Dobivamo: 1 = 4 ∙ 2 + 7 ∙ (-1) u = 2, v = -1

• Posebno rješenje jednadžbe: x 0 = 2 ∙ 16 = 32,

na 0 = -1 ∙ 16 = -16

metoda nabrajanja

riješiti jednadžbu 7 x + 12 y = 100

• 7x + 12y = 100
• 7x \u003d 100 - 12 god
• 100 - 12 godina višekratnik od 7

Posebno rješenje jednadžbe: x 0 = 4, y 0 = 6

100-12u

Način otpuštanja: 3x+8y=60

Izraziti

varijabla x

kroz na

Izraziti

varijabla x

kroz t

Odgovor:

Ispitivanje:

Metoda razmatranja ostataka od dijeljenja

• Riješite jednadžbu u cijelim brojevima 3x - 4y \u003d 1
• 3 x = 4 y + 1
• Lijeva strana jednadžbe djeljiva je s 3, tako da desna mora biti djeljiva s 3. Dijeljenje s 3 može rezultirati ostacima 0, 1 i 2.
• Razmotrimo 3 slučaja.

3x = 4 ∙ 3p + 1 = 12p + 1

y=3p+1

Nije djeljivo s 3

3x = 4 ∙ (3p + 1) +1 = 12p + 3

y=3p+2

Nije djeljivo s 3

3 x = 4 ∙ (3p + 2) +1 = 12p + 9

3x=3(4p+3)

x = 4 p + 3

Odgovor:

Djeljivo s 3

x = 4 p + 3 ; y=3p+2

Mogućnosti LDE teorije Pronađite sva cjelobrojna rješenja jednadžbe x 2 + 5g 2 + 34z 2 + 2xy - 10xz - 22uz =0

Što mi je projekt dao?

• Dobio uvid u rad na istraživačkom projektu.
• Upoznao se s poviješću razvoja Diofantovih jednadžbi i životopisom Diofanta.
• Proučavao metode za rješavanje LDE-a s dvije i tri nepoznanice.
• riješio skupinu zadataka koji su praktične naravi, a javljaju se i na olimpijadama, ispitima za tečaj osnovne škole
• Stekli vještine rješavanja nestandardnih problema.

Mislim da ću u budućnosti nastaviti proučavati Diofantove jednadžbe drugog stupnja i metode za njihovo rješavanje.

POPIS KORIŠTENIH IZVORA

• Matematika u pojmovima, definicijama i pojmovima. 1. dio. Vodič za učitelje. ur. L.V. Sabinina. M., "Prosvjeta", 1978. -320 str. (Knjižnica učitelja matematike.) Na poleđini naslovne knjige: O.V. Manturov, Yu.K. Solntsev, Yu.I. Sorokin, N.G. Fedin.
• Nagibin F.F., Kanin E.S. Matematička kutija: Vodič za učenike. – 4. izd., revidirano. i dodatni - M.: Prosvjetljenje, 1984. - 160s., ilustr.
• N.P. Tučnin. Kako postaviti pitanje? (O matematičkom stvaralaštvu učenika): knjiga za studente. - M .: Obrazovanje, 1993. - 192 str., ilustr.
• S.N.Olekhnik, Yu.V.Nesterenko, M.K.Potapov Antički zabavni problemi. –M.: Bustard, 2002. -176s., ilustr.
• Ya.I. Perelman. Zabavna algebra. - M.: Nauka, 1975. - 200s., ilustr.
• Izborni resurs: http :// www.yugzone.ru /x/ diofant-i-diofantovy-uravneniya / I.G. Bashmakova "Diofantske i diofantske jednadžbe".
• Izborni resurs: http :// www.goldenmuseum.com /1612Hilbert_eng.html Hilbertov 10. problem: povijest jednog matematičkog otkrića (Diofant, Fermat, Hilbert, Julije Robinson, Nikolaj Vorobjov, Jurij Matijasevič).
• Izborni izvor: http://ru.wikipedia.org/wiki/ Diofantove jednadžbe.
• Izborni resurs: http :// revolucija.allbest.ru / matematika /d00013924.html Belov Denis Vladimirovič Linearne diofantske jednadžbe.
• Izborni resurs: http :// revolucija.allbest.ru / matematika /d00063111.html Linearne diofantske jednadžbe
• Izborni resurs: http ://portfolio.1september.ru/work.php?id=570768 Zyuryukina Olga. Neodređene jednadžbe u cijelim brojevima ili Diofantove jednadžbe.
• Izborni resurs: http ://portfolio.1september.ru/work.php?id=561773 Aleksandar Arapov. Diofant i njegove jednadžbe.
• Izborni resurs: http :// en.wikipedia.org / wiki / Euklidov algoritam.

Danas predlažem razmišljanje o nekom zanimljivom matematičkom problemu.
Naime, zagrijmo se rješavanjem sljedeće linearne jednadžbe:

"Što je teško?" - pitaš. Doista, samo jedna jednadžba i čak četiri nepoznanice. Dakle, tri varijable su slobodne, a zadnja ovisi o njima. Pa izrazimo to brzo! Na primjer, preko varijable tada je skup rješenja sljedeći:

gdje je skup bilo kojih realnih brojeva.

Eto, rješenje se doista pokazalo previše trivijalnim. Tada ćemo zakomplicirati naš zadatak i učiniti ga zanimljivijim.

Prisjetimo se o linearne jednadžbe s cjelobrojnim koeficijentima i cjelobrojnim korijenima, koje su, zapravo, neka vrsta Diofantovih jednadžbi. Točnije, nametnut ćemo našoj jednadžbi odgovarajuće ograničenje na cjelobrojne koeficijente i korijene. Koeficijenti za nepoznanice već su cijeli brojevi (), ali same nepoznanice moraju biti ograničene na sljedeće:

gdje je skup cijelih brojeva.

Sada rješenje dobiveno na početku članka neće raditi, jer riskiramo da ga dobijemo kao racionalni (frakcijski) broj. Dakle, kako riješiti ovu jednadžbu? isključivo u cijelim brojevima?

Zainteresirani za rješavanje ovog problema, pitam pod kat.

I nastavljamo s vama. Pokušajmo napraviti neke elementarne transformacije željene jednadžbe:

Problem i dalje izgleda neshvatljivo, u takvim slučajevima matematičari obično rade neku vrstu zamjene. Idemo s vama:

Wow, postigli smo zanimljiv rezultat! Koeficijent sada kod nas jednako jedan, što znači da ti i ja tu nepoznanicu možemo izraziti preko ostalih nepoznanica u ovoj jednadžbi bez ikakvih podjela (što smo zgriješili na samom početku članka). Učinimo to:

Dopustite mi da primijetim da nam ovo govori da bez obzira na to što su (u okviru Diofantovih jednadžbi), oni će i dalje ostati cijeli broj, i to je u redu.

Prisjećajući se da je pošteno reći da . I zamjenjujući gore dobiveni rezultat, dobivamo:

Ovdje također vidimo da bez obzira na to što su, oni će i dalje ostati cijeli broj, i to je još uvijek u redu.

Tada nam pada na pamet briljantna ideja: deklarirajmo kao slobodne varijable, pa ćemo se izražavati kroz njih! Zapravo, već smo to učinili. Ostaje samo upisati odgovor u sustav rješenja:

Sada to možete vidjeti u sustavu odlučivanja nigdje podjele, što znači da će rješenja uvijek biti cijeli broj. Pokušajmo pronaći određeno rješenje izvorne jednadžbe, pretpostavivši, na primjer, da je:

Zamijenite u izvornoj jednadžbi:

Isto, super! Pokušajmo ponovno s drugim primjerom, hoćemo li?

Ovdje vidimo negativan koeficijent, može nam zadati priličnu količinu problema, pa se riješimo grijeha tako da ga zamijenimo, tada će jednadžba biti sljedeća:

Kao što se sjećamo, naš zadatak je napraviti takve transformacije da u našoj jednadžbi postoji nepoznanica s jediničnim koeficijentom na njoj (kako bismo je zatim izrazili kroz ostatak bez ikakvog dijeljenja). Da bismo to učinili, opet moramo uzeti nešto "iz zagrade", najbrže je uzeti koeficijente iz jednadžbe koji su najbliži jedinici. Međutim, morate razumjeti da samo onaj broj koji je nužno neki koeficijent jednadžbe (ni više, ni manje) može biti izbačen iz zagrade, inače ćemo naići na tautologiju/kontradikciju ili razlomke (drugim riječima, nemoguće je da se slobodne varijable pojavljuju negdje osim za posljednju promjenu). Tako:

Uvodimo zamjenu, a zatim dobivamo:

Opet ga izbacujemo iz zagrade i na kraju dobivamo nepoznanicu u jednadžbi s jediničnim koeficijentom:

Uvodimo zamjenu, zatim:

Izrazimo svoju usamljenu nepoznatost odavde:

Iz ovoga slijedi da što god uzmemo, to će i dalje ostati cijeli broj. Tada iz omjera nalazimo:

Slično, nalazimo iz relacije:

Na tome je sazrio naš sustav rješenja - izrazili smo apsolutno sve nepoznanice bez pribjegavanja dijeljenju, čime smo pokazali da će rješenje sigurno biti cjelobrojno. Također, ne zaboravite da moramo uvesti obrnutu zamjenu. Tada je konačni sustav rješenja sljedeći:

Dakle, ostaje odgovoriti na pitanje može li se ijedna slična jednadžba riješiti na ovaj način? Odgovor: ne, ako je jednadžba načelno nerješiva. To se događa u slučajevima kada slobodni član nije djeljiv s GCD svih koeficijenata za nepoznanice. Drugim riječima, s obzirom na jednadžbu:

Za rješavanje u cijelim brojevima dovoljno je ispuniti sljedeći uvjet:

(gdje je najveći zajednički djelitelj).

Dokaz

Dokaz nije razmatran u okviru ovog članka, jer je to razlog za poseban članak. Možete to vidjeti, na primjer, u prekrasnoj knjizi V. Sierpinskog "O rješavanju jednadžbi u cijelim brojevima" u §2.

Rezimirajući gore navedeno, pišemo algoritam radnji za rješavanje linearnih Diofantovih jednadžbi s bilo kojim brojem nepoznanica:

Zaključno, vrijedi reći da je također moguće dodati ograničenja na svaki član jednadžbe u obliku nejednadžbe na njemu (tada se sustavu rješenja dodaje sustav nejednadžbi, prema kojem će odgovor trebati prilagoditi) i dodati još nešto zanimljivo. Također ne treba zaboraviti da je algoritam rješenja strog i da se može napisati u obliku računalnog programa.

Peter je bio s tobom
hvala na pažnji.

Problem 1. Recimo da hobotnice i morske zvijezde žive u akvariju. Hobotnice imaju 8 nogu, a morske zvijezde 5. Ukupno ih ima 39. Koliko životinja ima u akvariju?

Riješenje. Neka je x broj morskih zvijezda, a y broj hobotnica. Tada sve hobotnice imaju 8 nogu, a sve zvijezde imaju 5 nogu. Napravimo jednadžbu: 5x + 8y = 39.

Imajte na umu da se broj životinja ne može izraziti necijelim ili negativnim brojevima. Stoga, ako je x nenegativan cijeli broj, tada y \u003d (39 - 5x) / 8 također mora biti cijeli broj i nenegativan, što znači da izraz 39 - 5x mora biti djeljiv s 8 bez ostatka. Jednostavan nabrajanje opcija pokazuje da je to moguće samo ako je x = 3, tada je y = 3. Odgovor: (3; 3).

Jednadžbe oblika ax + bu = c nazivaju se diofantske, prema starogrčkom matematičaru Diofantu iz Aleksandrije. Diofant je živio, po svemu sudeći, u 3. stoljeću. n. e., ostale činjenice iz njegove biografije koje su nam poznate iscrpljuju se ovakvom pjesmom-zagonetkom, prema legendi, uklesanom na njegovom nadgrobnom spomeniku:

Pepeo Diofantov grob počiva; čudi se njoj i kamenu

Starost pokojnika će mu reći mudrom umjetnošću.

Voljom bogova proživio je šestinu života kao dijete.

I dočekao je polovicu šeste s paperjem na obrazima.

Prošla je tek sedma, zaručio se s djevojkom.

S njom je, nakon pet godina provedenih, mudar čovjek čekao svog sina;

Njegov voljeni sin živio je samo pola života svog oca.

Od oca ga je rani grob uzeo.

Dva puta dvije godine roditelj je oplakivao tešku tugu,

Ovdje sam vidio granicu svog tužnog života.

Koliko je godina živio Diofant Aleksandrijski?

Zadatak 2. U skladištu se nalaze čavli u kutijama od 16,17 i 40 kg. Može li skladištar izdati 100 kg čavala bez otvaranja kutija? (metoda izravnog nabrajanja)

Analizirajmo metodu rješavanja s obzirom na jednu nepoznanicu.

Zadatak 3. U katalogu umjetničke galerije nalazi se 96 slika. Na nekim stranicama su 4 slike, a na nekima 6. Koliko stranica od svake vrste ima katalog?

Riješenje. Neka je x broj stranica sa četiri slike,

y je broj stranica sa šest slika,

Ovu jednadžbu rješavamo s obzirom na onu nepoznanica za koje je najmanji (modulo) koeficijent. U našem slučaju to je 4x, odnosno:

Cijelu jednadžbu dijelimo s ovim faktorom:

4x=96-6y | :4;

Ostaci pri dijeljenju s 4: 1,2,3. Zamijenite ove brojeve umjesto y.

Ako je y=1, onda je x=(96-6∙1):4=90:4 - Ne radi, rješenje nije u cijelim brojevima.

Ako je y=2, onda je x=(96-6∙2):4=21 - Prikladno.

Ako je y=3, onda je x=(96-6∙3):4=78:4 - Ne radi, rješenje nije u cijelim brojevima.

Dakle, posebno rješenje je par (21;2), što znači da su na 21 stranici 4 slike, a na 2 stranice 6 slika.

Analizirajmo metodu rješenja pomoću Euklidovog algoritma.

Zadatak 4. U trgovini se prodaju dvije vrste čokolade: mliječna i gorka. Sva čokolada se sprema u kutije. U skladištu je 7 kutija mliječne čokolade, a tamne 4. Poznato je da je bila još jedna tabla crne čokolade. Koliko je čokoladica u svakoj vrsti kutije?

Riješenje. Neka x bude broj pločica mliječne čokolade u jednoj kutiji,

y je broj štanglica tamne čokolade u jednoj kutiji,

Zatim, prema uvjetu ovog problema, možemo napisati jednadžbu:

Riješimo ovu jednadžbu pomoću Euklidovog algoritma.

Ekspresno 7=4∙1+3, => 3=7-4∙1.

Ekspresno 4=3∙1+1, => 1=4-3∙1=4-(7-4∙1)=4-7+4∙1=4∙ 2 -7∙1 =1.

Dakle, ispada x=1; y=2.

A to znači da je mliječna čokolada u kutiji od 1 komada, a gorka 2 komada.

Analizirajmo metodu pronalaženja određenog rješenja i opća formula rješenja.

Problem 5. U afričkom plemenu Tumbe-Yumbe dvoje domorodaca Tumba i Yumba rade kao frizeri, pri čemu Tumba svojim klijentima uvijek plete 7 pletenica, a Yumba po 4 pletenice. Koliko su mušterija majstori pojedinačno uslužili tijekom smjene, ako se zna da su zajedno ispleli 53 kikice?

Riješenje. Neka x bude broj Tumba kupaca,

y je broj Yumba klijenata,

tada je 7x+4y=53 (1).

Sada, kako bismo pronašli određena rješenja jednadžbe (,), zamijenit ćemo zbroj brojeva koji su nam dani s 1. To će uvelike pojednostaviti traženje odgovarajućih brojeva. Dobivamo:

Riješimo ovu jednadžbu metodom supstitucije.

4y \u003d 1-7x │: 4;

Ostaci kada se dijele s 4: 1, 2, 3. Zamijenite ove brojeve umjesto x:

Ako je x=1, tada y=(1-7):4 nije prikladno, jer rješenje nije u cijelim brojevima.

Ako je x=2, tada y=(1-7∙2):4 nije prikladno, jer rješenje nije u cijelim brojevima.

Ako je x=3, tada je y=(1-7∙3):4=-5 u redu.

Zatim pomnožimo dobivene vrijednosti s početnom vrijednošću zbroja koju smo zamijenili s 1, tj.

x=x 0 ∙53=3∙53=159;

y=y 0 ∙53=-5∙53=-265.

Našli smo posebno rješenje jednadžbe (1). Provjerimo to zamjenom početne jednadžbe:

7∙159+4∙(-265)=53; (3)

Odgovor se skupio. Kad bismo rješavali apstraktnu jednadžbu, tu bismo mogli stati. Međutim, mi rješavamo problem, a kako Tumba nije mogao isplesti negativan broj pletenica, moramo nastaviti rješavanje. Sada ćemo napisati formule za opće rješenje. Da bismo to učinili, od početne jednadžbe (1) oduzimamo jednadžbu sa zamijenjenim vrijednostima (3). Dobivamo:

Izbacimo uobičajene faktore iz zagrada:

7(x-159)+4(y+265)=0.

Premjestimo jedan od članova iz jednog dijela jednadžbe u drugi:

7(x-159)=-4(y+265).

Sada je postalo jasno da kako bi se jednadžba riješila (x-159) mora biti djeljivo s -4, a (y + 265) mora biti djeljivo sa 7. Uvedimo varijablu n, koja će prikazati ovo naše opažanje:

Premjestimo članove s jedne strane jednadžbe na drugu:

Dobili smo opće rješenje ove jednadžbe, sada možemo zamijeniti različite brojeve u nju i dobiti odgovarajuće odgovore.

Na primjer, neka je n=39

A to znači da je Tumba isplela kikice za 3 klijentice, a Yumba za 8 klijentica.

Rješavati probleme na razne načine.

Zadatak 6: Vovočka je kupio olovke za 8 rubalja i olovke za 5 rubalja. Štoviše, platio je 19 rubalja više za sve olovke nego za sve olovke. Koliko je olovaka i olovaka kupio mali Johnny? (metoda traženja općeg rješenja, rješenja za jednu nepoznanicu, korištenjem Euklidovog algoritma).

Problem 7. Flomasteri su kupljeni za 7 rubalja, a olovke za 4 rublje svaka, što ukupno iznosi 53 rublje. Koliko je kupljeno flomastera i olovaka?

Problem 8. (Općinski obilazak VOSH-a 2014-2015): na planetu C postoje dvije vrste kovanica: svaki od 16 tugrika i od 27 tugrika. Je li uz njihovu pomoć moguće kupiti robu po cijeni od 1 tugrika?

Problem 9. Šeherezada priča svoje priče velikom vladaru. Ukupno mora ispričati 1001 bajku. Koliko će noći trebati Šeherezadi da ispriča sve svoje priče, ako neke noći ispriča 3 priče, a neke 5? Za koliko noći će Šeherezada ispričati sve svoje priče ako to želi što prije? Koliko će noći trebati Šeherezadi ako joj je dosadno pričati pet priča za noć, pa takvih noći treba biti što manje?

Zadatak 10. (sjetite se "Aquariusa") Kako uliti 3 litre vode, imajući posudu od 9 i 5 litara?

Problem 11. Malom Johnnyju matematika ide odlično. U svom dnevniku ima samo petice i četvorke, a ima ih još petica. Zbroj svih Vovočkinih ocjena iz matematike je 47. Koliko je Vovočkinih petica, a koliko četvorki?

Problem 12. Koschey Besmrtni postavio je rasadnik za uzgoj zmija Gorynych. U zadnjem leglu ima 17-glavu i 19-glavu zmiju. Ukupno ovo leglo ima 339 golova. Koliko je 17-glavih, a koliko 19-glavih zmija uzgojio Koshchei?

Odgovori: Diofant je živio 84 godine;

zadatak 2: 4 kutije po 17 kg i 2 kutije po 16 kg;

zadatak 6: Kupljeno je 7 olovaka i 8 hemijskih, tj. (7,2) je partikularno rješenje i y = 2 + 5n, x = 7 + 8n, gdje je nê Z opće rješenje;

zadatak 7: (-53; 106) - pojedinačno rješenje, x=4n-53, y=-7n+106 - opća rješenja, s n=14, x=3, y=8, odnosno 3 flomastera kupljene su kemijske i 8 olovaka;

zadatak 8: na primjer, platite 3 kovanice od 27 tugrika i dobijete sitniš od 5 kovanica od 16 tugrika;

zadatak 9: (2002; -1001) - partikularno rješenje, x=-5 n+2002, y=3n-1001 - opće rješenje, s n=350, y=49, x=252, tj. 252 noći, 3 bajke svaka i 49 noći po 5 bajki - ukupno 301 noć; najbrža opcija: 2 noći po tri priče i 199 noći po 5 priča - ukupno 201 noć; najduža opcija: 332 noći po 3 bajke i 1 noć po 5 bajki - ukupno 333 noći.

zadatak 10: npr. staklenkom od 9 litara 2 puta prelijte vodu i staklenkom od 5 litara 3 puta zagrabite;

zadatak 11: Mali Johnny dobio 7 petica i 4 četvorke;

Problem 12: 11 zmija sa 17 glava i 8 zmija sa 19 glava.

Algebarske nejednadžbe ili njihovi sustavi s racionalnim koeficijentima čija se rješenja traže u integralnim ili cijelim brojevima. U pravilu je broj nepoznanica u Diofantovim jednadžbama veći. Stoga su također poznate kao neodređene nejednakosti. U modernoj matematici se gornji koncept primjenjuje na algebarske jednadžbe, čija se rješenja traže u algebarskim cijelim brojevima nekog proširenja polja Q-racionalnih varijabli, polja p-adičnih varijabli itd.

Porijeklo ovih nejednakosti

Proučavanje Diofantovih jednadžbi nalazi se na granici između teorije brojeva i algebarske geometrije. Pronalaženje rješenja u cjelobrojnim varijablama jedan je od najstarijih matematičkih problema. Već početkom drugog tisućljeća pr. stari Babilonci uspjeli su riješiti sustave jednadžbi s dvije nepoznanice. Ova grana matematike najviše je procvala u Drevna grčka. Diofantova aritmetika (oko 3. st. po Kr.) značajan je i glavni izvor koji sadrži Različite vrste i sustavi jednadžbi.

U ovoj je knjizi Diofant predvidio niz metoda za proučavanje nejednakosti drugog i trećeg stupnja koje su u potpunosti razvijene u 19. stoljeću. Stvaranje teorije racionalnih brojeva kod ovog istraživača antičke Grčke dovelo je do analize logičkih rješenja neodređenih sustava, koja se sustavno prate u njegovoj knjizi. Iako njegov rad sadrži rješenja specifičnih Diofantovih jednadžbi, postoji razlog za vjerovanje da je također bio upoznat s nekoliko općih metoda.

Proučavanje ovih nejednakosti obično je povezano s ozbiljnim poteškoćama. Zbog činjenice da sadrže polinome s cjelobrojnim koeficijentima F (x, y1,…, y n). Na temelju toga izvedeni su zaključci da ne postoji jedinstveni algoritam kojim bi bilo moguće za bilo koji zadani x odrediti je li jednadžba F (x, y 1 ,…., y n) zadovoljena. Situacija je rješiva ​​za y 1 , …, y n . Primjeri takvih polinoma mogu se zapisati.

Najjednostavnija nejednakost

ax + by = 1, gdje su a i b relativno cijeli i prosti brojevi, postoji ogroman broj izvršenja za to (ako je x 0, y 0 formiran rezultat, tada je par varijabli x = x 0 + b n i y = y 0 -an , gdje je n proizvoljan, također će se smatrati da ispunjava nejednakost). Drugi primjer Diofantovih jednadžbi je x 2 + y 2 = z 2 . Pozitivna integralna rješenja ove nejednadžbe su duljine malih stranica x, y i pravokutni trokuti, kao i hipotenuze z s cjelobrojnim bočnim dimenzijama. Ovi brojevi poznati su kao Pitagorini brojevi. Sve trojke s obzirom na gore navedene jednostavne varijable dane su formulama x=m 2 - n 2 , y = 2mn, z = m 2 + n 2 , gdje su m i n cijeli i prosti brojevi (m>n>0 ).

Diofant u svojoj Aritmetici traži racionalna (ne nužno integralna) rješenja posebnih vrsta svojih nejednadžbi. Opću teoriju za rješavanje Diofantovih jednadžbi prvog stupnja razvio je C. G. Baschet u 17. stoljeću. Drugi znanstvenici u početkom XIX stoljeća uglavnom su proučavane takve nejednakosti tipa ax 2 +bxy + cy 2 + dx +ey +f = 0, gdje su a, b, c, d, e i f zajednički, nehomogeni, s dvije nepoznanice drugi stupanj. Lagrange je koristio kontinuirane razlomke u svojoj studiji. Razvio Gauss za kvadratne oblike opća teorija u pozadini nekih vrsta rješenja.

U proučavanju ovih nejednakosti drugog stupnja značajniji napredak postignut je tek u 20. stoljeću. A. Thue je otkrio da je Diofantova jednadžba a 0 x n + a 1 x n-1 y +…+a n y n =c, gdje su n≥3, a 0 ,…,a n ,c cijeli brojevi, a a 0 t n + … + a n ne može imati beskonačan broj cjelobrojnih rješenja. Međutim, Thuova metoda nije bila pravilno razvijena. A. Baker stvorio je učinkovite teoreme koji daju procjene učinka nekih jednadžbi ove vrste. B. N. Delaunay predložio je drugu metodu istraživanja primjenjivu na užu klasu ovih nejednakosti. Konkretno, oblik ax 3 + y 3 = 1 potpuno je rješiv na ovaj način.

Diofantove jednadžbe: metode rješavanja

Diofantova teorija ima mnogo pravaca. Stoga je dobro poznati problem u ovom sustavu pretpostavka da ne postoji netrivijalno rješenje Diofantovih jednadžbi x n + y n = z n ako je n ≥ 3 (Fermatovo pitanje). Proučavanje cjelobrojnih ispunjenja nejednakosti prirodna je generalizacija problema Pitagorinih trojki. Euler je dobio pozitivno rješenje Fermatovog problema za n = 4. Na temelju ovog rezultata, to se odnosi na dokaz nedostajućeg cijelog broja koji nije nula studija jednadžbe ako je n neparan prost broj.

Elaborat u vezi s odlukom nije dovršen. Poteškoće s njegovom implementacijom povezane su s činjenicom da jednostavna faktorizacija u prstenu algebarskih cijelih brojeva nije jedinstvena. Teorija djelitelja u ovom sustavu za mnoge klase prostih eksponenata n omogućuje potvrdu valjanosti Fermatova teorema. Tako, postojeće metode i metode, linearna Diofantova jednadžba s dvije nepoznanice je zadovoljena.

Vrste i vrste opisanih zadataka

Aritmetika prstenova algebarskih cijelih brojeva također se koristi u mnogim drugim problemima i rješenjima Diofantovih jednadžbi. Na primjer, takve su metode primijenjene pri ispunjavanju nejednakosti oblika N(a 1 x 1 +…+ a n x n) = m, gdje je N(a) norma od a, a x 1 , …, x n su pronađene integralne racionalne varijable. . Ova klasa uključuje Pellovu jednadžbu x 2- dy 2 =1.

Vrijednosti a 1, ..., a n koje se pojavljuju, ove jednadžbe su podijeljene u dvije vrste. Prvi tip - takozvani potpuni oblici - uključuje jednadžbe u kojima među a postoji m linearno neovisnih brojeva nad poljem racionalnih varijabli Q, gdje je m = , u kojima postoji stupanj algebarskih eksponenata Q (a1,…, a n) preko Q. Nepotpune vrste su one kod kojih je najveći broj a i manji od m.

Puni obrasci su jednostavniji, njihovo proučavanje je završeno, a sva rješenja mogu se opisati. Drugi tip - nepotpuna vrsta - je kompliciraniji, a razvoj takve teorije još nije dovršen. Takve se jednadžbe proučavaju pomoću Diofantovih aproksimacija, koje uključuju nejednakost F(x,y)=C, gdje je F(x,y) - polinom stupnja n≥3 nesvodljiv, homogen. Dakle, možemo pretpostaviti da je y i → ∞. Prema tome, ako je y i dovoljno velik, tada će nejednakost proturječiti teoremu Thuea, Siegela i Rotha, iz kojeg slijedi da je F(x,y)=C, gdje je F oblik trećeg stupnja ili višeg, nesvodljivo ne može imaju beskonačan broj rješenja.

Ovaj primjer je prilično uska klasa među svima. Na primjer, unatoč njihovoj jednostavnosti, x 3 + y 3 + z 3 = N, kao ni x 2 + y 2 + z 2 + u 2 = N nisu uključeni u ovu klasu. Proučavanje rješenja je prilično pažljivo proučavana grana Diofantovih jednadžbi, gdje je osnova predstavljanje kvadratnim oblicima brojeva. Lagrange je stvorio teorem koji kaže da ispunjenje postoji za sve prirodne N. Svaki prirodni broj može se prikazati kao zbroj tri kvadrata (Gaussov teorem), ali ne smije biti u obliku 4 a (8K-1), gdje je i k su nenegativni cijeli brojevi.

Racionalna ili integralna rješenja sustava Diofantovih jednadžbi tipa F (x 1 , …, x n) = a, gdje je F (x 1 , …, x n) kvadratni oblik s cjelobrojnim koeficijentima. Dakle, prema Minkowski-Hasseovom teoremu, nejednadžba ∑a ij x i x j = b gdje su a ij i b racionalni, ima integralno rješenje u realnim i p-adičkim brojevima za svaki prosti broj p samo ako je rješiva ​​u ovoj strukturi .

Zbog inherentnih poteškoća, proučavanje brojeva s proizvoljnim oblicima trećeg i višeg stupnja proučavano je u manjoj mjeri. Glavna metoda izvođenja je metoda trigonometrijskih suma. U ovom slučaju, broj rješenja jednadžbe zapisan je eksplicitno u smislu Fourierovog integrala. Nakon toga se metodom okruženja izražava broj ispunjenosti nejednakosti odgovarajućih kongruencija. Metoda trigonometrijskih zbrojeva ovisi o algebarskim značajkama nejednadžbi. postoji veliki broj elementarne metode za rješavanje linearnih Diofantovih jednadžbi.

Diofantska analiza

Grana matematike čiji je predmet proučavanje integralnih i racionalnih rješenja sustava algebarskih jednadžbi metodama geometrije iz istog područja. U drugoj polovici 19. stoljeća pojava ove teorije brojeva dovela je do proučavanja Diofantovih jednadžbi iz proizvoljnog polja s koeficijentima, a rješenja su se razmatrala ili u njemu ili u njegovim prstenovima. Sustav algebarskih funkcija razvijao se paralelno s brojevima. Osnovna analogija između njih dvojice, koju su isticali D. Hilbert, a posebno L. Kronecker, dovela je do jedinstvene konstrukcije različitih aritmetičkih pojmova, koji se obično nazivaju globalnim.

Ovo je posebno vidljivo ako su algebarske funkcije koje se proučavaju nad konačnim poljem konstanti jedna varijabla. Koncepti kao što su teorija klasnog polja, djelitelj i grananje i rezultati dobra su ilustracija gore navedenog. Ovo je gledište usvojeno u sustavu Diofantovih nejednakosti tek kasnije, a sustavno istraživanje ne samo numeričkih koeficijenata, već i koeficijenata koji su funkcije, počelo je tek 1950-ih. Jedan od odlučujućih čimbenika u ovom pristupu bio je razvoj algebarske geometrije. Istodobno proučavanje područja brojeva i funkcija, koji se javljaju kao dva jednako važna aspekta istog predmeta, ne samo da je dalo elegantne i uvjerljive rezultate, već je dovelo do međusobnog obogaćivanja dviju tema.

U algebarskoj geometriji, pojam raznolikosti koristi se za zamjenu neinvarijantnog skupa nejednakosti nad danim poljem K, a njihova rješenja se zamjenjuju racionalnim točkama s vrijednostima u K ili u njegovom konačnom proširenju. Prema tome, može se reći da je temeljni problem Diofantove geometrije proučavanje racionalnih točaka algebarskog skupa X(K), gdje su X određeni brojevi u polju K. Izvršenje cijelog broja ima geometrijsko značenje u linearnim Diofantovim jednadžbama.

Studije nejednakosti i opcije

U proučavanju racionalnih (ili integralnih) točaka na algebarskim varijetetima javlja se prvi problem, a to je njihovo postojanje. Hilbertov deseti problem je formuliran kao problem pronalaženja opće metode za rješavanje ovog problema. U procesu stvaranja precizne definicije algoritma, a nakon što je dokazano da slična izvršenja za veliki broj zadaci ne postoje, problem je stekao očigledan negativan rezultat, i većina zanimljivo pitanje je definicija klasa Diofantovih jednadžbi za koje postoji gornji sustav. Najprirodniji pristup, s algebarske točke gledišta, je takozvani Hasseov princip: početno polje K proučava se zajedno sa svojim kompletiranjem K v za sve moguće procjene. Budući da su X(K) = X(K v) nužan uvjet postojanja, a točka K uzima u obzir da skup X(K v) nije prazan za sve v.

Važnost je u tome što spaja dva problema. Drugi je puno jednostavniji, rješiv je poznatim algoritmom. U posebnom slučaju kada je raznolikost X projektivna, Hanselova lema i njezine generalizacije omogućuju daljnju redukciju: problem se može svesti na proučavanje racionalnih točaka nad konačnim poljem. Zatim odlučuje izgraditi koncept, bilo dosljednim istraživanjem ili učinkovitijim metodama.

Posljednje važno razmatranje je da su skupovi X(K v) neprazni za sve osim za konačni broj v, tako da je broj uvjeta uvijek konačan i oni se mogu učinkovito testirati. Međutim, Hasseovo načelo ne vrijedi za krivulje stupnjeva. Na primjer, 3x 3 + 4y 3 =5 ima točke u svim poljima p-adičnih brojeva iu sustavu, ali nema racionalnih točaka.

Ova je metoda poslužila kao polazište za konstruiranje koncepta koji opisuje klase glavnih homogenih prostora Abelovih varijeteta za izvođenje "odstupanja" od Hasseovog principa. Opisuje se u smislu posebne strukture koja se može povezati sa svakom mnogostrukošću (Tate-Shafarevich grupa). Glavna poteškoća teorije leži u činjenici da je teško dobiti metode za izračunavanje grupa. Ovaj koncept je također proširen na druge klase algebarskih varijeteta.

Potražite algoritam za ispunjavanje nejednakosti

Još jedna heuristička ideja korištena u proučavanju Diofantovih jednadžbi je da ako je broj varijabli uključenih u skup nejednakosti velik, tada sustav obično ima rješenje. Međutim, to je vrlo teško dokazati za svaki pojedinačni slučaj. Opći pristup problemima ove vrste koristi se analitičkom teorijom brojeva i temelji se na procjenama za trigonometrijske zbrojeve. Ova metoda je izvorno primijenjena na posebne vrste jednadžbi.

Međutim, naknadno je uz njegovu pomoć dokazano da ako je oblik neparnog stupnja F, u d i n varijablama i s racionalnim koeficijentima, tada je n dovoljno velik u usporedbi s d, tako da projektivna hiperploha F = 0 ima racionalnu točku. Prema pretpostavci Artin, ovaj rezultat je točan čak i ako je n > d 2 . Ovo je dokazano samo za kvadratne oblike. Slični problemi mogu se postaviti i za druga polja. Središnji problem Diofantove geometrije je struktura skupa cijelih ili racionalnih točaka i njihovo proučavanje, a prvo pitanje koje treba razjasniti je je li taj skup konačan. U ovom problemu situacija obično ima konačan broj izvršenja ako je stupanj sustava mnogo veći od broja varijabli. Ovo je glavna pretpostavka.

Nejednakosti na pravcima i krivuljama

Grupa X(K) može se prikazati kao izravni zbroj slobodne strukture ranga r i konačne grupe reda n. Od 1930-ih proučava se pitanje jesu li ti brojevi ograničeni na skupu svih eliptičkih krivulja nad danim poljem K. Ograničenost torzije n demonstrirana je sedamdesetih godina. Postoje krivulje proizvoljno visokog ranga u funkcionalnom slučaju. U numeričkom slučaju na ovo pitanje još uvijek nema odgovora.

Konačno, Mordellova pretpostavka kaže da je broj integralnih točaka konačan za krivulju roda g>1. U funkcionalnom slučaju, ovaj koncept je demonstrirao Yu. I. Manin 1963. godine. Glavni alat koji se koristi u dokazivanju teorema konačnosti u Diofantovoj geometriji je visina. Od algebarskih varijeteta dimenzija većih od jedan, Abelovi varijeteti, koji su višedimenzionalni analozi eliptičkih krivulja, najtemeljitije su proučavani.

A. Weyl je generalizirao teorem o konačnosti broja generatora grupe racionalnih točaka na Abelove varijetete bilo koje dimenzije (koncept Mordell-Weila), proširivši ga. U 1960-ima se pojavila pretpostavka Bircha i Swinnerton-Dyera, koja je poboljšala ovu i grupnu i zeta funkciju mnogostrukosti. Brojčani dokazi podupiru ovu hipotezu.

Problem odlučivosti

Problem pronalaženja algoritma koji se može koristiti za određivanje ima li bilo koja Diofantova jednadžba rješenje. Bitna značajka postavljenog problema je potraga za univerzalnom metodom koja bi bila prikladna za svaku nejednakost. Takva bi metoda također omogućila rješavanje gornjih sustava, budući da je ekvivalentna P21+⋯+P2k=0.p1= 0 , ... , PK= 0p = 0,...,pK = 0 ili p21+ ⋯ + P2K= 0 . n12+⋯+pK2=0. Problem pronalaženja takvih univerzalni način rješenja za otkrivanje linearne nejednakosti u cijelim brojevima stavio je D. Gilbert.

Početkom 1950-ih pojavile su se prve studije koje su imale za cilj dokazati nepostojanje algoritma za rješavanje Diofantovih jednadžbi. U to se vrijeme pojavila Davisova pretpostavka, koja kaže da svaki nabrojivi skup također pripada grčkom znanstveniku. Zato što su primjeri algoritamski neodlučivih skupova poznati, ali su rekurzivno prebrojivi. Slijedi da je Davisova pretpostavka istinita i da problem rješivosti ovih jednadžbi ima negativno ispunjenje.

Nakon toga, za Davisovu pretpostavku, ostaje dokazati da postoji metoda za transformaciju nejednadžbe koja također (ili nije) u isto vrijeme ima rješenje. Pokazalo se da je takva promjena Diofantove jednadžbe moguća ako ima navedena dva svojstva: 1) u bilo kojoj otopini ovog tipa v≤uu; 2) za bilo koji k postoji izvršenje u kojem postoji eksponencijalni rast.

Primjer linearne Diofantove jednadžbe ove klase dovršio je dokaz. Problem postojanja algoritma za rješivost i prepoznavanje ovih nejednakosti u racionalnim brojevima još uvijek se smatra važnim i otvorenim pitanjem koje nije dovoljno proučeno.