Да се задачи с параметървключват например търсенето на решения на линейни и квадратни уравнения в общ изглед, изследването на уравнението за броя на наличните корени в зависимост от стойността на параметъра.
Без да давате подробни дефиниции, разгледайте следните уравнения като примери:
y = kx, където x, y са променливи, k е параметър;
y = kx + b, където x, y са променливи, k и b са параметри;
ax 2 + bx + c = 0, където x са променливи, a, b и c са параметри.
Да се реши уравнение (неравенство, система) с параметър означава, като правило, да се реши безкраен набор от уравнения (неравенства, системи).
Задачите с параметър могат условно да бъдат разделени на два вида:
а)условието казва: решете уравнението (неравенство, система) - това означава, че за всички стойности на параметъра се намерят всички решения. Ако поне един случай остане неизследван, такова решение не може да се счита за задоволително.
б)изисква се да се посочат възможните стойности на параметъра, за който уравнението (неравенство, система) има определени свойства. Например има едно решение, няма решения, има решения, които принадлежат на интервала и т. н. При такива задачи е необходимо ясно да се посочи при каква стойност на параметъра е изпълнено изискваното условие.
Параметърът, тъй като е неизвестно фиксирано число, като че ли има специална двойственост. На първо място, трябва да се има предвид, че предполагаемата слава предполага, че параметърът трябва да се възприема като число. Второ, свободата за обработка на параметър е ограничена от неговата неизвестност. Така, например, операции на разделяне чрез израз, в който има параметър или извличане на корена равномерна степенот такъв израз изискват предварително проучване. Следователно трябва да се внимава при работа с параметъра.
Например, за да сравним две числа -6a и 3a, трябва да се разгледат три случая:
1) -6a ще бъде по-голямо от 3a, ако a е отрицателно число;
2) -6a = 3a в случай, когато a = 0;
3) -6a ще бъде по-малко от 3a, ако a е положително число 0.
Решението ще бъде отговорът.
Нека е дадено уравнението kx = b. Това уравнение е съкратено за безкраен набор от уравнения в една променлива.
При решаване на такива уравнения може да има случаи:
1. Нека k е произволно реално числоненула и b е произволно число от R, тогава x = b/k.
2. Нека k = 0 и b ≠ 0, оригиналното уравнение ще приеме формата 0 · x = b. Очевидно това уравнение няма решения.
3. Нека k и b са числа, равни на нула, тогава имаме равенството 0 · x = 0. Неговото решение е всяко реално число.
Алгоритъмът за решаване на този тип уравнения:
1. Определете "контролните" стойности на параметъра.
2. Решете оригиналното уравнение за x със стойностите на параметъра, които са определени в първия параграф.
3. Решете оригиналното уравнение за x със стойности на параметри, които се различават от избраните в първия параграф.
4. Можете да запишете отговора в следната форма:
1) когато ... (стойност на параметъра), уравнението има корени ...;
2) когато ... (стойност на параметъра), няма корени в уравнението.
Пример 1
Решете уравнението с параметър |6 – x| = а.
Решение.
Лесно е да се види, че тук a ≥ 0.
По правилото на модул 6 – x = ±a, ние изразяваме x:
Отговор: x = 6 ± a, където a ≥ 0.
Пример 2
Решете уравнението a(x - 1) + 2(x - 1) = 0 по отношение на променливата x.
Решение.
Нека отворим скобите: ax - a + 2x - 2 = 0
Нека напишем уравнението в стандартен вид: x(a + 2) = a + 2.
Ако изразът a + 2 не е нула, т.е. ако a ≠ -2, имаме решението x = (a + 2) / (a + 2), т.е. х = 1.
Ако a + 2 е равно на нула, т.е. a = -2, тогава имаме истинско равенство 0 x = 0, така че x е всяко реално число.
Отговор: x \u003d 1 за a ≠ -2 и x € R за a = -2.
Пример 3
Решете уравнението x/a + 1 = a + x по отношение на променливата x.
Решение.
Ако a = 0, тогава преобразуваме уравнението във формата a + x = a 2 + ax или (a - 1) x = -a (a - 1). Последното уравнение за a = 1 има формата 0 · x = 0, следователно, x е произволно число.
Ако a ≠ 1, тогава последното уравнение ще приеме формата x = -a.
Това решение може да бъде илюстрирано на координатната линия (Фиг. 1)
Отговор: няма решения за a = 0; x - произволно число при a = 1; x \u003d -a с a ≠ 0 и a ≠ 1.
Графичен метод
Помислете за друг начин за решаване на уравнения с параметър - графичен. Този метод се използва доста често.
Пример 4
Колко корени, в зависимост от параметъра a, има уравнението ||x| – 2| = а?
Решение.
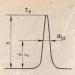
За да решим по графичен метод, ние изграждаме графики на функции y = ||x| – 2| и y = a (фиг. 2).
Чертежът ясно показва възможните случаи на местоположението на правата y = a и броя на корените във всеки от тях.
Отговор: уравнението няма да има корени, ако a< 0; два корня будет в случае, если a >2 и а = 0; уравнението ще има три корена в случай a = 2; четири корена - при 0< a < 2.
Пример 5
За което a уравнението 2|x| + |x – 1| = a има един корен?
Решение.
Нека начертаем графики на функции y = 2|x| + |x – 1| и y = a. За y = 2|x| + |x - 1|, разширявайки модулите по метода на празнината, получаваме:
(-3x + 1, при x< 0,
y = (x + 1, за 0 ≤ x ≤ 1,
(3x – 1, за x > 1.
На Фигура 3ясно се вижда, че уравнението ще има уникален корен само когато a = 1.
Отговор: а = 1.
Пример 6
Определете броя на решенията на уравнението |x + 1| + |x + 2| = a в зависимост от параметъра a?
Решение.
Графика на функцията y = |x + 1| + |x + 2| ще бъде прекъсната линия. Неговите върхове ще бъдат разположени в точките (-2; 1) и (-1; 1) (снимка 4).
Отговор: ако параметърът a е по-малък от единица, тогава уравнението няма да има корени; ако a = 1, тогава решението на уравнението е безкраен набор от числа от интервала [-2; -един]; ако стойностите на параметъра a са по-големи от един, тогава уравнението ще има два корена.
Имате ли някакви въпроси? Не знаете как да решавате уравнения с параметър?
За да получите помощта на преподавател - регистрирайте се.
Първият урок е безплатен!
сайт, с пълно или частично копиране на материала е необходима връзка към източника.
1. Системи линейни уравненияс параметър
Системите от линейни уравнения с параметър се решават по същите основни методи като конвенционалните системи от уравнения: методът на заместване, методът на добавяне на уравнения и графичният метод. Познания за графична интерпретация линейни системиулеснява отговора на въпроса за броя на корените и тяхното съществуване.
Пример 1
Намерете всички стойности на параметъра a, за които системата от уравнения няма решения.
(x + (a 2 - 3) y \u003d a,
(x + y = 2.
Решение.
Нека разгледаме няколко начина за решаване на този проблем.
1 начин.Използваме свойството: системата няма решения, ако съотношението на коефициентите пред x е равно на съотношението на коефициентите пред y, но не е равно на съотношението на свободните членове (a/a 1 = b/ b 1 ≠ c/c 1). тогава имаме:
1/1 \u003d (a 2 - 3) / 1 ≠ a / 2 или система
(и 2 - 3 = 1,
(а ≠ 2.
От първото уравнение a 2 \u003d 4, следователно, като се вземе предвид условието, че a ≠ 2, получаваме отговора.
Отговор: a = -2.
2 начин.Решаваме по метода на заместване.
(2 - y + (a 2 - 3) y \u003d a,
(x = 2 - y,
((a 2 - 3) y - y \u003d a - 2,
(x = 2 - y.
След като извадим общия фактор y от скобите в първото уравнение, получаваме:
((a 2 - 4) y \u003d a - 2,
(x = 2 - y.
Системата няма решения, ако първото уравнение няма решения, т.е
(и 2 - 4 = 0,
(a - 2 ≠ 0.
Очевидно е, че a = ±2, но като се вземе предвид второто условие се дава само отговорът с минус.
Отговор:а = -2.
Пример 2
Намерете всички стойности за параметър a, за който системата от уравнения има безкраен брой решения.
(8x + ay = 2,
(ax + 2y = 1.
Решение.
По свойство, ако съотношението на коефициентите при x и y е същото и е равно на съотношението на свободните членове на системата, тогава тя има безкраен брой решения (т.е. a / a 1 \u003d b / b 1 \u003d c / c 1). Следователно 8/a = a/2 = 2/1. Решавайки всяко от получените уравнения, откриваме, че \u003d 4 е отговорът в този пример.
Отговор:а = 4.
2. Системи от рационални уравнения с параметър
Пример 3
(3|x| + y = 2,
(|x| + 2y = a.
Решение.
Умножете първото уравнение на системата по 2:
(6|x| + 2y = 4,
(|x| + 2y = a.
Извадете второто уравнение от първото, получаваме 5|х| = 4 – а. Това уравнение ще има уникално решение за a = 4. В други случаи това уравнение ще има две решения (за a< 4) или ни одного (при а > 4).
Отговор: а = 4.
Пример 4
Намерете всички стойности на параметъра a, за които системата от уравнения има уникално решение.
(x + y = a,
(y - x 2 \u003d 1.
Решение.
Ще решим тази система с помощта на графичния метод. И така, графиката на второто уравнение на системата е парабола, повдигната нагоре по оста Oy с един единичен сегмент. Първото уравнение определя набора от линии, успоредни на правата y = -x (снимка 1). Фигурата ясно показва, че системата има решение, ако правата линия y \u003d -x + a е допирателна към параболата в точката с координати (-0,5; 1,25). Замествайки тези координати в уравнението на права линия вместо x и y, намираме стойността на параметъра a: 
1,25 = 0,5 + а;
Отговор: а = 0,75.
Пример 5
Използвайки метода на заместване, разберете при каква стойност на параметъра a системата има уникално решение.
(брадва - y \u003d a + 1,
(ax + (a + 2)y = 2.
Решение.
Изразете y от първото уравнение и го заместете във второто:
(y = ah - a - 1,
(ax + (a + 2) (ax - a - 1) = 2.
Привеждаме второто уравнение до вида kx = b, което ще има уникално решение за k ≠ 0. Имаме:
ax + a 2 x - a 2 - a + 2ax - 2a - 2 \u003d 2;
a 2 x + 3ax \u003d 2 + a 2 + 3a + 2.
Квадратният трином a 2 + 3a + 2 може да бъде представен като произведение на скоби
(a + 2)(a + 1), а отляво изваждаме x от скоби:
(a 2 + 3a) x \u003d 2 + (a + 2) (a + 1).
Очевидно, a 2 + 3a не трябва да е равно на нула, следователно,
a 2 + 3a ≠ 0, a(a + 3) ≠ 0, което означава a ≠ 0 и ≠ -3.
Отговор: a ≠ 0; ≠ -3.
Пример 6
Използвайки метода на графичното решение, определете при каква стойност на параметъра a системата има уникално решение.
(x 2 + y 2 = 9,
(y - |x| = a.
Решение.
Въз основа на условието изграждаме кръг с център в началото на координатите и радиус от 3 единични сегмента, именно този кръг задава първото уравнение на системата
x 2 + y 2 = 9. Второто уравнение на системата (y = |x| + a) е начупена линия. Като се използва фигура 2разглеждаме всички възможни случаи на местоположението му спрямо кръга. Лесно е да се види, че а = 3. 
Отговор: а = 3.
Имате ли някакви въпроси? Не знаете как да решавате системи от уравнения?
За да получите помощта на преподавател - регистрирайте се.
Първият урок е безплатен!
сайт, с пълно или частично копиране на материала е необходима връзка към източника.
AT последните годинина приемните изпити, на финалното тестване под формата на ЕГЭ се предлагат задачи с параметри. Тези задачи позволяват диагностициране на нивото на математическо и най-важното логическо мислене на кандидатите, способността за извършване на изследователски дейности, както и просто познаване на основните раздели училищен курсматематика.
Изгледът на параметъра като равна променлива се отразява в графичните методи. Всъщност, тъй като параметърът е „равен по права“ с променливата, тогава, разбира се, той може да „разпредели“ собствената си координатна ос. По този начин има координатна равнина. Отхвърлянето на традиционния избор на букви и за обозначаване на оси, определя един от най-ефективните методи за решаване на проблеми с параметри - „метод на домейн“. Наред с други методи, използвани при решаване на задачи с параметри, аз запознавам студентите си с графичните техники, като обръщам внимание на това как да разпознават „такива“ проблеми и как изглежда процесът на решаване на задача.
Повечето общи признаци, което ще помогне да се открият задачите, подходящи за разглеждания метод:
Задача 1. „За какви стойности на параметъра важи неравенството за всички?“
Решение. 1).
Нека разширим модулите, като вземем предвид знака на израза на подмодула: 
2). Записваме всички системи на получените неравенства:
а) 
б) 
в) 
ж) 
3). Нека покажем множеството точки, които удовлетворяват всяка система от неравенства (фиг. 1а).
четири). Комбинирайки всички области, показани на фигурата чрез щриховане, можете да видите, че неравенството не удовлетворява точките, лежащи вътре в параболите.
Фигурата показва, че за всяка стойност на параметъра можете да намерите областта, където лежат точките, чиито координати удовлетворяват първоначалното неравенство. Неравенството важи за всички, ако . Отговор: в.
Разглежданият пример е „отворен проблем“ - можете да разгледате решението на цял клас проблеми, без да променяте израза, разгледан в примера 
, в която вече са преодолени техническите трудности при зачертаването.
Задача. За какви стойности на параметъра уравнението няма решения? Отговор: в.
Задача. За какви стойности на параметъра уравнението има две решения? Запишете и двете решения, които намирате.
Отговор: тогава 
, 
;
Тогава 
; , тогава 
, .
Задача. При какви стойности на параметъра уравнението има един корен? Намерете този корен. Отговор: в в .
Задача. Решете неравенството.
(„Работни“ точки, разположени вътре в параболите).
, ; , няма решения;
Задача 2. Намерете всички стойности на параметрите а, за всяко от които системата от неравенства 
образува отсечка с дължина 1 на числовата права.
Решение. Пренаписваме оригиналната система в този вид 
Всички решения на тази система (двойки от формата) образуват определена област, ограничена от параболи 
и 
(Фигура 1).
Очевидно решението на системата от неравенства ще бъде отсечка с дължина 1 за и за . Отговор: ; .
Задача 3. Намерете всички стойности на параметъра, за които множеството решения на неравенството 
съдържа числото и също така съдържа два сегмента с дължина, които нямат общи точки.
Решение. Според значението на неравенството ; пренаписваме неравенството, като умножаваме и двете му части по (), получаваме неравенството:
, ,
(1)
Неравенството (1) е еквивалентно на комбинацията от две системи:
(фиг. 2).
Очевидно интервалът не може да съдържа сегмент с дължина. Това означава, че в интервала се съдържат два непресичащи се отсечки с дължина Това е възможно за , т.е. в . Отговор: .
Задача 4. Намерете всички стойности на параметъра, за всяка от които наборът от решения на неравенството 
съдържа сегмент с дължина 4 и също се съдържа в някакъв сегмент с дължина 7.
Решение. Нека извършим еквивалентни трансформации, като вземем предвид, че и .
, ,
; последното неравенство е еквивалентно на комбинацията от две системи:
Нека покажем областите, които отговарят на тези системи (фиг. 3).
1) За набор от решения е интервал с дължина по-малка от 4. За набор от решения е обединението на два интервала . Само един интервал може да съдържа отсечка с дължина 4 . Но тогава , и съюзът вече не се съдържа в нито един сегмент с дължина 7. Следователно, такива не отговарят на условието.
2) множеството от решения е интервалът . Той съдържа сегмент с дължина 4 само ако дължината му е по-голяма от 4, т.е. в . Той се съдържа в сегмент с дължина 7 само ако дължината му не е по-голяма от 7, т.е. в , тогава . Отговор: .
Задача 5. Намерете всички стойности на параметъра, за които множеството решения на неравенството 
съдържа числото 4 и също така съдържа два непресичащи се сегмента с дължина 4 всеки.
Решение. По условията. Умножаваме и двете части на неравенството по (). Получаваме еквивалентно неравенство, в което групираме всички термини от лявата страна и го трансформираме в продукт:
, ,
, 
.
От последното неравенство следва:
1) 
2)
Нека покажем областите, които отговарят на тези системи (фиг. 4).
а) За , получаваме интервал, който не съдържа числото 4. За , получаваме интервал, който също не съдържа числото 4.
б) За , Получаваме обединението на два интервала. Непресичащи се сегменти с дължина 4 могат да бъдат разположени само в интервала . Това е възможно само ако дължината на интервала е по-голяма от 8, т.е. За такива е изпълнено и друго условие: . Отговор: .
Задача 6. Намерете всички стойности на параметъра, за които има множество решения на неравенството 
съдържа някакъв сегмент с дължина 2, но не съдържа
няма сегмент с дължина 3.
Решение. Според смисъла на задачата умножаваме и двете части на неравенството по , групираме всички термини от лявата страна на неравенството и го преобразуваме в продукт:
, 
. От последното неравенство следва:
1) 
2) 
Нека покажем площта, която отговаря на първата система (фиг. 5).
Очевидно условието на задачата е изпълнено, ако 
. Отговор: .
Задача 7. Намерете всички стойности на параметъра, за които множеството решения на неравенството 1+ 
се съдържа в някакъв сегмент с дължина 1 и в същото време съдържа някакъв сегмент с дължина 0,5.
Решение. едно). Посочете ODZ на променливата и параметъра: 
2). Нека пренапишем неравенството във формата
, 
,
(един). Неравенството (1) е еквивалентно на комбинацията от две системи:
1) 
2) 
Като се вземе предвид ODZ, решенията на системите изглеждат така:
а) 
б) 
(фиг. 6).
а) 
б)
Нека покажем площта, съответстваща на системата а) (фиг. 7).Отговор: .
Задача 8. Шест числа образуват нарастваща аритметична прогресия. Първият, вторият и четвъртият член на тази прогресия са решения на неравенството 
, и останалото
не са решения на това неравенство. Намерете множеството от всички възможни стойности на първия член на такива прогресии.
Решение. I. Намерете всички решения на неравенството
а). ODZ: 
, т.е.
(в решението взехме предвид, че функцията се увеличава с ).
б). Върху неравенството на ODZ 
е еквивалентно на неравенството 
, т.е. 
, Какво дава:
1). 
2). 
Очевидно решението на неравенството служи като набор от ценности 
.
II. Нека илюстрираме втората част на задачата за условията на нарастваща аритметична прогресия с фигура ( ориз. осем , където е първият член, е вторият и т.н.). Забележи това:
Или имаме система от линейни неравенства:
Нека го решим графично. Ние изграждаме линии и , както и линии
Тогава, .. Първият, вторият и шестият член на тази прогресия са решения на неравенството 
, а останалите не са решения на това неравенство. Намерете множеството от всички възможни стойности на разликата на тази прогресия.
1. Задача.
При какви стойности на параметъра ауравнението ( а - 1)х 2 + 2х + а- 1 = 0 има точно един корен?
1. Решение.
В а= 1 уравнението има вида 2 х= 0 и очевидно има един корен х= 0. Ако а№ 1, то това уравнение е квадратно и има единичен корен за тези стойности на параметъра, за които дискриминантът на квадратния тричлен нула. Приравнявайки дискриминанта към нула, получаваме уравнение за параметъра а
4а 2 - 8а= 0, откъдето а= 0 или а = 2.
1. Отговор:уравнението има един корен при аО(0; 1; 2).
2. Задача.
Намерете всички стойности на параметрите а, за което уравнението има два различни корена х 2 +4брадва+8а+3 = 0.
2. Решение.
Уравнението х 2 +4брадва+8а+3 = 0 има два различни корена, ако и само ако д =
16а 2 -4(8а+3) > 0. Получаваме (след намаляване с общ коефициент 4) 4 а 2 -8а-3 > 0, откъдето
2. Отговор:
| а O (-Ґ ; 1 - | C 7 2 |
) И (1 + | C 7 2 |
; Ґ ). |
3. Задача.
Известно е, че
е 2 (х) = 6х-х 2 -6.
а) Графично изобразете функцията е 1 (х) при а = 1.
б) На каква стойност афункционални графики е 1 (х) и е 2 (х) имат една обща точка?
3. Решение.
3.a.Да се трансформираме е 1 (х) по следния начин
Графиката на тази функция а= 1 е показано на фигурата вдясно.
3.bВеднага отбелязваме, че функцията графики г =
kx+би г = брадва 2 +bx+° С
(а 0) се пресичат в една точка, ако и само ако квадратно уравнение kx+б =
брадва 2 +bx+° Сима един корен. Използване на View е 1 от 3.a, приравняваме дискриминанта на уравнението а = 6х-х 2 -6 до нула. От уравнение 36-24-4 а= 0 получаваме а= 3. Правете същото с уравнение 2 х-а = 6х-х 2 -6 намери а= 2. Лесно е да се провери дали тези стойности на параметрите удовлетворяват условията на задачата. Отговор: а= 2 или а = 3.
4. Задача.
Намерете всички стойности а, при което множеството от решения на неравенството х 2 -2брадва-3а i 0 съдържа сегмента .
4. Решение.
Първата координата на върха на параболата е(х) =
х 2 -2брадва-3ае равно на х 0 =
а. От имоти квадратична функциясъстояние е(х) i 0 на интервала е еквивалентно на съвкупността от три системи
има точно две решения?
5. Решение.
Нека пренапишем това уравнение във формата х 2 + (2а-2)х - 3а+7 = 0. Това е квадратно уравнение, то има точно две решения, ако неговият дискриминант е строго по-голям от нула. Изчислявайки дискриминанта, получаваме, че условието за наличието на точно два корена е изпълнението на неравенството а 2 +а-6 > 0. Решавайки неравенството, намираме а < -3 или а> 2. Първото от неравенствата очевидно е решения в естествени числаняма, а най-малкото естествено решение на второто е числото 3.
5. Отговор: 3.
6. Задача (10 клетки)
Намерете всички стойности а, за което графиката на функцията или, след очевидни трансформации, а-2 = |
2-а| . Последното уравнение е еквивалентно на неравенството ааз 2.
6. Отговор: ао)
