Міністерство освіти і науки Самарської області

Державне автономне освітня установадодаткового професійної освіти(підвищення кваліфікації) спеціалістів

САМАРСЬКИЙ ОБЛАСНИЙ ІНСТИТУТ ПІДВИЩЕННЯ КВАЛІФІКАЦІЇ

І ПЕРЕПІДГОТОВКИ ПРАЦІВНИКІВ ОСВІТИ

Підсумкова робота

На курсах підвищення кваліфікації

За ІОЧ СБ

«Методичні особливості навчання розв'язанню задач із параметром в умовах переходу до нових освітніх стандартів»

(15.06 – 19.06.2015р.)

Проектування багаторівневої системи завдань із параметром по темі:

«Похідна»

Виконала:

Валієва Ф.Г.,

вчитель математики

ДБОУ ЗОШ ім. М.К. Овсяннікова

с. Ісакли

Самара

2015 р.

ПОЯСНЮВАЛЬНА ЗАПИСКА

ПІБ (повністю)

Валієва Фанузя Галимзянівна

Місце роботи

ДБОУ ЗОШ ім. М.К. Овсяннікова с.Ісакли,

Ісаклінського району, Самарської області

Посада

Вчитель математики

Предмет

Математика

Клас

Цілі:

1. реалізація вимог ФГОС ТОВ щодо теми:«Похідна»

   Узагальнення та систематизація знань та способів діяльності на тему «Похідна»; формування умінь вирішувати завдання із параметрами.

   Розвиток дослідницької та пізнавальної діяльності.

Концепція духовно-морального розвитку та виховання особистості громадянина Росіїє методологічною основою розробки та реалізації федерального державного освітнього стандарту загальної освіти.

Федеральний державний освітній стандартосновної загальної освіти про шкільному курсіматематики.

В основі Стандарту лежитьсистемно-діяльнісний підхід.

Стандарт встановлює вимоги до результатів освоєння основний освітньої програмиосновної загальної освіти:

особистісним;

метапредметним;

предметним.

Завдання:

- Навчальні: аналізувати та осмислювати текст завдання, самостійне виділення та формулювання пізнавальної мети, переформулювати умову, будувати логічний ланцюжок міркувань, критично оцінювати отриману відповідь, усвідомлене і довільне побудова мовного висловлювання, вибір найбільш ефективного способувирішення завдань, постановка та формулювання проблеми, висування гіпотез та їх обґрунтування, смислове читання;

-розвиваючі: цілепокладання, планувати свою діяльність залежно від конкретних умов; рефлексія способів та умов дії, контроль та оцінка процесу та результатів діяльності, саморегуляція,через вирішення завдань, розвивати творчу та розумову діяльність учнів, інтелектуальні якості: здатність до “бачення” проблеми, оціночних дій, самостійності, гнучкості мислення;

-виховні: смислоутворення, вміння слухати та вступати в діалог, брати участь у колективному обговоренні проблем, виховувати відповідальність та акуратність.

Завдання з параметрами - це нестандартні завдання, тобто.незвичайні як за постановкою та змістом, так і за методами рішення. Роль такихзавдань, їх важливість та користь для розвитку логічного мислення, інтуїції,творчих здібностей учнів, формування у них високої математичноїкультури дуже великі. Відомо, що педагоги стикаються із серйознимиметодичними проблемами при навчанні вирішення таких завдань, незважаючи на наявність,досить великої кількостінавчальних посібників та журнальних статей. Причина цього досить очевидна: основна стратегія математичної освіти в школі - це розвиток умінь і навичок вирішення певного набору стандартних завдань, які здебільшого пов'язані з технікою алгебраїчних перетворень. Рівняння (нерівності) з параметрами ставляться до іншого типу завдань – завдань, на вирішення яких необхідно передусім вміння проводити – часом досить розгалужені – логічні побудови та дослідження.

Вирішення задач з параметрами вимагає дослідження, навіть якщо це слово не згадане у формулюванні завдання. Недостатньо механічного застосування формул, необхідне розуміння закономірностей, наявність навички аналізу конкретного випадку на основі відомих загальних властивостейоб'єкта, системність і послідовність у вирішенні, вмінні об'єднати аналізовані окремі випадки в єдиний результат. Цим зумовлені труднощі, які у учнів під час вирішення таких завдань.

Нині досить стала вельми поширеною отримала ідея поєднання навчання розв'язання завдань із навчанням їх конструюванню. Під конструюванням завдання – ми розумітимемо процес створення нового завдання. В основі конструювання завдання лежить уміння складати квадратний тричлен. При цьому використовуються різні прийоми: аналогія, варіювання коефіцієнтів квадратного тричлена, варіювання нової змінної, варіювання вимог задач. Як коефіцієнти і нової змінної можуть бути складніші функції. Тим самим можна використовувати такий квадратний тричлен, який допоможе в організації повторення більше складних функцій: показовою, логарифмічною, тригонометричною. З одного боку потрібно знати властивості квадратного тричлена, з другого боку повторюються властивості функції, цим досягається комбінованість завдання.

Вибір завдання з параметрами для навчання їх вирішенню та конструюванню можна пояснити такими обставинами:

під час вирішення завдань із параметрами відбувається повторення, як наслідок, глибше, міцне засвоєння програмних питань;

розв'язання задач із параметрами розширює математичний кругозір, дає нові підходи до розв'язання задач;

відбувається розвиток математичного, логічного мислення, вміння аналізувати, порівнювати, узагальнювати;

набувають навичок до дослідницьких робіт;

допомога при підготовці до іспитів;

відбувається формування таких якостей особистості, як працьовитість, цілеспрямованість, посидючість, сила волі, точність.

Формовані УУД у рамках ФГОС під час вирішення завдань із параметрами:

Етапи вирішення завдань

УУД, що формуються

Аналіз умови(Введення буквених позначень)

• цілепокладання;

  виділення суттєвої інформації;

  формулювання завдання та прогнозування способів розв'язання;

  абстрагування;

  аналогія;

  класифікація (типологізація);

  знакосимволічні дії.

Схематичний запис умови завдання у вигляді таблиці, схеми, графаіз введеними літерними позначеннями

• планування;

  систематизація;

  знакосимволічні дії;

  моделювання.

Складання моделі(Пошук аналога, залучення з математики чи фізики відомого закону)

• створення способу вирішення залачі;

  коригування умови;

  моделювання у графічному вигляді.

Рішення рівняння, системи та ін.(Пошук невідомого)

• аналіз та виявлення суттєвої інформації;

  виведення наслідків;

  побудова ланцюга міркувань;

  висування та перевірка гіпотез;

  перетворення моделі.

Інтерпретація моделі(перевірка та оцінка рішень, коріння)

• аналіз;

  виведення наслідків;

  конкретизація;

  знакосимволічну дію (інтерпретація).

Дослідження(Узагальнення задачі або способу її вирішення для видозмінених умов, інші підходи до вирішення)

• аналіз;

  синтез;

  пошук аналогів;

  побудова ланцюга міркувань;

  вміння стисло передати зміст;

  вміння схеми, символи, моделі;

  створення способів розв'язання проблем пошукового, творчого характеру.

Рефлексія

• смислоутворення;

  планування;

  контроль;

  корекція;

  оцінка;

  вольова саморегуляція;

  готовність до саморозвитку, самоосвіти;

  вміння самостійно визначати цілі навчання;

  ставити та формулювати для себе нові завдання;

  розвивати мотиви та інтереси своєї освітньої діяльності.

Багаторівнева система завдань

У основі методики навчання з урахуванням багаторівневої системи завдань лежить поетапне освоєння блоків її матриці. Основна особливість цієї методики у тому, що у кожному рівні, тобто. при освоєнні відповідного стовпця матриці, учень щоразу стикається з усіма трьома видами навчальних ситуацій, що виникають під час вирішення завдань.

Багаторівнева система завдань для кожної теми курсу формується за допомогою її матричного уявлення, шляхом виділення ранжованого переліку базових елементів змісту освіти та відповідних їм базових завдань, – з одного боку, та рівнів навченості, що відображають уміння вирішувати знайомі, модифіковані та незнайомі завдання, – з іншого .

Така матриця системи завдань теми містить 3 рядки, що відповідають трьом типам навчальних ситуацій, що виникають при вирішенні завдань, таN стовпців, що відбивають кількість базових завдань теми. Подібне табличне (матричне) уявлення системи завдань теми допомагає здійснити повноцінне наповнення на кожному рівні її математичного та діяльнісного (формування УУД) компонентів і цим реалізувати.критерії предметної та діяльнісної повноти (маючи на увазі пізнавальні УУД) формується система навчальних завдань. При цьому якщо базові завдання виконують у системі роль своєрідних інтеграторів предметно-змістовної компоненти, то при проектуванні та реалізації процесу навчання аналогічну роль мають відігравати універсальні навчальні дії(загальні методи та прийоми діяльності) у виділених ситуаціях.

Навчальна діяльність під час вирішення завдань, які входять у перший рядок матриці, носить репродуктивний характер (використовуються такі загальнонавчальні дії, як класифікація, підведення під поняття, виведення наслідків, дії, побудова логічного ланцюга міркувань, доказ тощо.). Завдання, що використовуються при цьому, відрізняютьсяявними зв'язками між даними та шуканими (відомими та невідомими) елементами. Учень ідентифікує (розпізнає знайомі завдання у ряді подібних), відтворює вивчені способи чи алгоритми дій, застосовує засвоєні знання на практичному плані деякого відомого класу завдань і отримує нову інформацію з урахуванням застосування засвоєного зразка діяльності

При вирішенні завдань другого рядка репродуктивна навчальна діяльністьпоєднується з реконструктивною, в якій зразки діяльності не просто відтворюються по пам'яті, а реконструюються в дещо видозмінених умовах (тут виявляються такі загальнонавчальні дії, як виділення та формулювання пізнавальної мети, пошук та виділення необхідної інформації, знаково-символічні дії, включаючи математичне моделювання, Структурування знання).

Нарешті, під час вирішення завдань третього рядка навчальна діяльність має дослідницький творчий характер. Учень повинен вміти орієнтуватися у нових ситуаціях та виробляти принципово нові програми дій (висувати гіпотезу, перевіряти: обґрунтовувати чи спростовувати, висувати нову і т.д., здійснювати дослідницьку діяльність). Розв'язання завдань відповідного блоку вимагає від учня володіння великим фондом відпрацьованих алгоритмів, що швидко розгортаються; вміння оперативно перекодувати інформацію із знаково-символічної форми у графічну та, навпаки, з графічної у знаково-символічну; системного бачення курсу Разом з тим, воно не просто передбачає використання старих алгоритмів у нових умовах та зростання технічної складності, а відрізняється неочевидністю застосування та комбінування вивчених алгоритмів. Завдання цього рівня мають ускладнену логічну структуру та характеризуються наявністюлатентних зв'язків між даними та шуканими елементами. Такі завдання зазвичай пропонуються як найважчі на вступних іспитах до вузів з високими вимогами до математичної підготовки абітурієнтів та у завданнях 17,18, 20, 21КІМів ЄДІ.

Багаторівнева система завдань на тему «Похідна»

№ п/п

Назва задачі

Тип завдання

Обчислення похідної за визначенням.

ЗЗ

МОЗ

НЗ

Знаходження похідних суми, твору, приватної функції

ЗЗ

МОЗ

НЗ

Дослідження монотонності функції

ЗЗ

функція зростає на всій числовій прямій?

МОЗ

При яких значеннях параметрафункція убуває всім значень ?

НЗ

Знайти множину всіх чисел a, при кожному з яких функціяf(x) = sin 2 x – 8(a + 1) sinx + (4 a 2 + 8 a – 14) xє зростаючою на всій числовій прямій і не має при цьому критичних точок.

Знаходження точок екстремуму

ЗЗ

має одну стаціонарну точку?

МОЗ

Визначте, за якого значення параметра максимум функціїдорівнює 9

НЗ

За яких значень параметра a функціяf(x) = (a 2 – 3 a + 2) (cos 2 – sin 2 + (a – 1) x + sin1 немає критичних точок?

Знаходження найбільшого та найменшого значень безперервної функції на проміжку, що диференціюється на інтервалі

ЗЗ

З'ясувати, за яких значень параметраа найменше значенняфункціїy = x 2 -12 x + a на відрізку дорівнює нулю.

МОЗ

При якому значенні параметра найменше значення функціїодно

НЗ

При яких значеннях параметрафункція приймає значення менше 5 для будь-яких

Повне дослідженнята побудова графіка

ЗЗ

3 + 3x 2

МОЗ

При якому значенні параметра a мінімум функції f(x) = ax 2 - 6ax + a 2 - 9 дорівнює 1?

НЗ

Рівняння щодо графіку функції в даній точці

ЗЗ

При яких значеннях параметрапряма є дотичною до графіка функції ?

МОЗ

При яких значеннях параметра щодо графіку функції відсікає від першої чверті рівнобедрений трикутник площею

НЗ

При яких значеннях параметра дотичні до графіку функції , проведені у точках його перетину з віссю, утворюють між собою кут

Застосування похідної для вирішення задач з геометрії, фізики та економіки

ЗЗ

Які мають бути сторони прямокутника з периметромPщоб його площа була максимальною?

МОЗ

Вікно має форму прямокутника, обмеженого зверху півколом (рисунок 3). Периметр вікна дорівнює P. Визначити радіус півкола R, при якому площа вікна є найбільшою.

НЗ

Картина висотою a підвішена на стіні таким чином, що її нижній край вище за рівень очей спостерігача наh одиниць. На якій відстані x від стіни повинен бути спостерігач, щоб кут огляду картини був найбільшим (рисунок 7a)?

Рішення

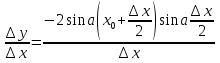
Рішення :

1. Функція f(x) зменшується для всіх значень x, якщо похідна

f′(x) = 6ax 2 + 18ax + 30a = 6a(x 2 + 3x + 5)< 0

всім x.

2. Звідси знаходимо, що a< 0.

3 . Відповідь: a (–∞; 0).

1. Знайти безліч всіх чисел a, при кожному з яких функція f(x) = sin 2x – 8(a + 1)sinx + (4a 2 + 8a – 14)x є зростаючою на всій числовій прямій і не має при цьому критичних точок.

1. При будь-якому фіксованому a дана функція диференційована в кожній точці числової прямої.

2. Оскільки функція f(x) зростає, то в кожній точці x повинна виконуватись нерівність f′(x) ≥ 0.

3. Оскільки, крім того, f(x) не має критичних точок, то за будь-якого x має бути виконана нерівність f′(x) ≠ 0.

4. Таким чином, якщо функція задовольняє умову задачі, то за всіх x має бути виконана нерівність f′(x) > 0.

5. З іншого боку, якщо за всіх x виконано нерівність f′(x) > 0, то функція, очевидно, не має критичних точок і зростає.

6. Знайдемо похідну цієї функції:

f′( x) = 2 cos 2 x – 8( a + 1) cosx + 4 a 2 + 8 a – 14.

Тепер завдання можна переформулювати так: знайти всі значення параметра a, при кожному з яких для будь-якого х виконано нерівність

cos 2x – 4(a + 1) cos x + 2a 2 + 4a - 7> 0.(1)

7. Враховуючи, що cos 2x = 2 cos 2 x – 1, і вважаючи cos x = t, де –1 ≤ t ≤ 1, перепишемо нерівність (1) таким чином:

2t 2 – 1 – 4(a + 1)t + 2a 2 + 4a - 7 > 0,

або

t 2 - 2(a + 1)t + a 2 + 2a - 4 > 0. (2)

8. Позначивши функцію в лівій частині нерівності (2) через ϕ(t), дамо нове формулювання вихідного завдання: знайти всі значення a, при кожному з яких найменше значення функції ϕ(t) на відрізку [–1; 1] позитивно.

9. Похідна ϕ′(t) = 2t – 2(a + 1) перетворюється на нуль при t 0 = a + 1.

10. Найменше значення функції ϕ(t) на відрізку [-1; 1] є:

ϕ (-1) = a 2 + 4a - 1,якщоa + 1 ≤ -1;

ϕ (a + 1) = -5,якщо –1 < a + 1 < 1;

ϕ(1) = a 2 – 5, якщо a + 1 ≥ 1.

11. Оскільки найменше значення функції ϕ(t) на відрізку [-1; 1] має бути позитивно, то значення параметра a, що задовольняють умові задачі, належать двом проміжкам: a ≤ –2 та a ≥ 0.

12. Якщо a ≤ –2, то значення параметра a задовольняють нерівності a 2 + 4a - 1> 0.

13. Якщо a ≥ 0, шукані значення параметра a задовольняють нерівності a 2 – 5 > 0.

14. Отже, безліч значень, що шукаються a є об'єднання рішень двох систем нерівностей:

(3)

а ≥ 0

а 2 -5 > 0 (4)

15. Безліч рішень системи (3) є проміжок –∞< a < –2 –√5 , а множество решений системы (4)- промежуток a >√5 .

16. Відповідь: a (–∞; –2 –√5) (√5; +∞).

1. Так як дана функція диференційована на всій числовій прямій, то критичними точками функції f(x) є точки, в яких похідна f′(x) = 0.

2. У разі маємо f′(x) =(a – 1)(a – 2) (–sin+ (a - 1).

3. Очевидно, що якщо a = 1, то f '(x) = 0 за будь-якого x R, тобто.

для заданої функціїкожна точка x R є критичним.

4. Припустимо, що a 1. Тоді рівняння f′(x) = 0 набуде вигляду

(a – 2) sin = 2. (1)

Звідси випливає, що й |a – 2|< 2, т. е. если a (0; 1) (1; 4),

то рівняння (1) немає коренів і, отже, при зазначених значеннях a функція f(x) немає критичних точок.

5 . Відповідь: a (0; 1) (1; 4).

Найменше значення чисельника та найбільше значеннязнаменника досягається за різних значень х. Тому знаходження найменшого значення функції зручно використовувати похідну. Перепишемо нерівність у вигляді

Деt=3- cos 2 x, t

Знайдемо найменше значення функціїf( t) = , на відрізку. Оскільки похіднаf "( t) = негативна приtтоfзменшується і набуває найменшого значення приt=3, f найм. = f(3) = .

Відповідь:a

При якому найменшому натуральному k рівняння x 3 + 3x 2 - 45x + k = 0 має рівно один корінь?

1. Побудуємо ескіз графіка функції y 1 = x 3 + 3x 2 – 45x і визначимо найменше натуральне значення k, коли цей графік перетинає пряму y 2 = -k рівно в одній точці.

2. а) D(y 1 ) = R;

б) у 1 / = 3x 2 + 6x - 45; 1 / в інтервалах (–∞; –5), (–5; 3) та (3; +∞) ілюструє рис. 1. На рис. 2 дано схематичне зображення графіка функції y 1 .

3. Очевидно, що це рівняння має єдине рішенняякщо -k > 175 або -k< –81, т. е. k < –175 или k >81. Найменше натуральне значення k дорівнює 82.

4. Відповідь: k = 82.

При якому значенні параметра a мінімум функції f(x) = ax2 – 6ax + a2 – 9 дорівнює 1?

1. f '(x) = -6x 2 + 6x + 12.

2. y′ = 0 при x 1 = 2.

6. Відповідь: a = 2.

При якому значенні параметра a мінімум функції f(x) = -2x 3 + 3x 2 + 12x + 4a дорівнює 1?

За яких значень параметра a пряма y=ax-2 є дотичною до графіка функції y=1+ln⁡ x?

При яких значеннях параметра a щодо графіку функції y=a-x^2 відсікає від першої чверті рівнобедрений трикутник площею 9/32

так як , за умовою дотична повинна перетинати функцію вчверті, значить. Трикутник рівнобедрений і прямокутний отже інші кути рівні, алезвідки дотична набуває вигляду точка торкання дотичної з графіком по осі абсцис дорівнює . за формулою щодо графіку тому що площа трикутника повинна дорівнювати , то так як чверть.Звідки

При яких значеннях параметра a дотичні до графіка функції y=4x^2-|a|x, проведені у точках його перетину з віссю x, утворюють між собою кут 60°

Якими мають бути сторони прямокутника з периметром P, щоб його площа була максимальною?

Вікно має форму прямокутника, обмеженого зверху півколом (рисунок 3). Периметр вікна дорівнює P. Визначити радіус півкола R, при якому площа вікна є найбільшою.

Картина висотою a підвішена на стіні таким чином, що її нижній край вище за рівень очей спостерігача наh одиниць. На якій відстані x від стіни повинен бути спостерігач, щоб кут огляду картини був найбільшим (рисунок 7a)?

Література

Азаров А.І., Барвенов С.А., Федосенко В.С.Методи вирішення завдань із параметрами. Математика для старшокласників. Мінськ: "Аверсев", 2003.

В.С. Висоцький, Завдання з параметрами для підготовки до ЄДІ

Горнштейн П.І., Полонський В.Б. Якір М.С. Завдання із параметрами. - К.: РІА "Текст"; МП "ОКО", 1992. -290 с.

Качалова Г. А. Про необхідність включення змістовно-методичної лінії «Завдання з параметрами» у навчальний модуль «Основи математики» //Materiał yMię dzynarodowejNaukowi- PraktycznejkonferencjiPostę pó wwnauce. Nowepoglą dy, problemy, innowacje. 29.07.2012. - 31.07.2012. Część 2. - Łódź, 2012. - С. 67-70.

Козко А. І., Панферов В. С, Сергєєв І. Н., Чирський В. Г. ЄДІ 2011. Математика. Завдання С5. Завдання з параметром/За ред. А. Л. Семенова та І. В.Ященко. - М: МЦНМО, 2011.-144 с.

Родіонов Є.М. Розв'язання задач із параметрами. М: МП «Русь-90», 1995

Вищої категорії

Санкт-Петербург

2006
Вступ

Вирішення завдань з параметрами є, мабуть, найважчим розділом курсу елементарної математики, причому як для школярів і абітурієнтів, а й у вчителів.

Це пояснюється тим, що основна стратегія математичної освіти в школі - це розвиток умінь і навичок вирішення певного набору стандартних завдань, здебільшого пов'язаних з технікою алгебраїчних перетворень. При розв'язанні задач з параметрами доводиться розглядати різні випадки, при кожному з яких методи розв'язання задачі часто суттєво відрізняються один від одного. При цьому слід чітко і послідовно стежити за збереженням рівносильності розв'язуваних рівнянь і нерівностей з урахуванням області визначення виразів, що входять до рівняння або нерівність, а також враховувати здійснюваність операцій. До того ж необхідно, перш за все, уміння виробляти – часом досить розгалужені логічні побудови. Крім того, арсенал стандартних перетворень має бути суттєво поповнений деякими специфічними перетвореннями.

Завдання з параметрами є дуже широке поле для повноцінної математичної діяльності, відкривають перед учнями значну кількість евристичних прийомів загального характеру, цінних для математичного розвитку особистості, які застосовуються в дослідженнях і на будь-якому іншому математичному матеріалі.

Завдання з параметрами показують, наскільки далеко відірвалася практика вступних іспитів від школи, наскільки помітні вимоги до випускника школи та вимоги, які пред'являє до абітурієнта ВНЗ.

Квадратична функція.

Будучи основним у шкільному курсі математики, квадратична функція, природно формує великий клас завдань із параметрами, різноманітних формою і змістом, але об'єднаних загальної ідеєю - основу їх вирішення лежать властивості y=ах2+bх+с.

Фактично всі важливі властивості квадратичні функціївизначаються таблицею.

Таблиця 1

Наведена схема досить ясно показує, що дискримінант D, старший коефіцієнта а, абсцис хо = - b/2a вершини параболи конструюють каркас, на якому будується теорія квадратичної функції. Далі розглянемо задачі, розв'язання яких пов'язане з дослідженням знаків D і a, задачі, розв'язання яких пов'язане зі становищем вершини параболи та задачі, пов'язані з розташуванням коренів квадратного тричлена.

Дискримінант, старший коефіцієнт.

https://pandia.ru/text/78/525/images/image013_18.jpg" align="left" width="179" height="216 src=">

Рішення:

Т. до. рівняння немає дійсних коренів, то графік функції y=ах2+bх+с розташований або повністю над віссю ОХ, або повністю під нею, тобто значення функції або більше нуля, або менше нуля для будь-яких значень х ( х - будь-яке число).

За умовою а+b+с<0, f (1) = а+b+с, то f (1) < 0, значит f (х) < 0 для всех значений х. с = f (0), т. е. с равно значению функции

Рис.2 y=f(х) при х=0. Висновок: з<0.

Відповідь:з<0.

Завдання 3.Нехай P(х)=2х2+ах+b, Q(х)= х2+сх+d та а2+ с2 +4d≤ 2ас + 4b(a, b, c-дійсні числа). Довести, що якщо рівняння P(х)=0 має дійсне коріння, то рівняння Q(х)=0, також має дійсне коріння.

Рішення:

Якщо рівняння P(х)=0 має дійсне коріння, то D = а2 – 8b≥0. Доведемо, що з нерівностей а2+ с2 +4d≤ 2ас + 4b і а2 – 8b≥0 випливає нерівність с2 – 4d ≥0. (х2+сх+d=0

D = с2 - 4d).

а2+ с2 +4d≤ 2ас + 4b · (-2)

2а2-2 с2 -8d ≥- 4ас -8b

А2+4ас≥ 2с2+8d або - а2+4ас - 4с2 ≥-2с2+8d; - а2+4ас - 4с2 = - (а2-4ас + 4с2) = - (а-с)2

с2 – 4d ≥ (а-с)2/2≥0, тобто дискримінант рівняння Q(х)=0, а це означає рівняння Q(х)=0 має рішення.

Завдання 4.

2y-х + хy = 0 (1)

(х + 2а - 4) y - ах + 5 = 0 (2)

має єдине рішення?

Рішення:

Очевидно, за жодних y пара (-2; y) не є рішенням даної системи. Тоді з рівняння (1) одержуємо y = х/(х + 2). Підставимо в рівняння (2), отримаємо:

(1 - а) х2 + х + 10 = 0 (3). Це рівняння має єдине рішення, якщо:

1). а - 1 = 0, а = 1,

2). D = 40а - 39 = 0, а = 39/40

3). Квадратне рівняння (3) має два різні корені, один з яких дорівнює -2. Підставимо х = -2 рівняння (3), отримаємо а = 3.

Відповідь:а = 1, а = 39/40, а = 3.

Завдання 5.При яких значеннях параметра система двох рівнянь

х2 -2х - y2 = 0 (1)

y = ах - а + b (2)

має єдине рішення за будь-яких значень b?

Рішення:

Підставимо y = ах – а + b (2) до рівняння (1), отримаємо:

(1-а2) х2 – 2(1-а2 + аb)х – (а - b)2=0 (3)

1). Якщо 1-а2 = 0, рівняння (3) має рішення ні за будь-яких значень. У цьому легко переконатись: нехай, наприклад, b = 0.

2) 1-а2≠0, тоді рівняння (3) квадратне. D = b2 – а2 + 1. Знайдемо ті значення параметра а, за яких нерівність b2 – а2 + 1≥0 за будь-яких значень b. Нерівність b2 ≥ а2-1 справедлива за будь-яких значень b, якщо а2-1≤0, тому що а = 1, а = -1 не підходить, то -1<а<1.

Відповідь: -1<а<1.

Завдання 6.При яких значеннях параметра графіки функцій y = 2ах + 1 y = (а-6)х2 –2 не перетинаються?

Рішення:

Відсутність точок перетину двох графіків функції рівносильна відсутності розв'язків системи двох рівнянь:

y = 2ах + 1 (1)

y = (а-6) х2 -2 (2)

2ах + 1 = (а-6)х2 –2 (3), щоб рівняння (3) не мало рішень виконаємо умову: D<0

4а2 + 12(а – 6)<0, -6<а<3.

Відповідь: -6<а<3.

Вершина параболи.

Завдання 7.Дійсні числа х, y, а такі, що умова х + y = 2а – 1(1) та умова

х2 + y2 = а2 + 2а - 3 (2), виконуються одночасно. При яких значеннях параметра а твір хy набуває найменшого значення?

Рішення:

хy = ((х + y)2 – (х2 + y2))/2 = ((2а – 1)2 – (а2 + 2а – 3))/2 = 3/2а2 – 3а +2

Розглянемо функцію f(а) = 3/2а2 – 3а +2

1). З'ясуємо, при яких значеннях параметра система двох рівнянь (1) і (2) має рішення.

Підставимо y = 2а – 1 – х до рівняння (2), отримаємо: 2 х2 +2х(1 – 2а) +3а2 - 6а +4 = 0. Щоб це рівняння мало рішення, виконаємо умову: D≥0, -2а2+ 8а – 7 ≥0,

https://pandia.ru/text/78/525/images/image017_29.gif" width="14">2-√2 / 2 ≤ а≤2 + √2 / 2

2).Знайдемо, за яких значень параметра а функція f(а) = 3/2а2 – 3а +2 приймає найменше значення на даному відрізку. Абсцис вершини параболи y = f(а) а = 1, 1<0, значит f(а) <0, тогда функция f(а) = 3/2а2 – 3а +2 принимает наименьшее значение при

Відповідь: 2 – √2/2.

Завдання 8.Знайти всі значення параметра а, за яких вершина двох парабол f(а) = 4х2 + 8ах – а та g(х) = 4ах2 – 8х + а –2 лежать по одну сторону від прямої y = -5.

Рішення:

З'ясуємо, при яких значеннях параметра ординати вершин даних парабол або одночасно більше -5, або одночасно менше -5. Нехай х1 - абсцис вершина параболи y = f (х), х1 = - а, f (х1) = -4а2 - а, х2 - абсцис вершина y = g (х), х2 = 1/а,

g(х2) =-4/а + а – 2. Виконаємо одночасно дві умови: -4а2 - а >-5 (1) -4/а + а – 2>-5(2)

або -4а2 - а<-5 (3), -4/а + а – 2<-5 (4). Для того, чтобы выполнить (1) и (2) одновременно или (3) и (4) одновременно достаточно решить неравенство (-4а2 - а+5)(-4/а + а – 2+5) >0,

а ця нерівність виконується при а<-4 или при-5/4<а<0.

Відповідь:а<-4; -5/4<а<0.

Завдання 9.Знайти найменше та найбільше значення функції y = 2-ах -3х2 при -1≤х≤1.

Рішення:

старший коефіцієнт -3<0, то ветви параболы направлены вниз и функция возрастает при х≤ хо и убывает при х≥хо, где хо =- b/2а - абсцисса вершины параболы. Результат в задаче зависит от положения абсциссы хо относительно отрезка [-1; 1], а не завсиит от знака дискриминанта. Выполним схематически рисунки (для D>0)

https://pandia.ru/text/78/525/images/image020_10.jpg" width="624" height="209 src=">

Для кожного із трьох випадків а), б), в) найменше значення функції f(t) = t2-8at+7a2

на відрізку досягається відповідно у точках при х = 1, х = 2а, х = 1/4. Тоді питання відповіді вирішення сукупності трьох систем:

1≤4а 1/4<4а<1 4а<1/4

f(1)<0 или f(4а)<0 или f(1/4)<0

а≥1/4 1/16<а<1/4 а≤1/16

1 - 8а + 7а2<0 или 16а2 – 32а2 + 7а2<0 или 1/16 – 2а + 7а2<0.

Відповідь: 1/28<а<1.

Тестові завдання

1). При яких значеннях параметра графіки функцій y = 2х – а та y = (а +1)х2 + 1 перетинаються тільки в одній точці?

2). Знайдіть усі значення параметра а, за яких графіки функцій y = (а +5)х2 – 1 і

y = (3а + 15) х – 4 не мають спільних точок?

3). За яких значень параметра а рівняння (а +4)х2 +6х –1 = 0 має єдине рішення?

4). За яких значень параметра а рівняння (2а +8)х2 –(а + 4)х +3 = 0 має єдине рішення?

5). При яких значеннях параметра рівняння має більше одного рішення?

а) (а +6) х2 - 8х + а = 0

б) а(2а + 4) х2 - (а +2) х - 5а - 10 = 0.

6). Знайдіть усі значення параметра до, за яких крива y = х2 + кх + 4 стосується осі ОХ.

7). При якому найменшому значенні параметра до квадратний тричлен

(к–2)х2+8х +к+4 позитивний за всіх дійсних значеннях х?

8). Числа х, y, а такі, що х + y = а –1, х2 + y2 = 5а2 – 3а + 0,5. При яких значеннях параметра а твір хy набуває найбільшого значення?

9). Числа х, y, а такі, що х + y = а +1, хy = а2 – 3а + 4. При яких значеннях параметра

а сума х2 + y2 набуває найбільшого значення?

10). Знайдіть найбільше та 1 найменше значення функції y = 2х2 – 2ах + на відрізку

11). Знайдіть найбільше значення квадратного тричлена 1–(а–2)х –х2 на відрізку

12). При яких значеннях параметра найменше значення функції y = х2 +(а+4) х+2а+3 на відрізку дорівнює –4?

13). При яких значеннях параметра найменше значення функції y = х2 –(а+2) х+а2 на відрізку [-1;1] дорівнює 4?

14). При яких значеннях параметра найбільше значення функції

f(х) = -(1/а)х +(7/а) · 3-х - 3а2 на відрізку [-1; 0] негативно?

Відповіді до тестового завдання

1) а = -2, а = -1, а = 0.

2) –19/3<а≤-5.

3) а = -4, а = -13.

5) а) -8<а<-6 и -6<а<2

б) а = -2; -1/40 0.

10) Якщо а<-2, то наименьшее значение функции при х=-1 и равно 3+2а, наибольшее значение функции при х=1 и равно 3–2а;

якщо -2≤а<0, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=1 и равно 3–2а;

якщо 0≤а<2, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=-1 и равно 3+2а;

якщо а≥2, то найменше значення функції при х = 1 і дорівнює 3-2а, найбільше значення функції при х = -1 і 3 +2а;

11) Якщо а≤0, то -6а2-а+2, якщо 0<а<8/5, то 2- 6а +а2/4, если а ≥8/5, то 19а-6а2 -14

13) а=-2 або а=(1+√21)/2

14) |а|>(7√3)/12.

Розташування коріння квадратного тричлена

Розглянемо ряд типових завдань, пов'язаних із розташуванням коренів квадратного тричлена ах2+bх+с. Усі міркування проведемо, припускаючи а>0. Якщо а<0,то рассуждения проводятся аналогично.

Завдання №1.

За яких умов обидва корені квадратного рівняння ах2+bх+с =0 (необов'язково різні) більші за деяке задане число до?

Рішення.

Побудуємо схематичні графіки функції квадратного тричлена y= ах2+bх+с, де х1 і х2 задовольняють умовам: х1>к, х2>к. Нехай f(х) = ах2 + bх + с. Графік y= f(х) або перетинає вісь ОХ (D>0), або стосується її (D=0). Тоді необхідно виконати умову: хо>к, y(к)>0. Якщо а< 0 условие: х1>до, х2>до визначаються системою нерівностей:

https://pandia.ru/text/78/525/images/image023_20.gif" width="14" height="86">

Рис.4

Завдання 11.Знайдіть усі значення параметра а, при яких усі корені рівняння

х2–6ах+2–2а+9а2 =0 більше 3.

Рішення.

При виконанні необхідної умови можливі такі положення параболи, яка є графіком функції f(х) = х2-6ах +2-2а +9а2

Рис.5

Розв'яжемо систему нерівностей:

https://pandia.ru/text/78/525/images/image026_8.jpg" align="left" width="324" height="239 src=">

Достатньо виконати умову: y(к)<0, если а >0.Прі а<0, y(к) > 0.

Мал. 6

Завдання 12.Знайдіть усі значення параметра а, за яких 1 лежить між корінням рівняння х2–2ах+3–4а+2а2=0.

Рішення.

старший коефіцієнт позитивний, достатньо виконати умову f(1)<0, где f(х)=х2–2ах+3–4а+2а2

4–6а+2а2<0, 1<а<2.

Відповідь: 1<а<2

Завдання №3.За яких умов рівно один корінь квадратного рівняння ах2+bх+с =0, що має різне коріння, лежить на інтервалі (к, е)?

Побудуємо схематично графіки у = ах2 + bх + с за умовою даної задачі для >0.

https://pandia.ru/text/78/525/images/image028_8.jpg" width="623" height="246 src=">

Розв'яжемо нерівність: f(1) · f(2)<0.

(а2+8а+7)(а2+14а+16)<0

7-√33< а<-7; -7+√33<а<-1.

Відповідь: -7-√33< а<-7; -7+√33<а<-1.

Завдання 14.Знайдіть усі значення параметра а, за яких рівняння 2cos(2x)+2asin(x)+a-1=0 має єдине рішення на проміжку (-π/2;0).

Рішення.

2cos(2x)+2a·sinx+a-1=0

2(1–2 sin2х)+ 2a·sinx+a–1=0

4 sin2х-2а sinx -a-1 = 0

Нехай sinx=t Т. до. -π/2<х<0, то -1< t <0

Знайдіть значення параметра а, при яких рівняння 4t2– 2at–a–1=0 має єдине рішення на проміжку (-1;0).

Рівняння 4t2-2at-a-1 = 0 має єдине рішення на проміжку (-1; 0), якщо:

1). D =0 D/4=(а+2)2 D =0 при а=-2.

2). Розглянемо функцію f(t) = 4t2-2at-a-1

Збудуємо схематично графік функції y=f(t)

https://pandia.ru/text/78/525/images/image030_16.gif" width="14" height="50 src=">

f(0) · f(1) ≤0 а≤-3; а≥-1

Відповідь:а≤-3; а≥-1; а=-2.

Завдання №4.За яких умов обидва корені (необов'язково різні) квадратного рівняння ах2+bх+с лежать на відрізку [к; е]. Розглянемо за умови а>0. Нехай функція f(х)= ах2+bх+с

https://pandia.ru/text/78/525/images/image032_14.gif" width="14" height="110"> D≥0

до≤ хо≤ е

Завдання 15. Знайдіть ті значення параметра а, за яких усі корені рівняння

х2-2(а-3)х-а +3 = 0 лежать в інтервалі (-3; 0).

Рішення.

За умови існування хоча б одного кореня графік функції f(х)= х2- 2(а–3)х–а +3 може бути схематично розташований одним із двох способів

https://pandia.ru/text/78/525/images/image034_12.gif" width="14" height="110"> D≥0 4(а – 3)(а – 2) ≥0

3<хо<0 3<а – 3 <0 1,2<а≤2.

f(-3) >0 5а – 6>0

f(0) >0 -а+3>0

Рівняння sin x − 1 + a = sin x − 2 . sin x − 2 sin x − 3 Рішення. Вважаючи t = sin x, наведемо рівняння до виду at2 − 5at + 6a − 1 = 0. Якщо a = 0, то рішень немає. При a = 0 і за умови a ∈ (−∞; −4] ∪ (0; +∞) √ напів- 2 + 4a чаєм коріння рівняння t1,2 = 5a ± 2aa. − 5at + 6a − 1 знаходиться в точці tв = 2 , 5 умова |t|1 для меншого з коренів виконуватиметься, якщо на кінцях відрізка [−1; 1] функція матиме різні знаки: f (−1)· f (1) 0 або (2a−1)(12a−1) 0. Рішенням останньої 1 нерівності є інтервал a ∈ 12 ; 1 .2 √ a2 Відповідь: Якщо a ∈ 12 ; 5a− 2a +4a +πn, n∈Z, 1 1 при інших a рішень немає Завдання 6.7 При яких значеннях параметра a функція f (x) = 8ax − a sin 6x − 7x − sin 5x зростає на всій числовій осі і не має критичних точок?Рішення Функція f(x) диференційована при будь-якому значенні a і f(x) = 8a − 6a cos 6x − 7 − 5 cos 5x Завдання можна переформулювати так: за яких a нерівність 6a cos 6x + 5 cos 5x< 8a − 7 справедливо для любого x? Так как последнее неравенство должно выполняться для любого значения x, оно должно быть справедливо и для x = 0, от- куда 6a + 5 < 8a − 7 или a >6. З огляду на тепер, що 6a cos 6x + 5 cos 5x 6|a| + 5< 8a − 7, приходим к выводу, что при a >6 нерівність справедлива для будь-якого x. Відповідь: a > 6. Завдання для самостійного рішенняЗавдання 6.8. (СДАУ) Залежно від значень параметра a розв'яжіть рівняння cos4 x − (a + 2) cos2 x √ a − 3 = 0. − Відповідь: Якщо a ∈ [−3; −2] : x = arccos a + 3 + πk, k ∈ Z, якщо a ∈ [−3; −2] : рішень немає. Завдання 6.9. (СДАУ) Залежно від значень параметра a розв'яжіть рівняння sin4 x + cos4 x + sin 2x + a = 0. 61 √ Відповідь: Якщо a ∈ − 3 ; 2: x = 1 (−1)k arcsin(1− 2a−3) + πk, 2 1 2 3 ; 1: рішень немає. якщо a ∈ − 2 2 k ∈ Z, завдання 6.10. (СДАУ) При яких значеннях параметра a рівняння (a2 +8a+16)(2−2 cos x− sin2 x)+(32+2a2 +16a)(cos x−1)+3a+10=0 не має рішень? Відповідь: a< − 10 ; −3 < a < −2. 3 Задача 6.11. (СГАУ) При каких значениях параметра a урав- нение loga−2 17 + cos x − sin x = 3 8 имеет решение? √ 2 3 Ответ: a ∈ 2 5 ; 3 ∪ 3; 2 + 26 . 2 Задача 6.12. (СГАУ) При каких значениях параметра a урав- нение loga+1 25 + cos x − 2 sin x = 3 8 2 имеет решение? √3 37 Ответ: a ∈ − 1 ; 0 ∪ 0; 2 − 1 . 2 Задача 6.13. (ЕГЭ) При каких значениях параметра a значение выражения 2+cos x·(3 cos x+a sin x) не равно нулю ни при каких значениях x? √ √ Ответ: a ∈ −2 10; 2 10 . Задача 6.14. (ЕГЭ) При каких значениях параметра a значение выражения 3 + sin x · (2 sin x + a cos x) будет равно −1 хотя бы при одном значении x? √ √ Ответ: a ∈ −∞; −4 6 ∪ 4 6; +∞ . Задача 6.15. (ЕГЭ) При каких значениях параметра a сумма loga (sin x + 2) и loga (sin x + 3) будет равна единице хотя бы при одном значении x? Ответ: a ∈ [ 2; 12 ]. Задача 6.16. (СГАУ) При каких значениях параметра α систе- ма 4 sin x · sin y · cos(x + y) − 0,5 = 0 x−y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. 62 Ответ: Если α = 2πn: x = ±π 6 + π(k+n) π y = ±6 + π(k−n); если α = π+2πn: x = ±π 3 + π + π(k+n) 2 y = ±π 3 − π + π(k−n), 2 n, k ∈ Z. Задача 6.17. (СГАУ) При каких значениях параметра α систе- ма 2 sin x · cos y · sin(x − y) + 0,25 = 0 x+y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. Ответ: Если α = π +2πn: x = (−1)k+1 π + π + π (2n+k) 2 12 4 2 k π + π + π (2n−k); y = (−1) 12 4 2 если α = − 2 π +2πn: x = (−1)k π − π + π (2n+k) 12 4 2 y = (−1) k+1 π − π + π (2n−k), 12 4 2 n, k ∈ Z. Задача 6.18. (СГАУ) При каких значениях параметра a нера- венство √ 2 2 (sin x − cos x) − a + 7 log 2a+34 15 <0 35 выполняется для любых значений x? 1 Ответ: a ∈ (−17; −12) ∪ 2 ; 3 . Задача 6.19. (СГАУ) При каких значениях параметра a нера- венство √ log 3−2a 3 sin x + 3 3 cos x − 2a − 12 >0 23 28 виконується для будь-яких значень x? Відповідь: a ∈ (−∞; −23) ∪ (−10; −9). Завдання 6.20. Залежно від значень параметра a розв'яжіть нерівність cos x 2 − a2 . Відповідь: | √ : x ∈ R, 1 1<|a| √3: x ∈ arccos(2−a2)+2πk; π− arccos(2−a2)+2πk , |a|>3: рішень немає. k∈Z Завдання 6.21. За яких значень параметра a рівняння tg x (a + 1) tg2 x − 2 cos x + a = 0 не має рішень? Відповідь: a −3; a 1. 63 Навчальний посібникЗАДАЧІ З ПАРАМЕТРАМИ Укладачі: Єфімов Євген Олександрович Коломієць Людмила Вадимівна Комп'ютерний набір та верстка О.О. Єфімов Самарський державний аерокосмічний університет імені академіка С.П. Корольова. 443086, Самара, Московське шосе, 34. - РІО Самарського державного аерокосмічного університету імені академіка С.П. Корольова. 443086, Самара, Московське шосе, 34

1. Завдання.
При яких значеннях параметра aрівняння ( a - 1)x 2 + 2x + a- 1 = 0 має рівно один корінь?

1. Рішення.
При a= 1 рівняння має вигляд 2 x= 0 і, очевидно, має єдиний корінь x= 0. Якщо a№ 1, то дане рівняння є квадратним і має єдиний корінь при тих значеннях параметра, за яких дискримінант квадратного тричлена дорівнює нулю. Прирівнюючи дискримінант до нуля, отримуємо рівняння щодо параметра a 4a 2 - 8a= 0, звідки a= 0 або a = 2.

1. Відповідь:рівняння має єдиний корінь при aПро (0; 1; 2).

2. Завдання.
Знайти всі значення параметра a, при яких має два різні корені рівняння x 2 +4ax+8a+3 = 0.
2. Рішення.
Рівняння x 2 +4ax+8a+3 = 0 має два різні корені тоді і тільки тоді, коли D = 16a 2 -4(8a+3) > 0. Отримуємо (після скорочення на загальний множник 4) 4 a 2 -8a-3 > 0, звідки

2. Відповідь:

aО (-Ґ ; 1 –

Ц 7 2

) І (1 +

Ц 7 2

; Ґ ).

3. Завдання.
Відомо що
f 2 (x) = 6x-x 2 -6.
а) Побудуйте графік функції f 1 (x) при a = 1.
б) При якому значенні aграфіки функцій f 1 (x) та f 2 (x) мають єдину загальну точку?

3. Рішення.
3.а.Перетворюємо f 1 (x) наступним чином
Графік цієї функції при a= 1 зображено малюнку праворуч.
3.б.Відразу зазначимо, що графіки функцій y = kx+bі y = ax 2 +bx+c (a№ 0) перетинаються в єдиній точці тоді і лише тоді, коли квадратне рівняння kx+b = ax 2 +bx+cмає єдине коріння. Використовуючи уявлення f 1 з 3.а, прирівняємо дискримінант рівняння a = 6x-x 2 -6 на нуль. З рівняння 36-24-4 a= 0 отримуємо a= 3. Зробивши те саме з рівнянням 2 x-a = 6x-x 2 -6 знайдемо a= 2. Неважко переконатися, що це значення параметра задовольняють умовам завдання. Відповідь: a= 2 або a = 3.

4. Завдання.
Знайти всі значення a, при яких безліч розв'язків нерівності x 2 -2ax-3aі 0 містить відрізок.

4. Рішення.
Перша координата вершини параболи f(x) = x 2 -2ax-3aдорівнює x 0 = a. З властивостей квадратичної функції умова f(x) і 0 на відрізку рівносильно сукупності трьох систем
має рівно два рішення?

5. Рішення.
Перепишемо це рівняння у вигляді x 2 + (2a-2)x - 3a+7 = 0. Це квадратне рівняння, воно має рівно два рішення, якщо його дискримінант строго більший за нуль. Обчислюючи дискримінант, отримуємо, що умовою наявності рівно двох коренів є виконання нерівності a 2 +a-6 > 0. Вирішуючи нерівність, знаходимо a < -3 или a> 2. Перше з нерівностей, очевидно, рішень у натуральних числахнемає, а найменшим натуральним рішенням другого є число 3.

5. Відповідь: 3.

6. Завдання (10 кл.)
Знайти всі значення a, при яких графік функції або після очевидних перетворень, a-2 = | 2-a| . Останнє рівняння рівносильне нерівності aі 2.

6. Відповідь: aПро )