Математическо очакване на случаен процес. случайни променливи. Дискретна случайна променлива.Математическо очакване. Закон за разпределението на дискретна случайна величина

Случайни (стохастични) процеси са външни смущения, флуктуационен шум на изхода на дискриминатора и други RAS устройства, вътрешни смущения в RAS: честотна нестабилност на PG, нестабилност на устройства с регулируемо време закъснение и др.

По принцип изследването на RAS при произволни въздействия може да се проведе по конвенционални методи, като се определят параметрите на качеството на RAS при най-неблагоприятните (максимални) стойности на смущението ( най-лошия случай ).

Въпреки това, тъй като максимална стойностпроизволна променлива е малко вероятно и ще се наблюдава рядко, очевидно ще бъдат наложени строги изисквания към RAS. По-рационални решения могат да бъдат получени чрез разглеждане най-вероятна стойност случайна величина.

Може да се разгледа законът за разпределение на флуктуационните компоненти в линейна RAS нормално (Гаусово). Нормалният закон за разпределение е характерен за вътрешните смущения. Когато произволен процес преминава през линейна система, законът за нормалното разпределение остава непроменен . Ако на входа на RAS или в която и да е друга точка (например на изхода на дискриминатора) има смущение със закон на разпределение, който се различава от нормалния и има широк спектър С(ω), това смущение е ефективно нормализира теснолентови PAC филтърни елементи.

Случаен процес с нормално разпределение се определя напълно от математическо очакване м(T) и корелационна функция Р(τ).

Очаквана стойност (очакване) на случаен процес х(T) е някои редовен функция mx(T), около който са групирани всички реализации на този процес ( е плътността на вероятността) . Нарича се още зададено средно (ансамбъл).

mx(T) = М{х(T)} = . (6.1)

произволен процес ( T) без обикновен компонент mx(T) е наречен центриран .

Да се вземе предвид степента на дисперсия на произволен процес спрямо неговата средна стойност mx(T) въведе понятието дисперсия :

Dx(T) = М{( (T)) 2 } = . (6.2)

Средната стойност на квадрата на произволен процес е свързана с неговото очакване mx(T) и дисперсия Dx(T) формула: .

На практика е удобно да се оцени произволен процес по статистически характеристики х добре(T) и s х(T) със същото измерение като самия процес.

RMS стойност х добре(T) произволен процес:

Стандартно отклонение x rms (t) произволен процес:

. (6.4)

Математическото очакване и дисперсията не дават достатъчна представа за естеството на индивидуалните реализации на случаен процес. За да се вземе предвид степента на променливост на процеса или връзката между неговите стойности в различни моменти от времето, концепцията за корелация ( автокорелация ) функции.

корелационна функцияцентриран процес ( T) е равно на

където е двумерната плътност на вероятността.

Функцията на корелация е дори : Р(τ ) = Р(–τ ).

Ако функциите на разпределение и плътността на вероятността на процеса не зависят от изместването на времето със същото количество аргументи за всички времеви, такъв случаен процес се нарича стационарен .

Ако стационарният процес има същите стойности зададено средно и средно време , такъв случаен процес се нарича ергодичен .

знаейки Р(τ) може да се определи дисперсията на стационарния процес:

Спектрална плътност Сл г(ω) изходен процес г(T) в линейна системаи спектрална плътност С l (ω) на входното действие са свързани с отношението:

. (6.7)

корелационна функция Р(τ) на стационарен случаен процес и неговата спектрална плътност С(ω) са свързани чрез трансформацията на Фурие, така че анализът често се извършва в честотната област. След извършване на преобразуването на Фурие за (6.7), получаваме израз за корелационната функция на изходния процес Рай(τ):

Спектрални плътности Сл г(ω) и С l (ω) са двустранно .

Можете да влезете едностранно спектрална плътност н(е), който се определя само за положителен честоти().

Паритет Р(τ) и формулите на Ойлер (6.8) могат да бъдат опростени:

. (6.9)

Качеството на работата на RAS е относително произволен сигнали и смущения се характеризират обща средноквадратична грешка (SKO).

Помислете за обобщена RAS, схемата на която е показана на фиг. 2.11. Отчитаме въздействието λ( T) детерминистичен, а смущението ξ( T) на изхода на дискриминатора е произволен процес. Използвайки формули (2.28)–(2.31), определяме TF за грешката при действието и смущението.

В общия случай между процесите на влияние и смущения може да съществуват корелация (Връзка). В този случай, освен автокорелация функции от вида (6.8) за всеки от процесите е необходимо да се вземат предвид взаимна корелация функции на процеса една спрямо друга. Чрез спектралните плътности по погрешка, данните за свързване се записват, както следва:

След заместване на израза (6.11) във формула (6.8), получаваме съответните компоненти на дисперсията:

Ако няма корелация между процесите, тогава С l x (ω) = С x l (ω) = 0, както и д l x = д x l = 0, а формулата (6.12) е опростена

Очакване на грешка х(T) е подобно на определението в стационарно състояние: .

Ако спектралната плътност S x(ω) се описва с рационална дробна функция по отношение на ω, след което се изчислява Dxтой е представен във формата:

където е полином, съдържащ дори степен иω до 2 н–2 включително; a е полином от степен н, чиито корени лежат в горната полуравнина на комплексната променлива ω.

Интегралите (6.14) могат да бъдат изчислени по формула (6.15):

, (6.15)

къде не старшият детерминант на Хурвиц от вида (4.7), съставен от коефициентите a j, а Qn– детерминанта от тип D н, където на първия ред коефициентите a jзаменен от b j.

За интеграла (6.15) има таблици със стойности за н ≤ 7.

Стойности при н≤ 4 се определят по формулите:

, , ,

Пример 6.1.Нека дефинираме RMS на PLL системата от пример 4.2.

Нека сигналът λ( T) = 1 + 0,1T, и смущението ξ( T) е бял шум с амплитуда N0= 1 mV ().

Процентите на грешки за даден PAC вече са открити в пример 5.1.

За PF грешката на смущенията от формула (2.30) след промяната на променливите Р ® иω получаваме ( К 1 = S d , к 0 = к 1 S d , к 1 = k f k и):

След заместване на формула (6.17) в (6.13) ( д l = 0) получаваме:

Сравнявайки (6.18) с израз (6.14), намираме реда и коефициентите на полиномите (6.14): н = 3, б 2 = 0, б 1\u003d - (T 2) 2, b 0 = 1; а 3 = T f T d, а 2 = T f+ T d , а 1 = 1 + к 0 Т2, а 0 = к 0 .

След заместване на числовите стойности резултатът е:

mx= 5×10 -4 (1/s), Dx\u003d 1,06 × 10 -3 (1 / s 2) (при к 0 = 200, S d = 10, к 1 = 20) или

mx= 5×10 -4 (1/s), Dx\u003d 0,66 (1 / s 2) (при к 0 = 200, S d = 0,4 , к 1 = 500).

От (6.3), (6.4) следва, че x скорост≈ с х= 0,032 (1/s) при S d= 10, докато S d = 0,4 x скорост≈ с х= 0,81 (1/s).

Пример 6.2.Нека определим RAS RAS от пример 4.5 за същите сигнали: λ( T) = 1 + 0,1Tи ξ( T) = N0= 1 mV. λ′( T) = λ 1 , λ″( T) = 0

Степента на грешки за даден RAS може да се намери с помощта на формулата (5.19): .

v = 0, d1 = 0, d0 = S d, б 3 = Т 1 Т 2 Т 3, б 2 = Т 1 Т 2+Т 2 Т 3+Т 1 Т 3, б 1 = Т 1 + Т 2 + Т 3, b 0 = 1.

От формули (5.19)–(5.22) получаваме

За PF грешката на смущенията от формула (2.30) след промяната на променливите p ® иω в (6.20) получаваме:

След заместване на формула (6.20) в (6.13) (D l = 0), получаваме:

Сравнявайки (6.21) с израза (6.14), намираме коефициентите на полиноми (6.14): н = 3, б 2 = б 1 = 0, b 0 = 1; а 3 = Т 1 Т 2 Т 3, а 2 = T 1 T 2 + T 2 T 3 + T 1 T 3, а 1 = Т 1 + Т 2 + Т 3, а 0 = S d + 1.

След заместване във формула (6.16) и трансформации получаваме:

След заместване на числовите стойности получаваме в резултат:

mx= (9,2 + 0,9 t)10 -2, Dx\u003d 4,2 × 10 -4.

6.2. Графоаналитичен метод за определяне на дисперсията.

Министерство на образованието и науката на Руската федерация

Череповец държавен университет

Инженерно-икономически институт

Концепцията за случаен процес в математиката

Изпълнено от ученик

група 5 GMU-21

Иванова Юлия

Череповец

Въведение

Главна част

Дефиниция на случаен процес и неговите характеристики

Стохастични процеси на Марков с дискретни състояния

Стационарни случайни процеси

Ергодично свойство на стационарни случайни процеси

литература

Въведение

Концепцията за произволен процес е въведена през 20-ти век и е свързана с имената на A.N. Колмогоров (1903-1987), А.Я. Хинчин (1894-1959), Е.Е. Слуцки (1880-1948), Н. Винер (1894-1965).

Тази концепция днес е една от централните не само в теорията на вероятностите, но и в естествените науки, инженерството, икономиката, организацията на производството и теорията на комуникацията. Теорията на случайните процеси принадлежи към категорията на най-бързо развиващите се математически дисциплини. Несъмнено това обстоятелство до голяма степен се определя от дълбоките му връзки с практиката. 20-ти век не може да се задоволи с идеологическото наследство, получено от миналото. Наистина, докато физик, биолог, инженер се интересуваше от процеса, т.е. промяната на изучаваното явление във времето, теорията на вероятностите ги предлага като математически апарат означава само, че изучават стационарни състояния.

За изучаване на промените във времето, теория на вероятностите края на XIX- началото на 20 век няма разработени частни схеми, още по-малко общи техники. А необходимостта от създаването им буквално почука по прозорците и вратите на математическата наука. Изучаването на Брауновото движение във физиката доведе математиката до прага на създаването на теория на случайните процеси.

Считам за необходимо да спомена още две важни групи изследвания, започнати по различно време и по различни причини.

Първо, тази работа на A.A. Марков (1856-1922) за изследване на верижните зависимости. Второ, произведенията на E.E. Слуцки (1880-1948) за теорията на случайните функции.

И двете посоки играха много съществена ролявъв формирането обща теорияпроизволни процеси.

За тази цел вече беше натрупан значителен първоначален материал и необходимостта от изграждане на теория сякаш виташе във въздуха.

Оставаше да се извърши задълбочен анализ на съществуващите произведения, изразените в тях идеи и резултати и на негова основа да се извърши необходимия синтез.

Дефиниция на случаен процес и неговите характеристики

Определение: произволен процес X(t) е процес, чиято стойност за всяка стойност на аргумента t е произволна променлива.

С други думи, произволен процес е функция, която в резултат на тестване може да приеме една или друга специфична форма, неизвестна предварително. За фиксирано t=t 0 X(t 0) е обикновена случайна променлива, т.е. разделпроизволен процес в момент t 0.

Примери за произволни процеси:

1. населението на района във времето;

2. броя на постъпилите заявления от сервиза за ремонт на фирмата във времето.

Случаен процес може да бъде записан като функция на две променливи X(t,ω), където ω€Ω, t€T, X(t, ω) € ≡ и ω е елементарно събитие, Ω е пространството на елементарните събития , Т е наборът от стойности на аргумента t, ≡ - набор от възможни стойности на произволния процес X(t, ω).

Изпълнениепроизволният процес X(t, ω) е неслучайна функция x(t), в която произволният процес X(t) се превръща в резултат на тестване (за фиксирано ω), т.е. специфична форма, взета от случайния процес X(t), неговата траектория.

По този начин, произволен процес X(t, ω) съчетава характеристиките на случайна променлива и функция.Ако фиксираме стойността на аргумента t, произволният процес се превръща в обикновена случайна променлива, ако фиксираме ω, тогава в резултат на всеки тест той се превръща в обикновена неслучайна функция. В това, което следва, ние пропускаме аргумента ω, но той ще бъде приет по подразбиране.

Фигура 1 показва няколко реализации на произволен процес. Нека напречното сечение на този процес за даден t е непрекъсната случайна величина. Тогава случайният процес X(t) за дадено t се определя напълно от вероятността φ(x‚ t). Очевидно плътността φ(x, t) не е изчерпателно описание на случайния процес X(t), тъй като не изразява зависимостта между неговите секции в различни моменти.

Случайният процес X(t) е колекция от всички секции за всички възможни стойности на t, следователно, за да го опишем, е необходимо да се разгледа многоизмерна случайна променлива (X(t 1), X(t 2), ..., X(t n)), състоящ се от всички комбинации на този процес. По принцип има безкрайно много такива комбинации, но за да се опише произволен процес, често е възможно да се мине с относително малък брой комбинации.

Казва се, че произволен процес има поръчкан, ако тя е напълно определена от плътността на съвместното разпределение φ(x 1, x 2 , …, x n ; t 1 , t 2 , …, t n) n произволни участъци от процеса, т.е. плътност на n-мерна случайна променлива (X(t 1), X(t 2), …, X(t n)), където X(t i) е комбинация от произволен процес X(t) в момент t i , i =1, 2 , …, n.

Подобно на случайна променлива, произволен процес може да бъде описан числени характеристики. Ако за произволна променлива тези характеристики са постоянни числа, тогава за случаен процес - неслучайни характеристики.

математическо очакванепроизволният процес X(t) е неслучайна функция a x (t), която за всяка стойност на променливата t е равна на математическото очакване на съответния участък от произволния процес X(t), т.е. ax(t)=M.

дисперсияслучаен процес X(t) е неслучайна функция D x (t), за всяка стойност на променливата t, равна на дисперсията на съответната комбинация от произволния процес X(t), т.е. Dx(t)=D.

Стандартно отклонениеσ x (t) на произволен процес X(t) е аритметичната стойност на корен квадратен от неговата дисперсия, т.е. σx(t)= Dx(t).

Математическото очакване на случаен процес характеризира средентраекторията на всички негови възможни реализации и неговата дисперсия или стандартно отклонение - разпръсна сереализации спрямо средната траектория.

Характеристиките на случайния процес, въведени по-горе, не са достатъчни, тъй като те се определят само от едномерен закон за разпределение. Ако произволен процес X 1 (t) се характеризира с бавна промяна в стойностите на реализациите с промяна в t, то за произволен процес X 2 (t) тази промяна е много по-бърза. С други думи, произволен процес X 1 (t) се характеризира с тясна вероятностна връзка между двете му комбинации X 1 (t 1) и X 1 (t 2), докато за случаен процес X 2 (t) тази зависимост между комбинации от X 2 (t 1) и X 2 (t 2) практически липсва. Тази зависимост между комбинациите се характеризира с корелационна функция.

определение: корелационна функцияпроизволният процес X(t) се нарича неслучайна функция

K x (t 1 , t 2) = M[(X(t 1) – a x (t 1))(X(t 2) – a x (t 2))] (1.)

две променливи t 1 и t 2 , което за всяка двойка променливи t 1 и t 2 е равно на ковариацията на съответните комбинации X(t 1) и X(t 2) на случайния процес.

Очевидно за произволен процес X (t 1) корелационната функция K x 1 (t 1, t 2) намалява, тъй като разликата t 2 - t 1 нараства много по-бавно от K x 2 (t 1, t 2) за a произволен процес X (t2).

Функцията на корелация K x (t 1, t 2) характеризира не само степента на стегнатост линейна зависимостмежду две комбинации, но също и разпространението на тези комбинации спрямо математическото очакване a x (t). Следователно се разглежда и нормализираната корелационна функция на случайния процес.

Нормализирана корелационна функцияпроизволният процес X(t) се нарича функция:

P x (t 1 , t 2) = K x (t 1 , t 2) / σ x (t 1)σ x (t 2) (2)

Пример №1

Случайният процес се дефинира с формулата X(t) = X cosωt, където X е произволна променлива. Намерете основните характеристики на този процес, ако M(X) = a, D(X) = σ 2 .

РЕШЕНИЕ:

Въз основа на свойствата на математическото очакване и дисперсия имаме:

a x (t) = M(X cosωt) = cosωt * M(X) = a cosωt,

D x (t) = D(X cosωt) = cos 2 ωt * D(X) = σ 2 cos 2 ωt.

Намираме корелационната функция по формулата (1.)

K x (t 1, t 2) = M[(X cosωt 1 - a cosωt 1) (X cos ωt 2 - a cosωt 2)] =

Cosωt 1 cosωt 2 * M[(X - a)(X - a)] = cosωt 1 cosωt 2 * D(X) = σ 2 cosωt 1 cosωt 2 .

Намираме нормализираната корелационна функция по формулата (2.):

P x (t 1, t 2) \u003d σ 2 cosωt 1 cosωt 2 / (σ cosωt 1) (σ cosωt 2) ≡ 1.

Случайните процеси могат да бъдат класифицирани в зависимост от това дали състоянията на системата, в която се случват, се променят плавно или рязко, разбира се (сброимо) или безкраен брой от тези състояния и т.н. Сред случайните процеси специално място заема случайният процес на Марков.

Теорема. Случаен процес X(t) е Хилберт, ако и само ако съществува R(t, t^) за всички (t, t^) e T*T.

Теорията на случайните процеси на Хилберт се нарича корелационна теория.

Забележете, че множеството T може да бъде дискретно и непрекъснато. В първия случай случайният процес X t се нарича процес с дискретно време, във втория - с непрекъснато време.

Съответно, комбинациите от X t могат да бъдат дискретни и непрекъснати случайни променливи.

Случайният процес се нарича X(t) селективнонеправилна, диференцируема и интегрируема в точка ω€Ω, ако нейната реализация x(t) = x(t, ω) е съответно непрекъсната, диференцируема и интегрируема.

Случайният процес X(t) се нарича непрекъснат: почти, вероятноако

P(A)=1, A = (ω € Ω : lim x(t n) = x(t))

AT среден квадрат,ако

Lim M[(X(t n) – X(t)) 2 ] = 0

По вероятност, ако

Aδ ≥ 0: limP[| X(t n) – X(t)| > δ] = 0

Средно квадратната конвергенция се обозначава и с:

X(t) = limX(t n)

Оказва се, че от селективната непрекъснатост следва приемствеността почти сигурно, от непрекъснатостта почти сигурно, а средноквадратично предполага приемственост във вероятността.

Теорема. Ако X(t) е хилбертов случаен процес, непрекъснат в средния квадрат, тогава m x (t) е непрекъсната функция и връзката

Lim M = M = M .

Теорема. Хилбертовият случаен процес X(t) е средноквадратичен непрекъснат, ако и само ако неговата ковариационна функция R(t, t^) е непрекъсната в точката (t, t).

Хилбертов случаен процес X(t) се нарича средноквадратично диференцируем, ако съществува произволна функция X(t) = dX(t)/dt, такава, че

X(t) = dX(t)/ dt = limX(t+∆t) – X(t) / ∆t

(t € T, t +∆t € T),

тези. кога

Lim M [((X(t + ∆t) – X(t) / (∆t)) – X(t)) 2 ] = 0

Случайната функция X(t) ще бъде извикана средно квадратна производнапроизволен процес X(t) съответно в точката t или на T.

Теорема. Хилбертов случаен процес X(t) е средноквадратично диференцируем в точка t, ако и само ако съществува

δ 2 R(t, t^) / δtδt^ в точката (t, t^). при което:

R x (t, t^) = M = δ 2 R(t, t^) / δtδt^.

Ако произволен процес на Хилберт е диференцируем върху T, тогава неговата средноквадратична производна също е случаен процес на Хилберт; ако извадковите траектории на процеса са диференцируеми на T с вероятност 1, то с вероятност 1 техните производни съвпадат със средноквадратичните производни на T.

Теорема. Ако X(t) е случаен процес на Хилберт, тогава

M = (d / dt) M = dm x (t) / dt.

Нека (0, t) е краен интервал, 0

X(t) - Хилбертов случаен процес.

Y n \u003d ∑ X (t i) (t i - t i-1) (n = 1.2, ...).

След това произволната променлива

max (t i – t i -1)→0

Наречен среден квадратен интегралпроцес X(t) върху (0, t) и се означава с:

Y(t) = ∫ X(τ)dτ.

Теорема . Средноквадратичният интеграл Y(t) съществува, ако и само ако ковариационната функция R(t, t^) на хилбертовия процес X(t) е непрекъсната на T×T и съществува интеграл

R y (t, t^) = ∫ ∫ R(τ, τ^) dτdτ^

Ако интегралът в средноквадратната функция X(t) съществува, тогава

M = ∫ Mdτ,

R Y (t, t^) = ∫ ∫ R(τ, τ^)dτdτ^

K y (t, t^) = ∫ ∫ K(τ, τ^)dτdτ^

Тук R y (t, t^) = M, K y (t, t^) = M са ковариационните и корелационни функции на случайния процес Y(t).

Теорема. Нека X(t) е случаен процес на Хилберт с ковариационна функция R(t, t^), φ(t) е реална функция и нека има интеграл

∫ ∫ φ(t)φ(t^)R(t, t^)dtdt^

Тогава съществува средноквадратичен интеграл

∫ φ(t)X(t)dt.

Случайни процеси:

X i (t) = V i φ i (t) (i = 1n)

Където φ i (t) са дадени реални функции

V i - случайни величини с характеристики

Те се наричат елементарни.

Канонична декомпозицияпроизволен процес X(t) се нарича негово представяне във формата

Където V i са коефициентите, а φ i (t) са координатните функции на каноничното разширение на процеса X(t).

От връзките:

M(V I = 0), D(V I) = D I , M(V i V j) = 0 (i ≠ j)

X(t) = m x (t) + ∑ V i φ i (t) (t € T)

K(t, t^) = ∑ D i φ i (t)φ i (t^)

Тази формула се нарича канонична декомпозициякорелационна функция на случаен процес.

В случая на уравнението

X(t) = m x (t) + ∑ V i φ i (t) (t € T)

Има формули:

X(t) = m x (t) + ∑ V i φ(t)

∫ x(τ)dt = ∫ m x (τ)dτ + ∑ V i ∫ φ i (t)dt.

По този начин, ако процесът X(t) е представен чрез неговото канонично разширение, тогава неговата производна и интеграл могат също да бъдат представени като канонични разширения.

Стохастични процеси на Марков с дискретни състояния

Случаен процес, протичащ в някаква система S с възможни състояния S 1 , S 2 , S 3 , ... се нарича Марковски, или произволен процес без последствия, ако за всеки момент от време t 0 вероятните характеристики на процеса в бъдеще (при t>t 0) зависят само от състоянието му в текущия момент t 0 и не зависят от това кога и как системата е дошла до това състояние ; тези. не зависят от поведението му в миналото (на т

Пример за процес на Марков: система S е брояч в такси. Състоянието на системата в момент t се характеризира с броя километри (десети от километрите), изминати от автомобила до този момент. Нека броячът показва S 0 в момента t 0 / Вероятността в момента t>t 0 броячът да покаже един или друг брой километри (по-точно съответния брой рубли) S 1 зависи от S 0 , но не зависи от това в кой момент, показанията на брояча са се променили до момента t 0 .

Много процеси могат да се разглеждат приблизително като процеси на Марков. Например процесът на игра на шах; система S е група от шахматни фигури. Състоянието на системата се характеризира с броя на фигурите на противника, оставащи на дъската в момента t 0 . Вероятността в момента t>t 0 материалното предимство да бъде на страната на един от опонентите зависи преди всичко от състоянието на системата в момента t 0, а не от това кога и в каква последователност фигурите с дъски нагоре до момента t 0 .

В някои случаи предисторията на разглежданите процеси може просто да бъде пренебрегната и за изследването им могат да се използват модели на Марков.

Марков случаен процес с дискретни състояния и дискретно време (или верига на Марков ) се нарича процес на Марков, при който възможните му състояния S 1 , S 2 , S 3, ... могат да бъдат изброени предварително и преходът от състояние в състояние става мигновено (скок), но само в определени моменти t 0, t 1, t 2, ... наречена стъпкипроцес.

Означете p ij – вероятност за преходпроизволен процес (система S) от състояние I към състояние j. Ако тези вероятности не зависят от номера на стъпката на процеса, тогава такава верига на Марков се нарича хомогенна.

Нека броят на състоянията на системата е краен и равен на m. Тогава може да се характеризира преходна матрица P 1 , който съдържа всички вероятности за преход:

p 11 p 12 … p 1m

п 21 п 22 ... п 2м

P m1 p m2 … p mm

Естествено, за всеки ред ∑ p ij = 1, I = 1, 2, …, m.

Означете p ij (n) като вероятността, че в резултат на n стъпки системата ще премине от състояние I към състояние j. В този случай за I = 1 имаме вероятностите за преход, образуващи матрицата P 1 , т.е. p ij (1) = p ij

Необходимо е, знаейки вероятностите за преход p ij , да се намери p ij (n) – вероятностите за преминаване на системата от състояние I в състояние j на n стъпки. За тази цел ще разгледаме междинно (между I и j) състояние r, т.е. приемаме, че системата ще премине от начално състояние I на k стъпки в междинно състояние r с вероятност p ir (k), след което в останалите n-k стъпкиот междинното състояние r ще премине в крайното състояние j с вероятност p rj (n-k). След това според формулата за общата вероятност

P ij (n) = ∑ p ir (k) p rj (n-k) е равенството на Марков.

Нека се уверим, че като знаем всички вероятности за преход p ij = p ij (1), т.е. матрица P 1 преход от състояние в състояние в една стъпка, можете да намерите вероятността p ij (2), т.е. матрица P 2 преход от състояние в състояние в две стъпки. И познавайки матрицата P 2 - намерете прехода на матрицата P 3 от състояние в състояние в три стъпки и т.н.

Наистина, като поставим n = 2 във формулата P ij (n) = ∑ p ir (k) p rj (n-k), т.е. k=1 (междинно състояние между стъпките), получаваме

P ij (2) = ∑ p ir (1)p rj (2-1) = ∑ p ir p rj

Полученото равенство означава, че P 2 = P 1 P 1 = P 2 1

Ако приемем n = 3, k = 2, по подобен начин получаваме P 3 = P 1 P 2 = P 1 P 1 2 = P 1 3 , а в общия случай P n = P 1 n

Пример

Съвкупността от семейства на определен регион може да бъде разделена на три групи:

1. семейства, които нямат кола и няма да я купуват;

2. семейства, които нямат автомобил, но възнамеряват да закупят такъв;

3. семейства с автомобил.

Проведеното статистическо проучване показа, че преходната матрица за интервал от една година има формата:

(В матрицата P 1 елементът p 31 = 1 означава вероятността семейство, което има кола, също ще има такава, а например елементът p 23 = 0,3 е вероятността семейство, което не е имало кола, но реши да придобие, да изпълни намерението си догодина и т.н.)

Намерете вероятността, че:

1. семейство, което не е имало кола и няма да купува такава, ще бъде в същото положение след две години;

2. Семейство, което не е имало кола, но възнамерява да си купи, ще има кола след две години.

РЕШЕНИЕ:намерете преходната матрица Р 2 за две години:

0,8 0,1 0,1 0,8 0,1 0,1 0,64 0,15 0,21

0 0,7 0,3 0 0,7 0,3 0 0,49 0,51

0 0 1 0 0 1 0 0 1

Тоест търсените вероятности в пример 1) и 2) са равни, съответно

p 11 = 0,64, p 23 = 0,51

След това помислете Стохастичен процес на Марков с дискретни състояния и непрекъснато време, в която, за разлика от веригата на Марков, разгледана по-горе, моментите на възможни преходи на системата от състояние не са фиксирани предварително, а са случайни.

При анализиране на случайни процеси с дискретни състояния е удобно да се използва геометрична схема – т.нар. график на събитията. Обикновено състоянията на системата се представят с правоъгълници (кръгове), а възможните преходи от състояние в състояние са представени със стрелки (ориентирани дъги), свързващи състоянията.

Пример. Постройте графика на състоянията на следния произволен процес: устройството S се състои от два възела, всеки от които може да се повреди в произволен момент от време, след което ремонтът на възела започва незабавно, като продължава за неизвестно преди това произволно време.

РЕШЕНИЕ.Възможни състояния на системата: S 0 – и двата възела работят; S 1 - първият възел е в ремонт, вторият е изправен; S 2 - вторият възел е в ремонт, първият е изправен; S 3 - и двата възела се ремонтират.

Стрелка, посоки, например от S 0 до S 1, означава преход на системата в момента на повреда на първия възел, от S 1 към S 0 - преходът в момента, в който ремонтът на този възел е завършен .

На графиката няма стрелки от S 0 до S 3 и от S 1 до S 2 . Това се обяснява с факта, че отказите на възли се приемат за независими една от друга и например вероятностите за едновременна повреда на два възела (преход от S 0 към S 3) или едновременно завършване на ремонт на два възела (преход от S 3 до S 0) може да се пренебрегне.

Стационарни случайни процеси

неподвижно в тесен смисъл, ако

F(x 1 , …, x n ; t 1 , …, t n) = F(x 1 , …, x n ; t 1 +∆, …, t n +∆)

За произволно

n≥1, x 1 , …, x n , t 1 , …, t n ; ∆; t 1 € T, t i + ∆ € T.

Тук F(x 1 , …, x n ; t 1 , …, t n) е n-мерната функция на разпределение на произволния процес X(t).

Извиква се произволен процес X(t). неподвижно в широк смисъл, ако

Очевидно стационарността в тесен смисъл предполага стационарност в широк смисъл.

От формули:

m(t) = m(t + ∆), K(t, t^) = K(t + ∆, t^ + ∆)

(t € T, t^ € T, t + ∆€ T), t^ + ∆€ T)

От това следва, че за процес, който е стационарен в широкия смисъл, може да се пише

m(t) = mx(0) = const;

D (t) = K(t, t) = K(0,0) = const;

K(t, t^) = K(t – t^, 0) = K (0, t^ - t)

По този начин, за процес, който е стационарен в широкия смисъл, математическото очакване и дисперсията не зависят от времето, а K(t, t^) е функция от вида:

Може да се види, че k(τ) е четна функция, докато

Тук D е дисперсията на стационарния процес

X(t), α i (I = 1, n) са произволни числа.

Първото равенство на системата

K(0) \u003d B \u003d σ 2; |k(τ)| ≤ k(0); ∑ ∑ ά i α j k(t i - t j) ≥ 0

следва от уравнението K(t, t^) = k(τ) = k(-τ), τ = t^ – t. Първо равенство

K(0) \u003d B \u003d σ 2; |k(τ)| ≤ k(0); ∑ ∑ ά i α j k(t i - t j) ≥ 0 е просто следствие от неравенството на Шварц за секциите X(t), X(t^) на стационарния случаен процес X(t). Последно неравенство:

K(0) \u003d B \u003d σ 2; |k(τ)| ≤ k(0); ∑ ∑ ά i α j k(t i - t j) ≥ 0

Вземете го така:

∑ ∑ α i α j k(t i - t j) = ∑ ∑ K(t i , t j)α i α j = ∑ ∑ M[(α i X i)(α j X j)] = M[(∑ α i X i) 2 ] ≥0

Като се вземе предвид формулата за корелационна функция на производната dX(t)/dt на случаен процес, за стационарен произволна функция X(t) получаваме

K 1 (t, t^) = M[(dX(t)/dt)*(dX(t^)/dt^)] = δ 2 K(t, t^) / δtδt^ = δ 2 k(t ^ - t) / δtδt^

Тъй като

δk(t^ - t) / δt = (δk(τ) / δτ) * (δτ / δτ) = - δk(τ) / δτ,

δ 2 k(t^ - t) / δtδt^ = - (δ 2 k(τ) / δτ 2) * (δτ / δt^) = - (δ 2 k(τ) / δτ 2)

тогава K 1 (t, t^) = k 1 (τ) = - (δ 2 k(τ) / δτ 2), τ = t^ – t.

Тук K 1 (t, t^) и k 1 (τ) е корелационната функция на първата производна на стационарния случаен процес X(t).

За n-то производно на стационарен случаен процес, формулата за корелационна функция е:

K n (τ) = (-1) n * (δ 2 n *k(τ) / δτ 2 n)

Теорема. Стационарен случаен процес X(t) с корелационна функция k(τ) е средноквадратичен непрекъснат в точка t ∈ T, ако и само ако

Limk(τ) = k(0)

За да го докажем, ние записваме очевидната верига от равенства:

M [|X(t+τ)-X(T)| 2 ] = M[|X(t)| 2 ] – 2M[|X(t+τ)X(t)|] + M =

2D-2k(τ) = 2.

Оттук е очевидно, че условието за непрекъснатост в средноквадратичния процес X(t) в точката t ∈ T

LimM[|X(t+τ) – X(t)| 2] = 0

Възниква, ако и само ако Lim k(τ) = k(0)

Теорема. Ако корелационната функция k(τ) на стационарен случаен процес X(t) е непрекъсната в средния квадрат в точката τ=0, тогава тя е непрекъсната в средния квадрат във всяка точка τ ∈ R 1 .

За да го докажем, записваме очевидните равенства:

k(τ+∆τ)-k(τ) = M – M =

M(X(t))

След това, прилагайки неравенството на Шварц към факторите в къдравата скоба и вземайки предвид отношенията:

K(t, t^) = k(τ) = k(-τ), τ = t^ – t.

K(0) \u003d B \u003d σ 2; |k(τ)| ≤ k(0); ∑ ∑ ά i α j k(t i - t j) ≥ 0

0 ≤ 2 ≤ MM[|X(t+τ+∆τ)-X(t+τ)| 2] =

Преминаване до предела като ∆τ→0 и отчитане на условието на теоремата за непрекъснатост k(τ) в точка τ=0, както и първото равенство на системата

K(0) \u003d B \u003d σ 2, намираме

Limk(τ+∆τ) = k(τ)

Тъй като тук τ е произволно число, теоремата трябва да се счита за доказана.

Ергодично свойство на стационарни случайни процеси

Нека X(t) е стационарен случаен процес на интервал от време с характеристики

τ = t^ – t, (t, t^) € T×T.

Ергодичното свойство на стационарния случаен процес е, че чрез достатъчно дълго изпълнение на процеса може да се прецени неговото математическо очакване, дисперсия, корелационна функция.

Ще бъде извикан по-строго стационарен случаен процес X(t). ергодичен в очакване,ако

Lim M (|(1 / T)∫ X(t)dt| 2 ) = 0

Теорема

Стационарен случаен процес X(t) с характеристики:

M = 0, K(t, t^) = M = k(τ),

τ = t^ – t, (t, t^) € T×T

е очакването ергодично, ако и само ако

Lim (2 / T) ∫ k(τ) (1 – τ/t)dτ = 0.

За да го докаже, очевидно е достатъчно да се провери, че равенството

Нека запишем очевидните отношения

C = M (|(1 / T)) ∫X(t)dt| 2 ) = (1 / T 2) ∫ ∫ k(t^ - t)dt^dt = (1/T) ∫ dt ∫ k(t^ - t)dt^.

Задавайки тук τ = t^ – t, dτ = dt^ и вземайки предвид условията (t^ = T) → (τ = T - t),

(t^ = 0)→(τ = -t), получаваме

С = (1/T 2) ∫ dt ∫ k(τ)dτ = (1/T 2) ∫ dt ∫ k(τ)dτ + (1/T 2) ∫ dt ∫ k(τ)dτ =

= -(1/T 2) ∫ dt ∫ k(τ)dτ - (1/T 2) ∫ dt ∫ k(τ)dτ

Приемайки съответно в първия и втория член от дясната страна на това равенство τ = -τ^, dτ = -dτ^, τ = T-τ^, dτ = -dτ^, намираме

С = (1/T 2) ∫ dt ∫ k(τ)dτ + (1/T 2) ∫ dt ∫ k(T - τ)dτ

Прилагайки формулата на Дирихле за двойни интеграли, пишем

С = (1/T 2) ∫ dt ∫ k(τ)dτ + (1/T 2) ∫ dt ∫ k(T - τ)dτ = (1/T 2) ∫ (T - τ) k(τ) dτ + (1/T 2) / τk (T – τ)dτ

Във втория член от дясната страна можем да поставим τ^ = T-τ, dτ = -dτ^, след което имаме

От това и от дефиницията на константите става ясно, че равенството

M((1 / T) ∫X(t)dt| 2 ) = (2 / T) ∫ k(τ) (1 – τ/t)dτ

честна.

Теорема

Ако корелационната функция k(τ) на стационарния случаен процес X(t) удовлетворява условието

Lim (1/T) ∫ |k(τ)| dt = 0

Тогава X(t) е ергодично очакване.

Наистина, като се има предвид съотношението

M((1 / T) ∫X(t)dt| 2 ) = (2 / T) ∫ k(τ) (1 – τ/t)dτ

Може да се пише

0 ≤ (2/Т) ∫ (1 – τ/t) k(τ)dτ ≤ (2/T) ∫ (1- τ/t) |k(τ)|dτ ≤ (1/T) ∫ |k (τ)|dτ

Това показва, че ако условието е изпълнено, тогава

Lim (2/T) ∫ (1 – τ/T) k(τ)dτ = 0

Сега, като се вземе предвид равенството

C \u003d (1 / T 2) ∫ (T - τ) k (τ) dτ - (1 / T 2) ∫ (T - τ) k (τ) dτ \u003d 2 / T ∫ (1- (τ / T) )k(τ)dτ

И условието Lim M (|(1 / T)∫ X(t)dt| 2 ) = 0

Ергодичност в очакване на стационарен случаен процес X(t), намираме, че изискваното е доказано.

Теорема.

Ако корелационната функция k(τ) на стационарен случаен процес

X(t) е интегрируема и намалява неограничено при τ → ∞, т.е. условието

За произволно ε > 0, тогава X(t) е стационарен произволен процес с ергодично очакване.

Наистина, предвид израза

За Т≥Т 0 имаме

(1/T) ∫ |k(τ)|dτ = (1/T)[ ∫ |k(τ)|dτ + ∫ |k(τ)|dτ ≤ (1/T) ∫ |k(τ)| dτ ε(1 – T 1 /T).

Преминавайки до предела при Т → ∞, намираме

0 ≤ lim ∫ |k(τ)|dτ = ε.

Тъй като тук ε > 0 е произволна, произволно малка стойност, условието за ергодичност по отношение на математическото очакване е изпълнено. Тъй като това следва от условието

При неограниченото намаляване на k(τ), тогава теоремата трябва да се счита за доказана.

Доказаните теореми установяват конструктивни критерии за ергодичност на стационарните случайни процеси.

X(t) = m + X(t), m=const.

Тогава M = m и ако X(t) е ергодичен стационарен случаен процес, тогава условието за ергодичност Lim M (|(1 / T)∫ X(t)dt| 2 ) = 0 след прости трансформации може да бъде представено като

LimM([(1/T) ∫ X(t)dt – m] 2 ) = 0

От това следва, че ако X(t) е стационарен случаен процес, ергодичен в очакване, тогава очакването на процеса X(t) = m + X(t) може да бъде приблизително изчислено по формулата

M = (1/T) / x(t)dt

Тук T е достатъчно дълъг период от време;

x(t) е изпълнението на процеса X(t) във времевия интервал .

Можем да разгледаме ергодичността на стационарния случаен процес X(t) по отношение на корелационната функция.

Извиква се стационарен случаен процес X(t). ергодичен в корелационната функция, ако

Lim M ([ (1/T) ∫ X(t) X(t + τ)dt – k(τ)] 2 ]) = 0

Това означава, че за стационарен случаен процес X(t) ергодичен в корелационната функция, можем да поставим

k (τ) = (1/T) ∫ x(t)x(t + τ)dt

с достатъчно голям T.

Оказва се, че условието

ограничеността на k(τ) е достатъчна за ергодичността в корелационната функция на стационарния нормално разпределен процес X(t).

Имайте предвид, че произволният процес се извиква нормално разпределениако някоя от неговите крайномерни функции на разпределение е нормална.

Необходимо и достатъчно условие за ергодичността на стационарен нормално разпределен случаен процес е отношението

τ 0: lim (1/T) ∫ (1 – τ/T)dτ = 0

литература

1. Н.Ш. Кремер "Теория на вероятностите и математическа статистика" / UNITI / Москва 2007 г.

2. Ю.В. Кожевников "Теория на вероятностите и математическа статистика" / Машиностроене / Москва 2002г.

3. B.V. Гнеденко "Курс по теория на вероятностите" / Основно издание на физико-математическата литература / Москва 1988 г.

Интерференцията в комуникационните системи се описва с методите на теорията на случайните процеси.

Една функция се нарича случайна, ако в резултат на експеримента приеме една или друга форма, не е известно предварително коя. Случайният процес е случайна функция на времето. Специфичната форма, която един произволен процес приема в резултат на експеримент, се нарича реализация на случаен процес.

На фиг. 1.19 показва набор от няколко (три) реализации на произволен процес , , . Такъв набор се нарича ансамбъл от реализации. С фиксирана стойност на момента на времето в първия експеримент получаваме конкретна стойност , във втория - , в третия - .

Случайният процес има двоен характер. От една страна, във всеки конкретен експеримент той е представен от собствена реализация – неслучайна функция на времето. От друга страна, случайният процес се описва от набор от случайни променливи.

Наистина, разгледайте произволен процес във фиксиран момент от време. След това във всеки експеримент приема една стойност и не е известно предварително коя. По този начин, произволен процес, разглеждан във фиксиран момент от време, е случайна променлива. Ако две точки във времето и са фиксирани, тогава във всеки експеримент ще получим две стойности и . В този случай съвместното разглеждане на тези стойности води до система от две случайни променливи. Когато анализираме случайни процеси в N точки във времето, стигаме до набор или система от N случайни променливи .

Математическо очакване, дисперсия и корелационна функция на случаен процес Тъй като произволен процес, разглеждан във фиксиран момент от време, е случайна променлива, можем да говорим за математическото очакване и дисперсията на случаен процес:

, .

Както и за случайна променлива, дисперсията характеризира разпространението на стойностите на произволен процес спрямо средната стойност. Колкото по-голям е, толкова по-голяма е вероятността от много големи положителни и отрицателни стойности на процеса. По-удобна характеристика е средно квадратното отклонение (MSD), което има същото измерение като самия произволен процес.

Ако произволен процес описва, например, промяна в разстоянието до обект, тогава математическото очакване е средното разстояние в метри; дисперсията се измерва в квадратни метри, а Sco - в метри и характеризира разпространението на възможните стойности на диапазона спрямо средното.

Средната стойност и дисперсията са много важни характеристики, които позволяват да се прецени поведението на произволен процес във фиксиран момент от време. Ако обаче е необходимо да се оцени "скоростта" на промяната в процеса, тогава наблюденията в даден момент не са достатъчни. За да направите това, използвайте две случайни променливи, разглеждани заедно. Точно както при случайните променливи, се въвежда характеристика на връзката или зависимостта между и. За произволен процес тази характеристика зависи от два момента във времето и се нарича корелационна функция: .

Стационарни случайни процеси. Много процеси в системите за управление протичат равномерно във времето. Основните им характеристики не се променят. Такива процеси се наричат стационарни. Точна дефиниция може да се даде, както следва. Случаен процес се нарича стационарен, ако някоя от неговите вероятностни характеристики не зависи от изместването на времевата референция. За стационарен случаен процес математическото очакване, дисперсията и стандартното отклонение са постоянни: , .

Корелационната функция на стационарния процес не зависи от началото t, т.е. зависи само от часовата разлика:

Функцията на корелация на стационарен случаен процес има следните свойства:

1) ; 2) ; 3) .

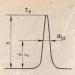
Често корелационните функции на процесите в комуникационните системи имат формата, показана на фиг. 1.20.

Ориз. 1.20. Функции на корелация на процесите

Интервалът от време, на който корелационната функция, т.е. величината на връзката между стойностите на произволен процес, намалява с M пъти, се нарича интервал или време на корелация на произволния процес. Обикновено или. Можем да кажем, че стойностите на произволен процес, които се различават във времето от интервала на корелация, са слабо свързани помежду си.

По този начин познаването на корелационната функция дава възможност да се прецени скоростта на промяна на произволен процес.

Друга важна характеристика е енергийният спектър на произволен процес. Дефинира се като преобразуване на Фурие на корелационната функция:

Очевидно е вярна и обратната трансформация:

Енергийният спектър показва разпределението на мощността на произволен процес, като шум, по оста на честотата.

При анализа на ACS е много важно да се определят характеристиките на произволен процес на изхода на линейна система с известни характеристики на процеса на входа на ACS. Да приемем, че линейната система е дадена от импулсната характеристика. Тогава изходният сигнал в момента се определя от интеграла на Дюамел:

където е процесът на входа на системата. За да намерим корелационната функция, пишем и след умножение намираме математическото очакване

Тук накратко разглеждаме основните въпроси на систематизацията (класификацията) на случайните процеси.

Случаен процес, протичащ (преминаващ) във всяка физическа система, е случаен преход на системата от едно състояние в друго. В зависимост от набора от тези състояния
от много стойности на аргумента всички произволни процеси са разделени на класове (групи):

1. дискретен процес (дискретно състояние) с дискретно време.

2. Дискретен процес с непрекъснато време.

3. Непрекъснат процес (непрекъснато състояние) с дискретно време.

4. Непрекъснат процес с непрекъснато време.

В 1-ви 3-ти калъфи комплект дискретно, т.е. аргумент приема дискретни стойности
обикновено
в 1-ви случай набор от стойности на произволни функции
са дефинирани от равенствата:, е дискретно множество
(Много
разбира се или изброими).

В третия случай комплектът
неизброими, т.е. напречно сечение на произволен процес по всяко време е непрекъсната случайна променлива.

Във 2-ри и 4-ти случай комплектът непрекъснато, във втория случай множеството състояния на системата
краен или изброим, а в четвъртия случай множеството
неизброими.

Ето няколко примера за произволни процеси от 1-4 класа, съответно:

1. Хокеист може или не може да вкара един или повече голове срещу съперник по време на мачове, играни в определени моменти (според графика на играта) от време

произволен процес
е броят отбелязани голове до момента .

2. Случаен процес
- броят на гледаните филми в кино Звезда

от началото на киното до момента във времето .

3. В определени моменти от времето
се измерва температурата
пациент в лечебен център.
- е случаен процес от непрекъснат тип с дискретно време.

4. Индикаторът за нивото на влажност на въздуха през деня в град А.

Могат да бъдат разгледани и други по-сложни класове случайни процеси. За всеки клас случайни процеси се разработват подходящи методи за тяхното изследване.

В учебниците могат да се намерят редица разнообразни и интересни примери за произволни потоци, [B. Feller, h 1.2] и в монографията. Тук ще се ограничим до това.

За произволни процеси се въвеждат и по-прости функционални характеристики в зависимост от параметъра , подобно на основните числови характеристики на случайните величини.

Познаването на тези характеристики е достатъчно за решаване на много проблеми (припомнете си, че пълна характеристика на случаен процес се дава от неговия многомерен (крайномерен) закон за разпределение.

За разлика от числените характеристики на случайните величини, в общия случай функционалните характеристики са определени функции.

4. Очакване и дисперсия на случаен процес

Математическото очакване на случаен процес

дефиниран за всяка фиксирана стойност на аргумента е равно на математическото очакване на съответния участък от произволния процес:

(12)
.

За кратко отбелязване на математическото очакване на s.p. също използвайте нотацията
.

Функция
характеризира поведението на произволен процес средно. Геометричното значение на математическото очакване
се интерпретира като "средна крива", около която са разположени кривите на реализация (виж фиг. 60).

(Виж Фиг. 60 Писмо.).

Въз основа на свойството на очакване на произволна променлива и като се вземе предвид това
произволен процес и
неслучайна функция, получаваме Имотиматематическо очакване произволен процес:

1. Математическото очакване на неслучайна функция е равно на самата функция:
.

2. Неслучаен множител (неслучайна функция) може да бъде изваден от знака на математическото очакване на случаен процес, т.е.

3. Математическото очакване на сбора (разликата) на два случайни процеса е равно на сумата

(разлика) на математическите очаквания на термините, т.е.

Имайте предвид, че ако коригираме аргумента (параметъра) , след това преминаваме от случаен процес към произволна променлива (т.е. преминаваме към напречното сечение на случаен процес), можем да намерим m.o. този процес с това фиксирано

Тъй като, ако напречното сечение на r.p.
дадено е непрекъсната р.в. с плътност
тогава математическото му очакване може да се изчисли по формулата

(13)
.

Пример 2Нека s.p. се определя по формулата, т.е.
r.v.,

Намерете математическото очакване на случаен процес

Решение.Свойство 2. имаме

защото
и следователно
.

Упражнение.Изчислете математическото очакване Ще използвам равенствата

,
,

и след това, въз основа на формула (13), изчислете интеграла и се уверете, че резултатът е същият.

Инструкция.Възползвайте се от равенството

Дисперсия на произволен процес.

Дисперсията на произволен процес
се нарича неслучайна функция

Дисперсия
s.p. разгледани, също така характеризират разсейването (разсейването) на възможните стойности на s.p. относно математическото му очакване.

Заедно с разпръскването на р.п. се взема предвид и стандартното отклонение

(кратко s.c.o.), което се определя от равенството

(15)

Функционално измерение
е равна на размера на s.p.
.

Стойностите на реализациите на р.с. на всеки се отклонява от очакването
с порядък
(виж фиг. 60).

Отбелязваме най-простите свойства на дисперсията на случайни процеси.

1. Дисперсия на неслучайна функция
равно на нула, т.е.

2. Дисперсия на случаен процес
неотрицателен, т.е.

3. Дисперсия на произведението на неслучайна функция
към произволна функция
е равно на произведението на квадрата на неслучайна функция и дисперсията на произволна функция, т.е.