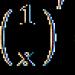Методът на Крамър се основава на използването на детерминанти при решаване на системи линейни уравнения. Това значително ускорява процеса на решение.
Методът на Крамър може да се използва за решаване на система от толкова линейни уравнения, колкото неизвестни има във всяко уравнение. Ако системният идентификатор не е такъв равно на нула, тогава методът на Крамър може да се използва в решението, но ако е равен на нула, тогава не може. В допълнение, методът на Cramer може да се използва за решаване на системи от линейни уравнения, имащи единствено решение.
Определение. Детерминанта, съставена от коефициенти за неизвестни, се нарича детерминанта на системата и се обозначава (делта).
Детерминанти
се получават чрез заместване на коефициентите на съответните неизвестни със свободни членове:
;
.
Теорема на Крамър. Ако детерминантата на системата е различна от нула, тогава системата от линейни уравнения има едно единствено решение и неизвестното е равно на отношението на детерминантите. Знаменателят съдържа детерминантата на системата, а числителят съдържа детерминантата, получена от детерминантата на системата чрез заместване на коефициентите на това неизвестно със свободни членове. Тази теорема е валидна за система от линейни уравнения от произволен ред.
Пример 1.Решете система от линейни уравнения:
Според Теорема на Крамърние имаме:
И така, решението на система (2):
онлайн калкулатор, метод на решаване на Cramer.
Три случая при решаване на системи от линейни уравнения
Както става ясно от Теорема на Крамър, при решаване на система от линейни уравнения могат да възникнат три случая:
Първи случай: система от линейни уравнения има уникално решение
(системата е последователна и категорична)
Втори случай: система от линейни уравнения има безкраен брой решения
(системата е последователна и несигурна)
** 
,
тези. коефициентите на неизвестните и свободните членове са пропорционални.
Трети случай: системата от линейни уравнения няма решения
(системата е непоследователна)
Така че системата млинейни уравнения с ннаречени променливи неставни, ако тя няма нито едно решение, и става, ако има поне едно решение. Нарича се едновременна система от уравнения, която има само едно решение определени, и повече от един – несигурен.
Примери за решаване на системи от линейни уравнения по метода на Крамер
Нека се даде системата
.
Въз основа на теоремата на Крамър
………….
,
Където 
-
системна детерминанта. Получаваме останалите детерминанти, като заменяме колоната с коефициентите на съответната променлива (неизвестна) със свободни условия:
Пример 2.
.
Следователно системата е категорична. За да намерим решението му, изчисляваме детерминантите
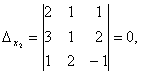
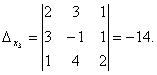
Използвайки формулите на Cramer намираме:
И така, (1; 0; -1) е единственото решение на системата.
За да проверите решенията на системи от уравнения 3 X 3 и 4 X 4, можете да използвате онлайн калкулатор, като използвате метода за решаване на Cramer.
Ако в система от линейни уравнения няма променливи в едно или повече уравнения, то в детерминантата съответните елементи са равни на нула! Това е следващият пример.
Пример 3.Решете система от линейни уравнения по метода на Крамер:
.
Решение. Намираме детерминантата на системата:
Разгледайте внимателно системата от уравнения и детерминантата на системата и повторете отговора на въпроса в кои случаи един или повече елементи от детерминантата са равни на нула. И така, детерминантата не е равна на нула, следователно системата е определена. За да намерим решението му, изчисляваме детерминантите за неизвестните
Използвайки формулите на Cramer намираме:
И така, решението на системата е (2; -1; 1).
За да проверите решенията на системи от уравнения 3 X 3 и 4 X 4, можете да използвате онлайн калкулатор, като използвате метода за решаване на Cramer.
Най-горе на страницата
Продължаваме заедно да решаваме системи, използвайки метода на Cramer
Както вече споменахме, ако детерминантата на системата е равна на нула, а детерминантите на неизвестните не са равни на нула, системата е непоследователна, тоест няма решения. Нека илюстрираме със следния пример.
Пример 6.Решете система от линейни уравнения по метода на Крамер:
Решение. Намираме детерминантата на системата:
Детерминантата на системата е равна на нула, следователно системата от линейни уравнения е или непоследователна и определена, или непоследователна, т.е. няма решения. За да изясним, ние изчисляваме детерминанти за неизвестни
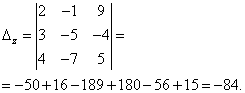
Детерминантите на неизвестните не са равни на нула, следователно системата е непоследователна, тоест няма решения.
За да проверите решенията на системи от уравнения 3 X 3 и 4 X 4, можете да използвате онлайн калкулатор, като използвате метода за решаване на Cramer.
При задачи, включващи системи от линейни уравнения, има и такива, в които освен букви, обозначаващи променливи, има и други букви. Тези букви представляват число, най-често реално. На практика задачите за търсене водят до такива уравнения и системи от уравнения общи свойствавсякакви явления или предмети. Тоест измислили ли сте някакви нов материалили устройство и за да опишете неговите свойства, които са общи, независимо от размера или броя на екземпляра, трябва да решите система от линейни уравнения, където вместо някои коефициенти за променливи има букви. Не е нужно да търсите далеч за примери.
Следващият пример е за подобен проблем, само броят на уравненията, променливите и буквите, обозначаващи някои реално число.
Пример 8.Решете система от линейни уравнения по метода на Крамер:
Решение. Намираме детерминантата на системата:
Намиране на детерминанти за неизвестни
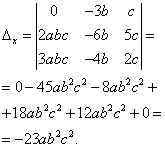
Раздел 3.3 показа ограниченията, които възникват при проследяване на сигнали с различна честота с помощта на система от втори ред. Нека сега разгледаме възможността за смекчаване на някои от тези ограничения чрез въвеждане на втори интегратор в системата. Оказва се, че процесът на улавяне за система от трети ред е по-малко стабилен, отколкото за система от втори ред, но с помощта на втория интегратор е възможно да се разшири обхватът на проследяване на система, която вече е била уловена в първоначалния момент. Функцията за трансфер на филтъра сега изглежда така
и от (3.1) следва:
След заместване този израз се свежда до формата
Нормализиране и въвеждане на означения, които получаваме
Обичайният метод на фазовата равнина не е приложим за диференциални уравнения от трети ред поради факта, че в този случай има три начални условия, съответстващи на три променливи: фаза, честота и скорост на промяна на честотата (в механични системи - преместване, скорост и ускорение). По принцип траекториите, определени от уравнение от трети ред, могат да бъдат представени в триизмерно пространство. Всеки опит да се проектират тези траектории за J набор от начални условия върху равнината би довел до толкова объркваща диаграма, че би било невъзможно да се направят общи заключения от нея.
От друга страна, ако се ограничим до един набор от начални условия, можем да получим проекция на траекторията върху равнината. От особено значение е следният набор от начални условия: С други думи, системата първоначално е заключена, така че честотните и фазовите грешки да са нула, когато референтната честота започне да се променя линейно.
Лесно е да се промени структурата на аналоговото изчислително устройство, за да се приспособи въвеждането на втори интегратор.
Ориз. 3.19. Проекции на траектории във фазовото пространство за контур от трети ред
(виж сканиране)
На фиг. Фигура 3.19 показва серия от траектории, проектирани върху равнината. Във всички разгледани случаи, т.н. В хипотетично триизмерно "фазово пространство" траекториите започват в точка и завършват в ос
На фиг. 3.19, а показва поведението на системата от втори ред при същите начални условия. Крайната или стационарна стойност на фазата е същата, както е показано в § 3.3. Въвеждането на втори интегратор води до намаляване на фазовата грешка в стационарно състояние до нула, колкото по-бързо, толкова повече.С нарастването си най-голямата фазова грешка също намалява, но поради намаляване на затихването на системата, което води до увеличаване на средноквадратичната фазова грешка (виж фиг. 3.19, b - 3.19, g). И накрая, когато системата стане нестабилна.
Подобрението, получено чрез увеличаване на реда на системата, е илюстрирано на фиг. 3.20. Тук както преди, но... В § 3.3 беше показано, че при тази или по-голяма скорост на линейна промяна на честотата, системата не може да извърши проследяване. Ориз. 3.20, но потвърждава това обстоятелство. От друга страна, дори и при най-малка степен на влияние на втория интегратор се получава нулева стационарна фазова грешка. Най-голямата моментна стойност на фазовото несъответствие намалява с увеличаване на коефициента, но когато коефициентът се увеличи, системата отново става нестабилна.
Подобни характеристики се виждат на фиг. 3.21-3.23, с изключение на факта, че с увеличаването на съотношението се изискват все по-големи стойности на коефициента, за да се поддържа системата в състояние на улавяне.В крайна сметка, когато съотношението се доближи до 2 или при, е необходимо да бъде около 1/2. Но от фиг. 3.19, g - 3.23, h е ясно, че при тази стойност системата е нестабилна. Диапазонът от стойности на коефициента, при който системата остава в състояние на улавяне, в зависимост от съотношението, е представен на фиг. 3.24-3.26 със стойности съответно. Диапазонът на допустимите стойности на коефициента е засенчен.Може да се види, че с линейна промяна на честотата въвеждането на система от трети ред направи възможно разширяването на диапазона, в който се получава проследяване, приблизително
Ориз. 3.20. Проекции на траектории във фазовото пространство за контур от трети ред
(виж сканиране)
Ориз. 3.21. Проекции на траектории във фазовото пространство за контур от трети ред
(виж сканиране)
Ориз. 3.22. Проекции на траектории във фазовото пространство за контур от трети ред
(виж сканиране)
Ориз. 3.23. Проекции на траектории във фазовото пространство за контур от трети ред
(виж сканиране)
Ориз. 3.24. Област на състояние на улавяне на системата от трети ред
Ориз. 3.25. Област на състояние на улавяне на системата от трети ред
Ориз. 3.26. Област на състояние на улавяне на системата от трети ред
два пъти повече в сравнение със система от втори ред при и дори повече при по-ниски стойности
Възможно е теоретично да се обясни осцилаторният характер на промяната на коефициента b, когато стойностите му са около или повече от 1/2. Диференцирайки уравнение (3.41), получаваме
За по-задълбочено разбиране на случващото се в тази статия можете да прочетете.Да разгледаме хомогенна система от диференциални уравнения от трети ред
Тук x(t), y(t), z(t) са търсените функции в интервала (a, b), а ij (i, j =1, 2, 3) са реални числа.
Нека напишем оригиналната система в матрична форма
,
Където 
Ще търсим решение на оригиналната система във формата
,
Където 
, C 1 , C 2 , C 3 са произволни константи.
За да намерите основната система от решения, трябва да решите така нареченото характеристично уравнение 
Това уравнение е алгебрично уравнение от трети ред, следователно има 3 корена. Възможни са следните случаи:
1. Корените (собствените стойности) са реални и различни.
2. Сред корените (собствените стойности) има комплексно спрегнати, нека
- истински корен
=
3. Корените (собствените стойности) са реални. Един от корените е кратно.
За да разберем как да действаме във всеки от тези случаи, ще ни трябва:
Теорема 1.
Нека са по двойки различни собствени стойности на матрица A и нека са съответните им собствени вектори. Тогава
формират фундаментална система от решения на оригиналната система.
Коментирайте
.
Нека е реалната собствена стойност на матрица A (реалният корен на характеристичното уравнение) и нека е съответният собствен вектор.
= - комплексни собствени стойности на матрица A, - съответстващ - собствен вектор. Тогава
(Re - реална част, Im - имагинерна част)
формират фундаментална система от решения на оригиналната система. (т.е. и = разглеждани заедно)
Теорема 3.
Нека е коренът на характеристичното уравнение с кратност 2. Тогава оригиналната система има 2 линейно независими решения от формата 
,
където са векторни константи. Ако кратността е 3, тогава има 3 линейно независими решения на формата
.
Векторите се намират чрез заместване на решения (*) и (**) в оригиналната система.
За да разберете по-добре метода за намиране на решения във формата (*) и (**), вижте типичните примери по-долу.
Сега нека разгледаме всеки от горните случаи по-подробно.
1. Алгоритъм за решаване на хомогенни системи диференциални уравнения от трети ред при различни реални корени на характеристичното уравнение.
Като се има предвид системата
1) Съставяме характеристично уравнение
- реални и отделни собствени стойности на 9-те корена на това уравнение).
2) Ние строим къде 
3) Ние строим къде
- собствен вектор на матрица A, съответстващ на , т.е. - всяко системно решение 
4) Ние строим къде
- собствен вектор на матрица A, съответстващ на , т.е. - всяко системно решение 
5)
представляват фундаментална система от решения. След това записваме общото решение на оригиналната система във формата
,
тук C 1, C 2, C 3 са произволни константи,
,
или в координатна форма 
Нека да разгледаме няколко примера:
Пример 1.
2) Намерете 
3) Намираме 
4) Векторни функции 
или в координатна нотация 
Пример 2.
1) Съставяме и решаваме характеристичното уравнение: 
2) Намерете 
3) Намираме 
4) Намерете 
5) Векторни функции 
образуват фундаментална система. Общото решение има формата 
или в координатна нотация 
2. Алгоритъм за решаване на хомогенни системи диференциални уравнения от трети ред при комплексно спрегнати корени на характеристичното уравнение.
- истински корен,
2) Ние строим къде
 |
3) Ние изграждаме
| - собствен вектор на матрица A, съответстващ на , т.е. удовлетворява системата |  |
Тук Re е истинската част
Im - въображаема част
4) представляват фундаментална система от решения. След това записваме общото решение на оригиналната система:
, Където
C 1, C 2, C 3 са произволни константи.
Пример 1.
1) Съставете и решете характеристичното уравнение 
2) Ние строим
3) Ние изграждаме
, Където
Нека намалим първото уравнение с 2. След това добавете първото уравнение, умножено по 2i, към второто уравнение и извадете първото, умножено по 2, от третото уравнение. 
По-нататък 
следователно 
4) - фундаментална система от решения. Нека запишем общото решение на оригиналната система: 
Пример 2.
1) Съставяме и решаваме характеристичното уравнение 
2) Ние строим
(т.е. и взети заедно), където
Умножете второто уравнение по (1-i) и намалете с 2. 
следователно 
3)
Общо решение на оригиналната система
или 
2. Алгоритъм за решаване на хомогенни системи диференциални уравнения от трети ред при множество корени на характеристичното уравнение.
Съставяме и решаваме характеристичното уравнение
Има два възможни случая: 
Разгледайте случай а) 1), където
| - собствен вектор на матрица A, съответстващ на , т.е. удовлетворява системата | |
2) Нека се позовем на теорема 3, от която следва, че има две линейно независими решения от вида 
,
където са постоянни вектори. Да ги вземем за.
3) - фундаментална система от решения. След това записваме общото решение на оригиналната система:
Разгледайте случай b):
1) Нека се позовем на теорема 3, от която следва, че има три линейно независими решения от вида
,
където , , са постоянни вектори. Да ги вземем за.
2) - фундаментална система от решения. След това записваме общото решение на оригиналната система.
За да разберете по-добре как да намерите решения във формата (*), разгледайте няколко типични примера.
Пример 1.
Съставяме и решаваме характеристичното уравнение: 
Имаме случай а)
1) Ние изграждаме 
, Където
От второто уравнение изваждаме първото:
? Третият ред е подобен на втория, зачеркваме го. Извадете второто от първото уравнение: 
2) = 1 (кратно на 2)
Според T.3 този корен трябва да съответства на две линейно независими решения от вида .
Нека се опитаме да намерим всички линейно независими решения, за които, т.е. решения на формата
.
Такъв вектор ще бъде решение тогава и само тогава, когато собственият вектор съответства на =1, т.е.
, или 
, вторият и третият ред са подобни на първия, изхвърлете ги. 
Системата е сведена до едно уравнение. Следователно има две свободни неизвестни, например и . Нека първо им дадем стойностите 1, 0; след това стойностите 0, 1. Получаваме следните решения: 
.
следователно 
.
3) - фундаментална система от решения. Остава да напишем общото решение на оригиналната система: 
. .. По този начин има само едно решение от формата Нека заместим X 3 в тази система: Задраскайте третия ред (той е подобен на втория). Системата е последователна (има решение) за всяко c. Нека c=1. 
или 
Габриел Крамер – математик, създател на едноименния метод за решаване на системи от линейни уравнения
Габриел Крамър е известен математик, който е роден на 31 юли 1704 г. Още като дете Габриел удивлява с интелектуалните си способности, особено в областта на математиката. Когато Крамър е на 20 години, той започва работа като преподавател на пълен работен ден в Женевския университет.
Докато пътува из Европа, Габриел се запознава с математика Йохан Бернули, който става негов ментор. Само благодарение на Йохан Крамер написа много статии по геометрия, история на математиката и философия. А в свободното си от работа време все повече учех математика.
Най-накрая дойде денят, когато Крамър намери начин, с който би било възможно лесно да се решават не само лесни, но и сложни системи от линейни уравнения.
През 1740 г. Крамър публикува няколко произведения, където решението е ясно заявено квадратни матриции е описан алгоритъм за намиране на обратната матрица. След това математикът описва намирането на линейни уравнения с различна сложност, където неговите формули могат да бъдат приложени. Затова и темата се казваше: „Решаване на системи от линейни уравнения по метода на Крамър“.
Ученият умира на 48-годишна възраст (през 1752 г.). Той имаше още много планове, но, за съжаление, така и не успя да ги осъществи.
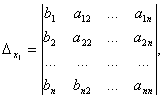
Нека е дадена система от линейни уравнения от тази форма:
където , , са неизвестни променливи, са числени коефициенти и са свободни членове.
Решението на SLAE (системи от линейни алгебрични уравнения) са онези неизвестни стойности, за които всички уравнения на дадена система се трансформират в идентичности.
Ако напишем системата в матрична форма, тогава получаваме , където
Тази основна матрица съдържа елементи, чиито коефициенти за неизвестни променливи,
Това е колонна матрица от свободни термини, но има и колонна матрица от неизвестни променливи:
След намирането на неизвестните променливи матрицата ще бъде решението на системата от уравнения и нашето равенство ще се трансформира в идентичност. . Ако умножите, тогава. Оказва се: .
Ако матрицата е неособена, т.е. нейният детерминант не е равен на нула, тогава SLAE има само едно уникално решение, което се намира с помощта на метода на Cramer.
Като правило, за решаване на системи от линейни уравнения с помощта на метода на Крамер, трябва да обърнете внимание на две свойства, на които се основава този метод:
1. Детерминантата на квадратна матрица е равна на сумата от продуктите на елементите на всеки от редовете (колоните) и техните алгебрични допълнения:
Тук – 1, 2, …, n; – 1, 2, 3, …, n.
2. Сумата от продуктите на елементите на дадена матрица от всеки ред или всяка колона от алгебричните допълнения на определени елементи от втория ред (колона) е равна на нула:
където – 1, 2, …, n; – 1, 2, 3, …, n. .
Така че сега можем да намерим първото неизвестно. За да направите това, е необходимо да умножите двете страни на първото уравнение на системата по, части от второто уравнение по, двете страни на третото уравнение по и т.н. Тоест всяко уравнение на една система трябва да бъде умножено по определени алгебрични допълнения на първата колона на матрицата:
Сега нека добавим всички леви страни на уравнението, да групираме членовете, като вземем предвид неизвестните променливи, и да приравним същата сума към сумата от дясната страна на системата от уравнения:
Можем да се обърнем към свойствата на детерминантите, описани по-горе, и тогава получаваме:
И предишното равенство вече изглежда така:
Ето откъде идва.
Откриваме подобно. За да направите това, трябва да умножите двете страни на уравненията по алгебрични добавки, които са във втората колона на матрицата.
Сега трябва да добавите всички уравнения на системата и да групирате членовете за неизвестни променливи. За да направите това, припомнете свойствата на детерминантата:
От къде идва?
Всички други неизвестни променливи се намират по подобен начин.
Ако посочим:
след това се получават формули, благодарение на които се намират неизвестни променливи по метода на Крамер:
Коментирайте.
Тривиално решение за може да съществува само ако системата от уравнения е хомогенна. Наистина, ако всички свободни членове са нула, тогава детерминантите са нула, тъй като съдържат колона с нула елементи. Разбира се, тогава формулите , , ще дадат
Метод на Крамер – теореми
Преди да решите уравнението, трябва да знаете:
- теорема за анулиране;
- теорема за заместване.
Теорема за заместване
Теорема
Сумата от продуктите на алгебричните добавки на всяка колона (ред) с произволни числа е равна на новата детерминанта, в която тези числа заместват съответните елементи на първоначалната детерминанта, които съответстват на тези алгебрични добавки.
Например,
където са алгебричните допълнения на елементите от първата колона на оригиналната детерминанта:
Теорема за анулиране
Теорема
Сумата от произведенията на елементите на един ред (колона) от алгебричните допълнения на съответните елементи на друг ред (колона) е равна на нула.
Например:
Алгоритъм за решаване на уравнения по метода на Крамер
Методът на Cramer е прост начин за решаване на линейни системи алгебрични уравнения. Тази опция се прилага изключително за SLAE, в които броят на уравненията съвпада с броя на неизвестните и детерминантата е различна от нула.
Така че, когато научите всички етапи, можете да преминете към алгоритъма за решаване на уравнения по метода на Cramer. Нека го запишем последователно:
Стъпка 1. Изчислете главния детерминант на матрицата
и трябва да се уверите, че детерминантата е различна от нула (не е равна на нула).
Стъпка 2. Намерете детерминанти
Това са детерминантите на матриците, които са получени от матрицата чрез замяна на колоните със свободни членове.
Стъпка 3. Изчислете неизвестни променливи
Сега нека си спомним формулите на Cramer, които използваме за изчисляване на корените (неизвестни променливи):
Стъпка 4. Проверете
Ние проверяваме решението, като използваме заместване в оригиналния SLAE. Абсолютно всички уравнения в системата трябва да се трансформират в тъждества. Можете също да изчислите произведението на матриците. Ако получената матрица е равна на , тогава системата е решена правилно. Ако не е равно, най-вероятно има грешка в едно от уравненията.
Нека първо да разгледаме система от две линейни уравнения, тъй като е по-проста и ще ви помогне да разберете как правилно да използвате правилото на Крамър. Ако разбирате прости и кратки уравнения, тогава можете да решавате по-сложни системи от три уравнения с три неизвестни.
Освен всичко друго, има системи от уравнения с две променливи, които могат да бъдат решени изключително благодарение на правилото на Крамър.
И така, дадена ни е система от две линейни уравнения:
Първо, изчисляваме основната детерминанта (детерминанта на системата):
Това означава, че ако , тогава системата или има много решения, или системата няма решения. В този случай няма смисъл да използвате правилото на Крамър, тъй като няма да има решение и трябва да запомните метода на Гаус, с помощта на който този пример се решава бързо и лесно.
Ако , тогава системата има само едно решение, но за това е необходимо да се изчислят още две детерминанти и да се намерят корените на системата.
Често на практика детерминантите могат да бъдат обозначени не само с , но и с латинската буква, което също ще бъде правилно.
Лесно е да намерите корените на уравнението, тъй като основното е да знаете формулите:
Тъй като успяхме да решим система от две линейни уравнения, сега можем лесно да решим система от три линейни уравнения и за това ще разгледаме системата:
Тук алгебричните допълнения на елементите са първата колона. Когато решавате, не забравяйте за допълнителни елементи. И така, в система от линейни уравнения трябва да намерите три неизвестни - с известни други елементи.
Нека създадем детерминанта на системата от коефициентите на неизвестните:
Нека умножим член по член на всяко уравнение съответно по , , – алгебрични допълнения на елементите от първата колона (коефициенти на ) и съберем и трите уравнения. Получаваме:
Съгласно теоремата за разширение, коефициентът при е равен на . Коефициентите на и ще бъдат равни на нула според теоремата за анулиране. Дясната страна на равенството по теоремата за заместване дава нова детерминанта, която се нарича спомагателна и се обозначава
След това можем да запишем равенството:
За да намерим и умножаваме всяко от уравненията на изходната система в първия случай съответно по , във втория - по и добавяме. Впоследствие получаваме:
Ако , тогава в резултат получаваме формулите на Крамер:
Процедурата за решаване на хомогенна система от уравнения
Специален случай са хомогенните системи:
Сред решенията на една хомогенна система може да има както нулеви решения, така и решения, различни от нула.
Теорема
Ако детерминантата на хомогенна система (3) е различна от нула, тогава такава система може да има само едно решение.
Наистина, спомагателни детерминанти, като тези, които имат нулева колона и следователно зад формулите на Крамър
Теорема
Ако една хомогенна система има ненулево решение, тогава нейният детерминант е нула
Наистина, нека едно от неизвестните, например, е различно от нула. Според хомогенността равенството (2) ще се запише: . Откъде идва това
Примери за решения по метода на Крамер
Нека разгледаме решението, като използваме метода на Cramer като пример и ще видите, че няма нищо сложно, но бъдете изключително внимателни, тъй като честите грешки в знаците водят до неправилен отговор.
Пример 1
Задача
Решение
Първото нещо, което трябва да направите, е да изчислите детерминантата на матрицата:
Както виждаме, следователно, според теоремата на Крамър, системата има уникално решение (системата е последователна). След това трябва да изчислите спомагателни детерминанти. За да направите това, заменете първата колона от детерминантата с колона със свободни коефициенти. Оказва се:
По подобен начин намираме останалите детерминанти:
И проверяваме:
Отговор
Пример 2
Задача
Решете системата от уравнения по метода на Крамер:
Решение
Намираме детерминантите:
Отговор
= = = = = =
Преглед
Уравнението има уникално решение.
Отговор
Пример 3
Задача
Решете системата с помощта на метода на Крамер
Решение
Както разбирате, първо намираме основната детерминанта:
Както виждаме, главният детерминант не е равен на нула и следователно системата има уникално решение. Сега можем да изчислим останалите детерминанти:
Използвайки формулите на Крамер, намираме корените на уравнението:
За да сте сигурни, че решението е правилно, трябва да проверите:
Както виждаме, замествайки решените корени в уравнението, получихме същия отговор като в началото на задачата, което показва правилното решение на уравненията.
Отговор
Системата от уравнения има единствено решение: , , .
Има примери, когато уравнението няма решения. Това може да е случаят, когато детерминантата на системата е равна на нула, а детерминантите на неизвестните не са равни на нула. В този случай те казват, че системата е непоследователна, тоест няма решения. Нека да видим в следния пример как може да се случи това.
Пример 4
Задача
Решете система от линейни уравнения по метода на Крамер:
Решение
Както в предишните примери, намираме основния детерминант на системата:
В тази система детерминантата е равна на нула, съответно системата е несъстоятелна и определена или несъгласувана и няма решения. За да изясним, трябва да намерим детерминанти за неизвестните, както направихме по-рано:
Намерихме детерминантите на неизвестните и видяхме, че всички те не са равни на нула. Следователно системата е непоследователна и няма решения.
Отговор
Системата няма решения.
Често в задачи върху системи от линейни уравнения има уравнения, в които няма еднакви букви, тоест освен буквите, които означават променливи, има и други букви и те означават някакво реално число. На практика такива уравнения и системи от уравнения се дължат на проблеми за търсене на общи свойства на всякакви явления или обекти. Тоест вие сте изобретили някакъв нов материал или устройство и за да опишете свойствата му, които са общи, независимо от размера или количеството на образеца, трябва да решите система от линейни уравнения, където вместо някои коефициенти за променливите там са писма. Нека да разгледаме този пример.
Използвайки формулите на Cramer, намираме:
Отговор
И накрая, преминаваме към най-сложната система от уравнения с четири неизвестни. Принципът на решението е същият като в предишните примери, но поради голямата система може да стане объркващо. Затова нека разгледаме това уравнение с пример.
В първоначалния детерминант от елементите на втория ред извадихме елементите на четвъртия ред, а от елементите на третия ред извадихме елементите на четвъртия ред, които бяха умножени по 2. Извадихме също от елементите на четвъртия ред елементите на първия ред, умножени по две. Трансформациите на началните детерминанти за първите три неизвестни се извършват по същата схема. Сега можете да намерите детерминанти за неизвестни:
За да трансформираме детерминантата за четвъртото неизвестно, извадихме елементите на четвъртия ред от елементите на първия ред.
Сега, като използвате формулите на Cramer, трябва да намерите:
Отговор
И така, намерихме корените на системата от линейни уравнения:
Нека обобщим
Използвайки метода на Крамер, можете да решавате системи от линейни алгебрични уравнения, ако детерминантата не е равна на нула. Този метод ви позволява да намерите детерминанти на матрици от същия ред като на благодарение на формулите на Cramer, когато трябва да намерите неизвестни променливи. Ако всички свободни членове са нула, тогава техните детерминанти са нула, тъй като съдържат колона с нула елементи. И разбира се, ако детерминантите са равни на нула, по-добре е системата да се реши чрез метода на Гаус Метод на Крамер в Excel от 2007 г. (XLSX)
Метод на Крамер - теорема, примери за решенияактуализиран: 22 ноември 2019 г. от: Научни статии.Ru
Матрици. Действия върху матрици. Свойства на операциите върху матрици. Видове матрици.
Матрици (и, съответно, математическата част - матрична алгебра)са важни в приложната математика, тъй като позволяват да се запише значителна част от математическите модели на обекти и процеси в доста проста форма. Терминът "матрица" се появява през 1850 г. Матриците са споменати за първи път през древен Китай, по-късно от арабски математици.
Матрица A=A mnред m*n се извиква правоъгълна таблица с числа, съдържаща m - реда и n - колони.
Матрични елементи aij,за които i=j се наричат диагонал и форма главен диагонал.
За квадратна матрица (m=n) главният диагонал се образува от елементите a 11, a 22,..., a nn.
Матрично равенство.
А=Б, ако матрицата нарежда АИ бса еднакви и a ij =b ij (i=1,2,...,m; j=1,2,...,n)
Действия върху матрици.
1. Събиране на матрици - поелементна операция
Матрично изваждане - поелементна операция
3. Произведението на матрица и число е поелементна операция
4. Умножение A*Bматрици според правилото ред към колона(броят на колоните на матрица A трябва да е равен на броя на редовете на матрица B)
A mk *B kn =C mnи всеки елемент с ijматрици Cmn равно на суматапроизведения на елементите на i-тия ред на матрица A и съответните елементи на j-тата колона на матрица B.
Нека покажем операцията на матрично умножение с помощта на пример:
6. Транспониране на матрица A. Транспонираната матрица се обозначава с A T или A"
Редовете и колоните са разменени
Пример
Свойства на операциите върху матрици
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
Видове матрици
1. Правоъгълен: мИ н- произволни цели положителни числа
2. Квадрат: m=n
3. Матричен ред: m=1. Например (1 3 5 7) - в много практически задачи такава матрица се нарича вектор
4. Матрична колона: n=1. Например
5. Диагонална матрица: m=nИ a ij =0, Ако i≠j. Например
6. Идентификационна матрица: m=nИ
7. Нулева матрица: a ij =0, i=1,2,...,m
j=1,2,...,n
8. Триъгълна матрица: всички елементи под главния диагонал са 0.
9. Квадратна матрица: m=nИ a ij =a ji(т.е. равни елементи са разположени на места, симетрични спрямо главния диагонал), и следователно А"=А
Например,
Обратна матрица- такава матрица A−1, когато се умножи по която оригиналната матрица Аводи до матрицата на идентичността д:
Квадратната матрица е обратима тогава и само ако не е сингулярна, т.е. нейният детерминант не е равен на нула. За неквадратни матрици и сингулярни матрици няма обратни матрици. Въпреки това е възможно да се обобщи тази концепция и да се въведат псевдообратни матрици, подобни на обратните в много свойства.
Примери за решаване на системи от линейни алгебрични уравнения с помощта на матричния метод.
Нека да разгледаме матричния метод с примери. В някои примери няма да описваме подробно процеса на изчисляване на детерминанти на матрици.
Пример.
Като се използва обратна матрицанамерете решението на системата от линейни уравнения
.
Решение.
В матрична форма оригиналната система ще бъде записана като, където 
. Нека изчислим детерминантата на основната матрица и се уверим, че е различна от нула. В противен случай няма да можем да решим системата с помощта на матричния метод. Ние имаме 
, следователно, за матрицата Аможе да се намери обратната матрица. Така, ако намерим обратната матрица, тогава дефинираме желаното решение на SLAE като . И така, задачата се свежда до изграждането на обратната матрица. Да я намерим.
Обратната матрица може да се намери с помощта на следната формула:
, където е детерминантата на матрица A, е транспонираната матрица от алгебрични допълнения на съответните елементи на матрица .
Концепцията за обратна матрица съществува само за квадратни матрици, матрици “две по две”, “три по три” и др.
Полярни координати. В полярната координатна система позицията на точка M
М
ПРАВОЪГЪЛНИ КООРДИНАТИ В ПРОСТРАНСТВОТО
ПРАВ
1. Общо уравнениеправ.Всяко уравнение от първа степен по отношение на x и y, т.е. уравнение от вида:
(1) Извика се Ax+Bu+C=0. общности по уравнението на правата линия ( + ≠0), A, B, C - ПОСТОЯННИ КОЕФИЦИЕНТИ.
КРИВИ ВТОРИ РЕД
1. Кръг.Окръжността е набор от точки в една равнина, разположени на еднакво разстояние -
на равно разстояние от дадена точка (център). Ако r е радиусът на окръжността, а точката C (a; b) е нейният център, тогава уравнението на окръжността има формата:
Хипербола. Хиперболата е набор от точки на равнина, абсолютът
величината на разликата в разстоянията до две дадени точки, наречена fo-
парчета, има постоянна стойност (тя се обозначава с 2а) и тази константа е по-малка от разстоянието между фокусите. Ако поставим фокусите на хиперболата в точките F1 (c; 0) и F2 (- c; 0), получаваме каноничното уравнение на хиперболата 
АНАЛИТИЧНА ГЕОМЕТРИЯ В ПРОСТРАНСТВОТО
РАВЕН И ПРАВ
равнина, наречена нормален вектор.
Повърхност от втори ред
Повърхност от втори ред- геометрично място на точки в тримерното пространство, чиито правоъгълни координати удовлетворяват уравнение от вида
в която поне един от коефициентите , , , , , е различен от нула.
Видове повърхности от втори ред
Цилиндрични повърхности
Повърхността се нарича цилиндрична повърхнина с образуваща, ако за която и да е точка от тази повърхност правата, минаваща през тази точка, успоредна на образуващата, принадлежи изцяло на повърхността.
Теорема (за уравнението на цилиндрична повърхност).
Ако в някаква декартова правоъгълна координатна система повърхнината има уравнението , то тя е цилиндрична повърхнина с образуваща, успоредна на оста.
Нарича се крива, определена от уравнение в равнината ръководствоцилиндрична повърхност.
Ако посоката на цилиндрична повърхност е дадена от крива от втори ред, тогава такава повърхност се нарича цилиндрична повърхност от втори ред .
| Елиптичен цилиндър: | Параболичен цилиндър: | Хиперболичен цилиндър: |
 |  |
|
 |  |  |
| Двойка съвпадащи редове: | Двойка съвпадащи равнини: | Двойка пресичащи се равнини: |
 |  |
Конични повърхнини
Конична повърхност.
Основна статия:Конична повърхност
Повърхността се нарича конична повърхностс връх в точка, ако за всяка точка от тази повърхност правата, минаваща през и принадлежи изцяло на тази повърхност.
Функцията се извиква хомогенен ред, ако е вярно следното:
Теорема (за уравнението на конична повърхнина).
Ако в някаква декартова правоъгълна координатна система повърхността е дадена от уравнението 
, където е хомогенна функция, тогава е конична повърхност с връх в началото.
Ако една повърхност е дефинирана от функция, която е хомогенен алгебричен полином от втори ред, тогава тя се нарича конична повърхност от втори ред .
· Каноничното уравнение на конус от втори ред има формата:
Повърхности на въртене]
Повърхността се нарича повърхност на въртене около ос, ако за някоя точка 
от тази повърхност окръжност, минаваща през тази точка в равнина с център в и радиус 
, принадлежи изцяло на тази повърхност.
Теорема (за уравнението на повърхността на въртене).
Ако в някаква декартова правоъгълна координатна система повърхността е дадена от уравнението, тогава е повърхност на въртене около оста.
| Елипсоид: | Еднолистов хиперболоид: | Двулистов хиперболоид: | Елиптичен параболоид: |
 |  |  |  |
 |  |  |  |
В случай изброените по-горе повърхности са повърхности на въртене.
Елиптичен параболоид
Уравнението на елиптичен параболоид е
Ако , тогава елиптичен параболоид е повърхност на въртене, образувана от въртенето на парабола, чийто параметър 
, около вертикална ос, минаваща през върха и фокуса на дадена парабола.
Пресечната точка на елиптичен параболоид с равнина е елипса.
Пресечната точка на елиптичен параболоид с равнина или е парабола.
Хиперболичен параболоид]
Хиперболичен параболоид.
Уравнението на хиперболичен параболоид има формата
Пресечната точка на хиперболичен параболоид с равнина е хипербола.
Пресечната точка на хиперболичен параболоид с равнина или е парабола.
Поради геометричното си сходство хиперболичният параболоид често се нарича "седло".
Централни повърхности
Ако центърът на повърхност от втори ред съществува и е уникален, тогава неговите координати могат да бъдат намерени чрез решаване на системата от уравнения:
По този начин знакът, който се приписва на минор на съответния елемент на детерминантата, се определя от следната таблица:
В горното равенство, изразяващо детерминанта от трети ред,
от дясната страна има сумата от произведенията на елементите от 1-ви ред на детерминанта и техните алгебрични добавки.
Теорема 1. Детерминантът от трети ред е равен на сумата от произведенията
елементи на който и да е от неговите редове или колони в техните алгебрични допълнения.
Тази теорема ви позволява да изчислите стойността на детерминантата, разкривайки я според
елементи на някой от неговите редове или колони.
Теорема 2. Сума от произведенията на елементи от всеки ред (колона)
детерминантата на алгебричните допълнения на елементи от друг ред (колона) е равна на нула.
Свойства на детерминантите.
1°. Детерминантата няма да се промени, ако редовете на детерминантата се заменят с колона
tsami, а колоните са съответните редове.
2°. Общият множител на елементите на всеки ред (или колона) може
да бъде взето отвъд определящия знак.
3°. Ако елементите на един ред (колона) от детерминантата, респ
са равни на елементите на друг ред (колона), то детерминантата е равна на нула.
4°. При пренареждане на два реда (колони) детерминантата променя знака на
противоположност.
5°. Детерминантата няма да се промени, ако елементите от същия ред (колона)
добавете съответните елементи от друг ред (колона), умножени по същото число (теоремата за линейната комбинация от паралелни серии на детерминантата).
Решаване на система от три линейни уравнения с три неизвестни.
намерени с помощта на формулите на Крамер
Приема се, че D ≠0 (ако D = 0, тогава оригиналната система е или несигурна, или непоследователна).
Ако системата е хомогенна, т.е. има формата 
и неговата детерминанта е различна от нула, тогава тя има уникално решение x = 0,
Ако детерминантата на хомогенна система е равна на нула, тогава системата е редуцирана
или към две независими уравнения (третото е тяхно следствие), или към
едно уравнение (другите две са неговите следствия). Първи случай
възниква, когато сред минорите на детерминантата на еднородна система има
поне едно е различно от нула, второто е, когато всички второстепенни на този детерминант са равни на нула. И в двата случая една хомогенна система има безкраен брой решения.
Изчислете детерминанта от трети ред
