Ministarstvo obrazovanja i znanosti Samarske regije

Državno autonomno obrazovna ustanova dodatni strukovno obrazovanje(napredno usavršavanje) specijalisti

SAMARA REGIONALNI INSTITUT NAPREDNIH STRUČNJAKA

I DOKVALIFIKACIJE PROSVJETNIH RADNIKA

Završni rad

Na naprednim tečajevima

Prema WB IOC

“Metodičke značajke nastave rješavanja problema s parametrom u kontekstu prijelaza na nove obrazovne standarde”

(15.06. - 19.06.2015.)

Dizajniranje sustava zadataka na više razina s parametrom na temu:

"izvedeno"

Izvedena:

Valieva F.G.,

profesorica matematike

Srednja škola GBOU nazvana po. M.K. Ovsjanikova

S. Isakli

Krilati plod

2015

OBJAŠNJENJE

Puno ime (puno ime)

Valieva Fanuzya Galimzyanovna

Mjesto rada

Srednja škola GBOU nazvana po. M.K. Ovsyannikov selo Isakly,

Isaklinski okrug, regija Samara

Naziv radnog mjesta

Profesor matematike

Artikal

Matematika

Klasa

Ciljevi:

1. provedba zahtjeva Saveznog državnog obrazovnog standarda LLC pri proučavanju teme: "Derivativa"

   Generalizacija i sistematizacija znanja i metoda aktivnosti na temu "Derivativa"; formiranje vještina rješavanja problema s parametrima.

   Razvoj istraživačke i obrazovne djelatnosti.

Koncept duhovnog i moralnog razvoja i obrazovanja osobnosti ruskog građaninaje metodološka osnova za razvoj i provedbu saveznog državnog obrazovnog standarda opće obrazovanje.

Savezna država obrazovni standard osnovno opće obrazovanje o školski tečaj matematika.

Standard se temeljisustavno-aktivni pristup.

Standard utvrđuje zahtjeve za rezultate učenika u svladavanju osnovnih obrazovni program osnovno opće obrazovanje:

osobni;

metasubjekt;

subjekt.

Zadaci:

- obrazovni: analizirati i razumjeti tekst problema, samostalno istaknuti i formulirati spoznajna svrha, preformulirati uvjet, izgraditi logički lanac razmišljanja, kritički procijeniti dobiveni odgovor, svjesno i dobrovoljno konstruirati govorni iskaz, odabrati naj učinkovit način rješavanje problema, postavljanje i formuliranje problema, postavljanje hipoteza i njihovo opravdanje, semantičko čitanje;

- razvijanje: postavljanje ciljeva, planiranje svojih aktivnosti ovisno o specifičnim uvjetima; promišljanje metoda i uvjeta djelovanja, kontrola i vrednovanje procesa i rezultata aktivnosti, samoregulacija,kroz rješavanje problema razvijati kreativnu i mentalnu aktivnost učenika, intelektualne kvalitete: sposobnost "vidjeti" problem, evaluacijske radnje, neovisnost, fleksibilnost mišljenja;

- obrazovni: smislenost, sposobnost slušanja i vođenja dijaloga, sudjelovanje u kolektivnoj raspravi o problemima, njegovanje odgovornosti i točnosti.

Zadaci s parametrima - ovo su nestandardni zadaci, tj.neobičan kako po postavci i sadržaju, tako i po načinima rješavanja. Uloga takvihzadataka, njihove važnosti i koristi za razvoj logično mišljenje, intuicija,kreativne sposobnosti učenika, formiranje visokih matematičkih vještina kod njihkulture su vrlo velike. Poznato je da se učitelji suočavaju s ozbiljnimmetodičkih problema u nastavi rješavanje takvih problema, unatoč prisutnosti,dovoljno velika količina udžbenici i članci u časopisima. Razlog za to je sasvim očit: glavna strategija matematičkog obrazovanja u školi je razvoj vještina i sposobnosti rješavanja određenog skupa standardnih problema, od kojih je većina povezana s tehnologijom algebarske transformacije. Jednadžbe (nejednadžbe) s parametrima pripadaju drugom tipu problema - problemima, čije rješenje zahtijeva, prije svega, sposobnost provođenja - ponekad prilično razgranatih - logičkih konstrukcija i istraživanja.

Rješavanje problema s parametrima zahtijeva istraživanje, čak i ako se ta riječ ne spominje u tvrdnji problema. Mehanička primjena formula nije dovoljna, potrebno je razumjeti obrasce i imati vještinu analize konkretnog slučaja na temelju poznatih opća svojstva objekt, sustavnost i dosljednost u rješenju, sposobnost kombiniranja pojedinačnih slučajeva koji se razmatraju u jedan rezultat. To objašnjava poteškoće s kojima se učenici susreću pri rješavanju takvih problema.

Trenutno je ideja kombiniranja učenja za rješavanje problema s učenjem za njihovu konstrukciju postala prilično raširena. Konstruiranjem zadatka razumjet ćemo proces stvaranja novog zadatka. Osnova za konstruiranje problema je sposobnost konstruiranja kvadratnog trinoma. U ovom slučaju koriste se različite tehnike: analogija, variranje koeficijenata kvadratnog trinoma, variranje nove varijable, variranje zahtjeva problema. Složenije funkcije mogu djelovati kao koeficijenti i nova varijabla. Dakle, možete koristiti takav kvadratni trinom, koji će vam pomoći u organiziranju ponavljanja više složene funkcije: eksponencijalni, logaritamski, trigonometrijski. S jedne strane potrebno je poznavati svojstva kvadratnog trinoma, as druge strane svojstva funkcije se ponavljaju čime se postiže kombinabilnost problema.

Izbor problema s parametrima za poučavanje njihovog rješavanja i dizajna može se objasniti sljedećim okolnostima:

pri rješavanju problema s parametrima dolazi do ponavljanja, a kao rezultat toga dolazi do dublje, trajnije asimilacije programskih pitanja;

rješavanje problema s parametrima proširuje matematičke horizonte i daje nove pristupe rješavanju problema;

razvija se matematičko i logičko mišljenje, sposobnost analize, usporedbe i generalizacije;

stječu se vještine za istraživački rad;

pomoć u pripremanju ispita;

dolazi do formiranja takvih osobina ličnosti kao što su naporan rad, odlučnost, ustrajnost, snaga volje, točnost.

Formiran UUD u okviru Saveznog državnog obrazovnog standarda pri rješavanju problema sa sljedećim parametrima:

Faze rješavanja problema

Formirana UUD

Analiza stanja(uvođenje slovnih oznaka)

• postavljanje ciljeva;

  isticanje bitnih informacija;

  formuliranje problema i predviđanje rješenja;

  apstrakcija;

  analogija;

  klasifikacija (tipologizacija);

  simboličke akcije.

Shematski zapis uvjeta problema u obliku tablice, dijagrama, grafikonas upisanim slovnim oznakama

• planiranje;

  sistematizacija;

  znakovno-simboličke radnje;

  modeliranje.

Izrada modela(traženje analogije, izvlačenje dobro poznatog zakona iz matematike ili fizike)

• stvaranje načina za rješavanje problema;

  podešavanje stanja;

  grafičko modeliranje.

Rješavanje jednadžbe, sustava itd.(potraga za nepoznatim)

• analiza i identifikacija značajnih informacija;

  izvođenje zaključaka;

  izgradnja lanca zaključivanja;

  postavljanje i testiranje hipoteza;

  transformacija modela.

Interpretacija modela(provjera i vrednovanje rješenja, korijeni)

• analiza;

  izvođenje zaključaka;

  specifikacija;

  znakovno-simboličko djelovanje (tumačenje).

Studija(generalizacija problema ili načina rješavanja za modificirane uvjete, drugi pristupi rješavanju)

• analiza;

  sinteza;

  traženje analoga;

  izgradnja lanca zaključivanja;

  sposobnost sažetog prenošenja sadržaja;

  vještina dijagrama, simbola, modela;

  stvaranje načina rješavanja problema tragačke i kreativne prirode.

Odraz

• stvaranje značenja;

  planiranje;

  kontrolirati;

  korekcija;

  razred;

  voljna samoregulacija;

  spremnost na samorazvoj, samoobrazovanje;

  sposobnost samostalnog određivanja ciljeva vlastitog učenja;

  postaviti i formulirati sebi nove zadatke;

  razvijati motive i interese svog obrazovnog djelovanja.

Višerazinski sustav zadataka

Metodika nastave koja se temelji na višerazinskom sustavu zadataka temelji se na postupnom svladavanju blokova svoje matrice. Glavna značajka ove tehnike je da na svakoj razini, tj. prilikom savladavanja odgovarajućeg stupca matrice učenik se svaki put susreće sa sve tri vrste situacije učenja koji nastaju prilikom rješavanja problema.

Višerazinski sustav zadataka za svaku temu kolegija formira se korištenjem njegove matrične reprezentacije, identificiranjem rangiranog popisa osnovnih elemenata obrazovnog sadržaja i osnovnih zadataka koji im odgovaraju, s jedne strane, i razine obuke, odražavajući sposobnost rješavati poznate, modificirane i nepoznate probleme, s druge strane.

Takva matrica tematskog problemskog sustava sadrži 3 retka koja odgovaraju trima vrstama situacija učenja koje se javljaju pri rješavanju problema iN stupci koji odražavaju broj osnovnih zadataka teme. Takav tablični (matrični) prikaz sustava zadataka teme pomaže u potpunosti popuniti njegove matematičke i aktivnosti (formiranje UUD) komponente na svakoj razini i time implementiratikriteriji za cjelovitost predmeta i aktivnosti (što znači kognitivni UUD) sustav koji se formira obrazovne zadatke. Štoviše, ako osnovni zadaci igraju ulogu jedinstvenih integratora predmetno-sadržajne komponente u sustavu, onda bi pri osmišljavanju i provedbi procesa učenja sličnu ulogu trebali imati i univerzalni aktivnosti učenja(opće metode i tehnike aktivnosti) u odabranim situacijama.

Obrazovne aktivnosti pri rješavanju problema koji se nalaze u prvom retku matrice reproduktivne su naravi (koriste se općeobrazovne aktivnosti kao što su klasifikacija, subsumiranje pojma, izvođenje konzekvencija, radnje, konstruiranje logičkog lanca zaključivanja, dokazivanje i sl.). Zadaci koji se koriste su različitiočite veze između podataka i traženih (poznatih i nepoznatih) elemenata. Učenik identificira (prepoznaje poznate zadatke među sličnim), reproducira naučene metode ili algoritme djelovanja, primjenjuje stečeno znanje u praksi za određenu poznatu klasu zadataka i dobiva nove informacije na temelju primjene naučenog obrasca aktivnosti.

Kod rješavanja problema druge linije, reproduktivne obrazovne aktivnosti u kombinaciji s rekonstruktivnim, u kojem se obrasci aktivnosti ne reproduciraju jednostavno iz sjećanja, već se rekonstruiraju pod malo izmijenjenim uvjetima (ovdje se takve općeobrazovne radnje očituju kao identificiranje i formuliranje kognitivnog cilja, traženje i isticanje potrebnih informacija, znakovno-simboličke radnje , uključujući matematičko modeliranje, strukturiranje znanja).

Konačno, pri rješavanju problema treće linije obrazovna je djelatnost istraživačke i kreativne prirode. Učenik mora biti sposoban snalaziti se u novim situacijama i razviti temeljno nove programe djelovanja (postaviti hipotezu, testirati: opravdati ili opovrgnuti, iznijeti novu itd., implementirati istraživačke aktivnosti). Rješavanje problema odgovarajućeg bloka zahtijeva od studenta opsežan fond provjerenih i brzo implementirajućih algoritama; sposobnost brzog prekodiranja informacija iz znakovno-simboličkog oblika u grafički oblik i, obrnuto, iz grafičkog u znakovno-simbolički oblik; sustavna vizija tečaja. Pritom ne podrazumijeva samo korištenje starih algoritama u novim uvjetima i povećanje tehničke složenosti, već ga karakterizira neočiglednost primjene i kombiniranja proučavanih algoritama. Zadaci na ovoj razini imaju kompliciranu logičku strukturu i karakterizira ih prisutnostlatentne veze između podataka i traženih elemenata. Takvi se problemi obično nude kao najteži na prijemnim ispitima na sveučilištima s visokim zahtjevima za matematičku pripremu kandidata i u zadacima 17,18, 20, 21 Jedinstvenog državnog ispita.

Višerazinski sustav problema na temu "Derivacija"

№ p/p

Naziv zadatka

Vrsta zadatka

Izračunavanje derivacije po definiciji.

ZZ

Ministarstvo zdravlja

NZ

Pronalaženje izvodnica zbroja, umnoška, ​​kvocijenta funkcija

ZZ

Ministarstvo zdravlja

NZ

Proučavanje monotonosti funkcije

ZZ

funkcija raste na cijelom brojevnom pravcu?

Ministarstvo zdravlja

Na kojim vrijednostima parametara funkcija opada za sve vrijednosti ?

NZ

Pronađite skup svih brojeva a, za svaki od njih funkcijaf(x) = grijeh 2 x – 8(a + 1) sinx + (4 a 2 + 8 a – 14) xraste na cijelom brojevnom pravcu i nema kritičnih točaka.

Pronalaženje ekstremnih točaka

ZZ

ima jednu stacionarnu točku?

Ministarstvo zdravlja

Odredite pri kojoj vrijednosti parametra maksimalna funkcija jednako 9

NZ

Pri kojim vrijednostima parametra a funkcionira funkcijaf(x) = (a 2 – 3 a + 2) (cos 2 – grijeh 2 + (a – 1) x + grijeh1 nema kritičnih točaka?

Pronalaženje najveće i najmanje vrijednosti kontinuirane funkcije na intervalu i diferencijabilne na intervalu

ZZ

Saznajte na kojim vrijednostima parametraA najmanja vrijednost funkcijeg = x 2 -12 x + a jednaka nuli na segmentu.

Ministarstvo zdravlja

Na kojoj vrijednosti parametra najmanja vrijednost funkcije jednaki

NZ

Na kojim vrijednostima parametara funkcija uzima vrijednosti manje od 5 za bilo koji

Cijela studija i planiranje

ZZ

3 + 3x 2

Ministarstvo zdravlja

Pri kojoj je vrijednosti parametra a minimum funkcije f(x) = ax 2 – 6ax + a 2 – 9 jednako 1?

NZ

Jednadžba tangente na graf funkcije u zadanoj točki

ZZ

Na kojim vrijednostima parametara ravno je tangenta na graf funkcije ?

Ministarstvo zdravlja

Na kojim vrijednostima parametara tangenta na graf funkcije odsijeca od prve četvrtine jednakokračni trokut s površinom

NZ

Na kojim vrijednostima parametara tangente na graf funkcije , nacrtana u točkama njezina sjecišta s osi, čine kut između sebe

Primjena izvoda na rješavanje problema u geometriji, fizici i ekonomiji

ZZ

Kolike bi trebale biti stranice pravokutnika s opsegom?Ptako da mu je površina najveća?

Ministarstvo zdravlja

Prozor ima oblik pravokutnika, s gornje strane omeđen polukrugom (slika 3). Opseg prozora je P. Odredi polumjer polukruga R na kojem je površina prozora najveća.

NZ

Slika visine a obješena je na zid tako da joj je donji rub h jedinica viši od razine očiju promatrača. Na kojoj udaljenosti x od zida mora biti promatrač da bi kut gledanja slike bio najveći (slika 7a)?

Rješenja

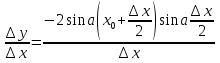
Riješenje :

1. Funkcija f(x) opada za sve vrijednosti x ako je izvod

f'(x) = 6ax 2 + 18ax + 30a = 6a(x 2 + 3x + 5)< 0

za sve x.

2. Odavde nalazimo da je a< 0.

3 . Odgovor: a (–∞; 0).

1. Nađite skup svih brojeva a od kojih je za svaki funkcija f (x) = sin 2x – 8(a + 1)sinx + (4a 2 + 8a – 14)x rastuća na cijelom brojevnom pravcu i nema kritične točke.

1. Za bilo koje fiksno a, ova je funkcija diferencijabilna u svakoj točki na brojevnom pravcu.

2. Budući da je funkcija f(x) rastuća, u svakoj točki x mora vrijediti nejednakost f′(x) ≥ 0.

3. Budući da, osim toga, f(x) nema kritičnih točaka, tada za svaki x mora biti zadovoljena nejednakost f′(x) ≠ 0.

4. Dakle, ako funkcija zadovoljava uvjete problema, tada za sve x mora biti zadovoljena nejednakost f′(x) > 0.

5. S druge strane, ako nejednakost f′(x) > 0 vrijedi za sve x, tada funkcija očito nema kritičnih točaka i raste.

6. Pronađite izvod ove funkcije:

f′( x) = 2 cos 2 x – 8( a + 1) cosx + 4 a 2 + 8 a – 14.

Sada se problem može preformulirati na sljedeći način: pronaći sve vrijednosti parametra a, za svaku od kojih nejednakost vrijedi za bilo koji x

cos 2x – 4(a + 1) cos x + 2a 2 + 4a – 7 > 0.(1)

7. S obzirom da je cos 2x = 2 cos 2 x – 1, a pretpostavljajući cos x = t, gdje je –1 ≤ t ≤ 1, prepisujemo nejednadžbu (1) na sljedeći način:

2t 2 – 1 – 4(a + 1)t + 2a 2 + 4a – 7 > 0,

ili

t 2 – 2(a + 1)t + a 2 + 2a – 4 > 0. (2)

8. Nakon što smo funkciju na lijevoj strani nejednadžbe (2) označili s ϕ(t), dajemo novu formulaciju izvornog problema: pronaći sve vrijednosti od a, za svaku od kojih je najmanja vrijednost funkcije ϕ (t) na intervalu [–1; 1] je pozitivan.

9. Derivacija ϕ′(t) = 2t – 2(a + 1) nestaje u t 0 = a + 1.

10. Najmanja vrijednost funkcije ϕ(t) na intervalu [–1; 1] je:

ϕ (–1) = a 2 + 4a – 1,Akoa + 1 ≤ –1;

ϕ (a + 1) = –5,Ako –1 < a + 1 < 1;

ϕ(1) = a 2 – 5 ako je a + 1 ≥ 1.

11. Budući da je najmanja vrijednost funkcije ϕ(t) na intervalu [–1; 1] moraju biti pozitivne, tada vrijednosti parametra a koje zadovoljavaju uvjete problema pripadaju dvama intervalima: a ≤ –2 i a ≥ 0.

12. Ako je a ≤ –2, tada željene vrijednosti parametra a zadovoljavaju nejednakost a 2 + 4a – 1 > 0.

13. Ako je a ≥ 0, tada željene vrijednosti parametra a zadovoljavaju nejednakost a 2 – 5 > 0.

14. Prema tome, skup željenih vrijednosti a je unija rješenja dvaju sustava nejednakosti:

(3)

a ≥ 0

A 2 -5 > 0 (4)

15. Skup rješenja sustava (3) je interval –∞< a < –2 –√5 , а множество решений системы (4)- промежуток a >√5 .

16. Odgovor: a (–∞; –2 –√5) (√5; +∞).

1. Kako je ova funkcija diferencijabilna na cijelom brojevnom pravcu, kritične točke funkcije f(x) su one točke u kojima je derivacija f′(x) = 0.

2. U ovom slučaju imamo f′(x) =(a – 1)(a – 2) (–sin+ (a – 1).

3. Očito, ako je a = 1, tada je f′(x) = 0 za bilo koji x R, tj.

Za dana funkcija svaka točka x R je kritičan.

4. Pretpostavimo da je a 1. Tada jednadžba f′(x) = 0 poprima oblik

(a – 2)grijeh = 2. (1)

Slijedi da ako je |a – 2|< 2, т. е. если a (0; 1) (1; 4),

tada jednadžba (1) nema korijene i, prema tome, za navedene vrijednosti a, funkcija f(x) nema kritične točke.

5 . Odgovor: a (0; 1) (1; 4).

Najmanja vrijednost brojnika i najveća vrijednost nazivnik se postiže pri različitim vrijednostima x. Stoga je za pronalaženje najmanje vrijednosti funkcije zgodno koristiti derivaciju. Prepišimo nejednakost u obliku

Gdjet=3- cos 2 x, t

Nađimo najmanju vrijednost funkcijef( t) = , na segmentu. Budući da izvedenicaf "( t) = negativno natDafopada i poprima najmanju vrijednost prit=3, f Ime = f(3) = .

Odgovor:a

Za koliko je najmanji prirodni k jednadžba x 3 + 3x 2 – 45x + k = 0 ima točno jedan korijen?

1. Konstruirajte skicu grafa funkcije y 1 = x 3 + 3x 2 – 45x i odredite najmanju prirodnu vrijednost k pri kojoj ovaj graf siječe pravac y 2 = –k u točno jednoj točki.

2. a) D(y 1 ) = R;

buu 1 / = 3x 2 + 6x – 45; 1 / u intervalima (–∞; –5), (–5; 3) i (3; +∞) ilustrirano je na sl. 1. Na sl. 2 prikazuje shematski prikaz grafa funkcije y 1 .

3. Očito, ova jednadžba ima jedina odluka, ako je –k > 175 ili –k< –81, т. е. k < –175 или k >81. Najmanja prirodna vrijednost k je 82.

4. Odgovor: k = 82.

Pri kojoj je vrijednosti parametra a minimum funkcije f(x) = ax2 – 6ax + a2 – 9 jednak 1?

1. f′(x) = –6x 2 + 6x + 12.

2. y′ = 0 na x 1 = 2.

6. Odgovor: a = 2.

Pri kojoj je vrijednosti parametra a minimalna funkcija f(x) = –2x 3 + 3x 2 + 12x + 4a jednako je 1?

Za koje vrijednosti parametra a je pravac y=ax-2 tangenta na graf funkcije y=1+ln⁡ x?

Pri kojim vrijednostima parametra a tangenta na graf funkcije y=a-x^2 odsijeca jednakokračni trokut površine 9/32 od prve četvrtine?

jer , prema uvjetu, tangenta mora presijecati funkciju načetvrtine, tj. Trokut je jednakokračan i pravokutan, pa su mu ostali kutovi jednaki, Aligdje tangenta poprima oblik dodirna točka tangente s grafom duž x-osi jednaka je . pomoću formule tangente na graf budući da površina trokuta mora biti jednaka , To jer četvrtina.Gdje

Pri kojim vrijednostima parametra a tangente na graf funkcije y=4x^2-|a|x, povučene u točkama njegovog sjecišta s osi x, međusobno sklapaju kut od 60°

Kolike trebaju biti stranice pravokutnika s opsegom P da bi njegova površina bila najveća?

Prozor ima oblik pravokutnika, s gornje strane omeđen polukrugom (slika 3). Opseg prozora je P. Odredi polumjer polukruga R na kojem je površina prozora najveća.

Slika visine a obješena je na zid tako da joj je donji rub h jedinica viši od razine očiju promatrača. Na kojoj udaljenosti x od zida mora biti promatrač da bi kut gledanja slike bio najveći (slika 7a)?

Književnost

Azarov A.I., Barvenov S.A., Fedosenko V.S.Metode rješavanja problema s parametrima. Matematika za srednjoškolce. Minsk: “Aversev”, 2003.

V.S. Vysotsky, Problemi s parametrima za pripremu za jedinstveni državni ispit

Gornshtein P.I., Polonsky V.B., Yakir M.S. Problemi s parametrima. - K.: RIA "Tekst"; MP "OKO", 1992. -290 str.

Kachalova G. A. O potrebi uključivanja sadržajno-metodološke linije „Problemi s parametrima” u obrazovni modul „Osnove matematike” //Materijał yMię dzynarodowejNaukowi- PraktycznejkonferencjiPostę stró wwnauce. Nowepoglą dy, problemy, innovacje. 29.07.2012. - 31.07.2012. Część 2. - Łódź, 2012. - str. 67–70.

Kozko A. I., Panferov V. S., Sergeev I. N., Chirsky V. G. Jedinstveni državni ispit 2011. Matematika. Zadatak C5. Problemi s parametrom / Ed. A. L. Semenova i I. V. Jaščenko. - M.: MTsNMO, 2011.-144 str.

Rodionov E.M. Rješavanje problema s parametrima. M.: MP "Rus-90", 1995

Najviša kategorija

Sankt Peterburg

2006
Uvod

Rješavanje problema s parametrima možda je najteži dio osnovnog tečaja matematike, ne samo za školarce i kandidate, već i za učitelje.

To se objašnjava činjenicom da je glavna strategija matematičkog obrazovanja u školi razvoj vještina i sposobnosti rješavanja određenog skupa standardnih problema, od kojih se većina odnosi na tehniku ​​algebarskih transformacija. Pri rješavanju problema s parametrima potrebno je razmotriti različite slučajeve, u svakom od kojih se metode rješavanja problema često međusobno značajno razlikuju. U tom slučaju treba jasno i dosljedno pratiti očuvanje ekvivalencije jednadžbi i nejednakosti koje se rješavaju, uzimajući u obzir opseg definicije izraza uključenih u jednadžbu ili nejednadžbu, a također uzeti u obzir izvedivost operacija izvedena. Osim toga, potrebna je, prije svega, sposobnost proizvodnje - ponekad prilično razgranatih logičkih konstrukcija. Osim toga, arsenal standardnih transformacija treba značajno nadopuniti nekim specifičnim transformacijama.

Problemi s parametrima predstavljaju vrlo široko polje za punopravnu matematičku aktivnost, učenicima otvaraju značajan broj heurističkih tehnika. Općenito, dragocjen za matematički razvoj pojedinca, primjenjiv u istraživanju i na bilo kojem drugom matematičkom materijalu.

Problemi s parametrima pokazuju koliko se praksa prijamnih ispita odvojila od škole, koliko se razlikuju zahtjevi za maturanta i zahtjevi za kandidata za fakultet.

Kvadratna funkcija.

Budući da je glavna u školskom tečaju matematike, kvadratna funkcija prirodno tvori široku klasu problema s parametrima, različitih oblika i sadržaja, ali ujedinjenih zajedničkom idejom - njihovo rješenje temelji se na svojstvima y = ax2 + bx + c .

Gotovo sva važna svojstva kvadratna funkcija određuju se tablicom.

stol 1

Gornji dijagram sasvim jasno pokazuje da diskriminant D, vodeći koeficijent a, apscisa xo = - b/2a, vrhovi parabole čine “okvir” na kojem je izgrađena teorija kvadratne funkcije. Zatim ćemo razmotriti probleme čije je rješenje vezano uz proučavanje predznaka D i a, probleme čije je rješenje vezano uz položaj vrha parabole i probleme vezane uz položaj korijena kvadratnog trinoma.

Diskriminant, seniorski koeficijent.

https://pandia.ru/text/78/525/images/image013_18.jpg" align="lijevo" width="179" height="216 src=">

Riješenje:

Budući da jednadžba nema stvarne korijene, graf funkcije y = ax2 + bx + c nalazi se ili potpuno iznad OX osi ili potpuno ispod nje, tj. vrijednosti funkcije su ili veće od nule ili manje nego nula za bilo koju vrijednost x ( x - bilo koji broj).

Prema uvjetu a+b+c<0, f (1) = а+b+с, то f (1) < 0, значит f (х) < 0 для всех значений х. с = f (0), т. е. с равно значению функции

Sl.2 y= f (x) pri x=0. Zaključak: sa<0.

Odgovor: S<0.

Zadatak 3. Neka je P(x)=2x2+ax+b, Q(x)= x2+cx+d i a2+ c2 +4d≤ 2ac + 4b(a, b, c su realni brojevi). Dokažite da ako jednadžba P(x)=0 ima realne korijene, onda i jednadžba Q(x)=0 također ima realne korijene.

Riješenje:

Ako jednadžba P(x)=0 ima realne korijene, tada je D = a2 – 8b≥0. Dokažimo da iz nejednakosti a2+ c2 +4d≤ 2ac + 4b i a2 – 8b≥0 slijedi nejednadžba c2 – 4d ≥0. (x2+cx+d=0

D = s2 – 4d).

a2+ c2 +4d≤ 2ac + 4b (-2)

2a2-2 s2 -8d ≥- 4as -8b

A2+4as≥ 2s2+8d ili - a2+4as - 4s2 ≥-2s2+8d; - a2+4ac - 4c2 = - (a2-4ac+ 4c2) = - (a-c)2

s2 – 4d ≥ (a-s)2/2≥0, tj. diskriminanta jednadžbe Q(x)=0, što znači da jednadžba Q(x)=0 ima rješenje.

Zadatak 4.

2y-x + xy = 0 (1)

(x + 2a – 4)y – ax + 5 = 0 (2)

ima jedno rješenje?

Riješenje:

Očito, ni za koji y par (-2; y) nije rješenje ovog sustava. Tada iz jednadžbe (1) dobivamo y = x/(x + 2). Zamjenom u jednadžbu (2) dobivamo:

(1 – a)x2 + x + 10 = 0(3). Ova jednadžba ima jedinstveno rješenje ako:

1). a – 1 = 0, a = 1,

2). D = 40a – 39 = 0, a = 39/40

3). Kvadratna jednadžba (3) ima dva različita korijena, od kojih je jedan –2. Zamijenimo x = -2 u jednadžbu (3), dobivamo a = 3.

Odgovor: a = 1, a = 39/40, a = 3.

Zadatak 5. Pri kojim vrijednostima parametra a funkcionira sustav dviju jednadžbi

x2 -2x - y2= 0 (1)

y = ax – a + b (2)

ima jedinstveno rješenje za bilo koju vrijednost b?

Riješenje:

Zamijenimo y = ax – a + b (2) u jednadžbu (1), dobivamo:

(1-a2) x2 – 2(1-a2 + ab)x – (a - b)2=0 (3)

1).Ako je 1-a2 = 0, jednadžba (3) ima rješenje za bilo koju vrijednost. To je lako provjeriti: neka je, na primjer, b = 0.

2) 1-a2≠0, tada je jednadžba (3) kvadratna. D = b2 – a2 + 1. Nađimo one vrijednosti parametra a za koje vrijedi nejednakost b2 – a2 + 1≥0 za bilo koju vrijednost b. Nejednakost b2 ≥ a2-1 vrijedi za bilo koju vrijednost b, ako je a2-1≤0, budući da a = 1, a = -1 nije prikladno, tada -1<а<1.

Odgovor: -1<а<1.

Zadatak 6. Pri kojim se vrijednostima parametra a ne sijeku grafovi funkcija y = 2ax + 1 y = (a-6)x2 –2?

Riješenje:

Nepostojanje sjecišnih točaka između dva grafa funkcije jednako je nepostojanju rješenja sustava dviju jednadžbi:

y = 2ax + 1 (1)

y = (a-6)x2 –2 (2)

2ax + 1 = (a-6)x2 –2 (3) tako da jednadžba (3) nema rješenja, ispunjavamo uvjet: D<0

4a2 + 12(a – 6)<0, -6<а<3.

Odgovor: -6<а<3.

Vrh parabole.

Zadatak 7. Realni brojevi x, y i takvi da je uvjet x + y = 2a – 1(1) i uvjet

x2 + y2 = a2 + 2a – 3 (2), izvode se istovremeno. Pri kojim vrijednostima parametra a umnožak xy poprima najmanju vrijednost?

Riješenje:

xy = ((x + y)2 – (x2 + y2))/2 = ((2a – 1)2 – (a2 + 2a – 3))/2 = 3/2a2 – 3a +2

Promotrimo funkciju f(a) = 3/2a2 – 3a +2

1). Otkrijmo pri kojim vrijednostima parametra a sustav dviju jednadžbi (1) i (2) ima rješenje.

Zamijenimo y = 2a – 1 – x u jednadžbu (2), dobivamo: 2 x2 +2x(1 – 2a) +3a2 - 6a +4 = 0. Da bi ova jednadžba imala rješenje, ispunjavamo uvjet: D≥ 0, -2a2+ 8a – 7 ≥0,

https://pandia.ru/text/78/525/images/image017_29.gif" width="14">2-√2 / 2 ≤ a≤2 + √2 / 2

2). Nađimo pri kojim vrijednostima parametra a funkcija f(a) = 3/2a2 – 3a +2 poprima najmanju vrijednost na danom segmentu. Apscisa vrha parabole y = f(a) a = 1, 1<0, значит f(а) <0, тогда функция f(а) = 3/2а2 – 3а +2 принимает наименьшее значение при

Odgovor: 2 - √2 / 2.

Zadatak 8. Nađite sve vrijednosti parametra a za koje vrh dviju parabola f(a) = 4x2 + 8ax – a i g(x) = 4ax2 – 8x + a –2 leži na istoj strani ravne linije y = -5.

Riješenje:

Otkrijmo pri kojim su vrijednostima parametra a ordinate vrhova ovih parabola ili veće od –5 ili istovremeno manje od –5. Neka je x1 vrh apscise parabole y = f(x), x1 = - a, f(x1) = -4a2 - a, x2 je vrh apscise y = g(x), x2 = 1/a,

g(x2) = -4/a + a – 2. Ispunimo dva uvjeta istovremeno: -4a2 - a > -5 (1) -4/a + a – 2> -5 (2)

ili -4a2 - a<-5 (3), -4/а + а – 2<-5 (4). Для того, чтобы выполнить (1) и (2) одновременно или (3) и (4) одновременно достаточно решить неравенство (-4а2 - а+5)(-4/а + а – 2+5) >0,

a ova nejednakost vrijedi za a<-4 или при-5/4<а<0.

Odgovor: A<-4; -5/4<а<0.

Zadatak 9. Odredi najmanju i najveću vrijednost funkcije y = 2–ax –3x2 za -1≤h≤1.

Riješenje:

Zato što je seniorski koeficijent -3<0, то ветви параболы направлены вниз и функция возрастает при х≤ хо и убывает при х≥хо, где хо =- b/2а - абсцисса вершины параболы. Результат в задаче зависит от положения абсциссы хо относительно отрезка [-1; 1], а не завсиит от знака дискриминанта. Выполним схематически рисунки (для D>0)

https://pandia.ru/text/78/525/images/image020_10.jpg" width="624" height="209 src=">

Za svaki od tri slučaja a), b), c) najmanja vrijednost funkcije f(t) = t2-8at+7a2

na segmentu postiže se u točkama na x = 1, x = 2a, x = 1/4. Tada je pitanje na koje treba odgovoriti rješenje za skup od tri sustava:

1≤4a 1/4<4а<1 4а<1/4

f(1)<0 или f(4а)<0 или f(1/4)<0

a≥1/4 1/16<а<1/4 а≤1/16

1 – 8a + 7a2<0 или 16а2 – 32а2 + 7а2<0 или 1/16 – 2а + 7а2<0.

Odgovor: 1/28<а<1.

Testni zadaci

1). Pri kojim se vrijednostima parametra a grafovi funkcija y = 2h – a i y = (a +1)h2 + 1 sijeku samo u jednoj točki?

2). Pronađite sve vrijednosti parametra a za koje su grafovi funkcija y = (a +5)x2 – 1 i

y = (3a + 15)x – 4 nemaju zajedničkih točaka?

3). Za koje vrijednosti parametra a jednadžba (a +4)x2 +6x –1 = 0 ima jedinstveno rješenje?

4). Za koje vrijednosti parametra a jednadžba (2a +8)x2 – (a + 4)x +3 = 0 ima jedinstveno rješenje?

5). Za koje vrijednosti parametra a jednadžba ima više od jednog rješenja?

a) (a +6)x2 - 8x +a = 0

b) a(2a + 4) x2 – (a +2)x – 5a – 10 = 0.

6). Nađite sve vrijednosti parametra k za koje krivulja y = x2 + kx + 4 dodiruje os OX.

7). Jer ono što je najmanja cjelobrojna vrijednost parametra k je kvadratni trinom

(k–2)x2+8x +k+4 je pozitivan za sve realne vrijednosti x?

8). Brojevi x, y, a su takvi da je x + y = a –1, x2 + y2 = 5a2 – 3a + 0,5. Pri kojim vrijednostima parametra a umnožak xy poprima najveću vrijednost?

9). Brojevi x, y, a su takvi da je x + y = a +1, xy = a2 – 3a + 4. Pri kojim vrijednostima parametra

a zbroj x2 + y2 ima najveću vrijednost?

10). Pronađite najveću i 1 najmanju vrijednost funkcije y = 2x2 – 2ax + na segmentu

jedanaest). Pronađite najveću vrijednost kvadratnog trinoma 1–(a–2)x –x2 na segmentu

12). Za koje je vrijednosti parametra a najmanja vrijednost funkcije y = x2 + (a+4) x+2a+3 na segmentu jednaka –4?

13). Za koje vrijednosti parametra a je najmanja vrijednost funkcije y = x2 –(a+2) x+a2 na segmentu [-1;1] jednaka 4?

14). Pri kojim je vrijednostima parametra a najveća vrijednost funkcije?

f(h) = -(1/a)h +(7/a) ·3-h – 3a2 na segmentu [-1;0] negativno?

Odgovori na ispitni zadatak

1) a=-2, a=-1, a=0.

2) –19/3<а≤-5.

3) a=-4, a=-13.

5) a) -8<а<-6 и -6<а<2

b) a=-2; -1/40 0.

10) Ako a<-2, то наименьшее значение функции при х=-1 и равно 3+2а, наибольшее значение функции при х=1 и равно 3–2а;

ako je -2≤a<0, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=1 и равно 3–2а;

ako je 0≤a<2, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=-1 и равно 3+2а;

ako je a≥2, tada je najmanja vrijednost funkcije pri x=1 jednaka 3–2a, najveća vrijednost funkcije pri x=-1 jednaka je 3+2a;

11) Ako je a≤0, tada je -6a2-a+2, ako je 0<а<8/5, то 2- 6а +а2/4, если а ≥8/5, то 19а-6а2 -14

13) a=-2 ili a=(1+√21)/2

14) |a|>(7√3)/12.

Položaj korijena kvadratnog trinoma

Razmotrimo nekoliko tipičnih problema vezanih uz položaj korijena kvadratnog trinoma ax2+bx+c. Provest ćemo sva razmišljanja pod pretpostavkom a>0. Ako a<0,то рассуждения проводятся аналогично.

Zadatak br. 1.

Pod kojim uvjetima su oba korijena kvadratne jednadžbe ax2+bx+c =0 (ne nužno različita) veća od nekog zadanog broja k?

Riješenje.

Konstruirajmo shematske grafove funkcije kvadratnog trinoma y= ax2+bx+c, gdje x1 i x2 zadovoljavaju uvjete: x1>k, x2>k. Neka je f(x)= ax2+bx+c. Graf y= f(x) ili siječe os OX (D > 0) ili je dodiruje (D = 0). Tada je potrebno ispuniti uvjet: xo>k, y(k) >0. Ako a< 0 условие: х1>k, x2>k određeni su sustavom nejednadžbi:

https://pandia.ru/text/78/525/images/image023_20.gif" width="14" height="86">

sl.4

Zadatak 11. Pronađite sve vrijednosti parametra a za koje su svi korijeni jednadžbe

x2–6ax+2–2a+9a2 =0 više od 3.

Riješenje.

Ako je traženi uvjet ispunjen mogući su sljedeći položaji parabole koja je graf funkcije f(x) = x2–6ax+2–2a+9a2

sl.5

Riješimo sustav nejednadžbi:

https://pandia.ru/text/78/525/images/image026_8.jpg" align="lijevo" width="324" height="239 src=">

Dovoljno je ispuniti uvjet: y(k)<0, если а >0. Na a<0, y(к) > 0.

Riža. 6

Zadatak 12. Pronađite sve vrijednosti parametra a za koje se 1 nalazi između korijena jednadžbe x2–2ax+3–4a+2a2=0.

Riješenje.

Budući da je vodeći koeficijent pozitivan, dovoljno je ispuniti uvjet f(1)<0, где f(х)=х2–2ах+3–4а+2а2

4–6a+2a2<0, 1<а<2.

Odgovor: 1<а<2

Zadatak br. 3. Pod kojim uvjetima točno jedan korijen kvadratne jednadžbe ax2+bx+c =0, koja ima različite korijene, leži na intervalu (k, e)?

Konstruirajmo shematski grafove y = ax2 + bx + c prema uvjetima ovog problema za a > 0.

https://pandia.ru/text/78/525/images/image028_8.jpg" width="623" height="246 src=">

Riješimo nejednadžbu: f(1) f(2)<0.

(a2+8a+7)(a2+14a+16)<0

7-√33< а<-7; -7+√33<а<-1.

Odgovor: -7-√33< а<-7; -7+√33<а<-1.

Zadatak 14. Pronađite sve vrijednosti parametra a za koje jednadžba 2cos(2x)+2asin(x)+a-1=0 ima jedinstveno rješenje na intervalu (-π/2;0).

Riješenje.

2cos(2x)+2a sinx+a-1=0

2(1–2 sin2x)+ 2a sinx+a–1=0

4 sin2h–2a sinx –a–1=0

Neka je sinx=t Jer -π/2<х<0, то -1< t <0

Nađite one vrijednosti parametra a za koje jednadžba 4t2– 2at–a–1=0 ima jedinstveno rješenje na intervalu (-1;0).

Jednadžba 4t2– 2at–a–1=0 ima jedinstveno rješenje na intervalu (-1;0) ako je:

1). D =0 D/4=(a+2)2 D =0 za a=-2.

2). Promotrimo funkciju f(t)= 4t2– 2at–a–1

Konstruirajmo shematski graf funkcije y=f(t)

https://pandia.ru/text/78/525/images/image030_16.gif" width="14" height="50 src=">

f(0) f(1) ≤0 a≤-3; a≥-1

Odgovor: a≤-3; a≥-1; a=-2.

Zadatak br. 4. Pod kojim uvjetima oba korijena (ne nužno različita) kvadratne jednadžbe ax2+bx+c leže na segmentu [k; e]. Razmotrimo uvjet a>0. Neka postoji funkcija f(x)= ax2+bx+c

https://pandia.ru/text/78/525/images/image032_14.gif" width="14" height="110"> D≥0

k≤ xo≤ e

Zadatak 15. Pronađite one vrijednosti parametra a za koje su svi korijeni jednadžbe

x2- 2(a–3)x–a +3=0 leže u intervalu (-3;0).

Riješenje.

Pod uvjetom da postoji barem jedan korijen, graf funkcije f(x) = x2- 2(a–3)x–a +3 može se shematski urediti na jedan od dva načina.

https://pandia.ru/text/78/525/images/image034_12.gif" width="14" height="110"> D≥0 4(a – 3)(a – 2) ≥0

3<хо<0 3<а – 3 <0 1,2<а≤2.

f(-3) >0 5a – 6>0

f(0) >0 -a+3>0

Jednadžba je sin x − 1 + a = sin x − 2. sin x − 2 sin x − 3 Rješenje. Uz pretpostavku t = sin x, jednadžbu svodimo na oblik at2 − 5at + 6a − 1 = 0. Ako je a = 0, tada nema rješenja. Za a = 0 i pod uvjetom a ∈ (−∞; −4] ∪ (0; +∞) √ dobivamo korijene jednadžbe t1,2 = 5a ± 2aa. Budući da je vrh parabole f (t) = at2 − 5at + 6a − 1 nalazi se u točki tv = 2, 5 uvjet |t| 1 za manji od korijena bit će zadovoljen ako na krajevima segmenta [−1; 1] funkcija ima različite predznake : f (−1) f (1) 0 ili (2a−1)(12a−1) 0. Rješenje posljednje 1 nejednadžbe je interval a ∈ 12 ;1 .2 √ a2 Odgovor: Ako je a ∈ 12 ; 2: x = (−1)n arcsin 5a− 2a +4a +πn, n∈Z, 1 1 za ostale a nema rješenja Zadatak 6.7 Za koje vrijednosti parametra a vrijedi funkcija f (x) = 8ax − a sin 6x − 7x − sin 5x raste na cijeloj osi realnih brojeva i nema kritičnih točaka Rješenje: Funkcija f (x) je diferencijabilna za bilo koju vrijednost a i f (x) = 8a − 6a cos 6x − 7 − 5 cos 5x Problem se može preformulirati na sljedeći način: za koliko vrijedi nejednadžba 6a cos 6x + 5 cos 5x< 8a − 7 справедливо для любого x? Так как последнее неравенство должно выполняться для любого значения x, оно должно быть справедливо и для x = 0, от- куда 6a + 5 < 8a − 7 или a >6. S obzirom da je 6a cos 6x + 5 cos 5x 6|a| + 5< 8a − 7, приходим к выводу, что при a >6 nejednakost vrijedi za bilo koji x. Odgovor: a > 6. Zadaci za neovisna odluka Problem 6.8. (SGAU) Ovisno o vrijednostima parametra a, riješiti jednadžbu cos4 x − (a + 2) cos2 x √ a − 3 = 0. − Odgovor: Ako je a ∈ [−3; −2] : x = arccos a + 3 + πk, k ∈ Z, ako je a ∈ [−3; −2] : nema rješenja. Problem 6.9. (SGAU) Ovisno o vrijednostima parametra a, riješiti jednadžbu sin4 x + cos4 x + sin 2x + a = 0. 61 √ Odgovor: Ako je a ∈ − 3 ; 2: x = 1 (−1)k arcsin(1− 2a−3) + πk, 2 1 2 3 ; 1: nema rješenja. ako je a ∈ − 2 2 k ∈ Z, zadatak 6.10. (SGAU) Za koje vrijednosti parametra a vrijedi jednadžba (a2 +8a+16)(2−2 cos x− sin2 x)+(32+2a2 +16a)(cos x−1)+3a+10 =0 rješenja? Odgovor: a< − 10 ; −3 < a < −2. 3 Задача 6.11. (СГАУ) При каких значениях параметра a урав- нение loga−2 17 + cos x − sin x = 3 8 имеет решение? √ 2 3 Ответ: a ∈ 2 5 ; 3 ∪ 3; 2 + 26 . 2 Задача 6.12. (СГАУ) При каких значениях параметра a урав- нение loga+1 25 + cos x − 2 sin x = 3 8 2 имеет решение? √3 37 Ответ: a ∈ − 1 ; 0 ∪ 0; 2 − 1 . 2 Задача 6.13. (ЕГЭ) При каких значениях параметра a значение выражения 2+cos x·(3 cos x+a sin x) не равно нулю ни при каких значениях x? √ √ Ответ: a ∈ −2 10; 2 10 . Задача 6.14. (ЕГЭ) При каких значениях параметра a значение выражения 3 + sin x · (2 sin x + a cos x) будет равно −1 хотя бы при одном значении x? √ √ Ответ: a ∈ −∞; −4 6 ∪ 4 6; +∞ . Задача 6.15. (ЕГЭ) При каких значениях параметра a сумма loga (sin x + 2) и loga (sin x + 3) будет равна единице хотя бы при одном значении x? Ответ: a ∈ [ 2; 12 ]. Задача 6.16. (СГАУ) При каких значениях параметра α систе- ма 4 sin x · sin y · cos(x + y) − 0,5 = 0 x−y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. 62 Ответ: Если α = 2πn: x = ±π 6 + π(k+n) π y = ±6 + π(k−n); если α = π+2πn: x = ±π 3 + π + π(k+n) 2 y = ±π 3 − π + π(k−n), 2 n, k ∈ Z. Задача 6.17. (СГАУ) При каких значениях параметра α систе- ма 2 sin x · cos y · sin(x − y) + 0,25 = 0 x+y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. Ответ: Если α = π +2πn: x = (−1)k+1 π + π + π (2n+k) 2 12 4 2 k π + π + π (2n−k); y = (−1) 12 4 2 если α = − 2 π +2πn: x = (−1)k π − π + π (2n+k) 12 4 2 y = (−1) k+1 π − π + π (2n−k), 12 4 2 n, k ∈ Z. Задача 6.18. (СГАУ) При каких значениях параметра a нера- венство √ 2 2 (sin x − cos x) − a + 7 log 2a+34 15 <0 35 выполняется для любых значений x? 1 Ответ: a ∈ (−17; −12) ∪ 2 ; 3 . Задача 6.19. (СГАУ) При каких значениях параметра a нера- венство √ log 3−2a 3 sin x + 3 3 cos x − 2a − 12 >0 23 28 vrijedi za bilo koju vrijednost x? Odgovor: a ∈ (−∞; −23) ∪ (−10; −9). Problem 6.20. Ovisno o vrijednostima parametra a, riješite nejednadžbu cos x 2 − a2. Odgovor: |a| √ : x ∈ R, 1 1<|a| √3: x ∈ arccos(2−a2)+2πk; π− arccos(2−a2)+2πk , |a|>3: nema rješenja. k∈Z Zadatak 6.21. Za koje vrijednosti parametra a jednadžba tan x (a + 1) tan2 x − 2 cos x + a = 0 nema rješenja? Odgovor: a −3; a 1,63 Tutorial PROBLEMI S PARAMETRIMA Sastavio: Efimov Evgeniy Aleksandrovich Kolomiets Lyudmila Vadimovna Računalno tipkanje i raspored E.A. Efimov Samara State Aerospace University nazvan po akademiku S.P. Kraljica. 443086, Samara, Moskovskoe autocesta, 34. – RIO Samara State Aerospace University nazvan po akademiku S.P. Kraljica. 443086, Samara, Moskovskoe autocesta, 34.

1. Zadatak.
Na kojim vrijednostima parametara a jednadžba ( a - 1)x 2 + 2x + a- Ima li 1 = 0 točno jedan korijen?

1. Rješenje.
Na a= 1 jednadžba je 2 x= 0 i očito ima jedan korijen x= 0. Ako a br. 1, onda je ova jednadžba kvadratna i ima jedan korijen za one vrijednosti parametara za koje je diskriminant kvadratnog trinoma jednaka nuli. Izjednačavajući diskriminantu s nulom, dobivamo jednadžbu za parametar a 4a 2 - 8a= 0, odakle a= 0 ili a = 2.

1. Odgovor: jednadžba ima jedan korijen na a O (0; 1; 2).

2. Zadatak.
Pronađite sve vrijednosti parametara a, za koju jednadžba ima dva različita korijena x 2 +4sjekira+8a+3 = 0.
2. Rješenje.
Jednadžba x 2 +4sjekira+8a+3 = 0 ima dva različita korijena ako i samo ako D = 16a 2 -4(8a+3) > 0. Dobivamo (nakon smanjenja za zajednički faktor 4) 4 a 2 -8a-3 > 0, odakle

2. Odgovor:

a O (-Ґ ; 1 –

Ts 7 2

) I (1 +

Ts 7 2

; Ґ ).

3. Zadatak.
Poznato je da
f 2 (x) = 6x-x 2 -6.
a) Grafički nacrtajte funkciju f 1 (x) na a = 1.
b) U kojoj vrijednosti a grafovi funkcija f 1 (x) I f 2 (x) imaju jednu zajedničku točku?

3. Rješenje.
3.a. Preobrazimo se f 1 (x) na sljedeći način
Graf ove funkcije na a= 1 prikazan je na slici desno.
3.b. Odmah napomenimo da grafovi funkcija g = kx+b I g = sjekira 2 +bx+c (a br. 0) sijeku se u jednoj točki ako i samo ako kvadratna jednadžba kx+b = sjekira 2 +bx+c ima jedan korijen. Korištenje Pogleda f 1 od 3.a, izjednačimo diskriminant jednadžbe a = 6x-x 2 -6 do nula. Iz jednadžbe 36-24-4 a= 0 dobivamo a= 3. Učinite isto s jednadžbom 2 x-a = 6x-x 2 -6 naći ćemo a= 2. Lako je provjeriti da ove vrijednosti parametara zadovoljavaju uvjete problema. Odgovor: a= 2 ili a = 3.

4. Zadatak.
Pronađite sve vrijednosti a, za koji je skup rješenja nejednadžbe x 2 -2sjekira-3a i 0 sadrži segment .

4. Rješenje.
Prva koordinata vrha parabole f(x) = x 2 -2sjekira-3a jednak x 0 = a. Od svojstava kvadratne funkcije uvjet f(x) i 0 na segmentu je ekvivalentan skupu od tri sustava
ima točno dva rješenja?

5. Rješenje.
Prepišimo ovu jednadžbu u obliku x 2 + (2a-2)x - 3a+7 = 0. Ovo je kvadratna jednadžba, ima točno dva rješenja ako je njezina diskriminanta strogo veća od nule. Izračunavajući diskriminantu, nalazimo da je uvjet za postojanje točno dva korijena ispunjenje nejednakosti a 2 +a-6 > 0. Rješavajući nejednadžbu, nalazimo a < -3 или a> 2. Prva od nejednadžbi je očito rješenja u prirodni brojevi nema, a najmanje prirodno rješenje drugog je broj 3.

5. Odgovor: 3.

6. Problem (10 tipki)
Pronađite sve vrijednosti a, za koji je graf funkcije ili, nakon očitih transformacija, a-2 = | 2-a| . Posljednja jednadžba je ekvivalentna nejednadžbi a ja 2.

6. Odgovor: a O )