Tehnička mehanika. Bilješke s predavanja. Osnovna mehanika za lutke. Uvod Bilješke s predavanja o teorijskoj mehanici riječ

državna autonomna institucija

Kalinjingradska regija

profesionalnim obrazovna organizacija

Visoka škola za usluge i turizam

Tečaj predavanja s primjerima praktičnih zadataka

"Osnove teorijske mehanike"

po discipliniTehnička mehanika

za studente3 tečaj

specijalitet20.02.04 Sigurnost od požara

Kalinjingrad

ODOBRITI

Zamjenik ravnatelja za SD GAU KO VEO KSTN.N. Myasnikov

ODOBRENO

Metodološko vijeće GAU KO VET KST

SMATRANO

Na sastanku PCC-a

Urednički tim:

Kolganova A.A., metodologinja

Falaleeva A.B., profesorica ruskog jezika i književnosti

Cvetaeva L.V., predsjednica PCC-aopće matematičke i prirodoslovne discipline

Sastavio:

Nezvanova I.V. Predavač GAU KO VET KST

Sadržaj

Dinamika: osnovni pojmovi i aksiomi

Bibliografija

Statika: osnovni pojmovi i aksiomi.

Teorijske informacije

Statika - dio teorijske mehanike, koji razmatra svojstva sila koje se primjenjuju na točke krutog tijela i uvjete za njihovu ravnotežu. Glavni zadaci:

1. Transformacija sustava sila u ekvivalentne sustave sila.

2. Određivanje uvjeta ravnoteže za sustave sila koje djeluju čvrsta.

materijalna točka naziva najjednostavnijim modelom materijalnog tijela

bilo koji oblik, čije su dimenzije dovoljno male i koji se može uzeti kao geometrijska točka određene mase. Mehanički sustav je bilo koji skup materijalnih točaka. Apsolutno kruto tijelo je mehanički sustav čiji se udaljenosti između točaka ne mijenjaju ni pod kakvim interakcijama.

Sila je mjera mehaničke interakcije materijalnih tijela jedno s drugim. Sila je vektorska veličina, jer je određena s tri elementa:

brojčana vrijednost;

smjer;

točka primjene (A).

Jedinica za snagu je Newton (N).

Slika 1.1

Sustav sila je skup sila koje djeluju na tijelo.

Uravnotežen (jednak nuli) sustav sila je sustav koji, primijenjen na tijelo, ne mijenja svoje stanje.

Sustav sila koje djeluju na tijelo može se zamijeniti jednom rezultantom koja djeluje kao sustav sila.

Aksiomi statike.

Aksiom 1: Ako se na tijelo primijeni uravnoteženi sustav sila, ono se giba jednoliko i pravocrtno ili miruje (zakon inercije).

Aksiom 2: Apsolutno kruto tijelo je u ravnoteži pod djelovanjem dviju sila ako i samo ako su te sile jednake po apsolutnoj vrijednosti, djeluju u jednoj ravnoj liniji i usmjerene su u suprotnim smjerovima. Slika 1.2

Aksiom 3: Mehaničko stanje tijela neće biti poremećeno ako se sustavu sila koje na njega djeluju pridodaju ili oduzmu uravnoteženi sustav sila.

Aksiom 4: Rezultanta dviju sila primijenjenih na tijelo jednaka je njihovom geometrijskom zbroju, odnosno izražena je u apsolutnoj vrijednosti i smjeru dijagonalom paralelograma izgrađenog na tim silama kao na stranicama.

Slika 1.3.

Aksiom 5: Sile kojima dva tijela djeluju jedno na drugo uvijek su jednake po apsolutnoj vrijednosti i usmjerene duž jedne ravne u suprotnim smjerovima.

Slika 1.4.

Vrste veza i njihove reakcije

veze nazivaju se svaka ograničenja koja sprječavaju kretanje tijela u prostoru. Tijelo, tražeći pod djelovanjem primijenjenih sila kretanje, koje je sprečeno vezom, djelovat će na njega određenom silom tzv. sila pritiska na spoj . Prema zakonu jednakosti djelovanja i reakcije, veza će na tijelo djelovati istim modulom, ali suprotno usmjerenom silom.
Zove se sila kojom ta veza djeluje na tijelo, sprječavajući jedno ili drugo kretanje sila reakcije (reakcija) veze .
Jedno od temeljnih načela mehanike je princip oslobođenja : svako neslobodno tijelo može se smatrati slobodnim, ako odbacimo veze i zamijenimo njihovo djelovanje reakcijama veza.

Reakcija veze je usmjerena u suprotnom smjeru od mjesta gdje veza ne dopušta tijelu da se kreće. Glavne vrste veza i njihove reakcije prikazane su u tablici 1.1.

Tablica 1.1

Vrste veza i njihove reakcije

Naziv komunikacije

Simbol

glatka površina (podrška) - površina (oslonac), trenje na kojem se dano tijelo može zanemariti.
Uz besplatnu podršku, reakcijaje usmjeren okomito na tangentu kroz točkuALI tjelesni kontakt1 s potpornom površinom2 .

Konac (fleksibilan, nerastegljiv). Veza, napravljena u obliku nerastavljive niti, ne dopušta tijelu da se odmakne od točke ovjesa. Stoga je reakcija niti usmjerena duž niti do točke njezina ovjesa.

bestežinski štap – štap čija se težina može zanemariti u usporedbi s percipiranim opterećenjem.
Reakcija bestežinskog zglobnog pravolinijskog štapa usmjerena je duž osi štapa.

Pomična šarka, zglobni pokretni oslonac. Reakcija je usmjerena duž normale na potpornu površinu.

Čvrsto zatvaranje. U ravnini krutog ugradnje bit će dvije komponente reakcije, i moment para sila, što sprječava okretanje grede1 u odnosu na točkuALI .
Kruta veza u prostoru oduzima svih šest stupnjeva slobode tijelu 1 - tri pomaka duž koordinatnih osi i tri rotacije oko tih osi.
U prostornoj krutoj ugradnji bit će tri komponente, , i tri momenta para sila.

Sustav konvergentnih sila

Sustav konvergirajućih sila naziva sustavom sila čije se linije djelovanja sijeku u jednoj točki. Dvije sile koje konvergiraju u jednoj točki, prema trećem aksiomu statike, mogu se zamijeniti jednom silom -rezultantna .
Glavni vektor sustava sila - vrijednost jednaka geometrijskom zbroju sila sustava.

Rezultanta ravninskog sustava sila koje se konvergiraju može se odreditigrafički i analitički.

Zbrajanje sustava sila . Zbrajanje ravnog sustava konvergentnih sila provodi se ili sukcesivnim zbrajanjem sila s konstrukcijom međurezultante (slika 1.5), ili konstruiranjem poligona sila (sl. 1.6).

Slika 1.5Slika 1.6

Projekcija sile na os - algebarska veličina jednaka umnošku modula sile i kosinusa kuta između sile i pozitivnog smjera osi.
ProjekcijaFx(sl.1.7) sile po osovini xpozitivan ako je α akutan, negativan ako je α tup. Ako snagaje okomita na os, tada je njegova projekcija na os nula.

Slika 1.7

Projekcija sile na ravninu Ohu– vektor , zaključen između projekcija početka i kraja silena ovaj avion. Oni. projekcija sile na ravninu je vektorska veličina koju karakterizira ne samo brojčana vrijednost, već i smjer u ravniniOhu (slika 1.8).

Slika 1.8

Zatim projekcijski modul do aviona Ohu bit će jednako:

Fxy = F cosα,

gdje je α kut između smjera sile i njegovu projekciju.
Analitički način specificiranja sila . Za analitičku metodu postavljanja silepotrebno je odabrati sustav koordinatnih osiOhz, u odnosu na koji će se odrediti smjer sile u prostoru.
Vektor koji prikazuje snagu, može se konstruirati ako su poznati modul ove sile i kutovi α, β, γ koje sila tvori s koordinatnim osi. TočkaALI primjena sile odvojeno svojim koordinatamax, na, z. Silu možete postaviti njezinim projekcijamafx, fy, fzna koordinatnim osovinama. Modul sile u ovom slučaju određuje se formulom:

i kosinus smjera:

, .

Analitička metoda zbrajanja sila : projekcija vektora zbroja na neku os jednaka je algebarski zbroj projekcije članova vektora na istu os, tj. ako:

zatim , , .
Znajući Rx, Ry, Rz, možemo definirati modul

i kosinus smjera:

, , .

Slika 1.9

Za ravnotežu sustava konvergirajućih sila potrebno je i dovoljno da rezultanta tih sila bude jednaka nuli.
1) Uvjet geometrijske ravnoteže za konvergentni sustav sila : za ravnotežu sustava konvergirajućih sila potrebno je i dovoljno da poligon sila konstruiran iz tih sila

je zatvoren (kraj vektora posljednjeg člana

sila se mora podudarati s početkom vektora prvog člana sile). Tada će glavni vektor sustava sila biti jednak nuli ()
2) Uvjeti analitičke ravnoteže . Modul glavnog vektora sustava sila određen je formulom. =0. Ukoliko , tada korijenski izraz može biti jednak nuli samo ako svaki član istovremeno nestane, t.j.

Rx= 0, Ry= 0, R z = 0.

Stoga je za ravnotežu prostornog sustava konvergirajućih sila potrebno i dovoljno da zbroji projekcija tih sila na svaku od tri koordinate osi budu jednaki nuli:

Za ravnotežu ravnog sustava konvergirajućih sila potrebno je i dovoljno da zbroj projekcija sila na svaku od dvije koordinatne osi bude jednak nuli:

Zbrajanje dviju paralelnih sila u istom smjeru.

Slika 1.9

Dvije paralelne sile usmjerene u istom smjeru svode se na jednu njima paralelnu rezultantnu silu i usmjerenu u istom smjeru. Veličina rezultante jednaka je zbroju veličina tih sila, a točka njezine primjene C dijeli udaljenost između linija djelovanja sila iznutra na dijelove obrnuto proporcionalne veličinama tih sila, tj.

B A C

R=F 1 +F 2

Zbrajanje dviju nejednakih paralelnih sila usmjerenih u suprotnim smjerovima.

Dvije nejednake antiparalelne sile svode se na jednu s njima paralelnu rezultantnu silu i usmjeravaju prema većoj sili. Veličina rezultante jednaka je razlici između veličina tih sila, a točka njezine primjene, C, dijeli udaljenost između linija djelovanja sila izvana na dijelove obrnuto proporcionalne veličinama tih sila, tj. je

Par sila i moment sile oko točke.

Trenutak sile u odnosu na točku O naziva se, uzet s odgovarajućim predznakom, umnožak veličine sile na udaljenosti h od točke O do pravca djelovanja sile . Ovaj proizvod se uzima sa znakom plus ako je sila teži rotaciji tijela u smjeru suprotnom od kazaljke na satu, a sa znakom - ako je sila teži rotaciji tijela u smjeru kazaljke na satu, tj . Duljina okomice h naziva serame snage točka O. Učinak djelovanja sile t.j. kutna akceleracija tijela je veća, što je veća veličina momenta sile.

Slika 1.11

Par sila Sustavom se naziva sustav koji se sastoji od dvije paralelne sile jednake veličine, usmjerene u suprotnim smjerovima. Udaljenost h između linija djelovanja sila naziva seramena parova . Moment para sila m(F,F") je umnožak vrijednosti jedne od sila koje čine par i kraka para, uzete s odgovarajućim predznakom.

Zapisuje se na sljedeći način: m(F, F")= ± F × h, pri čemu se umnožak uzima sa znakom plus ako par sila teži rotirati tijelo u smjeru suprotnom od kazaljke na satu i sa znakom minus ako par sila teži za rotiranje tijela u smjeru kazaljke na satu.

Teorem o zbroju momenata sila para.

Zbroj momenata sila para (F,F") u odnosu na bilo koju točku 0 uzetu u ravnini djelovanja para ne ovisi o izboru ove točke i jednak je momentu para.

Teorem o ekvivalentnim parovima. Posljedice.

Teorema. Dva para čiji su momenti međusobno jednaki su ekvivalentna, t.j. (F, F") ~ (P, P")

Posljedica 1 . Par sila može se prenijeti na bilo koje mjesto u ravnini svog djelovanja, kao i zarotirati pod bilo kojim kutom i promijeniti krak i veličinu sila para, uz zadržavanje momenta para.

Posljedica 2. Par sila nema rezultantu i ne može se uravnotežiti jednom silom koja leži u ravnini para.

Slika 1.12

Zbrajanje i uvjet ravnoteže za sustav parova na ravnini.

1. Teorem o zbrajanju parova koji leže u istoj ravnini. Sustav parova, proizvoljno smještenih u istoj ravnini, može se zamijeniti jednim parom, čiji trenutak jednak je zbroju trenutke ovih parova.

2. Teorem o ravnoteži sustava parova na ravnini.

Da bi apsolutno kruto tijelo mirovalo pod djelovanjem sustava parova, proizvoljno smještenih u istoj ravnini, potrebno je i dovoljno da zbroj momenata svih parova bude jednak nuli, tj.

Centar gravitacije

Gravitacija - rezultanta sila privlačenja na Zemlju, raspoređena po cijelom volumenu tijela.

Težište tijela - to je takva točka, koja je uvijek povezana s ovim tijelom, kroz koju prolazi linija djelovanja sile gravitacije danog tijela u bilo kojem položaju tijela u prostoru.

Metode za pronalaženje težišta

1. Metoda simetrije:

1.1. Ako je a homogeno tijelo ima ravninu simetrije, tada težište leži u ovoj ravnini

1.2. Ako homogeno tijelo ima os simetrije, onda težište leži na toj osi. Težište homogenog tijela okretanja leži na osi okretanja.

1.3 Ako homogeno tijelo ima dvije osi simetrije, tada je težište u točki njihova presjeka.

2. Metoda pregradnje: Tijelo se dijeli na najmanji broj dijelova, čija su sila gravitacije i položaj težišta poznati.

3. Metoda negativnih masa: Prilikom određivanja težišta tijela sa slobodnim šupljinama treba koristiti metodu pregradnje, ali masu slobodnih šupljina treba smatrati negativnom.

Koordinate težišta ravne figure:

Položaji težišta jednostavnih geometrijski oblici može se izračunati pomoću poznatih formula. (Slika 1.13)

Bilješka: Težište simetrije figure nalazi se na osi simetrije.

Težište štapa je na sredini visine.

1.2. Primjeri rješavanja praktičnih problema

Primjer 1: Uteg je ovješen na štap i u ravnoteži. Odredite sile u šipki. (Slika 1.2.1)

Odluka:

Sile koje nastaju u šipkama za pričvršćivanje jednake su po veličini silama kojima šipke podupiru opterećenje. (5. aksiom)

Određujemo moguće smjerove reakcija veza "krutih štapova".

Napori su usmjereni duž šipki.

Slika 1.2.1.

Oslobodimo točku A od veza, zamjenjujući djelovanje veza njihovim reakcijama. (Slika 1.2.2)

Započnimo konstrukciju s poznatom silom crtanjem vektoraFu nekom razmjeru.

Od kraja vektoraFcrtati linije paralelne s reakcijamaR 1 iR 2 .

Slika 1.2.2

Presijecajući se, linije stvaraju trokut. (Slika 1.2.3.). Poznavajući mjerilo konstrukcija i mjerenjem duljine stranica trokuta, moguće je odrediti veličinu reakcija u štapićima.

Za točnije izračune možete koristiti geometrijske odnose, posebno sinusni teorem: omjer stranice trokuta i sinusa suprotnog kuta je konstantna vrijednost

za ovaj slučaj:

Slika 1.2.3

Komentar: Ako se smjer vektora (reakcija spajanja) na zadanoj shemi i u trokutu sila ne podudara, tada bi reakcija na shemi trebala biti usmjerena u suprotnom smjeru.

Primjer 2: Odredite veličinu i smjer rezultantnog ravnog sustava sila koje se slijevaju na analitički način.

Odluka:

Slika 1.2.4

1. Određujemo projekcije svih sila sustava na Ox (slika 1.2.4)

Algebarskim zbrajanjem projekcija dobivamo projekciju rezultante na os Ox.

Znak označava da je rezultanta usmjerena ulijevo.

2. Određujemo projekcije svih sila na os Oy:

Algebarskim zbrajanjem projekcija dobivamo projekciju rezultante na os Oy.

Znak označava da je rezultanta usmjerena prema dolje.

3. Odredite modul rezultante prema veličinama projekcija:

4. Odredite vrijednost kuta rezultante s osi Ox:

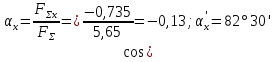
i vrijednost kuta s y-osom:

Primjer 3: Izračunajte zbroj momenata sila u odnosu na točku O (slika 1.2.6).

OA= AB= NAD=DE=CB=2m

Slika 1.2.6

Odluka:

1. Moment sile u odnosu na točku brojčano je jednak umnošku modula i kraka sile.

2. Moment sile jednak je nuli ako linija djelovanja sile prolazi kroz točku.

Primjer 4: Odredite položaj težišta figure prikazane na slici 1.2.7

Odluka:

Cifru dijelimo na tri:

1-pravokutnik

ALI 1 =10*20=200cm 2

2-trokut

ALI 2 =1/2*10*15=75cm 2

3 kruga

ALI 3 =3,14*3 2 =28,3 cm 2

Slika 1 CG: x 1 =10 cm, y 1 =5 cm

Slika 2 CG: x 2 =20+1/3*15=25cm, u 2 =1/3*10=3,3cm

Slika 3 CG: x 3 =10 cm, y 3 =5 cm

Slično je definiran za s =4,5 cm

Kinematika: osnovni pojmovi.

Osnovni kinematički parametri

Putanja - linija koju materijalna točka ocrtava pri kretanju u prostoru. Putanja može biti ravna i krivulja, ravna i prostorna crta.

Jednadžba putanje za gibanje ravnine: y =f ( x)

Prijeđena udaljenost. Put se mjeri duž puta u smjeru vožnje. Oznaka -S, mjerne jedinice - metri.

Jednadžba gibanja točke je jednadžba koja određuje položaj pokretne točke kao funkciju vremena.

Slika 2.1

Položaj točke u svakom trenutku vremena može se odrediti prema udaljenosti prijeđenom duž putanje od neke fiksna točka, smatra se referentnom točkom (slika 2.1). Ovakvo kretanje se zoveprirodnim . Dakle, jednadžba gibanja može se predstaviti kao S = f (t).

Slika 2.2

Položaj točke može se odrediti i ako su njene koordinate poznate kao funkcija vremena (slika 2.2). Zatim, u slučaju gibanja po ravnini, moraju se dati dvije jednadžbe:

U slučaju prostornog gibanja dodaje se i treća koordinataz= f 3 ( t)

Ovakvo kretanje se zoveKoordinirati .

Brzina putovanja je vektorska veličina koja u ovom trenutku karakterizira brzinu i smjer kretanja duž putanje.

Brzina je vektor usmjeren u svakom trenutku tangencijalno na putanju prema smjeru kretanja (slika 2.3).

Slika 2.3

Ako točka prelazi jednake udaljenosti u jednakim vremenskim intervalima, tada se kretanje nazivauniforma .

Prosječna brzina na putu ΔSdefinirano:

gdje∆S- put prijeđen u vremenu Δt; Δ t- vremenski interval.

Ako točka putuje nejednakim putovima u jednakim vremenskim intervalima, tada se kretanje nazivaneravnomjeran . U ovom slučaju brzina je promjenjiva i ovisi o vremenuv= f( t)

Trenutna brzina je definirana kao

točkasto ubrzanje - vektorska veličina koja karakterizira brzinu promjene brzine u veličini i smjeru.

Brzina točke pri kretanju od točke M1 do točke Mg mijenja se po veličini i smjeru. Prosječna vrijednost ubrzanja za ovaj vremenski period

Trenutno ubrzanje:

Obično se radi praktičnosti razmatraju dvije međusobno okomite komponente ubrzanja: normalna i tangencijalna (slika 2.4)

Normalno ubrzanje a n , karakterizira promjenu brzine za

smjer i definira se kao

Normalno ubrzanje je uvijek usmjereno okomito na brzinu prema središtu luka.

Slika 2.4

Tangencijalno ubrzanje a t , karakterizira promjenu brzine u veličini i uvijek je usmjeren tangencijalno na putanju; pri ubrzanju se njegov smjer poklapa sa smjerom brzine, a pri usporavanju je usmjeren suprotno od smjera vektora brzine.

Vrijednost punog ubrzanja definirana je kao:

Analiza tipova i kinematičkih parametara kretanja

Ujednačeno kretanje - ovaj pokret iz konstantna brzina:

Za pravolinijski jednoliko kretanje:

Za krivolinijsko jednoliko gibanje:

Zakon ravnomjernog gibanja :

Jednako-varijabilno gibanje – je gibanje s konstantnim tangencijalnim ubrzanjem:

Za pravolinijsko jednoliko gibanje

Za krivolinijsko jednoliko gibanje:

Zakon ravnomjernog gibanja:

Kinematički grafovi

Kinematički grafovi - Ovo su grafikoni promjena puta, brzine i ubrzanja ovisno o vremenu.

Ujednačeno kretanje (slika 2.5)

Slika 2.5

Jednako-varijabilno kretanje (slika 2.6)

Slika 2.6

Najjednostavniji pokreti krutog tijela

Kretanje naprijed naziva se kretanje krutog tijela, u kojem svaka ravna linija na tijelu tijekom kretanja ostaje paralelna sa svojim početnim položajem (slika 2.7)

Slika 2.7

U translacijskom gibanju sve se točke tijela gibaju na isti način: brzine i akceleracije su u svakom trenutku jednake.

Narotacijsko gibanje sve točke tijela opisuju kružnice oko zajedničkog fiksna osovina.

Fiksna os oko koje se okreću sve točke tijela naziva seos rotacije.

Samo za opisivanje rotacijskog gibanja tijela oko fiksne osikutne opcije. (Slika 2.8)

φ je kut rotacije tijela;

ω – kutna brzina, određuje promjenu kuta rotacije u jedinici vremena;

Određuje se promjena kutne brzine s vremenom kutno ubrzanje:

2.2. Primjeri rješavanja praktičnih problema

Primjer 1: Zadana je jednadžba gibanja točke. Odredite brzinu točke na kraju treće sekunde kretanja i prosječnu brzinu za prve tri sekunde.

Odluka:

1. Jednadžba brzine

2. Brzina na kraju treće sekunde (t=3 c)

3. Prosječna brzina

Primjer 2: Prema zadanom zakonu gibanja odredite vrstu gibanja, početnu brzinu i tangencijalno ubrzanje točke, vrijeme zaustavljanja.

Odluka:

1. Vrsta kretanja: jednako varijabilna ()
2. Pri usporedbi jednadžbi očito je da

- početni put prijeđen prije početka odbrojavanja 10m;

- početna brzina 20m/s

- konstantno tangencijalno ubrzanje

- ubrzanje je negativno, dakle, kretanje je sporo, ubrzanje je usmjereno u smjeru suprotnom brzini kretanja.

3. Možete odrediti vrijeme u kojem će brzina točke biti jednaka nuli.

3. Dinamika: osnovni pojmovi i aksiomi

Dinamika - dio teorijske mehanike u kojem se uspostavlja veza između gibanja tijela i sila koje na njih djeluju.

U dinamici se rješavaju dvije vrste problema:

odrediti parametre gibanja prema zadanim silama;

odrediti sile koje djeluju na tijelo, prema zadanim kinematičkim parametrima gibanja.

Pod, ispodmaterijalna točka podrazumijevaju određeno tijelo koje ima određenu masu (tj. sadrži određenu količinu materije), ali nema linearne dimenzije (beskonačno mali volumen prostora).
izolirani smatra se materijalna točka na koju druge materijalne točke ne utječu. U stvarnom svijetu izolirane materijalne točke, kao i izolirana tijela, ne postoje, ovaj koncept je uvjetovan.

Kod translatornog gibanja sve se točke tijela gibaju na isti način, pa se tijelo može uzeti kao materijalna točka.

Ako su dimenzije tijela male u odnosu na putanju, ono se može smatrati i materijalnom točkom, dok se točka poklapa s težištem tijela.

Tijekom rotacijskog gibanja tijela, točke se možda neće kretati na isti način, u ovom slučaju se neke odredbe dinamike mogu primijeniti samo na pojedinačne točke, a materijalni objekt se može smatrati skupom materijalnih točaka.

Stoga se dinamika dijeli na dinamiku točke i dinamiku materijalnog sustava.

Aksiomi dinamike

Prvi aksiom ( princip inercije): u svaka izolirana materijalna točka miruje ili ujednačena i pravolinijsko gibanje dok ga primijenjene sile ne izvedu iz ovog stanja.

Ovo stanje se zove državainercija. Uklonite točku iz ovog stanja, t.j. dajte mu malo ubrzanja, možda vanjsku silu.

Svako tijelo (točka) imainercija. Mjera inercije je masa tijela.

Masa pozvaokoličina materije u tijelu u klasičnoj mehanici smatra se konstantnom vrijednošću. Jedinica mase je kilogram (kg).

Drugi aksiom (Drugi Newtonov zakon je osnovni zakon dinamike)

F=ma

gdjet - masa točke, kg;a - ubrzanje točke, m/s 2 .

Ubrzanje koje materijalnoj točki daje sila proporcionalno je veličini sile i podudara se sa smjerom sile.

Gravitacija djeluje na sva tijela na Zemlji, daje ubrzanje tijelu. slobodan pad prema središtu zemlje:

G=mg

gdjeg- 9,81 m/s², ubrzanje slobodnog pada.

Treći aksiom (Treći Newtonov zakon): sSile međudjelovanja dvaju tijela jednake su po veličini i usmjerene duž iste ravne u različitim smjerovima.

U interakciji su akceleracije obrnuto proporcionalne masama.

Četvrti aksiom (zakon neovisnosti djelovanja sila): toSvaka sila sustava sila djeluje onako kako bi djelovala sama.

Ubrzanje koje točki daje sustav sila jednako je geometrijskom zbroju akceleracija koje svaka sila daje točki zasebno (slika 3.1):

Slika 3.1

Koncept trenja. Vrste trenja.

Trenje- otpor koji proizlazi iz kretanja jednog grubog tijela po površini drugog. Trenje klizanja rezultira trenjem klizanja, a trenje kotrljanja rezultira trenjem ljuljanja.

Trenje klizanja

Slika 3.2.

Razlog je mehanički zahvat izbočina. Sila otpora kretanju tijekom klizanja naziva se sila trenja klizanja (slika 3.2)

Zakoni trenja klizanja:

1. Sila trenja klizanja izravno je proporcionalna sili normalnog tlaka:

gdjeR- sila normalnog tlaka, usmjerena okomito na potpornu površinu;f- koeficijent trenja klizanja.

Slika 3.3.

U slučaju da se tijelo kreće duž nagnute ravni (slika 3.3)

trenje kotrljanja

Otpor kotrljanja povezan je s međusobnom deformacijom tla i kotača i mnogo je manji od trenja klizanja.

Za ravnomjerno kotrljanje kotača potrebno je primijeniti siluF dv (Slika 3.4)

Uvjet kotrljanja kotača je da moment kretanja ne smije biti manji od momenta otpora:

Slika 3.4.

Primjer 1: Primjer 2: Na dvije materijalne točke masem 1 =2kg im 2 = primjenjuju se 5 kg jednakih sila. Usporedite vrijednosti brže.

Odluka:

Prema trećem aksiomu, dinamika ubrzanja obrnuto je proporcionalna masama:

Primjer 3: Odredite rad sile teže pri pomicanju tereta od točke A do točke C po nagnutoj ravnini (slika 3. 7). Sila gravitacije tijela je 1500N. AB=6m, BC=4m. Primjer 3: Odrediti rad sile rezanja za 3 minute. Brzina rotacije obratka je 120 okretaja u minuti, promjer obratka je 40 mm, sila rezanja je 1kN. (Slika 3.8)

Odluka:

1. Rad s rotacijskim kretanjem:

2. kutna frekvencija rotacija 120 o/min

Slika 3.8.

3. Broj okretaja za dano vrijeme jez\u003d 120 * 3 \u003d 360 rev.

Kut rotacije za to vrijeme φ=2πz\u003d 2 * 3,14 * 360 \u003d 2261 rad

4. Radite za 3 okreta:W\u003d 1 * 0,02 * 2261 \u003d 45,2 kJ

Bibliografija

Olofinskaya, V.P. "Tehnička mehanika", Moskva "Forum" 2011

Erdedi A.A. Erdedi N.A. Teorijska mehanika. Čvrstoća materijala.- R-n-D; Feniks, 2010

1 slajd

Tečaj predavanja iz teorijske mehanike Dinamika (I dio) Bondarenko A.N. Moskva - 2007. Elektronički tečaj napisan je na temelju predavanja autora za studente koji studiraju na specijalnostima SZhD, PGS i SDM na NIIZhT i MIIT (1974.-2006.). Edukativni materijal odgovara kalendarskim planovima u obimu od tri semestra. Da biste u potpunosti implementirali efekte animacije tijekom prezentacije, morate koristiti preglednik Power Point koji nije niži od onog ugrađenog u Microsoft Office operativnog sustava Windows-XP Professional. Komentari i sugestije možete poslati na e-mail: [e-mail zaštićen]. Moskva Državno sveučilišteŽeljeznice (MIIT) Zavod za teorijsku mehaniku Znanstveno-tehnički centar prometnih tehnologija

2 slajd

Sadržaj Predavanje 1. Uvod u dinamiku. Zakoni i aksiomi dinamike materijalna točka. Osnovna jednadžba dinamike. Diferencijalne i prirodne jednadžbe gibanja. Dva glavna zadatka dinamike. Primjeri rješavanja izravnog problema dinamike Predavanje 2. Rješavanje inverznog problema dinamike. Opće upute za rješavanje inverznog problema dinamike. Primjeri rješavanja inverznog problema dinamike. Gibanje tijela bačenog pod kutom prema horizontu, bez uzimanja u obzir otpora zraka. Predavanje 3. Pravocrtne oscilacije materijalne točke. Uvjet za nastanak oscilacija. Klasifikacija vibracija. Slobodne vibracije bez uzimanja u obzir sila otpora. prigušene vibracije. Dekrement oscilacije. Predavanje 4. Prisilne oscilacije materijalne točke. Rezonancija. Utjecaj otpora gibanju tijekom prisilnih vibracija. Predavanje 5. Relativno gibanje materijalne točke. Sile inercije. Posebni slučajevi kretanja za različite vrste prijenosnih pokreta. Utjecaj Zemljine rotacije na ravnotežu i kretanje tijela. Predavanje 6. Dinamika mehaničkog sustava. mehanički sustav. Vanjske i unutarnje sile. Središte mase sustava. Teorem o gibanju središta mase. Zakoni o očuvanju. Primjer rješavanja problema korištenja teorema o kretanju središta mase. Predavanje 7. Impuls sile. Količina kretanja. Teorem o promjeni količine gibanja. Zakoni o očuvanju. Eulerov teorem. Primjer rješavanja zadatka o korištenju teorema o promjeni količine gibanja. moment zamaha. Teorem o promjeni kutnog momenta Predavanje 8. Zakoni održanja. Elementi teorije momenata tromosti. Kinetički moment krutog tijela. Diferencijalna jednadžba rotacije krutog tijela. Primjer rješavanja problema korištenja teorema o promjeni kutnog momenta sustava. Osnovna teorija žiroskopa. Preporučena literatura 1. Yablonsky A.A. Kolegij teorijske mehanike. 2. dio. M.: postdiplomske studije. 1977. 368 str. 2. Meshchersky I.V. Zbirka zadataka iz teorijske mehanike. M.: Znanost. 1986. 416 str. 3. Zbirka zadataka za seminarske radove /Ur. A.A. Yablonski. M.: Viša škola. 1985. 366 str. 4. Bondarenko A.N. “Teorijska mehanika u primjerima i zadacima. Dinamika” ( elektronički priručnik www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004.

3 slajd

Predavanje 1 Dinamika je dio teorijske mehanike koji proučava mehaničko gibanje s najopćenitijeg stajališta. Kretanje se razmatra u vezi sa silama koje djeluju na predmet. Dio se sastoji od tri dijela: Dinamika materijalne točke Dinamika mehaničkog sustava Analitička mehanika ■ Dinamika točke – proučava kretanje materijalne točke, uzimajući u obzir sile koje uzrokuju to kretanje. Glavni objekt je materijalna točka - materijalno tijelo s masom čije se dimenzije mogu zanemariti. Osnovne pretpostavke: - postoji apsolutni prostor (ima čisto geometrijska svojstva koja ne ovise o materiji i njenom kretanju. - postoji apsolutno vrijeme (ne ovisi o materiji i njenom kretanju). Iz ovoga slijedi: - postoji apsolutno nepomičan referentni okvir. - vrijeme ne ovisi o kretanju referentnog okvira - mase pokretnih točaka ne ovise o kretanju referentnog okvira. Ove se pretpostavke koriste u klasičnoj mehanici koju su stvorili Galileo i Newton Još uvijek ima prilično širok opseg, budući da mehanički sustavi koji se razmatraju u primijenjenim znanostima nemaju tako velike mase i brzine kretanja, za što je potrebno uzeti u obzir njihov utjecaj na geometriju prostora, vremena, gibanja, kao npr. se radi u relativističkoj mehanici (teorija relativnosti) ■ Osnovni zakoni dinamike - prvi otkrio Galileo i formulirao Newton čine osnovu svih metoda za opisivanje i analizu kretanja mehaničkih sustava i njihove dinamičke interakcije djelovanje pod utjecajem raznih sila. ■ Zakon inercije (Galileo-Newtonov zakon) - Izolirana materijalna točka tijela zadržava stanje mirovanja ili jednoliko pravocrtno gibanje sve dok ga primijenjene sile ne prisile da promijeni ovo stanje. To podrazumijeva ekvivalentnost stanja mirovanja i gibanja po inerciji (Galilejev zakon relativnosti). Referentni okvir, u odnosu na koji je zakon inercije ispunjen, naziva se inercijskim. Svojstvo materijalne točke da nastoji zadržati brzinu svog kretanja (svoje kinematičko stanje) nepromijenjenom naziva se inercija. ■ Zakon proporcionalnosti sile i ubrzanja (Osnovna jednadžba dinamike - Newtonov II zakon) - Ubrzanje koje se materijalnoj točki daje silom izravno je proporcionalno sili i obrnuto proporcionalno masi ove točke: ili Ovdje je m masa točke (mjera inercije), mjerena u kg, brojčano jednaka težini podijeljenoj s gravitacijskim ubrzanjem: F je sila koja djeluje, mjerena u N (1 N daje akceleraciju od 1 m/s2 točki mase 1 kg, 1 N \u003d 1/9. 81 kg-s). ■ Dinamika mehaničkog sustava - proučava kretanje skupa materijalnih točaka i krutih tijela, u kombinaciji opći zakoni interakcije, uzimajući u obzir sile koje uzrokuju ovo kretanje. ■ Analitička mehanika – proučava gibanje neslobodnih mehaničkih sustava korištenjem općih analitičkih metoda. jedan

4 slajd

Predavanje 1 (nastavak - 1.2) Diferencijalne jednadžbe gibanja materijalne točke: - diferencijalna jednadžba gibanja točke u vektorskom obliku. - diferencijalne jednadžbe gibanja točke u koordinatnom obliku. Taj se rezultat može dobiti formalnom projekcijom vektorske diferencijalne jednadžbe (1). Nakon grupiranja, vektorska relacija se razlaže u tri skalarne jednadžbe: U koordinatnom obliku: Koristimo odnos radijus-vektora s koordinatama i vektora sile s projekcijama: diferencijalna jednadžba gibanja na prirodnim (pokretnim) koordinatnim osi: ili: - prirodne jednadžbe gibanja točke. ■ Osnovna jednadžba dinamike: - odgovara vektorskom načinu zadavanja kretanja točke. ■ Zakon neovisnosti djelovanja sila - Ubrzanje materijalne točke pod djelovanjem više sila jednako je geometrijskom zbroju ubrzanja točke od djelovanja svake od sila posebno: ili Zakon vrijedi za bilo koje kinematičko stanje tijela. Sile interakcije koje se primjenjuju na različite točke (tijela) nisu uravnotežene. ■ Zakon jednakosti djelovanja i reakcije (Newtonov III zakon) - Svaka radnja odgovara jednakoj i suprotno usmjerenoj reakciji: 2

5 slajd

Dva glavna problema dinamike: 1. Izravni problem: Zadano je gibanje (jednadžbe gibanja, putanja). Potrebno je odrediti sile pod čijim djelovanjem dolazi do određenog kretanja. 2. Inverzni zadatak: Zadane su sile pod čijim djelovanjem dolazi do gibanja. Potrebno je pronaći parametre gibanja (jednadžbe gibanja, putanju kretanja). Oba problema rješavaju se osnovnom jednadžbom dinamike i njezinom projekcijom na koordinatne osi. Ako se razmatra gibanje neslobodne točke, tada se, kao u statici, koristi princip oslobađanja od veza. Kao rezultat reakcije, veze su uključene u sastav sila koje djeluju na materijalnu točku. Rješenje prvog problema povezano je s operacijama diferencijacije. Rješenje inverznog problema zahtijeva integraciju odgovarajućih diferencijalnih jednadžbi, a to je mnogo teže od diferencijacije. Inverzni problem je teži od izravnog problema. Rješenje izravnog problema dinamike - pogledajmo primjere: Primjer 1. Kabina s težinom G dizala podiže se sajlom s ubrzanjem a . Odredite napetost kabela. 1. Odaberite objekt (kabina dizala se kreće naprijed i može se smatrati materijalnom točkom). 2. Odbacimo spoj (kabel) i zamijenimo ga reakcijom R. 3. Sastavimo osnovnu jednadžbu dinamike: Odredimo reakciju sajle: Odredimo napetost kabela: Uz jednoliko kretanje kabine ay = 0 i napetost kabela jednaka je težini: T = G. Kada se sajla lomi T = 0 i ubrzanje kabine je jednako akceleraciji slobodnog pada: ay = -g. 3 4. Projiciramo osnovnu jednadžbu dinamike na y-os: y Primjer 2. Točka mase m giba se duž horizontalne površine (ravnina Oxy) prema jednadžbama: x = a coskt, y = b coskt. Odrediti silu koja djeluje na točku. 1. Odaberite objekt (materijalnu točku). 2. Odbacimo vezu (ravninu) i zamijenimo je reakcijom N. 3. Sustavu sila dodamo nepoznatu silu F. 4. Sastavimo osnovnu jednadžbu dinamike: 5. Projiciramo osnovnu jednadžbu dinamike na osi x,y: Odredite projekcije sila: Modul sile: Kosinus smjera: Dakle, veličina sile je proporcionalna udaljenosti točke do središta koordinata i usmjerena je prema središtu duž linije koja povezuje točku sa središtem. Putanja točke je elipsa sa središtem u ishodištu: O r Predavanje 1 (nastavak - 1.3)

6 slajd

Predavanje 1 (nastavak 1.4) Primjer 3: Teret težine G ovješen je na sajlu duljine l i giba se po kružnoj stazi u vodoravnoj ravnini određenom brzinom. Kut odstupanja kabela od vertikale jednak je. Odredite napetost sajle i brzinu opterećenja. 1. Odaberite objekt (teret). 2. Odbacite spoj (uže) i zamijenite ga reakcijom R. 3. Sastavite glavnu jednadžbu dinamike: Iz treće jednadžbe odredite reakciju kabela: Odredite napetost kabela: Zamijenite vrijednost reakcije užeta, normalno ubrzanje u drugu jednadžbu i odrediti brzinu tereta: 4. Projicirati dinamiku osovine glavne jednadžbe,n,b: Primjer 4: Automobil težine G kreće se po konveksnom mostu (radijus zakrivljenosti je R ) brzinom V. Odredi pritisak automobila na most. 1. Odabiremo objekt (automobil, zanemarujemo dimenzije i smatramo ga točkom). 2. Odbacimo vezu (hrapavu površinu) i zamijenimo je reakcijama N i silom trenja Ffr. 3. Sastavljamo osnovnu jednadžbu dinamike: 4. Osnovnu jednadžbu dinamike projiciramo na os n: Odavde određujemo normalnu reakciju: Određujemo pritisak automobila na most: Odavde možemo odrediti brzinu odgovara nultom pritisku na mostu (Q = 0): 4

7 slajd

Predavanje 2 Nakon zamjene pronađenih vrijednosti konstanti dobivamo: Dakle, pod djelovanjem istog sustava sila materijalna točka može izvršiti čitavu klasu kretanja određenih početnim uvjetima. Početne koordinate uzimaju u obzir početni položaj točke. Početna brzina, dana projekcijama, uzima u obzir utjecaj na njezino kretanje duž razmatranog odsječka putanje sila koje su djelovale na točku prije nego što su stigle u ovu dionicu, t.j. početno kinematičko stanje. Rješenje inverznog problema dinamike - U općem slučaju kretanja točke, sile koje djeluju na točku su varijable koje ovise o vremenu, koordinatama i brzini. Gibanje točke opisuje se sustavom od tri diferencijalne jednadžbe drugog reda: Nakon integracije svake od njih, postojat će šest konstanti C1, C2,…., C6: Vrijednosti konstanti C1, C2,… ., C6 nalaze se iz šest početnih uvjeta pri t = 0: Primjer 1 rješenja inverznog problema: Slobodna materijalna točka mase m giba se pod djelovanjem sile F koja je konstantna po veličini i veličini. . U početnom trenutku brzina točke bila je v0 i podudarala se u smjeru sa silom. Odrediti jednadžbu gibanja točke. 1. Sastavljamo osnovnu jednadžbu dinamike: 3. Snižavamo red derivacije: 2. Biramo kartezijanski referentni sustav, usmjeravajući os x duž smjera sile i projiciramo glavnu jednadžbu dinamike na ovu os: ili x y z 4. Odvojite varijable: 5. Izračunajte integrale iz oba dijela jednadžbe : 6. Predstavite projekciju brzine kao vremensku derivaciju koordinate: 8. Izračunajte integrale oba dijela jednadžbe: 7. Odvojite varijable: 9. Za određivanje vrijednosti konstanti C1 i C2 koristimo početne uvjete t = 0, vx = v0 , x = x0: Kao rezultat, dobivamo jednadžbu jednoliko promjenjivog gibanja (duž x os): 5

8 slajd

Opće upute za rješavanje izravnih i inverznih zadataka. Postupak rješavanja: 1. Sastavljanje diferencijalne jednadžbe gibanja: 1.1. Odaberite koordinatni sustav - pravokutni (fiksni) s nepoznatom putanjom kretanja, prirodni (pokretni) s poznatom putanjom, na primjer, kružnica ili ravna linija. U potonjem slučaju može se koristiti jedna pravocrtna koordinata. Referentnu točku treba kombinirati s početnim položajem točke (pri t = 0) ili s ravnotežnim položajem točke, ako postoji, na primjer, kada točka fluktuira. 6 1.2. Nacrtajte točku na poziciji koja odgovara proizvoljnom trenutku u vremenu (za t > 0) tako da koordinate budu pozitivne (s > 0, x > 0). Također pretpostavljamo da je projekcija brzine u ovom položaju također pozitivna. U slučaju oscilacija, projekcija brzine mijenja predznak, na primjer, kada se vraća u ravnotežni položaj. Ovdje treba pretpostaviti da se u razmatranom trenutku točka odmiče od ravnotežnog položaja. Primjena ove preporuke bitna je u budućnosti pri radu sa silama otpora koje ovise o brzini. 1.3. Oslobodite materijalnu točku od veza, zamijenite njihovo djelovanje reakcijama, dodajte aktivne sile. 1.4. Zapišite osnovni zakon dinamike u vektorskom obliku, projicirajte na odabrane osi, izrazite zadane ili reaktivne sile u terminima vremena, koordinata ili varijabli brzine, ako ovise o njima. 2. Rješenje diferencijalnih jednadžbi: 2.1. Smanjite derivaciju ako se jednadžba ne svede na kanonski (standardni) oblik. na primjer: ili 2.2. Odvojene varijable, na primjer: ili 2.4. Izračunajte neodređene integrale na lijevoj i desnoj strani jednadžbe, na primjer: 2.3. Ako u jednadžbi postoje tri varijable, promijenite varijable, na primjer: i zatim odvojite varijable. Komentar. Umjesto kalkulacije neodređeni integrali moguće je izračunati određene integrale s promjenjivom gornjom granicom. Donje granice predstavljaju početne vrijednosti varijabli (početne uvjete). Tada nema potrebe zasebno pronaći konstantu, koja se automatski uključuje u rješenje, na primjer: Koristeći početne uvjete, na primjer, t = 0 , vx = vx0, odrediti konstantu integracije: 2.5. Izrazite brzinu u smislu vremenske derivacije koordinate, na primjer, i ponovite korake 2.2 -2.4 Napomena. Ako se jednadžba svede na kanonski oblik koji ima standardno rješenje, tada se koristi ovo gotovo rješenje. Konstante integracije se još uvijek nalaze iz početnih uvjeta. Vidi npr. oscilacije (predavanje 4, str. 8). Predavanje 2 (nastavak 2.2)

9 slajd

Predavanje 2 (nastavak 2.3) Primjer 2 rješavanja inverznog problema: Sila ovisi o vremenu. Teret težine P počinje se kretati duž glatke horizontalne površine pod djelovanjem sile F čija je veličina proporcionalna vremenu (F = kt). Odrediti put koji je prešao teret u vremenu t. 3. Sastavite osnovnu jednadžbu dinamike: 5. Smanjite redoslijed derivacije: 4. Projektirajte osnovnu jednadžbu dinamike na os x: ili 7 6. Odvojite varijable: 7. Izračunajte integrale oba dijela jednadžba: 9. Predstavite projekciju brzine kao derivaciju koordinate s obzirom na vrijeme: 10. Izračunajte integrale oba dijela jednadžbe: 9. Odvojite varijable: 8. Odredite vrijednost konstante C1 iz početni uvjet t = 0, vx = v0=0: Kao rezultat dobivamo jednadžbu gibanja (duž osi x), koja daje vrijednost prijeđene udaljenosti za vrijeme t: 1. Odaberite referentni sustav ( Kartezijanske koordinate) tako da tijelo ima pozitivnu koordinatu: 2. Predmet gibanja uzimamo kao materijalnu točku (tijelo se kreće naprijed), oslobađamo ga od veze (referentne ravnine) i zamjenjujemo reakcijom (normalna reakcija glatke površina): 11. Odrediti vrijednost konstante C2 iz početnog uvjeta t = 0, x = x0=0: Primjer inverznog zadatka 3: Sila ovisi o koordinati. Materijalna točka mase m izbačena je prema gore sa Zemljine površine brzinom v0. Sila gravitacije Zemlje obrnuto je proporcionalna kvadratu udaljenosti od točke do težišta (centra Zemlje). Odrediti ovisnost brzine o udaljenosti y do središta Zemlje. 1. Odabiremo referentni sustav (kartezijanske koordinate) tako da tijelo ima pozitivnu koordinatu: 2. Sastavljamo osnovnu jednadžbu dinamike: 3. Osnovnu jednadžbu dinamike projiciramo na os y: ili Koeficijent proporcionalnosti može može se pronaći pomoću težine točke na površini Zemlje: R Stoga diferencijal jednadžba izgleda ovako: ili 4. Smanji redoslijed derivacije: 5. Promijeni varijablu: 6. Odvoji varijable: 7. Izračunaj integrali obje strane jednadžbe: 8. Zamijenite granice: Kao rezultat, dobivamo izraz za brzinu kao funkciju koordinate y: Maksimalna visina leta može se naći izjednačavanjem brzine s nulom: Maksimalna visina leta kada se nazivnik okrene na nulu: Odavde, pri postavljanju polumjera Zemlje i ubrzanja slobodnog pada, dobiva se II kozmička brzina:

10 slajd

Predavanje 2 (nastavak 2.4) Primjer 2 rješavanja inverznog zadatka: Sila ovisi o brzini. Brod mase m imao je brzinu v0. Otpor vode kretanju broda proporcionalan je brzini. Odredite vrijeme potrebno da se brzina broda prepolovi nakon gašenja motora, kao i udaljenost koju je brod priješao do potpunog zaustavljanja. 8 1. Odabiremo referentni sustav (kartezijanske koordinate) tako da tijelo ima pozitivnu koordinatu: 2. Uzimamo objekt gibanja kao materijalnu točku (brod se kreće naprijed), oslobađamo ga od veza (vode) i zamjenjujemo s reakcijom (sila uzgona - Arhimedova sila), a također i sila otpora kretanju. 3. Dodajte aktivnu silu (gravitaciju). 4. Sastavljamo glavnu jednadžbu dinamike: 5. Glavnu jednadžbu dinamike projiciramo na os x: ili 6. Spuštamo red derivacije: 7. Odvajamo varijable: 8. Računamo integrale iz oba dijelove jednadžbe: 9. Zamjenjujemo granice: Dobiva se izraz koji povezuje brzinu i vrijeme t, iz kojeg se može odrediti vrijeme kretanja: Vrijeme kretanja, tijekom kojeg će brzina pasti za polovicu: To je zanimljivo je primijetiti da kada se brzina približi nuli, vrijeme kretanja teži beskonačnosti, t.j. konačna brzina ne može biti nula. Zašto ne "perpetual motion"? Međutim, u ovom slučaju, prijeđena udaljenost do zaustavljanja je konačna vrijednost. Da bismo odredili prijeđenu udaljenost, okrenemo se izrazu dobivenom nakon snižavanja reda derivacije i izvršimo promjenu varijable: Nakon integracije i zamjene granica, dobivamo: Prijeđenu udaljenost do zaustavljanja: ■ Kretanje točke bačene u kut prema horizontu u jednoličnom gravitacijskom polju bez uzimanja u obzir otpora zraka Eliminirajući vrijeme iz jednadžbi gibanja, dobivamo jednadžbu putanje: Vrijeme leta određuje se izjednačavanjem koordinate y s nulom: Domet leta određuje se zamjenom vrijeme leta:

11 slajd

Predavanje 3 Pravocrtne oscilacije materijalne točke - Oscilatorno kretanje materijalne točke događa se pod uvjetom da postoji sila vraćanja koja teži vratiti točku u ravnotežni položaj za svako odstupanje od tog položaja. 9 Postoji povratna sila, ravnotežni položaj je stabilan. Nema povratne sile, ravnotežni položaj je nestabilan. Nema povratne sile, ravnotežni položaj je indiferentan Uvijek je usmjerena prema ravnotežnom položaju, vrijednost je izravno proporcionalna linearnom istezanju (skraćenju) opruge, jednaka odstupanju tijela od ravnotežnog položaja: c je koeficijent krutosti opruge, brojčano jednake po snazi, pod čijim djelovanjem opruga mijenja svoju duljinu za jedan, mjeri se u N / m u SI sustavu. x y O Vrste vibracija materijalne točke: 1. Slobodne vibracije (bez uzimanja u obzir otpora medija). 2. Slobodne oscilacije uzimajući u obzir otpor medija (prigušene oscilacije). 3. Prisilne vibracije. 4. Prisilne oscilacije uzimajući u obzir otpor medija. ■ Slobodne oscilacije – nastaju pod djelovanjem samo povratne sile. Zapišimo osnovni zakon dinamike: Odaberemo koordinatni sustav sa središtem u ravnotežnom položaju (točka O) i projiciramo jednadžbu na os x: Dovedemo rezultirajuću jednadžbu u standardni (kanonski) oblik: Ova jednadžba je homogena linearna diferencijalna jednadžba drugog reda, čiji je oblik rješenja određen korijenima karakteristike jednadžbe dobivene univerzalnom zamjenom: Korijeni karakteristične jednadžbe su imaginarni i jednaki: Opće rješenje diferencijalne jednadžbe ima oblik: Brzina točke: Početni uvjeti: Definirajte konstante: Dakle, jednadžba slobodnih vibracija ima oblik: Jednadžba se može prikazati jednočlanim izrazom: gdje je a amplituda, - početna faza. Nove konstante a i - povezane su s konstantama C1 i C2 relacijama: Definirajmo a i: Razlog nastanka slobodnih oscilacija je početni pomak x0 i/ili početna brzina v0.

12 slajd

10 Predavanje 3 (nastavak 3.2) Prigušene oscilacije materijalne točke - Oscilatorno kretanje materijalne točke događa se uz prisutnost povratne sile i sile otpora kretanju. Ovisnost sile otpora kretanju o pomaku ili brzini određena je fizičkom prirodom medija ili veze koja ometa kretanje. Najjednostavnija ovisnost je linearna ovisnost na brzinu (viskozni otpor): - koeficijent viskoznosti x y O Osnovna jednadžba dinamike: Projekcija jednadžbe dinamike na os: Dovodimo jednadžbu u standardni oblik: gdje Karakteristična jednadžba ima korijene: Opće rješenje ove diferencijalne jednadžbe ima različit oblik ovisno o vrijednostima korijena: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - slučaj velike viskozne otpornosti: - pravi korijeni, različiti. ili - ove funkcije su aperiodične: 3. n = k: - korijeni su realni, višestruki. ove funkcije su također aperiodične:

13 slajd

Predavanje 3 (nastavak 3.3) Klasifikacija rješenja slobodnih oscilacija. Opružne veze. ekvivalentna tvrdoća. y y 11 Dif. Jednadžbeni lik. Korijeni jednadžbe char. jednadžba Rješavanje diferencijalne jednadžbe Graf nk n=k

14 slajd

Predavanje 4 Prisilne vibracije materijalne točke - Uz povratnu silu djeluje i sila koja se povremeno mijenja, koja se naziva sila smetnji. Uznemirujuća sila može imati drugačiju prirodu. Na primjer, u određenom slučaju, inercijski učinak neuravnotežene mase m1 rotacionog rotora uzrokuje harmonično promjenjive projekcije sile: Glavna jednadžba dinamike: Projekcija jednadžbe dinamike na os: Dovedite jednadžbu na standard oblik: 12 Rješenje ove nehomogene diferencijalne jednadžbe sastoji se od dva dijela x = x1 + x2: x1 je opće rješenje odgovarajuće homogene jednadžbe, a x2 je posebno rješenje nehomogene jednadžbe: Odabiremo posebno rješenje u obliku desna strana: Rezultirajuća jednakost mora biti zadovoljena za bilo koji t . Tada: ili Dakle, uz istodobno djelovanje povratne i remećejuće sile, materijalna točka vrši složeno oscilatorno gibanje, koje je rezultat zbrajanja (superpozicije) slobodnih (x1) i prisilnih (x2) vibracija. Ako str< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (prisilne oscilacije visoke frekvencije), tada je faza oscilacija suprotna fazi sile koja remeti:

15 slajd

Predavanje 4 (nastavak 4.2) 13 Dinamički koeficijent - omjer amplitude prisilne vibracije na statičko odstupanje točke pod djelovanjem konstantne sile H = const: Amplituda prisilnih oscilacija: Statičko odstupanje se može naći iz jednadžbe ravnoteže: Ovdje: Dakle: Dakle, na p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (visoka frekvencija prisilnih titranja) dinamički koeficijent: Rezonancija – nastaje kada se frekvencija prisilnih titranja poklopi s frekvencijom vlastitih oscilacija (p = k). To se najčešće događa prilikom pokretanja i zaustavljanja rotacije loše uravnoteženih rotora postavljenih na elastične ovjese. Diferencijalna jednadžba oscilacija jednakih frekvencija: Ne može se uzeti određeno rješenje u obliku desne strane, jer dobit će se linearno ovisno rješenje (vidi opće rješenje). Opće rješenje: Zamjena u diferencijalnoj jednadžbi: Uzmimo određeno rješenje u obliku i izračunajmo derivacije: Tako se dobiva rješenje: ili Prisilne oscilacije u rezonanciji imaju amplitudu koja se neograničeno povećava proporcionalno vremenu. Utjecaj otpora gibanju tijekom prisilnih vibracija. Diferencijalna jednadžba u prisutnosti viskoznog otpora ima oblik: Opće rješenje se bira iz tablice (predavanje 3, str. 11) ovisno o omjeru n i k (vidi). Uzimamo određeno rješenje u obliku i izračunavamo derivacije: Zamjena u diferencijalnoj jednadžbi: Izjednačavanje koeficijenata na istom trigonometrijske funkcije dobivamo sustav jednadžbi: Dizanjem obje jednadžbe na stepen i njihovim zbrajanjem dobivamo amplitudu prisilnih oscilacija: Dijeljenjem druge jednadžbe s prvom dobivamo fazni pomak prisilnih oscilacija: Dakle, jednadžba gibanja za prisilne oscilacije, uzimajući u obzir otpor kretanju, na primjer, na n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 slajd

Predavanje 5 Relativno gibanje materijalne točke - Pretpostavimo da se pokretni (neinercijski) koordinatni sustav Oxyz giba po nekom zakonu u odnosu na fiksni (inercijski) koordinatni sustav O1x1y1z1. Gibanje materijalne točke M (x, y, z) u odnosu na pokretni sustav Oxyz je relativno, u odnosu na nepomični sustav O1x1y1z1 je apsolutno. Gibanje mobilnog sustava Oxyz u odnosu na fiksni sustav O1x1y1z1 je prijenosno gibanje. 14 z x1 y1 z1 O1 x y M x y z O Osnovna jednadžba dinamike: Apsolutna akceleracija točke: Zamijeni apsolutna akceleracija točke u glavnu jednadžbu dinamike: Prenesimo članove s translacijskim i Coriolisovim ubrzanjem na desnu stranu: preneseni pojmovi imaju dimenziju sila i smatraju se odgovarajućim inercijskim silama, jednakim: Tada se relativno gibanje točke može smatrati apsolutnim ako se djelujućim silama dodaju translacijske i Coriolisove sile inercije: U projekcijama na osi gibljivog koordinatnog sustava imamo: rotacija je jednolika, tada je εe = 0: 2. Translacijsko krivuljasto gibanje: Ako je gibanje pravocrtno, tada = : Ako je gibanje pravocrtno i jednoliko, tada je sustav kretanja inercijalan i relativni gibanje se može smatrati apsolutnim: nikakve mehaničke pojave ne mogu otkriti pravocrtnu uniformu gibanje (načelo relativnosti klasične mehanike). Utjecaj Zemljine rotacije na ravnotežu tijela – Pretpostavimo da je tijelo u ravnoteži na površini Zemlje na proizvoljnoj geografskoj širini φ (paralele). Zemlja rotira oko svoje osi od zapada prema istoku kutnom brzinom: polumjer Zemlje je oko 6370 km. S R je ukupna reakcija neglatke površine. G - sila privlačenja Zemlje prema centru. F - centrifugalna sila inercije. Uvjet relativne ravnoteže: Rezultanta sila privlačenja i inercije je sila gravitacije (težina): Veličina sile gravitacije (težine) na površini Zemlje je P = mg. Centrifugalna sila inercije je mali djelić sile gravitacije: Odstupanje sile gravitacije od smjera sile privlačenja je također malo: Dakle, utjecaj Zemljine rotacije na ravnotežu tijela izuzetno je mali. i ne uzima se u obzir u praktičnim proračunima. Maksimalna vrijednost inercijalne sile (pri φ = 0 - na ekvatoru) iznosi samo 0,00343 vrijednosti gravitacije

17 slajd

Predavanje 5 (nastavak 5.2) 15 Utjecaj Zemljine rotacije na kretanje tijela u Zemljinom gravitacijskom polju - Pretpostavimo da tijelo padne na Zemlju s određene visine H iznad Zemljine površine na geografskoj širini φ . Odaberimo pokretni referentni okvir, kruto povezan sa Zemljom, usmjeravajući osi x, y tangencijalno na paralelu i na meridijan: Relativna jednadžba gibanja: Ovdje je malenost centrifugalne sile inercije u usporedbi sa silom gravitacije jednaka uzeti u obzir. Dakle, sila gravitacije se poistovjećuje sa silom gravitacije. Osim toga, pretpostavljamo da je gravitacija usmjerena okomito na Zemljinu površinu zbog malog otklona, kao što je gore razmotreno. Coriolisovo ubrzanje je jednako i usmjereno je paralelno s y-osi prema zapadu. Coriolisova sila inercije usmjerena je u suprotnom smjeru. Projiciramo jednadžbu relativnog gibanja na os: Rješenje prve jednadžbe daje: Početni uvjeti: Rješenje treće jednadžbe daje: Početni uvjeti: Treća jednadžba ima oblik: Početni uvjeti: Njeno rješenje daje: Rezultirajuće rješenje pokazuje da tijelo prilikom pada skreće prema istoku. Izračunajmo vrijednost ovog odstupanja, na primjer, pri padu s visine od 100 m. Vrijeme pada nalazimo iz rješenja druge jednadžbe: Dakle, utjecaj Zemljine rotacije na kretanje tijela izuzetno je mali. za praktične visine i brzine i ne uzima se u obzir u tehničkim proračunima. Rješenje druge jednadžbe također podrazumijeva postojanje brzine duž y-osi, koja bi također trebala uzrokovati i uzrokovati odgovarajuće ubrzanje i Coriolisovu inercijsku silu. Utjecaj ove brzine i s njom povezane sile tromosti na promjenu gibanja bit će čak i manji od razmatrane Coriolisove sile tromosti povezane s okomitom brzinom.

18 slajd

Predavanje 6 Dinamika mehaničkog sustava. Sustav materijalnih točaka ili mehanički sustav - Skup materijalnih točaka ili onih materijalnih točaka ujedinjenih općim zakonima interakcije (položaj ili kretanje svake od točaka ili tijela ovisi o položaju i kretanju svih ostalih) sustav slobodnih točaka - čije kretanje nije ograničeno nikakvim vezama (na primjer, planetarni sustav, u kojem se planeti smatraju materijalnim točkama). Sustav neslobodnih točaka ili neslobodni mehanički sustav – kretanje materijalnih točaka ili tijela ograničeno je ograničenjima koja su nametnuta sustavu (na primjer, mehanizam, stroj itd.). 16 Sile koje djeluju na sustav. Uz dosadašnju klasifikaciju sila (aktivne i reaktivne sile), uvodi se nova klasifikacija sila: 1. Vanjske sile (e) - djeluju na točke i tijela sustava iz točaka ili tijela koja nisu dio ovog sustav. 2. Unutarnje sile (i) - sile interakcije između materijalnih točaka ili tijela uključenih u dati sustav. Ista sila može biti i vanjska i unutarnja sila. Sve ovisi o tome koji se mehanički sustav razmatra. Na primjer: U sustavu Sunca, Zemlje i Mjeseca sve su gravitacijske sile između njih unutarnje. Kada se razmatra sustav Zemlje i Mjeseca, gravitacijske sile koje se primjenjuju sa strane Sunca su vanjske: C Z L Na temelju zakona djelovanja i reakcije, svaka unutarnja sila Fk odgovara drugoj unutarnjoj sili Fk', jednakoj po apsolutnoj vrijednosti i suprotnoj u smjer. Iz ovoga proizlaze dva izvanredna svojstva unutarnjih sila: Glavni vektor svih unutarnjih sila sustava jednak je nuli: Glavni moment svih unutarnjih sila sustava u odnosu na bilo koje središte jednak je nuli: Ili u projekcijama na koordinatu osi: Napomena. Iako su ove jednadžbe slične jednadžbama ravnoteže, nisu, budući da se unutarnje sile primjenjuju na različite točke ili tijela sustava i mogu uzrokovati da se te točke (tijela) pomiču jedna u odnosu na drugu. Iz ovih jednadžbi proizlazi da unutarnje sile ne utječu na gibanje sustava koji se promatra kao cjelina. Središte mase sustava materijalnih točaka. Za opisivanje gibanja sustava u cjelini uvodi se geometrijska točka, nazvana središte mase, čiji je radijus-vektor određen izrazom, gdje je M masa cijelog sustava: Ili u projekcijama na koordinatu osi: Formule za središte mase slične su onima za težište. Međutim, pojam centra mase je općenitiji, budući da nije povezan sa silama gravitacije ili silama gravitacije.

19 slajd

Predavanje 6 (nastavak 6.2) 17 Teorem o gibanju središta mase sustava - Razmotrimo sustav od n materijalnih točaka. Sile koje djeluju na svaku točku dijelimo na vanjske i unutarnje i zamjenjujemo ih odgovarajućim rezultantama Fke i Fki. Zapišimo za svaku točku osnovnu jednadžbu dinamike: ili Zbrojimo ove jednadžbe po svim točkama: Na lijevoj strani jednadžbe uvest ćemo mase pod znakom derivacije i zamijeniti zbroj derivacija derivacijom od zbroja: Iz definicije središta mase: Zamijenite u rezultirajuću jednadžbu: dobivamo ili: Umnožak mase sustava i akceleracije njegove središnje mase jednak je glavnom vektoru vanjskih sila. U projekcijama na koordinatne osi: Središte mase sustava giba se kao materijalna točka s masom jednakom masi cijelog sustava na koju se primjenjuju sve vanjske sile koje djeluju na sustav. Posljedice iz teorema o gibanju središta mase sustava (zakoni održanja): 1. Ako je u vremenskom intervalu glavni vektor vanjskih sila sustava nula, Re = 0, tada je brzina centra mase je konstantna, vC = const (središte mase giba se jednoliko pravolinijsko - zakon održanja gibanja središta mase). 2. Ako je u vremenskom intervalu projekcija glavnog vektora vanjskih sila sustava na os x jednaka nuli, Rxe = 0, tada je brzina središta mase duž x osi konstantna, vCx = const (središte mase giba se jednoliko duž osi). Slične tvrdnje vrijede za y i z osi. Primjer: Dvije osobe mase m1 i m2 nalaze se u čamcu mase m3. U početnom trenutku čamac s ljudima mirovao je. Odredi pomak čamca ako se osoba mase m2 pomaknula do pramca čamca na udaljenosti a. 3. Ako je u vremenskom intervalu glavni vektor vanjskih sila sustava jednak nuli, Re = 0, a u početnom trenutku brzina centra mase je nula, vC = 0, tada je vektor radijusa od središte mase ostaje konstantno, rC = const (središte mase miruje je zakon održanja položaja središta mase). 4. Ako je u vremenskom intervalu projekcija glavnog vektora vanjskih sila sustava na os x jednaka nuli, Rxe = 0, a u početnom trenutku brzina središta mase duž ove osi je nula , vCx = 0, tada koordinata središta mase duž osi x ostaje konstantna, xC = const (središte mase se ne pomiče duž ove osi). Slične tvrdnje vrijede za y i z osi. 1. Predmet gibanja (čamac s ljudima): 2. Odbacujemo veze (voda): 3. vezu zamjenjujemo reakcijom: 4. Zbrajamo aktivne sile: 5. Zapiši teorem o središtu mase: Projicirajte na os x: O Odredite koliko daleko trebate prijeći do osobe mase m1, tako da čamac ostane na mjestu: Čamac će se pomaknuti za udaljenost l u suprotnom smjeru.

20 slajd

7. predavanje Impuls sile je mjera mehaničke interakcije koja karakterizira prijenos mehaničko kretanje od sila koje djeluju na točku u određenom vremenskom razdoblju: 18 U projekcijama na koordinatne osi: U slučaju stalne sile: U projekcijama na koordinatne osi: Zamah rezultante jednak je geometrijskom zbroju impulsi sila koje se primjenjuju na točku za isto vremensko razdoblje: dt: Integrirajmo na zadanom vremenskom intervalu: Količina pomaka točke je mjera mehaničkog kretanja, određena vektorom, jednak proizvodu masa točke na njezinom vektoru brzine: Teorem o promjeni količine gibanja sustava - Razmotrimo sustav od n materijalnih točaka. Sile koje djeluju na svaku točku dijelimo na vanjske i unutarnje i zamjenjujemo ih odgovarajućim rezultantama Fke i Fki. Napišimo za svaku točku osnovnu jednadžbu dinamike: ili Količina gibanja sustava materijalnih točaka - geometrijski zbroj količina gibanja materijalnih točaka: Po definiciji središta mase: Vektor količine gibanja sustava jednak je umnošku mase cijelog sustava i vektora brzine središta mase sustava. Zatim: U projekcijama na koordinatne osi: Vremenska derivacija vektora zamaha sustava jednaka je glavnom vektoru vanjskih sila sustava. Zbrojimo ove jednadžbe po svim točkama: Na lijevoj strani jednadžbe uvodimo mase pod znakom derivacije i zamjenjujemo zbroj derivacija derivacijom zbroja: Iz definicije količine gibanja sustava: U projekcijama na koordinatne osi:

21 slajd

Eulerov teorem - Primjena teorema o promjeni količine gibanja sustava na kretanje kontinuiranog medija (vode). 1. Kao objekt kretanja odabiremo volumen vode koji se nalazi u krivuljastom kanalu turbine: 2. Odbacujemo spojeve i zamjenjujemo njihovo djelovanje reakcijama (Rpov - rezultanta površinskih sila) 3. Dodajemo aktivne sile (Rb - rezultanta tjelesnih sila): 4. Zapišite teorem o promjeni količine gibanja sustava: Količina gibanja vode u trenucima t0 i t1 predstavit će se kao zbroji: Promjena količine gibanja vode u vremenskom intervalu : Promjena količine gibanja vode u beskonačno malom vremenskom intervalu dt: , gdje je F1 F2 Uzimajući umnožak gustoće, površine poprečnog presjeka i brzine po sekundi mase, dobivamo: Zamjena diferencijala količine gibanja sustava u teorem promjene , dobivamo: Posljedice iz teorema o promjeni količine gibanja sustava (zakoni održanja): 1. Ako je u vremenskom intervalu glavni vektor vanjskih sila sustava jednak nuli, Re = 0, tada kvantitet vektorskog gibanja je konstantan, Q = const je zakon održanja količine gibanja sustava). 2. Ako je u vremenskom intervalu projekcija glavnog vektora vanjskih sila sustava na os x jednaka nuli, Rxe = 0, tada je projekcija količine gibanja sustava na os x konstantna, Qx = konst. Slične tvrdnje vrijede za y i z osi. Predavanje 7 (nastavak 7.2) Primjer: Granata mase M, koja je letjela brzinom v, eksplodirala je na dva dijela. Brzina jednog od ulomaka mase m1 porasla je u smjeru gibanja na vrijednost v1. Odredite brzinu drugog fragmenta. 1. Predmet kretanja (granata): 2. Objekt je slobodan sustav, nema veza i njihovih reakcija. 3. Dodajte aktivne sile: 4. Zapišite teorem o promjeni količine gibanja: Projektirajte na os: β Podijelite varijable i integrirajte: Desni integral je gotovo nula, jer vrijeme eksplozije t

22 slajd

Predavanje 7 (nastavak 7.3) 20 Kutni moment točke ili kinetički moment gibanja u odnosu na određeno središte je mjera mehaničkog gibanja, određena vektorom jednakim vektorskom umnošku vektora radijusa materijalne točke i vektor njegovog zamaha: Kinetički moment sustava materijalnih točaka u odnosu na određeno središte je geometrijski zbroj momenata broja gibanja svih materijalnih točaka u odnosu na isto središte: U projekcijama na os: U projekcijama na os: Teorem o promjeni momenta zamaha sustava - Razmotrimo sustav od n materijalnih točaka. Sile koje djeluju na svaku točku dijelimo na vanjske i unutarnje i zamjenjujemo ih odgovarajućim rezultantama Fke i Fki. Zapišimo za svaku točku osnovnu jednadžbu dinamike: ili Zbrojimo ove jednadžbe za sve točke: Zamijenimo zbroj derivacija derivacijom zbroja: Izraz u zagradi je moment količine gibanja sustava. Odavde: Vektorski pomnožimo svaku od jednakosti s radijus vektorom s lijeve strane: Pogledajmo je li moguće uzeti predznak derivacije izvan vektorski proizvod: Tako smo dobili: Derivat vektora zamaha sustava u odnosu na određeno središte u vremenu jednak je glavnom momentu vanjskih sila sustava u odnosu na isto središte. U projekcijama na koordinatne osi: Derivat momenta gibanja sustava u odnosu na neku os u vremenu jednak je glavnom momentu vanjskih sila sustava u odnosu na istu os.

23 slajd

Predavanje 8 21 ■ Posljedice iz teorema o promjeni kutne količine gibanja sustava (zakoni održanja): 1. Ako je u vremenskom intervalu vektor glavnog momenta vanjskih sila sustava u odnosu na određeno središte jednak. na nulu, MOe = 0, tada je vektor kutne količine gibanja sustava u odnosu na isto središte konstantan, KO = const je zakon održanja količine gibanja sustava). 2. Ako je u vremenskom intervalu glavni moment vanjskih sila sustava u odnosu na os x jednak nuli, Mxe = 0, tada je kutni moment sustava u odnosu na os x konstantan, Kx = const. Slične tvrdnje vrijede za y i z osi. 2. Moment tromosti krutog tijela oko osi: Moment tromosti materijalne točke oko osi jednak je umnošku mase točke i kvadrata udaljenosti točke od osi. Trenutak tromosti krutog tijela oko osi jednak je zbroju proizvoda mase svake točke i kvadrata udaljenosti te točke od osi. ■ Elementi teorije momenata tromosti - Kod rotacijskog gibanja krutog tijela mjera tromosti (otpora promjeni gibanja) je moment tromosti oko osi rotacije. Razmotrimo osnovne pojmove definicije i metode za izračunavanje momenata tromosti. 1. Moment tromosti materijalne točke oko osi: Pri prijelazu iz diskretne male mase u beskonačno malu masu točke, granica takvog zbroja određena je integralom: aksijalni moment tromosti krutog tijela. . Osim aksijalnog momenta tromosti krutog tijela, postoje i druge vrste momenata tromosti: centrifugalni moment tromosti krutog tijela. polarni moment tromosti krutog tijela. 3. Teorem o momentima tromosti krutog tijela oko paralelnih osi - formula za prijelaz na paralelne osi: Moment tromosti oko referentne osi Statički momenti tromosti oko referentnih osi Masa tijela Udaljenost između osi z1 i z2 Dakle : trenuci su nula:

24 slajd

Predavanje 8 (nastavak 8.2) 22 Moment tromosti jednolične šipke konstantnog presjeka oko osi: x z L Odabrati elementarni volumen dV = Adx na udaljenosti x: x dx Elementarna masa: Izračunati moment tromosti oko središnje osi (prolazeći kroz težište), dovoljno je promijeniti položaj osi i postaviti granice integracije (-L/2, L/2). Ovdje demonstriramo formulu za prijelaz na paralelne osi: zS 5. Moment tromosti homogenog čvrstog cilindra oko osi simetrije: H dr r Izdvojimo elementarni volumen dV = 2πrdrH (tanki cilindar polumjera r) : Elementarna masa: Ovdje koristimo formulu volumena cilindra V=πR2H. Za izračunavanje momenta tromosti šupljeg (debelog) cilindra dovoljno je postaviti granice integracije od R1 do R2 (R2> R1): 6. Moment inercije tankog cilindra oko osi simetrije (t

25 slajd

Predavanje 8 (nastavak 8.3) 23 ■ Diferencijalna jednadžba rotacije krutog tijela oko osi: Napišimo teorem o promjeni kutnog momenta krutog tijela koje rotira oko fiksne osi: Moment rotacije krutog tijela je: Moment vanjskih sila oko osi rotacije jednaka je momentu (reakcije i sila ne stvaraju gravitacijske momente): Zamjenjujemo kinetički moment i moment u teorem Primjer: Dvije osobe iste težine G1 = G2 vise na bačenom užetu nad čvrstim blokom težine G3 = G1/4. U nekom trenutku, jedan od njih se počeo penjati po užetu relativnom brzinom u. Odredite brzinu podizanja svake osobe. 1. Odaberite objekt kretanja (blok s ljudima): 2. Odbacite spojeve (noseći uređaj bloka): 3. Zamijenite vezu s reakcijama (ležaj): 4. Dodajte aktivne sile (gravitaciju): 5. Zapišite teorem o promjeni kinetičkog momenta sustava s obzirom na os rotacije bloka: R Budući da je moment vanjskih sila jednak nuli, kinetički moment mora ostati konstantan: U početnom trenutku vremena t = 0, postoji bio je ravnotežan i Kz0 = 0. Nakon početka gibanja jedne osobe u odnosu na uže, cijeli se sustav počeo kretati, ali sustav kinetičkog momenta mora ostati nula: Kz = 0. Kutni moment sustava je zbroj kutnih momenata ljudi i bloka: Ovdje je v2 brzina druge osobe, jednaka brzini kabel, Primjer: Odrediti period malih slobodnih titranja homogene šipke mase M i duljine l, obješene na jednom kraju o fiksnu os rotacije. Ili: U slučaju malih oscilacija sinφ φ: Period titranja: Moment inercije štapa:

26 slajd

Predavanje 8 (nastavak 8.4 - dodatni materijal ) 24 ■ Elementarna teorija žiroskopa: Žiroskop je kruto tijelo koje rotira oko osi materijalne simetrije, čija je jedna od točaka nepomična. Slobodni žiroskop je fiksiran na način da mu središte mase ostaje nepomično, a os rotacije prolazi kroz središte mase i može zauzeti bilo koji položaj u prostoru, t.j. os rotacije mijenja svoj položaj kao i os vlastite rotacije tijela tijekom sfernog gibanja. Glavna pretpostavka aproksimativne (elementarne) teorije žiroskopa je da se vektor zamaha (kinetički moment) rotora smatra usmjerenim duž vlastite osi rotacije. Dakle, unatoč činjenici da u općem slučaju rotor sudjeluje u tri rotacije, u obzir se uzima samo kutna brzina vlastite rotacije ω = dφ/dt. Razlog tome je što se u modernoj tehnologiji rotor žiroskopa rotira kutnom brzinom reda 5000-8000 rad/s (oko 50000-80000 o/min), dok su druge dvije kutne brzine povezane s precesijom i nutacijom vlastite osi. vrtnje desetke tisuća puta manje od ove brzine. Glavno svojstvo slobodnog žiroskopa je da os rotora zadržava isti smjer u prostoru u odnosu na inercijski (zvjezdani) referentni sustav (demonstriran Foucaultovim njihalom, koji drži ravninu ljuljanja nepromijenjenom u odnosu na zvijezde, 1852.). To proizlazi iz zakona održanja kinetičkog momenta u odnosu na središte mase rotora, pod uvjetom da se zanemari trenje u ležajevima osi ovjesa rotora, vanjskog i unutarnjeg okvira: Djelovanje sile na os slobodnog žiroskop. U slučaju primjene sile na os rotora, moment vanjskih sila u odnosu na središte mase nije jednak nuli: ω ω S sila, a prema vektoru momenta te sile, t.j. neće se rotirati oko x-osi (unutarnji ovjes), već oko y-osi (vanjski ovjes). Po prestanku sile, os rotora će ostati u istom položaju, što odgovara posljednjem vremenu djelovanja sile, jer od ovog trenutka, moment vanjskih sila ponovno postaje jednak nuli. U slučaju kratkotrajnog djelovanja sile (udara), os žiroskopa praktički ne mijenja svoj položaj. Dakle, brza rotacija rotora daje žiroskopu mogućnost suprotstavljanja slučajnim utjecajima koji nastoje promijeniti položaj osi rotacije rotora, a uz stalno djelovanje sile održava položaj ravnine okomite na djelujuća sila u kojoj leži os rotora. Ova svojstva se koriste u inercijski sustavi navigacija.

Predavanja iz teorijske mehanike

Dinamika točaka

Predavanje 1

Osnovni pojmovi dinamike

U poglavlju Dinamika proučava se kretanje tijela pod djelovanjem sila koje se na njih primjenjuju. Stoga, pored onih pojmova koji su uvedeni u odjeljku Kinematika, ovdje je potrebno koristiti nove koncepte koji odražavaju specifičnosti utjecaja sila na razna tijela i reakcija tijela na te utjecaje. Razmotrimo glavne od ovih koncepata.

a) snaga

Sila je kvantitativni rezultat utjecaja drugih tijela na određeno tijelo. Sila je vektorska veličina (slika 1).

Točka A početka vektora sile F pozvao točka primjene sile. Zove se pravac MN na kojem se nalazi vektor sile linija sile. Duljina vektora sile, mjerena na određenoj skali, naziva se brojčana vrijednost ili modul vektora sile. Modul sile se označava kao ili . Djelovanje sile na tijelo očituje se ili u njegovoj deformaciji, ako tijelo miruje, ili u davanju ubrzanja kada se tijelo kreće. Na tim manifestacijama sile temelji se uređaj različitih instrumenata (mjera sile ili dinamometara) za mjerenje sila.

b) sustav sila

Razmatrani skup sila se formira sustav sila. Svaki sustav koji se sastoji od n sila može se zapisati u sljedećem obliku:

c) slobodno tijelo

Tijelo koje se može kretati u prostoru u bilo kojem smjeru, a da ne doživi izravnu (mehaničku) interakciju s drugim tijelima naziva se besplatno ili izolirani. Utjecaj jednog ili drugog sustava sila na tijelo može se razjasniti samo ako je ovo tijelo slobodno.

d) rezultantna sila

Ako bilo koja sila ima isti učinak na slobodno tijelo kao neki sustav sila, tada se ta sila naziva rezultanta ovog sustava sila. Ovo je napisano kako slijedi:

što znači ekvivalencija utjecaj na isto slobodno tijelo rezultante i nekog sustava n sila.

Prijeđimo sada na razmatranje složenijih pojmova vezanih uz kvantitativno određivanje rotacijskih učinaka sila.

e) moment sile u odnosu na točku (centar)

Ako se tijelo pod djelovanjem sile može rotirati oko neke fiksne točke O (slika 2), tada se za kvantificiranje ovog rotacijskog učinka uvodi fizička veličina koja se naziva moment sile oko točke (centra).

Zove se ravnina koja prolazi kroz zadanu fiksnu točku i liniju djelovanja sile ravnina sile. Na slici 2 to je ravnina OAV.

Moment sile u odnosu na točku (središte) je vektorska veličina jednaka vektorskom umnošku vektora radijusa točke primjene sile vektorom sile:

( 1)

Prema pravilu vektorskog množenja dvaju vektora, njihov vektorski umnožak je vektor okomit na ravninu položaja vektora faktora (u ovom slučaju ravninu trokuta OAB), usmjeren u smjeru iz kojeg je najkraći zaokret od prvi faktor vektor u drugi faktor vektor vidljivo na satu (slika 2). Ovim redoslijedom vektora faktora križnog proizvoda (1) rotacija tijela pod djelovanjem sile bit će vidljiva prema satu (slika 2) Budući da je vektor okomit na ravninu sile , njegov položaj u prostoru određuje položaj ravnine sile Brojčana vrijednost vektora momenta sile u odnosu na središte jednaka je dvostrukoj površini OAV i može se odrediti formulom:

, (2)

gdje veličinah, jednaka najkraćoj udaljenosti od zadane točke O do linije djelovanja sile, naziva se krakom sile.

Ako položaj ravnine djelovanja sile u prostoru nije bitan za karakterizaciju rotacijskog djelovanja sile, onda u ovom slučaju, za karakterizaciju rotacijskog djelovanja sile, umjesto vektora momenta sile, algebarski moment sile:

(3)

Algebarski moment sile u odnosu na zadano središte jednak je umnošku modula sile i njenog ramena, uzetog sa predznakom plus ili minus. U tom slučaju pozitivan moment odgovara rotaciji tijela pod djelovanjem zadane sile prema satu, a negativni moment odgovara rotaciji tijela u smjeru sata. Iz formula (1), (2) i (3) slijedi da moment sile u odnosu na točku jednak je nuli samo ako je krak ove silehnula. Takva sila ne može rotirati tijelo oko određene točke.

f) Moment sile oko osi

Ako se tijelo pod djelovanjem sile može rotirati oko neke fiksne osi (na primjer, rotacija okvira vrata ili prozora u šarkama kada se otvore ili zatvore), tada se uvodi fizička veličina za kvantificiranje ovog rotacijskog učinka, koja Zove se moment sile oko date osi.

 b Fxy

Slika 3 prikazuje dijagram u skladu s kojim se određuje moment sile oko z-osi:

Kut  čine dva okomita smjera z i na ravnine trokuta O ab i OAV, respektivno. Budući da  O ab je projekcija OAV na xy ravninu, tada prema teoremu o stereometriji o projekciji ravne figure na zadanu ravninu imamo:

gdje znak plus odgovara pozitivnoj vrijednosti cos, tj. oštri uglovi, a znak minus odgovara negativnoj vrijednosti cos, tj. tupim kutovima , zbog smjera vektora . Zauzvrat, SO ab=1/2abh, gdje h  ab . Vrijednost segmenta ab jednaka je projekciji sile na xy ravninu, tj. . ab = F xy .

Na temelju prethodno navedenog, kao i jednakosti (4) i (5), određujemo moment sile oko z-osi na sljedeći način:

Jednakost (6) nam omogućuje da formuliramo sljedeću definiciju momenta sile oko bilo koje osi: Moment sile oko dane osi jednak je projekciji na ovu os vektora momenta te sile u odnosu na bilo koju točku ovu os i definira se kao umnožak projekcije sile na ravninu okomitu na zadanu os, uzetu sa predznakom plus ili minus na ramenu ove projekcije u odnosu na točku presjeka osi s ravninom projekcije. U ovom slučaju, predznak trenutka smatra se pozitivnim ako se, gledajući iz pozitivnog smjera osi, rotacija tijela oko ove osi vidi u odnosu na sat. Inače, moment sile oko osi uzima se kao negativan. Budući da je ovu definiciju momenta sile u odnosu na os prilično teško zapamtiti, preporuča se zapamtiti formulu (6) i sl. 3, koja objašnjava ovu formulu.

Iz formule (6) proizlazi da moment sile oko osi je nula ako paralelna je s osi (u ovom slučaju njena projekcija na ravninu okomitu na os jednaka je nuli), ili linija djelovanja sile siječe os (tada krak projekcije h=0). To u potpunosti odgovara fizičkom značenju momenta sile oko osi kao kvantitativne karakteristike rotacijskog djelovanja sile na tijelo s osi rotacije.

g) tjelesna težina

Odavno je zapaženo da pod utjecajem sile tijelo postupno povećava brzinu i nastavlja se kretati ako se sila ukloni. To svojstvo tijela, da se odupiru promjeni svog gibanja, zvalo se tromosti ili tromosti tijela. Kvantitativna mjera tromosti tijela je njegova masa. Osim, masa tijela je kvantitativna mjera djelovanja gravitacijskih sila na dano tijelo što je masa tijela veća, to veća sila gravitacije djeluje na tijelo. Kao što će biti prikazano u nastavku, uh Ove dvije definicije tjelesne težine su povezane.

Drugi koncepti i definicije dinamike bit će raspravljeni kasnije u odjeljcima gdje se prvi put pojavljuju.

2. Veze i reakcije veza

Ranije u odjeljku 1 točka (c) dan je koncept slobodnog tijela, kao tijela koje se može kretati u prostoru u bilo kojem smjeru, a da nije u izravnom kontaktu s drugim tijelima. Većina stvarnih tijela koja nas okružuju u izravnom je kontaktu s drugim tijelima i ne mogu se kretati u jednom ili drugom smjeru. Tako se, na primjer, tijela koja se nalaze na površini stola mogu kretati u bilo kojem smjeru, osim u smjeru okomitom na površinu stola prema dolje. Vrata sa šarkama mogu se okretati, ali se ne mogu kretati naprijed itd. Tijela koja se ne mogu kretati u prostoru u jednom ili drugom smjeru nazivaju se nije besplatno.

Sve što ograničava kretanje danog tijela u prostoru naziva se vezama. To mogu biti neka druga tijela koja sprječavaju kretanje ovog tijela u nekim smjerovima ( fizičke veze); šire gledano, to mogu biti neki uvjeti nametnuti kretanju tijela, ograničavajući to kretanje. Dakle, možete postaviti uvjet da se kretanje materijalne točke dogodi duž zadane krivulje. U ovom slučaju, veza je određena matematički u obliku jednadžbe ( jednadžba veze). U nastavku će se detaljnije razmotriti pitanje o vrstama poveznica.

Većina veza nametnutih tijelima su praktički fizičke veze. Stoga se postavlja pitanje interakcije datog tijela i povezanosti nametnute tom tijelu. Na ovo pitanje odgovara aksiom o međudjelovanju tijela: Dva tijela djeluju jedno na drugo silama jednakim po veličini, suprotnog smjera i smještene na istoj pravoj liniji. Te se sile nazivaju interakcijske sile. Interakcione sile se primjenjuju na različita tijela koja djeluju. Tako, na primjer, tijekom interakcije zadanog tijela i veze, jedna od interakcijskih sila primjenjuje se sa strane tijela na spoj, a druga sila interakcije primjenjuje se sa strane veze na dano tijelo. . Ova posljednja moć se zove sila reakcije veze ili jednostavno, reakcija veze.

Pri rješavanju praktičnih zadataka dinamike potrebno je znati pronaći smjer reakcija različite vrste veze. Opće pravilo za određivanje smjera reakcije veze ponekad može pomoći u tome: Reakcija veze je uvijek usmjerena suprotno od smjera u kojem ta veza sprječava kretanje danog tijela. Ako se ovaj smjer može definitivno odrediti, tada će reakcija veze biti određena smjerom. Inače, smjer reakcije veze je neodređen i može se pronaći samo iz odgovarajućih jednadžbi gibanja ili ravnoteže tijela. Detaljnije treba proučiti pitanje vrsta veza i smjera njihovih reakcija prema udžbeniku: S.M. Targ Kratki tečaj teorijske mehanike "Viša škola", M., 1986. Pogl.1, §3.

U odjeljku 1, točka (c), rečeno je da se učinak bilo kojeg sustava sila može u potpunosti odrediti samo ako se ovaj sustav sila primijeni na slobodno tijelo. Budući da većina tijela, zapravo, nije slobodna, onda se u svrhu proučavanja kretanja tih tijela postavlja pitanje kako ta tijela učiniti slobodnima. Na ovo pitanje je odgovoreno aksiom povezanosti predavanja na filozofija kod kuće. Predavanja bili... socijalna psihologija i etnopsihologije. 3. Teorijski rezultati u socijaldarvinizmu bili su...

teorijski Mehanika

Vodič >> Fizika

Sažetak predavanja na predmet TEORIJSKI MEHANIKA Za studente specijalnosti: 260501,65 ... - redoviti Sažetak predavanja sastavljeno na temelju: Butorin L.V., Busygina E.B. teorijski Mehanika. Edukativni i praktični vodič...

Unutar bilo kojeg tečaj Studij fizike počinje mehanikom. Ne iz teorijske, ne iz primijenjene i ne računske, već iz dobre stare klasične mehanike. Ova mehanika se također naziva Newtonovom mehanikom. Prema legendi, znanstvenik je šetao vrtom, vidio kako jabuka pada, a upravo ga je taj fenomen potaknuo da otkrije zakon gravitacija. Naravno, zakon je oduvijek postojao, a Newton mu je samo dao oblik razumljiv ljudima, ali njegova je zasluga neprocjenjiva. U ovom članku nećemo što detaljnije opisivati zakone Newtonove mehanike, već ćemo iznijeti osnove, osnovna znanja, definicije i formule koje vam uvijek mogu igrati na ruku.

Mehanika je grana fizike, znanost koja proučava kretanje materijalnih tijela i međudjelovanja među njima.

Sama riječ je grčkog porijekla i prevodi se kao "umjetnost građenja strojeva". Ali prije izgradnje strojeva, još nam je dug put, pa krenimo stopama naših predaka, pa ćemo proučavati kretanje kamenja bačenog pod kutom prema horizontu i jabuka koje padaju na glave s visine h.

Zašto studij fizike počinje s mehanikom? Jer potpuno je prirodno, a ne krenuti iz termodinamičke ravnoteže?!

Mehanika je jedna od najstarijih znanosti, a povijesno je proučavanje fizike počelo upravo s temeljima mehanike. Smješteni u okvire vremena i prostora, ljudi, zapravo, nisu mogli krenuti od nečega drugog, koliko god željeli. Pokretna tijela su prva stvar na koju obraćamo pažnju.

Što je kretanje?

Mehaničko gibanje je promjena položaja tijela u prostoru jedno u odnosu na drugo tijekom vremena.

Nakon ove definicije sasvim prirodno dolazimo do koncepta referentnog okvira. Promjena položaja tijela u prostoru jedno u odnosu na drugo. Ključne riječi ovdje: jedni prema drugima . Uostalom, putnik u automobilu se kreće u odnosu na osobu koja stoji uz cestu određenom brzinom, i odmara se u odnosu na svog susjeda na obližnjem sjedištu i kreće se nekom drugom brzinom u odnosu na putnika u automobilu koji prestiže ih.

Zato nam je potrebno, kako bismo normalno mjerili parametre pokretnih objekata i ne bismo se zbunili referentni sustav - kruto međusobno povezano referentno tijelo, koordinatni sustav i sat. Na primjer, Zemlja se kreće oko Sunca u heliocentričnom referentnom okviru. U svakodnevnom životu gotovo sva naša mjerenja provodimo u geocentričnom referentnom sustavu povezanom sa Zemljom. Zemlja je referentno tijelo u odnosu na koje se kreću automobili, avioni, ljudi, životinje.

Mehanika, kao znanost, ima svoju zadaću. Zadaća mehanike je u svakom trenutku znati položaj tijela u prostoru. Drugim riječima, mehanika gradi matematički opis gibanja i pronalazi veze između njih fizičke veličine karakterizirajući ga.

Da bismo krenuli dalje, potreban nam je pojam “ materijalna točka ". Kažu da je fizika egzaktna znanost, ali fizičari znaju koliko je aproksimacija i pretpostavki potrebno napraviti da bi se složili upravo oko ove točnosti. Nitko nikada nije vidio materijalnu točku ili nanjušio idealan plin, ali oni postoje! S njima je jednostavno puno lakše živjeti.

Materijalna točka je tijelo čija se veličina i oblik mogu zanemariti u kontekstu ovog problema.

Odjeljci klasične mehanike

Mehanika se sastoji od nekoliko dijelova

Kinematika
Dinamika
Statika

Kinematika s fizičke točke gledišta, proučava točno kako se tijelo kreće. Drugim riječima, ovaj dio se bavi kvantitativnim karakteristikama kretanja. Pronađi brzinu, put - tipični zadaci kinematike

Dinamika rješava pitanje zašto se kreće na način na koji se kreće. To jest, razmatra sile koje djeluju na tijelo.

Statika proučava ravnotežu tijela pod djelovanjem sila, odnosno odgovara na pitanje: zašto uopće ne pada?

Granice primjenjivosti klasične mehanike

Klasična mehanika više ne tvrdi da je znanost koja sve objašnjava (početkom prošlog stoljeća sve je bilo potpuno drugačije), i ima jasan opseg primjenjivosti. Općenito, zakoni klasične mehanike vrijede za svijet koji nam je poznat po veličini (makrosvijet). Prestaju djelovati u slučaju svijeta čestica, kada se klasični zamijeni kvantna mehanika. Također, klasična mehanika je neprimjenjiva na slučajeve kada se kretanje tijela događa brzinom bliskom brzini svjetlosti. U takvim slučajevima dolazi do izražaja relativistički učinak. Grubo rečeno, u okviru kvantne i relativističke mehanike – klasične mehanike, ovo je poseban slučaj kada su dimenzije tijela velike, a brzina mala.

Općenito govoreći, kvantni i relativistički efekti nikada ne nestaju, oni se također odvijaju tijekom uobičajenog gibanja makroskopskih tijela brzinom mnogo manjom od brzine svjetlosti. Druga je stvar što je djelovanje tih učinaka toliko malo da ne ide dalje od najtočnijih mjerenja. Klasična mehanika tako nikada neće izgubiti svoju temeljnu važnost.

Nastavit ćemo proučavati fizičke temelje mehanike u budućim člancima. Za bolje razumijevanje mehanike, uvijek se možete obratiti naši autori , koji su pojedinačno rasvijetlili tamnu točku najtežeg zadatka.

Kako pronaći aritmetičku sredinu broja u Excelu Kako pronaći aritmetičku sredinu velikog broja brojeva

Istina i mitovi o podvigu podolskih kadeta