държавна автономна институция
професионален образователна организация
Колеж по обслужване и туризъм
Лекционен курс с примерни практически задачи
"Основи на теоретичната механика"
по дисциплинаТехническа механика
за студенти3 курс
специалности20.02.04 Пожарна безопасност
Калининград
ОДОБРЯВАМ
Заместник-директор по SD GAU KO VEO KSTN.N. Мясников
ОДОБРЕНО
Методически съвет на GAU KO VET KST
РАЗГЛЕЖДАН
На заседание на ПКК
Редакционен екип:
Колганова А.А., методолог
Фалалеева А.Б., учител по руски език и литература
Цветаева Л.В., председател на PCCобщоматематически и природонаучни дисциплини
съставен от:
Незванова И.В. Преподавател GAU KO VET KST
Съдържание
Теоретична информация
Теоретична информация
Примери за решаване на практически задачи
Динамика: основни понятия и аксиоми
Теоретична информация
Примери за решаване на практически задачи
Библиография
Теоретична информация
Статика: основни понятия и аксиоми.
Статика - раздел на теоретичната механика, който разглежда свойствата на силите, приложени към точките на твърдо тяло, и условията за тяхното равновесие. Основни цели:
1. Преобразуване на системи от сили в еквивалентни системи от сили.
2. Определяне на условията за равновесие на системи от действащи сили твърдо.
материална точка наречен най-прост модел на материално тяло
всяка форма, чиито размери са достатъчно малки и която може да се приеме като геометрична точка с определена маса. Механична система е всеки набор от материални точки. Абсолютно твърдото тяло е механична система, чиито разстояния между точките не се променят при никакви взаимодействия.
Сила е мярка за механичното взаимодействие на материалните тела едно с друго. Силата е векторно количество, тъй като се определя от три елемента:
числова стойност;
посока;
точка на приложение (A).
Единицата за сила е нютон (N).

Фигура 1.1
Система от сили е набор от сили, действащи върху тялото.
Балансирана (равна на нула) система от сили е система, която, приложена към тяло, не променя състоянието си.
Системата от сили, действащи върху тялото, може да бъде заменена с една резултатна, действаща като система от сили.
Аксиоми на статиката.
Аксиома 1: Ако върху тялото се приложи уравновесена система от сили, то се движи равномерно и праволинейно или е в покой (законът за инерцията).
Аксиома 2:
Абсолютно твърдо тяло е в равновесие под действието на две сили тогава и само ако тези сили са равни по абсолютна стойност, действат в една права линия и са насочени в противоположни посоки. Фигура 1.2
Аксиома 3:
Механичното състояние на тялото няма да се наруши, ако към системата от сили, действащи върху него, се добави или извади балансирана система от сили.
Аксиома 4: Резултатът от двете сили, приложени към тялото, е равен на техния геометричен сбор, т.е. изразява се в абсолютна стойност и посока чрез диагонала на успоредника, изграден върху тези сили като върху страните.
Фигура 1.3.
Аксиома 5:
Силите, с които две тела действат едно върху друго, винаги са равни по абсолютна стойност и са насочени по една права линия в противоположни посоки.
Фигура 1.4.
Видове връзки и техните реакции
връзки
се наричат всякакви ограничения, които пречат на движението на тялото в пространството. Тялото, стремящо се под действието на приложените сили да се движи, което се възпрепятства от връзката, ще действа върху него с определена сила, т.нар. сила на натиск върху връзката
. Съгласно закона за равенство на действието и реакцията връзката ще действа върху тялото със същия модул, но противоположно насочена сила.
Силата, с която тази връзка действа върху тялото, предотвратявайки едно или друго движение, се нарича силата на реакция (реакция) на връзката
.
Един от основните принципи на механиката е освободителен принцип
:
всяко несвободно тяло може да се счита за свободно, ако отхвърлим връзките и заменим тяхното действие с реакциите на връзките.
Реакцията на връзката е насочена в посока, обратна на тази, в която връзката не позволява на тялото да се движи. Основните видове връзки и техните реакции са показани в таблица 1.1.
Таблица 1.1
Видове връзки и техните реакции
Име на комуникацията
1
Гладка повърхност (опора)
- повърхността (опората), триенето върху която даденото тяло може да се пренебрегне.
С безплатна поддръжка, реакциятае насочена перпендикулярно на допирателната през точкатаНО
телесен контакт1
с опорна повърхност2
.

2
Нишка (гъвкава, неразтеглива). Връзката, направена под формата на неразтеглива нишка, не позволява на тялото да се отдалечи от точката на окачване. Следователно реакцията на нишката е насочена по нишката до точката на нейното окачване.

3
безтегловен прът
– прът, чието тегло може да бъде пренебрегнато в сравнение с възприеманото натоварване.
Реакцията на безтегловен шарнирен праволинеен прът е насочена по оста на пръта.

4
Подвижна панта, шарнирна подвижна опора. Реакцията е насочена по нормалата към опорната повърхност.

7
Твърдо затваряне.
В равнината на твърдото вграждане ще има два компонента на реакцията,
и момент на двойка сили, което предотвратява завъртането на гредата1
спрямо точкатаНО
.
Твърдото закрепване в пространството отнема всичките шест степени на свобода от тялото 1 - три премествания по координатните оси и три завъртания около тези оси.
Ще има три компонента в пространственото твърдо вграждане,
,
и три момента на двойки сили![]() .
.

Конвергентна силова система
Система от събиращи се сили
наречена система от сили, чиито линии на действие се пресичат в една точка. Две сили, събиращи се в една точка, според третата аксиома на статиката, могат да бъдат заменени с една сила -резултатна
.
Основният вектор на системата от сили
- стойност, равна на геометричната сума на силите на системата.
Резултатът от равнинна система от събиращи се сили може да се определиграфично и аналитично.
Добавяне на система от сили . Добавянето на плоска система от сближаващи се сили се извършва или чрез последователно добавяне на сили с изграждането на междинен резултат (фиг. 1.5), или чрез конструиране на силов многоъгълник (фиг. 1.6).


Фигура 1.5 Фигура 1.6
Проекция на сила върху оста
- алгебрична величина, равна на произведението на модула на силата и косинуса на ъгъла между силата и положителната посока на оста.
ПроекцияЕх(фиг.1.7) сили на ос хположително, ако α е остро, отрицателно, ако α е тъпо. Ако силатае перпендикулярна на оста, тогава неговата проекция върху оста е нула.

Фигура 1.7
Проекция на сила върху равнина Оху– вектор , сключен между проекциите на началото и края на силатакъм този самолет. Тези. проекцията на силата върху равнината е векторна величина, характеризираща се не само с числова стойност, но и с посоката в равнинатаОху (фиг. 1.8).

Фигура 1.8
След това прожекционният модулдо самолета Оху ще бъде равно на:
Еxy = Ф cosα,
където α е ъгълът между посоката на силатаи неговата проекция.
Аналитичен начин за определяне на силите
.
За аналитичния метод за настройка на силатанеобходимо е да се избере система от координатни осиОхз, спрямо които ще се определи посоката на силата в пространството.
Вектор, изобразяващ сила, може да се построи, ако са известни модулът на тази сила и ъглите α, β, γ, които силата образува с координатните оси. ТочкаНОприлагане на сила зададено отделно по своите координатих,
при,
z. Можете да зададете силата по нейните проекцииfx,
fy,
fzпо координатните оси. Модулът на силата в този случай се определя по формулата:
![]()
и насочващи косинуси:
,
.
Аналитичен метод за добавяне на сили : проекцията на вектора на сумата върху някаква ос е равна на алгебрична сумапроекции на членове на вектори върху една и съща ос, т.е. ако:
тогава , , .
знаейки Rx, Ry, Rz, можем да дефинираме модула
![]()
и насочващи косинуси:
, , .
Фигура 1.9
За равновесието на система от събиращи се сили е необходимо и достатъчно резултантната на тези сили да е равна на нула.1) Геометрично равновесно условие за събираща се система от сили : за равновесието на система от сближаващи се сили е необходимо и достатъчно силовият многоъгълник, изграден от тези сили
беше затворен (края на вектора на последния член
силата трябва да съвпада с началото на вектора на първия член на силата). Тогава основният вектор на системата от сили ще бъде нула ()
2)
Аналитични условия на равновесие
.
Модулът на главния вектор на системата от сили се определя по формулата.
![]() =0. Тъй като , тогава коренният израз може да бъде равен на нула само ако всеки член едновременно изчезва, т.е.
=0. Тъй като , тогава коренният израз може да бъде равен на нула само ако всеки член едновременно изчезва, т.е.
Rx= 0, Рай= 0, Р z = 0.
Следователно за равновесието на пространствената система от събиращи се сили е необходимо и достатъчно сумите от проекциите на тези сили върху всяка от трите координати на осите да бъдат равни на нула:
За равновесието на плоска система от събиращи се сили е необходимо и достатъчно сумата от проекциите на силите върху всяка от двете координатни оси да е равна на нула:
Събиране на две успоредни сили в една и съща посока.

Фигура 1.9
Две успоредни сили, насочени в една и съща посока, се свеждат до една равностойна сила, успоредна на тях и насочена в една и съща посока. Големината на резултата е равна на сумата от големините на тези сили, а точката на нейното приложение C разделя разстоянието между линиите на действие на силите вътрешно на части, обратно пропорционални на величините на тези сили, т.е.B A C
R=F 1 +F 2
Събиране на две неравни успоредни сили, насочени в противоположни посоки.
Две неравни противоуспоредни сили се свеждат до една успоредна на тях резултантна сила, насочена към по-голямата сила. Големината на резултантната е равна на разликата между величините на тези сили и точката на нейното приложение, С, разделя разстоянието между линиите на действие на силите отвън на части, обратно пропорционални на величините на тези сили, че е
Двойка сили и момент на сила спрямо точка.
Силов момент
спрямо точка O се нарича, взето със съответния знак, произведението на големината на силата от разстоянието h от точката O до линията на действие на силата . Този продукт се приема със знак плюс, ако силата има тенденция да върти тялото обратно на часовниковата стрелка и със знака -, ако силата има тенденция да върти тялото по посока на часовниковата стрелка, т.е . Дължината на перпендикуляра h се наричарамо на силата
точка О. Ефектът от действието на силата т.е. ъгловото ускорение на тялото е толкова по-голямо, колкото по-голяма е величината на момента на силата.
Фигура 1.11
Няколко сили Система се нарича система, състояща се от две успоредни сили с еднаква големина, насочени в противоположни посоки. Разстоянието h между линиите на действие на силите се наричараменни двойки . Момент на двойка сили m(F,F") е произведението на стойността на една от силите, съставляващи двойката, и рамото на двойката, взети със съответния знак.Записва се по следния начин: m(F, F")= ± F × h, където продуктът се взема със знак плюс, ако двойката сили се стреми да върти тялото обратно на часовниковата стрелка и със знак минус, ако двойката сили се стреми за въртене на тялото по часовниковата стрелка.
Теоремата за сумата от моментите на силите на двойка.
Сумата от моментите на силите на двойката (F,F") по отношение на всяка точка 0, взета в равнината на действие на двойката, не зависи от избора на тази точка и е равна на момента на двойката.
Теорема за еквивалентни двойки. Последствия.
Теорема. Две двойки, чиито моменти са равни един на друг, са еквивалентни, т.е. (F, F") ~ (P, P")
Следствие 1 . Една двойка сили може да бъде прехвърлена на произволно място в равнината на нейното действие, както и да се завърти под произволен ъгъл и да се промени рамото и големината на силите на двойката, като същевременно се запази моментът на двойката.
Следствие 2. Двойка сили няма резултатна и не може да бъде балансирана от една сила, лежаща в равнината на двойката.

Фигура 1.12
Събиране и условие за равновесие на система от двойки в равнина.
1. Теорема за събирането на двойки, лежащи в една и съща равнина. Система от двойки, произволно разположени в една и съща равнина, може да бъде заменена с една двойка, моментът на която е равно на суматамоменти от тези двойки.
2. Теорема за равновесието на система от двойки в равнина.
За да бъде абсолютно твърдо тяло в покой под действието на система от двойки, произволно разположени в една и съща равнина, е необходимо и достатъчно сумата от моментите на всички двойки да е равна на нула, т.е.
Център на тежестта
Земно притегляне - резултата от силите на привличане към Земята, разпределени по целия обем на тялото.
Център на тежестта на тялото - това е такава точка, неизменно свързана с това тяло, през която минава линията на действие на силата на тежестта на дадено тяло при всяко положение на тялото в пространството.
Методи за намиране на центъра на тежестта
1. Метод на симетрия:
1.1. Ако хомогенно тялоима равнина на симетрия, тогава центърът на тежестта лежи в тази равнина
1.2. Ако хомогенното тяло има ос на симетрия, тогава центърът на тежестта лежи на тази ос. Центърът на тежестта на хомогенно тяло на въртене лежи върху оста на въртене.
1.3 Ако едно хомогенно тяло има две оси на симетрия, тогава центърът на тежестта е в точката на тяхното пресичане.
2. Метод на разделяне: Тялото се разделя на най-малък брой части, чиито сили на тежестта и положението на центровете на тежестта са известни.
3. Метод на отрицателните маси: При определяне на центъра на тежестта на тяло със свободни кухини трябва да се използва методът на разделяне, но масата на свободните кухини трябва да се счита за отрицателна.
Координати на центъра на тежестта на плоска фигура:

Позициите на центровете на тежестта на прост геометрични формиможе да се изчисли по известни формули. (Фигура 1.13)

Забележка: Центърът на тежестта на симетрията на фигурата е върху оста на симетрия.
Центърът на тежестта на пръта е в средата на височината.
1.2. Примери за решаване на практически задачи
Пример 1:
Тежест е окачена на прът и е в равновесие. Определете силите в пръта. (Фигура 1.2.1)
Решение:
Силите, които възникват в закрепващите пръти, са равни по големина на силите, с които прътите поддържат товара. (5-та аксиома)
Определяме възможните посоки на реакциите на връзките "твърди пръти".
Усилията са насочени по прътите.
Фигура 1.2.1.
Нека освободим точка А от връзки, като заменим действието на връзките с техните реакции. (Фигура 1.2.2)
Нека започнем конструкцията с известна сила, като начертаем векторЕв някакъв мащаб.
От края на вектораЕначертайте линии, успоредни на реакциитеР 1 иР 2 .
Фигура 1.2.2
Пресичайки се, линиите образуват триъгълник. (Фигура 1.2.3.). Познавайки мащаба на конструкциите и измервайки дължината на страните на триъгълника, е възможно да се определи величината на реакциите в прътите.
За по-точни изчисления можете да използвате геометрични връзки, по-специално синусовата теорема: съотношението на страната на триъгълника към синуса на противоположния ъгъл е постоянна стойност
![]()
За този случай:
Фигура 1.2.3
![]()
коментар: Ако посоката на вектора (реакция на свързване) по дадена схема и в триъгълника на силите не съвпада, тогава реакцията по схемата трябва да бъде насочена в обратна посока.
Пример 2:
Определете големината и посоката на получената плоска система от събиращи се сили по аналитичен начин.
Решение:
Фигура 1.2.4
1. Определяме проекциите на всички сили на системата върху Ox (Фигура 1.2.4)Алгебрично събирайки проекциите, получаваме проекцията на резултата върху оста Ox.

Знакът показва, че резултатната е насочена наляво.
2. Определяме проекциите на всички сили върху оста Oy:
Алгебрично събирайки проекциите, получаваме проекцията на резултата върху оста Oy.
Знакът показва, че резултатът е насочен надолу.
3. Определете модула на резултата от величините на проекциите:
4. Определете стойността на ъгъла на резултата с оста Ox:
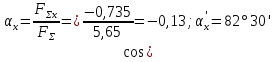
и стойността на ъгъла с оста y:

Пример 3:
Изчислете сумата от моментите на силите спрямо точка O (Фигура 1.2.6).
ОА= AB= ATD=DE=CB=2м
Фигура 1.2.6
Решение:
1. Момент на сила спрямо точка числено е равно на произведениетомодул на рамото на силата.
2. Моментът на силата е равен на нула, ако линията на действие на силата минава през точка.
Пример 4:
Определете позицията на центъра на тежестта на фигурата, показана на фигура 1.2.7
Решение:
Разделяме фигурата на три:
1-правоъгълник
НО 1 =10*20=200см 2
2-триъгълник
НО 2 =1/2*10*15=75см 2
3-обиколка
НО 3 =3,14*3 2 =28,3 см 2
Фигура 1 CG: x 1 =10 см, y 1 =5 см
Фигура 2 CG: x 2 =20+1/3*15=25см, u 2 =1/3*10=3,3 см
Фигура 3 CG: x 3 =10 см, y 3 =5 см
По подобен начин се определя и за с =4,5 см
Кинематика: основни понятия.
Основни кинематични параметри
Траектория - линията, която материална точка очертава при движение в пространството. Траекторията може да бъде права и крива, плоска и пространствена линия.
Уравнение на траекторията за равнинно движение: y =f ( х)
Изминато разстояние. Пътят се измерва по пътя в посоката на движение. Обозначаване -С, мерни единици - метри.
Уравнение за движение на точка е уравнение, което определя позицията на движеща се точка като функция на времето.
Фигура 2.1
Позицията на точка във всеки момент от времето може да се определи от разстоянието, изминато по траекторията от някои фиксирана точка, разглеждана като референтна точка (Фигура 2.1). Този вид движение се наричаестествено . По този начин уравнението на движението може да бъде представено като S = f (t).

Фигура 2.2
Позицията на точка може също да бъде определена, ако нейните координати са известни като функция на времето (Фигура 2.2). Тогава, в случай на движение в равнина, трябва да се дадат две уравнения:В случай на пространствено движение се добавя и трета координатаz= f 3 ( T)
Този вид движение се наричакоординирам .
Скорост на пътуване е векторна величина, която характеризира в момента скоростта и посоката на движение по траекторията.
Скоростта е вектор, насочен във всеки момент тангенциално към траекторията към посоката на движение (Фигура 2.3).
Фигура 2.3
Ако една точка покрива равни разстояния за равни интервали от време, тогава движението се наричауниформа .Средна скорост по пътя ΔСдефиниран:
където∆S- изминато разстояние във времето ΔT; Δ T- времеви интервал.
Ако една точка измине различни пътища за равни интервали от време, тогава движението се наричанеравен . В този случай скоростта е променлива и зависи от времетоv= f( T)
Текущата скорост се определя като
точково ускорение - векторно количество, характеризиращо скоростта на промяна на скоростта по големина и посока.
Скоростта на точка при движение от точка M1 към точка Mg се променя по големина и посока. Средната стойност на ускорението за този период от време
Текущо ускорение:
Обикновено за удобство се разглеждат два взаимно перпендикулярни компонента на ускорението: нормален и тангенциален (Фигура 2.4)
Нормално ускорение a н , характеризира промяната в скоростта с
посока и се определя като
Нормалното ускорение винаги е насочено перпендикулярно на скоростта към центъра на дъгата.
Фигура 2.4
Тангенциално ускорение а T , характеризира промяната на скоростта по големина и винаги е насочена тангенциално към траекторията; при ускорение посоката му съвпада с посоката на скоростта, а при забавяне е насочена обратно на посоката на вектора на скоростта.![]()
Стойността на пълното ускорение се определя като:
Анализ на видовете и кинематичните параметри на движенията
Равномерно движение - това движение от постоянна скорост:
За праволинейни равномерно движение:
За криволинейно равномерно движение:
![]()
Закон за равномерното движение :
Равнопроменливо движение – е движение с постоянно тангенциално ускорение:
За праволинейно равномерно движение
За криволинейно равномерно движение:
![]()
Закон за равномерното движение:
![]()
Кинематични графики
Кинематични графики - Това са графики на промените в пътя, скоростта и ускорението в зависимост от времето.
Равномерно движение (Фигура 2.5)

Фигура 2.5
Равнопроменливо движение (фигура 2.6)

Фигура 2.6
Най-простите движения на твърдо тяло
Движение напред наречено движение на твърдо тяло, при което всяка права линия на тялото по време на движение остава успоредна на първоначалното си положение (Фигура 2.7)

Фигура 2.7
При постъпателно движение всички точки на тялото се движат по един и същ начин: скоростите и ускоренията са еднакви във всеки един момент.
Привъртеливо движение
всички точки на тялото описват окръжности около обща фиксирана ос.

Нарича се неподвижната ос, около която се въртят всички точки на тялотоос на въртене.
Само за описание на въртеливото движение на тяло около неподвижна осъглови опции. (Фигура 2.8)
φ е ъгълът на завъртане на тялото;
ω – ъглова скорост, определя промяната на ъгъла на въртене за единица време;
Определя се изменението на ъгловата скорост с времето ъглово ускорение:
2.2. Примери за решаване на практически задачи
Пример 1: Дадено е уравнението на движението на точка. Определете скоростта на точката в края на третата секунда от движението и средната скорост за първите три секунди.
![]()
Решение:
1. Уравнение на скоростта
2. Скорост в края на третата секунда (T=3 ° С)
3. Средна скорост
Пример 2: Според дадения закон за движение определете вида на движението, началната скорост и тангенциалното ускорение на точката, времето за спиране.
![]()
Решение:
1. Тип движение: еднакво променливо (![]() )
)
2. При сравняване на уравненията е очевидно, че
- началният път, изминат преди началото на обратното броене 10m;
- начална скорост 20m/s
- постоянно тангенциално ускорение ![]()
- ускорението е отрицателно, следователно движението е бавно, ускорението е насочено в посока, обратна на скоростта на движение.
3. Можете да определите времето, в което скоростта на точката ще бъде равна на нула.
3. Динамика: основни понятия и аксиоми
Динамика - раздел от теоретичната механика, в който се установява връзка между движението на телата и силите, действащи върху тях.
В динамиката се решават два вида задачи:
определят параметрите на движение по зададените сили;
определят силите, действащи върху тялото, според дадените кинематични параметри на движение.
Подматериална точка
предполагат определено тяло, което има определена маса (т.е. съдържа определено количество материя), но няма линейни размери (безкрайно малък обем пространство).
Изолиран
разглежда се материална точка, която не се влияе от други материални точки. В реалния свят изолирани материални точки, както и изолирани тела не съществуват, това понятие е условно.
При постъпателното движение всички точки на тялото се движат по един и същи начин, така че тялото може да се приеме за материална точка.
Ако размерите на тялото са малки спрямо траекторията, то също може да се разглежда като материална точка, като точката съвпада с центъра на тежестта на тялото.
По време на въртеливото движение на тялото точките може да не се движат по същия начин, в този случай някои разпоредби на динамиката могат да се прилагат само към отделни точки, а материалният обект може да се разглежда като набор от материални точки.
Следователно динамиката се разделя на динамика на точка и динамика на материална система.
Аксиоми на динамиката
Първа аксиома ( принцип на инерцията): в всяка изолирана материална точка е в покой или еднаква и праволинейно движениедокато приложените сили не го изведат от това състояние.
Това състояние се нарича състояниеинерция. Премахнете точката от това състояние, т.е. дайте му малко ускорение, може би външна сила.
Всяко тяло (точка) имаинерция. Мярката за инерция е масата на тялото.
маса Нареченколичеството материя в тялото в класическата механика се счита за постоянна стойност. Единицата за маса е килограм (kg).
Втора аксиома (Вторият закон на Нютон е основният закон на динамиката)
F=ma
къдетоT - маса на точката, kg;а - точково ускорение, m/s 2 .
Ускорението, придадено на материална точка от сила, е пропорционално на големината на силата и съвпада с посоката на силата.
Гравитацията действа върху всички тела на Земята, тя придава ускорение на тялото. свободно паданекъм центъра на земята:
G=mg
къдетоg- 9,81 m/s², ускорение при свободно падане.
Трета аксиома (трети закон на Нютон): сСилите на взаимодействие на две тела са равни по големина и са насочени по една и съща права линия в различни посоки.
При взаимодействие ускоренията са обратно пропорционални на масите.
Четвърта аксиома (закон за независимостта на действието на силите): доВсяка сила от системата от сили действа така, както би действала самостоятелно.
Ускорението, придадено на точката от системата от сили, е равно на геометричната сума от ускоренията, придадени на точката от всяка сила поотделно (Фигура 3.1):

Фигура 3.1
Концепцията за триене. Видове триене.
триене-
съпротивление, възникващо от движението на едно грапаво тяло върху повърхността на друго. Триенето при плъзгане води до триене при плъзгане, а триенето при търкаляне води до триене при люлеене.
Триене при плъзгане
Фигура 3.2.
Причината е механичното зацепване на издатините. Силата на съпротивление при движение по време на плъзгане се нарича сила на триене при плъзгане (Фигура 3.2)Закони на триенето при плъзгане:
1. Силата на триене при плъзгане е право пропорционална на силата на нормалното налягане: 
къдетоР- сила на нормален натиск, насочена перпендикулярно на опорната повърхност;f- коефициент на триене при плъзгане.
Фигура 3.3.
В случай на движение на тяло по наклонена равнина (Фигура 3.3)триене при търкаляне
Съпротивлението при търкаляне е свързано с взаимната деформация на земята и колелото и е много по-малко от триенето при плъзгане.
За равномерно търкаляне на колелото е необходимо да се приложи силаЕ дв (Фигура 3.4)
Условието за търкаляне на колелото е, че движещият момент не трябва да бъде по-малък от момента на съпротивление:
Фигура 3.4.
Пример 1: Пример 2: Към две материални точки на масам 1 =2 кг им 2 = 5 kg са приложени равни сили. Сравнете стойностите по-бързо.Решение:
Според третата аксиома динамиката на ускорението е обратно пропорционална на масите: ![]()
Пример 3:
Определете работата на гравитацията при преместване на товар от точка А до точка С по наклонена равнина (Фигура 3. 7). Силата на тежестта на тялото е 1500N. AB=6m, BC=4m.Пример 3:
Определете работата на силата на рязане за 3 минути. Скоростта на въртене на детайла е 120 rpm, диаметърът на детайла е 40 mm, силата на рязане е 1 kN. (Фигура 3.8)
Решение:
1. Работа с въртеливо движение:
2. Ъглова скорост 120 об/мин
Фигура 3.8.
3. Броят на оборотите за дадено време еz\u003d 120 * 3 \u003d 360 об.Ъгъл на завъртане през това време φ=2πz\u003d 2 * 3,14 * 360 \u003d 2261 rad
4. Работете за 3 оборота:У\u003d 1 * 0,02 * 2261 \u003d 45,2 kJ
Библиография
Олофинская, В.П. "Техническа механика", Москва "Форум" 2011 г
Ердеди А.А. Ердеди Н.А. Теоретична механика. Съпротивление на материалите.- Р-н-Д; Финикс, 2010 г
1 слайд
Курс на лекции по теоретична механика Динамика (I част) Бондаренко A.N. Москва - 2007 г. Електронният курс за обучение е написан на базата на лекции, изнесени от автора за студенти, обучаващи се по специалностите на SZhD, PGS и SDM в NIIZhT и MIIT (1974-2006). Учебен материалсъответства на календарните планове в обем от три семестъра. За пълното прилагане на анимационните ефекти по време на презентацията трябва да използвате програма за преглед на Power Point не по-ниска от вградената в Microsoft Office на операционната система Windows XP Professional. Коментари и предложения можете да изпращате на имейл: [имейл защитен]. Москва Държавен университетЖелезници (MIIT) Департамент по теоретична механика Научно-технически център по транспортни технологии

2 слайд
Съдържание Лекция 1. Въведение в динамиката. Закони и аксиоми на динамиката материална точка. Основно уравнение на динамиката. Диференциални и естествени уравнения на движението. Две основни задачи на динамиката. Примери за решаване на пряката задача на динамиката Лекция 2. Решаване на обратната задача на динамиката. Общи указания за решаване на обратната задача на динамиката. Примери за решаване на обратната задача на динамиката. Движението на тяло, хвърлено под ъгъл спрямо хоризонта, без да се взема предвид съпротивлението на въздуха. Лекция 3. Праволинейни трептения на материална точка. Условието за възникване на трептения. Класификация на вибрациите. Свободни вибрации без отчитане на силите на съпротивление. гасени вибрации. Декремент на трептене. Лекция 4. Принудени трептения на материална точка. Резонанс. Влияние на съпротивлението на движение при принудителни вибрации. Лекция 5. Относително движение на материална точка. Сили на инерцията. Частни случаи на движение за различни видове преносими механизми. Влияние на въртенето на Земята върху равновесието и движението на телата. Лекция 6. Динамика на механична система. механична система. Външни и вътрешни сили. Център на масата на системата. Теорема за движението на центъра на масата. Закони за опазване. Пример за решаване на проблема с използването на теоремата за движението на центъра на масата. Лекция 7. Импулс на сила. Количеството движение. Теорема за промяната на импулса. Закони за опазване. Теорема на Ойлер. Пример за решаване на проблема с използването на теоремата за промяната на импулса. момент на импулс. Теорема за промяна на ъгловия момент Лекция 8. Закони за запазване. Елементи на теорията на инерционните моменти. Кинетичен момент на твърдо тяло. Диференциално уравнение на въртене на твърдо тяло. Пример за решаване на проблема с използването на теоремата за промяна на ъгловия момент на системата. Елементарна теория на жироскопа. Препоръчителна литература 1. Yablonsky A.A. Курс по теоретична механика. Част 2. М.: висше училище. 1977. 368 стр. 2. Мещерски И.В. Сборник задачи по теоретична механика. М.: Наука. 1986 416 стр. 3. Сборник задачи за курсови работи/ Ед. А.А. Яблонски. М.: Висше училище. 1985. 366 стр. 4. Бондаренко A.N. “Теоретична механика в примери и задачи. Динамика” ( електронен наръчник www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004 г.

3 слайд
Лекция 1 Динамиката е раздел от теоретичната механика, който изучава механичното движение от най-обща гледна точка. Движението се разглежда във връзка със силите, действащи върху обекта. Разделът се състои от три раздела: Динамика на материална точка Динамика Динамика на механична система Аналитична механика ■ Динамика на точка - изучава движението на материална точка, като се вземат предвид силите, които предизвикват това движение. Основният обект е материална точка - материално тяло с маса, чиито размери могат да бъдат пренебрегнати. Основни допускания: - има абсолютно пространство (то има чисто геометрични свойства, които не зависят от материята и нейното движение. - има абсолютно време (не зависи от материята и нейното движение). От това следва: - има абсолютно неподвижна отправна система - времето не зависи от движението на отправната система - масите на движещите се точки не зависят от движението на отправната система Тези допускания се използват в класическата механика, създадена от Галилей и Нютон , Той все още има доста широк обхват, тъй като механичните системи, разглеждани в приложните науки, нямат толкова големи маси и скорости на движение, за които е необходимо да се вземе предвид тяхното влияние върху геометрията на пространството, времето, движението, като се прави в релативистката механика (теорията на относителността) ■ Основните закони на динамиката - открити за първи път от Галилей и формулирани от Нютон, формират основата на всички методи за описание и анализ на движението на механичните системи и тяхното динамично взаимодействие действие под въздействието на различни сили. ■ Закон за инерцията (закон на Галилео-Нютон) - Изолирана материална точка от тяло запазва състоянието си на покой или равномерно праволинейно движение, докато приложените сили не я принудят да промени това състояние. Това предполага еквивалентност на състоянието на покой и движение по инерция (законът на относителността на Галилей). Отправната система, по отношение на която се изпълнява законът на инерцията, се нарича инерционна. Свойството на материалната точка да се стреми да запази скоростта на своето движение (кинематичното си състояние) непроменена се нарича инерция. ■ Законът за пропорционалност на силата и ускорението (Основно уравнение на динамиката - закон на Нютон II) - Ускорението, придадено на материална точка от сила, е право пропорционално на силата и обратно пропорционално на масата на тази точка: или Тук m е маса на точката (мярка за инерция), измерена в kg, числено равна на теглото, разделено на гравитационното ускорение: F е действащата сила, измерена в N (1 N придава ускорение от 1 m / s2 на точка с a маса от 1 kg, 1 N \u003d 1/9. 81 kg-s). ■ Динамика на механична система - изучава движението на набор от материални точки и твърди тела, комбинирани общи законивзаимодействия, като се вземат предвид силите, предизвикващи това движение. ■ Аналитична механика - изучава движението на несвободни механични системи с помощта на общ аналитични методи. 1

4 слайд
Лекция 1 (продължение - 1.2) Диференциални уравнения на движение на материална точка: - диференциално уравнение на движение на точка във векторна форма. - диференциални уравнения на движение на точка в координатна форма. Този резултат може да бъде получен чрез формална проекция на векторното диференциално уравнение (1). След групирането векторната връзка се разлага на три скаларни уравнения: В координатна форма: Използваме връзката на радиус-вектора с координатите и вектора на силата с проекциите: диференциално уравнение на движение върху естествени (подвижни) координатни оси: или: - естествени уравнения на движение на точка. ■ Основно уравнение на динамиката: - съответства на векторния начин за определяне на движението на точка. ■ Закон за независимостта на действието на силите - Ускорението на материална точка под действието на няколко сили е равно на геометричната сума на ускоренията на точка от действието на всяка от силите поотделно: или Законът е в сила за всяко кинематично състояние на телата. Силите на взаимодействие, приложени към различни точки (тела), не са балансирани. ■ Законът за равенството на действието и реакцията (трети закон на Нютон) - Всяко действие съответства на еднаква и противоположно насочена реакция: 2

5 слайд
Две основни задачи на динамиката: 1. Пряка задача: Дадено е движение (уравнения на движение, траектория). Необходимо е да се определят силите, под действието на които възниква дадено движение. 2. Обратна задача: Дадени са силите, под действието на които възниква движението. Необходимо е да се намерят параметри на движение (уравнения на движение, траектория на движение). И двете задачи се решават с помощта на основното уравнение на динамиката и неговата проекция върху координатните оси. Ако се разглежда движението на несвободна точка, тогава, както в статиката, се използва принципът на освобождаване от връзки. В резултат на реакцията връзките се включват в състава на силите, действащи върху материалната точка. Решението на първия проблем е свързано с операции за диференциране. Решението на обратната задача изисква интегриране на съответните диференциални уравнения, а това е много по-трудно от диференцирането. Обратната задача е по-трудна от директната задача. Решението на директната задача на динамиката - да разгледаме примери: Пример 1. Кабина с тегло G на асансьор се повдига с въже с ускорение a . Определете напрежението на кабела. 1. Изберете обект (кабината на асансьора се движи напред и може да се разглежда като материална точка). 2. Изхвърляме връзката (кабела) и я заменяме с реакцията R. 3. Съставете основното уравнение на динамиката: Определете реакцията на кабела: Определете напрежението на кабела: При равномерно движение на кабината ay = 0 и напрежението на кабела е равно на теглото: T = G. При скъсване на кабела T = 0 и ускорението на кабината е равно на ускорението на свободното падане: ay = -g. 3 4. Проектираме основното уравнение на динамиката върху оста y: y Пример 2. Точка с маса m се движи по хоризонтална повърхност (равнина Oxy) съгласно уравненията: x = a coskt, y = b coskt. Определете силата, действаща върху точката. 1. Изберете обект (материална точка). 2. Изхвърляме връзката (равнината) и я заместваме с реакцията N. 3. Добавяме неизвестна сила F към системата от сили 4. Съставяме основното уравнение на динамиката: 5. Проектираме основното уравнение на динамиката върху оси x,y: Определете проекциите на силата: Модулът на силата: Косинусите на посоката: По този начин големината на силата е пропорционална на разстоянието на точката до центъра на координатите и е насочена към центъра по линията, свързваща точката с центъра. Траекторията на движението на точката е елипса с център в началото: O r Лекция 1 (продължение - 1.3)

6 слайд
Лекция 1 (продължение 1.4) Пример 3: Товар с тегло G е окачен на кабел с дължина l и се движи по кръгова траектория в хоризонтална равнина с определена скорост. Ъгълът на отклонение на кабела от вертикалата е равен на. Определете напрежението на кабела и скоростта на товара. 1. Изберете обект (товар). 2. Изхвърлете връзката (въжето) и я заменете с реакцията R. 3. Съставете основното уравнение на динамиката: От третото уравнение определете реакцията на кабела: Определете напрежението на кабела: Заменете стойността на реакцията на кабела, нормално ускорение във второто уравнение и определете скоростта на товара: 4. Проектирайте основното уравнение axle dynamics,n,b: Пример 4: Автомобил с тегло G се движи по изпъкнал мост (радиусът на кривината е R ) със скорост V. Определете натиска на автомобила върху моста. 1. Избираме обект (автомобил, пренебрегваме размерите и го разглеждаме като точка). 2. Изхвърляме връзката (грапава повърхност) и я заменяме с реакциите N и силата на триене Ffr. 3. Съставяме основното уравнение на динамиката: 4. Проектираме основното уравнение на динамиката върху оста n: От тук определяме нормалната реакция: Определяме натиска на автомобила върху моста: От тук можем да определим скоростта съответстващо на нулево налягане върху моста (Q = 0): 4

7 слайд
Лекция 2 След като заместим намерените стойности на константите, получаваме: По този начин, под действието на една и съща система от сили, материална точка може да извърши цял клас движения, определени от началните условия. Началните координати отчитат началната позиция на точката. Началната скорост, дадена от проекциите, отчита влиянието върху нейното движение по разглеждания участък от траекторията на силите, които са действали върху точката преди пристигането в този участък, т.е. начално кинематично състояние. Решение на обратната задача на динамиката - В общия случай на движение на точка, силите, действащи върху точката, са променливи, които зависят от времето, координатите и скоростта. Движението на точка се описва от система от три диференциални уравнения от втори ред: След интегриране на всяко от тях ще има шест константи C1, C2,…., C6: Стойностите на константите C1, C2,… ., C6 се намират от шест начални условия при t = 0: Пример 1 на обратната задача на решението: Свободна материална точка с маса m се движи под действието на сила F, която е постоянна по големина и големина. . В началния момент скоростта на точката е v0 и съвпада по посока със силата. Определете уравнението на движение на точка. 1. Съставете основното уравнение на динамиката: 3. Намалете порядъка на производната: 2. Изберете декартова отправна система, насочвайки оста x по посока на силата и проектирайте основното уравнение на динамиката върху тази ос: или x y z 4 Разделете променливите: 5. Изчислете интегралите на двете части на уравнението: 6. Нека представим проекцията на скоростта като производна на координатата по отношение на времето: 8. Изчислете интегралите на двете части на уравнението: 7. Разделете променливите: 9. За да определим стойностите на константите C1 и C2, използваме началните условия t = 0, vx = v0 , x = x0: В резултат на това получаваме уравнението на равномерно променливо движение (по протежение на ос x): 5

8 слайд
Общи указания за решаване на прави и обратни задачи. Процедура за решаване: 1. Съставяне на диференциалното уравнение на движението: 1.1. Изберете координатна система - правоъгълна (неподвижна) с неизвестна траектория на движение, естествена (подвижна) с известна траектория, например кръг или права линия. В последния случай може да се използва една праволинейна координата. Референтната точка трябва да се комбинира с началната позиция на точката (при t = 0) или с равновесната позиция на точката, ако съществува, например, когато точката се колебае. 6 1.2. Начертайте точка в позиция, съответстваща на произволен момент от времето (за t > 0), така че координатите да са положителни (s > 0, x > 0). Предполагаме също, че проекцията на скоростта в тази позиция също е положителна. В случай на трептене проекцията на скоростта променя знака, например при връщане в равновесно положение. Тук трябва да се приеме, че в разглеждания момент точката се отдалечава от равновесното положение. Изпълнението на тази препоръка е важно в бъдеще при работа със съпротивителни сили, които зависят от скоростта. 1.3. Освободете материалната точка от връзките, заменете тяхното действие с реакции, добавете активни сили. 1.4. Напишете основния закон на динамиката във векторна форма, проектирайте върху избраните оси, изразете зададените или реактивни сили чрез променливите време, координати или скорости, ако зависят от тях. 2. Решаване на диференциални уравнения: 2.1. Редуцирайте производната, ако уравнението не се редуцира до каноничната (стандартна) форма. например: или 2.2. Отделни променливи, например: или 2.4. Изчислете неопределените интеграли от лявата и дясната страна на уравнението, например: 2.3. Ако има три променливи в уравнението, тогава направете промяна на променливите, например: и след това разделете променливите. Коментирайте. Вместо да пресмятате неопределени интеграливъзможно е да се изчислят определени интеграли с променлива горна граница. Долните граници представляват началните стойности на променливите (началните условия).Тогава няма нужда да се намира отделно константата, която автоматично се включва в решението, например: Използвайки началните условия, например, t = 0 , vx = vx0, определяме константата на интегриране: 2.5. Изразете скоростта по отношение на времевата производна на координатата например и повторете стъпки 2.2 -2.4 Забележка. Ако уравнението се сведе до канонична форма, която има стандартно решение, тогава се използва това готово решение. Константите на интегриране все още се намират от началните условия. Вижте например трептенията (лекция 4, стр. 8). Лекция 2 (продължение 2.2)

9 слайд
Лекция 2 (продължение 2.3) Пример 2 за решаване на обратна задача: Силата зависи от времето. Товар с тегло P започва да се движи по гладка хоризонтална повърхност под действието на сила F, чиято величина е пропорционална на времето (F = kt). Определете разстоянието, изминато от товара за време t. 3. Съставяме главното уравнение на динамиката: 5. Понижаваме порядъка на производната: 4. Проектираме основното уравнение на динамиката върху оста x: или 7 6. Разделяме променливите: 7. Изчисляваме интегралите от двете части на уравнението: 9. Представяме проекцията на скоростта като производна на координатата по време: 10. Изчисляваме интегралите на двете части на уравнението: 9. Разделяме променливите: 8. Определете стойността на константата C1 от началното условие t = 0, vx = v0=0: В резултат на това получаваме уравнението на движението (по оста x), което дава стойността на изминатото разстояние за време t: 1. Изберете референтната система ( Декартови координати), така че тялото да има положителна координата: 2. Вземаме обекта на движение като материална точка (тялото се движи напред), освобождаваме го от връзката (референтна равнина) и го заместваме с реакцията (нормална реакция на гладка повърхност): 11. Определете стойността на константата C2 от началното условие t = 0, x = x0=0: Пример за обратна задача 3: Силата зависи от координатата. Материална точка с маса m е изхвърлена нагоре от повърхността на Земята със скорост v0. Силата на гравитацията на Земята е обратно пропорционална на квадрата на разстоянието от точката до центъра на тежестта (центъра на Земята). Определете зависимостта на скоростта от разстоянието y до центъра на Земята. 1. Избираме отправна система (декартови координати), така че тялото да има положителна координата: 2. Съставяме основното уравнение на динамиката: 3. Проектираме основното уравнение на динамиката върху оста y: или Коефициентът на пропорционалност може да се намери с помощта на теглото на точка на повърхността на Земята: R Следователно диференциалът, уравнението изглежда така: или 4. Намалете реда на производната: 5. Променете променливата: 6. Разделете променливите: 7. Изчислете интеграли от двете страни на уравнението: 8. Заместете границите: В резултат на това получаваме израз за скоростта като функция на координатата y: Максималната височина на полета може да се намери чрез приравняване на скоростта на нула: Максималната височина на полета когато знаменателят стане нула: Оттук при задаване на радиуса на Земята и ускорението на свободното падане се получава II космическа скорост:

10 слайд
Лекция 2 (продължение 2.4) Пример 2 за решаване на обратна задача: Силата зависи от скоростта. Кораб с маса m има скорост v0. Съпротивлението на водата при движението на кораба е пропорционално на скоростта. Определете времето, за което скоростта на кораба намалява наполовина след изключване на двигателя, както и разстоянието, изминато от кораба до пълно спиране. 8 1. Избираме референтна система (декартови координати), така че тялото да има положителна координата: 2. Вземаме обекта на движение като материална точка (корабът се движи напред), освобождаваме го от връзки (вода) и го заместваме с реакция (плаваща сила - Архимедова сила), а също и силата на съпротивление при движение. 3. Добавете активна сила (гравитация). 4. Съставяме основното уравнение на динамиката: 5. Проектираме основното уравнение на динамиката върху оста x: или 6. Понижаваме реда на производната: 7. Разделяме променливите: 8. Изчисляваме интегралите от двете части на уравнението: 9. Заменяме границите: Получава се израз, който свързва скоростта и времето t, от което можете да определите времето на движение: Времето на движение, през което скоростта ще падне наполовина: интересно е да се отбележи, че когато скоростта се доближи до нула, времето на движение клони към безкрайност, т.е. крайната скорост не може да бъде нула. Защо не "перпетуум мобиле"? В този случай обаче изминатото разстояние до спирката е крайна стойност. За да определим изминатото разстояние, се обръщаме към израза, получен след понижаване реда на производната, и правим промяна на променливата: След интегриране и заместване на границите, получаваме: Изминато разстояние до спиране: ■ Преместване на точка, хвърлена в ъгъл спрямо хоризонта в равномерно гравитационно поле, без да се взема предвид съпротивлението на въздуха. Елиминирайки времето от уравненията на движението, получаваме уравнението на траекторията: Времето на полета се определя чрез приравняване на координатата y на нула: Обхватът на полета се определя чрез заместване времето на полета:

11 слайд
Лекция 3 Праволинейни трептения на материална точка - Осцилаторното движение на материална точка възниква при условие: има възстановяваща сила, която се стреми да върне точката в равновесно положение при всяко отклонение от това положение. 9 Има възстановяваща сила, равновесното положение е стабилно Няма възстановяваща сила, равновесното положение е нестабилно Няма възстановяваща сила, равновесното положение е безразлично Тя винаги е насочена към равновесното положение, стойността е право пропорционална на линейното удължение (скъсяване) на пружината, което е равно на отклонението на тялото от равновесното положение: c е коефициентът на твърдост на пружината, числено равни по сила, под действието на което пружината променя дължината си с единица, се измерва в N / m в системата SI. x y O Видове вибрации на материална точка: 1. Свободни вибрации (без да се отчита съпротивлението на средата). 2. Свободни трептения с отчитане на съпротивлението на средата (затихващи трептения). 3. Принудени вибрации. 4. Принудени трептения с отчитане на съпротивлението на средата. ■ Свободни трептения – възникват под действието само на възстановяваща сила. Нека запишем основния закон на динамиката: Нека изберем координатна система с център в позицията на равновесие (точка O) и проектираме уравнението върху оста x: Нека приведем полученото уравнение в стандартната (канонична) форма: Това уравнение е хомогенно линейно диференциално уравнение от втори ред, формата на решението на което се определя от корените на характеристиката на уравнението, получено чрез универсалното заместване: Корените на характеристичното уравнение са въображаеми и равни: Общото решение на диференциалното уравнение има формата: Скоростта на точката: Начални условия: Определете константите: И така, уравнението на свободните вибрации има формата: Уравнението може да бъде представено чрез едночленен израз: където a е амплитудата, - начална фаза. Новите константи a и - са свързани с константите C1 и C2 чрез съотношенията: Нека дефинираме a и: Причината за възникване на свободни трептения е началното преместване x0 и/или началната скорост v0.

12 слайд
10 Лекция 3 (продължение 3.2) Затихващи трептения на материална точка - Осцилаторното движение на материална точка възниква при наличието на възстановяваща сила и сила на съпротивление на движението. Зависимостта на силата на съпротивление на движението от преместването или скоростта се определя от физическата природа на средата или връзката, която възпрепятства движението. Най-простата зависимост е линейна зависимоствърху скоростта (вискозно съпротивление): - коефициент на вискозитет x y O Основно уравнение на динамиката: Проекция на уравнението на динамиката върху оста: Привеждаме уравнението към стандартната форма: където Характеристичното уравнение има корени: Общото решение на това диференциално уравнение има различна форма в зависимост от стойностите на корените: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - случай на високо вискозно съпротивление: - истински корени, различни. или - тези функции са апериодични: 3. n = k: - корените са реални, кратни. тези функции също са апериодични:

13 слайд
Лекция 3 (продължение 3.3) Класификация на решения на свободни трептения. Пружинни връзки. еквивалентна твърдост. y 11 Разл. Характер на уравнението. Корени на уравнението char. уравнение Решаване на диференциално уравнение Графика nk n=k

14 слайд
Лекция 4 Принудени вибрации на материална точка - Заедно с възстановяващата сила действа периодично променяща се сила, наречена смущаваща сила. Смущаващата сила може да има различен характер. Например, в конкретен случай инерционният ефект на небалансирана маса m1 на въртящ се ротор причинява хармонично променящи се проекции на силата: Основното уравнение на динамиката: Проекцията на уравнението на динамиката върху оста: Нека приведем уравнението към стандарта форма: 12 Решението на това нехомогенно диференциално уравнение се състои от две части x = x1 + x2: x1 е общото решение на съответното хомогенно уравнение и x2 е частно решение на нехомогенното уравнение: Избираме конкретното решение под формата на дясната страна: Полученото равенство трябва да бъде изпълнено за всяко t . Тогава: или Така, при едновременното действие на възстановяващите и смущаващите сили, материалната точка извършва сложно колебателно движение, което е резултат от събирането (суперпозицията) на свободни (x1) и принудени (x2) вибрации. Ако p< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (принудителни трептения висока честота), тогава фазата на трептенията е противоположна на фазата на смущаващата сила:

15 слайд
Лекция 4 (продължение 4.2) 13 Динамичен коефициент - отношение на амплитудата принудителни вибрациикъм статичното отклонение на точка под действието на постоянна сила H = const: Амплитуда на принудените трептения: Статичното отклонение може да се намери от уравнението на равновесието: Тук: Следователно: Така при p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (висока честота на принудените трептения) динамичен коефициент: Резонанс - възниква, когато честотата на принудените трептения съвпада с честотата на собствените трептения (p = k). Най-често това се случва при стартиране и спиране на въртенето на лошо балансирани ротори, монтирани на еластични окачвания. Диференциалното уравнение на трептенията с равни честоти: Не може да се вземе частно решение под формата на дясната страна, т.к. ще се получи линейно зависимо решение (виж общото решение). Общо решение: Заместете в диференциалното уравнение: Вземете конкретно решение във формата и изчислете производните: Така се получава решението: или Принудените трептения при резонанс имат амплитуда, която нараства неограничено пропорционално на времето. Влияние на съпротивлението на движение при принудителни вибрации. Диференциалното уравнение при наличие на вискозно съпротивление има формата: Общото решение се избира от таблицата (лекция 3, стр. 11) в зависимост от съотношението на n и k (виж). Взимаме определено решение във формата и изчисляваме производните: Заместване в диференциалното уравнение: Приравняване на коефициентите при едни и същи тригонометрични функцииполучаваме система от уравнения: Като повдигнем двете уравнения на степен и ги добавим, получаваме амплитудата на принудените трептения: Като разделим второто уравнение на първото, получаваме фазовото изместване на принудителните трептения: Така уравнението на движение за принудителни трептения, като се вземе предвид съпротивлението на движение, например при n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 слайд
Лекция 5 Относително движение на материална точка - Да приемем, че подвижната (неинерциална) координатна система Oxyz се движи по някакъв закон спрямо неподвижната (инерциална) координатна система O1x1y1z1. Движението на материална точка M (x, y, z) спрямо подвижната система Oxyz е относително, спрямо неподвижната система O1x1y1z1 е абсолютно. Движението на мобилната система Oxyz спрямо неподвижната система O1x1y1z1 е преносимо движение. 14 z x1 y1 z1 O1 x y M x y z O Основно уравнение на динамиката: Абсолютно ускорение на точка: Заместете абсолютното ускорение на точка в основното уравнение на динамиката: Нека прехвърлим членовете с транслационното и Кориолисовото ускорение в дясната страна: прехвърлените членове имат размерността на силите и се разглеждат като съответните инерционни сили, равни: Тогава относителното движение на точка може да се счита за абсолютно, ако добавим транслационните и Кориолисовите инерционни сили към действащите сили: В проекции върху оси на подвижната координатна система имаме: въртенето е равномерно, тогава εe = 0: 2. Транслационно криволинейно движение: Ако движението е праволинейно, тогава = : Ако движението е праволинейно и равномерно, тогава движещата се система е инерционна и относителното движение може да се разглежда като абсолютно: никакви механични явления не могат да открият праволинейна униформа движение (принцип на относителността на класическата механика). Влияние на въртенето на Земята върху равновесието на телата - Да приемем, че тялото е в равновесие върху земната повърхност на произволна географска ширина φ (паралели). Земята се върти около оста си от запад на изток с ъглова скорост: Радиусът на Земята е около 6370 km. S R е общата реакция на негладка повърхност. G - силата на привличане на Земята към центъра. Ф - центробежна инерционна сила. Условие на относително равновесие: Резултатът от силите на привличане и инерция е силата на гравитацията (теглото): Големината на силата на гравитацията (теглото) върху повърхността на Земята е P = mg. Центробежната сила на инерцията е малка част от силата на гравитацията: Отклонението на силата на гравитацията от посоката на силата на привличане също е малко: По този начин влиянието на въртенето на Земята върху баланса на телата е изключително малко и не се взема предвид в практическите изчисления. Максималната стойност на инерционната сила (при φ = 0 - на екватора) е само 0,00343 от стойността на гравитацията

17 слайд
Лекция 5 (продължение 5.2) 15 Влияние на въртенето на Земята върху движението на телата в гравитационното поле на Земята - Да предположим, че едно тяло пада на Земята от определена височина H над земната повърхност на ширина φ . Нека изберем подвижна референтна система, твърдо свързана със Земята, насочваща осите x, y тангенциално към паралела и към меридиана: Уравнение на относителното движение: Тук се взема предвид малката центробежна сила на инерцията в сравнение с гравитацията . Така силата на гравитацията се идентифицира със силата на гравитацията. В допълнение, ние приемаме, че гравитацията е насочена перпендикулярно на повърхността на Земята поради малкото нейно отклонение, както беше обсъдено по-горе. Ускорението на Кориолис е равно на и насочено успоредно на оста y на запад. Инерционната сила на Кориолис е насочена в обратна посока. Проектираме уравнението на относителното движение върху оста: Решението на първото уравнение дава: Начални условия: Решението на третото уравнение дава: Начални условия: Третото уравнение приема формата: Начални условия: Неговото решение дава: Полученото решение показва, че тялото се отклонява на изток, когато пада. Нека изчислим стойността на това отклонение, например при падане от височина 100 м. Намираме времето на падане от решението на второто уравнение: По този начин влиянието на въртенето на Земята върху движението на телата е изключително малко за практически височини и скорости и не се взема предвид в техническите изчисления. Решението на второто уравнение също предполага наличието на скорост по оста y, която също трябва да причинява и причинява съответното ускорение и инерционната сила на Кориолис. Влиянието на тази скорост и свързаната с нея инерционна сила върху промяната в движението ще бъде дори по-малко от разглежданата инерционна сила на Кориолис, свързана с вертикалната скорост.

18 слайд
Лекция 6 Динамика на механична система. Система от материални точки или механична система - Набор от материални точки или онези материални точки, обединени от общи закони на взаимодействие (позицията или движението на всяка от точките или тялото зависи от позицията и движението на всички останали) Системата от свободни точки - чието движение не е ограничено от никакви връзки (например планетарна система, в която планетите се считат за материални точки). Система от несвободни точки или несвободна механична система - движението на материални точки или тела е ограничено от ограниченията, наложени на системата (например механизъм, машина и др.). 16 Сили, действащи върху системата. В допълнение към предишната класификация на силите (активни и реактивни сили) се въвежда нова класификация на силите: 1. Външни сили (e) - действащи върху точки и тела на системата от точки или тела, които не са част от тази система. 2. Вътрешни сили (i) - сили на взаимодействие между материални точки или тела, включени в дадената система. Една и съща сила може да бъде както външна, така и вътрешна сила. Всичко зависи от това коя механична система се разглежда. Например: В системата на Слънцето, Земята и Луната всички гравитационни сили между тях са вътрешни. Когато разглеждаме системата Земя и Луна, гравитационните сили, приложени от страната на Слънцето, са външни: C Z L Въз основа на закона за действие и реакция всяка вътрешна сила Fk съответства на друга вътрешна сила Fk', равна по абсолютна стойност и противоположна по посока. Две забележителни свойства на вътрешните сили следват от това: Главният вектор на всички вътрешни сили на системата е равен на нула: Главният момент на всички вътрешни сили на системата спрямо всеки център е равен на нула: Или в проекции върху координатата оси: Забележка. Въпреки че тези уравнения са подобни на уравненията на равновесието, те не са, тъй като вътрешните сили се прилагат към различни точки или тела на системата и могат да накарат тези точки (тела) да се движат една спрямо друга. От тези уравнения следва, че вътрешните сили не влияят на движението на системата, разглеждана като цяло. Центърът на масата на системата от материални точки. За да се опише движението на системата като цяло, се въвежда геометрична точка, наречена център на масата, чийто радиус вектор се определя от израза, където M е масата на цялата система: Или в проекции върху координатата оси: Формулите за центъра на масата са подобни на тези за центъра на тежестта. Концепцията за центъра на масата обаче е по-обща, тъй като не е свързана със силите на гравитацията или силите на гравитацията.

19 слайд
Лекция 6 (продължение 6.2) 17 Теорема за движението на центъра на масата на системата - Да разгледаме система от n материални точки. Разделяме силите, приложени към всяка точка, на външни и вътрешни и ги заместваме със съответните резултанти Fke и Fki. Нека запишем за всяка точка основното уравнение на динамиката: или Нека сумираме тези уравнения по всички точки: От лявата страна на уравнението ще въведем масите под знака на производната и ще заменим сумата от производните с производната на сумата: От дефиницията на центъра на масата: Заместете в полученото уравнение: получаваме или: Произведението на масата на системата и ускорението на нейния център на маса е равно на главния вектор на външните сили. В проекции върху координатните оси: Центърът на масата на системата се движи като материална точка с маса, равна на масата на цялата система, към която се прилагат всички външни сили, действащи върху системата. Следствия от теоремата за движението на центъра на масата на системата (закони за запазване): 1. Ако в интервала от време главният вектор на външните сили на системата е равен на нула, Re = 0, то скоростта на центърът на масата е постоянен, vC = const (центърът на масата се движи равномерно праволинейно - законът за запазване на центъра на движение на масата). 2. Ако в интервала от време проекцията на главния вектор на външните сили на системата върху оста x е равна на нула, Rxe = 0, тогава скоростта на центъра на масата по оста x е постоянна, vCx = const (центърът на масата се движи равномерно по оста). Подобни твърдения са верни за осите y и z. Пример: Двама души с маси m1 и m2 са в лодка с маса m3. В началния момент лодката с хора е била в покой. Определете водоизместването на лодката, ако човек с маса m2 се придвижи до носа на лодката на разстояние a. 3. Ако в интервала от време основният вектор на външните сили на системата е равен на нула, Re = 0, а в началния момент скоростта на центъра на масата е равна на нула, vC = 0, тогава радиус векторът на центъра на масата остава постоянен, rC = const (центърът на масата е в покой е законът за запазване на позицията на центъра на масата). 4. Ако в интервала от време проекцията на главния вектор на външните сили на системата върху оста x е равна на нула, Rxe = 0, а в началния момент скоростта на центъра на масата по тази ос е нула , vCx = 0, тогава координатата на центъра на масата по оста x остава постоянна, xC = const (центърът на масата не се движи по тази ос). Подобни твърдения са верни за осите y и z. 1. Обект на движение (лодка с хора): 2. Изхвърлете връзките (вода): 3. Заменете връзката с реакция: 4. Добавете активни сили: 5. Запишете теоремата за центъра на масата: Проектирайте върху оста x : O Определете колко разстояние трябва да прехвърлите на човек с маса m1, така че лодката да остане на място: Лодката ще се движи на разстояние l в обратна посока.

20 слайд
Лекция 7 Импулсът на сила е мярка за механично взаимодействие, която характеризира предаването механично движениеот силите, действащи върху точката за даден период от време: 18 В проекции върху координатните оси: В случай на постоянна сила: В проекции върху координатните оси: dt: Нека интегрираме върху даден интервал от време: Импулсът на точка е мярка за механично движение, определена от вектор, равен на произведението на масата на точката и нейния вектор на скоростта: Теорема за промяната на импулса на системата - Да разгледаме система от n материални точки. Разделяме силите, приложени към всяка точка, на външни и вътрешни и ги заместваме със съответните резултанти Fke и Fki. Нека напишем за всяка точка основното уравнение на динамиката: или Импулсът на системата от материални точки е геометричната сума на количествата на движение на материалните точки: По дефиниция на центъра на масата: Векторът на импулса на системата е равна на произведението на масата на цялата система и вектора на скоростта на центъра на масата на системата. Тогава: В проекции върху координатните оси: Производната по време на вектора на импулса на системата е равна на главния вектор на външните сили на системата. Нека сумираме тези уравнения по всички точки: От лявата страна на уравнението въвеждаме масите под знака на производната и заместваме сумата на производните с производната на сумата: От дефиницията на импулса на системата: В проекции върху координатните оси:

21 слайд
Теорема на Ойлер - Приложение на теоремата за промяната на импулса на система към движението на непрекъсната среда (вода). 1. Избираме като обект на движение обема вода, намиращ се в криволинейния канал на турбината: 2. Изхвърляме връзките и заменяме действието им с реакции (Rpov - резултатът от повърхностните сили) 3. Добавяме активни сили (Rb - резултантната на силите на тялото): 4. Запишете теоремата за промяната в импулса на системата: Импулсът на водата в моменти t0 и t1 се представя като суми: Промяна в импулса на водата в интервала от време : Промяна в импулса на водата за безкрайно малък интервал от време dt: , където F1 F2 Вземайки произведението на плътността, площта на напречното сечение и скоростта за секунда маса, получаваме: Замествайки диференциала на импулса на системата в теоремата за промяната, получаваме : Следствия от теоремата за изменението на импулса на системата (закони за запазване): 1. Ако в интервала от време главният вектор на външните сили на системата е равен на нула, Re = 0, тогава векторът на величината движение е константа, Q = const е законът за запазване на импулса на системата). 2. Ако в интервала от време проекцията на главния вектор на външните сили на системата върху оста x е равна на нула, Rxe = 0, тогава проекцията на импулса на системата върху оста x е постоянна, Qx = конст. Подобни твърдения са верни за осите y и z. Лекция 7 (продължение на 7.2) Пример: Граната с маса M, летяща със скорост v, експлодира на две части. Скоростта на един от фрагментите с маса m1 нараства по посока на движението до стойност v1. Определете скоростта на втория фрагмент. 1. Обект на движение (граната): 2. Обектът е свободна система, няма връзки и техните реакции. 3. Добавете активни сили: 4. Запишете теоремата за промяната на импулса: Проектирайте върху оста: β Разделете променливите и интегрирайте: Десният интеграл е почти нула, т.к. време на експлозия t

22 слайд
Лекция 7 (продължение 7.3) 20 Ъгловият момент на точка или кинетичният момент на движение спрямо определен център е мярка за механично движение, определена от вектор, равен на векторното произведение на радиус вектора на материална точка и вектор на неговия импулс: Кинетичният момент на система от материални точки спрямо определен център е геометрична сумата от моментите на импулса на всички материални точки спрямо същия център: В проекции на оста: В проекции на оста : Теорема за изменението на момента на импулса на системата - Да разгледаме система от n материални точки. Разделяме силите, приложени към всяка точка, на външни и вътрешни и ги заместваме със съответните резултанти Fke и Fki. Нека напишем за всяка точка основното уравнение на динамиката: или Нека сумираме тези уравнения по всички точки: Нека заменим сумата от производните с производната на сумата: Изразът в скобите е моментът на импулса на системата. Оттук: Нека векторно умножим всяко от равенствата по радиус вектора отляво: Да видим дали е възможно да изнесем знака на производната навън векторен продукт: Така получаваме: Производната на вектора на импулса на системата спрямо определен център във времето е равна на главния момент на външните сили на системата спрямо същия център. В проекции върху координатните оси: Производната на момента на импулса на системата спрямо дадена ос във времето е равна на главния момент на външните сили на системата спрямо същата ос.

23 слайд
Лекция 8 21 ■ Следствия от теоремата за изменението на ъгловия момент на системата (закони за запазване): 1. Ако във времевия интервал векторът на главния момент на външните сили на системата спрямо определен център е равен до нула, MOe = 0, тогава векторът на ъгловия импулс на системата спрямо същия център е постоянен, KO = const е законът за запазване на импулса на системата). 2. Ако в интервала от време главният момент на външните сили на системата спрямо оста x е равен на нула, Mxe = 0, то ъгловият момент на системата спрямо оста x е постоянен, Kx = const. Подобни твърдения са верни за осите y и z. 2. Инерционен момент на твърдо тяло спрямо ос: Инерционният момент на материална точка спрямо ос е равен на произведението от масата на точката и квадрата на разстоянието на точката до оста. Инерционният момент на твърдо тяло спрямо ос е равен на сумата от произведенията на масата на всяка точка и квадрата на разстоянието на тази точка от оста. ■ Елементи на теорията на инерционните моменти - При въртеливото движение на твърдо тяло мярката за инерция (съпротивление срещу промяна на движението) е инерционният момент около оста на въртене. Разгледайте основните понятия на дефиницията и методите за изчисляване на моментите на инерция. 1. Инерционен момент на материална точка спрямо оста: При прехода от дискретна малка маса към безкрайно малка маса на точка, границата на такава сума се определя от интеграла: аксиален инерционен момент на твърдо тяло . В допълнение към аксиалния инерционен момент на твърдо тяло има и други видове инерционни моменти: центробежен инерционен момент на твърдо тяло. полярен момент на инерция на твърдо тяло. 3. Теоремата за инерционните моменти на твърдо тяло спрямо успоредни оси - формулата за прехода към успоредни оси: Инерционен момент спрямо базовата ос Статични моменти на инерция спрямо базовите оси Моментите на масата на тялото са нула:

24 слайд
Лекция 8 (продължение 8.2) 22 Инерционен момент на еднакъв прът с постоянно сечение около оста: x z L Изберете елементарния обем dV = Adx на разстояние x: x dx Елементарна маса: За да изчислите инерционния момент около централната ос (преминаваща през центъра на тежестта), достатъчно е да промените местоположението на оста и да зададете границите на интегриране (-L/2, L/2). Тук демонстрираме формулата за преход към успоредни оси: zС 5. Инерционният момент на хомогенен твърд цилиндър спрямо оста на симетрия: H dr r Нека отделим елементарния обем dV = 2πrdrH (тънък цилиндър с радиус r) : Елементарна маса: Тук използваме формулата за обем на цилиндър V=πR2H. За да се изчисли инерционният момент на кух (дебел) цилиндър, е достатъчно да се зададат границите на интегриране от R1 до R2 (R2> R1): 6. Инерционният момент на тънък цилиндър спрямо оста на симетрия (t

25 слайд
Лекция 8 (продължение 8.3) 23 ■ Диференциално уравнение на въртене на твърдо тяло около ос: Нека напишем теорема за промяна на ъгловия импулс на твърдо тяло, въртящо се около неподвижна ос: Импулсът на въртящо се твърдо тяло е: Моментът на външните сили около оста на въртене е равен на въртящия момент (реакциите и силата не създават гравитационни моменти): Заместваме кинетичния момент и въртящия момент в теоремата Пример: Двама души с еднакво тегло G1 = G2 висят на въже хвърлен върху твърд блок с тежест G3 = G1/4. В един момент един от тях започна да се катери по въжето с относителна скорост u. Определете скоростта на повдигане на всеки човек. 1. Избираме обекта на движение (блок с хора): 2. Изхвърляме връзките (поддържащото устройство на блока): 3. Заменяме връзката с реакции (лагер): 4. Добавяме активни сили (гравитация): 5. Запишете теоремата за промяната на кинетичния момент на системата спрямо оста на въртене на блока: R Тъй като моментът на външните сили е равен на нула, кинетичният момент трябва да остане постоянен: В началния момент от време t = 0, имаше равновесие и Kz0 = 0. След началото на движението на един човек спрямо въжето, цялата система започна да се движи, но кинетичният момент на системата трябва да остане равен на нула: Kz = 0. Ъгловият момент на системата е сумата от ъгловите моменти на хората и блока: Тук v2 е скоростта на втория човек, равно на скоросттакабел, Пример: Определете периода на малки свободни трептения на хомогенен прът с маса M и дължина l, окачен в единия край на фиксирана ос на въртене. Или: В случай на малки трептения sinφ φ: Период на трептене: Инерционен момент на пръта:

26 слайд
Лекция 8 (продължение 8.4 - допълнителен материал) 24 ■ Елементарна теория на жироскопа: Жироскопът е твърдо тяло, въртящо се около оста на материална симетрия, една от точките на което е фиксирана. Свободният жироскоп е фиксиран по такъв начин, че неговият център на масата остава неподвижен, а оста на въртене минава през центъра на масата и може да заема произволно положение в пространството, т.е. оста на въртене променя позицията си подобно на оста на собственото въртене на тялото по време на сферично движение. Основното предположение на приблизителната (елементарна) теория на жироскопа е, че векторът на импулса (кинетичния момент) на ротора се счита за насочен по собствената му ос на въртене. Така, въпреки факта, че в общия случай роторът участва в три завъртания, се взема предвид само ъгловата скорост на собственото му въртене ω = dφ/dt. Причината за това е, че в съвременните технологии роторът на жироскопа се върти с ъглова скорост от порядъка на 5000-8000 rad/s (около 50000-80000 rpm), докато другите два ъглови скоростисвързана с прецесията и нутацията на собствената си ос на въртене е десетки хиляди пъти по-малка от тази скорост. Основното свойство на свободния жироскоп е, че оста на ротора поддържа постоянна посока в пространството по отношение на инерциалната (звездна) референтна система (демонстрирано от махалото на Фуко, което поддържа равнината на люлеене непроменена по отношение на звездите, 1852 г.). Това следва от закона за запазване на кинетичния момент спрямо центъра на масата на ротора, при условие че се пренебрегне триенето в лагерите на осите на окачване на ротора, външната и вътрешната рамка: Силово действие върху оста на свободен жироскоп. В случай на сила, приложена към оста на ротора, моментът на външните сили спрямо центъра на масата не е равен на нула: ω ω С сила, а към вектора на момента на тази сила, т.е. ще се върти не около оста x (вътрешно окачване), а около оста y (външно окачване). При прекратяване на силата, оста на ротора ще остане в същото положение, съответстващо на последното време на силата, т.к. от този момент моментът на външните сили отново става равен на нула. При краткотрайно действие на сила (удар) оста на жироскопа практически не променя позицията си. По този начин бързото въртене на ротора дава на жироскопа способността да противодейства на случайни влияния, които се стремят да променят позицията на оста на въртене на ротора, и с постоянно действие на силата поддържа позицията на равнината, перпендикулярна на действащата сила, в която лежи оста на ротора. Тези свойства се използват в инерционни системинавигация.
Лекции по теоретична механика
Точкова динамика
Лекция 1
Основни понятия на динамиката
В глава Динамикаизучава се движението на телата под действието на приложени към тях сили. Следователно, в допълнение към тези понятия, които бяха въведени в раздел кинематика,тук е необходимо да се използват нови понятия, отразяващи спецификата на въздействието на силите върху различни телаи реакцията на телата към тези влияния. Нека разгледаме основните от тези понятия.
а) сила
Силата е количественият резултат от въздействието върху дадено тяло от други тела.Силата е векторна величина (фиг. 1).
![]()
![]()
Точка А от началото на вектора на силата ЕНаречен точка на прилагане на сила. Правата MN, върху която е разположен векторът на силата, се нарича силова линия.Дължината на вектора на силата, измерена в определен мащаб, се нарича числена стойност или модул на вектора на силата. Модулът на силата се означава като или. Действието на сила върху тялото се проявява или в неговата деформация, ако тялото е неподвижно, или в придаване на ускорение при движение на тялото. На тези прояви на сила се основава устройството на различни инструменти (силомери или динамометри) за измерване на сили.
б) система от сили
Разглежданата съвкупност от сили формира силова система.Всяка система, състояща се от n сили, може да бъде записана в следната форма: ![]()
в) свободно тяло
Нарича се тяло, което може да се движи в пространството във всяка посока, без да изпитва пряко (механично) взаимодействие с други тела Безплатноили изолиран. Влиянието на една или друга система от сили върху едно тяло може да се изясни само ако това тяло е свободно.
г) резултатна сила
Ако някоя сила има същия ефект върху свободно тяло като някаква система от сили, тогава тази сила се нарича резултат от тази система от сили. Това е написано по следния начин:
![]() ,
,
което означава еквивалентноствъздействието върху същото свободно тяло на резултантната и някаква система от n сили.
Нека сега се обърнем към разглеждането на по-сложни концепции, свързани с количественото определяне на ротационните ефекти на силите.
д) момент на сила спрямо точка (център)
Ако тялото под действието на сила може да се върти около някаква фиксирана точка O (фиг. 2), то за количествено определяне на този ротационен ефект се въвежда физична величина, която се нарича момент на сила около точка (център).

Нарича се равнината, минаваща през дадена фиксирана точка и линията на действие на силата равнина на силата. На фиг.2 това е равнината ОАВ.
Моментът на сила спрямо точка (център) е векторно количество, равно на векторното произведение на радиус вектора на точката на прилагане на силата от вектора на силата:
![]() ( 1)
( 1)
Съгласно правилото за векторно умножение на два вектора, техният векторен продукт е вектор, перпендикулярен на равнината на местоположението на факторните вектори (в този случай равнината на триъгълника OAB), насочен в посоката, от която е най-късият завой на първия фактор вектор към втория фактор вектор видими срещу часовника (фиг. 2).При този ред на векторите на факторите на кръстосаното произведение (1), въртенето на тялото под действието на силата ще бъде видимо срещу часовника (фиг. 2). Тъй като векторът е перпендикулярен на равнината на сила, разположението й в пространството определя положението на равнината на силата Числената стойност на вектора на момента на силата спрямо центъра е равна на удвоената площ ОАВ и може да се определи по формулата:
![]() ,
(2)
,
(2)
където величинач, равно на най-късото разстояние от дадена точка О до линията на действие на силата, се нарича рамо на силата.
Ако положението на равнината на действие на силата в пространството не е от съществено значение за характеризиране на въртеливото действие на силата, тогава в този случай, за да се характеризира въртеливото действие на силата, вместо вектора на момента на силата, алгебричен момент на сила:
![]() (3)
(3)
Алгебричният момент на сила спрямо даден център е равен на произведението на модула на силата и нейното рамо, взети със знак плюс или минус. В този случай положителният момент съответства на въртенето на тялото под действието на дадена сила срещу часовника, а отрицателният момент съответства на въртенето на тялото в посоката на часовника. От формули (1), (2) и (3) следва, че моментът на сила спрямо точка е равен на нула само ако рамото на тази силачнула. Такава сила не може да завърти тялото около дадена точка.
е) Силов момент около оста
Ако едно тяло под действието на сила може да се върти около някаква фиксирана ос (например въртенето на рамката на врата или прозорец в пантите, когато те се отварят или затварят), тогава се въвежда физическо количество, за да се определи количествено този ротационен ефект, който е наречен момент на сила около дадена ос.
 z
z
b Fxy
Фигура 3 показва диаграма, в съответствие с която се определя моментът на сила около оста z:
Ъгълът се образува от две перпендикулярни посоки z и на равнините на триъгълници O аби OAV, съответно. Тъй като O абе проекцията на ОАВ върху равнината xy, то съгласно стереометричната теорема за проекцията на плоска фигура върху дадена равнина имаме:
където знакът плюс съответства на положителна стойност на cos, т.е. остри ъгли, а знакът минус съответства на отрицателната стойност на cos, т.е. тъпи ъгли , поради посоката на вектора. На свой ред SO аб=1/2abh, където ч аб . Стойността на сегмента абе равна на проекцията на силата върху равнината xy, т.е. . аб = Е xy .
Въз основа на гореизложеното, както и на равенствата (4) и (5), определяме момента на силата около оста z, както следва:
Равенството (6) ни позволява да формулираме следната дефиниция на момента на силата спрямо всяка ос: Моментът на силата около дадена ос е равен на проекцията върху тази ос на вектора на момента на тази сила спрямо всяка точка от дадена ос и се определя като произведението на проекцията на силата върху равнина, перпендикулярна на дадената ос, взета със знак плюс или минус на рамото на тази проекция спрямо точката на пресичане на оста с равнината на проекцията. В този случай знакът на момента се счита за положителен, ако, гледайки от положителната посока на оста, въртенето на тялото около тази ос се вижда срещу часовника. В противен случай моментът на силата около оста се приема за отрицателен. Тъй като тази дефиниция на момента на сила спрямо оста е доста трудна за запомняне, се препоръчва да запомните формулата (6) и фиг. 3, която обяснява тази формула.
От формула (6) следва, че моментът на силата около оста е нула, акотя е успоредна на оста (в този случай нейната проекция върху равнина, перпендикулярна на оста, е равна на нула), или линията на действие на силата пресича оста (тогава рамото на проекцията ч=0). Това напълно отговаря на физическия смисъл на момента на силата около оста като количествена характеристика на ротационното действие на сила върху тяло с ос на въртене.
ж) телесно тегло
Отдавна е отбелязано, че под въздействието на сила тялото постепенно набира скорост и продължава да се движи, ако силата бъде премахната. Това свойство на телата, да се противопоставят на промяна в движението си, се нарича инерция или инерция на телата. Количествената мярка за инертността на тялото е неговата маса.Освен това, телесната маса е количествена мярка за ефекта на гравитационните сили върху дадено тяло колкото по-голяма е масата на тялото, толкова по-голяма гравитационна сила действа върху тялото.Както ще бъде показано по-долу, ъъъТези две определения за телесно тегло са свързани.
Други понятия и дефиниции на динамиката ще бъдат обсъдени по-късно в разделите, където се срещат за първи път.
2. Връзки и реакции на връзки
По-рано в раздел 1, точка (c) беше дадена концепцията за свободно тяло, като тяло, което може да се движи в пространството във всяка посока, без да е в пряк контакт с други тела. Повечето от реалните тела, които ни заобикалят, са в пряк контакт с други тела и не могат да се движат в една или друга посока. Така например телата, разположени на повърхността на масата, могат да се движат във всяка посока, с изключение на посоката, перпендикулярна на повърхността на масата надолу. Вратите с панти могат да се въртят, но не могат да се движат напред и т.н. Телата, които не могат да се движат в пространството в една или друга посока, се наричат не е безплатно.
Всичко, което ограничава движението на дадено тяло в пространството, се нарича връзки.Това могат да бъдат някои други тела, които пречат на движението на това тяло в някои посоки ( физически връзки); в по-широк план това може да са някои условия, наложени върху движението на тялото, ограничаващи това движение. Така че можете да зададете условие за движението на материална точка по дадена крива. В този случай връзката се определя математически под формата на уравнение ( уравнение на връзката). Въпросът за видовете връзки ще бъде разгледан по-подробно по-долу.
Повечето от връзките, наложени на телата, са практически физически връзки. Следователно възниква въпросът за взаимодействието на дадено тяло и връзката, наложена на това тяло. На този въпрос отговаря аксиомата за взаимодействието на телата: Две тела действат едно на друго с равни по големина сили, противоположни по посока и разположени на една и съща права линия. Тези сили се наричат сили на взаимодействие. Силите на взаимодействие се прилагат към различни взаимодействащи тела. Така например по време на взаимодействието на дадено тяло и връзка една от силите на взаимодействие се прилага от страната на тялото към връзката, а другата сила на взаимодействие се прилага от страната на връзката към даденото тяло . Тази последна власт се нарича сила на реакция на връзкатаили просто, реакция на свързване.
При решаването на практически проблеми на динамиката е необходимо да можете да намерите посоката на реакциите различни видовевръзки. Общото правило за определяне на посоката на реакцията на връзката понякога може да помогне за това: Реакцията на връзката винаги е насочена противоположно на посоката, в която тази връзка предотвратява движението на дадено тяло. Ако тази посока може да бъде определена определено, тогава реакцията на връзката ще се определя от посоката. В противен случай посоката на реакцията на връзката е неопределена и може да се намери само от съответните уравнения на движение или равновесие на тялото. По-подробно въпросът за видовете връзки и посоката на техните реакции трябва да се проучи според учебника: S.M. Targ Кратък курс по теоретична механика "Висше училище", М., 1986 г. гл.1, §3.
В раздел 1, точка (c) беше казано, че ефектът от всяка система от сили може да бъде напълно определен само ако тази система от сили се приложи към свободно тяло. Тъй като повечето тела всъщност не са свободни, тогава, за да се изследва движението на тези тела, възниква въпросът как да направим тези тела свободни. Този въпрос е отговорен аксиома за връзки на лекции Нафилософия у дома. Лекцииса били... социална психологияи народопсихология. 3. Теоретиченрезултатите в социалния дарвинизъм бяха ...
теоретичен Механика
Урок >> ФизикаРезюме лекции Напредмет ТЕОРЕТИЧЕН МЕХАНИКАЗа студенти от специалността: 260501.65 ... - редовно Реферат лекциисъставен въз основа на: Butorin L.V., Busygina E.B. теоретичен Механика. Образователно-практическо ръководство...
В рамките на всяка курс на обучениеИзучаването на физиката започва с механиката. Не от теоретична, не от приложна и не изчислителна, а от добрата стара класическа механика. Тази механика се нарича още Нютонова механика. Според легендата един учен се разхождал в градината, видял падаща ябълка и именно това явление го подтикнало да открие закона земно притегляне. Разбира се, законът винаги е съществувал и Нютон му е дал само разбираема за хората форма, но неговата заслуга е безценна. В тази статия няма да опишем законите на Нютоновата механика възможно най-подробно, но ще очертаем основите, основните знания, определенията и формулите, които винаги могат да ви помогнат.
Механиката е дял от физиката, наука, която изучава движението на материалните тела и взаимодействията между тях.
Самата дума има гръцки произходи се превежда като "изкуството за изграждане на машини". Но преди да изградим машини, все още имаме да извървим дълъг път, така че нека следваме стъпките на нашите предци и ще изучаваме движението на камъни, хвърлени под ъгъл спрямо хоризонта, и ябълки, падащи върху глави от височина h.

Защо изучаването на физиката започва с механиката? Защото е напълно естествено, да не го тръгнем от термодинамичното равновесие?!
Механиката е една от най-старите науки и исторически изучаването на физиката започва именно с основите на механиката. Поставени в рамките на времето и пространството, хората всъщност не биха могли да започнат от нещо друго, колкото и да им се искаше. Движещите се тела са първото нещо, на което обръщаме внимание.
Какво е движение?
Механичното движение е промяна в положението на телата в пространството едно спрямо друго във времето.
След това определение съвсем естествено стигаме до понятието референтна рамка. Промяна на положението на телата в пространството едно спрямо друго.Ключови думи тук: един спрямо друг . В крайна сметка, пътник в кола се движи спрямо човек, стоящ отстрани на пътя, с определена скорост и почива спрямо съседа си на седалка наблизо и се движи с друга скорост спрямо пътник в кола, която ги изпреварва.

Ето защо, за да измерваме нормално параметрите на движещи се обекти и да не се объркаме, имаме нужда отправна система - твърдо свързани помежду си отправно тяло, координатна система и часовник. Например, земята се движи около слънцето в хелиоцентрична референтна система. В ежедневието ние извършваме почти всички наши измервания в геоцентрична референтна система, свързана със Земята. Земята е еталонно тяло, спрямо което се движат автомобили, самолети, хора, животни.

Механиката като наука има своя задача. Задачата на механиката е да знае положението на тялото в пространството по всяко време. С други думи, механиката изгражда математическо описание на движението и намира връзки между физични величинихарактеризирайки го.
За да продължим по-нататък, имаме нужда от понятието „ материална точка ". Казват, че физиката е точна наука, но физиците знаят колко много приближения и предположения трябва да се направят, за да се постигне съгласие относно точно тази точност. Никой никога не е виждал материална точка или е подушвал идеален газ, но те съществуват! Просто с тях се живее много по-лесно.
Материална точка е тяло, чийто размер и форма могат да бъдат пренебрегнати в контекста на тази задача.
Раздели на класическата механика
Механиката се състои от няколко раздела
- Кинематика
- Динамика
- Статика
Кинематикаот физическа гледна точка, изучава как точно се движи тялото. С други думи, този раздел се занимава с количествените характеристики на движението. Намерете скорост, път - типични задачи на кинематиката
Динамикарешава въпроса защо се движи по този начин. Тоест, той отчита силите, действащи върху тялото.
Статикаизучава равновесието на телата под действието на силите, тоест отговаря на въпроса: защо изобщо не пада?
Граници на приложимост на класическата механика
Класическата механика вече не претендира да бъде наука, която обяснява всичко (в началото на миналия век всичко беше съвсем различно) и има ясен обхват на приложимост. Като цяло законите на класическата механика са валидни за света, познат ни по размери (макросвят). Те спират да работят в случая на света на частиците, когато класическият се замени с квантова механика. Също така класическата механика е неприложима за случаите, когато движението на телата се извършва със скорост, близка до скоростта на светлината. В такива случаи релативистките ефекти стават ясно изразени. Грубо казано, в рамките на квантовата и релативистката механика - класическата механика, това е частен случай, когато размерите на тялото са големи, а скоростта е малка.

Най-общо казано, квантовите и релативистичните ефекти никога не изчезват; те се проявяват и при обичайното движение на макроскопични тела със скорост, много по-ниска от скоростта на светлината. Друго нещо е, че действието на тези ефекти е толкова малко, че не надхвърля най-точните измервания. По този начин класическата механика никога няма да загуби фундаменталното си значение.
Ще продължим да изучаваме физическите основи на механиката в бъдещи статии. За по-добро разбиране на механиката винаги можете да се обърнете към нашите автори , които поотделно хвърлят светлина върху тъмното петно на най-трудната задача.










