Министерство на образованието и науката на Самарска област

Държавно автономно образователна институциядопълнителен професионално образование(повишено обучение) специалисти

САМАРСКИ РЕГИОНАЛЕН ИНСТИТУТ ЗА НАПРЕДНАЛИ ПРОФЕСИОНАЛИСТИ

И ПРЕКВАЛИФИКАЦИЯ НА РАБОТНИЦИ В ОБРАЗОВАНИЕТО

Финална работа

На курсове за напреднали

Според WB IOC

„Методически особености на обучението за решаване на задачи с параметър в контекста на прехода към нови образователни стандарти“

(15.06 - 19.06.2015 г.)

Проектиране на многостепенна система от задачи с параметър по темата:

"Производна"

Изпълнено:

Валиева Ф.Г.,

учител по математика

GBOU Средно училище им. М.К. Овсянникова

с. Исаклий

Самара

2015 г

ОБЯСНИТЕЛНА ЗАПИСКА

пълно име (пълно име)

Валиева Фанузя Галимзяновна

Месторабота

GBOU Средно училище им. М.К. село Овсянников Исакли,

Исаклински район, Самарска област

Длъжност

Учител по математика

Вещ

Математика

Клас

Цели:

1. изпълнение на изискванията на Федералния държавен образователен стандарт LLC при изучаване на темата: „Производна“

   Обобщаване и систематизиране на знанията и методите на дейност по темата „Производна”; формиране на умения за решаване на задачи с параметри.

   Развитие на изследователска и образователна дейност.

Концепцията за духовно-нравствено развитие и възпитание на личността на руския гражданине методологическата основа за разработването и прилагането на федералния държавен образователен стандарт общо образование.

Федерална държава образователен стандартосновно общо образование за училищен курсматематика.

Стандартът се основава насистемно-дейностен подход.

Стандартът установява изисквания към резултатите от усвояването на осн образователна програмаосновно общо образование:

лични;

метасубект;

предмет.

Задачи:

- образователни: анализират и разбират текста на проблема, самостоятелно подчертават и формулират познавателна цел, преформулиране на условието, изграждане на логическа верига от разсъждения, критична оценка на получения отговор, съзнателно и доброволно изграждане на речево изказване, избор на най- ефективен начинрешаване на проблеми, поставяне и формулиране на проблем, поставяне на хипотези и тяхното обосноваване, смислов прочит;

-разработване: поставяне на цели, планиране на вашите дейности в зависимост от конкретни условия; размисъл върху методите и условията на действие, контрол и оценка на процеса и резултатите от дейността, саморегулация,чрез решаване на проблеми, развиват творческата и умствената активност на учениците, интелектуалните качества: способността да „виждат“ проблем, оценъчни действия, независимост, гъвкавост на мисленето;

- образователни: осмисляне, способност за слушане и диалог, участие в колективно обсъждане на проблеми, култивиране на отговорност и точност.

Задачи с параметри - това са нестандартни задачи, т.е.необичайни както по обстановка и съдържание, така и по методи на решение. Ролята на такивазадачи, тяхното значение и ползи за развитието логично мислене, интуиция,творческите способности на учениците, формирането на високи математически умения у тяхкултурите са много големи. Известно е, че учителите са изправени пред сериозниметодически проблеми в преподаването решаване на такива проблеми, въпреки наличието,достатъчно голямо количествоучебници и статии в списания. Причината за това е съвсем очевидна: основната стратегия на обучението по математика в училище е развитието на умения и способности за решаване на определен набор от стандартни задачи, повечето от които са свързани с технологиите алгебрични трансформации. Уравненията (неравенствата) с параметри принадлежат към различен тип проблеми - проблеми, чието решение изисква преди всичко способност за извършване - понякога доста разклонени - логически конструкции и изследвания.

Решаването на проблеми с параметри изисква проучване, дори ако тази дума не се споменава в изложението на проблема. Механичното прилагане на формули не е достатъчно, необходимо е да се разберат закономерностите и да има умението да се анализира конкретен случай въз основа на известни общи свойстваобект, систематичност и последователност в решението, способност за комбиниране на разглежданите частни случаи в един резултат. Това обяснява трудностите, които учениците срещат при решаването на подобни задачи.

Понастоящем идеята за комбиниране на обучение за решаване на проблеми с обучение за конструирането им стана доста широко разпространена. Чрез конструирането на задача ще разберем процеса на създаване на нова задача. Основата за конструиране на задача е способността да се конструира квадратен трином. В този случай се използват различни техники: аналогия, промяна на коефициентите на квадратен трином, промяна на нова променлива, промяна на изискванията на задачите. По-сложните функции могат да действат като коефициенти и нова променлива. По този начин можете да използвате такъв квадратен тричлен, който ще помогне при организирането на повторението на повече сложни функции: експоненциална, логаритмична, тригонометрична. От една страна, трябва да знаете свойствата на квадратен трином, а от друга страна, свойствата на функцията се повтарят, като по този начин се постига комбинираемостта на проблема.

Изборът на проблем с параметри за преподаване на тяхното решение и дизайн може да се обясни със следните обстоятелства:

при решаване на задачи с параметри възниква повторение и в резултат на това се получава по-дълбоко, по-трайно усвояване на програмните въпроси;

решаването на задачи с параметри разширява математическите хоризонти и дава нови подходи за решаване на проблеми;

има развитие на математическо и логическо мислене, способност за анализ, сравнение и обобщение;

придобиват се умения за изследователска работа;

помощ при подготовка за изпити;

възниква формирането на такива качества на личността като трудолюбие, решителност, постоянство, воля, точност.

Формиран UUD в рамките на Федералния държавен образователен стандарт при решаване на задачи със следните параметри:

Етапи на решаване на проблема

Сформиран UUD

Анализ на състоянието(въвеждане на буквени означения)

• поставяне на цели;

  подчертаване на съществена информация;

  формулиране на проблема и прогнозиране на решения;

  абстракция;

  аналогия;

  класификация (типологизация);

  символични действия.

Схематично записване на условията на проблема под формата на таблица, диаграма, графикас въведени буквени означения

• планиране;

  систематизиране;

  знаково-символични действия;

  моделиране.

Изготвяне на модел(търсене на аналог, рисуване на добре познат закон от математиката или физиката)

• създаване на начин за решаване на проблеми;

  настройка на състоянието;

  графично моделиране.

Решаване на уравнение, система и др.(търсене на неизвестното)

• анализ и идентифициране на значима информация;

  правене на заключения;

  изграждане на верига от разсъждения;

  поставяне и тестване на хипотези;

  трансформация на модела.

Интерпретация на модела(проверка и оценка на решения, корени)

• анализ;

  правене на заключения;

  спецификация;

  знаково-символно действие (интерпретация).

Проучване(обобщаване на проблема или метод за решаването му за модифицирани условия, други подходи за решение)

• анализ;

  синтез;

  търсене на аналози;

  изграждане на верига от разсъждения;

  способност за кратко предаване на съдържанието;

  умение за диаграми, символи, модели;

  създаване на начини за решаване на проблеми от търсещ и творчески характер.

Отражение

• създаване на смисъл;

  планиране;

  контрол;

  корекция;

  степен;

  волева саморегулация;

  готовност за саморазвитие, самообразование;

  способността самостоятелно да определя целите на своето обучение;

  поставяйте и формулирайте нови задачи за себе си;

  развиват мотивите и интересите на своята образователна дейност.

Многостепенна система от задачи

Методиката на преподаване, базирана на многостепенна система от задачи, се основава на поетапното овладяване на блоковете на нейната матрица. Основната характеристика на тази техника е, че на всяко ниво, т.е. при усвояване на съответната колона на матрицата ученикът всеки път среща и трите вида учебни ситуациивъзникващи при решаване на проблеми.

Формира се многостепенна система от задачи за всяка тема на курса, като се използва нейното матрично представяне, чрез идентифициране на класиран списък от основни елементи на учебното съдържание и съответстващите им основни задачи, от една страна, и нива на обучение, отразяващи способността за решаване на познати, променени и непознати проблеми, от друга страна.

Такава матрица на тематичната проблемна система съдържа 3 реда, съответстващи на три вида учебни ситуации, които възникват при решаването на проблеми, ин колони, отразяващи броя на основните задачи на темата. Такова таблично (матрично) представяне на системата от задачи на темата помага да се запълнят напълно нейните математически и дейностни (формиране на UUD) компоненти на всяко ниво и по този начин да се реализиракритерии за пълнота на предмета и дейността (което означава когнитивна UUD) системата, която се формира образователни задачи. Освен това, ако основните задачи играят ролята на уникални интегратори на предметно-съдържателния компонент в системата, тогава при проектирането и реализирането на учебния процес подобна роля трябва да играят универсалните учебни дейности(общи методи и техники на дейност) в избрани ситуации.

Образователните дейности при решаване на задачи, включени в първия ред на матрицата, имат репродуктивен характер (използват се общообразователни дейности като класификация, включване на понятие, извеждане на следствия, действия, изграждане на логическа верига от разсъждения, доказателство и др.). Използваните задачи са различниочевидни връзки между данните и търсените (известни и неизвестни) елементи. Ученикът идентифицира (разпознава познати задачи сред подобни), възпроизвежда научените методи или алгоритми на действие, прилага придобитите знания на практика за определен известен клас задачи и получава нова информация въз основа на прилагането на научения модел на дейност.

При решаване на задачи от втори ред, репродуктивен образователна дейносткомбиниран с реконструктивен, при който моделите на дейност не се възпроизвеждат просто от паметта, а се реконструират при леко модифицирани условия (тук се проявяват такива общообразователни действия като идентифициране и формулиране на познавателна цел, търсене и подчертаване на необходимата информация, знаково-символични действия , включително математическо моделиране, структуриране на знания).

И накрая, при решаването на задачи от третата линия образователната дейност има изследователски и творчески характер. Ученикът трябва да може да се ориентира в нови ситуации и да разработи принципно нови програми за действие (предложи хипотеза, тест: обосновете или опровергайте, изложете нова и т.н., приложете изследователска дейност). Решаването на проблемите на съответния блок изисква студентът да има богат набор от доказани и бързо внедряеми алгоритми; способността за бързо прекодиране на информация от знаково-символна форма в графична форма и, обратно, от графична в знаково-символична форма; системна визия на курса. В същото време той не включва просто използване на стари алгоритми в нови условия и увеличаване на техническата сложност, но се характеризира с неочевидност на приложението и комбинацията от изследваните алгоритми. Задачите на това ниво имат сложна логическа структура и се характеризират с присъствиелатентни връзки между данните и търсените елементи. Такива задачи обикновено се предлагат като най-трудни на приемните изпити в университети с високи изисквания към математическата подготовка на кандидатите и в задачи 17,18, 20, 21 от Единния държавен изпит.

Многостепенна система от проблеми по темата „Производна“

№ п/п

Име на задачата

Тип задача

Изчисляване на производната по дефиниция.

ZZ

МЗ

Нова Зеландия

Намиране на производни на сбор, произведение, частно на функции

ZZ

МЗ

Нова Зеландия

Изследване на монотонността на функция

ZZ

функция нараства на цялата числова ос?

МЗ

При какви стойности на параметритефункция намалява за всички стойности ?

Нова Зеландия

Намерете множеството от всички числа a, за всяко от които функциятаf(х) = грях 2 х – 8(а + 1) sinx + (4 а 2 + 8 а – 14) хнараства по цялата числова ос и няма критични точки.

Намиране на екстремни точки

ZZ

има една неподвижна точка?

МЗ

Определете при каква стойност на параметъра максимална функцияе равно на 9

Нова Зеландия

При какви стойности на параметъра a изпълнява функциятаf(х) = (а 2 – 3 а + 2) (cos 2 – грях 2 + (а – 1) х + грях1 няма критични точки?

Намиране на най-големите и най-малките стойности на непрекъсната функция на интервал и диференцируема на интервал

ZZ

Разберете при какви стойности на параметъраА най-малка стойностфункцииг = х 2 -12 х + а е равно на нула на сегмента.

МЗ

При каква стойност на параметъра най-малката стойност на функциятаравно на

Нова Зеландия

При какви стойности на параметритефункция приема стойности по-малки от 5 за всяко

Пълно проучванеи чертане

ZZ

3 + 3x 2

МЗ

При каква стойност на параметъра a е минимумът на функцията f(x) = ax 2 – 6ax + a 2 – 9 е равно на 1?

Нова Зеландия

Уравнение на допирателната към графиката на функция в дадена точка

ZZ

При какви стойности на параметритеправ е допирателна към графиката на функцията ?

МЗ

При какви стойности на параметрите допирателна към графиката на функция отрязва от първата четвърт равнобедрен триъгълник с площ

Нова Зеландия

При какви стойности на параметрите допирателни към графиката на функция , начертана в точките на пресичането му с оста, образуват ъгъл помежду си

Приложение на производната за решаване на задачи в геометрията, физиката и икономиката

ZZ

Какви трябва да бъдат страните на правоъгълник с периметър?Птака че площта му да е максимална?

МЗ

Прозорецът има формата на правоъгълник, ограничен отгоре с полукръг (Фигура 3). Периметърът на прозореца е P. Определете радиуса на полукръга R, при който площта на прозореца е най-голяма.

Нова Зеландия

Картина с височина a е окачена на стената по такъв начин, че долният й ръб да е с h единици по-високо от нивото на очите на наблюдателя. На какво разстояние х от стената трябва да бъде наблюдателят, за да бъде ъгълът на видимост на картината най-голям (Фигура 7а)?

Решения

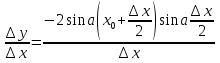
Решение :

1. Функцията f(x) намалява за всички стойности на x, ако производната

f′(x) = 6ax 2 + 18ax + 30a = 6a(x 2 + 3x + 5)< 0

за всички x.

2. От тук намираме, че a< 0.

3 . Отговор: а (–∞; 0).

1. Намерете множеството от всички числа a, за всяко от които функцията f (x) = sin 2x – 8(a + 1)sinx + (4a 2 + 8a – 14)x е нарастваща на цялата числова ос и няма критични точки.

1. За всяко фиксирано a тази функция е диференцируема във всяка точка на реалната права.

2. Тъй като функцията f(x) нараства, неравенството f′(x) ≥ 0 трябва да е в сила във всяка точка x.

3. Освен това, тъй като f(x) няма критични точки, тогава за всяко x трябва да е в сила неравенството f′(x) ≠ 0.

4. Така, ако функцията удовлетворява условието на задачата, тогава за всички x неравенството f (x) > 0 трябва да бъде изпълнено.

5. От друга страна, ако неравенството f′(x) > 0 е в сила за всички x, тогава функцията очевидно няма критични точки и нараства.

6. Намерете производната на тази функция:

f′( х) = 2 cos 2 х – 8( а + 1) cosx + 4 а 2 + 8 а – 14.

Сега проблемът може да бъде преформулиран по следния начин: намерете всички стойности на параметъра a, за всяка от които неравенството е валидно за всяко x

cos 2x – 4(a + 1) cos x + 2a 2 + 4a – 7 > 0.(1)

7. Като се има предвид, че cos 2x = 2 cos 2 x – 1 и приемайки cos x = t, където –1 ≤ t ≤ 1, пренаписваме неравенство (1), както следва:

2т 2 – 1 – 4(a + 1)t + 2a 2 + 4a – 7 > 0,

или

T 2 – 2(a + 1)t + a 2 + 2a – 4 > 0. (2)

8. След като обозначихме функцията от лявата страна на неравенството (2) с ϕ(t), даваме нова формулировка на първоначалния проблем: намираме всички стойности на a, за всяка от които най-малката стойност на функцията ϕ (t) на интервала [–1; 1] е положителен.

9. Производната ϕ′(t) = 2t – 2(a + 1) изчезва при t 0 = а + 1.

10. Най-малката стойност на функцията ϕ(t) на интервала [–1; 1] е:

ϕ (–1) = а 2 + 4а – 1,Акоa + 1 ≤ –1;

ϕ (a + 1) = –5,Ако –1 < a + 1 < 1;

ϕ(1) = a 2 – 5, ако a + 1 ≥ 1.

11. Тъй като най-малката стойност на функцията ϕ(t) на интервала [–1; 1] трябва да е положителен, тогава стойностите на параметъра a, които отговарят на условията на проблема, принадлежат на два интервала: a ≤ –2 и a ≥ 0.

12. Ако a ≤ –2, тогава желаните стойности на параметъра a отговарят на неравенството a 2 + 4a – 1 > 0.

13. Ако a ≥ 0, тогава желаните стойности на параметъра a отговарят на неравенството a 2 – 5 > 0.

14. Следователно наборът от желани стойности a е обединението на решения на две системи от неравенства:

(3)

a ≥ 0

А 2 -5 > 0 (4)

15. Множеството от решения на система (3) е интервалът –∞< a < –2 –√5 , а множество решений системы (4)- промежуток a >√5 .

16. Отговор: а (–∞; –2 –√5) (√5; +∞).

1. Тъй като тази функция е диференцируема на цялата числова ос, критичните точки на функцията f(x) са онези точки, в които производната f′(x) = 0.

2. В този случай имаме f′(x) =(a – 1)(a – 2) (–sin+ (а – 1).

3. Очевидно, ако a = 1, тогава f′(x) = 0 за всяко x R, т.е.

За дадена функциявсяка точка x R е критичен.

4. Да предположим, че a 1. Тогава уравнението f′(x) = 0 приема формата

(а – 2) грях = 2. (1)

От това следва, че ако |a – 2|< 2, т. е. если a (0; 1) (1; 4),

тогава уравнение (1) няма корени и следователно за посочените стойности на a функцията f(x) няма критични точки.

5 . Отговор: а (0; 1) (1; 4).

Най-малката стойност на числителя и най-висока стойностзнаменателят се постига при различни стойности на x. Следователно, за да намерите най-малката стойност на функция, е удобно да използвате производната. Нека пренапишем неравенството във формата

КъдетоT=3- cos 2 х, T

Нека намерим най-малката стойност на функциятаf( T) = , на сегмента. Тъй като производнатаf "( T) = отрицателен приTЧеfнамалява и приема най-малка стойност приT=3, f име = f(3) = .

Отговор:а

За какво е най-малкото естествено k уравнението x 3 + 3x 2 – 45x + k = 0 има точно един корен?

1. Постройте скица на графиката на функцията y 1 = х 3 + 3x 2 – 45x и определете най-малката естествена стойност на k, при която тази графика пресича правата y 2 = –k точно в една точка.

2. а) D(y 1 ) = R;

буу 1 / = 3x 2 + 6x – 45; 1 / в интервалите (–∞; –5), (–5; 3) и (3; +∞) е илюстрирано на фиг. 1. На фиг. 2 показва схематично представяне на графиката на функция y 1 .

3. Очевидно това уравнение има единствено решение, ако –k > 175 или –k< –81, т. е. k < –175 или k >81. Най-малката естествена стойност на k е 82.

4. Отговор: k = 82.

При каква стойност на параметъра a минимумът на функцията f(x) = ax2 – 6ax + a2 – 9 е равен на 1?

1. f′(x) = –6x 2 + 6x + 12.

2. y′ = 0 при x 1 = 2.

6. Отговор: a = 2.

При каква стойност на параметър a е минималната функция f(x) = –2x 3 + 3x 2 + 12x + 4a е равно на 1?

За какви стойности на параметъра a правата y=ax-2 е допирателна към графиката на функцията y=1+ln⁡ x?

При какви стойности на параметъра a допирателната към графиката на функцията y=a-x^2 отрязва равнобедрен триъгълник с площ 9/32 от първата четвърт?

защото , според условието допирателната трябва да пресича функцията причетвъртинки, т.е. Триъгълникът е равнобедрен и правоъгълен, следователно останалите ъгли са равни, Нокъдето допирателната приема формата точката на контакт на допирателната с графиката по оста x е равна на . използвайки формулата на допирателната към графиката тъй като площта на триъгълника трябва да е равна на , Че защото четвърт.Където

При какви стойности на параметъра a допирателните към графиката на функцията y=4x^2-|a|x, начертани в точките на пресичането й с оста x, образуват ъгъл от 60° помежду си

Какви трябва да бъдат страните на правоъгълник с обиколка P, за да е максималната му площ?

Прозорецът има формата на правоъгълник, ограничен отгоре с полукръг (Фигура 3). Периметърът на прозореца е P. Определете радиуса на полукръга R, при който площта на прозореца е най-голяма.

Картина с височина a е окачена на стената по такъв начин, че долният й ръб да е с h единици по-високо от нивото на очите на наблюдателя. На какво разстояние х от стената трябва да бъде наблюдателят, за да бъде ъгълът на видимост на картината най-голям (Фигура 7а)?

Литература

Азаров А.И., Барвенов С.А., Федосенко В.С.Методи за решаване на задачи с параметри. Математика за гимназисти. Минск: "Аверсев", 2003 г.

СРЕЩУ. Висоцки, Проблеми с параметри за подготовка за Единния държавен изпит

Gornshtein P.I., Polonsky V.B., Yakir M.S. Проблеми с параметрите. – К.: РИА „Текст”; МП "ОКО", 1992. -290 с.

Качалова Г. А. За необходимостта от включване на съдържателно-методическата линия „Задачи с параметри“ в образователния модул „Основи на математиката“ //материяł yMię dzynarodowejNaukowi- PraktycznejkonferencjiPostę стрó wwnauce. Nowepoglą dy, проблеми, innovacje. 29.07.2012. - 31.07.2012. Część 2. - Łóдź, 2012. - с. 67–70.

Козко А. И., Панферов В. С., Сергеев И. Н., Чирски В. Г. Единен държавен изпит 2011. Математика. Задача C5. Проблеми с параметър / Ed. А. Л. Семенова и И. В. Ященко. - М.: МЦНМО, 2011.-144 с.

Родионов Е.М. Решаване на задачи с параметри. М.: МП "Рус-90", 1995 г

Най-висока категория

Санкт Петербург

2006
Въведение

Решаването на задачи с параметри е може би най-трудната част от началния курс по математика не само за ученици и кандидати, но и за учители.

Това се обяснява с факта, че основната стратегия на математическото образование в училище е развитието на умения и способности за решаване на определен набор от стандартни задачи, повечето от които са свързани с техниката на алгебричните трансформации. При решаването на задачи с параметри трябва да се разглеждат различни случаи, във всеки от които методите за решаване на проблема често се различават значително един от друг. В същото време трябва ясно и последователно да се следи запазването на еквивалентността на решаваните уравнения и неравенства, като се вземе предвид областта на дефиниране на изразите, включени в уравнението или неравенството, и също така да се вземе предвид осъществимостта на извършени операции. Освен това е необходимо, на първо място, способността да се произвеждат - понякога доста разклонени логически конструкции. В допълнение, арсеналът от стандартни трансформации трябва да бъде значително допълнен от някои специфични трансформации.

Проблемите с параметри представляват много широко поле за пълноценна математическа дейност, отварят значителен брой евристични техники за учениците. общ, ценни за математическото развитие на индивида, приложими в изследванията и върху всякакъв друг математически материал.

Задачите с параметри показват доколко практиката на приемните изпити се е отдалечила от училището, доколко се различават изискванията за завършил училище и изискванията, които университетът предявява към кандидата.

Квадратична функция.

Като основна в училищния курс по математика, квадратната функция естествено образува обширен клас задачи с разнообразни по форма и съдържание параметри, но обединени от обща идея - свойствата y=ax2+bx+c формират основата на тяхното решение.

На практика всички важни свойства квадратична функциясе определят от таблицата.

маса 1

Горната диаграма показва съвсем ясно, че дискриминантът D, водещият коефициент a, абсцисата xo = - b/2a, върховете на параболата изграждат „рамката“, върху която е изградена теорията на квадратичната функция. След това ще разгледаме задачи, чието решение е свързано с изучаването на знаците на D и a, задачи, чието решение е свързано с положението на върха на парабола и задачи, свързани с местоположението на корените на квадратен тричлен.

Дискриминант, старши коефициент.

https://pandia.ru/text/78/525/images/image013_18.jpg" align="left" width="179" height="216 src=">

Решение:

Тъй като уравнението няма реални корени, графиката на функцията y = ax2 + bx + c се намира или напълно над оста OX, или напълно под нея, т.е. стойностите на функцията са или по-големи от нула, или по-малки отколкото нула за всякакви стойности на x ( x - всяко число).

По условие a+b+c<0, f (1) = а+b+с, то f (1) < 0, значит f (х) < 0 для всех значений х. с = f (0), т. е. с равно значению функции

Фиг.2 y= f (x) при x=0. Заключение: с<0.

Отговор:с<0.

Задача 3.Нека P(x)=2x2+ax+b, Q(x)= x2+cx+d и a2+ c2 +4d≤ 2ac + 4b(a, b, c са реални числа). Докажете, че ако уравнението P(x)=0 има реални корени, то уравнението Q(x)=0 също има реални корени.

Решение:

Ако уравнението P(x)=0 има реални корени, тогава D = a2 – 8b≥0. Нека докажем, че от неравенствата a2+ c2 +4d≤ 2ac + 4b и a2 – 8b≥0 следва неравенството c2 – 4d ≥0. (x2+cx+d=0

D = с2 – 4d).

a2+ c2 +4d≤ 2ac + 4b (-2)

2а2-2 с2 -8d ≥- 4ас -8b

А2+4ас≥ 2с2+8d или - а2+4ас - 4с2 ≥-2с2+8d; - a2+4ac - 4c2 = - (a2-4ac+ 4c2) = - (a-c)2

с2 – 4d ≥ (а-с)2/2≥0, т.е. дискриминанта на уравнението Q(x)=0, което означава, че уравнението Q(x)=0 има решение.

Задача 4.

2y-x + xy = 0 (1)

(x + 2a – 4)y – ax + 5 = 0 (2)

има едно единствено решение?

Решение:

Очевидно за всяко y двойката (-2; y) не е решение на тази система. Тогава от уравнение (1) получаваме y = x/(x + 2). Замествайки в уравнение (2), получаваме:

(1 – a)x2 + x + 10 = 0(3). Това уравнение има уникално решение, ако:

1). a – 1 = 0, a = 1,

2). D = 40a – 39 = 0, a = 39/40

3). Квадратното уравнение (3) има два различни корена, единият от които е –2. Заместете x = -2 в уравнение (3), получаваме a = 3.

Отговор: a = 1, a = 39/40, a = 3.

Задача 5.При какви стойности на параметъра a системата от две уравнения

x2 -2x - y2= 0 (1)

y = ax – a + b (2)

има уникално решение за всякакви стойности на b?

Решение:

Заместете y = ax – a + b (2) в уравнение (1), получаваме:

(1-a2) x2 – 2(1-a2 + ab)x – (a - b)2=0 (3)

1). Ако 1-a2 = 0, уравнение (3) има решение за всякакви стойности. Това е лесно да се провери: нека, например, b = 0.

2) 1-a2≠0, тогава уравнение (3) е квадратно. D = b2 – a2 + 1. Нека намерим онези стойности на параметъра a, за които неравенството b2 – a2 + 1≥0 за всякакви стойности на b. Неравенството b2 ≥ a2-1 е валидно за всякакви стойности на b, ако a2-1≤0, тъй като a = 1, a = -1 не е подходящо, тогава -1<а<1.

Отговор: -1<а<1.

Задача 6.При какви стойности на параметъра a не се пресичат графиките на функциите y = 2ax + 1 y = (a-6)x2 –2?

Решение:

Липсата на пресечни точки между две графики на функция е еквивалентна на липсата на решения на система от две уравнения:

y = 2ax + 1 (1)

y = (a-6)x2 –2 (2)

2ax + 1 = (a-6)x2 –2 (3), така че уравнение (3) да няма решения, изпълняваме условието: D<0

4a2 + 12(a – 6)<0, -6<а<3.

Отговор: -6<а<3.

Върхът на параболата.

Задача 7.Реални числа x, y и такива, че условието x + y = 2a – 1(1) и условието

x2 + y2 = a2 + 2a – 3 (2), се изпълняват едновременно. При какви стойности на параметъра a продуктът xy приема най-малка стойност?

Решение:

xy = ((x + y)2 – (x2 + y2))/2 = ((2a – 1)2 – (a2 + 2a – 3))/2 = 3/2a2 – 3a +2

Да разгледаме функцията f(a) = 3/2a2 – 3a +2

1). Нека разберем при какви стойности на параметъра a системата от две уравнения (1) и (2) има решение.

Заместете y = 2a – 1 – x в уравнение (2), получаваме: 2 x2 +2x(1 – 2a) +3a2 - 6a +4 = 0. За да има решение на това уравнение, ние изпълняваме условието: D≥ 0, -2a2+ 8a – 7 ≥0,

https://pandia.ru/text/78/525/images/image017_29.gif" width="14">2-√2 / 2 ≤ a≤2 + √2 / 2

2). Да намерим при какви стойности на параметъра a функцията f(a) = 3/2a2 – 3a +2 приема най-малката стойност на даден сегмент. Абсцисата на върха на параболата y = f(a) a = 1, 1<0, значит f(а) <0, тогда функция f(а) = 3/2а2 – 3а +2 принимает наименьшее значение при

Отговор: 2 - √2 / 2.

Задача 8.Намерете всички стойности на параметъра a, за които върхът на две параболи f(a) = 4x2 + 8ax – a и g(x) = 4ax2 – 8x + a –2 лежи от една и съща страна на правата линия y = -5.

Решение:

Нека разберем при какви стойности на параметъра a ординатите на върховете на тези параболи са по-големи от –5 или едновременно по-малки от –5. Нека x1 е абсцисният връх на параболата y = f(x), x1 = - a, f(x1) = -4a2 - a, x2 е абсцисният връх y = g(x), x2 = 1/a,

g(x2) = -4/a + a – 2. Нека изпълним две условия едновременно: -4a2 - a > -5 (1) -4/a + a – 2> -5 (2)

или -4a2 - a<-5 (3), -4/а + а – 2<-5 (4). Для того, чтобы выполнить (1) и (2) одновременно или (3) и (4) одновременно достаточно решить неравенство (-4а2 - а+5)(-4/а + а – 2+5) >0,

и това неравенство е в сила за a<-4 или при-5/4<а<0.

Отговор:А<-4; -5/4<а<0.

Задача 9.Намерете най-малката и най-голямата стойност на функцията y = 2–ax –3x2 за -1≤х≤1.

Решение:

Тъй като старши коефициентът е -3<0, то ветви параболы направлены вниз и функция возрастает при х≤ хо и убывает при х≥хо, где хо =- b/2а - абсцисса вершины параболы. Результат в задаче зависит от положения абсциссы хо относительно отрезка [-1; 1], а не завсиит от знака дискриминанта. Выполним схематически рисунки (для D>0)

https://pandia.ru/text/78/525/images/image020_10.jpg" width="624" height="209 src=">

За всеки от трите случая a), b), c) най-малката стойност на функцията f(t) = t2-8at+7a2

върху сегмента се постига съответно в точки при x = 1, x = 2a, x = 1/4. Тогава въпросът, на който трябва да се отговори, е решението на набор от три системи:

1≤4a 1/4<4а<1 4а<1/4

е (1)<0 или f(4а)<0 или f(1/4)<0

a≥1/4 1/16<а<1/4 а≤1/16

1 – 8а + 7а2<0 или 16а2 – 32а2 + 7а2<0 или 1/16 – 2а + 7а2<0.

Отговор: 1/28<а<1.

Тестови задачи

1). При какви стойности на параметъра a графиките на функциите y = 2х – а и y = (а +1)х2 + 1 се пресичат само в една точка?

2). Намерете всички стойности на параметъра a, за които графиките на функциите y = (a +5)x2 – 1 и

y = (3a + 15)x – 4 нямат общи точки?

3). За какви стойности на параметъра a уравнението (a +4)x2 +6x –1 = 0 има единствено решение?

4). За какви стойности на параметъра a уравнението (2a + 8) x2 - (a + 4) x + 3 = 0 има уникално решение?

5). За какви стойности на параметъра a уравнението има повече от едно решение?

а) (a +6)x2 - 8x +a = 0

б) a(2a + 4) x2 – (a +2)x – 5a – 10 = 0.

6). Намерете всички стойности на параметъра k, за които кривата y = x2 + kx + 4 докосва оста x.

7). Защото най-малкото цяло число на параметъра k е квадратният трином

(k–2)x2+8x +k+4 е положителен за всички реални стойности на x?

8). Числата x, y, a са такива, че x + y = a –1, x2 + y2 = 5a2 – 3a + 0,5. При какви стойности на параметъра a продуктът xy приема максимална стойност?

9). Числата x, y, a са такива, че x + y = a +1, xy = a2 – 3a + 4. При какви стойности на параметъра

и сумата x2 + y2 приема най-голяма стойност?

10). Намерете най-голямата и 1 най-малка стойност на функцията y = 2x2 – 2ax + върху отсечката

единадесет). Намерете най-голямата стойност на квадратния трином 1–(a–2)x –x2 на отсечката

12). При какви стойности на параметъра a най-малката стойност на функцията y = x2 + (a + 4) x + 2a + 3 на сегмента е равна на -4?

13). При какви стойности на параметъра a най-малката стойност на функцията y \u003d x2 - (a + 2) x + a2 на сегмента [-1; 1] е равна на 4?

14). При какви стойности на параметъра a е най-голямата стойност на функцията?

f(х) = -(1/а)х +(7/а) ·3-х – 3а2 на отсечката [-1;0] отрицателно?

Отговори на тестовата задача

1) a=-2, a=-1, a=0.

2) –19/3<а≤-5.

3) a=-4, a=-13.

5) а) -8<а<-6 и -6<а<2

б) а=-2; -1/40 0.

10) Ако а<-2, то наименьшее значение функции при х=-1 и равно 3+2а, наибольшее значение функции при х=1 и равно 3–2а;

ако -2≤a<0, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=1 и равно 3–2а;

ако 0≤a<2, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=-1 и равно 3+2а;

ако a≥2, тогава най-малката стойност на функцията при x= 1 и равна на 3–2a, най-голямата стойност на функцията при x=-1 и равна на 3+2a;

11) Ако a≤0, тогава -6a2-a+2, ако е 0<а<8/5, то 2- 6а +а2/4, если а ≥8/5, то 19а-6а2 -14

13) a=-2 или a=(1+√21)/2

14) |a|>(7√3)/12.

Местоположение на корените на квадратния тричлен

Разгледайте редица типични проблеми, свързани с местоположението на корените на квадратния трином ax2 + bx + c. Ще извършим всички разсъждения, като приемем, че a>0. Ако<0,то рассуждения проводятся аналогично.

Задача No1.

При какви условия и двата корена на квадратното уравнение ax2+bx+c =0 (не непременно различни) са по-големи от дадено число k?

Решение.

Нека построим схематични графики на функцията на квадратен тричлен y= ax2+bx+c, където x1 и x2 отговарят на условията: x1>k, x2>k. Нека f(x)= ax2+bx+c. Графиката y= f(x) или пресича оста OX (D > 0), или я докосва (D = 0). Тогава е необходимо да се изпълни условието: xo>k, y(k) >0. Ако< 0 условие: х1>k, x2>k се определят от системата от неравенства:

https://pandia.ru/text/78/525/images/image023_20.gif" width="14" height="86">

Фиг.4

Задача 11.Намерете всички стойности на параметъра a, за които всички корени на уравнението

x2–6ax+2–2a+9a2 =0 повече от 3.

Решение.

Ако изискваното условие е изпълнено, са възможни следните позиции на параболата, която е графиката на функцията f(x) = x2–6ax+2–2a+9a2

Фиг.5

Да решим системата от неравенства:

https://pandia.ru/text/78/525/images/image026_8.jpg" align="left" width="324" height="239 src=">

Достатъчно е да се изпълни условието: y(k)<0, если а >0.На а<0, y(к) > 0.

Ориз. 6

Задача 12.Намерете всички стойности на параметъра a, за които 1 е между корените на уравнението x2–2ax+3–4a+2a2=0.

Решение.

Тъй като водещият коефициент е положителен, достатъчно е да се изпълни условието f(1)<0, где f(х)=х2–2ах+3–4а+2а2

4–6а+2а2<0, 1<а<2.

Отговор: 1<а<2

Задача No3.При какви условия точно един корен на квадратното уравнение ax2 + bx + c = 0, което има различни корени, лежи на интервала (k, e)?

Нека да изградим схематично графики y = ax2 + bx + c според условията на тази задача за a > 0.

https://pandia.ru/text/78/525/images/image028_8.jpg" width="623" height="246 src=">

Нека решим неравенството: f(1) f(2)<0.

(a2+8a+7)(a2+14a+16)<0

7-√33< а<-7; -7+√33<а<-1.

Отговор: -7-√33< а<-7; -7+√33<а<-1.

Задача 14.Намерете всички стойности на параметъра a, за които уравнението 2cos(2x)+2asin(x)+a-1=0 има уникално решение в интервала (-π/2;0).

Решение.

2cos(2x)+2a sinx+a-1=0

2(1–2 sin2x)+ 2a sinx+a–1=0

4 sin2х–2а sinx –a–1=0

Нека sinx=t, защото -π/2<х<0, то -1< t <0

Намерете онези стойности на параметъра a, за които уравнението 4t2– 2at–a–1=0 има единствено решение в интервала (-1; 0).

Уравнението 4t2– 2at–a–1=0 има уникално решение на интервала (-1;0), ако:

1). D =0 D/4=(a+2)2 D =0 за a=-2.

2). Да разгледаме функцията f(t)= 4t2– 2at–a–1

Нека построим схематична графика на функцията y=f(t)

https://pandia.ru/text/78/525/images/image030_16.gif" width="14" height="50 src=">

f(0) f(1) ≤0 а≤-3; а≥-1

Отговор:а≤-3; а≥-1; а=-2.

Задача No4.При какви условия и двата корена (не непременно различни) на квадратното уравнение ax2+bx+c лежат на отсечката [k; д]. Нека разгледаме условието a>0. Нека има функция f(x)= ax2+bx+c

https://pandia.ru/text/78/525/images/image032_14.gif" width="14" height="110"> D≥0

k≤ xo≤ e

Задача 15. Намерете тези стойности на параметъра a, за които всички корени на уравнението

x2- 2(a–3)x–a +3=0 лежат в интервала (-3;0).

Решение.

При условие, че съществува поне един корен, графиката на функцията f (x) \u003d x2- 2 (a-3) x-a + 3 може да бъде схематично разположена по един от двата начина

https://pandia.ru/text/78/525/images/image034_12.gif" width="14" height="110"> D≥0 4(a – 3)(a – 2) ≥0

3<хо<0 3<а – 3 <0 1,2<а≤2.

f(-3) >0 5a – 6>0

f(0) >0 -а+3>0

Уравнението е sin x − 1 + a = sin x − 2. sin x − 2 sin x − 3 Решение. Ако приемем, че t = sin x, редуцираме уравнението до формата at2 − 5at + 6a − 1 = 0. Ако a = 0, тогава няма решения. За a = 0 и при условие a ∈ (−∞; −4] ∪ (0; +∞) √ получаваме корените на уравнението t1,2 = 5a ± 2aa. Тъй като върхът на параболата f (t) = at2 − 5at + 6a − 1 се намира в точката tв = 2, 5 условие |t| 1 за по-малкия от корените ще бъде изпълнено, ако в краищата на отсечката [−1; 1] функцията има различни знаци : f (−1) f (1) 0 или (2a−1)(12a−1) 0. Решението на последното 1 неравенство е интервалът a ∈ 12 ;1 .2 √ a2 Отговор: Ако a ∈ 12 ; 2: x = (−1)n arcsin 5a− 2a +4a +πn, n∈Z, 1 1 за други a няма решения Задача 6.7 За какви стойности на параметъра a е функцията f (x) = 8ax − a sin 6x − 7x − sin 5x нараства по цялата ос на реалните числа и няма критични точки? Решение: Функцията f (x) е диференцируема за всяка стойност на a и f (x) = 8a − 6a cos 6x − 7 − 5 cos 5x Задачата може да се преформулира по следния начин: за какво е неравенството 6a cos 6x + 5 cos 5x< 8a − 7 справедливо для любого x? Так как последнее неравенство должно выполняться для любого значения x, оно должно быть справедливо и для x = 0, от- куда 6a + 5 < 8a − 7 или a >6. Имайки предвид сега, че 6a cos 6x + 5 cos 5x 6|a| + 5< 8a − 7, приходим к выводу, что при a >6 неравенството е валидно за всяко x. Отговор: а > 6. Задачи за независимо решениеЗадача 6.8. (SGAU) В зависимост от стойностите на параметъра a, решете уравнението cos4 x − (a + 2) cos2 x √ a − 3 = 0. − Отговор: Ако a ∈ [−3; −2] : x = arccos a + 3 + πk, k ∈ Z, ако a ∈ [−3; −2] : няма решения. Задача 6.9. (SGAU) В зависимост от стойностите на параметъра a, решете уравнението sin4 x + cos4 x + sin 2x + a = 0. 61 √ Отговор: Ако a ∈ − 3 ; 2: x = 1 (−1)k arcsin(1− 2a−3) + πk, 2 1 2 3 ; 1: няма решения. ако a ∈ − 2 2 k ∈ Z, задача 6.10. (SGAU) За какви стойности на параметъра a се прилага уравнението (a2 +8a+16)(2−2 cos x− sin2 x)+(32+2a2 +16a)(cos x−1)+3a+10 =0 решения? Отговор: а< − 10 ; −3 < a < −2. 3 Задача 6.11. (СГАУ) При каких значениях параметра a урав- нение loga−2 17 + cos x − sin x = 3 8 имеет решение? √ 2 3 Ответ: a ∈ 2 5 ; 3 ∪ 3; 2 + 26 . 2 Задача 6.12. (СГАУ) При каких значениях параметра a урав- нение loga+1 25 + cos x − 2 sin x = 3 8 2 имеет решение? √3 37 Ответ: a ∈ − 1 ; 0 ∪ 0; 2 − 1 . 2 Задача 6.13. (ЕГЭ) При каких значениях параметра a значение выражения 2+cos x·(3 cos x+a sin x) не равно нулю ни при каких значениях x? √ √ Ответ: a ∈ −2 10; 2 10 . Задача 6.14. (ЕГЭ) При каких значениях параметра a значение выражения 3 + sin x · (2 sin x + a cos x) будет равно −1 хотя бы при одном значении x? √ √ Ответ: a ∈ −∞; −4 6 ∪ 4 6; +∞ . Задача 6.15. (ЕГЭ) При каких значениях параметра a сумма loga (sin x + 2) и loga (sin x + 3) будет равна единице хотя бы при одном значении x? Ответ: a ∈ [ 2; 12 ]. Задача 6.16. (СГАУ) При каких значениях параметра α систе- ма 4 sin x · sin y · cos(x + y) − 0,5 = 0 x−y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. 62 Ответ: Если α = 2πn: x = ±π 6 + π(k+n) π y = ±6 + π(k−n); если α = π+2πn: x = ±π 3 + π + π(k+n) 2 y = ±π 3 − π + π(k−n), 2 n, k ∈ Z. Задача 6.17. (СГАУ) При каких значениях параметра α систе- ма 2 sin x · cos y · sin(x − y) + 0,25 = 0 x+y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. Ответ: Если α = π +2πn: x = (−1)k+1 π + π + π (2n+k) 2 12 4 2 k π + π + π (2n−k); y = (−1) 12 4 2 если α = − 2 π +2πn: x = (−1)k π − π + π (2n+k) 12 4 2 y = (−1) k+1 π − π + π (2n−k), 12 4 2 n, k ∈ Z. Задача 6.18. (СГАУ) При каких значениях параметра a нера- венство √ 2 2 (sin x − cos x) − a + 7 log 2a+34 15 <0 35 выполняется для любых значений x? 1 Ответ: a ∈ (−17; −12) ∪ 2 ; 3 . Задача 6.19. (СГАУ) При каких значениях параметра a нера- венство √ log 3−2a 3 sin x + 3 3 cos x − 2a − 12 >0 23 28 важи за всякакви стойности на x? Отговор: a ∈ (−∞; −23) ∪ (−10; −9). Задача 6.20. В зависимост от стойностите на параметъра a, решете неравенството cos x 2 − a2. Отговор: |a| √ : x ∈ R, 1 1<|a| √3: x ∈ arccos(2−a2)+2πk; π− arccos(2−a2)+2πk , |a|>3: няма решения. k∈Z Задача 6.21. За какви стойности на параметъра a уравнението tan x (a + 1) tan2 x − 2 cos x + a = 0 няма решения? Отговор: a −3; 1,63 УрокПРОБЛЕМИ С ПАРАМЕТРИ Съставител: Ефимов Евгений Александрович Коломиец Людмила Вадимовна Компютърно въвеждане и оформление E.A. Ефимов Самарски държавен аерокосмически университет на името на академик S.P. кралица. 443086, Самара, Московско шосе, 34. – RIO Самарски държавен аерокосмически университет на името на академик S.P. кралица. 443086, Самара, Московско шосе, 34.

1. Задача.
При какви стойности на параметрите ауравнението ( а - 1)х 2 + 2х + а- 1 = 0 има ли точно един корен?

1. Решение.
При а= 1 уравнението е 2 х= 0 и очевидно има един корен х= 0. Ако а№ 1, тогава това уравнение е квадратно и има един корен за тези стойности на параметрите, за които дискриминантът на квадратния трином нула. Приравнявайки дискриминанта на нула, получаваме уравнение за параметъра а 4а 2 - 8а= 0, откъдето а= 0 или а = 2.

1. Отговор:уравнението има един корен при аО (0; 1; 2).

2. Задача.
Намерете всички стойности на параметрите а, за което уравнението има два различни корена х 2 +4брадва+8а+3 = 0.
2. Разтвор.
Уравнението х 2 +4брадва+8а+3 = 0 има два различни корена тогава и само ако д = 16а 2 -4(8а+3) > 0. Получаваме (след намаляване с общ множител 4) 4 а 2 -8а-3 > 0, откъдето

2. Отговор:

а O (-Ґ ; 1 –

Ts 7 2

) И (1 +

Ts 7 2

; Ґ ).

3. Задача.
Известно е, че
f 2 (х) = 6х-х 2 -6.
а) Графика на функцията f 1 (х) при а = 1.
б) На каква стойност афункционални графики f 1 (х) И f 2 (х) имат една обща точка?

3. Разтвор.
3.а.Да се ​​трансформираме f 1 (х) по следния начин
Графиката на тази функция при а= 1 е показано на фигурата вдясно.
3.б.Нека веднага да отбележим, че графиките на функциите г = kx+bИ г = брадва 2 +bx+° С (а№ 0) се пресичат в една точка тогава и само ако квадратно уравнение kx+b = брадва 2 +bx+° Сима един корен. Използване на View f 1 от 3.а, нека приравним дискриминанта на уравнението а = 6х-х 2-6 на нула. От уравнение 36-24-4 а= 0 получаваме а= 3. Направете същото с уравнение 2 х-а = 6х-х 2 -6 ще намерим а= 2. Лесно е да се провери дали тези стойности на параметрите отговарят на условията на проблема. Отговор: а= 2 или а = 3.

4. Задача.
Намерете всички стойности а, за които множеството от решения на неравенството х 2 -2брадва-3а i 0 съдържа сегмента.

4. Разтвор.
Първа координата на върха на параболата f(х) = х 2 -2брадва-3аравна на х 0 = а. От свойствата на квадратична функция условието f(х) i 0 на сегмента е еквивалентен на набор от три системи
има точно две решения?

5. Разтвор.
Нека пренапишем това уравнение във формата х 2 + (2а-2)х - 3а+7 = 0. Това е квадратно уравнение, то има точно две решения, ако неговият дискриминант е строго по-голям от нула. Изчислявайки дискриминанта, установяваме, че условието за наличието на точно два корена е изпълнението на неравенството а 2 +а-6 > 0. Решавайки неравенството, намираме а < -3 или а> 2. Първото от неравенствата очевидно е решения в естествени числаняма, а най-малкото естествено решение на второто е числото 3.

5. Отговор: 3.

6. Проблем (10 ключа)
Намерете всички стойности а, за която графиката на функцията или, след очевидни трансформации, а-2 = | 2-а| . Последното уравнение е еквивалентно на неравенството ааз 2.

6. Отговор: аОТНОСНО )