Predavanja iz Teorijske mehanike
Dinamika točke
Predavanje 1
Osnovni pojmovi dinamike
U poglavlju Dinamika proučava se kretanje tijela pod djelovanjem sila koje na njih djeluju. Stoga, uz one pojmove koji su uvedeni u odjeljku Kinematika, ovdje je potrebno koristiti nove pojmove koji odražavaju specifičnosti utjecaja sila na razna tijela te reakcija tijela na te utjecaje. Razmotrimo glavne od ovih koncepata.
a) snaga
Sila je kvantitativni rezultat utjecaja drugih tijela na određeno tijelo. Sila je vektorska veličina (slika 1).
![]()
![]()
Točka A početka vektora sile F nazvao točka primjene sile. Pravac MN na kojem se nalazi vektor sile naziva se linija sile. Duljina vektora sile, mjerena u određenom mjerilu, naziva se brojčana vrijednost ili modul vektora sile. Modul sile se označava kao ili . Djelovanje sile na tijelo očituje se ili u njegovoj deformaciji, ako tijelo miruje, ili u pridavanju ubrzanja pri gibanju tijela. Na tim manifestacijama sile temelji se uređaj raznih instrumenata (silometara ili dinamometra) za mjerenje sila.
b) sustav sila
Razmatrani skup sila čini sustav sila. Bilo koji sustav koji se sastoji od n sila može se napisati u sljedećem obliku: ![]()
c) slobodno tijelo
Tijelo koje se može kretati u prostoru u bilo kojem smjeru bez izravnog (mehaničkog) međudjelovanja s drugim tijelima naziva se besplatno ili izolirani. Utjecaj jednog ili drugog sustava sila na tijelo može se razjasniti samo ako je to tijelo slobodno.
d) rezultantna sila
Ako bilo koja sila djeluje na slobodno tijelo jednako kao neki sustav sila, tada se ta sila naziva rezultanta ovog sustava sila. Ovo je napisano na sljedeći način:
![]() ,
,
što znači jednakovrijednost utjecaj na isto slobodno tijelo rezultante i nekog sustava n sila.
Prijeđimo sada na razmatranje složenijih koncepata koji se odnose na kvantitativno određivanje rotacijskih učinaka sila.
e) moment sile u odnosu na točku (središte)
Ako se tijelo pod utjecajem sile može okretati oko neke fiksna točka O (sl. 2), tada se za kvantitativnu procjenu ovog rotacijskog učinka uvodi fizikalna veličina koja se naziva moment sile oko točke (središta).

Zove se ravnina koja prolazi kroz zadanu fiksnu točku i pravac djelovanja sile ravnina sile. Na slici 2 to je ravnina OAV.
Moment sile u odnosu na točku (središte) je vektorska veličina jednaka vektorskom umnošku radijus vektora točke primjene sile i vektora sile:
![]() ( 1)
( 1)
Prema pravilu vektorskog množenja dva vektora, njihov vektorski umnožak je vektor okomit na ravninu položaja faktor vektora (u ovom slučaju ravninu trokuta OAB), usmjeren u smjeru iz kojeg polazi najkraći zavoj prvog faktorskog vektora drugom faktorskom vektoru vidljivo naspram sata (slika 2). S ovim redoslijedom vektora faktora umnoška (1), rotacija tijela pod djelovanjem sile bit će vidljiva u odnosu na sat (slika 2). Budući da je vektor okomit na ravninu sile , njegov položaj u prostoru određuje položaj ravnine sile Brojčana vrijednost vektora momenta sile u odnosu na središte jednaka je dvostrukoj površini OAV i može se odrediti formulom:
![]() ,
(2)
,
(2)
Gdje veličinah, jednaka najkraćoj udaljenosti od zadane točke O do linije djelovanja sile, naziva se krak sile.
Ako položaj ravnine djelovanja sile u prostoru nije bitan za karakterizaciju rotacijskog djelovanja sile, tada se u ovom slučaju za karakterizaciju rotacijskog djelovanja sile, umjesto vektora momenta sile, koristi vektor momenta sile. algebarski moment sile:
![]() (3)
(3)
Algebarski moment sile u odnosu na dano središte jednak je umnošku modula sile i njezinog ramena, uzetog s predznakom plus ili minus. U tom slučaju pozitivni moment odgovara rotaciji tijela pod djelovanjem zadane sile protiv sata, a negativni moment odgovara rotaciji tijela u smjeru sata. Iz formula (1), (2) i (3) slijedi da moment sile oko točke nula samo ako rame ove silehnula. Takva sila ne može rotirati tijelo oko zadane točke.
f) Moment sile oko osi
Ako se tijelo pod utjecajem sile može okretati oko neke fiksna osovina(na primjer, rotacija okvira vrata ili prozora u šarkama kada se otvaraju ili zatvaraju), tada se uvodi fizička veličina za kvantificiranje ovog rotacijskog učinka, koji se naziva moment sile oko date osi.
 z
z
b Fxy
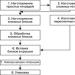
Slika 3 prikazuje dijagram prema kojem se određuje moment sile oko z-osi:
Kut tvore dva okomita pravca z i na ravnine trokuta O ab odnosno OAV. Od O ab je projekcija OAV na ravninu xy, tada prema stereometrijskom teoremu o projekciji ravnog lika na zadanu ravninu imamo:
gdje znak plus odgovara pozitivnoj vrijednosti cos, tj. oštri kutovi, a znak minus odgovara negativnoj vrijednosti cos, tj. tupim kutovima , zbog smjera vektora . Zauzvrat, SO ab=1/2abh, Gdje h ab . Vrijednost segmenta ab jednaka je projekciji sile na xy ravninu, tj. . ab = F xy .
Na temelju prethodnog, kao i jednakosti (4) i (5), određujemo moment sile oko z-osi na sljedeći način:
Jednakost (6) nam omogućuje da formuliramo sljedeću definiciju momenta sile oko bilo koje osi: Moment sile oko dane osi jednak je projekciji na tu os vektora momenta te sile u odnosu na bilo koju točku zadanu os i definira se kao umnožak projekcije sile na ravninu okomitu na zadanu os, uz znak plus ili minus na rubu te projekcije u odnosu na točku presjeka osi s ravninom projekcije. U ovom slučaju, znak trenutka se smatra pozitivnim ako je, gledajući iz pozitivnog smjera osi, rotacija tijela oko ove osi vidljiva u odnosu na sat. Inače se moment sile oko osi uzima kao negativan. Budući da je ovu definiciju momenta sile u odnosu na os prilično teško zapamtiti, preporuča se zapamtiti formulu (6) i sl. 3, koja objašnjava ovu formulu.
Iz formule (6) proizlazi da moment sile oko osi jednak je nuli ako paralelna je s osi (u ovom slučaju njezina projekcija na ravninu okomitu na os jednaka je nuli), ili pravac djelovanja sile siječe os (tada krak projekcije h=0). To u potpunosti odgovara fizičkom značenju momenta sile oko osi kao kvantitativnoj karakteristici rotacijskog djelovanja sile na tijelo s osi rotacije.
g) tjelesna težina
Odavno je uočeno da pod utjecajem sile tijelo postupno ubrzava i nastavlja se kretati ako se sila ukloni. Ovo svojstvo tijela, da se odupiru promjeni svoga gibanja, zvalo se tromost ili tromost tijela. Kvantitativna mjera tromosti tijela je njegova masa. Osim, masa tijela je kvantitativna mjera djelovanja gravitacijskih sila na određeno tijelo što je masa tijela veća, to na tijelo djeluje veća gravitacijska sila. Kao što će biti prikazano u nastavku, uh Ove dvije definicije tjelesne težine su povezane.
O drugim pojmovima i definicijama dinamike raspravljat ćemo kasnije u odjeljcima u kojima se prvi put pojavljuju.
2. Veze i reakcije veza
Ranije u odjeljku 1 točka (c) dan je koncept slobodnog tijela, kao tijela koje se može kretati u prostoru u bilo kojem smjeru, a da nije u izravnom kontaktu s drugim tijelima. Većina stvarnih tijela koja nas okružuju u izravnom su kontaktu s drugim tijelima i ne mogu se kretati u jednom ili drugom smjeru. Tako se, na primjer, tijela koja se nalaze na površini stola mogu kretati u bilo kojem smjeru, osim u smjeru okomitom na površinu stola prema dolje. Vrata na šarkama mogu se okretati, ali se ne mogu kretati naprijed itd. Tijela koja se ne mogu kretati u prostoru u jednom ili drugom smjeru nazivamo nije besplatno.
Sve što ograničava kretanje određenog tijela u prostoru naziva se vezama. To mogu biti neka druga tijela koja sprječavaju kretanje ovog tijela u nekim smjerovima ( fizičke veze); šire, to mogu biti neki uvjeti nametnuti kretanju tijela, ograničavajući to kretanje. Dakle, možete postaviti uvjet za kretanje materijalne točke duž zadane krivulje. U ovom slučaju, veza je određena matematički u obliku jednadžbe ( jednadžba veze). U nastavku ćemo detaljnije razmotriti pitanje vrsta poveznica.
Većina veza nametnutih tijelima praktički su fizičke veze. Stoga se postavlja pitanje međudjelovanja danog tijela i veze koja je nametnuta tom tijelu. Na ovo pitanje odgovara aksiom o međudjelovanju tijela: Dva tijela djeluju jedno na drugo jednakim silama, suprotnog smjera i smještena na istoj ravnoj liniji. Te se sile nazivaju interakcijskim silama. Sile međudjelovanja djeluju na različita tijela koja međusobno djeluju. Tako npr. pri međudjelovanju zadanog tijela i spoja jedna od sila međudjelovanja djeluje sa strane tijela na spoj, a druga sila interakcije djeluje sa strane spoja na zadano tijelo . Ova zadnja moć zove se sila reakcije veze ili jednostavno, reakcija veze.
Pri rješavanju praktičnih problema dinamike potrebno je znati pronaći smjer reakcija različite vrste veze. U tome ponekad može pomoći opće pravilo za određivanje smjera reakcije veze: Reakcija veze uvijek je usmjerena suprotno od smjera u kojem ta veza sprječava kretanje određenog tijela. Ako se ovaj smjer može odrediti definitivno, tada će reakcija veze biti određena smjerom. Inače, smjer reakcije veze je neodređen i može se pronaći samo iz odgovarajućih jednadžbi gibanja ili ravnoteže tijela. Detaljnije, pitanje vrsta veza i smjera njihovih reakcija treba proučiti prema udžbeniku: S.M. Targ Kratki tečaj teorijske mehanike "Viša škola", M., 1986. Poglavlje 1, §3.
U odjeljku 1. točki (c) rečeno je da se učinak bilo kojeg sustava sila može u potpunosti odrediti samo ako se taj sustav sila primijeni na slobodno tijelo. Budući da većina tijela zapravo nije slobodna, onda se za proučavanje kretanja tih tijela postavlja pitanje kako ta tijela učiniti slobodnima. Na ovo pitanje je odgovoreno aksiom povezanosti predavanja Po filozofija kod kuće. Predavanja bili... socijalna psihologija i etnopsihologije. 3. Teorijski Rezultati socijalnog darvinizma bili su ...
teoretski Mehanika
Udžbenik >> FizikaSažetak predavanja Po subjekt TEORIJSKI MEHANIKA Za studente specijalnosti: 260501,65 ... - redoviti Sažetak predavanja sastavljeno na temelju: Butorin L.V., Busygina E.B. teoretski Mehanika. Edukativno-praktični vodič...
Pogled: ovaj članak je pročitan 32852 puta
Pdf Odaberite jezik... Ruski Ukrajinski Engleski
Cijeli materijal se preuzima iznad, nakon odabira jezika
- Statika
- Osnovni pojmovi statike
- Vrste sila
- Aksiomi statike
- Veze i njihove reakcije
- Sustav konvergentnih sila
- Metode određivanja rezultantnog sustava konvergentnih sila
- Uvjeti ravnoteže sustava konvergentnih sila
- Moment sile oko središta kao vektor
- Algebarska vrijednost momenta sile
- Svojstva momenta sile oko središta (točke)
- Teorija parova sila
- Zbrajanje dviju paralelnih sila u istom smjeru
- Zbrajanje dviju paralelnih sila usmjerenih u suprotnim smjerovima
- Parovi snage
- Nekoliko teorema o silama
- Uvjeti ravnoteže sustava parova sila
- Ruka poluge
- Proizvoljni ravninski sustav sila
- Slučajevi svođenja ravnog sustava sila na jednostavniji oblik
- Analitički uvjeti ravnoteže
- Centar paralelnih sila. Centar gravitacije
- Centar paralelnih sila
- Težište krutog tijela i njegove koordinate
- Težište volumena, ravnine i pravci
- Metode određivanja položaja težišta
- Osnove trkača snage
- Problemi i metode otpornosti materijala
- Klasifikacija opterećenja
- Klasifikacija konstrukcijskih elemenata
- Deformacije štapa
- Glavne hipoteze i načela
- Unutarnje sile. Metoda presjeka
- napon
- Napetost i kompresija
- Mehanička svojstva materijala
- Dopuštena naprezanja
- Tvrdoća materijala
- Dijagrami uzdužnih sila i naprezanja
- Shift
- Geometrijske karakteristike presjeka
- Torzija
- saviti se
- Diferencijalne ovisnosti kod savijanja
- Čvrstoća na savijanje
- normalna naprezanja. Proračun čvrstoće
- Posmični naponi pri savijanju
- Krutost na savijanje
- Elementi opće teorije stanja naprezanja
- Teorije čvrstoće
- Savijanje s uvijanjem
- Kinematika
- Kinematika točke
- Putanja točke
- Metode zadavanja kretanja točke
- Brzina točke
- točkasto ubrzanje
- Kinematika krutog tijela
- Translatorno gibanje krutog tijela
- Rotacijsko gibanje krutog tijela
- Kinematika prijenosnih mehanizama
- Planparalelno gibanje krutog tijela
- Složeno kretanje točke
- Kinematika točke
- Dinamika
- Osnovni zakoni dinamike
- Dinamika točke
- Diferencijalne jednadžbe slobodnog materijalna točka
- Dva problema dinamike točke
- Dinamika krutog tijela
- Klasifikacija sila koje djeluju na mehanički sustav
- Diferencijalne jednadžbe gibanja mehaničkog sustava
- Opći teoremi dinamike
- Teorem o gibanju središta mase mehaničkog sustava
- Teorem o promjeni količine gibanja
- Teorem o promjeni kutne količine gibanja
- Teorem o promjeni kinetičke energije
- Sile koje djeluju u strojevima
- Sile u zahvatu čeličnog zupčanika
- Trenje u mehanizmima i strojevima
- Trenje klizanja
- trenje kotrljanja
- Učinkovitost
- Dijelovi strojeva
- Mehanički prijenosi
- Vrste mehaničkih prijenosnika
- Osnovni i izvedeni parametri mehaničkih prijenosnika
- zupčanici
- Zupčanici s fleksibilnim vezama
- Osovine
- Namjena i klasifikacija
- Projektni proračun
- Provjerite proračun osovina
- Ležajevi
- Klizni ležajevi
- Kotrljajući ležajevi
- Spajanje strojnih dijelova
- Vrste rastavljivih i nerastavljivih spojeva
- Spojevi s ključem
- Mehanički prijenosi
- Standardizacija normi, zamjenjivost
- Tolerancije i slijetanja
- jedan sustav tolerancije i slijetanja (ESDP)
- Odstupanje oblika i položaja
Format: pdf
Veličina: 4 MB
ruski jezik
Primjer proračuna čeonog zupčanika
Primjer proračuna čeonog zupčanika. Proveden je izbor materijala, proračun dopuštenih naprezanja, proračun kontaktne i savojne čvrstoće.
Primjer rješavanja problema savijanja grede
U primjeru su ucrtani dijagrami poprečnih sila i momenata savijanja, pronađen opasni presjek i odabrana I-nosača. U problemu se analizira konstrukcija dijagrama pomoću diferencijalnih ovisnosti, provodi se komparativna analiza različitih presjeka grede.
Primjer rješavanja problema torzije vratila
Zadatak je ispitati čvrstoću čelične osovine za zadani promjer, materijal i dopuštena naprezanja. Tijekom rješavanja izrađuju se dijagrami momenta, posmičnih naprezanja i kutova uvijanja. Vlastita težina osovine nije uzeta u obzir
Primjer rješavanja zadatka napetost-stlačenje štapa
Zadatak je ispitati čvrstoću čelične šipke pri zadanim dopuštenim naprezanjima. Tijekom rješavanja grade se krivulje uzdužnih sila, normalnih naprezanja i pomaka. Vlastita težina šipke se ne uzima u obzir
Primjena teorema o održanju kinetičke energije
Primjer rješavanja problema primjene teorema o očuvanju kinetičke energije mehaničkog sustava
Određivanje brzine i ubrzanja točke prema zadanim jednadžbama gibanja
Primjer rješavanja zadatka određivanja brzine i ubrzanja točke pomoću zadane jednadžbe pokreta
Određivanje brzina i ubrzanja točaka krutog tijela tijekom planparalelnog gibanja
Primjer rješavanja problema određivanja brzina i ubrzanja točaka krutog tijela tijekom planparalelnog gibanja
Određivanje sila u planarnim rešetkastim šipkama
Primjer rješavanja problema određivanja sila u šipkama ravne rešetke metodom Ritter i metodom rezanja čvorova
Teorijska mehanika je grana mehanike koja postavlja osnovne zakone mehaničko kretanje i mehaničko međudjelovanje materijalnih tijela.
Teorijska mehanika je znanost u kojoj se proučavaju gibanja tijela u vremenu (mehanička gibanja). Služi kao osnova za druge dijelove mehanike (teorija elastičnosti, otpor materijala, teorija plastičnosti, teorija mehanizama i strojeva, hidroaerodinamika) i mnoge tehničke discipline.
mehaničko kretanje- ovo je promjena tijekom vremena relativnog položaja materijalnih tijela u prostoru.
Mehanička interakcija- ovo je takva interakcija, uslijed koje se mijenja mehaničko kretanje ili se mijenja relativni položaj dijelova tijela.
Statika krutog tijela
Statika- To je grana teorijske mehanike, koja se bavi problemima ravnoteže čvrstih tijela i transformacije jednog sustava sila u drugi, njemu ekvivalentan.
- Osnovni pojmovi i zakoni statike
- Apsolutno čvrsta (čvrsto tijelo, tijelo) je materijalno tijelo, udaljenost između bilo koje točke u kojem se ne mijenja.
- Materijalna točka je tijelo čije se dimenzije, prema uvjetima zadatka, mogu zanemariti.
- labavo tijelo je tijelo čije kretanje nema ograničenja.
- Neslobodno (vezano) tijelo je tijelo čije je kretanje ograničeno.
- Veze- to su tijela koja sprječavaju kretanje predmeta koji se razmatra (tijelo ili sustav tijela).
- Reakcija komunikacije je sila koja karakterizira djelovanje veze na kruto tijelo. Ako silu kojom kruto tijelo djeluje na vezu smatramo djelovanjem, tada je reakcija veze protudjelstvo. U ovom slučaju sila - djelovanje djeluje na spoj, a reakcija spoja na čvrsto tijelo.
- mehanički sustav je skup međusobno povezanih tijela ili materijalnih točaka.
- Čvrsto može se smatrati mehaničkim sustavom čiji se položaji i udaljenosti između točaka ne mijenjaju.
- Sila je vektorska veličina koja karakterizira mehaničko djelovanje jednog materijalnog tijela na drugo.
Silu kao vektor karakterizira točka primjene, smjer djelovanja i apsolutna vrijednost. Jedinica mjere za modul sile je Newton. - linija sile je pravac duž kojeg je usmjeren vektor sile.
- Koncentrirana moć je sila primijenjena u jednoj točki.
- Distribuirane sile (raspodijeljeno opterećenje)- to su sile koje djeluju na sve točke volumena, površine ili dužine tijela.
Raspodijeljeno opterećenje dano je silom koja djeluje po jedinici volumena (površina, duljina).
Dimenzija raspodijeljenog opterećenja je N / m 3 (N / m 2, N / m). - Vanjska sila je sila koja djeluje iz tijela koje ne pripada razmatranom mehaničkom sustavu.
- unutarnja snaga je sila koja djeluje na materijalnu točku mehaničkog sustava iz druge materijalne točke koja pripada sustavu koji se razmatra.
- Sustav sila je ukupnost sila koje djeluju na mehanički sustav.
- Ravni sustav sila je sustav sila čije linije djelovanja leže u istoj ravnini.
- Prostorni sustav sila je sustav sila čiji pravci djelovanja ne leže u istoj ravnini.
- Sustav konvergentnih sila je sustav sila čije se linije djelovanja sijeku u jednoj točki.
- Proizvoljni sustav sila je sustav sila čije se linije djelovanja ne sijeku u jednoj točki.
- Ekvivalentni sustavi sila- to su sustavi sila čija zamjena jedne za drugu ne mijenja mehaničko stanje tijela.
Prihvaćena oznaka: . - Ravnoteža Stanje u kojem tijelo miruje ili se giba jednoliko pravocrtno pod djelovanjem sila.
- Uravnoteženi sustav sila- to je sustav sila koji djelovanjem na slobodno čvrsto tijelo ne mijenja njegovo mehaničko stanje (ne dovodi ga u ravnotežu).
 .
. - rezultantna sila je sila čije je djelovanje na tijelo ekvivalentno djelovanju sustava sila.
 .
. - Trenutak moći je vrijednost koja karakterizira rotacionu sposobnost sile.
- Snažni par je sustav dviju paralelno jednakih po apsolutnoj vrijednosti suprotno usmjerenih sila.
Prihvaćena oznaka: .
Pod djelovanjem par sila tijelo će izvršiti rotacijsko gibanje. - Projekcija sile na os- ovo je segment zatvoren između okomica povučenih od početka i kraja vektora sile na ovu os.
Projekcija je pozitivna ako se smjer segmenta poklapa s pozitivnim smjerom osi. - Projekcija sile na ravninu je vektor na ravnini zatvorenoj između okomica povučenih s početka i kraja vektora sile na tu ravninu.
- Zakon 1 (zakon inercije). Izolirana materijalna točka miruje ili se giba jednoliko i pravocrtno.
Jednoliko i pravocrtno gibanje materijalne točke je gibanje po inerciji. Stanje ravnoteže materijalne točke i krutog tijela shvaća se ne samo kao stanje mirovanja, već i kao gibanje po inerciji. Za kruto tijelo postoje različite vrste gibanja po inerciji, na primjer jednolika rotacija krutog tijela oko nepomične osi. - Zakon 2. Kruto tijelo je u ravnoteži pod djelovanjem dviju sila samo ako su te sile jednake po veličini i usmjerene u suprotnim smjerovima duž zajedničke linije djelovanja.
Ove dvije sile se nazivaju uravnotežene.
Općenito se kaže da su sile uravnotežene ako kruto tijelo na koje te sile djeluju miruje. - Zakon 3. Bez narušavanja stanja (riječ "stanje" ovdje označava stanje gibanja ili mirovanja) krutog tijela, mogu se dodavati i odbacivati sile ravnoteže.
Posljedica. Bez narušavanja stanja krutog tijela, sila se može prenijeti duž njegove linije djelovanja na bilo koju točku tijela.
Dva sustava sila nazivaju se ekvivalentnima ako se jedan od njih može zamijeniti drugim bez narušavanja stanja krutog tijela. - Zakon 4. Rezultanta dviju sila koje djeluju na jednu točku djeluje na istu točku, jednaka je u apsolutnoj vrijednosti dijagonali paralelograma izgrađenog na tim silama i usmjerena je duž ove
dijagonale.
Modul rezultante je: - Zakon 5 (zakon jednakosti akcije i reakcije). Sile kojima dva tijela djeluju jedno na drugo jednake su veličine i usmjerene u suprotnim smjerovima duž jedne ravne crte.
Treba imati na umu da akcijski- sila primijenjena na tijelo B, I protivljenje- sila primijenjena na tijelo A, nisu uravnoteženi, jer su pričvršćeni za različita tijela. - Zakon 6 (zakon otvrdnjavanja). Ravnoteža nečvrstog tijela nije poremećena kada se skrutne.
Ne treba zaboraviti da su uvjeti ravnoteže, koji su nužni i dovoljni za kruto tijelo, nužni, ali ne i dovoljni za odgovarajuće nekruto tijelo. - Zakon 7 (zakon oslobađanja od obveznica). Neslobodno čvrsto tijelo može se smatrati slobodnim ako je mentalno oslobođeno veza, zamjenjujući djelovanje veza odgovarajućim reakcijama veza.
- Veze i njihove reakcije
- Glatka površina ograničava kretanje po normali na površinu oslonca. Reakcija je usmjerena okomito na površinu.
- Zglobni pokretni nosač ograničava kretanje tijela po normali na referentnu ravninu. Reakcija je usmjerena duž normale na površinu nosača.
- Zglobni fiksni nosač suprotstavlja se svakom gibanju u ravnini okomitoj na os rotacije.
- Zglobni bestežinski štap suprotstavlja se kretanju tijela duž linije štapa. Reakcija će biti usmjerena duž linije štapa.
- Slijepi prekid suprotstavlja se svakom kretanju i rotaciji u ravnini. Njegovo djelovanje može se zamijeniti silom predstavljenom u obliku dvije komponente i para sila s momentom.




Kinematika
Kinematika- odjeljak teorijske mehanike, koji razmatra opća geometrijska svojstva mehaničkog gibanja, kao procesa koji se odvija u prostoru i vremenu. Objekti koji se kreću smatraju se geometrijskim točkama ili geometrijskim tijelima.
- Osnovni pojmovi kinematike
- Zakon gibanja točke (tijela) je ovisnost položaja točke (tijela) u prostoru o vremenu.
- Putanja točke je geometrijsko mjesto položaja točke u prostoru tijekom njezina kretanja.
- Brzina točke (tijela).- ovo je karakteristika promjene u vremenu položaja točke (tijela) u prostoru.
- Ubrzanje točke (tijela).- ovo je karakteristika promjene brzine točke (tijela) u vremenu.
- Određivanje kinematičkih karakteristika točke
- Putanja točke
U vektorskom referentnom sustavu trajektorija je opisana izrazom: .
U koordinatnom referentnom sustavu putanja je određena prema zakonu gibanja točke i opisana je izrazima z = f(x,y) u prostoru, odn y = f(x)- u avionu.
U prirodnom referentnom sustavu putanja je unaprijed određena. - Određivanje brzine točke u vektorskom koordinatnom sustavu
Pri određivanju gibanja točke u vektorskom koordinatnom sustavu omjer gibanja i vremenskog intervala naziva se prosječna vrijednost brzine u tom vremenskom intervalu: .
Uzimajući vremenski interval kao infinitezimalnu vrijednost, dobivamo vrijednost brzine u danom trenutku (trenutačna vrijednost brzine): .
.
Vektor prosječne brzine usmjeren je duž vektora u smjeru kretanja točke, vektor trenutna brzina usmjerena tangencijalno na putanju u smjeru kretanja točke.
Zaključak: brzina točke je vektorska veličina jednaka derivaciji zakona gibanja s obzirom na vrijeme.
Izvedeno svojstvo: vremenska derivacija bilo koje vrijednosti određuje brzinu promjene ove vrijednosti. - Određivanje brzine točke u koordinatnom referentnom sustavu
Stopa promjene koordinata točke: .
.
Modul pune brzine točke s pravokutnim koordinatnim sustavom bit će jednak: .
.
Smjer vektora brzine određen je kosinusima kutova upravljanja: ,
,
gdje su kutovi između vektora brzine i koordinatnih osi. - Određivanje brzine točke u prirodnom referentnom sustavu
Brzina točke u prirodnom referentnom sustavu definirana je kao derivacija zakona gibanja točke: .
Prema prethodnim zaključcima, vektor brzine usmjeren je tangencijalno na putanju u smjeru kretanja točke i u osi je određen samo jednom projekcijom.
- Kinematika krutog tijela
- U kinematici krutih tijela rješavaju se dva glavna problema:
1) zadatak kretanja i određivanje kinematičkih karakteristika tijela u cjelini;
2) određivanje kinematičkih karakteristika točaka tijela. - Translatorno gibanje krutog tijela
Translatorno gibanje je gibanje pri kojem pravac povučen kroz dvije točke tijela ostaje paralelan sa svojim prvobitnim položajem.
Teorema: kod translatornog gibanja sve točke tijela gibaju se istim putanjama i u svakom trenutku imaju istu brzinu i akceleraciju po apsolutnoj vrijednosti i smjeru.
Zaključak: translatorno gibanje krutog tijela određeno je gibanjem bilo koje njegove točke, pa se stoga zadatak i proučavanje njegovog gibanja svodi na kinematiku točke. - Rotacijsko gibanje krutog tijela oko nepomične osi
Rotacijsko gibanje krutog tijela oko nepomične osi je gibanje krutog tijela kod kojeg dvije točke koje pripadaju tijelu ostaju nepomične za cijelo vrijeme gibanja.
Položaj tijela određen je kutom zakreta. Mjerna jedinica za kut je radijan. (radijan - središnji kut kružnica čija je duljina luka jednaka polumjeru, sadrži ukupni kut kružnice 2π radijan.)
Zakon rotacijskog gibanja tijela oko nepomične osi.
kutna brzina i kutno ubrzanje tijela su definirana metodom diferenciranja:
— kutna brzina, rad/s;
— kutno ubrzanje, rad/s².
Ako tijelo presječemo ravninom okomitom na os, izaberemo točku na osi rotacije S i proizvoljna točka M, onda točka M opisat će oko točke S polumjer kruga R. Tijekom dt postoji elementarna rotacija kroz kut , dok je točka M kretat će se duž putanje za udaljenost .
.
Modul linearne brzine: .
.
točkasto ubrzanje M s poznatom putanjom određuju njegove komponente: ,
,
Gdje .
.
Kao rezultat toga dobivamo formule
tangencijalno ubrzanje: ;
;
normalno ubrzanje: .
.

Dinamika
Dinamika- Ovo je grana teorijske mehanike, koja proučava mehanička gibanja materijalnih tijela, ovisno o uzrocima koji ih uzrokuju.
- Osnovni pojmovi dinamike
- inercija je svojstvo materijalnih tijela da održavaju stanje mirovanja ili uniformnosti pravocrtno gibanje dok vanjske sile ne promijene ovo stanje.
- Težina je kvantitativna mjera tromosti tijela. Jedinica mase je kilogram (kg).
- Materijalna točka je tijelo s masom čije se dimenzije zanemaruju pri rješavanju ovog problema.
- Središte mase mehaničkog sustava — geometrijska točka, čije su koordinate određene formulama:
Gdje m k , x k , y k , z k- masa i koordinate k- ta točka mehaničkog sustava, m je masa sustava.
U jednoličnom gravitacijskom polju položaj središta mase poklapa se s položajem težišta. - Moment tromosti materijalnog tijela oko osi je kvantitativna mjera tromosti tijekom rotacijskog gibanja.
Moment tromosti materijalne točke oko osi jednak je umnošku mase točke i kvadrata udaljenosti točke od osi: .
.
Moment tromosti sustava (tijela) oko osi jednak je aritmetičkom zbroju momenata tromosti svih točaka:
- Sila tromosti materijalne točke je vektorska veličina koja je u apsolutnoj vrijednosti jednaka umnošku mase točke i modula ubrzanja i usmjerena suprotno od vektora ubrzanja:
- Sila tromosti materijalnog tijela je vektorska veličina koja je po apsolutnoj vrijednosti jednaka umnošku mase tijela i modula akceleracije centra mase tijela i usmjerena suprotno od vektora akceleracije centra mase: ,
gdje je akceleracija centra mase tijela. - Impuls elementarne sile je vektorska veličina jednaka umnošku vektora sile s infinitezimalnim vremenskim intervalom dt:
.
Ukupni impuls sile za Δt jednak je integralu elementarnih impulsa: .
. - Elementarni rad sile je skalar dA, jednako skalaru
1 slajd
Tečaj predavanja iz teorijske mehanike Dinamika (I dio) Bondarenko A.N. Moskva - 2007 Elektronički tečaj napisano na temelju predavanja koje je autor održao za studente koji studiraju na specijalnostima SZhD, PGS i SDM na NIIZhT i MIIT (1974-2006). Obrazovni materijal odgovara kalendarskim planovima u obimu od tri semestra. Za potpunu implementaciju animacijskih efekata tijekom prezentacije, morate koristiti Power Point preglednik koji nije niži od onog ugrađenog u Microsoft Office operativnog sustava Windows XP Professional. Primjedbe i sugestije možete slati na e-mail: [e-mail zaštićen]. Moskva Državno sveučilišteŽeljeznice (MIIT) Odjel za teorijsku mehaniku Znanstveno-tehnički centar prometnih tehnologija

2 slajd
Sadržaj predavanja 1. Uvod u dinamiku. Zakoni i aksiomi dinamike materijalne točke. Osnovna jednadžba dinamike. Diferencijalne i prirodne jednadžbe gibanja. Dvije glavne zadaće dinamike. Primjeri rješavanja izravnog problema dinamike Predavanje 2. Rješavanje inverznog problema dinamike. Opće upute za rješavanje inverznog problema dinamike. Primjeri rješavanja inverznog problema dinamike. Gibanje tijela bačenog pod kutom prema horizontu, bez uzimanja u obzir otpora zraka. Predavanje 3. Pravocrtne oscilacije materijalne točke. Uvjet za pojavu oscilacija. Klasifikacija vibracija. Slobodne vibracije bez uzimanja u obzir sila otpora. prigušene vibracije. Dekrement oscilacije. Predavanje 4. Prisilne oscilacije materijalne točke. Rezonancija. Utjecaj otpora gibanju tijekom prisilnih vibracija. Predavanje 5. Relativno gibanje materijalne točke. Sile inercije. Posebni slučajevi kretanja za razne vrste prijenosnih pokreta. Utjecaj Zemljine rotacije na ravnotežu i gibanje tijela. Predavanje 6. Dinamika mehaničkog sustava. mehanički sustav. Vanjske i unutarnje sile. Središte mase sustava. Teorem o gibanju centra mase. Zakoni očuvanja. Primjer rješenja zadatka korištenjem teorema o kretanju središta mase. Predavanje 7. Impuls sile. Količina kretanja. Teorem o promjeni količine gibanja. Zakoni očuvanja. Eulerov teorem. Primjer rješavanja problema korištenjem teorema o promjeni količine gibanja. moment zamaha. Teorem o promjeni kutne količine gibanja Predavanje 8. Zakoni očuvanja. Elementi teorije momenata tromosti. Kinetički moment krutog tijela. Diferencijalna jednadžba rotacije krutog tijela. Primjer rješavanja problema korištenjem teorema o promjeni kutne količine gibanja sustava. Elementarna teorija žiroskopa. Preporučena literatura 1. Yablonsky A.A. Kolegij teorijske mehanike. 2. dio. M.: postdiplomske studije. 1977. 368 str. 2. Meshchersky I.V. Zbirka zadataka iz teorijske mehanike. M.: Znanost. 1986. 416 str. 3. Zbirka zadataka za seminarski radovi/ Ed. A.A. Jablonski. M.: Viša škola. 1985. 366 str. 4. Bondarenko A.N. “Teorijska mehanika u primjerima i zadacima. Dinamika” ( elektronički priručnik www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004.

3 slajd
Predavanje 1. Dinamika je dio teorijske mehanike koji proučava mehaničko gibanje s najopćenitijeg gledišta. Kretanje se razmatra u vezi sa silama koje djeluju na objekt. Dio se sastoji od tri cjeline: Dinamika materijalne točke Dinamika Dinamika mehaničkog sustava Analitička mehanika ■ Dinamika točke - proučava gibanje materijalne točke, uzimajući u obzir sile koje uzrokuju to gibanje. Glavni objekt je materijalna točka - materijalno tijelo s masom čije se dimenzije mogu zanemariti. Osnovne pretpostavke: - postoji apsolutni prostor (ima čisto geometrijska svojstva koja ne ovise o materiji i njenom kretanju. - postoji apsolutno vrijeme (ne ovisi o materiji i njenom kretanju). Iz ovoga slijedi: - postoji apsolutno nepomičan referentni okvir - vrijeme ne ovisi o gibanju referentnog okvira - mase pokretnih točaka ne ovise o gibanju referentnog okvira Ove se pretpostavke koriste u klasičnoj mehanici koju su stvorili Galileo i Newton Još uvijek ima prilično širok opseg, budući da mehanički sustavi koji se razmatraju u primijenjenim znanostima nemaju tako velike mase i brzine kretanja, za što je potrebno uzeti u obzir njihov utjecaj na geometriju prostora, vremena, kretanja, kao radi se u relativističkoj mehanici (teoriji relativnosti) ■ Osnovni zakoni dinamike - prvi ih je otkrio Galileo, a formulirao Newton čine osnovu svih metoda za opisivanje i analizu kretanja mehaničkih sustava i njihove dinamičke interakcije pod djelovanjem različitih snage. ■ Zakon tromosti (Galileo-Newtonov zakon) - Izolirana materijalna točka tijela zadržava stanje mirovanja ili ravnomjernog pravocrtnog gibanja sve dok je primijenjene sile ne prisile da promijeni to stanje. To implicira istovjetnost stanja mirovanja i gibanja po inerciji (Galilejev zakon relativnosti). Referentni okvir, u odnosu na koji je ispunjen zakon inercije, naziva se inercijalni. Svojstvo materijalne točke da nastoji zadržati nepromijenjenu brzinu svog gibanja (njezino kinematičko stanje) naziva se inercija. ■ Zakon proporcionalnosti sile i akceleracije (Osnovna jednadžba dinamike - Newtonov II zakon) - Akceleracija koju sila prenosi na materijalnu točku izravno je proporcionalna sili i obrnuto proporcionalna masi te točke: ili Ovdje je m masa točke (mjera tromosti), mjerena u kg, brojčano jednaka težini podijeljenoj s akceleracijom slobodan pad: F je djelujuća sila, mjerena u N (1 N daje točki s masom od 1 kg ubrzanje od 1 m / s2, 1 N \u003d 1 / 9,81 kg-s). ■ Dinamika mehaničkog sustava - proučava kretanje skupa materijalnih točaka i krutih tijela, zajedno opći zakoni interakcije, uzimajući u obzir sile koje uzrokuju to kretanje. ■ Analitička mehanika – proučava gibanje neslobodnih mehaničkih sustava koristeći opće analitičke metode. 1

4 slajd
Predavanje 1 (nastavak - 1.2) Diferencijalne jednadžbe gibanja materijalne točke: - diferencijalna jednadžba gibanja točke u vektorskom obliku. - diferencijalne jednadžbe gibanja točke u koordinatnom obliku. Taj se rezultat može dobiti formalnom projekcijom vektorske diferencijalne jednadžbe (1). Nakon grupiranja vektorska relacija se rastavlja na tri skalarne jednadžbe: U koordinatnom obliku: Koristimo odnos radijus-vektora s koordinatama i vektora sile s projekcijama: diferencijalna jednadžba gibanja po prirodnim (pokretnim) koordinatnim osima: ili: - prirodne jednadžbe gibanja točke. ■ Osnovna jednadžba dinamike: - odgovara vektorskom načinu zadavanja gibanja točke. ■ Zakon neovisnosti o djelovanju sila - Ubrzanje materijalne točke pod djelovanjem više sila jednako je geometrijskom zbroju ubrzanja točke od djelovanja svake od sila zasebno: ili Vrijedi zakon. za bilo koje kinematičko stanje tijela. Sile međudjelovanja, koje se primjenjuju na različite točke (tijela) nisu uravnotežene. ■ Zakon jednakosti akcije i reakcije (Newtonov III zakon) - Svakoj akciji odgovara jednaka i suprotno usmjerena reakcija: 2

5 slajd
Dva glavna problema dinamike: 1. Izravni problem: Zadano je gibanje (jednadžbe gibanja, putanja). Potrebno je odrediti sile pod čijim djelovanjem nastaje određeno gibanje. 2. Inverzni zadatak: Zadane su sile pod čijim djelovanjem nastaje gibanje. Potrebno je pronaći parametre gibanja (jednadžbe gibanja, putanje gibanja). Oba problema rješavaju se temeljnom jednadžbom dinamike i njezinom projekcijom na koordinatne osi. Ako se razmatra gibanje neslobodne točke, tada se, kao iu statici, koristi princip oslobađanja od veza. Kao rezultat reakcije, veze se uključuju u sastav sila koje djeluju na materijalnu točku. Rješenje prvog problema povezano je s operacijama diferenciranja. Rješenje inverznog problema zahtijeva integraciju odgovarajućih diferencijalnih jednadžbi, a to je puno teže od diferencijacije. Inverzni problem je teži od izravnog problema. Rješenje izravnog zadatka dinamike - pogledajmo primjere: Primjer 1. Kabina s utegom G dizala podiže se sajlom s akceleracijom a . Odredite napetost kabela. 1. Odaberite objekt (kabina dizala se kreće naprijed i može se smatrati materijalnom točkom). 2. Odbacimo spoj (uže) i zamijenimo ga reakcijom R. 3. Sastavimo osnovnu jednadžbu dinamike: Odredimo reakciju užeta: Odredimo napetost užeta: Pri jednolikom kretanju kabine ay = 0 i napetost sajle jednaka je težini: T = G. Pri kidanju sajle T = 0 i akceleracija kabine jednaka je akceleraciji slobodnog pada: ay = -g. 3 4. Osnovnu jednadžbu dinamike projiciramo na os y: y Primjer 2. Točka mase m giba se po horizontalnoj površini (ravnina Oxy) prema jednadžbama: x = a coskt, y = b coskt. Odredite silu koja djeluje na točku. 1. Odaberite objekt (materijalnu točku). 2. Odbacimo vezu (ravninu) i zamijenimo je reakcijom N. 3. Sustavu sila dodamo nepoznatu silu F. 4. Sastavimo osnovnu jednadžbu dinamike: 5. Projiciramo osnovnu jednadžbu dinamike na osi x,y: Odredite projekcije sile: Modul sile: Kosinus smjera: Dakle, veličina sile proporcionalna je udaljenosti točke od središta koordinata i usmjerena je prema središtu duž crte koja povezuje točku sa središtem. Putanja gibanja točke je elipsa sa središtem u ishodištu: O r Predavanje 1 (nastavak - 1.3)

6 slajd
1. predavanje (nastavak 1.4) Primjer 3: Teret težine G obješen je na sajlu duljine l i giba se po kružnoj putanji u horizontalnoj ravnini određenom brzinom. Kut odstupanja kabela od okomice jednak je. Odredite napetost užeta i brzinu tereta. 1. Odaberite objekt (teret). 2. Odbacite spoj (uže) i zamijenite ga reakcijom R. 3. Sastavite osnovnu jednadžbu dinamike: Iz treće jednadžbe odredite reakciju sajle: Odredite napetost sajle: Zamijenite vrijednost reakcije kabela, normalno ubrzanje u drugu jednadžbu i odredite brzinu tereta: 4. Projicirajte glavnu jednadžbu axle dynamics,n,b: Primjer 4: Automobil težine G giba se po konveksnom mostu (polumjer zakrivljenosti je R ) brzinom V. Odredite pritisak automobila na most. 1. Odaberemo objekt (auto, zanemarimo dimenzije i smatramo ga točkom). 2. Odbacujemo vezu (hrapavu površinu) i nadomještamo je reakcijama N i silom trenja Ffr. 3. Sastavljamo osnovnu jednadžbu dinamike: 4. Osnovnu jednadžbu dinamike projiciramo na n os: Odavde određujemo normalnu reakciju: Određujemo pritisak automobila na most: Odavde možemo odrediti brzinu koji odgovara nultom tlaku na mostu (Q = 0): 4

7 slajd
2. predavanje Nakon zamjene pronađenih vrijednosti konstanti dobivamo: Dakle, pod djelovanjem istog sustava sila materijalna točka može izvršiti čitavu klasu gibanja određenih početnim uvjetima. Početne koordinate uzimaju u obzir početni položaj točke. Početna brzina, dana projekcijama, uzima u obzir utjecaj sila koje su djelovale na točku prije dolaska na ovu dionicu na njeno kretanje duž razmatranog odsječka putanje, tj. početno kinematičko stanje. Rješenje inverznog problema dinamike - U općem slučaju gibanja točke, sile koje djeluju na točku su varijable koje ovise o vremenu, koordinatama i brzini. Gibanje točke opisuje se sustavom od tri diferencijalne jednadžbe drugog reda: Nakon integracije svake od njih, bit će šest konstanti C1, C2,…., C6: Vrijednosti konstanti C1, C2,… ., C6 nalaze se iz šest početnih uvjeta pri t = 0: Primjer 1 rješenja inverznog problema: Slobodna materijalna točka mase m giba se pod djelovanjem sile F, koja je konstantne veličine i veličine. . U početnom trenutku brzina točke bila je v0 i poklapala se po smjeru sa silom. Odredite jednadžbu gibanja točke. 1. Sastavite osnovnu jednadžbu dinamike: 3. Snizite red derivacije: 2. Odaberite kartezijev referentni sustav, usmjeravajući os x duž smjera sile i projicirajte osnovnu jednadžbu dinamike na tu os: ili x y z 4 .Razdvojite varijable: 5. Izračunajte integrale oba dijela jednadžbe: 6. Predstavimo projekciju brzine kao derivaciju koordinate u odnosu na vrijeme: 8. Izračunajte integrale oba dijela jednadžbe: 7. Odvojite varijable: 9. Za određivanje vrijednosti konstanti C1 i C2 koristimo početne uvjete t = 0, vx = v0 , x = x0: Kao rezultat toga, dobivamo jednadžbu jednoliko promjenjivog gibanja (duž x os): 5

8 slajd
Opće upute za rješavanje izravnih i inverznih zadataka. Postupak rješavanja: 1. Sastavljanje diferencijalne jednadžbe gibanja: 1.1. Odaberite koordinatni sustav - pravokutni (fiksni) s nepoznatom putanjom kretanja, prirodni (pokretni) s poznatom putanjom, na primjer, krug ili ravna linija. U potonjem slučaju može se koristiti jedna pravocrtna koordinata. Referentnu točku treba kombinirati s početnim položajem točke (pri t = 0) ili s ravnotežnim položajem točke, ako postoji, na primjer, kada točka fluktuira. 6 1.2. Nacrtajte točku u položaju koji odgovara proizvoljnom trenutku u vremenu (pri t > 0) tako da su koordinate pozitivne (s > 0, x > 0). Također pretpostavljamo da je projekcija brzine u tom položaju također pozitivna. U slučaju oscilacija, projekcija brzine mijenja predznak, npr. pri povratku u ravnotežni položaj. Ovdje treba pretpostaviti da se u promatranom trenutku točka udaljava od ravnotežnog položaja. Primjena ove preporuke važna je u budućnosti kada se radi sa silama otpora koje ovise o brzini. 1.3. Oslobodite materijalnu točku od veza, njihovo djelovanje zamijenite reakcijama, dodajte aktivne sile. 1.4. Napišite osnovni zakon dinamike u vektorskom obliku, projicirajte ga na odabrane osi, izrazite zadane ili reaktivne sile varijablama vrijeme, koordinate ili brzine, ako o njima ovise. 2. Rješenje diferencijalnih jednadžbi: 2.1. Reducirajte izvod ako se jednadžba ne svodi na kanonski (standardni) oblik. na primjer: ili 2.2. Odvojite varijable, na primjer: ili 2.4. Izračunajte neodređene integrale na lijevoj i desnoj strani jednadžbe, na primjer: 2.3. Ako u jednadžbi postoje tri varijable, tada napravite promjenu varijabli, na primjer: i zatim razdvojite varijable. Komentar. Umjesto da kalkulira neodređeni integrali moguće je izračunati određene integrale s promjenjivom gornjom granicom. Donje granice predstavljaju početne vrijednosti varijabli (početni uvjeti). Tada nema potrebe posebno pronaći konstantu, koja se automatski uključuje u rješenje, na primjer: Korištenje početnih uvjeta, na primjer, t = 0 , vx = vx0, odredimo konstantu integracije: 2.5. Izrazite brzinu u smislu vremenske derivacije koordinate, na primjer, i ponovite korake 2.2 -2.4 Napomena. Ako se jednadžba svede na kanonski oblik koji ima standardno rješenje, tada se koristi ovo gotovo rješenje. Konstante integracije još uvijek se nalaze iz početnih uvjeta. Vidi, na primjer, oscilacije (predavanje 4, str. 8). Predavanje 2 (nastavak 2.2)

9 slajd
2. predavanje (nastavak 2.3) Primjer 2 rješavanja inverznog problema: Sila ovisi o vremenu. Teret težine P počinje se gibati po glatkoj horizontalnoj površini pod djelovanjem sile F čija je veličina proporcionalna vremenu (F = kt). Odrediti put koji teret prijeđe u vremenu t. 3. Sastavljamo glavnu jednadžbu dinamike: 5. Spuštamo red derivacije: 4. Glavnu jednadžbu dinamike projiciramo na x-os: ili 7 6. Odvajamo varijable: 7. Računamo integrale iz oba dijela jednadžbe: 9. Projekciju brzine predstavimo kao derivaciju koordinate u odnosu na vrijeme: 10. Izračunajmo integrale oba dijela jednadžbe: 9. Razdvojimo varijable: 8. Odredimo vrijednost konstante C1 iz početnog uvjeta t = 0, vx = v0=0: Kao rezultat dobivamo jednadžbu gibanja (po x osi), koja daje vrijednost prijeđenog puta za vrijeme t: 1. Odaberite referentni sustav ( Kartezijeve koordinate) tako da tijelo ima pozitivnu koordinatu: 2. Predmet gibanja uzmemo kao materijalnu točku (tijelo se giba naprijed), oslobodimo ga veze (referentne ravnine) i zamijenimo reakcijom (normalna reakcija glatke površina): 11. Odredite vrijednost konstante C2 iz početnog uvjeta t = 0, x = x0=0: Primjer inverznog zadatka 3: Sila ovisi o koordinati. Materijalna točka mase m bačena je uvis sa Zemljine površine brzinom v0. Sila gravitacije Zemlje obrnuto je proporcionalna kvadratu udaljenosti od točke do težišta (središta Zemlje). Odredite ovisnost brzine o udaljenosti y od središta Zemlje. 1. Odaberemo referentni sustav (Kartezijeve koordinate) tako da tijelo ima pozitivnu koordinatu: 2. Sastavimo osnovnu jednadžbu dinamike: 3. Osnovnu jednadžbu dinamike projiciramo na y os: ili Koeficijent proporcionalnosti može pronaći koristeći težinu točke na površini Zemlje: R Stoga diferencijalna jednadžba izgleda ovako: ili 4. Smanjite red derivacije: 5. Promijenite varijablu: 6. Odvojite varijable: 7. Izračunajte integrali obje strane jednadžbe: 8. Zamijenite granice: Kao rezultat, dobivamo izraz za brzinu kao funkciju y koordinate: Maksimalna visina leta može se pronaći izjednačavanjem brzine s nulom: Maksimalna visina leta kada se nazivnik pretvori u nulu: Odavde se pri postavljanju polumjera Zemlje i ubrzanja slobodnog pada dobiva II kozmička brzina:

10 slajd
2. predavanje (nastavak 2.4) Primjer 2 rješavanja inverznog problema: Sila ovisi o brzini. Brod mase m imao je brzinu v0. Otpor vode gibanju broda proporcionalan je brzini. Odredite vrijeme za koje se brzina broda smanji za pola nakon gašenja motora, kao i put koji prijeđe brod do potpunog zaustavljanja. 8 1. Odaberemo referentni sustav (kartezijeve koordinate) tako da tijelo ima pozitivnu koordinatu: 2. objekt gibanja uzmemo kao materijalnu točku (brod se giba naprijed), oslobodimo ga veza (voda) i zamijenimo s reakcijom (sila uzgona - Arhimedova sila), a također i sila otpora kretanju. 3. Dodajte aktivnu silu (gravitaciju). 4. Sastavljamo glavnu jednadžbu dinamike: 5. Projiciramo glavnu jednadžbu dinamike na x-os: ili 6. Spuštamo red derivacije: 7. Odvajamo varijable: 8. Računamo integrale iz oba dijela jednadžbe: 9. Zamjenjujemo granice: Dobiva se izraz koji povezuje brzinu i vrijeme t, iz kojeg možete odrediti vrijeme gibanja: Vrijeme gibanja, tijekom kojeg će brzina pasti za pola: To Zanimljivo je primijetiti da kada se brzina približi nuli, vrijeme kretanja teži beskonačnosti, tj. konačna brzina ne može biti nula. Zašto ne "perpetum mobile"? Međutim, u ovom slučaju, udaljenost prijeđena do zaustavljanja je konačna vrijednost. Da bismo odredili prijeđenu udaljenost, okrećemo se izrazu dobivenom nakon spuštanja reda derivacije i mijenjamo varijablu: Nakon integracije i zamjene granica, dobivamo: Prijeđenu udaljenost do zaustavljanja: ■ Kretanje točke bačene na kut prema horizontu u ravnomjernom gravitacijskom polju bez uzimanja u obzir otpora zraka Eliminacijom vremena iz jednadžbi gibanja dobivamo jednadžbu putanje: Vrijeme leta se određuje izjednačavanjem koordinate y s nulom: Domet leta se određuje zamjenom vrijeme leta:

11 slajd
Predavanje 3 Pravocrtne oscilacije materijalne točke - Oscilatorno gibanje materijalne točke događa se pod uvjetom: postoji povratna sila koja nastoji vratiti točku u ravnotežni položaj za svako odstupanje od tog položaja. 9 Postoji sila vraćanja, položaj ravnoteže je stabilan Nema sile vraćanja, položaj ravnoteže je nestabilan Nema sile vraćanja, položaj ravnoteže je ravnodušan Uvijek je usmjeren prema ravnotežnom položaju, vrijednost je izravno proporcionalna linearnom izduženju (skraćenju) opruge, koje je jednako odstupanju tijela od ravnotežnog položaja: c je koeficijent krutosti opruge, brojčano jednak sila pod kojom opruga mijenja svoju duljinu za jedan, mjerena u N/m u sustavu SI. x y O Vrste vibracija materijalne točke: 1. Slobodne vibracije (bez uzimanja u obzir otpora medija). 2. Slobodne oscilacije uzimajući u obzir otpor medija (prigušene oscilacije). 3. Prisilne vibracije. 4. Prisilne oscilacije uzimajući u obzir otpor medija. ■ Slobodne oscilacije - nastaju pod djelovanjem samo povratne sile. Zapišimo osnovni zakon dinamike: Odaberimo koordinatni sustav sa središtem u položaju ravnoteže (točka O) i projicirajmo jednadžbu na os x: Dovedimo dobivenu jednadžbu u standardni (kanonski) oblik: Ova jednadžba je homogena linearna diferencijalna jednadžba drugog reda čiji je oblik rješenja određen korijenima karakteristike jednadžbe dobivene univerzalnom supstitucijom: Korijeni karakteristične jednadžbe su imaginarni i jednaki: Opće rješenje diferencijalne jednadžbe ima oblik: Brzina točke: Početni uvjeti: Definirajte konstante: Dakle, jednadžba slobodnih titraja ima oblik: Jednadžba se može prikazati jednočlanim izrazom: gdje je a amplituda, - početna faza. Nove konstante a i - povezane su s konstantama C1 i C2 relacijama: Definirajte a i: Razlog za pojavu slobodnih oscilacija je početni pomak x0 i/ili početna brzina v0.

12 slajd
10 Predavanje 3 (nastavak 3.2) Prigušene oscilacije materijalne točke - Oscilatorno gibanje materijalne točke događa se uz prisutnost povratne sile i sile otpora gibanju. Ovisnost sile otpora gibanju o pomaku ili brzini određena je fizičkom prirodom medija ili spoja koji ometa kretanje. Najjednostavnija ovisnost je linearna ovisnost na brzinu (viskozni otpor): - koeficijent viskoznosti x y O Osnovna jednadžba dinamike: Projekcija jednadžbe dinamike na os: Jednadžbu dovodimo u standardni oblik: gdje Karakteristična jednadžba ima korijene: Opće rješenje ove diferencijalne jednadžbe ima različit oblik ovisno o vrijednostima korijena: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - slučaj visoke otpornosti na viskoznost: - pravi korijeni, različiti. ili - ove funkcije su aperiodične: 3. n = k: - korijeni su pravi, višestruki. ove funkcije su također aperiodične:

13 slajd
Predavanje 3 (nastavak 3.3) Klasifikacija rješenja slobodnih oscilacija. Opružni priključci. ekvivalentna tvrdoća. y 11 Razl. Znak jednadžbe. Korijeni jednadžbe char. jednadžba Rješavanje diferencijalne jednadžbe Grafikon nk n=k

14 slajd
Predavanje 4 Prisilne vibracije materijalne točke - Uz povratnu silu djeluje periodički promjenjiva sila koja se naziva perturbirajuća sila. Uznemirujuća sila može imati različitu prirodu. Na primjer, u konkretnom slučaju, inercijski učinak neuravnotežene mase m1 rotirajućeg rotora uzrokuje harmonijski promjenjive projekcije sile: Glavna jednadžba dinamike: Projekcija jednadžbe dinamike na os: Dovedimo jednadžbu na standardnu oblik: 12 Rješenje ove nehomogene diferencijalne jednadžbe sastoji se od dva dijela x = x1 + x2: x1 je opće rješenje odgovarajuće homogene jednadžbe, a x2 je partikularno rješenje nehomogene jednadžbe: Odaberemo partikularno rješenje u obliku desna strana: Rezultirajuća jednakost mora biti zadovoljena za bilo koje t . Tada: ili Dakle, uz istovremeno djelovanje povratne i uznemirujuće sile, materijalna točka izvodi složeno oscilatorno gibanje, koje je rezultat zbrajanja (superpozicije) slobodnih (x1) i prisilnih (x2) vibracija. Ako str< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (prisilne oscilacije visoka frekvencija), tada je faza oscilacija suprotna fazi uznemirujuće sile:

15 slajd
Predavanje 4 (nastavak 4.2) 13 Omjer dinamički koeficijent - amplituda prisilne vibracije na statički otklon točke pod djelovanjem konstantne sile H = const: Amplituda prisilnih oscilacija: Statički otklon može se pronaći iz jednadžbe ravnoteže: Ovdje: Dakle: Dakle, na p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (visoka frekvencija prisilnih oscilacija) dinamički koeficijent: Rezonancija – nastaje kada se frekvencija prisilnih oscilacija poklopi s frekvencijom vlastitih oscilacija (p = k). To se najčešće događa kod pokretanja i zaustavljanja vrtnje loše uravnoteženih rotora postavljenih na elastične ovjese. Diferencijalna jednadžba oscilacija s jednakim frekvencijama: Ne može se uzeti posebno rješenje u obliku desne strane, jer dobit će se linearno ovisno rješenje (vidi opće rješenje). Opće rješenje: Zamjena u diferencijalnoj jednadžbi: Uzmite određeno rješenje u obliku i izračunajte derivacije: Tako se dobije rješenje: ili Prisilne oscilacije pri rezonanciji imaju amplitudu koja neograničeno raste proporcionalno vremenu. Utjecaj otpora gibanju tijekom prisilnih vibracija. Diferencijalna jednadžba u prisutnosti viskoznog otpora ima oblik: Opće rješenje se odabire iz tablice (predavanje 3, str. 11) ovisno o omjeru n i k (vidi). Uzimamo određeno rješenje u obliku i izračunavamo derivacije: Zamjena u diferencijalnoj jednadžbi: Izjednačavanje koeficijenata pri istoj trigonometrijske funkcije dobivamo sustav jednadžbi: Dizanjem obje jednadžbe na potenciju i njihovim zbrajanjem dobivamo amplitudu prisilnih oscilacija: Dijeljenjem druge jednadžbe s prvom dobivamo fazni pomak prisilnih oscilacija: Dakle, jednadžba gibanja za prisilne oscilacije, uzimajući u obzir otpor gibanju, na primjer, kod n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 slajd
Predavanje 5 Relativno gibanje materijalne točke - Pretpostavimo da se pokretni (neinercijalni) koordinatni sustav Oxyz giba prema nekom zakonu u odnosu na nepomični (inercijalni) koordinatni sustav O1x1y1z1. Gibanje materijalne točke M (x, y, z) u odnosu na pokretni sustav Oxyz je relativno, u odnosu na nepomični sustav O1x1y1z1 je apsolutno. Gibanje mobilnog sustava Oxyz u odnosu na fiksni sustav O1x1y1z1 prijenosno je gibanje. 14 z x1 y1 z1 O1 x y M x y z O Osnovna jednadžba dinamike: Apsolutna akceleracija točke: Zamijenimo apsolutnu akceleraciju točke u osnovnu jednadžbu dinamike: Prenesimo članove s translatornom i Coriolisovom akceleracijom na desnu stranu: preneseni članovi imaju dimenziju sila i smatraju se odgovarajućim inercijskim silama, jednakim: Tada se relativno gibanje točke može smatrati apsolutnim, ako djelovajućim silama dodamo translacijsku i Coriolisovu silu tromosti: U projekcijama na osi gibljivog koordinatnog sustava imamo: rotacija je jednolika, tada je εe = 0: 2. Translatorno krivuljasto gibanje: Ako je gibanje pravocrtno, tada je = : Ako je gibanje pravocrtno i jednoliko, tada je gibljivi sustav inercijalan i relativno gibanje može se smatrati apsolutnim: nijedan mehanički fenomen ne može otkriti pravocrtni jednoliko kretanje(princip relativnosti klasične mehanike). Utjecaj rotacije Zemlje na ravnotežu tijela - Pretpostavimo da je tijelo u ravnoteži na površini Zemlje na proizvoljnoj geografskoj širini φ (paralele). Zemlja se okreće oko svoje osi od zapada prema istoku kutnom brzinom: Polumjer Zemlje je oko 6370 km. S R je ukupna reakcija neglatke površine. G - sila privlačenja Zemlje prema središtu. F - centrifugalna sila tromosti. Uvjet relativne ravnoteže: Rezultanta sila privlačenja i tromosti je sila teže (težine): Veličina sile teže (težine) na površini Zemlje je P = mg. Centrifugalna sila tromosti je mali djelić sile teže: Odstupanje sile teže od smjera sile privlačenja također je malo: Dakle, utjecaj Zemljine rotacije na ravnotežu tijela je izuzetno malen. i ne uzima se u obzir u praktičnim proračunima. Najveća vrijednost inercijske sile (kod φ = 0 - na ekvatoru) iznosi samo 0,00343 vrijednosti sile teže

17 slajd
Predavanje 5 (nastavak 5.2) 15 Utjecaj Zemljine rotacije na kretanje tijela u Zemljinom gravitacijskom polju - Pretpostavimo da tijelo padne na Zemlju s određene visine H iznad Zemljine površine na geografskoj širini φ . Odaberimo pokretni referentni okvir, kruto povezan sa Zemljom, usmjeravajući x, y osi tangencijalno na paralelu i meridijan: Jednadžba relativnog gibanja: Ovdje se uzima u obzir malenost centrifugalne sile tromosti u usporedbi s gravitacijom . Dakle, sila gravitacije se poistovjećuje sa silom gravitacije. Osim toga, pretpostavljamo da je gravitacija usmjerena okomito na Zemljinu površinu zbog malog otklona, kao što je gore objašnjeno. Coriolisovo ubrzanje jednako je i usmjereno paralelno s osi y prema zapadu. Coriolisova tromost je usmjerena u suprotnom smjeru. Projiciramo jednadžbu relativnog gibanja na os: Rješenje prve jednadžbe daje: Početne uvjete: Rješenje treće jednadžbe daje: Početne uvjete: Treća jednadžba ima oblik: Početni uvjeti: Njeno rješenje daje: Rezultirajuće rješenje pokazuje da tijelo pri padu skrene prema istoku. Izračunajmo kolika je vrijednost tog odstupanja npr. pri padu s visine od 100 m. Vrijeme pada nalazimo iz rješenja druge jednadžbe: Dakle, utjecaj rotacije Zemlje na kretanje tijela izuzetno je malen. za praktične visine i brzine i ne uzima se u obzir u tehničkim proračunima. Rješenje druge jednadžbe također implicira postojanje brzine duž y-osi, koja bi također trebala uzrokovati i uzrokuje odgovarajuću akceleraciju i Coriolisovu tromost. Utjecaj ove brzine i s njom povezane sile tromosti na promjenu gibanja bit će čak manji od razmatrane Coriolisove sile tromosti povezane s okomitom brzinom.

18 slajd
Predavanje 6 Dinamika mehaničkog sustava. Sustav materijalnih točaka ili mehanički sustav - Skup materijalnih točaka ili onih materijalnih točaka ujedinjenih općim zakonima interakcije (položaj ili kretanje svake od točaka ili tijela ovisi o položaju i kretanju svih ostalih) slobodne točke - čije kretanje nije ograničeno nikakvim vezama (na primjer, planetarni sustav , u kojem se planeti smatraju materijalnim točkama). Sustav neslobodnih točaka ili neslobodni mehanički sustav - kretanje materijalnih točaka ili tijela ograničeno je ograničenjima koja su nametnuta sustavu (na primjer, mehanizam, stroj itd.). 16 Sile koje djeluju na sustav. Uz dosadašnju klasifikaciju sila (aktivne i reaktivne sile) uvodi se nova klasifikacija sila: 1. Vanjske sile (e) - djeluju na točke i tijela sustava iz točaka ili tijela koja nisu dio ovog sustava. sustav. 2. Unutarnje sile (i) - sile međudjelovanja između materijalnih točaka ili tijela uključenih u zadani sustav. Ista sila može biti i vanjska i unutarnja sila. Sve ovisi o tome koji se mehanički sustav razmatra. Na primjer: U sustavu Sunca, Zemlje i Mjeseca sve gravitacijske sile između njih su unutarnje. Kada se razmatra sustav Zemlje i Mjeseca, gravitacijske sile koje djeluju sa strane Sunca su vanjske: C Z L Na temelju zakona akcije i reakcije, svaka unutarnja sila Fk odgovara drugoj unutarnjoj sili Fk', jednakoj u apsolutnoj vrijednosti i suprotnoj u smjer. Iz ovoga slijede dva izvanredna svojstva unutarnjih sila: Glavni vektor svih unutarnjih sila sustava jednak je nuli: Glavni moment svih unutarnjih sila sustava u odnosu na bilo koje središte jednak je nuli: Ili u projekcijama na koordinatu sjekire: Napomena. Iako su ove jednadžbe slične jednadžbama ravnoteže, one to nisu, budući da unutarnje sile djeluju na različite točke ili tijela sustava i mogu uzrokovati međusobno pomicanje tih točaka (tijela). Iz ovih jednadžbi proizlazi da unutarnje sile ne utječu na gibanje sustava promatranog kao cjeline. Središte mase sustava materijalnih točaka. Za opis gibanja sustava kao cjeline uvodi se geometrijska točka, nazvana centar mase, čiji je radijus vektor određen izrazom, gdje je M masa cijelog sustava: Ili u projekcijama na koordinatu osi: Formule za središte mase slične su onima za težište. Međutim, koncept središta mase je općenitiji, jer nije povezan sa silama gravitacije ili silama gravitacije.

19 slajd
Predavanje 6 (nastavak 6.2) 17 Teorem o gibanju središta mase sustava - Promotrimo sustav od n materijalnih točaka. Sile koje djeluju na svaku točku dijelimo na vanjske i unutarnje i zamjenjujemo ih odgovarajućim rezultantama Fke i Fki. Zapišimo za svaku točku osnovnu jednadžbu dinamike: ili Zbrojimo te jednadžbe po svim točkama: Na lijevoj strani jednadžbe uvest ćemo mase pod predznakom derivacije, a zbroj derivacija zamijeniti derivacijom zbroja: Iz definicije središta mase: Zamijenimo u dobivenu jednadžbu: dobivamo ili: Umnožak mase sustava i akceleracije njegova središta mase jednak je glavnom vektoru vanjskih sila. U projekcijama na koordinatne osi: Središte mase sustava giba se kao materijalna točka s masom jednakom masi cijelog sustava, na koju djeluju sve vanjske sile koje djeluju na sustav. Posljedice iz teorema o gibanju središta mase sustava (zakoni očuvanja): 1. Ako je u vremenskom intervalu glavni vektor vanjskih sila sustava jednak nuli, Re = 0, tada je brzina središte mase je konstantno, vC = const (središte mase giba se jednoliko pravocrtno – zakon očuvanja gibanja centra mase). 2. Ako je u vremenskom intervalu projekcija glavnog vektora vanjskih sila sustava na os x jednaka nuli, Rxe = 0, tada je brzina centra mase duž osi x konstantna, vCx = const (središte mase giba se jednoliko po osi). Slične tvrdnje vrijede za osi y i z. Primjer: U čamcu mase m3 nalaze se dvije osobe masa m1 i m2. U početnom trenutku brod s ljudima je mirovao. Odredi deplasman čamca ako se osoba mase m2 pomaknula do pramca čamca na udaljenosti a. 3. Ako je u vremenskom intervalu glavni vektor vanjskih sila sustava jednak nuli, Re = 0, a u početnom trenutku brzina centra mase jednaka nuli, vC = 0, tada je radijus vektor centra mase ostaje konstantan, rC = const (centar mase miruje je zakon o održanju položaja centra mase). 4. Ako je u vremenskom intervalu projekcija glavnog vektora vanjskih sila sustava na os x jednaka nuli, Rxe = 0, au početnom trenutku brzina centra mase duž ove osi je nula. , vCx = 0, tada koordinata središta mase duž x osi ostaje konstantna, xC = const (centar mase se ne pomiče duž ove osi). Slične tvrdnje vrijede za osi y i z. 1. Objekt gibanja (čamac s ljudima): 2. Odbaciti veze (voda): 3. Zamijeniti vezu reakcijom: 4. Dodati aktivne sile: 5. Zapisati teorem o središtu mase: Projicirati na x-os : O Odredite koliku udaljenost treba prenijeti osoba mase m1 da čamac ostane na mjestu: čamac će se pomaknuti za udaljenost l u suprotnom smjeru.

20 slajd
Predavanje 7. Impuls sile je mjera mehaničke interakcije koja karakterizira prijenos mehaničkog gibanja od sila koje djeluju na točku u određenom vremenskom razdoblju: 18 U projekcijama na koordinatne osi: U slučaju konstantne sile: U projekcije na koordinatne osi: na točku sile u istom vremenskom intervalu: pomnožiti s dt: integrirati kroz zadani vremenski interval: količina pomaka točke je mjera mehaničkog pomaka, određena vektorom, jednak umnošku masa točke na njen vektor brzine: Teorem o promjeni količine gibanja sustava - Promotrimo sustav od n materijalnih točaka. Sile koje djeluju na svaku točku dijelimo na vanjske i unutarnje i zamjenjujemo ih odgovarajućim rezultantama Fke i Fki. Napišimo za svaku točku osnovnu jednadžbu dinamike: ili Količina gibanja sustava materijalnih točaka je geometrijski zbroj količina gibanja materijalnih točaka: Po definiciji centra mase: Vektor količine gibanja sustava je jednaka umnošku mase cijelog sustava i vektora brzine centra mase sustava. Tada: U projekcijama na koordinatne osi: Vremenska derivacija vektora količine gibanja sustava jednaka je glavnom vektoru vanjskih sila sustava. Zbrojimo ove jednadžbe po svim točkama: Na lijevoj strani jednadžbe uvedemo mase pod predznakom derivacije i zbroj derivacija zamijenimo derivacijom zbroja: Iz definicije količine gibanja sustava: U projekcijama na koordinatne osi:

21 slajd
Eulerov teorem - Primjena teorema o promjeni količine gibanja sustava na gibanje kontinuiranog medija (vode). 1. Odaberemo kao predmet gibanja volumen vode koji se nalazi u zakrivljenom kanalu turbine: 2. Odbacimo veze i zamijenimo njihovo djelovanje reakcijama (Rpov - rezultanta površinskih sila) 3. Dodamo aktivne sile (Rb - rezultanta tjelesnih sila): 4. Zapišite teorem o promjeni količine gibanja sustava: Količina gibanja vode u trenucima t0 i t1 prikazuje se kao zbrojevi: Promjena količine gibanja vode u vremenskom intervalu : Promjena u količina gibanja vode u infinitezimalnom vremenskom intervalu dt: , gdje F1 F2 Uzimajući umnožak gustoće, površine poprečnog presjeka i brzine po sekundi mase, dobivamo: Zamjenom diferencijala količine gibanja sustava u teorem o promjeni dobivamo : Posljedice iz teorema o promjeni količine gibanja sustava (zakoni očuvanja): 1. Ako je u vremenskom intervalu glavni vektor vanjskih sila sustava jednak nuli, Re = 0, tada je gibanje vektora količine je konstantan, Q = const je zakon očuvanja količine gibanja sustava). 2. Ako je u vremenskom intervalu projekcija glavnog vektora vanjskih sila sustava na os x jednaka nuli, Rxe = 0, tada je projekcija količine gibanja sustava na os x konstantna, Qx = konst. Slične tvrdnje vrijede za osi y i z. Predavanje 7 (nastavak 7.2) Primjer: Granata mase M leteći brzinom v eksplodirala je na dva dijela. Brzina jednog od fragmenata mase m1 povećala se u smjeru gibanja na vrijednost v1. Odredite brzinu drugog fragmenta. 1. Objekt kretanja (granata): 2. Objekt je slobodan sustav, nema veza i njihovih reakcija. 3. Dodati aktivne sile: 4. Zapisati teorem o promjeni količine gibanja: Projicirati na os: β Podijeliti varijable i integrirati: Desni integral je skoro nula, jer vrijeme eksplozije t

22 slajd
Predavanje 7 (nastavak 7.3) 20 Kutna količina gibanja točke ili kinetički moment gibanja u odnosu na određeno središte je mjera mehaničkog gibanja, određena vektorom jednakim vektorskom umnošku radijus vektora materijalne točke i vektor njegove količine gibanja: Kinetički moment sustava materijalnih točaka u odnosu na određeno središte je geometrijski zbroj momenata količine gibanja svih materijalnih točaka u odnosu na isto središte: U projekcijama na os: U projekcijama na os : Teorem o promjeni momenta količine gibanja sustava - Promotrimo sustav od n materijalnih točaka. Sile koje djeluju na svaku točku dijelimo na vanjske i unutarnje i zamjenjujemo ih odgovarajućim rezultantama Fke i Fki. Napišimo za svaku točku osnovnu jednadžbu dinamike: ili Zbrojimo ove jednadžbe po svim točkama: Zbroj derivacija zamijenimo derivacijom zbroja: Izraz u zagradi je moment količine gibanja sustava. Odavde: Vektorski pomnožimo svaku od jednakosti s radijus vektorom lijevo: Da vidimo je li moguće predznak derivacije uzeti izvan vektorski proizvod: Dakle, dobili smo: Derivacija vektora količine gibanja sustava u odnosu na određeno središte u vremenu jednaka je glavnom momentu vanjskih sila sustava u odnosu na isto središte. U projekcijama na koordinatne osi: Derivacija momenta količine gibanja sustava u odnosu na neku os u vremenu jednaka je glavnom momentu vanjskih sila sustava u odnosu na istu os.

23 slajd
Predavanje 8 21 ■ Posljedice iz teorema o promjeni kutne količine gibanja sustava (zakoni očuvanja): 1. Ako je u vremenskom intervalu vektor glavnog momenta vanjskih sila sustava u odnosu na neko središte jednak na nulu, MOe = 0, tada je vektor kutne količine gibanja sustava u odnosu na isto središte konstantan, KO = const je zakon očuvanja količine gibanja sustava). 2. Ako je u vremenskom intervalu glavni moment vanjskih sila sustava u odnosu na os x jednak nuli, Mxe = 0, tada je kutna količina gibanja sustava u odnosu na os x konstantna, Kx = const. Slične tvrdnje vrijede za osi y i z. 2. Moment tromosti krutog tijela oko osi: Moment tromosti materijalne točke oko osi jednak je umnošku mase točke i kvadrata udaljenosti točke od osi. Moment tromosti krutog tijela oko osi jednak je zbroju umnožak mase svake točke i kvadrata udaljenosti te točke od osi. ■ Elementi teorije o momentima tromosti - Kod rotacijskog gibanja krutog tijela mjera tromosti (otpora promjeni gibanja) je moment tromosti oko osi rotacije. Razmotriti osnovne koncepte definicije i metode za izračunavanje momenata tromosti. 1. Moment tromosti materijalne točke oko osi: Pri prijelazu iz diskretne male mase u beskonačno malu masu točke granica takvog zbroja određena je integralom: osni moment tromosti krutog tijela . Osim osnog momenta tromosti krutog tijela postoje i druge vrste momenata tromosti: centrifugalni moment tromosti krutog tijela. polarni moment tromosti krutog tijela. 3. Teorem o momentima tromosti krutog tijela oko paralelnih osi - formula za prijelaz na paralelne osi: Moment tromosti oko referentne osi Statički momenti tromosti oko referentne osi Momenti mase tijela jednaki su nuli:

24 slajd
Predavanje 8 (nastavak 8.2) 22 Moment tromosti jednolikog štapa konstantnog presjeka oko osi: x z L Odaberite elementarni volumen dV = Adx na udaljenosti x: x dx elementarna masa: Za izračun momenta tromosti oko središnje osi (koja prolazi kroz težište), dovoljno je promijeniti položaj osi i postaviti granice integracije (-L/2, L/2). Ovdje demonstriramo formulu za prijelaz na paralelne osi: zS 5. Moment tromosti homogenog čvrstog cilindra oko osi simetrije: H dr r Izdvojimo elementarni volumen dV = 2πrdrH (tanki cilindar polumjera r) : Elementarna masa: Ovdje koristimo formulu volumena cilindra V=πR2H. Za izračun momenta tromosti šupljeg (debelog) cilindra dovoljno je postaviti granice integracije od R1 do R2 (R2> R1): 6. Moment tromosti tankog cilindra oko osi simetrije (t

25 slajd
Predavanje 8 (nastavak 8.3) 23 ■ Diferencijalna jednadžba rotacije krutog tijela oko osi: Napišimo teorem o promjeni momenta količine gibanja krutog tijela koje rotira oko nepomične osi: Moment količine rotacije krutog tijela je: Moment vanjskih sila oko osi rotacije jednak momentu (reakcije i sila ne stvaraju gravitacijske momente): kinetički moment i moment zamijenimo u teorem Primjer: Dvije osobe iste težine G1 = G2 vise na užetu bačen preko čvrstog bloka s utegom G3 = G1/4. U nekom se trenutku jedan od njih počeo penjati po užetu relativnom brzinom u. Odredite brzinu dizanja svake osobe. 1. Odaberemo objekt gibanja (blok s ljudima): 2. Odbacimo veze (nosač bloka): 3. Zamijenimo vezu reakcijama (ležište): 4. Dodamo aktivne sile (gravitaciju): 5. Zapišite teorem o promjeni kinetičkog momenta sustava u odnosu na os rotacije bloka: R Budući da je moment vanjskih sila jednak nuli, kinetički moment mora ostati konstantan: U početnom trenutku vremena t = 0, došlo je do ravnoteže i Kz0 = 0. Nakon početka gibanja jedne osobe u odnosu na uže, cijeli sustav se počeo gibati, ali kinetički moment sustava mora ostati jednak nuli: Kz = 0. Kutni moment sustava je zbroj kutnih momenata i ljudi i bloka: Ovdje je v2 brzina druge osobe, jednako brzini kabel, Primjer: Odredite period malih slobodnih oscilacija homogenog štapa mase M i duljine l, obješenog na jednom kraju o nepomičnu os rotacije. Ili: U slučaju malih oscilacija sinφ φ: Period titranja: Moment tromosti štapa:

26 slajd
Predavanje 8 (nastavak 8.4 - dodatni materijal) 24 ■ Osnovna teorija žiroskopa: Žiroskop je kruto tijelo koje rotira oko osi materijalne simetrije, a jedna od točaka je nepomična. Slobodni žiroskop je fiksiran tako da mu središte mase miruje, a os rotacije prolazi kroz središte mase i može zauzeti bilo koji položaj u prostoru, tj. os rotacije mijenja svoj položaj poput osi vlastite rotacije tijela tijekom sfernog gibanja. Glavna pretpostavka aproksimativne (elementarne) teorije žiroskopa je da se vektor količine gibanja (kinetički moment) rotora smatra usmjerenim duž njegove vlastite osi rotacije. Dakle, unatoč činjenici da u općem slučaju rotor sudjeluje u tri rotacije, uzima se u obzir samo kutna brzina vlastite rotacije ω = dφ/dt. Razlog tome je što se u modernoj tehnologiji rotor žiroskopa okreće kutnom brzinom reda 5000-8000 rad/s (oko 50000-80000 o/min), dok druga dva kutne brzine povezana s precesijom i nutacijom vlastite osi rotacije je desetke tisuća puta manja od ove brzine. Glavno svojstvo slobodnog žiroskopa je da os rotora održava konstantan smjer u prostoru u odnosu na inercijalni (zvjezdani) referentni sustav (pokazano Foucaultovim njihalom, koje održava ravninu ljuljanja nepromijenjenom u odnosu na zvijezde, 1852.). To proizlazi iz zakona održanja kinetičkog momenta u odnosu na središte mase rotora, uz uvjet da se zanemari trenje u ležajevima osi ovjesa rotora, vanjskog i unutarnjeg okvira: Djelovanje sile na os slobodnog žiroskop. U slučaju sile koja djeluje na os rotora, moment vanjskih sila u odnosu na centar mase nije jednak nuli: ω ω S sila, a prema vektoru momenta te sile, tj. neće se okretati oko x-osi (unutarnji ovjes), već oko y-osi (vanjski ovjes). Nakon prestanka djelovanja sile, os rotora će ostati u istom položaju, što odgovara zadnjem vremenu djelovanja sile, jer od ove točke u vremenu, moment vanjskih sila ponovno postaje jednak nuli. U slučaju kratkotrajnog djelovanja sile (udarca), os žiroskopa praktički ne mijenja svoj položaj. Dakle, brza rotacija rotora daje žiroskopu mogućnost suprotstavljanja slučajnim utjecajima koji nastoje promijeniti položaj osi rotacije rotora, te uz konstantno djelovanje sile održava položaj ravnine okomite na operativna sila, koji sadrži os rotora. Ova svojstva se koriste u inercijski sustavi navigacija.